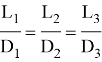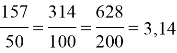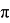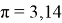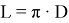Как с помощью нитки найти длину окружности

Как измерить длину окружности ниткой

С помощью тонкой нити измерьте длину окружности стакана, измерьте длину диаметра?

Математика | 5 — 9 классы

С помощью тонкой нити измерьте длину окружности стакана, измерьте длину диаметра.

Найдите отношение длины окружности к длине диаметра и сравните полученный результат с числом п.

Только в подробнастях.

Какие тут могут быть подробности?

Меряете длину окружности (нитка вокруг стакана) и длину диаметра (нитка поперёк стакана), делите длину окружности на длину диаметра, получаете 3, 14.

Это число равно числу пи, так как пи — это отношение длины окружности к её радиусу.

С спомощью тонкой нити измерьте длину какой — нибудь окружности ( на стакане ведре тарелке) измерьте длину диаметра?

С спомощью тонкой нити измерьте длину какой — нибудь окружности ( на стакане ведре тарелке) измерьте длину диаметра.

Найдите отношение длины окружности к длине диаметра и сравните полученный результат с числом пи.

Найдите отношение длины окружности к длине диаметра и сравните полученный результат пи?

Найдите отношение длины окружности к длине диаметра и сравните полученный результат пи.

С помощью тонкой нити измерьте длину какой — нибудь окружности ( на стакане, ведре, тарелке), измерьтедлину диаметра?

С помощью тонкой нити измерьте длину какой — нибудь окружности ( на стакане, ведре, тарелке), измерьтедлину диаметра.

Найдите отношение длины окружности к длине диаметра и сравните полученный результат с числом п.

ЗАДАЧА № 867 6 КЛАСС ВИЛЕНКИН ( с помощью нитки измерьте длину какой нибудь окружности, измерьте длину диаметра?

ЗАДАЧА № 867 6 КЛАСС ВИЛЕНКИН ( с помощью нитки измерьте длину какой нибудь окружности, измерьте длину диаметра.

Найдите отношение длины окружности к длине диаметра и сравните полученный результат с числом (что — то на подобе н)).

С помщью тонкой нити измерьте длину какой — нибудь окружности (на стакане, ведре, тарелке) измерьте длину диаметра?

С помщью тонкой нити измерьте длину какой — нибудь окружности (на стакане, ведре, тарелке) измерьте длину диаметра.

Найдите отношение длины окружности к длине диаметра и сравните полученный результат с числом п.

Помогите срочно надо.

С помощью нитки измерить стакан(при измерение получилось 21 см), измерить длину диаметра?

С помощью нитки измерить стакан(при измерение получилось 21 см), измерить длину диаметра.

Найдите отношение длины окружности к длине диаметра и сравните полученный результат с числом пи.

С помощью тонкой нити измерьте длину какой нибудь окружности ( на стакане , ведре , тарелки ) измерьте длину диаметра ?

С помощью тонкой нити измерьте длину какой нибудь окружности ( на стакане , ведре , тарелки ) измерьте длину диаметра .

Найдите отношение длины окружности к длине диаметра и сравните полученный результат с п.

С помощью тонкой нити измерьте длину какой — нибудь окружности (на стакане, ведре, тарелке, ), измерьте длину диаметра?

С помощью тонкой нити измерьте длину какой — нибудь окружности (на стакане, ведре, тарелке, ), измерьте длину диаметра.

Найдите отношение длины окружности к длине диаметра и сравните полученный результат с числом пи.

Помогите , пожалуйста, решить задачу?

Помогите , пожалуйста, решить задачу.

С помощью тонкой нити измерьте длину какой нибудь окружности ( на стакане, ведре, тарелке), измерте длину даметра.

Найдите отношение длины окружности к длине диаметра и сравните полученный результат с числом Π.

С помощью тонкой нити измерьте длину какой — нибудь окружности (стакана, тарелки и т?

С помощью тонкой нити измерьте длину какой — нибудь окружности (стакана, тарелки и т.

Д. ), измерьте длину диаметра.

Найдите отношение длины окружности к длине диаметра и сравните полученный результат с числом ПИ.

Ребят даю 60 баллов, Помогите пожалуйста.

Перед вами страница с вопросом С помощью тонкой нити измерьте длину окружности стакана, измерьте длину диаметра?, который относится к категории Математика. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Измерьте диаметр и длину окружности у пяти предметов цилиндрической формы с помощью нити и линейки

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,845
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Как посчитать длину окружности

Онлайн калькулятор

Как посчитать длину окружности зная диаметр

Какая длина у окружности если

Какова длина окружности (С) если её диаметр d?

Формула

С = π⋅d , где π ≈ 3.14

Пример

Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная радиус

Какая длина у окружности если

Какова длина окружности (С) если её радиус r?

Формула

С = 2⋅π⋅r , где π ≈ 3.14

Пример

Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.

Как посчитать длину окружности зная её площадь

Какая длина у окружности если

Какова длина окружности (С) если её площадь S?

Формула

С = 2π⋅ √ S /_π , где π ≈ 3.14

Пример

Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.

Начертите окружность радиусом 3 см и измерьте её длину с помощью нити. 2) Длину окружности приближённо можно найти, умножив её радиус на 6.

Ваш ответ

решение вопроса

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,937
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

На этой странице сайта, в категории Математика размещен ответ на вопрос
Как найти длину окружности с помощью нитки?. По уровню сложности вопрос рассчитан на учащихся
10 — 11 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.

На этом уроке мы познакомимся с числом .
Выведем формулу длины окружности. Научимся решать задачи с использованием
формулы длины окружности.

Ещё в 5-ом классе вы познакомились с одной
замечательной линией, как окружность и её элементами. Наверняка
вы уже хорошо научились строить окружности с помощью циркуля.

Но не всегда такой прибор, как циркуль существовал в
нашей жизни. Как вы думаете, можно ли начертить окружность без циркуля?
Конечно, да!

Давайте проведём небольшой опыт. Возьмём монетку,
положим её на лист бумаги и проведём по её контуру карандашом.

Смотрите, на листе остался след. Что это за фигура?
Да! Это окружность! С помощью линейки можно измерить её диаметр.

Диаметр нашей монетки равен 5,5
см.

Скажите, а можно ли измерить длину самой окружности?
Ведь линейку к ней не приложишь.

Но можно поступить иначе. Если взять нитку, обмотать
ею монетку, потом разрезать эту нитку и измерить ее линейкой, то получим длину
окружности. Проделаем это с нашей монеткой.

Смотрите, длина окружности монеты равна 17,27 см.

Ещё чтобы вы имели представление о длине окружности,
можно взять кольцо, сделанное из проволоки, разрезать его и разогнуть
проволоку. Линия, которая у нас получится и отображает длину окружности.

Можно заметить, что длина нитки примерно в 3 раза больше длины диаметра монеты.

Обозначим длину окружности буквой С, а её диаметр буквой D. Оказывается, какую бы окружность мы ни
взяли, частное от деления С на D всегда одно и то же. Сначала было
замечено, что длина любой окружности примерно в 3 раза
больше диаметра. Затем этот результат был уточнен – в  раза,
но и тогда математики знали, что это число тоже не является точным.

Чтобы не было проблем при записях расчётов,
математики Древней Греции стали обозначать его греческой буквой  (читается
«пи» – начальная буква греческого слова perimetron,
которое и означает «окружность»).

Было доказано, что число
 относится
к таким числам, точное значение которых записать невозможно ни с помощью обыкновенных,
ни с помощью десятичных дробей.

Можно записать приближённое значение числа  с
точностью до миллионных, до миллиардных. Поэтому в формулах используют букву , а для
практических вычислений его приближённое значение.

Определение

Отношение длины окружности к длине её
диаметра является одним и тем же числом для любой окружности.

Обозначив длину окружности буквой С, а её диаметр буквой D, получаем:

Обычно формулу длины окружности записывают через
радиус

Заметим, что число  – это отношение
длины окружности к длине её диаметра.

Задача

В Лондоне была построена самая большая в мире
часовая башня, которая имеет название Биг-Бен. Длина диаметра циферблата часов
на башне равна 7 метров. Определите длину
окружности часов, если число  ≈
3,14.
Ответ округлите с точностью до целых.

Решение:

Задача

Минутная стрелка описывает окружность длиной 18 см. Определите длину минутной стрелки, если
число  =
3,14.
Результат округлите до десятых.

Решение:

Задача

Спортсмен пробежал расстояние 42000 м, причём сделал полных 105 оборотов. Определите радиус стадиона, границей
которого является беговая дорожка, по которой бежал спортсмен. Число  =
3,14.
Результат округлите до целых.

Решение:

Итоги

Итак, сегодня на уроке мы познакомились с интересным
числом ,
вывели формулу длины окружности и научились решать задачи с использованием этой
формулы.



В своей повседневной жизни мы часто сталкиваемся с задачами, которые связаны с вычислением периметра, то есть суммы длин сторон различных геометрических фигур. В случае, если геометрическая фигура — многоугольник, нахождение его периметра не составляет особого труда: для этого достаточно с помощью линейки измерить длину каждой из сторон и сложить полученные результаты. Что же делать, если необходимо узнать длину окружности? Ответу на этот вопрос посвящена данная статья.

Окружность является самой распространённой кривой практически во всех областях человеческой деятельности. Форму окружности или круга мы встречаем повсюду: это и колесо машины, и линия горизонта, и диск Луны. Многие вещи, окружающие нас, имеют круглую форму, например: обруч, кольцо, мяч, тарелка.

В свободное время я люблю заниматься моделированием из бумаги, пластилина и, особенно, из деталей конструктора Лего. Иногда, для того чтобы подготовить нужную заготовку для модели, необходимо знать длину сторон фигуры, которую хочешь получить. Никогда эта задача не вызывала у меня затруднений, пока я не столкнулся с определением длины окружности.

В учебнике по геометрии 7 класса рассматривается вопрос определения длины окружности. Существует формула, при помощи которой решается эта задача. Мне стало интересно, а как же раньше, в древности, люди находили длину окружности, можно ли ее найти экспериментальным путем без помощи известной формулы, какая существует связь между размером окружности (диаметром) и длиной окружности, и какое практическое применение может иметь решение этой задачи.

Ещё в давние времена люди сталкивались с практическими задачами, для решения которых необходимо было уметь находить длину окружности. Например, для того чтобы изготовить металлический обод для колеса телеги, определить вместительность сосуда, при строительстве зданий, для изготовления ювелирных изделий, при пошиве одежды.

В источниках [1, 4] сказано, что уже 4 тысячи лет назад люди знали, что длина окружности примерно равна трём его диаметрам. В дальнейшем, более 2 тыс. лет назад, большой вклад в развитие геометрии, в том числе в изучение геометрических фигур — окружности и круга — внесли древнегреческий математик Евклид, а позже — Архимед.

Целью исследования является изучение различных способов нахождения длины окружности и получение взаимосвязи между диаметром окружности и её длиной.

Гипотеза исследования: формулу длины окружности можно получить самостоятельно экспериментальным путем.

Основные понятия

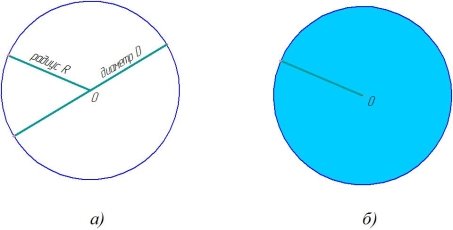
Окружность — это замкнутая плоская кривая линия, все точки которой находятся на одинаковом расстоянии от заданной точки О. Эта точка называется центром окружности (рисунок 1,а).

Круг — часть плоскости, ограниченная окружностью (рисунок 1,б).

Можно сказать, что окружность является границей круга.

Основные линии окружности — радиус и диаметр (рисунок 1,а).

Радиус R окружности — это отрезок, соединяющий центр О с любой точкой окружности.

Диаметр D окружности — отрезок, который соединяет две точки окружности и проходит через ее центр.

Рис. 1. Окружность и круг

Способы нахождения длины окружности

Рассмотрим некоторые возможные способы нахождения длины окружности.

Нахождение длины окружности с








помощью нити

Когда я впервые задумался над решением данной задачи, первое и самое простое, что пришло на ум — это приложить нить к окружности, а затем при помощи линейки измерить ее длину. Подготовиться к эксперименту мне помог папа: он вырезал на станке металлические круги разных диаметров.

Проведем измерение круга диаметром 50 мм. Я обернул круг нитью, шариковой ручкой сделал отметки и при помощи линейки измерил длину нити между отметками (рисунок 2).

Длина нити оказалась равной 158 мм. При измерении я обратил внимание на то, что результат получается приблизительным, так как зависит от силы натяжения нити и ее толщины. И самое главное — не каждую окружность можно измерить таким способом.

То есть данный экспериментальный способ не решает поставленной задачи. Необходимо получить универсальную формулу, при помощи которой можно было бы найти длину окружности любого диаметра.

Рис. 2. Нахождение длины окружности с помощью нити

Нахождение длины окружности с








помощью квадратов

Следующий способ, который я решил применить: представить окружность в виде квадрата (рисунок 3).

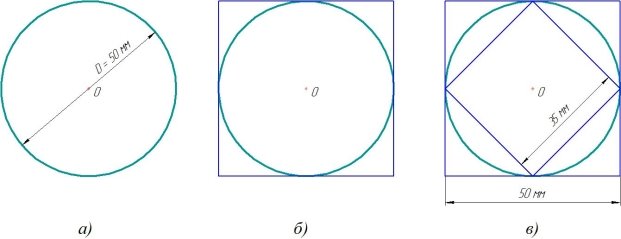
Продолжаем исследовать окружность диаметром 50 мм (рисунок 3,а).

Построим вокруг окружности квадрат так, чтобы он касался окружности в 4-х точках (рисунок 3,б), то есть сторона квадрата равна диаметру окружности.

Но на рисунке видно, что периметр квадрата явно больше длины вписанной окружности. А что, если внутри окружности построить еще один квадрат? Тогда, возможно, длина окружности будет средней величиной между периметрами двух квадратов.

Рис. 3

Измерим длины сторон квадратов с помощью линейки (рисунок 3,в). Длина стороны внутреннего квадрата равна 35 мм, наружного — 50 мм.

Найдем периметры квадратов:

Периметр внутреннего квадрата Р

_внутр

= 35+35+35+35 = 435= 140 (мм);

Периметр внешнего квадрата Р

_внешн

= 50+50+50+50= 450 = 200 (мм).

Предположим, что длина окружности — это средняя величина двух периметров. Найдём, чему она равна: (140+200):2 = 170 (мм).

Это значение намного отличается от длины окружности, полученной при измерении с помощью нити — 158 мм, что говорит о невысокой точности этого метода.

Нахождение длины окружности с








помощью многоугольников

Далее я предположил, что если внутри окружности построить многоугольник с большим количеством сторон, то его периметр будет больше приближен к длине описанной окружности.

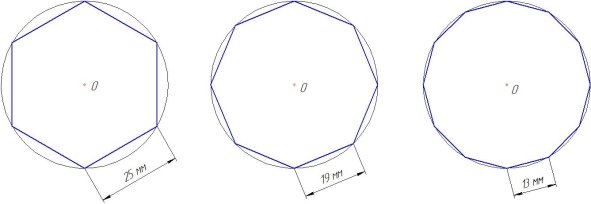
Для того чтобы подтвердить своё предположение, я решил исследовать несколько геометрических фигур: шестиугольник, восьмиугольник, двенадцатиугольник. Диаметр окружности — 50 мм (рисунок 4).

Рис. 4

Измерим линейкой длины сторон и с помощью калькулятора найдем периметры построенных фигур.

Периметр шестиугольника (обозначим его Р

₆

) равен:

Р

₆

= 25+25+25+25+25+25= 625 = 150 (мм).

Найдем периметры восьмиугольника Р

₈

и


двенадцатиугольника Р

₁₂

:

Р

₈

= 19+19+19+19+19+19+19+19 = 819 = 152 (мм);

Р

₁₂

= 13+13+13+13+13+13+13+13+13+13+13+13 = 1213 = 156 (мм).

Из полученных результатов можно сделать вывод, что чем больше сторон имеет многоугольник, тем больше его периметр будет приближен к реальной длине окружности, в которую он вписан.

Получение формулы длины окружности экспериментальным методом

От геометрических построений переходим к практическому исследованию и попробуем ответить на вопрос: существует ли связь между диаметром окружности и его длиной.

Экспериментальным способом найдём длины 3-х окружностей диаметром 50, 100 и 200 мм.

Для эксперимента нам понадобятся: 3 металлических круга диаметром 50, 100 и 200 мм, простой карандаш, цветные карандаши, лист ватмана, линейка, рулетка, корпус шариковой ручки, выполняющий роль оси вращения (рисунок 5).

Рис. 5. Подготовка к эксперименту

Для нахождения длины окружности мы будем катить металлический круг, как колесо, по прямой линии, проведенной на листе ватмана. На круге сделана насечка для того, чтобы можно было отметить, когда круг сделает полный оборот. Расстояние, которое пройдет круг за один оборот, и будет являться длиной окружности соответствующего диаметра (рисунок 6).

Рис. 6. Проведение эксперимента

В ходе эксперимента мы получили следующие результаты (рисунок 7).

Длина окружности, диаметр которой D

₁

= 50мм, равна 157мм, то есть L

₁

=157 мм.

Длина окружности диаметром D

₂

=100 мм равна L

₂

=314 мм.

Длина окружности диаметром D

₃

=200 мм равна L

₃

=628 мм.

Рис. 7. Результаты эксперимента

Представим полученные результаты в виде таблицы.

Диаметр окружности, мм	50	100	200
Длина окружности, мм	157	314	628

Сравним полученные результаты. Из таблицы видно, что при увеличении диаметра окружности в 2 раза, длина окружности увеличивается также в 2 раза. Отсюда можно сделать вывод, что отношение длины окружности к её диаметру — одинаковая величина для любой окружности, то есть:

С помощью калькулятора выполним расчет:

Экспериментальным методом мы определили, что отношение длины к диаметру окружности — постоянная величина, приблизительно равная 3,14.

Уже более 2 тыс. лет назад древнегреческий математик Архимед в своих научных трудах доказал, что отношение длины окружности к её диаметру является постоянной величиной, равной 3,14.

В 1706 году британский математик Уильям Джонс предложил это отношение обозначать греческой буквой

(пи), от первой буквы греческого слова “periferia (периферия)” — круг:

Зная отношение длины окружности к диаметру, получим формулу для нахождения длины окружности:

При помощи этой формулы можно вычислить длину любой окружности, насколько бы велика или мала она не была, или решить обратную задачу для нахождения радиуса окружности, если известна её длина.

Заключение

Таким образом, были исследованы различные способы нахождения длины окружности: с помощью нити, методом квадратов, с помощью многоугольников, в результате чего мы пришли к выводу, что метод многоугольников позволяет найти наиболее точное значение длины окружности.

Экспериментальным путем найдена взаимосвязь между диаметром окружности и её длиной и получена формула для нахождения длины окружности

, где

, что подтверждает нашу гипотезу.

Литература:

1. Энциклопедический словарь юного математика/Сост. А. П. Савин. — М.: Педагогика, 1989. — 352 с.: ил.
2. Что такое. Кто такой: В 3 т. Т. 1–4-е изд., перераб. и доп. — М.: Педагогика-Пресс, 1998. — 384 с.: ил.
3. Что такое. Кто такой: В 3 т. Т. 2–4-е изд., перераб. И доп. — М.: Педагогика-Пресс, 1998. — 416 с.: ил.
4. Окружность: история // ВикипедиЯ. URL: https://ru.wikipedia.org/wiki/ %D0 %9E %D0 %BA %D1 %80 %D1 %83 %D0 %B6 %D0 %BD %D0 %BE %D1 %81 %D1 %82 %D1 %8C (дата обращения: 11.12.2019).

Подпишись на наш канал в телеграм. Там мы даём ещё больше полезной информации для школьников!