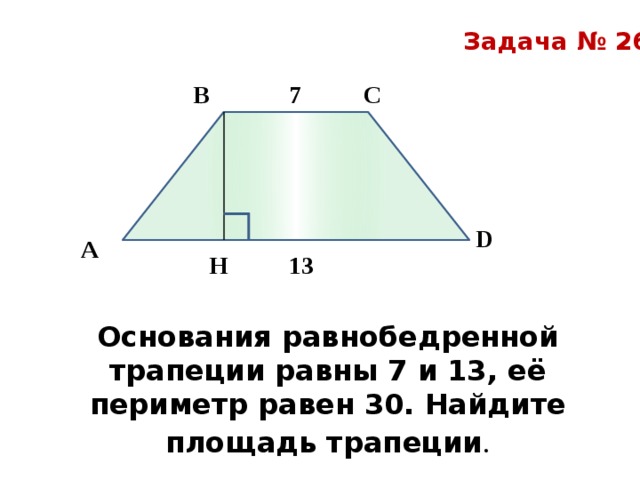
Для начала найдем длины боковых сторон равнобедренной трапеции. Равнобедренная трапеция имеет две параллельные стороны (основания) и две равные не параллельные стороны (боковые стороны). Зная основания и периметр трапеции, мы можем найти длину каждой из боковых сторон.
Основания равны 8 и 18, а периметр равен 52. Обозначим длины боковых сторон трапеции как a и b.
Так как это равнобедренная трапеция, a = b.
Теперь найдем длины боковых сторон:
a + b + 8 + 18 = 52
a + a + 26 = 52
2a = 26
a = 13
Теперь, когда у нас есть длины боковых сторон, давайте найдем высоту трапеции. Высота трапеции опускается перпендикулярно к основаниям. Разделите трапецию на два равнобедренных треугольника. В таком случае, можно использовать теорему Пифагора для одного из этих треугольников.
Разность оснований равна 18 — 8 = 10. Таким образом, каждый из равнобедренных треугольников имеет основание, равное 10/2 = 5.
Теперь используем теорему Пифагора:
a^2 = h^2 + b^2
13^2 = h^2 + 5^2
169 = h^2 + 25
h^2 = 144
h = 12
Теперь, когда у нас есть высота и основания трапеции, мы можем найти её площадь. Формула для площади трапеции:
S = ((a + b) / 2) * h
S = ((8 + 18) / 2) * 12
S = (26 / 2) * 12
S = 13 * 12
S = 156
Площадь равнобедренной трапеции равна 156 квадратных единиц.
Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.
Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.
Площадь трапеции, можно измерить, в единицах
измерения в квадрате: мм2, см2, м2 и км2 и так далее.
Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.
Содержание
- Формулы площади трапеции
- Площадь любых трапеций
- Площадь равнобедренной трапеции
- Определения трапеции
- Элементы трапеции
Формулы площади трапеции
Площадь любых трапеций
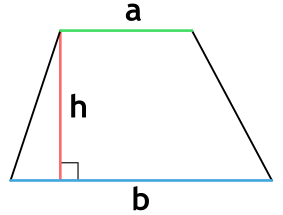
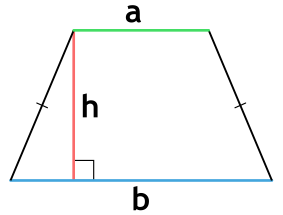
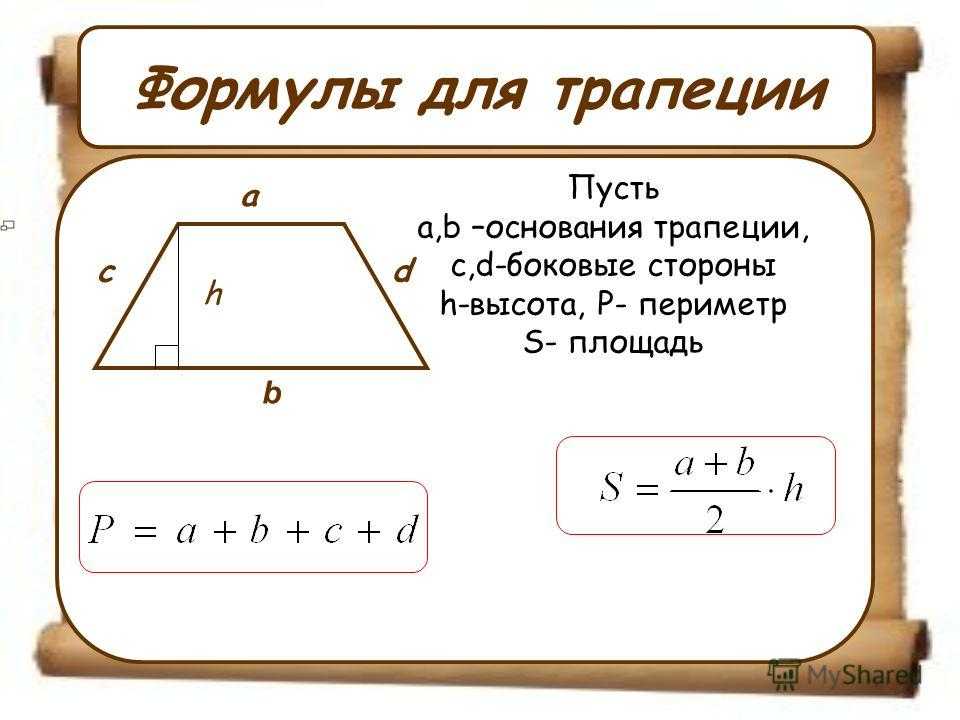
Ⅰ. Площадь трапеции через основания и высоту:
[ S = frac{a+b}{2} cdot h ]
a,b — основания трапеции;
h — высота трапеции;
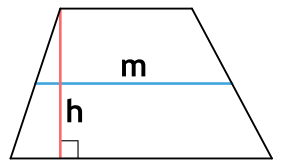
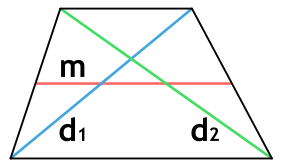
Ⅱ. Площадь трапеции через высоту и среднюю линию:
[ S = mh ]
m — средняя линия трапеции;
h — высота трапеции;
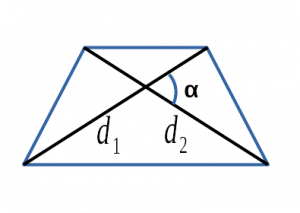
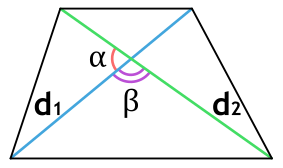
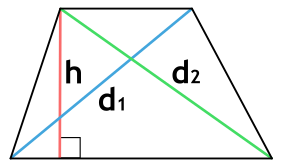
Ⅲ. Площадь трапеции через диагонали и угол между ними:
[ S =frac{1}{2}d_1d_2 cdot sin alpha ]
( d_1, d_2 )- диагонали трапеции;
sin α — синус угла альфа в трапеции;
Ⅳ. Площадь трапеции через периметр, высоту и боковые стороны:
[ S = frac{P-(c+d)}{2}h ]
P — периметр трапеции;
c,d — боковые стороны трапеции;
h — высота трапеции;
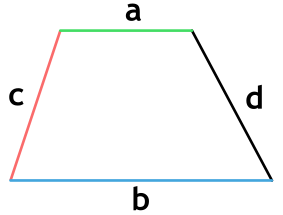
Ⅴ. Площадь трапеции через основания и боковые стороны:
[ S = frac{a+b}{2} cdot sqrt{c^2-(frac{(a+b)^2+c^2-d^2}{2a-2b})^2} ]
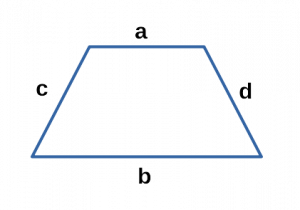
a,b — основания трапеции;
с,d — боковые стороны трапеции;
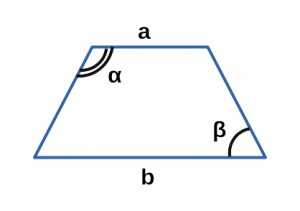
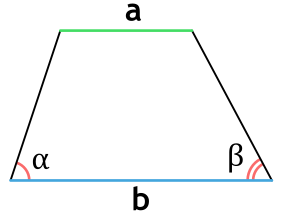
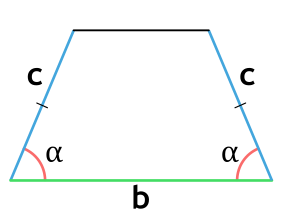
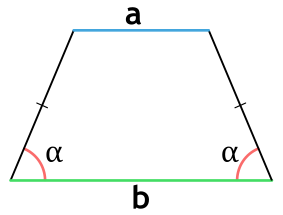
Ⅵ. Площадь трапеции через основания и углы:
[ S = frac{b^2-a^2}{2} cdot frac{sin α cdot sin β}{sin( α + β)} ]
a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;
Площадь равнобедренной трапеции
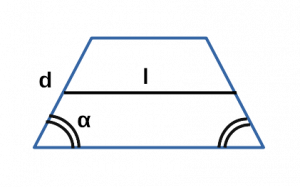
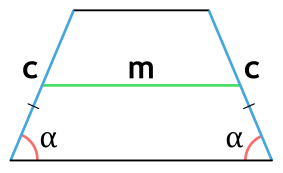
Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:
[ S = ld cdot sin α ]
l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
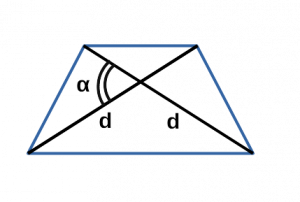
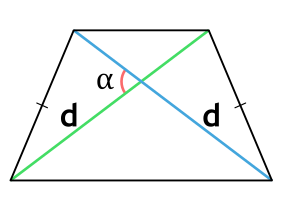
Ⅱ. Площадь трапеции через диагонали и синус угла:
[ S = frac{d^2}{2} cdot sin α ]
d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
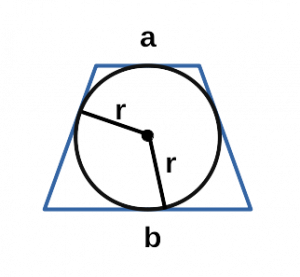
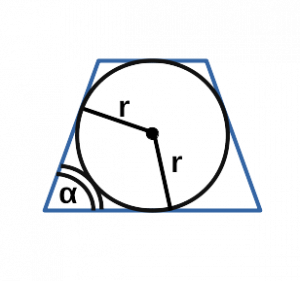
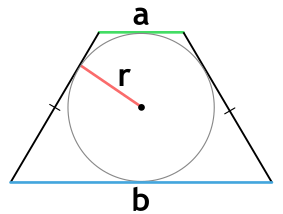
Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:
[ S = r( a+b) ]
r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
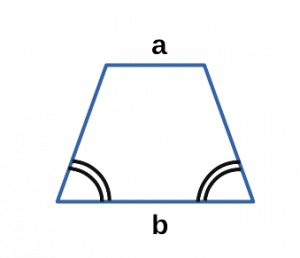
Ⅳ. Площадь трапеции через основания:
[ S = sqrt{ab} cdot {frac{a+b}{2}} ]
a, b — основания равнобедренной трапеции;
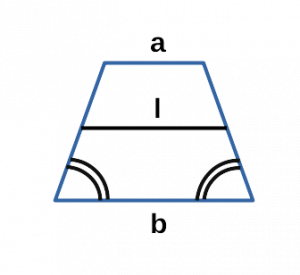
Ⅴ. Площадь трапеции через основания и среднюю линию:
[ S = lsqrt{ab} ]
l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
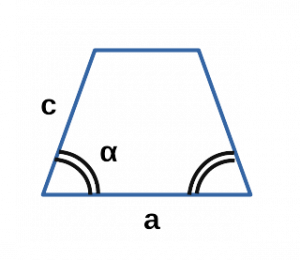
Ⅵ. Площадь трапеции через синус угла и стороны:
[ S = c cdot sin α cdot (a-c cdot cos α) ]
a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;
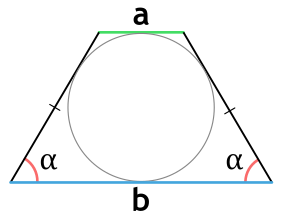
Ⅶ. Площадь трапеции через угол и радиус вписанной окружности:
[ S = frac{4r^2}{sin α} ]
r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Определения трапеции
Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.
Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:
- Обычная / стандартная трапеция: четыре угла и четыре стороны не равны.
- Равнобедренная / равнобочная / равнобоковая трапеция:
два угла при основании равны, две боковые стороны равны. - Прямоугольная / прямая трапеция: один из углов прямой.
Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.
Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.
Элементы трапеции
Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.
Основание трапеции — это сторона, противолежащая
сторона которой параллельна.
Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.
Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.
Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.
Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.
Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.
Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.
Площадь трапеции
Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.
Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.
Площадь трапеции, можно измерить, в единицах
измерения в квадрате: мм 2 , см 2 , м 2 и км 2 и так далее.
Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.
Формулы площади трапеции
Площадь любых трапеций
Ⅰ. Площадь трапеции через основания и высоту:
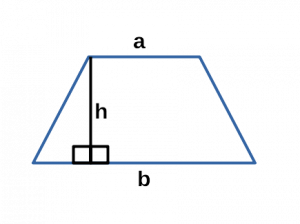
[ S = frac <2>cdot h ]
a,b — основания трапеции;
h — высота трапеции;
Ⅱ. Площадь трапеции через высоту и среднюю линию:
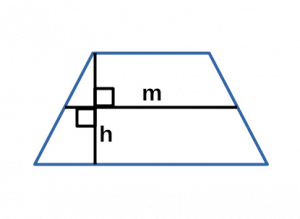
[ S = mh ]
m — средняя линия трапеции;
h — высота трапеции;
Ⅲ. Площадь трапеции через диагонали и угол между ними:
[ S =frac<1><2>d_1d_2 cdot sin alpha ]
( d_1, d_2 ) - диагонали трапеции;
sin α — синус угла альфа в трапеции;
Ⅳ. Площадь трапеции через периметр, высоту и боковые стороны:
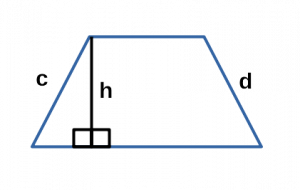
[ S = frac<2>h ]
P — периметр трапеции;
c,d — боковые стороны трапеции;
h — высота трапеции;
Ⅴ. Площадь трапеции через основания и боковые стороны:
[ S = frac <2>cdot sqrt<2a-2b>)^2> ]
a,b — основания трапеции;
с,d — боковые стороны трапеции;
Ⅵ. Площадь трапеции через основания и углы:
a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;
Площадь равнобедренной трапеции
Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:
[ S = ld cdot sin α ]
l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅱ. Площадь трапеции через диагонали и синус угла:
[ S = frac <2>cdot sin α ]
d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:
r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅳ. Площадь трапеции через основания:
a, b — основания равнобедренной трапеции;
Ⅴ. Площадь трапеции через основания и среднюю линию:
l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅵ. Площадь трапеции через синус угла и стороны:
[ S = c cdot sin α cdot (a-c cdot cos α) ]
a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;
Ⅶ. Площадь трапеции через угол и радиус вписанной окружности:
r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Определения трапеции
Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.
Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:
- Обычная / стандартная трапеция: четыре угла и четыре стороны не равны.
- Равнобедренная / равнобочная / равнобоковая трапеция:
два угла при основании равны, две боковые стороны равны. - Прямоугольная / прямаятрапеция: один из углов прямой.
Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.
Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.
Элементы трапеции
Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.
Основание трапеции — это сторона, противолежащая
сторона которой параллельна.
Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.
Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.
Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.
Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.
Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.
Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.
Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) |
| a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
a — большее основание
Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как найти площадь трапеции
Как найти площадь трапеции? Для этого в зависимости от данных условия можно использовать несколько формул.
1. Площадь трапеции равна произведению полусуммы её оснований на высоту.
Для трапеции ABCD, AD ∥ BC, с высотой BF площадь равна
Если AD=a, BC=b, BF=h, формула для нахождения площади трапеции
2. Площадь трапеции равна произведению её средней линии на высоту.
Если MN=m, BF=h, формула для нахождения площади трапеции через среднюю линию и высоту
3. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.
Если AC=d1, BD=d2, ∠COD=φ, то формула для нахождения площади трапеции через диагонали —
Если диагонали трапеции перпендикулярны,
так как sin 90º=1,
то формула площади трапеции
4. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.
Так как в трапецию можно вписать окружность, если суммы ее противолежащих сторон равны, то AB+CD=AD+BC. Следовательно, полупериметр трапеции равен сумме её оснований: p=AD+BC или p=a+b.
Таким образом, получаем еще одну формулу для нахождения площади трапеции через радиус вписанной окружности:
(Так как радиус вписанной в трапецию окружности равен половине высоты трапеции:
то эта формула может быть получена непосредственно из формулы из пункта 1).
http://ru.onlinemschool.com/math/formula/trapezium/
{S = dfrac{1}{2} (a + b) cdot h}
Площадь трапеции можно найти множеством способов. Для вас мы собрали все возможные варианты нахождения площади. Для вашего удобства для каждой формулы создан калькулятор, который поможет рассчитать площадь трапеции по известным данным. От вас требуется только подставить значения и в режиме онлайн мгновенно получить ответ. Формулы и калькуляторы сгруппированы по типам трапеций — обычная, равнобедренная (равнобокая).
- Калькулятор площади трапеции
- Площадь трапеции
- через основания и высоту
- через среднюю линию и высоту
- через диагонали и среднюю линию
- через 4 стороны
- через диагонали и угол между ними
- через основания и углы при основании
- через площади треугольников
- через диагонали и высоту
- через радиус вписанной окружности и основания
- через перпендикулярные диагонали
- Площадь равнобедренной (равнобокой) трапеции
- через основания и высоту
- через 3 стороны (формула Брахмагупты)
- через верхнее основание, боковую сторону и угол при нижнем основании
- через нижнее основание, боковую сторону и угол при нижнем основании
- через основания и угол
- через диагонали и угол между ними
- через боковую сторону, угол при основании и среднюю линию
- через радиус вписанной окружности и угол при основании
- Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
- через высоту (диаметр вписанной окружности) и угол при основании
- через основания и угол при основании
- через основания и радиус вписанной окружности
- через основания
- через основания и боковую сторону
- через основания и среднюю линию
- Примеры задач
Площадь трапеции
Трапеция — выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Площадь трапеции через основания и высоту
{S = dfrac{1}{2} (a + b) cdot h}
a и b — основания трапеции
h — высота, проведенная к основанию
Площадь трапеции через среднюю линию и высоту
{S = m cdot h}
m — средняя линия трапеции
h — высота трапеции
Площадь трапеции через диагонали и среднюю линию
{S = sqrt{p(p-d_1)(p-d_2)(p-2m)}}
{p = dfrac{d_1+d_2+2m}{2}}
d1 и d2 — диагонали трапеции
m — средняя линия трапеции
Площадь трапеции через 4 стороны
{S = dfrac{a+b}{2} sqrt{c^2 — {Big( dfrac{(a-b)^2 + c^2 — d^2}{2(a-b)} Big)}^2}}
a, b, c и d — стороны трапеции
Площадь трапеции через диагонали и угол между ними
{S = dfrac{d_1 cdot d_2}{2}cdot sin(alpha); S = dfrac{d_1 cdot d_2}{2}cdot sin(beta)}
d1 и d2 — диагонали трапеции
α или β — угол между диагоналями трапеции
Площадь трапеции через основания и углы при основании
{S = dfrac{b^2 — a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(alpha + beta)}}
a и b — основания трапеции
α или β — прилежащие к основанию трапеции углы
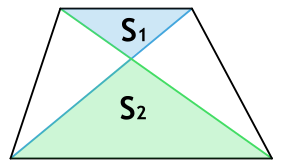
Площадь трапеции через площади треугольников
{S = (sqrt{S_1} + sqrt{S_2})^2}
S1 и S2 — площади образованных пересечением диагоналей трапеции треугольников
Площадь трапеции через диагонали и высоту
{S = dfrac{sqrt{{d_2}^2-h^2}+sqrt{{d_1}^2-h^2}}{2} cdot h}
d1 и d2 — диагонали трапеции
h — высота трапеции
Площадь трапеции через радиус вписанной окружности и основания
{S = (a+b)cdot r}
a и b — основания трапеции
r — радиус вписанной в трапецию окружности
Площадь трапеции через перпендикулярные диагонали
{S = dfrac{1}{2} cdot d_1 cdot d_2}
d1 и d2 — перпендикулярные диагонали трапеции
Площадь равнобедренной (равнобокой) трапеции
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Площадь равнобедренной трапеции через основания и высоту
{S = dfrac{a+b}{2} cdot h}
a и b — основания равнобедренной трапеции
h — высота, проведенная к основанию равнобедренной трапеции
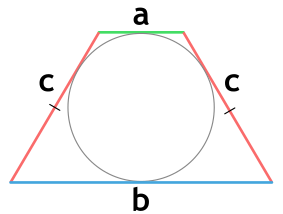
Площадь равнобедренной трапеции через 3 стороны (формула Брахмагупты)
{S = sqrt{(p-a)(p-b)(p-c)^2}}
{p = dfrac{a+b+2c}{2}}
a и b — основания равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании
{S = c cdot sin(alpha) cdot (a+c cdot cos(alpha))}
a — верхнее основание равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
α — прилежащие к нижнему основанию трапеции углы
Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании
{S = c cdot sin(alpha) cdot (b-c cdot cos(alpha))}
b — нижнее основание равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
α — прилежащий к нижнему основанию трапеции угол
Площадь равнобедренной трапеции через основания и угол
{S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha)}
a и b — основания равнобедренной трапеции
α — прилежащий к основанию трапеции угол
Площадь равнобедренной трапеции через диагонали и угол между ними
{S = dfrac{1}{2}d^2 cdot sin(alpha)}
a — диагональ равнобедренной трапеции
α — угол между диагоналями равнобедренной трапеции
Площадь равнобедренной трапеции через боковую сторону, угол при основании и среднюю линию
{S = m cdot c cdot sin(alpha)}
m — средняя линия равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
α — угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции через радиус вписанной окружности и угол при основании
{S = dfrac{4r^2}{sin(alpha)}}
r — радиус вписанной окружности
α — угол при основании равнобедренной трапеции
Площадь равнобедренной (равнобокой) трапеции, в которую можно вписать окружность
В трапецию можно вписать окружность тогда и только тогда, когда суммы ее противоположных сторон равны.
Площадь равнобедренной трапеции, в которую можно вписать окружность, через высоту (диаметр вписанной окружности) и угол при основании
{S = dfrac{h^2}{sin(alpha)}}
h — высота равнобедренной трапеции
α — угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и угол при основании
{S = dfrac{a cdot b}{sin(alpha)}}
a и b — основания равнобедренной трапеции
α — угол при основании равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и радиус вписанной окружности
{S = r(a+b); r=dfrac{sqrt{a cdot b}}{2}}
a и b — основания равнобедренной трапеции
r — радиус вписанной окружности
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания
{S = sqrt{a cdot b} cdot dfrac{a+b}{2}}
a и b — основания равнобедренной трапеции
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и боковую сторону
{S = c cdot sqrt{a cdot b}}
a и b — основания равнобедренной трапеции
c — боковая сторона равнобедренной трапеции
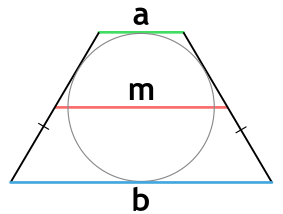
Площадь равнобедренной трапеции, в которую можно вписать окружность, через основания и среднюю линию
{S = m cdot sqrt{a cdot b}}
a и b — основания равнобедренной трапеции
m — средняя линия равнобедренной трапеции
Примеры задач на нахождение площади трапеции
Задача 1
Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.
Решение
Для решения задачи воспользуемся первой формулой.
S = dfrac{1}{2} (a + b) cdot h = dfrac{1}{2} (6 + 9) cdot 5 = dfrac{1}{2} cdot 15 cdot 5 = dfrac{1}{2} cdot 75 = 37dfrac{1}{2} : см^2
Ответ: 37.5 см²
Полученный ответ легко проверить с помощью калькулятора .
Задача 2
Найдите площадь трапеции средняя линия которой равна 18 см, а высота 9 см.
Решение
С решением этой задачи нам поможет вторая формула.
S = m cdot h = 18 cdot 9 = 162 : см^2
Ответ: 162 см²
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите площадь трапеции диагонали которой равны 10 и 8, а средняя линия равна 3.
Решение
Для решения этой задачи нам поможет третья формула.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{10+8+2 cdot 3}{2} = dfrac{10+8+6}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-10)(12-8)(12-2 cdot 3)} = sqrt{12 cdot 2 cdot 4 cdot 6} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Осталось проверить полученный ответ.
Задача 4
Найдите площадь трапеции диагонали которой равны 17 и 15, а средняя линия равна 4.
Решение
Задача похожа на ту, что мы только что решили. Поэтому повторим шаги.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{17+15+ 2 cdot 4}{2} = dfrac{17+15+8}{2} = dfrac{40}{2} = 20
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{20(20-17)(20-15)(20-2 cdot 4)} = sqrt{20 cdot 3 cdot 5 cdot 12} = sqrt{3600} = 60 : см^2
Ответ: 60 см²
Проверка .
Задача 5
Найдите площадь трапеции диагонали которой равны 8 и 6 а средняя линия равна 5.
Решение
Еще одна типовая задача. Повторим действия как в задачах выше.
На первом этапе вычислим p:
p = dfrac{d_1+d_2+2m}{2} = dfrac{8+6+ 2 cdot 5}{2} = dfrac{8+6+10}{2} = dfrac{24}{2} = 12
А теперь можно вычислить площадь трапеции:
S = sqrt{p(p-d_1)(p-d_2)(p-2m)} = sqrt{12(12-8)(12-6)(12-2 cdot 5)} = sqrt{12 cdot 4 cdot 6 cdot 2} = sqrt{576} = 24 : см^2
Ответ: 24 см²
Проверка .
Задача 6
Найдите площадь равнобедренной трапеции если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.
Решение
Для решения этой задачи используем формулу Брахмагупты.
Сначала вычислим p:
p = dfrac{a+b+2c}{2} = dfrac{5+17+2 cdot 10}{2} = dfrac{22+20}{2} = dfrac{42}{2} = 21
А теперь можно вычислить площадь трапеции:
S = sqrt{(p-a)(p-b)(p-c)^2} = sqrt{(21-5)(21-17)(21-10)^2} = sqrt{16 cdot 4 cdot 11^2} = sqrt{16 cdot 4 cdot 121} = sqrt{7744}= 88 : см^2
Ответ: 88 см²
Проверка .
Задача 7
Острый угол равнобедренной трапеции равен 45°, а основания равны 8 и 6 см. Найдите площадь трапеции.
Решение
Для решения этой задачи воспользуемся формулой.
S = dfrac{1}{2}(b^2-a^2) cdot tg(alpha) = dfrac{1}{2}(8^2-6^2) cdot tg(45°)
Тангенс 45° = 1, продолжим вычисления:
S = dfrac{1}{2}(8^2-6^2) cdot tg(45°) = dfrac{1}{2}(64-36) cdot 1 = dfrac{1}{2} cdot 28 = 14 : см^2
Ответ: 14 см²
Убедиться в правильности решения нам поможет калькулятор .
формула с основаниями, без высоты
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение площади трапеции: формула и примеры
Трапеция – это геометрическая фигура; четырехугольник, имеющий 2 параллельные и 2 непараллельные стороны.
-
Формулы вычисления площади
- По длине оснований и высоте
- Через длины всех сторон (Формула Герона)
- Через диагонали и угол между ними
- Примеры задач
Формулы вычисления площади
По длине оснований и высоте
Площадь трапеции (S) равняется половине суммы ее оснований, умноженной на высоту, проведенную к ним.
Через длины всех сторон (Формула Герона)
Для вычисления площади трапеции необходимо знать длины всех ее сторон:
p – полупериметр трапеции, считается по формуле:
Через диагонали и угол между ними
Площадь трапеции равна половине произведения диагоналей и синуса угла между ними. Вычисляется по одной из двух формул ниже:
Примеры задач
Задание 1
Найдите площадь трапеции, если ее основания равны 4 и 7 см, а высота – 4 см.
Решение:
Используем первую формулу, рассмотренную выше: S = 1/2
* (4 см + 7 см) * 4 см = 22 см2.
Задание 2
Найдите площадь трапеции, если ее основания равны 6 и 12 см, а боковые стороны – 8 и 10 см.
Решение:
Т.к. нам известны длины всех сторон, применим формулу Герона:
S = (6+12) / |6-12| * √(18-6)(18-12)(18-6-8)(18-6-10) = 18 / 6 * √576 = 72 см2.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Найти большее основание трапеции
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-10-28
Найти большее основание трапеции.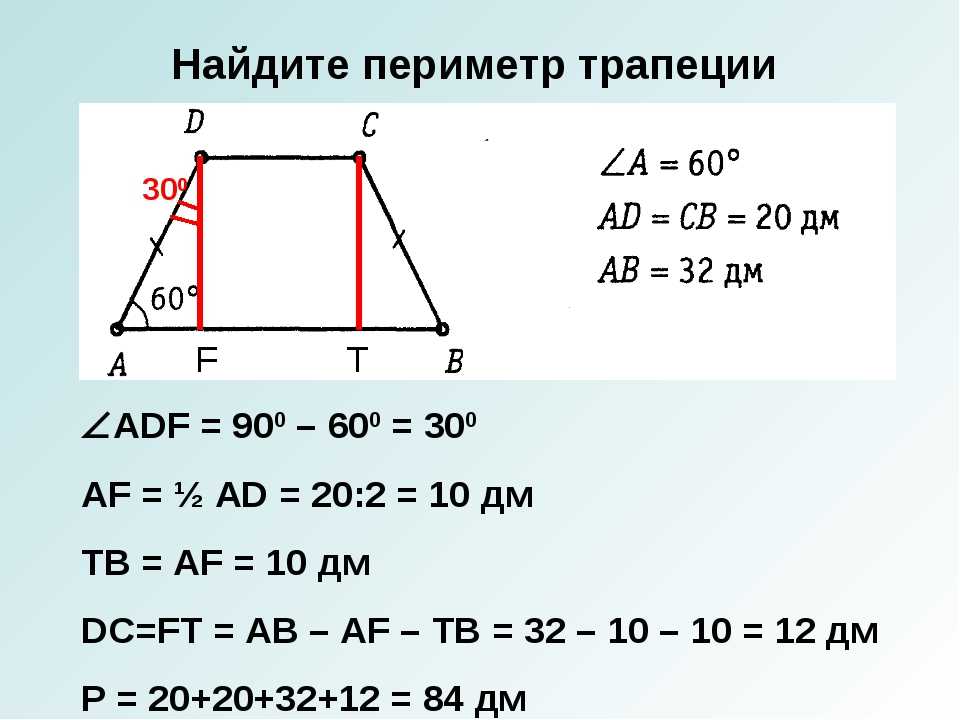
Здравствуйте! В той статье разберём группу задач связанных с площадью трапеции. Часть задачек решается устно, другая часть нет, но всё же быстро. Перед решением стоит посмотреть статью «Углы равнобедренной трапеции», и информацию о выводе формулы площади. Сама формула:
Рассмотрим задачи:
27627. Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
Площадь трапеции (формула):
Нам известны основания и площадь, можем записать:
Ответ: 8
27628. Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.
Формула площади при данных обозначениях вершин:
Нам известны основание, площадь и высота, можем записать:
Ответ: 7
*Заметьте, что в условии не сказано какое именно дано основание меньшее и большее, да это и не важно для процесса вычисления.
27630. Средняя линия трапеции равна 12, площадь равна 96.
Найдите высоту трапеции.
Формула площади при данных обозначениях вершин:
Нам известны средняя линя и площадь, можем записать:
Ответ: 8
27632. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
Для того, что бы найти периметр нам необходимо найти чему равна боковая сторона. Как известно, у равнобедренной трапеции боковые стороны равны.
Используя данные в условии мы можем вычислить высоту:
Опустим высоту из точки D к основанию АВ и точку пересечения обозначим как Е:
Теперь мы можем вычислить отрезок AH и по теореме Пифагора в прямоугольном треугольнике ADH найти гипотенузу AD (боковую сторону трапеции):
По теореме Пифагора:
Таким образом периметр будет равен 7+13+5+5 = 30
Ответ: 30
27635. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
Для вычисления площади нам необходимо найти высоту.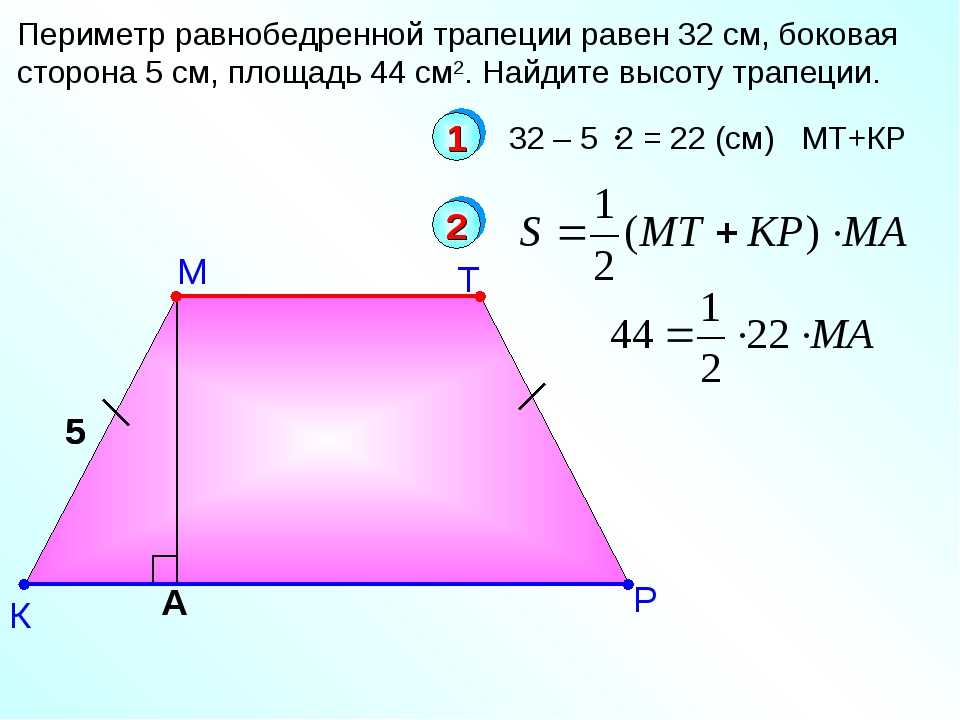
Выполним дополнительные построения:
Нижнее основание будет разбито на отрезки 6, 14 и 6. По теореме Пифагора мы можем вычислить высоту:
Таким образом площадь будет равна:
Ответ: 160
27636. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
Задача обратная предыдущей. Из данных в условии мы можем вычислить высоту:
Теперь выполним дополнительные построения (опустим высоты):
Большее основание разбивается ими на отрезки 3, 7 и 3. По теореме Пифагора можем вычислить боковую сторону:
Ответ: 5
27637. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 1500. Найдите площадь трапеции.
Для вычисления площади необходимо найти высоту. Это мы можем сделать рассмотрев прямоугольный треугольник АВН:
Высоту нашли, вычисляем площадь:
Ответ: 42
27593.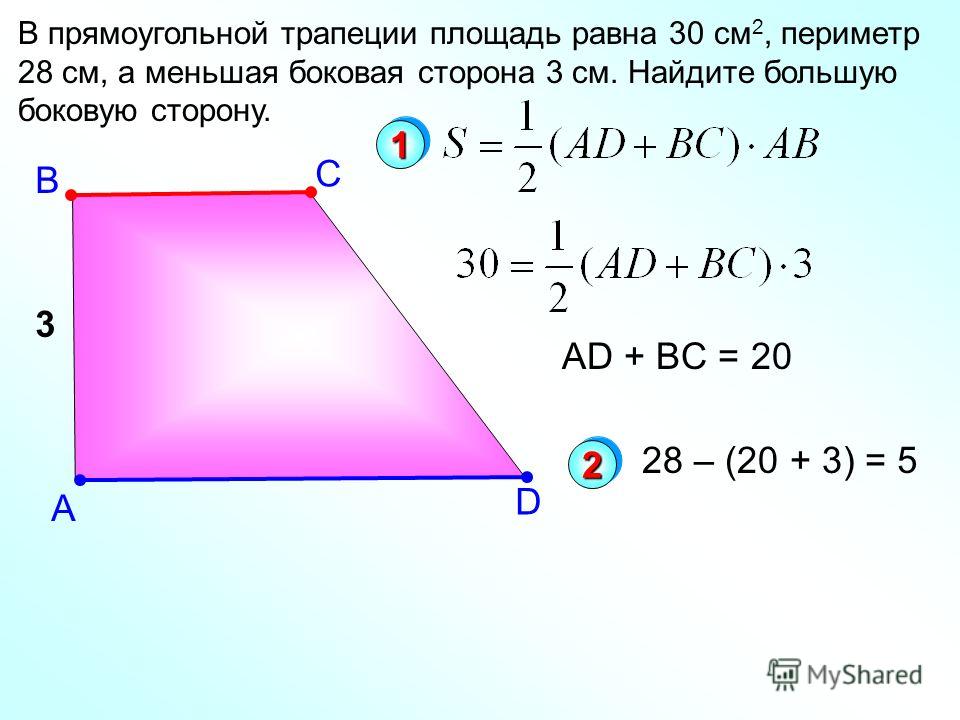
Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции.
Посмотреть решение
27594. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
Посмотреть решение
27629. Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
Посмотреть решение
27631. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Посмотреть решение
27633. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 450.
Посмотреть решение
27634. Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.
Посмотреть решение
27638. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне.
Ответ выразите в градусах.
Посмотреть решение
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
P.S: Расскажите о статье и сайте в социальных сетях.
Категория: Четырёхугольники | ЕГЭ-№1ПлощадьТрапеция
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Калькулятор площади трапеции
Площадь трапеции — Площадь трапеции равна 1/2 высоты, умноженной на сумму оснований (b1 + b2)
Вход на базу (база 1)
сммкминмийдфтмм
Вход на базу (база 2)
сммкминмийдфтмм
Введите высоту
сммкминмийдфтмм
Вот некоторые примеры расчетов площади трапеции
Площадь трапеции Калькулятор:
Вы когда-нибудь думали, что запомнить формулы на уроке геометрии так сложно? Если да, то наш простой в использовании Калькулятор площади трапеции поможет вам найти площадь за считанные секунды.
Всего несколько нажатий достаточно, чтобы вычислить площадь трапеции с помощью нашего калькулятора. Итак, зачем искать другие ресурсы, просто попробуйте наш бесплатный онлайн-калькулятор площади трапеции и легко получите вывод площади. Если вам интересно узнать, «как найти площадь и периметр трапеции», не смотрите дальше — просто продолжайте читать, чтобы узнать!
Трапеция – это четырехсторонняя геометрическая фигура, две стороны которой параллельны друг другу. И мы назвали эти две стороны (a и b) основаниями трапеции. Две другие стороны (c и d) называются катетами. Высота трапеции представлена как «h». Высота (или высота) трапеции — это перпендикулярное расстояние между двумя основаниями. Все внутренние углы трапеции в сумме дают 360°. Кроме того, углы с одной и той же стороны катета называются смежными и всегда составляют в сумме 180°, что определяется в уравнениях как
α + β = 180°
γ + δ = 180°
Площадь трапеции в основном равна средней ширине, умноженной на высоту, или по формуле:
Площадь = 1/2 * высота * (основание1 + основание2)
где
b1, b2 – длины каждого основания
h – высота (высота)
Четырехсторонняя геометрическая фигура, имеющая одну пару параллельных сторон, называется трапецией.
В большинстве случаев основания параллельны. Чтобы найти площадь трапеции, все, что вам нужно сделать, это просто выполнить шаги, указанные ниже:0005
- Прежде всего, запишите заданные параметры, такие как длина сторон и высота.
- На следующем шаге добавьте параллельные базы, т. е. base1 и base2.
- Теперь сложите сумму оснований и высоту трапеции.
- После завершения шага просто разделите результат на 2.
- Наконец, вы получите площадь трапеции в качестве выходных данных
Для большей ясности о том, как найти площадь трапеции, мы собираемся привести решенный пример ниже:
Пример:
Найдите площадь трапеции, у которой основание1 равно 23 см, основание2 равно 12 см, а высота равна 6 см?
Решение:
Заданные параметры, такие как основание1 b1 = 23 см, основание2 b2 = 12 см и высота h = 6 см
Подставляем значения оснований (b1 = 23 см и b2 = 12 см ) и высоты h = 6 см в формулу площади трапеции
Площадь = 1/2 * высота * (основание1 + основание2)
Подставьте значение основания и значение высоты в формулу площади.
Площадь = 1/2 * (6 см) * (23 + 12) см
Добавьте базовое значение b1 = 23 см и b2 = 12 см
Площадь = 1/2 * 6 см * (35,0 см )
Умножение 6 см и 35,0 см
Площадь = 1/2 * 210,0 см 2
Разделение 210,0 см 2 на 2
Область = 105,0 CM 2
Таким параметры 23 см, 12 см и 6 см 105,0 см 2
Наша площадь трапеции очень проста и удобна в использовании. Все, что вам нужно сделать, это ввести необходимые параметры в поля ввода, расположенные на экране. Наряду с входными данными также установите метрику единицы с помощью раскрывающегося списка. После того, как вы ввели необходимые параметры в поля, просто нажмите на кнопку под названием «Площадь». Наконец, он отображает результаты площади трапеции после выполнения всех внутренних вычислений.
Кроме того, вам будут известны шаги расчета площади трапеции в подробном объяснении. Итак, используйте этот бесплатный онлайн-инструмент Калькулятор площади трапеции и с легкостью получите результаты.
Знайте, что у вас достаточно информации о том, как это работает и как это помогает вам найти площадь трапеции при наличии необходимых параметров.
1. По какой формуле находится площадь трапеции?
Площадь трапеции находится по формуле A=(a+b)/2 x h.
2. Как найти площадь трапеции?
Вы можете легко найти результаты площади трапеции, введя заданные параметры в поля ввода Калькулятор площади трапеции .
3. Калькулятор площади трапеции является бесплатным онлайн-инструментом или нет?
Да, наш калькулятор площади трапеции — это бесплатный онлайн-инструмент, который помогает учащимся выполнять вычисления площади трапеции намного проще и быстрее.
4. Какая формула для периметра трапеции?
Вы также можете использовать эту площадь калькулятора трапеции для вычисления периметра этой четырехсторонней геометрической фигуры. Просто суммируйте все длины сторон вместе, то есть P = a + b + c + d.
Площадь — Площадь трапеций
До сих пор мы имели дело с вариациями одной и той же формулы площади A = bh . Мы изменили его на A = lw для прямоугольников и даже A = s 2 для квадратов, но по сути это одно и то же. Сколько раз можно умножить два числа вместе?
Пришло время сходить с ума. Нет, не супер причудливый, но много причудливого. Например, иметь две базы — не две головы — вместо одной.
Мы говорим не о чем ином, как о трапециях , которые очень легко найти. Пока только две из четырех ее сторон параллельны друг другу, мы получили трапецию. Они даже не обязательно должны быть одинаковой длины, что означает, что другие стороны могут делать все, что захотят, в значительной степени. Ничего похожего на параллелограммы или прямоугольники.
Мы говорили вам. Причудливый. На самом деле настолько причудливые, что мы должны называть их фриказоидами.
Они все равно выглядят по-разному. Даже если бы мы могли использовать одно уравнение для расчета площади для всех из них, с чего бы мы начали? Это как пытаться попасть из Небраски в страну Оз. (Возможно, это не лучший пример. Объезд через Канзас и мы в золоте.)
Возьмем общую характеристику всех трапеций: параллельные стороны. Мы знаем, что две параллельные линии всегда будут находиться на одном и том же расстоянии друг от друга, поэтому давайте назовем это расстояние высота . Ради согласованности мы будем использовать h для высоты… снова.
Мы знаем, что две параллельные стороны не будут иметь одинаковую длину, потому что тогда у нас будет параллелограмм. Итак, мы назовем эти две стороны основаниями , b 1 и b 2 . (Иногда вы увидите B и b вместо b 1 и b 2 . Это просто разные способы различения двух оснований.
) Наша формула площади для любой трапеции с высотой h and bases b 1 and b 2 is:
A = ½( b 1 + b 2 ) h
Thankfully, we можно игнорировать шаткие стороны, которые не параллельны друг другу.
Пример задачи
Если основания трапеции имеют длину 4 и 5, а высоту 2, какова площадь трапеции?
Используя уравнение площади трапеции, все, что нам нужно сделать, это подставить длины оснований и высоты.
A = ½ ( B 1 + B 2 ) H
A = ½ (4 + 5) × 2
A = ½ (4 5) × 2
A = ½ (4 5) × 2
1 A = ½ (4 5) × 2
1. A = ½ (4 5) × 2
A = ½ (4 5) × 2
A = ½ (4 5) × 2
A = ½ (4 5) × 2
A 9027 A = 9 единиц 2
Пример задачи
Найдите высоту трапеции, имеющей площадь 7 единиц 2 и основания 7 единиц и длину 21 единицу.
Мы можем использовать ту же формулу площади для трапеции. На этот раз вместо решения A мы можем найти высоту 9.0271 ч . Замените 21 единицу на b 1 , 7 единиц на b 2 и 7 единиц 2 на A . Вы знаете, что делать.
a = ½ ( B 1 + B 2 ) H
7 = ½ (21 + 7) H
7 = ½ (21 + 7) H
7 = ½ (21 + 7) H
7 = ½ (21 + 7). h
Высота трапеции 0,5 ед.
Какими бы причудливыми ни были трапеции, вы, наверное, уже знаете, что они бывают разных типов. Равнобедренные трапеции пытаются стать нормальными, делая две непараллельные стороны одинаковой длины. Прямоугольные трапеции имеют стороны, образующие прямые углы с обоими основаниями.
Знание этих специфических типов трапеций не меняет формулы расчета площади. Это по-прежнему A = ½( b 1 + b 2 ) h .
С другой стороны, это может быть полезно, если у вас нет b 1 , b 2 и h переданы вам сразу.
Пример задачи
Каковы площадь и периметр этой трапеции?
Это прямоугольная трапеция, поэтому мы можем рассматривать ее как прямоугольник и прямоугольный треугольник, соединенные вместе. Гипотенуза треугольника равна 5, и мы можем найти один из катетов, вычитая малое основание из большого основания, что дает нам длину 3.
Мы знаем гипотенузу и один из катетов прямоугольного треугольника. . Можете ли вы сказать: «Теорема Пифагора»? Мы уверены, что можем. Просто замените a with 3, b with h , and c with 5.
a 2 + b 2 = c 2
3 2 + h 2 = 5 2
h 2 = 16
h = 4 ед. быть легким ветерком.