Как составить алгебраическое выражение

Математические термины

Алгебра — это наука, изучающая действия над числовыми и буквенными величинами. Кроме того, она занимается решениями уравнений и связанными с ними действиями. Под буквенными величинами обычно понимают конкретные или переменные числовые значения. Входящие в состав записи буквы могут иметь различные числовые величины. Например, в формуле S * 4 + 12 символом S может быть заменена известная или неизвестная величина или даже целое выражение.

Математики под алгебраическим выражением понимают запись, составленную со смыслом, состоящую из букв и цифр, обозначающих числа. При этом она может содержать скобки и знаки арифметических действий. Исходя из этого простейшего определения можно утверждать, что формулы 2 * k — s, 4 * (y — 3/2), 0,89 * a — g * (9a + 4b), a² и (29p — 56) / log (a + c) являются примерами алгебраических выражений. Так как буквы в записях обозначают различные числа, то их считают переменными, а само уравнение — выражением с переменной.

Если же значение переменной известно и его можно подставить на место буквенного обозначения, то результат, полученный после выполнения указанных в уравнении действий, называется ответом алгебраического выражения. Но если число, подставляемое вместо буквы, приводит к бессмысленности записи, то оно считается недопустимым. Из этого можно сделать вывод, что одна и та же алгебраическая запись при различных величинах букв может иметь отличные значения.

На практике приходится сталкиваться с довольно сложными и громоздкими алгебраическими выражениями, поэтому над ними приходится выполнять ряд действий, правил, законов или использовать свойства для упрощения записи.

Кроме определений здесь применяется понятие «тождественность». Под ним понимают два выражения, для которых при любых значениях переменных, входящих в их состав, будет справедливо их равенство, например, 56* (x+с) = 56 * x + 56 * с.

Эти два выражения можно заменить друг другом или, выражаясь математическим языком, — «выполнить тождественное преобразование».

Виды выражений

В школе на уроках алгебры приходится сталкиваться с различными видами выражений. Обычно они состоят из нескольких членов. В математике существует группирование, объединяющее сходные элементы. Обучение понятиям начинают в седьмом классе с того, что приводят следующие определения:

1. Одночленом называют числа или переменные, а также степени, имеющие натуральные показатели. Таким образом, одночленами могут быть просто числа или составленные из них произведения, например, 3, 5 * x, 5b / (6 * b).
2. Многочленом считается запись, состоящая из суммы одночленов, например, 2x+4, 16b / 23 + b.

Многочлен всегда подразумевает выполнение действий. При описании понятия используют и такие термины, как коэффициент, член, степень. Во время работы с одночленами применяют тождественное их приведение к стандартному виду.

В нём выражение представляют как произведение числового множителя и натуральной степени разных переменных, например, 2 * a, −x * 3.

Выражения в алгебре могут быть следующих видов:

1. Рациональные (алгебраические) дроби. Это запись, в которой числитель и знаменатель представляют в виде многочлена. Следует понимать, что любая обыкновенная дробь будет алгебраической.
2. Целые рациональные. Математические записи, в которых не содержится деление на уравнения с переменными или выражения с отрицательной степенью.
3. Степенные. Формулы, в состав которых входит одночлен или многочлен, возводимый в степень.
4. Иррациональные с корнями. Записи уравнений, содержащие подкоренные члены.
5. Тригонометрические. К ним относят уравнения, связанные с прямыми и обратными тригонометрическими функциями.
6. Логарифмические выражения. Формулы, которые содержат логарифмы.

Все указанные виды относят к простым, но с 7 класса алгебраические выражения будут усложняться. Сложный вид записи обычно состоит из многочлена, включающего в себя извлечение корня, логарифмы и возведение в степень, например, ln (x² — 1) * tg ((x + p) / cos x). И хоть среди них попадаются перечисленные типы, их относят к общему виду.

Вычисление сложных выражений подразумевает выполнение преобразований, которые позволят проще решить задание и найти правильный ответ.

Алгебраические действия

Решая задачу, приходится выполнять те или иные преобразования. Чаще всего сложность задания определяется громоздкостью и объёмом соответствующих преобразований, поэтому в школе на уроках элементарной математики часто попадаются задачи на упрощения.

Основу всех алгебраических действий составляют три закона. Это правила, касающиеся сложения и умножения: переставное, соединительное и распределительное. Но наряду с ними применяют и формулы сокращённого умножения.

На начальном этапе обучения рекомендуется даже записать данные правила отдельно на листик и пользоваться им, пока применение законов не дойдёт до автоматизма. Вот некоторые практические рекомендации, решаться с которыми примеры будут намного легче:

1. Выполнять вычисления и преобразования нужно последовательно, шаг за шагом, на каждом этапе максимально упрощая полученный результат.
2. Важным элементом преобразований, необходимым для решения различных задач с любых разделов, является умение раскладывать на множители те или иные одночлены или многочлены. Как правило, результат достигается благодаря удачной группировке слагаемых.
3. При возможности всегда нужно использовать правило замены переменных, то есть вводить условные равенства. Переход к новым обозначениям и заменам — это нужный приём, с помощью которого решают не только различные задачи элементарной, но и высшей математики.
4. Сильно упростить выражение позволяет приведение подобных членов. Если слагаемые имеют одинаковые буквенные части, то их числовые коэффициенты прилагаются, а буквенная часть сохраняется: 9* a²b — 3 * a²b — 4a²b = (9 — 3 — 4) * a²b = 2 * a²b.
5. Используя правила распределительного закона, можно осуществить вынесение множителя за скобки и их раскрытие. В этом также помогают теоремы действий со степенями: 4ax²y + 3 * а²bxy² — 2 * abx² = ax * (4 * xy + 3 * aby² — 2 * bx²).
6. Во время преобразований нужно помнить о знаках. Так, если множитель перед скобками имеет отрицательный знак, то при их раскрытии знак изменится у всех слагаемых на противоположный.

Не стоит забывать и о такой операции, как деление многочлена. Для этого используют метод столбика. Заключается он в размещении слагаемых многочлена в порядке убывания степени переменной и разделения первого слагаемого числителя многочлена на первое слагаемое знаменателя.

Затем результат умножают на делитель и отнимают ответ от делимого.

Применение преобразований

Алгебраические выражения, показывающие, что одна величина больше другой или равна ей, называют уравнениями и равенствами. При этом их используют для составления формул, то есть для записи, выражающей зависимость между двумя или несколькими переменными. Это удобно, так как преобразования позволяют привести формулу к простому для запоминания виду.

При решении примеров важно знать все существующие методы. Какой из них применять, конкретно указать нельзя, всё зависит от личных предпочтений и опыта решения подобных заданий. Например, пусть нужно упростить сложное выражение (a³ (b — c) + b³ (c — a) + c³ (a — b)) / (a² (b — c) + b² (c — a) + c² (a — b)).

Сначала можно попробовать разложить на множители делитель и делимое. Один из вариантов преобразования числителя следующий:

a³ (b — c) + b³ (c — a) + c³ (a — b) = a³b — b³c — a³c + b³c + c³(a — b) = ab (a^{2 —} b²) = ab (a² — b²) — c (a³ — b³) + c³(a — b) = (a — b) (ab (a + b) — c (a² + ab + b²) + c³ = (a — b) (a²b — a²c + ab² — abc + c³ — cb²) = (a — b) (a² (b — c) + ab (b — c) — c (b² — c²) = (a — b) (b — c) (a² — c² + ab — cb) = (a — b) (b — c) (a — c) (a + b + c).

По аналогии раскладывая знаменатель, можно прийти к результату: (a — b) (b — c) (a — c). В итоге получится равенство (a³ (b — c) + b³ (c — a) + c³ (a — b)) / (a² (b — c) + b² (c — a) + c² (a — b)) = ((a — b) (b — c) (a — c) (a + b + c)) / ((a — b)(b — c)(a — c)) = a + b + c.

В числителе возможно выделить множитель (a — b) на том основании, что делимое равно нулю, когда a совпадает с b. Обычно в двух взаимно обратных операциях выполнение одной сложнее, чем другой. Это касается, в частности, выполнения умножения алгебраических выражений и разложения на множители или возведения в степень с извлечением корня. Например, легко увидеть, что (5 + 3 √2)² = 43 + 30 √2, но значительно труднее прочитать это равенство справа налево.

Следует помнить, что когда при решении задачи встречается выражение подкоренного вида √с + n * √k или √a + b√k, то необходимо попытаться добыть соответствующий корень. Если же это невозможно, то нужно воспользоваться подбором.

Если нужно упростить выражение √11 + 6 √ 2, то его можно представить как c + b √2. Следовательно, справедливо будет следующее равенство: 11 + 6 √2 = с² + 2b² + 2 cb √2. Поиск целых (рациональных) c и b приведёт к решению системы: a² + 2b² = 11, ab = 3.

При этом подобрать нужную пару целых легко: a = 3, b = 1, то есть можно записать равенство как √11 + 6√ 2 = 3 + √2.

Algebraic expression started in the 9th century. In the beginning, it was more in statement form and not mathematical at all. For instance, algebraic equations used to be written as “5 times the thing added with 3 gives 18, which is 5x + 3 = 18. This type of equation which was not mathematical was Babylonian algebra. Algebra evolved with time and with the different forms provided. It started with Egyptian algebra, then came Babylonian algebra, then came Greek geometrical algebra, moved to diophantine algebra, followed by Hindu algebra, then came Arabic algebra, and followed by abstract algebra. Today, the easiest and most convenient form of algebra is taught in classes for better understanding.

What are Algebraic Expressions?

Algebraic expressions are the expressions obtained from the combination of variables, constants, and mathematical operations like addition, subtraction, multiplication, division, and so on. An algebraic expression is made up of terms, there can be one or more than one terms present in the equation. Let’s learn about the basic terms used in algebraic expressions.

Algebraic Terms, Constants, Variables, and Coefficients

In the algebraic expression, fixed numerals are called constants. Constants do not have any variables attached to them. For example, 3x – 1 has a constant -1 to it. Variables are the unknown values that are present in the algebraic expression. For instance, 4y + 5z has y and z as variables. Coefficients are the fixed values (real numbers) attached to the variables. They are multiplied by the variables. For example, 5x² + 3 has 5 as the coefficient of x². A term can be a constant, a variable, or a combination of both. Each term is separated by either addition or subtraction. For example, 3x + 5, 3x, and 5 are the terms.

Types of Algebraic Expressions

There are various types of algebraic expressions based on the number of terms.

Type of Algebraic Expression	Definition	Examples
Monomial	A monomial algebraic expression is an algebraic expression that has only one term.	2xy, 5y3, 7a, 2b, etc
Binomial	A binomial algebraic expression is an algebraic expression that has two unlike terms or two monomials.	6x + 8y, 3a2 + 2ab, etc.
Trinomial	A trinomial algebraic expression is an algebraic expression that has three unlike terms or three monomials.	x + y + z, 11x2 – 5y + z, etc
Polynomial	A polynomial algebraic expression is an algebraic expression that has two or more terms with non-negative integral exponents of a variable.	3x + 4y + 5z, ax3 + bx2 + cx + d, etc
Multinomial	A multinomial algebraic expression is an algebraic expression that has one or more than one term. Here, the exponent of variable can be negative also.	x + y-2, 5x2 + 6z-1

Simplifying Algebraic Expressions

Simplifying algebraic expressions is easy and very basic. First, understand what are like and unlike terms. Like terms have the same sign and unlike terms have opposite signs. To simplify the given algebraic expression, first, find out the terms having the same power. Then, if the terms are like terms, add them; if they are unlike terms, find the difference between the terms. The most simplified form of an algebraic expression is the one where no same power terms are not repeated. 

For instance, lets simplify 4x⁵ + 3x³ – 8x² + 67 – 4x² + 6x³, the same powers that are repeated are cubic and square, upon combining them together, the expression becomes, 4x⁵ + (3x³ + 6x³) – (8x² – 4x²) + 67. Now, simplifying the expression, the final answer obtained is 4x⁵ + 9x³ – 12x² + 67. This term does not have any terms repeated that have the same power.

Addition of Algebraic Expressions

When an addition operation is performed on two algebraic expressions, like terms are added with like terms only, i.e., coefficients of the like terms are added.

Example: Add (25x + 34y + 14z) and (9x − 16y + 6z + 17).

Solution:

(25x + 34y + 14z) + (9x − 16y + 6z + 17)

By writing like terms together, we get

= (25x + 9x) + (34y − 16y) + (14z + 6z) + 17

By adding like terms, we get

= 34x + 18y + 20z + 17.

Hence, (25x + 34y + 14z) + (9x − 16y + 6z + 17) = 34x + 18y + 20z + 17.

Subtraction of Algebraic Expressions

To subtract an algebraic expression from another, we have to add the additive inverse of the second expression to the first expression.

Example: Subtract (5b² + 6b + from (3b² − 5b).

Solution:

(5b² + 6b + − (3b² − 5b)

= (5b² + 6b + + (−3b² + 5b)

= (5b² − 3b²) + (6b + 5b) + 8 = 2b² + 11b + 8

Multiplication of Algebraic Expressions

When a multiplication operation is performed on two algebraic expressions, we have to multiply every term of the first expression with every term of the second expression and then combine all the products.

Example: Multiply (3x + 2y) with (4x + 6y − 8z)

Solution:

(3x + 2y)(4x + 6y − 8z) = 3x(4x) + 3x(6y) − 3x(8z) + 2y(4x) + 2y(6y) − 2y(8z)

= 12x² + 18xy − 24xz + 8xy + 12y² − 16yz

= 12x² + 12y² + 26xy − 16yz − 24xz

Division of Algebraic Expressions

When we have to divide an algebraic expression from another, we can factorize both the numerator and the denominator, then cancel all the possible terms, and simplify the rest, or we can use the long division method when we cannot factorize the algebraic expressions.

Example: Solve: (x² + 5x + 6)/(x + 2)

Solution:

= (x² + 5x + 6)/(x + 2)

(x² + 5x + 6) = (x + 2) (x + 3)

= [(x + 2) (x + 3)]/(x + 2)

= (x + 3)

Algebraic Formulas

The general algebraic formulas we use for solving the expressions or equations are:

1. (x + a) (x + b) = x² + x(a + b) + ab
2. (a + b)² = a² + 2ab + b²
3. (a – b)² = a² – 2ab + b²
4. (a + b)² + (a – b)² = 2 (a² + b²)
5. (a + b)² – (a – b)² = 4ab
6. a² – b² = (a – b)(a + b)
7. (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
8. (a + b)³ = a³ + b³ + 3ab(a + b)
9. (a – b)³ = a³ – b³ – 3ab(a – b) 
10. a³ – b³ = (a – b)(a² + ab + b²)
11. a³ + b³ = (a + b)(a² – ab + b²)
12. a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – ab – bc – ca))

Solved Examples on Algebraic Expressions

Problem 1: Find out the constant from the following algebraic expressions,

1. x³ + 4x² – 6
2. 9 + y⁵

Answer: 

Constants are the terms that do not have any variable attached to them, therefore, in the first case, -6 is the constant, and in the second case, 9 is the constant.

Problem 2: Find out the number of terms present in the following expressions,

1. 4x² + 7x – 8
2. 5y⁷ – 12

Answer:

Terms are separated by each other either by addition or subtraction sign. Therefore, in the first case, there are 3 terms and in the second case, there are 2 terms.

Problem 3: Simplify the algebraic term, z⁵ + z³ – y⁶ + 7z⁵ – 8y⁶ + 34 + 10z³

Solution:

In the expression, there are terms with the same power and same variable that are repeated, first bring them together,

(z⁵ + 7z⁵) + (z³ + 10z³) – (y⁶ – 8y⁶) + 34.

Now, simplify the expression,

8z⁵ + 11z³ – 9y⁶ + 34.

Problem 4: Add (13x² + 11), ( – 25x² + 26x + 42) and (–33x – 29).

Solution:

(13x² + 11) + ( – 25x² + 26x + 42) + (–33x – 29)

= 13x² – 25x² + 26x – 33x + 11 + 42 – 29

Now, add like terms

= –12x² – 7x + 24

Hence, (13x² + 11) + ( – 25x² + 26x + 42) + (–33x – 29) = –12x² – 7x + 24.

Problem 5: Solve (5x + 4y + 6z)² + (3y – 7x)².

Solution:

Given,

(5x + 4y + 6z)² + (3y – 7x)²

From algebraic formulae, we have

(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

(a – b)² = a² – 2ab + b²

= (5x)² + (4y)² + (6z)² + 2(5x)(4y) + 2(4y)(6z) + 2(6z)(5x) + [(3y)² – 2(3y)(7x) + (7x)²]

= 25x² + 16y² + 36z² + 40xy + 48yz + 60zx +9y2 – 42xy + 49x²

Now, combine the like terms.

= 74x² + 25y² + 36z² – 2xy + 48yz + 60zx

Hence, (5x + 4y + 6z)² + (3y – 7x)² = 74x² + 25y² + 36z² – 2xy + 48yz + 60zx.

FAQs on Algebraic Expressions

Question 1: What are the types of algebraic expressions?

Answer:

The three main types of algebraic expressions are

• Monomial: A monomial is an expression that has only one non-zero term. 2xy, 5y3, 7a, 2b, etc are some examples of monomials.
• Binomial: A binomial is an expression that has two non-zero terms. For example, 2a + 3 has two monomials 2a and 3 and hence it is a binomial.
• Polynomial: A polynomial is an expression that has more than two non-zero, unlike terms. For example, x-4y+ 8z has three monomials x, 4y, and z, hence it is a polynomial.

Question 2: Are all algebraic expressions polynomials?

Answer:

Not all algebraic expressions are polynomials but all polynomials are algebraic expressions i.e. there exist some algebraic expressions that are not polynomials. Example: πx + 1 is an algebraic expression but not a polynomial.

Question 3: How are algebraic expressions defined?

Answer:

An algebraic expression is an idea of representing numbers using letters such as x, y, z, etc. without specifying their actual values. It is a mathematical statement that we get when arithmetic operations such as addition, subtraction, multiplication, or division are operated upon on variables and constants. In simple terms, an algebraic expression is a mathematical statement where variables have been combined using fundamental arithmetic operations.

Example: Ram’s age is three times the age of Akash, and their total age is 48. Express it as an algebraic equation.

Solution: Let the age of Akash be x. Then Ram’s age is 3x

3x + x = 48

4x = 48

Question 4: What are variables in an algebraic expression?

Answer:

In an algebraic expression, a variable is a symbol that doesn’t have a fixed value. For example, in the equation, 3x + 7 = 0, x is the variable that can take any value. In mathematics, a, b, m, n, x, y, z, etc are some examples of variables.

Часть I

Выражения, в которых наряду с буквами могут быть использованы числа, знаки арифметических действий и скобки, называются алгебраическими выражениями.

Примеры алгебраических выражений:

2m -n;     3·(2a + b);     0,24x;     0,3a -b · (4a + 2b);     a²– 2ab;

Так как букву в алгебраическом выражении можно заменить какими то различными числами, то букву называют переменной, а само алгебраическое выражение — выражением с переменной.

Часть II

Если в алгебраическом выражении буквы (переменные) заменить их значениями и выполнить указанные действия, то полученное в результате число называется значением алгебраического выражения.

Примеры. Найти значение выражения:

1) a + 2b -c при a = -2; b = 10; c = -3,5.

2) |x| + |y| -|z| при x = -8; y = -5; z = 6.

Решение.

1) a + 2b -c при a = -2; b = 10; c = -3,5. Вместо переменных подставим их значения. Получим:

— 2+ 2 · 10- (-3,5) = -2 + 20 +3,5 = 18 + 3,5 = 21,5.

2) |x| + |y| -|z|  при x = -8; y = -5; z = 6. Подставляем указанные значения. Помним, что модуль отрицательного числа равен противоположному ему числу, а модуль положительного числа равен самому этому числу. Получаем:

|-8| + |-5| -|6| = 8 + 5 -6 = 7.

Часть III

Значения буквы (переменной), при которых алгебраическое выражение имеет смысл, называют допустимыми значениями буквы (переменной).

Примеры. При каких значениях переменной выражение не имеет смысла?

Решение. Мы знаем, что на нуль делить нельзя, поэтому, каждое из данных выражений не будет иметь смысла при том значении буквы (переменной), которая обращает знаменатель дроби в нуль!

В примере 1) это значение а = 0. Действительно, если вместо а подставить 0, то нужно будет число 6 делить на 0, а этого делать нельзя. Ответ: выражение 1) не имеет смысла при а = 0.

В примере 2) знаменатель х — 4 = 0 при х = 4, следовательно, это значение х = 4 и нельзя брать. Ответ: выражение 2) не имеет смысла при х = 4.

В примере 3) знаменатель х + 2 = 0 при х = -2. Ответ: выражение 3) не имеет смысла при х = -2.

В примере 4) знаменатель 5 -|x| = 0 при  |x| = 5. А так как |5| = 5 и |-5| = 5, то нельзя брать х = 5 и х = -5. Ответ: выражение 4) не имеет смысла при х = -5 и при х = 5.

Часть IV

Два выражения называются тождественно равными, если при любых допустимых значениях переменных соответственные значения этих выражений равны.

Пример: 5 (a – b) и 5a – 5b тожественно равны, так как равенство 5 (a – b) = 5a – 5b будет верным при любых значениях a и b. Равенство 5 (a – b) = 5a – 5b есть тождество.

Тождество

Тождество – это равенство, справедливое при всех допустимых значениях входящих в него переменных. Примерами уже известных вам тождеств являются, например,  свойства сложения и умножения, распределительное свойство.

Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. Тождественные преобразования выражений с переменными выполняются на основе свойств действий над числами.

Примеры.

a) преобразуйте выражение в тождественно равное, используя распределительное свойство умножения:

1) 10·(1,2х + 2,3у);    2) 1,5·(a -2b + 4c);  3) a·(6m -2n + k).

Решение. Вспомним распределительное свойство (закон) умножения:

1) 10·(1,2х + 2,3у) = 10 · 1,2х + 10 · 2,3у = 12х + 23у.

2) 1,5·(a -2b + 4c) = 1,5а -3b + 6c.

3) a·(6m -2n + k) = 6am -2an +ak.

б) преобразуйте выражение в тождественно равное, используя переместительное и сочетательное  свойства (законы) сложения:

4) х + 4,5 +2х + 6,5;      5) (3а + 2,1) + 7,8;      6) 5,4с -3 -2,5 -2,3с.

Решение. Применим законы (свойства) сложения:

4) х + 4,5 +2х + 6,5 = (х + 2х) + (4,5 + 6,5) = 3х + 11.

5) (3а + 2,1) + 7,8 = 3а + (2,1 + 7,8) = 3а + 9,9.

6) 6) 5,4с -3 -2,5 -2,3с = (5,4с -2,3с) + (-3 -2,5) = 3,1с -5,5.

в) преобразуйте выражение в тождественно равное, используя переместительное и сочетательное  свойства (законы) умножения:

7) 4 · х · (-2,5);       -3,5 · 2у · (-1);      9) 3а · (-3) · 2с.

Решение. Применим законы (свойства) умножения:

7) 4 · х · (-2,5) = -4 · 2,5 · х = -10х.

8 ) -3,5 · 2у · (-1) = 7у.

9) 3а · (-3) · 2с = -18ас.

Если алгебраическое выражение дано в виде сократимой дроби, то пользуясь правилом сокращения дроби его можно упростить, т.е. заменить тождественно равным ему более простым выражением.

Решение. Сократить дробь — это значит разделить ее числитель и знаменатель на одно и то же число (выражение), отличное от нуля. Дробь 10) сократим на 3b; дробь 11) сократим на а и дробь 12) сократим на 7n. Получаем:

Алгебраические выражения применяют для составления формул.

Формула – это алгебраическое выражение, записанное в виде равенства и выражающее зависимость между двумя или несколькими переменными. Пример: известная вам формула пути s=v·t  (s — пройденный путь, v — скорость, t — время). Вспомните, какие еще формулы вы знаете.

Алгебраические выражения составляются из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень и извлечения корня и с помощью скобок.

Рассмотрим некоторые примеры алгебраических выражений:

2a²b – 3ab²(a + b)

a + b + c/5

(1/a + 1/b – c/3)³.

Существует несколько видов алгебраических выражений.

Целым называется такое алгебраическое выражение, которое не содержит деления на переменные и извлечения корня из переменных (в том числе, возведения в степень с дробным показателем).

2a²b – 3ab²(a + b) является целым алгебраическим выражением.

(1/a + 1/b – c/3)³ не является целым алгебраическим выражением, т.к. содержит деление на переменную.

Дробным называется такое алгебраическое выражение, которое составлено из чисел и переменных с помощью действий сложения, вычитания, умножения, возведения в степень с натуральным показателем и деления.

(1/a + 1/b – c/3)³ является дробным алгебраическим выражением.

Рациональными алгебраическими выражениями называются целые и дробные выражения.

Значит, и 2a²b – 3ab²(a + b), и (1/a + 1/b – c/3)³ – это рациональные алгебраические выражения.

Иррациональное алгебраическое выражение – это такое алгебраическое выражение, в котором используются извлечение корня из переменных (или возведение переменных в дробную степень).

a ^2/3 – b ^2/3 – иррациональное алгебраическое выражение.

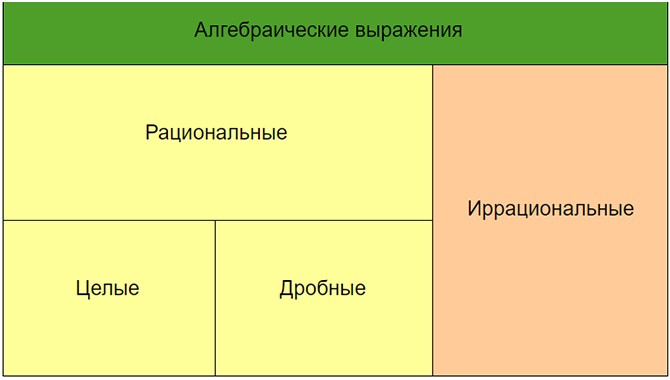
Иными словами, все алгебраические выражения делятся на две большие группы: рациональные и иррациональные алгебраические выражения. Рациональные выражения, в свою очередь, делятся на целые и дробные.

Допустимым значением переменных называется такое значение переменных, при котором алгебраическое выражение имеет смысл. Множество всех допустимых значений переменной – это область определения алгебраического выражения.

Целые выражения имеют смысл при любых значениях его переменных. Например, 2a²b – 3ab²(a + b) имеет смысл и при a = 0, b = 1, и при a = 3, b = 6 и др.

Предположим, что a = 0, b = 1, и попробуем найти решение выражения

2a²b – 3ab²(a + b).

Если a = 0, b = 1, то 2 ∙ 0² ∙ 1 – 3 ∙ 0 ∙ 1² ∙ (0 + 1) = 0 ∙ 0 = 0.

Значит, при a = 0, b = 1 выражение равно 0.

Дробные выражения имеют смысл только в том случае, если значения не обращают переменные в нуль: вспомним наше «золотое правило» – на нуль делить нельзя.

Выражение (1/a + 1/b – c/3)³ имеет смысл при a и b не равных нулю (а ≠ 0, b ≠ 0). В противном случае мы получим деление на нуль.

Иррациональное выражение не будет иметь смысл при значениях переменных, которые обращают в отрицательное число выражение, содержащееся под знаком корня четной степени или под знаком возведения в дробную степень.

Выражение a ^2/3 – b ^2/3 имеет смысл при a ≥ 0 и b ≥ 0. В противном случае мы столкнемся с возведением в дробную степень отрицательного числа.

Значением алгебраического выражения называется числовое выражение, получившееся в результате того, что переменным придали допустимые значения.

Найдем значение алгебраического выражения

a + b + c/5 при a = 6, b = 3, c = 5.

1. Выражение a + b + c/5 является целым алгебраическим выражением → все значения являются допустимыми.

2. Подставим числовые значения переменных и получим:

6 + 3 + 5/5 = 9 + 1 = 10.

Итак, ответ: 10.

Тождеством называют равенство, которое верно при всех допустимых значениях входящих в него переменных.

Тождественно равными называются выражения, соответственные значения которых совпадают при всех допустимых значениях переменных. Так, выражения x⁵ и x² ∙ x³, a + b + c и b + c + a являются тождественно равными между собой.

Понятие тождественно равных выражений приводит нас к еще одному важному понятию – тождественное преобразование выражений.

Тождественным преобразованием выражения называется замена одного выражения другим, тождественно равным ему.

Это значит, выражение x⁵ можно тождественно преобразовать в выражение x² ∙ x³.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Алгебраическое выражение – это конечная комбинация символов, подчиняющаяся определенным правилам. Если эти правила нарушаются, то выражение нельзя считать алгебраическим.

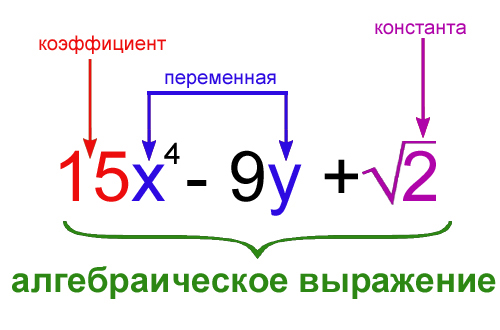
Состав алгебраического выражения

Алгебраическое выражение строится из констант и переменных, которые соединены друг с другом алгебраическими операциями.

Константа – это величина, имеющая постоянное значение. Традиционно для обозначения констант используются первые буквы латинского алфавита (a, b, c и т. д.).

Переменная – это величина, которая может принимать разные значения. В алгебраических выражениях переменные представляются некими символами (обычно буквами). Если вместо переменной подставить в выражение число, то можно вычислить численное значение алгебраического выражения.

Под алгебраической операцией, когда речь идет об алгебраическом выражении, понимаются следующие операции:

• сложение;
• вычитание;
• умножение;
• деление;
• возведение в степень, причем показатель степени обязательно должен быть целым числом;
• извлечение корня, причем показатель корня должен быть обязательно целым числом.

Примеры алгебраических выражений:

Данное определение алгебраического выражения приводит к интересным случаям, когда одно и то же выражение может считаться алгебраическим относительно одной входящей в него переменной, но неалгебраическим относительно другой переменной. Вот пример такого выражения:

Это выражение является алгебраическим относительно переменной х и неалгебраическим относительно переменной у.

Следующая иллюстрация показывает общую схему алгебраического выражения:

Следует подчеркнуть, что нужно различать алгебраическое выражение и математическую формулу:

• математическая формула – это высказывание, записанное специальными символами;
• алгебраическое выражение – это математический объект, соответствующий определенным требованиям.

Поясним на примере:

В состав алгебраического выражения входят алгебраические члены. Члены алгебраического выражения.

Алгебраический член – это число или переменная, или числа и переменные, связанные операцией умножения или деления, или возведения в степень. Выражение может состоять только из одного члена, либо из нескольких членов, связанных друг с другом операциями сложения или вычитания.

Пример в таблице:

Чем отличаются алгебраические и арифметические выражения. Понятие алгебраического выражения шире, чем понятие арифметического выражения. Арифметическое выражение может включать в себя только константы, скобки и знаки арифметических операций.

Порядок действий в алгебраическом выражении

Порядок выполнения вычислений полностью однозначно определяется расстановкой скобок. При этом у операций нет приоритета: сначала выполняется действие в самых вложенных скобках. Таким образом, никаких разночтений возникнуть не может.

Но на практике часто по умолчанию используется приоритет операций, позволяющий существенно сократить количество скобок в записях. В порядке убывания приоритета операции располагаются следующим образом:

• возведение в степень (наивысший приоритет – выполняются в первую очередь);
• смена знака (унарный минус);
• умножение, деление – обладают одинаковым приоритетом;
• сложение и вычитание.

Операции с одинаковым приоритетом выполняются слева направо.

Таким образом, если мы хотим вычислить значение выражения 9/3*(2+3), то порядок действий должен быть следующим:

1. 2 + 3 = 5;
2. 9 / 3 = 3;
3. 3 * 5 = 15.

Но если дополнительно расставить скобки (9/3) * (2+3) вероятность допустить ошибку существенно снизится. Поэтому лучше не пренебрегать «лишними» скобками в записях громоздких или ненаглядных выражений.

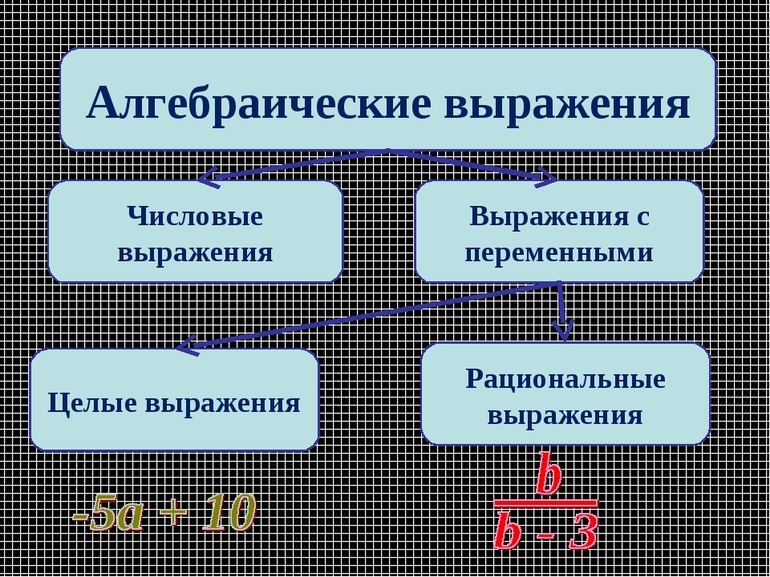
Виды алгебраических выражений

Алгебраические выражения подразделяются на следующие виды:

Пояснение к схеме:

• Целые алгебраические выражения: к переменным применяются только операции сложения, вычитания, умножения и возведения в целую степень, т. е. нет деления на переменную (но деление на константу может присутствовать) и нет извлечения корня из переменной;
• Дробные алгебраические выражения: обязательно содержат деление на переменную в целой степени;
• Рациональные алгебраические выражения: объединяют в себе целые и дробные выражения;
• Иррациональные (радикальные) алгебраические выражения: обязательно содержат извлечение корня из переменной.

Видео по теме:

Как разложить на множители квадратный трехчлен читайте в нашей статье.