Как составить алгоритм нахождения произведения чисел

При вычислении
суммы или произведения ряда чисел
пользуются соответствующими формулами.

ФОРМУЛА
СУММЫ

S_i=S_i-1+x_i

Сумма равна
предыдущей сумме плюс аргумент. Начальная
сумма равна нулю. При нахождении
количества аргумент равен одному.

ФОРМУЛА
ПРОИЗВЕДЕНИЯ

P_i=P_i-1*x_i

Произведение равно
предыдущему произведению, умноженному
на аргумент. Начальное произведение
всегда равно единице.

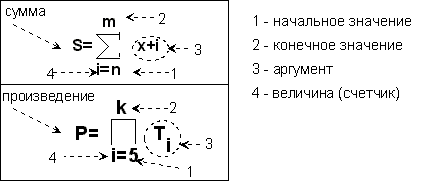
Математически
данные формулы записываются так (рис.
9.14).

Если в аргументе
около имени какой-нибудь величины стоит
индекс
счетчика,
то внутри цикла необходимо поставить
блок ввода этой величины.

Рис.
9. 14. Формулы для вычисления суммы и
произведения

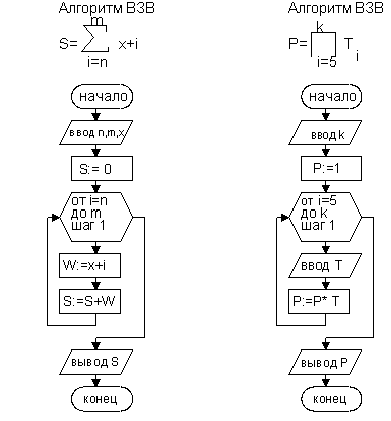
В качестве примера
рассмотрим блок-схемы алгоритмов для
приведенных на рис. 9.14 примеров.

9.3.1.4. Вложенные циклы

Возможны случаи,
когда внутри тела цикла необходимо
повторять некоторую последовательность
операторов, т. е. организовать внутренний
цикл. Такая структура получила название
цикла
в цикле
или вложенных
циклов.
Глубина вложения циклов (то есть
количество вложенных друг в друга
циклов) может быть различной.

Рис.
9. 15. Блок-схемы алгоритмов вычисления
суммы и произведения

При использовании
такой структуры для экономии машинного
времени необходимо выносить из внутреннего
цикла во внешний все операторы, которые
не зависят от параметра внутреннего
цикла.

Рассмотрим два
примера вычисления вложенных циклов.

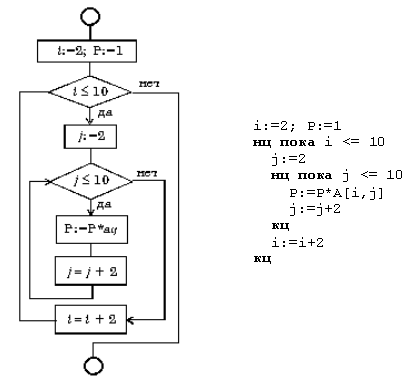
Рис.
9. 16. Вложенный цикл «до»

Вложенный
цикл «до»

Пример

Вычислите
произведение тех элементов заданной
матрицы A(10,10),
которые расположены на пересечении
четных строк и четных столбцов (рис.
9.16).

Вложенный
цикл «пока»

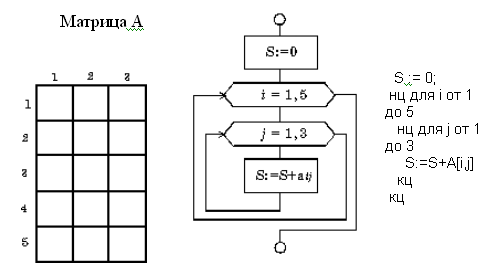
Рис.
9. 17. Вложенный цикл «пока»

Пример

Вычислите сумму
элементов заданной матрицы А(5,3)
– рис. 9.17.

9.4. Языки программирования

9.4.1. Программный способ записи алгоритмов. Уровни языка программирования

При записи алгоритма
в словесной форме, в виде блок-схемы или
на псевдокоде допускается некоторый
произвол при изображении команд. Вместе
с тем такая запись точна настолько, что
позволяет человеку понять суть дела и
исполнить алгоритм.

Однако на практике
в качестве исполнителей алгоритмов
используются специальные автоматы —
компьютеры. Поэтому алгоритм,
предназначенный для исполнения на
компьютере, должен быть записан на
понятном ему языке. И здесь на первый
план выдвигается необходимость точной
записи команд, не оставляющей места для
произвольного толкования их исполнителем.

Следовательно,
язык для
записи алгоритмов должен быть формализован.
Такой язык принято называть языком
программирования,
а запись алгоритма на этом языке —
программой
для компьютера.

В настоящее время
в мире существует несколько сотен
реально используемых языков
программирования. Для каждого есть своя
область применения.

Любой алгоритм
есть последовательность предписаний,
выполнив которые можно за конечное
число шагов перейти от исходных данных
к результату. В зависимости от степени
детализации предписаний обычно
определяется уровень языка программирования
— чем меньше детализация, тем выше
уровень языка.

По этому критерию
можно выделить следующие уровни языков
программирования:

• машинные;

• машинно-оpиентиpованные
  (ассемблеpы);

• машинно-независимые
  (языки высокого уровня).

Машинные языки
и машинно-ориентированные языки —
это языки низкого
уровня,
требующие указания мелких деталей
процесса обработки данных. Языки же
высокого
уровня
имитируют естественные языки, используя
некоторые слова разговорного языка и
общепринятые математические символы.
Эти языки более удобны для человека.

Языки высокого
уровня делятся на:

• Процедурные
  (алгоритмические)
  (Basic, Pascal, C и др.), которые предназначены
  для однозначного описания алгоритмов;
  для решения задачи процедурные языки
  требуют в той или иной форме явно
  записать процедуру ее решения.

• Логические
  (Prolog, Lisp и др.), которые ориентированы
  не на разработку алгоритма решения
  задачи, а на систематическое и
  формализованное описание задачи с тем,
  чтобы решение следовало из составленного
  описания.

• Объектно-ориентированные
  (Object Pascal, C++, Java и др.), в основе которых
  лежит понятие
  объекта, сочетающего в себе данные и
  действия над нами.
  Программа на объектно-ориентированном
  языке, решая некоторую задачу, по сути,
  описывает часть мира, относящуюся к
  этой задаче. Описание действительности
  в форме системы взаимодействующих
  объектов естественнее, чем в форме
  взаимодействующих процедур.

При программировании
на машинном
языке программист может держать под
своим контролем каждую команду и каждую
ячейку памяти, использовать все
возможности имеющихся машинных операций.

Но процесс написания
программы на машинном языке очень
трудоемкий
и утомительный.
Программа получается громоздкой,
труднообозримой, ее трудно отлаживать,
изменять и развивать.

Поэтому в случае,
когда нужно
иметь эффективную программу,
в максимальной степени учитывающую
специфику конкретного компьютера,
вместо машинных языков используют
близкие к ним машинно-ориентированные
языки (ассемблеры)
или языки
высокого уровня.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Разберём чуть более сложную задачу. Итак, вам дана последовательность неотрицательных целых чисел $a_1, dots, a_{n}$. Вычислите

$$
maxlimits_{1 le i neq j le n}a_i cdot a_j , .
$$

Обратите внимание, что $i$ и $j$ должны быть разными, хотя в каких-то случаях можно наблюдать, что $a_i=a_j$.

• Формат ввода: Первая строка содержит целое число $n$. Следующая строка содержит $n$ неотрицательных целых чисел $a_1, dotsc, a_{n}$ (разделены пробелами).
• Формат вывода: Максимальное попарное произведение.
• Ограничения: $2 le n le 2cdot10^5$; $0 le a_1, dots, a_{n} le 2cdot 10^5$.
• Примеры

Пример 1

Ввод	Вывод
3 1 2 3	6

Пример 2

Ввод	Вывод
10 7 5 14 2 8 8 10 1 2 3	140

Наивный подход

Наивный способ решить задачу Максимальное произведение — перебрать все возможные пары вводных элементов $A[1dotsc n]=[a_1,dotsc, a_n]$ и найти пару, которая даёт наибольшее произведение.

MaxPairwiseProductNaive(A[1..n]):
    product = 0
    for i from 1 to n
        for j from 1 to n
            if i != j
                if product < A[i] * A[j]
                    product = A[i] * A[j]
    return product

Этот код можно оптимизировать и сократить следующим образом.

MaxPairwiseProductNaive(A[1..n]):
    product = 0
    for i from 1 to n
        for j from i+1 to n
            product = max(product, A[i] * A[j])
    return product

Реализуйте этот алгоритм, используя ваш любимый язык программирования. Если вы используете C++, Java или Python3, вам могут пригодиться начальные заготовки (для всех задач из книги мы предлагаем стартовые заготовки с использованием этих трёх языков в интерфейсе тестирующей системы).
С другими языками вам понадобится сделать работу с нуля.

Стартовые заготовки решений для C++, Java и Python3 представлены ниже.

C++

#include <iostream>
#include <vector>
#include <algorithm>

int MaxPairwiseProduct(const std::vector<int>& numbers) {
    int max_product = 0;
    int n = numbers.size();

    for (int first = 0; first < n; ++first) {
        for (int second = first + 1; second < n; ++second) {
            max_product = std::max(max_product,
                numbers[first] * numbers[second]);
        }
    }

    return max_product;
}

int main() {
    int n;
    std::cin >> n;
    std::vector<int> numbers(n);
    for (int i = 0; i < n; ++i) {
        std::cin >> numbers[i];
    }

    std::cout << MaxPairwiseProduct(numbers) << "n";
    return 0;
}

Java

import java.util.*;
import java.io.*;

public class MaxPairwiseProduct {
    static int getMaxPairwiseProduct(int[] numbers) {
        int max_product = 0;
        int n = numbers.length;

        for (int first = 0; first < n; ++first) {
            for (int second = first + 1; second < n; ++second) {
                max_product = Math.max(max_product,
                    numbers[first] * numbers[second]);
            }
        }

        return max_product;
    }

    public static void main(String[] args) {
        FastScanner scanner = new FastScanner(System.in);
        int n = scanner.nextInt();
        int[] numbers = new int[n];
        for (int i = 0; i < n; i++) {
            numbers[i] = scanner.nextInt();
        }
        System.out.println(getMaxPairwiseProduct(numbers));
    }

    static class FastScanner {
        BufferedReader br;
        StringTokenizer st;

        FastScanner(InputStream stream) {
            try {
                br = new BufferedReader(new
                    InputStreamReader(stream));
            } catch (Exception e) {
                e.printStackTrace();
            }
        }

        String next() {
            while (st == null || !st.hasMoreTokens()) {
                try {
                    st = new StringTokenizer(br.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return st.nextToken();
        }

        int nextInt() {
            return Integer.parseInt(next());
        }
    }

}

Python

def max_pairwise_product(numbers):
    n = len(numbers)
    max_product = 0
    for first in range(n):
        for second in range(first + 1, n):
            max_product = max(max_product,
                numbers[first] * numbers[second])

    return max_product


if __name__ == '__main__':
    _ = int(input())
    input_numbers = list(map(int, input().split()))
    print(max_pairwise_product(input_numbers))

После проверки вы можете увидеть такое сообщение:

Failed case #4/17: time limit exceeded

Дело в том, что мы проверяем ваше решение на тестовых примерах — это помогает убедиться, что программа работает быстро и без ошибок.
В результате мы, как правило, знаем, какие ошибки вы допустили.
Сообщение выше говорит о том, что предложенная программа превышает ограничение по времени в 4-м тестовом примере из 17.

💡 Остановитесь и подумайте:
Почему решение не укладывается в ограничение по времени?

MaxPairwiseProductNaive выполняет порядка $n^2$ шагов при последовательности длиной $n$.
При максимальном возможном значении $n=2cdot 10^5$ количество шагов будет порядка $4cdot 10^{10}$.
Так как большинство современных компьютеров выполняют около $10^8$–$10^9$ базовых операций в секунду (разумеется, это зависит от компьютера),
выполнение MaxPairwiseProductNaive может занять десятки секунд.
Это превысит временное ограничение задачи.

Нам нужен более быстрый алгоритм!

Быстрый алгоритм

А что если внимательнее рассмотреть более мелкие примеры— скажем, $[5,6,2,7,4]$? Эврика! Достаточно помножить два самых больших элемента массива — $7$ и $6$.

То есть нам достаточно просканировать последовательность лишь дважды. При первом сканировании мы найдем самый большой элемент, затем — второй по величине.

MaxPairwiseProductFast(A[1..n]):
    index_1 = 1
    for i from 2 to n
        if A[i] > A[index_1]
            index_1 = i
    index_2 = 1
    for i from 2 to n
        if A[i] != A[index_1] and A[i] > A[index_1]
            index_1 = i
    return A[index_1] * A[index_2]

Тестирование и отладка

Реализуйте этот алгоритм и протестируйте его на вводе $A=[1,2]$. Как и ожидалось, алгоритм выводит $2$.
Затем проверьте на вводе $A=[2,1]$. На удивление, алгоритм выводит $4$.
Изучив код, вы обнаружите, что после первого цикла $index_1=1$. Далее алгоритм инициализирует $index_2$ значением $1$, и цикл for не обновляет $index_2$.
В результате перед возвратом $index_1=index_2$. Чтобы этого избежать, необходимо изменить псевдокод следующим образом:

MaxPairwiseProductFast(A[1..n]):
    index_1 = 1
    for i from 2 to n
        if A[i] > A[index_1]:
            index_1 = i
    if index_1 = 1
        index_2 = 2
    else:
        index_2 = 1
    for i from 1 to n
        if A[i] != A[index_1] and A[i] > A[index_1]
            index1 = i
    return A[index_1] * A[index_2]

Опробуйте этот код на маленьких наборах данных $[7,4,5,6]$, чтобы убедиться, что он выдает правильные результаты. Затем попробуйте ввод.

2  
100000 90000  

Может оказаться, что программа выдает что-то вроде $410,065,408$ или даже отрицательное число вместо правильного результата — $9,000,000,000$.
Вероятнее всего, это вызвано целочисленным переполнением. Например, на языке C++ такое большое число, как $9,000,000,000$, не умещается в стандартный тип int, который занимает 4 байта на большинстве компьютеров и варьируется от $-2^{31}$ до $2^{31}-1$ при
$$
2^{31}=2,147,483,648 ,.
$$

Соответственно, вместо использования типа int в C++ при вычислении произведения и сохранении результата вам нужно использовать тип int64_t.
Это предотвратит целочисленное переполнение, так как тип int64_t занимает 8 байтов и хранимые значения варьируются от $-2^{63}$ до $2^{63}-1$ при

$$
2^{63}=9,223,372,036,854,775,808 , .
$$

Затем протестируйте вашу программу с большими наборами данных, например, с массивом $A[1 dotsc 2 cdot 10^5]$, где $A[i]=i$ для всех $1 le i le 2 cdot 10^5$.
Это можно сделать двумя способами:

• Создать массив в программе и передать его MaxPairwiseProductFast (чтобы не считывать его из стандартного ввода).
• Создать отдельную программу, которая запишет такой массив в файл dataset.txt. Затем передать этот набор данных вашей программе из консоли:

yourprogram < dataset.txt

Убедитесь, что при обработке данных ваша программа укладывается в ограничение по времени и выдаёт верный результат: $39,999,800,000$.
Теперь вы можете быть уверенным, что ваша программа работает!

Однако система оценки снова ругается:

Failed case #5/17: wrong answer

Но как создать такой тестовый сценарий, который приведет к сбою программы и поможет понять, что с ней не так?

А в чём ошибка?

Вероятно, вас интересует, почему мы не предоставили 5-й набор данных из 17 — тот, который привел к сбою программы?
Причина проста: в реальности вам не будут показывать тестовые примеры.

Даже опытные программисты при решении задач с алгоритмами часто совершают ошибки, которые трудно обнаружить.
Поэтому важно научиться находить баги как можно раньше.
Когда авторы этой книги только начинали программировать, они ошибочно полагали, что почти все их программы правильные.
Сейчас же мы знаем, что при первом запуске наши программы почти никогда не верны.

Когда разработчик уверен в работе своей программы, он зачастую использует всего лишь несколько примеров для тестирования.
Если результаты выглядят приемлемо, он считает свою работу законченной — но это путь к катастрофе.
Если вы хотите убедиться, что ваша программа работает всегда, то советуем тщательно подобрать примеры для тестирования.
Реализация алгоритмов, а также их тестирование и отладка будут бесценным навыком для вашей будущей карьеры программиста.

Стресс-тестирование

Представляем вам стресс-тестирование — технику, которая позволяет генерировать тысячи тестовых сценариев. С её помощью можно найти тот, из-за которого провалилось ваше решение.

Стресс-тестирование состоит из четырёх частей:

• Реализация алгоритма.
• Альтернативная, банальная и медленная, но правильная реализация алгоритма для той же самой задачи.
• Генератор случайных тестов.
• Бесконечный цикл, генерирующий тесты и передающий их обоим вариантам реализации для сравнения результатов. Если результаты разнятся, выводятся оба результата и пример для тестирования, а программа останавливается. В ином случае цикл повторяется.

Стресс-тестирование основано на идее, что две правильных реализации
с каждым тестом должны приводить к одному ответу (при условии, что ответ на задачу уникален).
Однако если одна из реализаций неправильна, должен существовать такой тест, который приводит к разным ответам.
Единственный случай, при котором это не так, — когда в обеих реализациях есть одна и та же ошибка.
Но это маловероятно — если ошибка не где-то в программе ввода/вывода, общей для обоих решений.
Действительно, если одно решение правильно, а другое — нет, то существует сценарий тестирования, при котором они различаются.
Если оба решения неверны, но баги отличаются — скорее всего, есть тест, при котором два решения дают разные результаты.

Продемонстрируем стресс-тестирование MaxPairwiseProductFast,
используя

MaxPairwiseProductNaive в качестве тривиальной реализации:

StressTest(N, M):
    while true:
        n = ... // случайное целое число между 2 и N
        // создать массив A[1..n]
        for i from 1 to n
            A[i] = ... // случайное целое число между 0 и M
        print(A[1..n])
        result_1 = MaxPairwiseProductNaive(A)
        result_2 = MaxPairwiseProductFast(A)
        if result_1 = result_2:
            print("OK")
        else:
            print("Wrong answer:", result_1, result_2)
            return

Представленный выше цикл while сначала генерирует длину вводной последовательности $n$, случайное число между $2$ и $N$.
Оно должно быть не менее $2$: формулировка задачи гласит, что $n ge 2$.
Параметр $N$ должен быть достаточно маленьким, чтобы позволить нам рассмотреть множество тестов, несмотря на то, что наши решения медленные.

Сгенерировав $n$, мы генерируем массив $A$ с $n$ целыми числами от $0$ до $M$ и выводим его, чтобы по ходу бесконечного цикла мы всегда знали,
какой тест проходит сейчас. Это упростит нахождение ошибок в коде для генерации теста. Затем мы вызываем два алгоритма для $A$ и сравниваем результаты.
Если результаты отличаются, мы их печатаем и останавливаемся. В ином случае мы продолжаем цикл while.

Давайте запустим StressTest(10, 100'000) и скрестим пальцы в надежде, что он выдаст Wrong answer.
Для нас это выглядит как-то так (результат может отличаться на вашем компьютере из-за другого генератора случайных чисел).

...  
OK  
67232 68874 69499  
OK  
6132 56210 45236 95361 68380 16906 80495 95298  
OK  
62180 1856 89047 14251 8362 34171 93584 87362 83341 8784  
OK  
21468 16859 82178 70496 82939 44491  
OK 
68165 87637 74297 2904 32873 86010 87637 66131 82858 82935  
Wrong answer: 7680243769 7537658370  

Ура! Мы нашли пример, в котором MaxPairwiseProductNaive и MaxPairwiseProductFast приводят к разным результатам, и теперь можем проверить, что именно пошло не так.
Затем мы отлаживаем это решение через этот пример, находим баг, исправляем его и повторяем стресс-тестирование.

💡 Остановитесь и подумайте:
Видите что-то подозрительное в найденном наборе данных?

Обратите внимание, что генерировать тесты автоматически и проводить стресс-тестирование легко, но находить и исправлять баги — сложно.
Прежде чем углубиться в отладку багов, давайте попробуем сгенерировать тестовый пример поменьше — это упростит нам работу.
Для этого мы поменяем $N$ с 10 на 5 и $M$ с $100,000$ на $9$.

💡 Остановитесь и подумайте:
Почему мы сначала запустили StressTest с большими параметрами $N$ и $M$, а теперь хотим запустить с маленькими?

Затем мы заново начинаем стресс-тестирование и получаем следующее:

...  
7 3 6  
OK  
2 9 3 1 9  
2 3  
Wrong answer: 81 27  

Медленный алгоритм MaxPairwiseProductNaive даёт верный ответ $81$ ( $9 cdot 9 = 81$ ), но быстрый MaxPairwiseProductFast — неверный ($27$).

💡 Остановитесь и подумайте:
Как может выйти, что MaxPairwiseProductFast выдаёт $27$?

Чтобы избавиться от багов в первом решении, давайте проверим, какие два числа он считает наибольшими.
Для этого мы добавим следующую строку перед return в функции MaxPairwiseProductFast:

print(index_1, index_2)

Когда мы снова начинаем стресс-тестирование, мы получаем следующее:

...  
7 3 6  
OK  
2 9 3 1 9  
2 3  
Wrong answer: 81 27  

Обратите внимание, что наши решения работали и давали сбой на одних и тех же примерах тестирования, так как мы ничего не меняли в генераторе тестов.
Он использует псевдослучайные числа при создании тестов вместо действительно случайных.
Это значит, что последовательность выглядит случайной, но она одинакова каждый раз, когда работает программа.
Такое свойство удобно и важно. Советуем вам использовать эту практику, потому что в детерминированных программах (тех, что всегда выдают одинаковый результат при одинаковых вводных данных) легче находить баги, чем в недетерминированных.

Давайте теперь рассмотрим $index_1=2$ и $index_2=3$. Если мы обратим внимание на код для определения второго максимального числа, то заметим неочевидный баг.
Когда мы использовали условие для $i$ (число не должно быть таким же, как предыдущее самое большое), вместо сравнения $i$ и $index_1$ мы сравнили $A[i]$ и $A[index_1]$.
Это означает, что второе максимальное число отличается от первого по значению, а не по индексу элемента, который мы выбрали для решения задачи.
Так, наше решение не работает при любом тесте, в котором второе самое большое число равно первому.
Теперь изменим условие: вместо

A[i] != A[index_1]

мы используем

i != index_1

Проведя стресс-тестирование еще раз, мы видим на экране шквал сообщений OK. Ждём минуту, пока нам не надоест, и заключаем, что MaxPairwiseProductFast наконец-то работает правильно!

Однако не стоит останавливаться на этом, так как вы сгенерировали только очень маленькие тесты с $N=5$ и $M=10$.
Теперь нужно проверить, работает ли наша программа при большем $n$ и бо́льших элементах массива.
Таким образом, мы меняем $N$ на $1,000$ (при большем $N$ примитивное решение будет довольно медленным из-за квадратичного времени выполнения).
Мы также меняем $M$ на $200,000$ и запускаем программу.
Ещё раз наблюдаем, как экран заполняется сообщениями OK. Затем ждём минуту, а потом решаем, что MaxPairwiseProductFast действительно работает верно.
После этого мы сдаём получившееся решение системе оценки и успешно проходим тест!

Как вы можете заметить, даже при решении такой простой задачи как Максимальное попарное произведение сложно избежать
труднораспознаваемых ошибок на этапе проектирования и реализации алгоритма. Приведённый ниже псевдокод — это пример более надежного способа реализации алгоритма.

MaxPairwiseProductFast(A[1..n]):
    index = 1
    for i from 2 to n
        if A[i] > A[index]:
            index = i
    swap(A[index], A[n]) // поставим наибольшее значение в конец массива
    index = 1:
    for i from 2 to n - 1
        if A[i] > A[index]:
            index = i
    swap(A[index], A[n - 1]) // поставим второй по величине элемент предпоследним
    return A[n - 1] * A[n]

В этой книге вы узнаете, как проектировать и реализовывать алгоритмы так, чтобы минимизировать вероятность ошибок. А заодно научитесь тестировать вашу реализацию.

Ещё более быстрый алгоритм

Алгоритм MaxPairwiseProductFast находит два самых больших числа примерно за $2n$ сравнений.

💡 Остановитесь и подумайте:
Найдите два самых больших элемента в массиве за $1.5n$ сравнений.

Когда вы решите эту задачу, вас ждет ещё более сложное упражнение. Попробуйте с ним справиться!

💡 Остановитесь и подумайте:
Найдите два самых наибольших элемента в массиве за $n + lceil log_2 n rceil — 2$ сравнений.

Если это упражнение показалось вам слишком простым, посмотрите задачи ниже. Они вполне могут оказаться на следующем собеседовании!

✒️ Упражнение:
Докажите, что не существует алгоритма, которому потребуется менее $n + lceil log_2 n rceil — 2$ сравнений, чтобы найти два самых больших элемента массива.

✒️ Упражнение:
Какой алгоритм найдёт три самых больших элемента быстрее всего?

Более компактный алгоритм

Задачу Максимальное попарное произведение можно решить с помощью следующего компактного алгоритма, который использует сортировку (в неубывающем порядке).

MaxPairwiseProductBySorting(A[1..n]):
    Sort(A)
    return A[n-1]*A[n]

Этот алгоритм делает даже больше, чем нам нужно: вместо того, чтобы найти два самых больших элемента, он сортирует весь массив.
Поэтому его время выполнения $O(nlog n)$, а не $O(n)$. Однако для таких ограничений ($2 le n le 2 cdot 10^5$) он достаточно быстрый, чтобы выполнить задачу за секунду и успешно пройти тесты в нашей систему оценки.

«Универсальная» блок-схема и 3 типовых алгоритма

Дважды за день заходила речь об одном и том же, да и жаль выкидывать пару картинок, могут ещё понадобиться. Речь шла об изображении базовых типовых алгоритмов, связанных с расчётом какой-либо элементарной характеристики последовательности (массива) — суммы, количества, произведения, максимума, минимума и т.п.
В картинках не показаны «начало» и «конец», только содержательная часть.

ГОСТовские «перевёртыши» на практике крайне неудобны, классическое изображение с помощью «ромбика» часто сбивает начинающих с толку похожестью на обычное ветвление (плюс они забывают делать шаг в конце тела цикла),
а вот значок «цикла с параметром», если отказаться от паскалевского шага, непременно равного единице, удобен и нормально воспринимается.

I Алгоритм табулирования (составление списка или таблицы)

Алгоритм табулирования (составление списка или таблицы)

Что писать в фигурках вместо цифр?

1. Примем, что управляющая переменная цикла называется x, а здесь зададим её начальное (x1) и конечное (x2) значения, а также шаг изменения dx. Это можно записать присваиванием x1=0,x2=1,dx=0.1 или поставить вместо прямоугольника параллелограмм (оператор ввода) с подписью «ввод x1,x2,dx«;

2. Обычно внутри значка «цикл с параметром» (цикл, пределы изменения и шаг управляющей переменной которого известны) пишут что-то вроде псевдокода: «для x от x1 до x2 шаг dx» или то же самое в форме x=x1,x1+dx..x2 или просто x=x1,x2,dx ;

3. Для очередного x вычислить y=f(x). Этот шаг может включать несколько действий и предполагать вставку дополнительных блоков «расчёт» или условных операторов;

4. Вывести строку таблицы: вывод x, f(x)


II. Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности

Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности

Вместо цифр в элементах блок-схему указываем:

1. Для каждой искомой величины задать по переменной и присвоить ей начальные значения: сумме s=0, количеству k=0, произведению p=1 (на самом деле, это не совсем корректно, но для обсуждаемого уровня сойдёт);

2. Выполняется как в задаче I;

3. Считаем очередной элемент последовательности y=f(x), с тем же замечанием, что к задаче I;

4-5. Если y отвечает условию задачи (проверка на шаге 4), сумма на шаге 5 ищется в виде s=s+f(x), количество в виде k=k+1, произведение в виде p=p*f(x). При нескольких искомых величинах блок вида 4-5 может повторяться несколько раз;

6. По выходе из цикла выводим найденную величину или величины.

III. Алгоритм поиска максимума или минимума

Блок схема задачи II годится и для этого случая.

1. Для каждого максимума или минимума задать по переменной (примем, что минимум обозначен min, а максимум — max) и присвоить каждой переменной начальные значения: максимуму – заведомо малое значение (например, -10³⁰, оператор будет иметь вид Max=-1030) или первый элемент последовательности (массива); минимуму присвоить заведомо большое значение (например, 10³⁰) или первый элемент последовательности;

2-3. Выполняются как в задачах I-II, с теми же замечаниями.

4-5. Для поиска максимума проверяется условие 4 f(x)>max, выполняется действие 5 вида max=f(x), дли минимума проверяется условие 4 f(x)<min и выполняется действие 5 вида min=f(x). С чем сравнивали max или min, то им и присваиваем.Могут понадобиться дополнительные условия, связанные логической операцией «И» либо «ИЛИ» с основным, например, поиск максимального из отрицательных элементов предполагает проверку y<0 and y>max;

6. По выходе из цикла выводим найденную величину или величины.

Несмотря на обилие средств для рисования блок-схем, удобнее простого Paint из Win7 и выше для этой цели ничего пока не придумали

IV. Схема ввода и обработки элементов одномерного массива

Как правило, ввод, обработка или вывод одномерного массива (вектора, списка) выполняется поэлементно с помощью цикла с параметром (цикла «for»). Счётчиком цикла служит номер элемента в массиве (обычно применяется нумерация с единицы). Ниже показаны ввод и обработка массива x из 6 элементов.

Схема ввода и обработки элементов одномерного массива

V. Реализация алгоритма в кратных (вложенных) циклах

Основное отличие – все действия над матрицей (таблицей) выполняются поэлементно в двойном цикле следующего вида:

Блок-схема двойного цикла с параметром

Здесь показан ввод матрицы A из 6 строк и 4 столбцов, а счётчиками внешнего и внутреннего цикла с параметром служат номера строки (i) и столбца (j) в матрице. Обработка и вывод элементов матрицы могут быть реализованы аналогичными конструкциями, часто, если элементы обрабатываются последовательно и независимо друг от друга, ввод и обработку или обработку и вывод можно объединить.

31.10.2016, 21:46 [10934 просмотра]

---