Как составить алгоритм по математике 4 класс

 «Алгоритмы письменных приёмов умножения и деления 3-4 классы. УМК
«Школа России»»

      Изучение
алгоритма письменного умножения трёхзначного числа на однозначное число
происходит после того, как изучен алгоритм письменного сложения и вычитания
многозначных чисел в 3 классе. Прежде чем изучить алгоритм письменного
умножения, учащиеся знакомятся с приёмами устного умножения и деления. Этот
период можно назвать подготовительной работой.  Устные приёмы умножения и
деления основаны на умении раскладывать  многозначное число на разрядные
слагаемые, а также умножение и деление суммы на однозначное число. И, конечно
же, успешное овладение и устными и письменными приёмами будет тогда, когда
таблица умножения прочно усвоена детьми.

Например:  32 ∙ 4
= (30 +2) ∙ 4=(30 ∙ 4) + (2 ∙ 4) = 120 + 8= 128

     Как видно из
представленного примера, умножать двузначное число на однозначное достаточно
легко. Но стоит предложить детям  в качестве первого множителя многозначное
число, как сразу же возникают сложности и неуверенность. Таким образом, мы
знакомим  третьеклассников с понятием письменного приёма умножения.

234 ∙ 2 =(200 + 30
+ 4) ∙ 2 =  200 ∙ 2 + 30 ∙ 2 + 4 ∙ 2= 400 + 60 + 8 = 468

После этого
предлагается сравнить две записи и сделать вывод, какой способ удобнее.

 
×234       Совместно с детьми составляем алгоритм умножения трехзначного

        2         числа на однозначное
число с опорой на учебник.

    468                                              

Алгоритм

1.    
Пишу единицы под единицами.

2.    
Умножаю единицы на число 2. Результат пишу
под единицами.

3.    
Умножаю десятки на число 2. Результат пишу
под десятками.

4.    
Умножаю сотни на число 2. Результат пишу
под сотнями.

5.    
Читаю ответ: произведение равно 468.

Далее можно
предложить умножение с переходом через разряд.

 

       В начале 4 класса учащиеся
закрепляют  письменный приём умножения на однозначное число. Единственное
отличие от третьего класса, что первый множитель может быть представлен
многозначным числом. Алгоритм изменяется только в том, что после умножения  сотен
на число, необходимо умножать следующие разрядные единицы (единицы тысяч,
десятки тысяч, сотни тысяч и т.д.)

     Затем
учащиеся знакомятся с приёмом письменного умножения многозначного числа,
оканчивающегося нулями на однозначное число, а также приёмом умножения на
число, оканчивающееся нулями.

     С алгоритмом
умножения на двузначное и трехзначное число учащиеся знакомятся позже. Сначала предлагается
вычислить, применяя устные приёмы вычислений.

46 ∙ 73 = 46 ∙ (70
+3)= 46 ∙ 70 + 46 ∙3 =46 ∙ 3 + 46 ∙ 70

В результате
делается вывод, что это неудобно.

Знакомим с записью
в столбик, при этом составляем алгоритм работы, с опорой на учебник.

Алгоритм
умножения на двузначное число.

1.                
Пишу
единицы под единицами, а десятки под десятками.

2.    
 Умножу
первый множитель (46) на число единиц второго
множителя (3).

Получу первое неполное произведение (138)

3.    
 Умножу
первый множитель (46) на число десятков второго
множителя (7)

Получу второе  неполное произведение (322 дес.)

Начну
подписывать второе неполное произведение под десятками.

4.    
Сложу
неполные произведения, используя алгоритм сложения.

5.    
Читаю
ответ: произведение равно 3358

       
Алгоритм письменного умножения на трёхзначное число похож на предыдущий, но в
нём есть три неполных произведения, так как первый множитель мы будем умножать
на единицы, десятки и сотни  второго множителя.

Алгоритм 
умножения на трёхзначное число.

1.    
Умножу первый множитель на число единиц второго
множителя.

Получу первое неполное произведение.

2.    
Умножу первый множитель на число десятков
второго множителя.

Начну подписывать второе неполное
произведение под десятками.

Получу второе  неполное произведение.

3.    
Умножу первый множитель на число сотен второго
множителя.

Начну подписывать третье неполное
произведение под десятками.

Получу третье  неполное произведение.

4.    
Сложу
неполные произведения.

5.    
 Читаю ответ….

      
Теоретической основой письменного деления на однозначно число

служит
правило деления суммы на число. Поэтому прежде необходимо повторить:

ü
смысл действия деления и его взаимосвязь с
умножением;

ü
табличные случаи умножения и соответствующие
случаи деления, случаи умножения и деления с нулем и единицей;

ü
правило деления суммы на число и деление с
остатком.

Знакомство с новой
записью деления (деление в столбик) уместно начать с использования устных
приёмов деления.

Попутно знакомим с новыми
математическими символами.

     На
следующем уроке целесообразно познакомить с алгоритмом письменного деления. В
учебнике «Математика. 3 класс» не даётся понятие неполное делимое, но я в своей
работе знакомлю учащихся с понятием неполное делимое уже на этом этапе. 

       
Учащиеся начальных классов часто допускают ошибки при подборе числа в частном.
Поэтому прежде чем учащиеся приступят к делению, необходимо научить их
определять количество цифр в частном.

        
Если первое неполное делимое — однозначное число (первая цифра в делимом
обозначает число, которое равно делителю или больше него), то в частном будет
столько цифр, сколько в делимом. Если первое неполное делимое — двузначное
число (первая цифра в делимом обозначает число, которое меньше делителя, и
поэтому необходимо начинать действие с деления числа, записанного двумя первыми
цифрами), то в частном будет на одну цифру меньше, чем в делимом.

      
Учащиеся определяют, каким числом (однозначным или двузначным) является первое
неполное делимое, и ставят на месте записи частного точку, далее они ставят
столько точек, сколько еще цифр в делимом. Предварительная
прикидка количества цифр в частном предотвращает возможность пропуска нуля в
частном.

        
В 4 классе учащиеся знакомятся с алгоритмом деления на двузначное и трёхзначное
число. Проверку правильности выполненного деления можно провести умножением
частного на делитель или делением делимого на частное.

Подготовила:
Мельниченко И.В.

учитель
начальных классов

МАОУ
СОШ№6 г. Холмска

Цели урока:

• Образовательные:
  • закрепление приёмов письменного умножения и
    деления, умения решать примеры;
  • решение уравнений и задач, используя алгоритмы.
• Развивающие:
  • развитие памяти, речи, навыков устных и
    письменных вычислений;
  • развитие мыслительных операций: внимания,
    логического мышления, анализа.
• Воспитательные: воспитание внимательного
  отношения друг к другу, умения работы в парах,
  группах.

Формы проведения урока: учебный
диалог, фронтальная работа, работа в парах,
работа в группах, индивидуальная работа.

Оборудование: мультимедиа;
записи на доске. Таблички со словами: примеры,
уравнения, задачи; табличка с примером 406958: 67.
Вырезанные из цветной бумаги жёлтые
треугольники (лучи солнца), жёлтый круг (солнце),
красные цветы, голубые бабочки.

ХОД УРОКА

I. Оргмомент

– Давайте улыбнемся  друг другу и
начнём урок с хорошего настроения.

II. Устный счёт

– Вычислите устно и вы узнаете ключевое
слово сегодняшнего урока.

3) – Какое число я задумала?

4) – Продолжи ряд на одно число:

С помощью компьютера на экран заранее
выносятся  ответы к заданиям  в порядке
возрастания. По ходу правильных ответов напротив
каждого числа появляется буква:

Рис. 1

III. Актуализация знаний

– Вы узнали ключевое слово урока. Что
означает слово алгоритм, вы расскажете немного
позже. А сейчас откройте тетради, запишите число.
– Скажите, пожалуйста, чему мы учимся на
уроках математики? (Решать примеры, уравнения,
задачи, думать, рассуждать)

Учитель по ходу ответов учеников
вывешивает на доску таблички со словами: примеры,
уравнения, задачи.

– Посмотрите внимательно на доску:

– Ученик решил пример. Согласны ли вы с
решением данного примера? Почему?
– Вы заметили ошибки. Запишите пример в тетради и
решите его.

Ученики решают пример в тетради.

– Какие ошибки были допущены учеником? (Ошибки
при умножении числа 6 на число 4, при сложении
чисел 4 и 8, число236 не умножили на 5 сотен)
– Что помешало ученику решить пример правильно? (Не
знает таблицу умножения, таблицу сложения, был
невнимательным, не рассуждал по алгоритму)
– Каким алгоритмом вы пользовались при решении
данного примера? (Алгоритмом умножения на
трёхзначное число.)
– Что вы делали сначала? Потом?

 Дети называют совершённые
действия по порядку, и они одновременно
выносятся на экран с помощью компьютера.

1. Алгоритм умножения на трёхзначное
число:

1) Число умножаем на единицы.
2) Число умножаем на десятки.
3) Число умножаем на сотни.
4) Результаты складываем.
5) Получившееся число делим на классы.

IV. Тема, цель урока

– Что такое алгоритм? (Порядок
действий)
– Так что же мы должны уметь, чтобы справиться с
заданиями? (Уметь рассуждать по алгоритму)
– Сформулируйте тему урока. (Использование
алгоритмов при решении примеров, уравнений и
задач)
– Все ли из вас научились рассуждать по
алгоритму?
– Сформулируйте цель урока. (Продолжить
учиться решать примеры, уравнения, задачи на
основе рассуждения по алгоритмам)
– Те из ребят, которые считают, что они уже этому
научились, еще раз проверят свои знания.

V. Работа по теме

2. Алгоритм деления

– Давайте вспомним алгоритм деления.

1. Находим первое неполное делимое.
2. Определяем  число цифр в частном.
3. Делим методом подбора, начиная с наибольшего
числа.
4. Находим остаток.
5. Сносим следующую цифру.

Ученики устно проговаривают алгоритм,
учитель по ходу ответов учеников выносит 
порядок действий на экран с помощью компьютера.

–  Запишите пример на деление: 69861 : 73 =

– Может быть, кто-то из вас
продемонстрирует своё умение рассуждать по
алгоритму? (К доске выходит ученица)

а) Индивидуальная работа

Далее в  роли учителя выступает
ученица.

– Давайте проверим, все ли умеют
рассуждать при решении примеров. Я приготовила
для вас пример на деление: 406958:67. Решите его в
тетради и ответ запишите на жёлтых
треугольниках.
– Давайте «оденем» солнышко. Выйдите те, у кого
получился ответ 6074.

VI. Физминутка

– По моей команде вы должны
объединиться в группы. Слушайте меня
внимательно.
– Объединитесь в группы по 4 человека, по 2
человека, по 8 человек.

VII. Продолжение работы по теме

Учитель: Скажите, пожалуйста,
для чего нужно хорошо  уметь умножать, делить,
вычитать, складывать? Где могут пригодиться ваши
умения? (При решении уравнений, задач)

3. Алгоритм составного уравнения

– Какое уравнение называется составным?
– Давайте вспомним алгоритм составного
уравнения.

1. Составляем программу действий.
2. Выделяем части, целое.
3. Находим неизвестный компонент (часть или целое)
по правилу.
4. Находим корень уравнения.
5. Делаем проверку.
6. Записываем ответ.

Ученики устно проговаривают алгоритм,
учитель по ходу ответов учеников выносит 
порядок действий на экран с помощью компьютера.

б) Работа в парах

26 х (х + 427) = 15756

–  Давайте проверим, все ли умеют
рассуждать при решении составных уравнений. У
вас на партах лежат цветы, на которых вы должны
записать корень уравнения. Для этого вы должны
сначала решить уравнение в тетради. Работать
нужно в парах.

После решения:

– Давайте «оденем» полянку. Выйдите те,
у кого корень уравнения равен 179.

Дети выходят с цветами красного цвета
и прикрепляют их на ватман с изображением
солнышка и полянки.

4. Алгоритм задачи

– Давайте вспомним алгоритм решения
задач.

1. Внимательно читаем задачу 2 раза.
2. Думаем о чём задача.
3. Чертим схему.
4. Находим  главные слова и отмечаем их на
схеме.
5. «Одеваем » схему, читая задачу по частям.
6. Комментируя, показываем на схеме то, что
известно и то, что неизвестно (часть, целое.)
7. Находим неизвестную часть или неизвестное
целое по правилу.
8. Записываем решение, пояснение к задаче.
9. Записываем ответ задачи.

Ученики устно проговаривают алгоритм,
учитель по ходу ответов учеников выносит 
порядок действий на экран с помощью компьютера.

в) Работа в группах

– Давайте проверим, умеете ли вы
рассуждать при решении задач. У вас на парте
лежат бабочки, на которых вы должны записать
ответ задачи. Для этого вы должны сначала решить
задачу в тетради. Работать нужно в группах.

Задача:

В одной пачке 55 тетрадей, что на 20
тетрадей больше, чем во второй и на 15 тетрадей
больше, чем в третьей. Сколько тетрадей было в
трёх пачках?

? т.
______________________________         
I               
II                    
III
_______/_______________/____________
55 т.         (55 – 20)
т.             (55 – 15)
т.

После решения:

– Выйдите те, у кого ответ задачи: 130
тетрадей.

Дети выходят с бабочками  и
прикрепляют их на ватман над цветами.

Рис. 2

VIII. Итог урока

– Чему продолжали учиться?
– Что было главным для каждого из вас на уроке?

IХ. Рефлексия

– Выразите своё отношение к уроку. (Понравился
урок или не понравился? Почему? Что больше всего
понравилось?)

– Спасибо всем за активную работу на
уроке.

Математика, 4 класс

Урок № 33.Повторение пройденного материала по теме «Алгоритмы письменного умножения и деления»

Перечень вопросов, рассматриваемых в теме:

— каковы алгоритмы письменного умножения и деления?

— как решаются уравнения и задачи изученных видов?

Глоссарий по теме:

Задача – это сформулированный словами вопрос, ответ на который может быть получен с помощью арифметических действий

Уравнение – это равенство, содержащее неизвестное число

Алгоритм – последовательность действия (шагов)

Умножение – действие, при котором одно число повторяется столько раз, сколько в другом содержится единиц, и находится сумма этих слагаемых.

Деление – действие, обратное умножению.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.1 — М.; Просвещение, 2015. – с.91-95

2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – с.79-80

3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.50

Теоретический материал для самостоятельного изучения

На уроке мы вспомним:

Алгоритмы письменного умножения и деления многозначного числа на однозначное.

Сможем:

Совершенствовать вычислительные навыки в процессе решения задач, выражений, уравнений.

Повторим: алгоритм умножения многозначного числа на однозначное.

Повторим алгоритм деления многозначного числа на однозначное

Повторим письменный прием умножения многозначного числа на однозначное, умножим 15 719 ∙ 5

Записываем числа друг под другом: единицы под единицами

Умножаем единицы 9 на 5, получится 45.

45 – это 4 десятка и 5 единиц

5 единиц пишем под единицами

4 десятка запоминаем,

его позже прибавим к десяткам

Умножаем десятки 1 ∙ 5 = 5 и прибавляем 4 десятка, который получился при умножении десятков, получится 9

Записываем десятки под десятками

Умножаем сотни 7 ∙ 5 = 35.

35 – это 5сотен и 3 тысячи.

Записываем 5 сотен под сотнями, 3 тысячи запоминаем. Их позже прибавим к тысячам.

Умножаем тысячи: 5 ∙ 5=25 и прибавляем 3 тысячи, которые получились при умножении сотен. Получается 28.

8 тысяч записываем под тысячами, а 2десятка тысяч запоминаем. Их позже прибавим к десяткам тысяч.

Умножаем десятки тысяч: 1 ∙ 5 = 5 и прибавляем 2 десятка тысяч, которые получились при умножении тысяч. Получается 7. Записываем под десятками тысяч.

Получилось 78595.

Повторим письменный прием деления многозначного числа на однозначное

83 216 : 4

Помним, что при письменном делении запись ведется в столбик

Делим десятки тысяч.

Разделим: 8 : 4, в частном будет 2 десятка тысяч.

Умножим 4 на 2 = 8, это значит, что разделили 8десятков тысяч.

Вычтем из 8 -8=0.

Делим тысячи:

3:4. В частном будет 0 тысяч

Сносим 2 сотни. 32 сотни делим на 4, получается 8.

8 ∙ 4 = 32. Вычтем 32 – 32 = 0

Делим десятки: 1 : 4 = 0. Остаток 1. Сносим 6 единиц. 16:4 = 4.

Умножаем 4 на 4, получается 16.

16 – 16 = 0.

Деление закончили.

Читаем ответ: 20 804.

Задания тренировочного модуля:

1. Найдите значение выражений:

Правильный вариант:

824 · 9 = 7416

916 · 3 = 2748

2. Найдите значение выражений:

Правильный вариант:

7410 : 3 = 2470

4850 : 5 = 970

Рассказываем о требованиях программы по текстовым задачам. Показываем типовые задачи по математике 4 класс и алгоритмы их решения.

Содержание учебной деятельности по текстовым задачам

Типы задач по математике 4 класс и алгоритмы их решения

Результаты освоения программы по решению задач

Учебное занятие по математике в 4 классе

Тема   «Решение задач с применением
алгоритмов»

Цель
 : сформировать у учащихся
умение применять общий алгоритм  для решения любой задачи и алгоритм при
решении конкретной задачи.

Образовательные
задачи:

-закрепить
умение решать составные задачи, анализируя их состав;

Воспитательные
задачи:

-воспитывать
интерес к математическим знаниям;

-воспитывать
ответственность за выполнение коллективной работы.

Развивающие
задачи (УУД).

Регулятивные
УУД:

—
уметь организовывать свою деятельность;

-принимать
и ставить учебно-познавательную задачу;

-строить
логические рассуждения;

-планировать
свои действия.

Познавательные
УУД:

-учиться 
применять алгоритм при решении задач.

Коммуникативные
УУД:

-уметь
использовать математическую речь при объяснении своих действий;

-осуществлять
взаимный контроль и оказывать необходимую помощь товарищам.

Тип
занятия:
Урок рефлексии  (комбинированный)

Методы: словесные,
наглядные, практические, частично поисковые, сравнение, аналогия и обобщение.

Медиапродукт: презентация к
уроку.

Средства
обучения:
компьютер, мультимедийный проектор, презентация Power Point, карточки –
алгоритмы , карточки – самооценка.

 Ход
занятия

1.     Мотивационный
этап.

—
Я
рада всех вас видеть на нашем уроке. Я желаю вам хорошего настроения и отличных
ответов. Повернитесь друг к другу, улыбнитесь и пожелайте взаимной удачи.

Начнём
занятие  с девиза:  

«Мы
сможем, мы сумеем, и у нас всё получится!» (слайд 2)

У каждого из вас
на столе лежит конверт. В нём есть карточка – самооценка. В конце
урока подведёте  итог своей работы и оцените себя.

2. Актуализация
прежних знаний.

      А сейчас небольшая
разминка перед серьёзной работой.   (слайд 3)

Положите перед
собой индивидуальные досточки, возьмите маркер и настройтесь на работу. Я буду
произносить математические выражения, а вы, в качестве ответа, будете
записывать только знак действия. (Ответ показывают учителю)

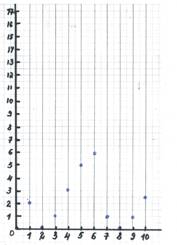
На слайде: 1. Диаграмма,
в которую я буду заносить результаты ваших ответов. Она поможет увидеть
ошибочные ответы и сделать вывод: в чём вы ещё затрудняетесь, и что надо будет
повторить на следующих уроках. 

2. Математические
выражения, которые я буду называть. Они нам нужны будут при подведении  итога 
этой работы.  (слайд 4)

                    
1.
Увеличение числа в несколько раз

                    
2. Нахождение целого

                    
3. Уменьшение на несколько единиц

                    
4. Приведение к единице

                    
5. Нахождение части от числа

                    
6. Нахождение числа по его части

                    
7. Разностное сравнение

                    
8. Уменьшение числа в несколько раз

                    
9. Нахождение остатка

                   
10.Кратное сравнение

Во время работы
учитель отмечает на слайде маркером точку, обозначающую количество детей, у
которых была допущена ошибка,  напротив номера задания.

Проверим работу. По диаграмме мы
видим, что больше всего ошибок на 5-е и 6-е задание. Какой вывод сделаем? (…)
Правильно, надо ликвидировать пробелы путём повторения.

                                    

А что мы вспомнили,
выполняя эту работу?  (Дети: мы повторили виды простых задач)
Правильно. А если объединить несколько простых задач, то, что получится? (Дети:
получится составная задача).  Можно сказать, что мы закрепляли умения определять
знаки действий при решении простых задач?  (Дети: да)

Вспомните, что мы
используем при решении составной задачи? (Дети: алгоритм).

Вы можете сказать, чем мы
будем заниматься сегодня на уроке?  (Дети: решать составные задачи с
применением алгоритма).

Тема нашего занятия:
«Решение задач с применением алгоритма».  Мы уже умеем применять алгоритм для
решения задачи, т.е. основной и обязательный алгоритм для решения любой
задачи. А сегодня мы продолжим работу по применению алгоритмов более глубоко.

Задачи:
продолжить учиться применять алгоритм для решения любой  задачи, а так же
учиться составлять алгоритм при подготовке к конкретному виду задач.

Ребята, а что такое АЛГОРИТМ? 
(Дети:    Алгоритм – это последовательность действий   или план 
достижения цели.  Алгоритм  состоит из отдельных шагов.  Каждый  шаг содержит
одну  команду.)  

Как вы считаете, только
ли  на математике применяется алгоритм? (Дети: нет. Алгоритм  можно
применять на любом уроке. И не только на уроках, но и в жизненных ситуациях.
)  Приведите примеры из жизни. (Учащиеся приводят примеры). Например:  подготовка
домашнего задания;  утренние сборы в школу; заваривание чая, кофе;
строительство дома и т. д.

Вывод:  Алгоритм
– это универсальное действие. (слайд 5)

А теперь приступим к
решению задачи.  Но сначала повторим главный алгоритм для решения любой задачи (слайд
 6)

         Алгоритм работы над
задачей

1.    
Читаю
условие задачи.    Читаю вопрос.

2.    
Представляю
ситуацию, описанную в задаче.

3.    
Нахожу
данные задачи, выделяю опорные слова.

4.    
Определяю
искомое задачи (конечная цель).

5.    
Определяю состав задачи.

              Простая    
                                      Составная

1.     
Моделирую
задачу.                  1. Моделирую задачу.

2.     
Записываю
решение .               2. Определяю кол-во простых.

3.     
Записываю
ответ.                      3. Указываю  действия.

4.     
________________                   
4. Записываю решение.

5.     
________________                   
5. Записываю ответ.

6.     
________________                   
6. Записываю выражение. 

Задача 1.     В школьном саду посадили 30
яблонь, слив в 2 раза меньше, а вишен на 12 деревьев больше, чем слив.    
Сколько всего деревьев посадили в школьном саду?

Работаем по алгоритму. 

Дети:  сначала мы
прочитаем условие задачи, вопрос. Затем представим, о чем идёт речь в
задаче.  (В школьном саду высаживают деревья: яблони, вишни   и сливы.) Находим
опорные слова: (яблони, вишни, сливы). Называем  что известно, а что не
известно. (Известно,  сколько яблонь — их  30.  Не известно —  сколько вишен
и груш). Искомое задачи – главный вопрос задачи. Определяем состав
задачи. (Задача составная. Состоит из трёх простых)

Моделируем задачу. Выбираем словесную модель.
(Можно  также использовать чертёж, рисунок,  …)  Определим,  сколько в ней
простых  задач (их три). Указываем действия каждой простой задачи  (
: ,  +,  +)      (слайд 7)

Яблонь
– 30 (д.)

Вишен 
— ?,  в 2 раза меньше, чем яблонь  (:)

Груш 
— ?,  на 12 д. больше, чем вишен (+)

Всего
деревьев — ? (+)                                                            

Записываем
решение задачи:

1).  30 :
2 = 15 (д.) – вишнёвых.

2). 1 5 +
12 = 27 (д.) – грушевых.

3).  30 +
15 + 27 = 72 (д.) – всего деревьев.

Записываем  ответ:
72 дерева посадили школьники.

Составляем и
записываем выражение к задаче:

30 +
30 : 2 + (30 : 2 + 12) =72 (д.)

Задача решена
с помощью алгоритма. А в жизни  процесс посадки деревьев проходит в строгой
последовательности или действия посадки можно менять? ( Дети: действия
посадки деревьев тоже проходят в определённой последовательности. )

Посмотрите
как это происходит.   (слайд

Чтобы решить следующую задачу, давайте кое- что
вспомним.

На   (слайде 9) появляется  запись:   мм 
см  дм  м  км    Что это?   Дети: (единицы измерения длины). 
Далее появляется:    мм²  см²  дм²   м²  км²   А
это что?  (единицы измерения площади.  Как связаны между
собой  эти   единицы измерения? (единицы площади зависят от линейных
размеров)

Вот вам задание: выразите  6 км²  в  м².
Можно ли и в этом случае применить алгоритм?   Дети: да, можно.   
1). 1км = 1000м  

                                                      
2). (1000 х 1000=1000 000)

                                                      
2). 1км² = 1000 000 м²

                                                      
3). 6км² = 6 000 000 м²

Эти знания нам нужны для решения задачи на нахождение
площади.

Решим простую задачу.  Текст задачи на  (слайде 10)    
 ( Работа в паре)                                                                                                                 

      Задача. 
На участке, длина которого 400м, а ширина 300 м  посадили яблони.      

                      На какой площади
были посажены яблони?  

  Ребята, для решения этой задачи  (нахождение
площади прямоугольника), кроме основного алгоритма для решения задач,
применяется алгоритм конкретно для данной задачи.  Поработайте в парах ,
составьте алгоритм и приготовьтесь презентовать задачу).

Дети должны составить алгоритм для решения данной   задачи
(на нахождение площади прямоугольника).    По истечении времени пара
выходит к доске и презентует задачу по составленному алгоритму. Алгоритм должен
быть таким:

1.      Вспомним
определение площади.

2.      Запишем
формулу нахождения площади прямоугольника.

3.      Запишем
решение задачи.

4.      Запишем
ответ задачи.

400 х 300 =
12000(м²)

Какую работу ещё можно выполнить в данном случае?  (Дети:
перевести в гектары)

Применяя алгоритм, переведите в   га.

—  1га
это квадрат со стороной 100 м

—  100
х 100 = 10 000м²,    т.е.    1 га = 10000 м²

—  12 000
: 10 000 + 12 (га) —  площадь равна 12 га

Подведём итог нашей работы.

Какую цель ставили в начале урока? (ответы детей)

 -Кому был полезен
этот урок?

 -В чём испытывали
затруднения?

-На что ещё надо
обратить внимание?

Заполните карточку – самооценку.

Урок окончен. Спасибо всем за работу.