Муниципальное Бюджетное образовательное учреждение
средняя образовательная школа №15 г.Нерюнгри
учебное-методическое пособие
Основы работы в программе «кумир»
Харьковская
Ольга Константиновна
учитель
информатики и ИКТ
Нерюнгри,
2018
Содержание
Введение……………………………………………………………………….3
1.
Лекция 1. Основы
алгоритмизации……………………………………….4
2.
Лекция 2. Способы записи
алгоритмов…………………………………..5
3.
Лекция 3. Разработка
алгоритма с помощью «Исполнителя Робот»……7
4.
Практические работы…………………………………………………….15
4.1.
Линейный алгоритм………………………………………………..15
4.2.
Циклический алгоритм. Цикл N
раз………………………………18
4.3.
Циклический алгоритм с предусловием «ПОКА»……………….22
4.4.
Команды ветвления (если, выбор)…………………………………28
СПИСОК
ЛИТЕРАТУРЫ……………………………………………………….35
ВВЕДЕНИЕ
Учебно-методическое
пособие «Основы работы в программе Кумир» предназначено для учителей
и обучающихся 8-9 классов общеобразовательных школ, изучающих раздел
информатики: «Основы алгоритмизации».
Эти материалы могут быть
полезны при подготовке к основному и единому государственному экзамену по
информатике.
В пособие включен
цикл лабораторных работ, основными целями для
проведения которых являются:
·
Углубление, обобщение и
систематизация знаний по блок-схемам;
·
Развитие алгоритмического
мышления через составление блок-схем;
·
Закрепление навыков
составления всевозможных алгоритмов фиксированной длины на алгоритмическом
языке для формального исполнителя с заданной системой команд;
·
Закрепление навыков работы на
персональном компьютере в среде программирования КУМИР;
·
Развитие информационно-коммуникационной компетентности обучающихся
Лекция 1. Основы алгоритмизации
Известно
множество областей применения компьютера: обработка текстов и графики, передача
и получение информации, создание справочников, произведение расчетов. Еще одно
из важнейших направлений применения компьютеров – управление.
Управление – это
целенаправленное воздействие одних объектов, которые являются управляющими, на
другие объекты – управляемые. Все управляющие воздействия производятся с
определенной целью с помощью команд. Таким образом, алгоритмом управления – это
последовательность команд по управлению объектом, приводящую к достижению заранее
поставленной цели.
Объект
управления – исполнитель алгоритма, в данном случае исполнитель алгоритма –
устройство. Все исполнители, которые относятся к такому типу, называются
формальные. Формальный исполнитель не понимает смысл команд, в информатике
рассматривают только формальных исполнителей.
Алгоритм –это
точное описание последовательности шагов в решении задачи, приводящих от
исходных данных к требуемому результату.
Алгоритм применительно к вычислительной
технике должен обладать свойствами, которые обеспечивали бы его автоматическое
выполнение:
1) Процесс решения задачи
должен быть разбит на последовательность отдельно выполняемых шагов
–дискретность (прерывность).
2) Алгоритм для данного исполнителя
содержит только те команды, которые входят в систему его команд –понятность.
3) Каждое правило алгоритма
должно быть четким и однозначным –определенность (точность).
4) Исполнение алгоритма должно
завершиться за определенное количество шагов конечность (результативность).
5) Алгоритм должен выполняться
для любого набора исходных данных из некоторой области, удовлетворяющих условию
задачи (массовость).
Лекция 2. Способы записи
алгоритмов
Существуют
различные способы записи алгоритмов. Основными среди них являются:
·
Словесные
·
Графические
·
На алгоритмических языках.
1.
Словесные способы записи
алгоритма. Самой простой является запись алгоритма в виде набора высказываний
на обычном разговорном языке. Но алгоритм в словесной форме может оказаться
очень объемным и трудным для восприятия.
2.
Блок-схема представляет собой
графический документ, дающий представление о порядке работы алгоритма.
|
Название блока |
Название блока |
Название блока |
|
Начало, остановка |
|
Начало и конец блок |
|
данные |
|
Ввод-вывод данных |
|
процесс |
|
Вычислительное действие |
|
Решение |
|
Проверка условия |
|
подготовка |
|
Начало цикла |
|
дисплей |
|
Вывод результата на экран |
|
документ |
|
Вывод результата на печать |
3.
Алгоритмические языки –
школьный алгоритмический язык,
Алгоритм применительно к вычислительной
технике должен обладать свойствами, которые обеспечивали бы его автоматическое
выполнение:
1) Процесс решения задачи
должен быть разбит на последовательность отдельно выполняемых шагов
–дискретность (прерывность).
2) Алгоритм для данного исполнителя
содержит только те команды, которые входят в систему его команд
–понятность.
3) Каждое правило алгоритма
должно быть четким и однозначным –определенность (точность).
4) Исполнение алгоритма должно
завершиться за определенное количество шагов конечность (результативность).
5) Алгоритм должен выполняться
для любого набора исходных данных из некоторой области, удовлетворяющих условию
задачи (массовость).
Лекция 3. Разработка
алгоритма с помощью «Исполнителя Робот»
Прежде чем
говорить о реализации алгоритмов для исполнителя, нужно понимать, что такое
программа и чем она отличается от алгоритма.
Программа – алгоритм,
записанный на языке программирования.
Как мы помним,
алгоритмы могут иметь различные формы представления, а программа должна быть записана
на языке исполнителя. Любому учебному исполнителю свойственна среда деятельности,
система команд управления и режимы работы.

клетчатое поле, между клетками которого могут быть препятствия (стены) рисунок
1.
Система команд исполнителя
Робот:
Простые команды: вверх, вниз, влево, вправо, закрасить.
Команды логические: (проверки условия)
сверху свободно, снизу
свободно, слева свободно, справа свободно.
Логические связки: И, НЕ, ИЛИ (сложные условия)
Пример: (не слева
свободно) или (не справа свободно)
команда ветвления: команда цикла:
если условие то
нц пока условие
серия
команд серия команд
всё
кц
Важно помнить, что исполнитель Робот двигается по клеточкам, получая
простую команду, робот выполняет движение на одну клетку и ждет следующей
команды.
И так,
запустив программу Кумир, откройте меню Вставка, выберите исполнителя Робот.
Далее, прежде чем начать писать программу для Робота, нужно настроить «поле» по
которому Исполнитель Робот будет двигаться выполняя программу.

обстановку (рис.1),
Рисунок 1 –
выбор команды Редактировать обстановку
Далее, справа диалоговое окно обстановка
Робот, становиться синего цвета, и появляются кнопки управления (рис.2),
которыми можно добавить или убрать
Рисунок 2 –
Редактирование поля
клетки поля (при первом
запуске поле имеет размер 7 х 7 клеток).

мыши (рис.3) выставляем препятствия для Робота.
Рисунок 3 – Окончание редактирования
После того
как обстановка для исполнителя Робот готова, нужно её сохранить. Заходим в меню
Робот, выбираем команду Сохранить обстановку. Далее в открывшемся
диалоговом окне, выбираем куда сохранить файл (например, Рабочий стол или
личная папка учащегося), даем название файлу и сохраняем.

выбираем команду Загрузить обстановку, поле для Робота становиться
зеленого цвета (рис.4) и нет кнопок управления.
Второе – составляем по условию
задачи алгоритм для Робота, для этого в левой части окна программы выполняем
следующее:
1. меню Вставка команда Использовать Робот, слово робот закрашивается
зеленым цветом;
2. составляем нужный алгоритм по условию задачи;
3. проверяем работает ли составленный алгоритм, для этого на панели
инструментов нажимаем кнопку Обычное или клавишу F9.
Для каждой конкретной задачи
используется свой алгоритм. Как помним, алгоритмы есть линейные, циклические,
алгоритмы ветвления.
Рассмотрим примеры с
исполнителем Робот, для каждого алгоритма по отдельности.
1. Линейные программы для исполнителя
Задача: Робот в произвольной
точке поля. Передвинуть Робота на 5 клеток влево, закрасив их (рис.5). Напишем
программу для Робота:
использовать Робот
алг лабиринт
нач
влево; закрасить
влево; закрасить
влево; закрасить
влево; закрасить
влево; закрасить

Рисунок 5 –
Выполнение алгоритма «Лабиринт»
Как видно, клетки, первоначально находящиеся слева от Робота закрашены.
В данном случае показан пример создания линейной программы для исполнителя.
2. Циклические алгоритмы для исполнителя
Цикл «пока»
Задача:
закрасить все клетки справа от Робота, при условии, сто справа на неизвестном
расстоянии есть стена и количество клеток, которые нужно закрасить неизвестно.
Очевидно, что
пока будет выполняться условие справа свободно, нужно выполнять команды:
закрасить; вправо (рис.6)
Рисунок 6 –
Использование цикла «Пока»
Для оформления таких
последовательностей действий используется специальная конструкция
алгоритмического языка — цикл «пока».
Цикл «раз»
Задача: нарисовать букву «П»
размер высотой 6 клеток, шириной 4 клетки с помощью исполнителя Робот. Исходное
положение Робота показано на рисунке 7. В этом алгоритме известно количество
шагов исполнителя, поэтому используем цикл «раз». Его конструкция в общем виде
выглядит так:
НЦ количество РАЗ

Рисунок 7 –
«Буква»
По аналогии с предыдущим
примером Робот должен закрашивать очередную клетку, а затем переходить на
следующую – сначала вверх, затем вправо и вниз.
Программа для Робота:
использовать Робот
алг буква
нач
нц 5
раз
закрасить;
вверх
кц
закрасить
нц 3
раз
вправо;
закрасить
кц
нц 5
раз
вниз;
закрасить
кц
кон
3.
Алгоритм ветвление для
исполнителя Робот
Вспомним, что
форма организации действий, при которой в зависимости от выполнения или
невыполнения некоторого условия совершается либо одна,
либо другая последовательность
действий, называется ветвлением.
Для организации ветвлений исполнителя
Робота предусмотрена специальная
команда ЕСЛИ. Ее общий вид:
ЕСЛИ <условие> ТО
<серия действий 1>
ИНАЧЕ <серия действий 2>
КОНЕЦ
Задача: Робот
находится в горизонтальном коридоре, нижняя граница

имеются выходы (рис. 8). Требуется провести Робота через весь коридор и
закрасить клетки коридора, не имеющие границ сверху.
Рисунок 8 –
«Коридор»
Единственным
признаком коридора является наличие границы сверху, значит, условие НЕ сверху свободно
должно выполняться. Если при этом выполняется условие снизу свободно, то клетку
нужно закрасить, иначе — закрашивать не надо. Известно, что слева и справа от горизонтального
коридора есть клетки.
Таким образом, рассмотрев примеры
написания трех основных типов алгоритмов и ознакомившись с пошаговым примером
работы с исполнителем Робот, можно приступить к выполнению практической части.
Практические работы
для самостоятельного выполнения
1.
Линейные алгоритмы
Задания рассчитаны на группу в 10 человек. Каждая карточка
содержит 3 задания разной степени сложности.
Вариант 1
1. Составьте программу закрашивания прямоугольника 3×4, считая, что
Робот находится где-то в центре поля.
2. Необходимо перевести Робота из начального положения (◊) в точку A
за минимальное число шагов любым из возможных способов.
2. Необходимо
перевести Робота по лабиринту из начального положения (◊) в точку A.
Вариант 2
1.
Составьте программу закрашивания прямоугольника 4×2, считая, что
Робот находится где-то в центре поля.
2.
Необходимо перевести Робота из начального положения (◊) в точку A
за минимальное число шагов любым из возможных способов.
3. Необходимо
перевести Робота по лабиринту из начального положения (◊) в точку A.
Вариант 3
1. Составьте программу закрашивания
периметра квадрата 3×3, считая, что Робот находится где-то в центре поля.
2. Необходимо перевести Робота из
начального положения (◊) в точку A за минимальное число шагов любым из
возможных способов.
3. Необходимо
перевести Робота по лабиринту из начального положения (◊) в точку A.
Вариант 4
1. Составьте программу закрашивания
квадрата 3×3, считая, что Робот находится где-то в центре поля.
2. Необходимо перевести Робота из
начального положения (◊) в точку A за минимальное число шагов любым из
возможных способов.
3. Необходимо
перевести Робота по лабиринту из начального положения (◊) в точку A.
Вариант 5
1. Составьте программу закрашивания
буквы «Г», состоящей из трех вертикальных и двух горизонтальных
клеток. Начальное положение Робота — где-то в центре поля.
2. Необходимо перевести Робота из
начального положения (◊) в точку A за минимальное число шагов любым из
возможных способов.
3. Необходимо
перевести Робота по лабиринту из начального положения (◊) в точку A.
Вариант 6
1. Составьте программу закрашивания
буквы «П», размерами три клетки по вертикали и две по горизонтали.
Начальное положение Робота — где-то в центре поля.
2. Необходимо перевести Робота из
начального положения (◊) в точку A за минимальное число шагов любым из
возможных способов.
3. Необходимо
перевести Робота по лабиринту из начального положения (◊) в точку A.
Вариант 7
1. Составьте программу закрашивания
буквы «Т», размерами четыре клетки по вертикали и три по горизонтали.
Начальное положение Робота — где-то в центре поля.
2. Необходимо перевести Робота из начального
положения (◊) в точку A за минимальное число шагов любым из возможных способов.
3. Необходимо
перевести Робота по лабиринту из начального положения (◊) в точку A.
Вариант 8
1. Составьте программу
закрашивания клеток, отмеченных звездочкой. Начальное положение Робота — где-то
в центре поля.
2. Необходимо
перевести Робота из начального положения (◊) в точку A за минимальное число
шагов любым из возможных способов.
3. Необходимо
перевести Робота по лабиринту из начального положения (◊) в точку A.
Вариант 9
1. Составьте программу
закрашивания клеток, отмеченных звездочкой. Начальное положение Робота — где-то
в центре поля.
2. Необходимо
перевести Робота из начального положения (◊) в точку A за минимальное число
шагов любым из возможных способов.
3. Необходимо
перевести Робота по лабиринту из начального положения (◊) в точку A.
Вариант 10
1. Составьте программу
закрашивания клеток, отмеченных звездочкой. Начальное положение Робота — где-то
в центре поля.
2. Необходимо
перевести Робота из начального положения (◊) в точку A за минимальное число
шагов любым из возможных способов.
3. Необходимо
перевести Робота по лабиринту из начального положения (◊) в точку A.
1.
Циклические алгоритмы. Цикл N раз.
Задания расчитаны на
группу в 10 человек. Каждая карточка содержит 3 задания разной степени
сложности.
Вариант 1
1. Составьте программу закрашивания 6-ти клеток
вправо от Робота, считая, что изначально Робот находится у левого края поля.
2. Необходимо провести Робота по лабиринту из
начального положения (◊) в точку A.
3. Составьте
программу закрашивания клеток поля, отмеченных звездочкой. Начальное положение
Робота где-то в центре поля.
Вариант 2
1. Составьте
программу закрашивания 5-ти клеток влево от Робота, считая, что изначально
Робот находится у правого края поля.
2. Необходимо
провести Робота по лабиринту из начального положения (◊) в точку A.
3. Составьте
программу закрашивания клеток поля, отмеченных звездочкой. Начальное положение
Робота где-то в центре поля.
Вариант 3
1. Составьте
программу закрашивания 5-ти клеток по диагонали вправо вниз от Робота, считая,
что изначально Робот находится в левом верхнем углу поля.
2. Необходимо
провести Робота по лабиринту из начального положения (◊) в точку A.
3. Составьте
программу закрашивания клеток поля, отмеченных звездочкой. Начальное положение
Робота где-то в центре поля.
Вариант 4
1. Составьте
программу закрашивания 7-ти клеток по диагонали вправо вверх от Робота, считая,
что изначально Робот находится в левом нижнем углу поля.
2. Необходимо
провести Робота по лабиринту из начального положения (◊) в точку A.
3. Составьте
программу закрашивания клеток поля, отмеченных звездочкой. Начальное положение
Робота где-то в центре поля.
Вариант 5
1. Составьте
программу закрашивания 4-х клеток по диагонали влево вверх от Робота, считая,
что изначально Робот находится в правом нижнем углу поля.
2. Необходимо
провести Робота по лабиринту из начального положения (◊) в точку A.
3. Считая,
что Робот находится в левом нижнем углу поля, составьте программу закрашивания
клеток поля в виде буквы «Т» высотой в 6 клеток.
Вариант 6
1. Составьте программу закрашивания клеток поля,
отмеченных *. Начальное положение Робота обозначено значком ◊.
2. Необходимо
провести Робота по лабиринту из начального положения (◊) в точку A.
3. Считая,
что Робот находится в левом нижнем углу поля, составьте программу закрашивания
клеток поля в виде буквы «О» высотой в 6 клеток.
Вариант 7
1. Составьте программу закрашивания клеток поля,
отмеченных *. Начальное положение Робота обозначено значком ◊.
2. Необходимо
провести Робота вверх по лестнице из начального положения (◊) в точку A.
3. Считая,
что Робот находится в левом нижнем углу поля, составьте программу закрашивания
клеток поля в виде буквы «Г» высотой в 6 клеток.
Вариант 8
1. Составьте программу закрашивания всех клеток
поля вдоль нижней горизонтальной стены. Изначально Робот находится в правом
нижнем углу поля.
2. Необходимо провести Робота вверх по лестнице
из начального положения (◊) в точку A.
3. Считая,
что Робот находится в левом нижнем углу поля, составьте программу закрашивания
клеток поля в виде буквы «Е» высотой в 5 клеток.
Вариант 9
1. Составьте программу закрашивания всех клеток
поля вдоль правой вертикальной стены. Изначально Робот находится в правом
верхнем углу поля.
2. Необходимо провести Робота вниз по лестнице
из начального положения (◊) в точку A.
3. Считая,
что Робот находится в левом нижнем углу поля, составьте программу закрашивания
клеток поля в виде буквы «Р» высотой в 6 клеток.
Вариант 10
1. Составьте программу закрашивания 3-х клеток
по диагонали вправо вверх от Робота, считая, что изначально Робот находится
где-то в центре поля.
2. Необходимо провести Робота вдоль коридора из
начального положения (◊) до точки A, заглядывая в каждый боковой коридор.
2.
Считая, что Робот находится в
левом нижнем углу поля, составьте программу закрашивания клеток поля в виде
буквы «Ш» высотой в 4 клетки.
3.Цикл с предусловием (цикл ПОКА)
Задания расcчитаны на
группу в 10 человек. Каждая карточка содержит по два задания.
Вариант 1
1. Необходимо перевести Робота из начального
положения (◊) в точку A, закрашивая при этом указанные клетки поля. Размеры
стен и расстояние между ними могут быть произвольны.
2. Где-то
в поле Робота находится вертикальная стена, размеры которой неизвестны. Робот
из верхнего левого угла поля должен дойти до стены и закрасить все клетки
вокруг нее. Пример результата работы программы показан на рисунке.
Вариант 2
1. Необходимо перевести Робота из начального
положения (◊) в точку A, закрашивая при этом указанные клетки поля. Размеры
стен и расстояние между ними могут быть произвольны.
2. Где-то
в поле Робота находится прямоугольник, размеры которой неизвестны. Робот из
верхнего левого угла поля должен дойти до прямоугольника и закрасить все клетки
по периметру вокруг него. Пример результата работы программы показан на
рисунке.
Вариант 3
1. Необходимо перевести Робота из начального
положения (◊) в точку A, закрашивая при этом указанные клетки поля. Размеры
стен и расстояние между ними могут быть произвольны.
2. Где-то
в поле Робота находится горизонтальная стена с отверстием в одну клетку,
размеры которой неизвестны. Робот из произвольной клетки над стеной, но
обязательно напротив нее, должен дойти до стены и закрасить все клетки под ней,
как показано на рисунке.
Вариант 4
1. Необходимо перевести Робота из начального
положения (◊) в точку A, закрашивая при этом указанные клетки поля. Размеры
стен и расстояние между ними могут быть произвольны.
2. Где-то
в поле Робота находится вертикальная стена с отверстием в одну клетку, размеры
которой неизвестны. Робот из произвольной клетки справа от стены, но
обязательно напротив нее, должен дойти до стены и закрасить клетки за стеной,
как показано на рисунке.
Вариант 5
1. Необходимо перевести Робота из начального
положения (◊) в точку A, закрашивая при этом указанные клетки поля. Размеры
стен и расстояние между ними могут быть произвольны.
2. Где-то
в поле Робота находятся две горизонтальные стены смещенные друг относительно
друга, размеры которых неизвестны. Робот из произвольной клетки над верхней
стеной, но обязательно напротив нее, должен дойти до стены и закрасить все
клетки между стенами, как показано на рисунке.
Вариант 6
1. Необходимо перевести Робота из начального
положения (◊) в точку A, закрашивая при этом указанные клетки поля. Размеры
стен и расстояние между ними могут быть произвольны.
2. Где-то
в поле Робота находятся две вертикальный стены равной, но неизвестной длины,
расположенные одна за другой. Робот из произвольной клетки справа от правой
стены, но обязательно напротив нее, должен дойти до стены и закрасить клетки
между стенами, как показано на рисунке.
Вариант 7
1. Необходимо перевести Робота из начального положения
(◊) в точку A, закрашивая при этом указанные клетки поля. Размеры стен и
расстояние между ними могут быть произвольны.
2. Где-то
в поле Робота находится стена в виде уголка, размеры которой неизвестны. Робот
из произвольной клетки слева от стены, но обязательно напротив нее, должен
дойти до стены и закрасить все клетки вдоль стены за ней, как показано на
рисунке.
Вариант 8
1. Необходимо перевести Робота из начального
положения (◊) в точку A, закрашивая при этом указанные клетки поля. Размеры
стен и расстояние между ними могут быть произвольны.
2. Где-то
в поле Робота находится горизонтальный коридор шириной в одну клетку
неизвестной длины. Робот из верхнего левого угла поля должен дойти до коридора
и закрасить клетки внутри него, как показано на рисунке. По полю Робота в
произвольном порядке располагаются стены, но расстояние между ними больше одной
клетки.
Вариант 9
1. Необходимо перевести Робота из начального
положения (◊) в точку A, закрашивая при этом указанные клетки поля. Размеры
стен и расстояние между ними могут быть произвольны.
2. Где-то
в поле Робота находятся две стены равной, но неизвестной длины. В правой стене
имеется отверстие шириной в одну клетку. Робот из произвольной клетки справа от
правой стены, но обязательно напротив нее, должен дойти до стены и закрасить
все клетки между двумя стенами, как показано на рисунке.
Вариант 10
1. Необходимо перевести Робота из начального
положения (◊) в точку A, закрашивая при этом указанные клетки поля. Размеры
стен и расстояние между ними могут быть произвольны.
2. Где-то
в поле Робота находится прямоугольник неизвестного размера, в верхней стенке
которого имеется отверстие шириной в одну клетку. Робот из верхнего левого угла
поля должен дойти до прямоугольника и закрасить клетки внутри него по
периметру, как показано на рисунке.
4.Команды
ветвления (если, выбор)
Задания рассчитаны на
группу в 10 человек. Каждая карточка содержит по два задания.
Вариант 1
1. Необходимо провести Робота по коридору
шириной в одну клетку из начального положения (◊) до конца коридора, закрашивая
при этом все клетки коридора, которые имеют выход. Выходы размером в одну
клетку располагаются произвольно по всей длине коридора. Коридор заканчивается
тупиком. Коридор имеет два горизонтальных и диагональный участки в форме . Пример коридора
показан на рисунке.
2. Робот
движется вдоль стены, профиль которой показан на рисунке, от начального
положения (◊) до конца стены. Необходимо закрасить все внутренние углы стены,
как показано на примере. Размеры стены могут быть произвольны.
Вариант 2
1. Необходимо провести Робота по коридору
шириной в одну клетку из начального положения (◊) до конца коридора, закрашивая
при этом все клетки коридора, которые имеют выход. Выходы размером в одну
клетку располагаются произвольно по всей длине коридора. Коридор заканчивается
тупиком. Коридор имеет два горизонтальных и диагональный участки в форме . Пример коридора
показан на рисунке.
2. Робот
движется вдоль стены, профиль которой показан на рисунке, от начального
положения (◊) до конца стены. Необходимо закрасить все внутренние углы стены,
как показано на примере. Размеры стены могут быть произвольны.
Вариант 3
1. Необходимо провести Робота по коридору
шириной в одну клетку из начального положения (◊) до конца коридора, закрашивая
при этом все клетки коридора, которые имеют выход. Выходы размером в одну
клетку располагаются произвольно по всей длине коридора. Коридор заканчивается
тупиком. Коридор имеет два горизонтальных и диагональный участки в форме . Пример коридора
показан на рисунке.
2. Робот
движется вдоль стены от начального положения (◊) до конца стены. Стена
располагается по диагонали от правого верхнего к левому нижнему углу поля.
Необходимо закрасить все внутренние углы стены, как показано на примере.
Размеры стены могут быть произвольны.
Вариант 4
1. Необходимо провести Робота по коридору
шириной в одну клетку из начального положения (◊) до конца коридора, закрашивая
при этом все клетки коридора, которые имеют выход. Выходы размером в одну
клетку располагаются произвольно по всей длине коридора. Коридор заканчивается
тупиком. Коридор имеет два горизонтальных и диагональный участки в форме . Пример коридора
показан на рисунке.
2. Робот
движется вдоль стены от начального положения (◊) до конца стены. Стена
располагается по диагонали от правого нижнего к левому верхнему углу поля.
Необходимо закрасить все внутренние углы стены, как показано на примере.
Размеры стены могут быть произвольны.
Вариант 5
1. Необходимо провести Робота по коридору
шириной в одну клетку из начального положения (◊) до конца коридора, закрашивая
при этом все клетки коридора, которые имеют выход. Выходы размером в одну
клетку располагаются произвольно по всей длине коридора. Коридор заканчивается
тупиком. Коридор имеет два вертикальных и диагональный участки в форме . Пример коридора
показан на рисунке.
2. Робот
движется вдоль стены от начального положения (◊) до конца стены. Стена
располагается по диагонали от правого верхнего к левому нижнему углу поля.
Необходимо закрасить все внутренние углы стены, как показано на примере.
Размеры стены могут быть произвольны.
Вариант 6
1. Необходимо провести Робота по коридору
шириной в одну клетку из начального положения (◊) до конца коридора, закрашивая
при этом все клетки коридора, которые имеют выход. Выходы размером в одну
клетку располагаются произвольно по всей длине коридора. Коридор заканчивается
тупиком. Коридор имеет горизонтальный, вертикальный и диагональный участки в
форме . Пример коридора
показан на рисунке.
2. Робот
движется вдоль стены от начального положения (◊) до конца стены. Стена
располагается по диагонали от правого нижнего к левому верхнему углу поля.
Необходимо закрасить все внутренние углы стены, как показано на примере.
Размеры стены могут быть произвольны.
Вариант 7
1. Необходимо провести Робота по коридору
шириной в одну клетку из начального положения (◊) до конца коридора, закрашивая
при этом все клетки коридора, которые имеют выход. Выходы размером в одну
клетку располагаются произвольно по всей длине коридора. Коридор заканчивается
тупиком. Коридор имеет горизонтальный, вертикальный и диагональный участки в
форме . Пример коридора
показан на рисунке.
2. Робот
движется вдоль стены, профиль которой показан на рисунке, от начального
положения (◊) до конца стены. Необходимо закрасить все внутренние углы стены,
как показано на примере. Размеры стены могут быть произвольны.
Вариант 8
1. Необходимо провести Робота по коридору
шириной в одну клетку из начального положения (◊) до конца коридора, закрашивая
при этом все клетки коридора, которые имеют выход. Выходы размером в одну
клетку располагаются произвольно по всей длине коридора. Коридор заканчивается
тупиком. Коридор имеет горизонтальный, вертикальный и диагональный участки в
форме . Пример коридора
показан на рисунке.
2. Робот
движется вдоль стены, профиль которой показан на рисунке, от начального
положения (◊) до конца стены. Необходимо закрасить все внутренние углы стены,
как показано на примере. Размеры стены могут быть произвольны.
Вариант 9
1. Необходимо провести Робота по коридору
шириной в одну клетку из начального положения (◊) до конца коридора, закрашивая
при этом все клетки коридора, которые имеют выход. Выходы размером в одну
клетку располагаются произвольно по всей длине коридора. Коридор заканчивается
тупиком. Коридор имеет горизонтальный, вертикальный и диагональный участки в
форме . Пример коридора
показан на рисунке.
2. Робот
движется вдоль стены, профиль которой показан на рисунке, от начального
положения (◊) до конца стены. Необходимо закрасить все клетки стены, которые
огорожены с трех сторон, как показано на примере. Размеры стены могут быть
произвольны.
Вариант 10
1. Необходимо провести Робота по коридору
шириной в одну клетку из начального положения (◊) до конца коридора, закрашивая
при этом все клетки коридора, которые имеют выход. Выходы размером в одну
клетку располагаются произвольно по всей длине коридора. Коридор заканчивается
тупиком. Коридор имеет два вертикальных и диагональный участки в форме . Пример коридора показан
на рисунке.
2. Робот
движется вдоль стены, профиль которой показан на рисунке, от начального
положения (◊) до конца стены. Необходимо закрасить все углы стены, которые
огорожены только с двух сторон, как показано на примере. Размеры стены могут быть
произвольны.
Список литературы
1. Босова Л.Л. Информатика: уч. для 9 кл. –2-е изд., испр. – М.:
БИНОМ. Лаборатория знаний, 2014
2. Камалова Н.А.http://festival.1september.ru/articles/594645/
3. Нурмухамедов Г.М. Информатика. Теоретические основы: учеб. Пос.
для подготовки к ЕГЭ. – СПб.: БХВ-Петербург, 2012
4. Поляков К.Ю., Еремин Е.А. Информатика. Углубленный уровень: уч.
5. для 10кл.: в 2 ч. Ч.1. – М.: БИНОМ. Лаборатория знаний, 2013
6. Семакин И.Г., Залогова Л.А., Русаков С.В. Информатика и ИКТ: уч.
для 9 кл. – М.: БИНОМ. Лаборатория знаний, 2012
7. Сухих Н.А.Поурочные разработки по информатике: 9 класс. –М.: ВАКО,
2012.
Конструирование алгоритмов
Последовательное построение алгоритма
Существуют различные методы конструирования
(разработки, построения) алгоритмов. Мы познакомимся с одним из них — методом последовательного построения (уточнения) алгоритма. Иначе он называется методом разработки «сверху вниз», нисходящим
методом или методом пошаговой детализации.
Процесс последовательного построения алгоритма
выглядит следующим образом.
На первом шаге мы считаем, что перед нами
совершенный исполнитель, который «всё знает и всё умеет». Поэтому достаточно определить исходные данные и результаты алгоритма, а сам алгоритм представить в виде единого предписания — постановки
задачи (рис. 2.4).

Рис. 2.4.
Линейный алгоритм, являющийся результатом первого этапа детализации задачи
Если исполнитель не обучен исполнять заданное
предписание, то необходимо представить это предписание в виде совокупности более простых предписаний (команд).
Для этого:
• задачу разбивают на несколько частей, каждая из
которых проще всей задачи;
• решение каждой части задачи формулируют в
отдельной команде, которая также может выходить за рамки системы команд исполнителя;
• при наличии в алгоритме предписаний, выходящих за
пределы возможностей исполнителя, такие предписания вновь представляются в виде совокупности ещё более простых предписаний.
Процесс продолжается до тех пор, пока все
предписания не будут понятны исполнителю.
Объединяя полученные предписания в единую
совокупность выполняемых в определённой последовательности команд, получаем требуемый алгоритм решения исходной задачи.
Разработка алгоритма методом последовательного
уточнения для исполнителя Робот
Вы уже знакомы с исполнителем Робот. Он действует на
клетчатом поле, между клетками которого могут быть стены.
Система команд исполнителя
Робот:

В одном условии можно использовать несколько команд,
применяя логические операции И, ИЛИ, НЕ.
Известно, что Робот находится где-то в
горизонтальном коридоре. Ни одна из клеток коридора не закрашена.

Составим алгоритм, под управлением которого Робот
закрасит все клетки этого коридора и вернётся в исходное положение.

Представим план действий Робота следующими
укрупнёнными шагами (модулями):

Детализируем каждый из пяти модулей.
1. Чтобы закрасить все клетки коридора, находящиеся
левее Робота, прикажем Роботу шагнуть влево и выполнить цикл — ПОКА:
влево
нц пока сверху стена и снизу стена закрасить; влево
кц
Под управлением этого алгоритма Робот закрасит все
клетки коридора, находящиеся левее от него, и окажется в клетке левее коридора.

2. Командой вправо вернём Робота в коридор. Наша
задача — вернуть Робота в исходную клетку. Эта клетка — первая незакрашенная клетка, находящаяся правее Робота. Поэтому пока занимаемая Роботом клетка оказывается закрашенной, будем перемещать
его вправо.
вправо
нц пока клетка закрашена вправо
кц
Под управлением этого алгоритма Робот окажется в
исходной клетке.

3. Выполнив команду вправо, Робот пройдёт исходную
клетку и займёт клетку правее исходной. Теперь можно закрашивать клетки коридора, расположенные правее исходной.
вправо
нц пока сверху стена и снизу стена закрасить; вправо
кц

4. Так как, выполнив предыдущий алгоритм, Робот
оказался правее коридора, командой влево вернём его в коридор. Возвращение в исходную клетку обеспечивается алгоритмом:
влево
нц пока клетка закрашена влево
кц

5. По команде закрасить Робот закрашивает исходную
клетку. Полностью программа управления Роботом выглядит так:

Вспомогательные алгоритмы
При построении новых алгоритмов нередко возникают
ситуации, когда в разных местах алгоритма необходимо выполнение одной и той же последовательности шагов обработки данных. Для такой последовательности шагов создают отдельный алгоритм, называемый
вспомогательным. В качестве вспомогательных могут использоваться алгоритмы, ранее разработанные для решения других задач.
Вспомогательный алгоритм — алгоритм, целиком
используемый в составе другого алгоритма.
Пример 1. В среде КуМир составим алгоритм для исполнителя Робот, под
управлением которого он нарисует узор:

Начальное положение Робота отмечено звёздочкой. В
алгоритме использован вспомогательный алгоритм фигура.

При представлении алгоритмов с помощью блок-схем для
обозначения команды вызова вспомогательного алгоритма используется блок «предопределённый процесс» (рис. 2.5), внутри которого записывается название (имя) вспомогательного алгоритма, после
которого в скобках перечисляются параметры — входные данные и результаты.

Рис. 2.5. Блок «предопределённый
процесс»
Вспомогательный алгоритм делает структуру алгоритма
более понятной.
Пример 2. Вспомним алгоритм вычисления степени с натуральным показателем
у = аn. Соответствующая блок-схема:

Степень с целым показателем у = ах, где х
— целое число, а ≠ 0 вычисляется так:

В приведённой записи дважды фигурирует вычисление
степени с натуральным показателем. Поэтому в алгоритм вычисления степени с целым показателем можно включить вызов вспомогательного алгоритма вычисления степени с натуральным показателем.
Соответствующая блок-схема:

Алгоритм, представленный на блок-схеме, является
основным по отношению к вызываемому в нём вспомогательному алгоритму.
Параметрами используемого вспомогательного алгоритма
являются величины а, n, у. Это формальные параметры, они используются при описании алгоритма. При конкретном обращении к вспомогательному алгоритму формальные параметры заменяются фактическими
параметрами, т. е. именно теми величинами, для которых будет исполнен вспомогательный алгоритм. Типы, количество и порядок следования формальных и фактических параметров должны совпадать.
Команда вызова вспомогательного алгоритма
исполняется следующим образом (рис. 2.6):
1) формальные входные данные вспомогательного алгоритма заменяются
значениями фактических входных данных, указанных в команде вызова вспомогательного алгоритма;
2) для заданных входных данных исполняются команды вспомогательного
алгоритма;
3) полученные результаты присваиваются переменным с именами
фактических результатов;
4) осуществляется переход к следующей команде основного
алгоритма.

Рис. 2.6. Схема выполнения команды вызова
вспомогательного алгоритма
Алгоритм, в котором прямо или косвенно содержится
ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.
Рассмотрим несколько примеров рекурсивных
алгоритмов.
Пример 3. Алгоритм вычисления степени с натуральным показателем п для
любого вещественного числа а можно представить в виде рекурсивного:

Число а в степени n (n-я степень числа а) есть не
что иное, как произведение аn-1 • а; в свою очередь, аn-1 = аn-2 • а и т. д.
Пример 4. Рекурсивный алгоритм положен в основу эффективного решения
головоломки «Ханойская башня».

Интерактивная игра «Ханойские башни» (195747)
поможет вам вспомнить условие и алгоритм решения головоломки (http://sc.edu.ru/).
Пример 5. Рассмотрим алгоритм построения геометрической фигуры, которая
называется снежинкой Коха. Шаг процедуры построения состоит в замене средней трети каждого из имеющихся отрезков двумя новыми такой же длины, как показано на рисунке:

С каждым шагом фигура становится всё причудливее.
Граница снежинки Коха — положение кривой после выполнения бесконечного числа шагов.
Попробуйте подсчитать, сколько рёбер в границе
снежинки Коха после четвёртого шага; после пятого шага.
§ 2.3. Конструирование алгоритмов
Информатика. 9 класса. Босова Л.Л. Оглавление
Ключевые слова:
- последовательное построение алгоритма
- вспомогательный алгоритм
- формальные параметры
- фактические параметры
- рекурсивный алгоритм
Последовательное построение алгоритма
Существуют различные методы конструирования (разработки, построения) алгоритмов. Мы познакомимся с одним из них — методом последовательного построения (уточнения) алгоритма. Иначе он называется методом разработки «сверху вниз», нисходящим методом или методом пошаговой детализации.
Процесс последовательного построения алгоритма выглядит следующим образом.
На первом шаге мы считаем, что перед нами совершенный исполнитель, который «всё знает и всё умеет». Поэтому достаточно определить исходные данные и результаты алгоритма, а сам алгоритм представить в виде единого предписания — постановки задачи (рис. 2.2).

Если исполнитель не обучен исполнять заданное предписание, то необходимо представить это предписание в виде совокупности более простых предписании (команд). Для этого:
- задачу разбивают на несколько частей, каждая из которых проще всей задачи;
- решение каждой части задачи формулируют в отдельной команде, которая также может выходить за рамки системы команд исполнителя;
- при наличии в алгоритме предписаний, выходящих за пределы возможностей исполнителя, такие предписания вновь представляются в виде совокупности ещё более простых предписаний.
Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.
Объединяя полученные предписания в единую совокупность выполняемых в определённой последовательности команд, получаем требуемый алгоритм решения исходной задачи.
Разработка алгоритма методом последовательного уточнения для исполнителя Робот
Вы уже знакомы с исполнителем Робот. Он действует на клетчатом поле, между клетками которого могут быть стены.
Система команд исполнителя Робот:


В одном условии можно использовать несколько команд, применяя логические операций И, ИЛИ, НЕ.
Известно, что Робот находится где-то в горизонтальном коридоре. Ни одна из клеток коридора не закрашена.

Составим алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернётся в исходное положение.

Представим план действий Робота следующими укрупнёнными шагами (модулями):

Детализируем каждый из пяти модулей.
1. Чтобы закрасить все клетки коридора, находящиеся левее Робота, прикажем Роботу шагнуть влево и выполнить цикл-ПОКА:
- влево
- нц пока сверху стена и снизу стена
- закрасить; влево
- кц
Под управлением этого алгоритма Робот закрасит все клетки коридора, находящиеся левее от него, и окажется на клетке рядом с левой границей коридора.

2. Командой вправо вернём Робота в коридор. Наша задача — вернуть Робота в исходную точку. Эта точка имеет единственный отличительный признак — она не закрашена. Поэтому пока занимаемая Роботом клетка оказывается закрашенной, будем перемещать его вправо.
- вправо.
- вправо
- нц пока клетка закрашена
- вправо
- кц
Под управлением этого алгоритма Робот окажется в исходной клетке.

4. Так как, выполнив предыдущий алгоритм, Робот оказался правее коридора, командой влево вернём его в коридор. Возвращение в исходную точку обеспечивается алгоритмом:
- влево
- нц пока клетка закрашена
- влево
- кц

5. По команде закрасить Робот закрашивает исходную клетку.
Полностью программа управления Роботом выглядит так:
- алг
- нач
- влево
- нц пока сверху стена и снизу стена
- закрасить; влево
- кц
- вправо
- нц пока клетка закрашена
- вправо
- кц
- вправо
- нц пока сверху стена и снизу стена
- закрасить; вправо
- кц
- влево
- нц пока клетка закрашена
- влево
- кц
- закрасить
- кон
Вспомогательные алгоритмы
При построении новых алгоритмов нередко возникают ситуации, когда в разных местах алгоритма необходимо выполдение одной и той же последовательности шагов обработки данных. Для такой последовательности шагов создают отдельный алгоритм, называемый вспомогательным. В качестве вспомогательных могут использоваться алгоритмы, ранее разработанные для решения других задач.
Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма.
Пример 1. В среде КуМир составим алгоритм для исполнителя Робот, под управлением которого он нарисует узор:

Начальное положение Робота отмечено звёздочкой. В алгоритме использован вспомогательный алгоритм фигура.
- использовать Робот
- алг узор
- нач
- фигура
- вправо; вниз
- фигура
- вправо; вниз
- фигура
- кон
- алг фигура
- нач
- закрасить; вниз
- закрасить; вправо; закрасить; вправо; закрасить
- вверх; закрасить
- кон
При представлении алгоритмов с помощью блок-схем для обозначения команды вызова вспомогательного алгоритма используется блок «предопределённый процесс» (рис. 2.3), внутри которого записывается название (имя) вспомогательного алгоритма, после которого в скобках перечисляются параметры — входные данные и результаты.

Вспомогательный алгоритм делает структуру алгоритма более понятной.
Пример 2.
Вспомним алгоритм вычисления степени с натуральным показателем у = аn. Соответствующая блок-схема:

Степень с целым показателем у = ах, где х — целое число, а ? 0 вычисляется так:

В приведённой записи дважды фигурирует вычисление степени с натуральным показателем. Поэтому в алгоритм вычисления степени с целым показателем можно включить вызов вспомогательного алгоритма вычисления степени с натуральным показателем. Соответствующая блок-схема:

Алгоритм, представленный на блок-схеме, является основным по отношению к вызываемому в нём вспомогательному алгоритму.
Параметрами используемого вспомогательного алгоритма являются величины а, n, у. Это формальные параметры, они используются при описании алгоритма. При конкретном обращении к вспомогательному алгоритму формальные параметры заменяются фактическими параметрами, т. е. именно теми величинами, для которых будет исполнен вспомогательный алгоритм. Типы, количество и порядок следования формальных и фактических параметров должны совпадать.
Команда вызова вспомогательного алгоритма исполняется следующим образом (рис. 2.4):
- 1) формальные входные данные вспомогательного алгоритма заменяются значениями фактических входных данных, указанных в команде вызова вспомогательного алгоритма;
- 2) для заданных входных данных исполняются команды вспомогательного алгоритма;
- 3) полученные результаты присваиваются переменным с именами фактических результатов;
- 4) осуществляется переход к следующей команде основного алгоритма.

Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.
Рассмотрим несколько примеров рекурсивных алгоритмов.
Пример 3. Алгоритм вычисления степени с натуральным показателем n для любого вещественного числа а можно представить в виде рекурсивного:

n-я степень числа а есть не что иное, как произведение аn-1 • а; в свою очередь, аn-1 = аn-2 • а и т. д.
Пример 4. Рекурсивный алгоритм положен в основу эффективно го решения головоломки «Ханойская башня».

- Интерактивная игра «Ханойские башни» (195747) поможет вам вспомнить условие и алгоритм решения головоломки (http://sc.edu.ru/).
Пример 5. Рассмотрим алгоритм построения геометрической фигуры, которая называется снежинкой Коха. Шаг процедуры построения состоит в замене средней трети каждого из имеющихся отрезков двумя новыми такой же длины, как показано на рисунке:

С каждым шагом фигура становится всё причудливее. Граница снежинки Коха — положение кривой после выполнения бесконечного числа шагов.
Попробуйте подсчитать, сколько рёбер в границе снежинки Коха после четвёртого шага; после пятого шага.
САМОЕ ГЛАВНОЕ
Один из основных методов конструирования алгоритмов — метод последовательного построения алгоритма. Его суть состоит в том, что: исходная задача разбивается на несколько частей, каждая из которых проще всей задачи, и решение каждой части формулируется в отдельной команде; если получаются команды, выходящие за пределы возможностей исполнителя, то они представляются в виде совокупности ещё более простых предписаний. Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма.Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?
2. Почему при решении сложной задачи затруднительно сразу конкретизировать все необходимые действия?
3. В чём заключается метод последовательного уточнения при построении алгоритма?
4. Какая связь между методом последовательного построения алгоритма и такими процессами, как написание сочинения или подготовка к многодневному туристическому походу?
5. Известен рост каждого из n учеников 9А класса и m учеников 9Б класса. Опишите укрупнёнными блоками алгоритм сравнения среднего роста учеников этих классов.
6. В ряду из десяти клеток правее Робота некоторые клетки закрашены. Последняя закрашенная клетка может примыкать к стене. Составьте алгоритм, который закрашивает клетки выше и ниже каждой закрашенной клетки. Проверьте работу алгоритма в следующих случаях
7. Для чего нужны вспомогательные алгоритмы?
8. Опишите процесс выполнения команды вызова вспомогательного алгоритма в основном алгоритме.
9. Сталкивались ли вы с идеей формальных и фактических параметров при изучении математики и физики? Приведите пример.
10. Какие алгоритмы называют рекурсивными? Приведите пример рекурсии из жизни.
11. Составьте алгоритмы, под управлением которых Робот закрасит указанные клетки. При необходимости используйте вспомогательный алгоритм.
§ 2.2. Одномерные массивы целых чисел
§ 2.3. Конструирование алгоритмов
§ 2.4. Запись вспомогательных алгоритмов на языке Паскаль
Линейные алгоритмы в КуМир.
Линейные алгоритмы в КуМир.
Какие операторы неправильные? 2 алг
Какие операторы неправильные?
2
алг Ошибки
нач
цел a, b
вещ x, y
a := 5
10 := x
y := 7,8
b := 2.5
x := 2*(a + y)
a := b + x
кон
имя переменной должно быть слева от знака :=
целая и дробная часть отделяются точкой
нельзя записывать вещественное значение в целую переменную
Что будет выведено? 3 цел a = 1, b = 3 вывод «a+», b, «=a+b» a+3=a+b цел a = 1, b = 3 вывод a,…
Что будет выведено?
3
цел a = 1, b = 3
вывод «a+», b, «=a+b»
a+3=a+b
цел a = 1, b = 3
вывод a, «=F(«, b, «)»
1=F(3)
цел a = 1, b = 3
вывод «a=F(«, b, «);»
цел a = 1, b = 3
вывод a+b, «>», b, «!»
цел a = 1, b = 3
вывод «F(«, b, «)=X(«, a, «)»
a=F(3)
4>3!
F(3)=X(1)
Как записать оператор «вывод»? 4 цел a = 1, b = 3 вывод «X(«, b, «=», a
Как записать оператор «вывод»?
4
цел a = 1, b = 3
вывод «X(«, b, «=», a
X(3)=1
4=1+3
f(1)>f(3)
<1<>3>
1+3=?
цел a = 1, b = 3
вывод a+b, «=», a, «+», b
цел a = 1, b = 3
вывод «f(«, a, «)>f(«, b, «)»
цел a = 1, b = 3
вывод «<«, a, «<>», b, «>»
цел a = 1, b = 3
вывод a, «+», b, «=?»
Блок-схема линейного алгоритма 5 начало конец действие ввод блок «начало» блок «ввод» блок «процесс» блок «вывод» блок «конец» вывод
Блок-схема линейного алгоритма
5
начало
конец
действие
ввод
блок «начало»
блок «ввод»
блок «процесс»
блок «вывод»
блок «конец»
вывод
По данной блок-схеме вычисления значения некоторой функции, восстановите условие задачи; напишите формулу вычисления значения функции
По данной блок-схеме вычисления значения некоторой функции, восстановите условие задачи; напишите формулу вычисления значения функции.
Постановка задачи: Составить программу вычисления площади треугольника, если заданы координаты его сторон: x1, y1; x2, y2; x3,y3
Постановка задачи:
Составить программу вычисления площади треугольника, если заданы координаты его сторон: x1, y1; x2, y2; x3,y3.
2. Математическая модель:
ФОРМУЛА ГЕРОНА:
Где a, b, c – длины сторон треугольника, p — полупериметр
Формула Герона
Длина стороны вычисляется по формуле:
НАЧАЛО Ввод координат вершин треугольника x1, y1, x2, y2, x3, y3
НАЧАЛО
Ввод координат вершин треугольника
x1, y1, x2, y2, x3, y3
Построение алгоритма
P=(a+b+c)/2
Вывод значения S
конец
Домашнее задание Составить блок –схему и программу для решения следующей задачи:
Домашнее задание
Составить блок –схему и программу для решения следующей задачи:
Двум переменным А и В заданы разные значения. Поменяйте эти значе-ния местами
1) с использованием третьей переменной,
2) без использования других переменных.
Программирование на алгоритмическом языке (7 класс)
- Введение
- Ветвления
- Сложные условия
- Циклы
- Циклы с переменной
- Графика
- Вспомогательные алгоритмы
- Анимация
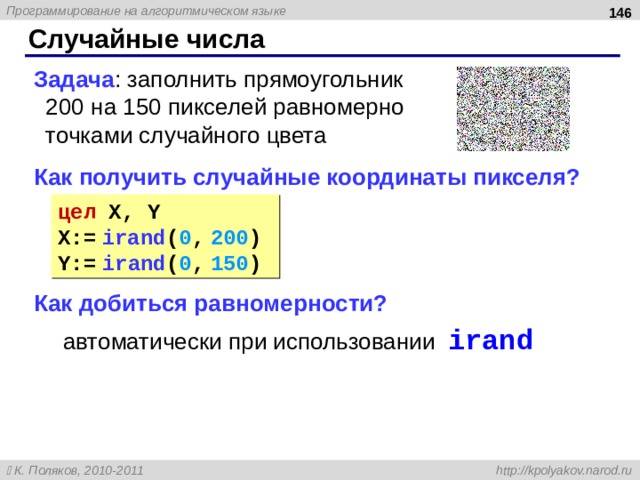
- Случайные числа
Программирование на алгоритмическом языке
Тема 1. Введение
Алгоритм
Алгоритм – это четко определенный план решения задачи для исполнителя.
Свойства алгоритма
- дискретность : состоит из отдельных шагов (команд) понятность : должен включать только команды, известные исполнителю конечность : позволяет получить решение задачи за конечное число шагов определенность : при одинаковых исходных данных всегда выдает один и тот же результат массовость : может применяться при различных исходных данных
- дискретность : состоит из отдельных шагов (команд)
- понятность : должен включать только команды, известные исполнителю
- конечность : позволяет получить решение задачи за конечное число шагов
- определенность : при одинаковых исходных данных всегда выдает один и тот же результат
- массовость : может применяться при различных исходных данных
Программа
Программа – это
- алгоритм, записанный на каком-либо языке программирования набор команд для исполнителя
- алгоритм, записанный на каком-либо языке программирования
- набор команд для исполнителя
Команда – это описание действий, которые должен выполнить исполнитель.
- откуда взять исходные данные? что нужно с ними сделать?
- откуда взять исходные данные?
- что нужно с ними сделать?
Простейшая программа
название алгоритма
алг Первый
нач | начало алгоритма
кон | конец алгоритма
комментарии после | не обрабатываются
?
Что делает эта программа ?
5
5
Вывод текста на экран
алг Вывод на экран
нач
вывод «2+»
вывод «2=?» , нс
вывод «Ответ: 4»
кон
новая строка
Протокол :
2+2=?
Ответ: 4
5
Задания
«4»: Вывести на экран текст «лесенкой»
Вася
пошел
гулять
«5»: Вывести на экран рисунок из букв
Ж
ЖЖЖ
ЖЖЖЖЖ
ЖЖЖЖЖЖЖ
HH HH
ZZZZZ
Переменные
Задача. Ввести с клавиатуры два числа и найти их сумму.
Протокол :
Введите два целых числа
25 30
25+30=55
компьютер
пользователь
компьютер считает сам!
?
- Как ввести числа в память?
- Где хранить введенные числа ?
- Как вычислить?
- Как вывести результат?
8
Программа
алг Сумма
нач
| ввести два числа
| вычислить их сумму
| вывести сумму на экран
кон
Псевдокод – алгоритм на русском языке с элементами языка программирования.
!
Компьютер не может исполнить псевдокод!
9
9
Переменные
Переменная – это величина, имеющая имя, тип и значение. Значение переменной можно изменять во время работы программы.
Значение
Другой тип данных
?
Поместится?
!
В переменной хранятся данные определенного типа!
Имя
10
Имена переменных
МОЖНО использовать
- латинские буквы ( A-Z) , русские буквы (А-Я) цифры знак подчеркивания _
- латинские буквы ( A-Z) , русские буквы (А-Я)
- цифры
- знак подчеркивания _
заглавные и строчные буквы различаются
имя не может начинаться с цифры
Какие имена правильные?
AXby R&B 4Wheel Вася “PesBarbos” TU154 [QuQu] _ABBA A+B
Объявление переменных
Типы переменных:
- цел | целая вещ | вещественная и другие…
- цел | целая
- вещ | вещественная
- и другие…
выделение места в памяти
Объявление переменных:
тип – целые
список имен переменных
цел a, b, c
Как записать значение в переменную?
Оператор присваивания
!
При записи нового значения старое стирается!
5
a := 5
Оператор – это команда языка программирова-ния (инструкция).
Оператор присваивания – это команда для записи нового значения в переменную.
13
Блок-схема линейного алгоритма
начало
блок «начало»
ввод a , b
блок «ввод»
c := a + b
блок «процесс»
вывод c
блок «вывод»
конец
блок «конец»
Как ввести значение с клавиатуры?
Оператор ввода
5
ввод a
!
- Программа ждет, пока пользователь введет значение и нажмет Enter .
- Введенное значение записывается в переменную a .
15
Ввод значений двух переменных
Ввод значений двух переменных .
ввод a, b
через пробел:
25 30
через запятую:
25,30
a
25
b
30
a
25
b
30
16
Изменение значения переменной
Пример:
алг Тест
нач
цел a, b
a := 5
b := a + 2
a := (a + 2 )*(b – 3 )
b := b + 1
кон
a
5
?
5
b
?
5+2
7
a
7*4
28
5
b
7
7+1
8
Арифметические операции
+ сложение – вычитание
* умножение / деление
- + сложение – вычитание * умножение / деление
цел a, b
- цел a, b
a := 7 * 3 – 4
a := a * 5
- a := 7 * 3 – 4 a := a * 5
Вывод данных
| вывод значения | переменной a
вывод a
| вывод значения | переменной a и переход | на новую строчку
вывод a , нс
| вывод текста
вывод ‘ Привет! ‘
вывод ‘ Ответ: ‘ , c
| вывод текста и значения переменной c
вывод a, ‘+’ , b, ‘=’ , c
Задача: сложение чисел
Задача. Ввести два целых числа и вывести на экран их сумму.
Простое решение:
алг Сумма
нач
цел a, b, c
ввод a, b
c := a + b
вывод c
кон
?
Что плохо?
20
Полное решение
алг Сумма
нач
цел a, b, c
вывод «Введите два целых числа»
ввод a, b
c := a + b
вывод a, «+» , b, «=» , c
кон
подсказка
компьютер
Протокол :
Введите два целых числа
25 30
25+30=55
пользователь
Задания
«3»: Ввести три числа, найти их сумму.
Пример:
Введите три числа:
4 5 7
4+5+7=16
«4»: Ввести три числа, найти их сумму и произведение.
Пример:
Введите три числа:
4 5 7
4+5+7=16
4*5*7=140
Задания
«5»: Ввести три числа, найти их сумму, произведение и среднее арифметическое.
Пример:
Введите три числа:
4 5 7
4+5+7=16
4*5*7=140
(4+5+7) / 3 =5.33 3333
Какие операторы неправильные?
алг Ошибки
нач
цел a, b
вещ x, y
a := 5
10 := x
y := 7 , 8
b := 2.5
x := 2 *(a + y)
a := b + x
кон
имя переменной должно быть слева от знака :=
целая и дробная часть отделяются точкой
нельзя записывать вещественное значение в целую переменную
Арифметические операции
+ сложение – вычитание
* умножение / деление
div деление нацело (остаток отбрасывается)
mod остаток от деления
- + сложение – вычитание * умножение / деление div деление нацело (остаток отбрасывается) mod остаток от деления
цел a, b
- цел a, b
a := 7 * 3 — 4 | 17
a := a * 5 | 85
b := div ( a, 10 ) | 8
a := mod (a, 10 ) | 5
- a := 7 * 3 — 4 | 17 a := a * 5 | 85 b := div ( a, 10 ) | 8 a := mod (a, 10 ) | 5
Порядок выполнения операций
- вычисление выражений в скобках умножение, деление, div , mod слева направо сложение и вычитание слева направо
- вычисление выражений в скобках
- умножение, деление, div , mod слева направо
- сложение и вычитание слева направо
1 2 4 5 3 6
- 1 2 4 5 3 6
z := ( 5 *a+c)/a*(b-c)/ b
- z := ( 5 *a+c)/a*(b-c)/ b
2 3 5 4 1 10 6 9 8 7
- 2 3 5 4 1 10 6 9 8 7
x:= ( 5 *c*c-d*(a+b))/((c+d)*(d- 2 *a))
- x:= ( 5 *c*c-d*(a+b))/((c+d)*(d- 2 *a))
Ручная прокрутка программы
алг Тест
нач
цел a, b
a := 5
b := a + 2
a := (a + 2 )*(b – 3 )
b := div (a, 5 )
a := mod (a,b)
a := a + 1
b := mod (a+ 14 , 7 )
кон
a
b
?
?
5
7
28
5
3
4
4
Команда «вывод»
цел a = 1, b = 3
вывод a, «+» , b, «=» , a+b
список вывода
- элементы разделяются запятыми элементы в кавычках – выводятся без изменений выражения (элементы без кавычек) вычисляются и выводится их результат
- элементы разделяются запятыми
- элементы в кавычках – выводятся без изменений
- выражения (элементы без кавычек) вычисляются и выводится их результат
?
Что будет выведено?
1+3=4
28

Что будет выведено?
цел a = 1, b = 3
вывод » a +» , b, «= a+b »
a +3= a+b
цел a = 1, b = 3
вывод a , «= F( » , b, » )»
1= F(3)
цел a = 1, b = 3
вывод » a = F( » , b, » );»
a = F(3);
цел a = 1, b = 3
вывод a+b , » » , b, » !»
4 3!
цел a = 1, b = 3
вывод » F( » , b, » ) = X( » , a, » )»
F(3) = X(1)

Как записать оператор «вывод»?
цел a = 1, b = 3
вывод » X( » , b, » ) =» , a
X(3)=1
цел a = 1, b = 3
вывод a + b, » = » , a , » + » , b
4=1+ 3
цел a = 1, b = 3
вывод » f( » , a , » )f( » , b , » ) »
f(1)f(3)
цел a = 1, b = 3
вывод » » , b , » »
3
цел a = 1, b = 3
вывод a , » + » , b, » =? »
1+3 = ?
Программирование на алгоритмическом языке
Тема 2. Ветвления
Разветвляющиеся алгоритмы
Задача. Ввести два целых числа и вывести на экран наибольшее из них.
Идея решения: надо вывести на экран первое число, если оно больше второго, или второе, если оно больше первого.
Особенность: действия исполнителя зависят от некоторых условий ( если … иначе … ).
Алгоритмы, в которых последовательность шагов зависит от выполнения некоторых условий, называются разветвляющимися.
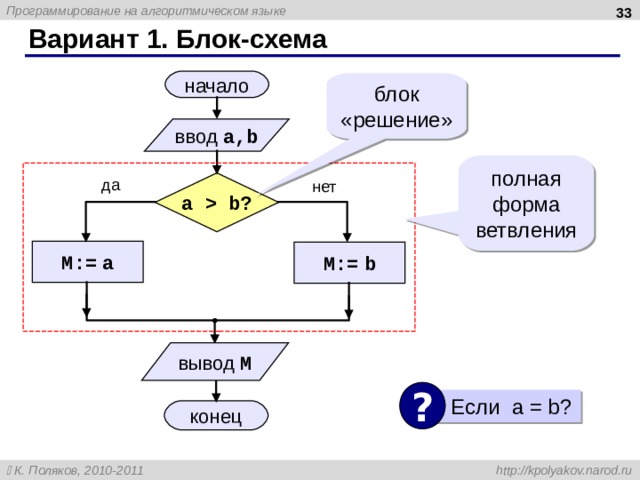
Вариант 1. Блок-схема
начало
блок «решение»
ввод a,b
полная форма ветвления
да
нет
a b?
M:= a
M:= b
вывод M
?
Если a = b?
конец
33
33
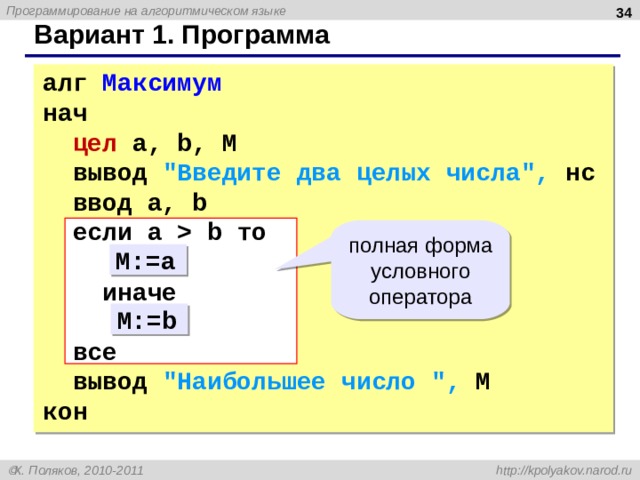
Вариант 1. Программа
алг Максимум нач цел a, b, M вывод «Введите два целых числа», нс ввод a, b если a b то иначе все вывод «Наибольшее число «, M кон
полная форма условного оператора
M:=a
M:=b
33
33
Условный оператор
если условие то
| что делать, если условие верно
иначе
| что делать, если условие неверно
все
!
Вторая часть (иначе) может отсутствовать!
35
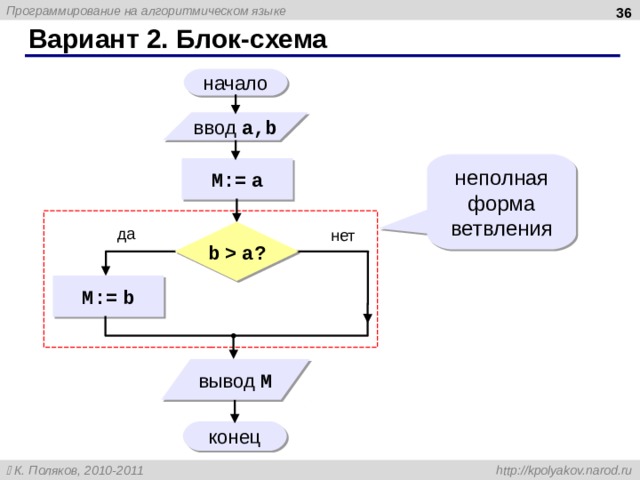
Вариант 2 . Блок-схема
начало
ввод a,b
неполная форма ветвления
M:= a
да
нет
b a?
M:= b
вывод M
конец
Вариант 2. Программа
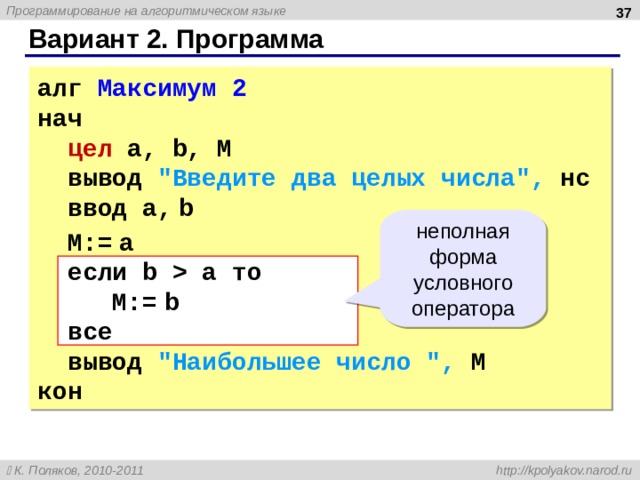
алг Максимум 2 нач цел a, b, M вывод «Введите два целых числа», нс ввод a, b
M:= a если b a то M:= b все вывод «Наибольшее число «, M кон
неполная форма условного оператора

Вариант 2б. Программа
алг Максимум 2 б нач цел a, b, M вывод «Введите два целых числа», нс ввод a, b
M:= b если ??? то ??? все вывод «Наибольшее число «, M кон
a b
M:= a
Задания
« 3 »: Ввести два числа и вывести их в порядке возрастания.
Пример:
Введите два числа:
15 9
Ответ: 9 15
«4»: Ввести три числа и найти наибольшее из них.
Пример:
Введите три числа:
4 15 9
Наибольшее число 15
Задания
«5»: Ввести пять чисел и найти наибольшее из них.
Пример:
Введите пять чисел:
4 15 9 56 4
Наибольшее число 5 6
Программирование на алгоритмическом языке
Тема 3. Сложные условия
Сложные условия
Задача. Фирма набирает сотрудников от 25 до 40 лет включительно. Ввести возраст человека и определить, подходит ли он фирме (вывести ответ «подходит» или «не подходит» ) .
Особенность: надо проверить, выполняются ли два условия одновременно.
?
Можно ли решить известными методами ?
42
42
Вариант 1. Алгоритм
начало
ввод x
да
нет
x = 25?
да
нет
x
“ подходит ”
“ не подходит ”
“ не подходит ”
конец
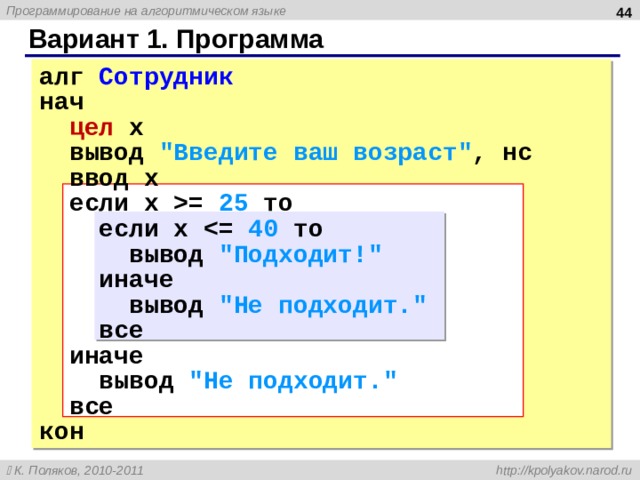
Вариант 1. Программа
алг Сотрудник
нач
цел x
вывод «Введите ваш возраст» , нс
ввод x
если x = 25 то
если x
вывод «Подходит!»
иначе
вывод «Не подходит.»
все
иначе
вывод «Не подходит.»
все
кон
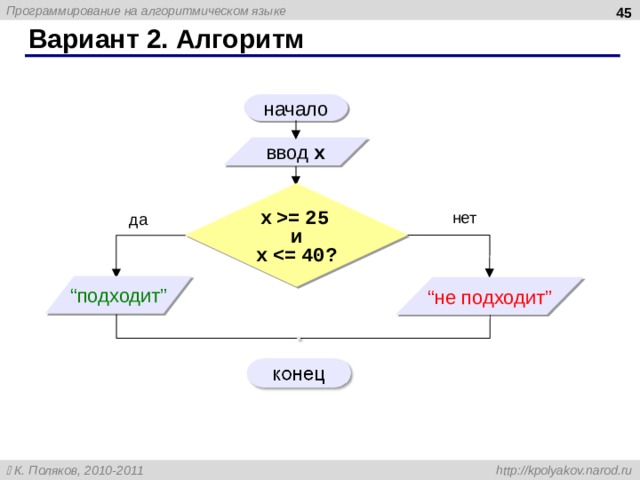
Вариант 2. Алгоритм
начало
ввод x
x = 25 и
x
нет
да
“ подходит ”
“ не подходит ”

Вариант 2 . Программа
алг Сотрудник
нач
цел x
вывод «Введите ваш возраст» , нс
ввод x
если x = 25 и x
вывод «Подходит!»
иначе
вывод «Не подходит.»
все
кон
сложное условие

Сложные условия
Простые условия (отношения)
= =
Сложное условие – это условие, состоящее из нескольких простых условий (отношений), связанных с помощью логических операций :
- И – одновременное выполнение условий
- И – одновременное выполнение условий
x = 25 И x
- x = 25 И x
- ИЛИ – выполнение хотя бы одного из условий
- ИЛИ – выполнение хотя бы одного из условий
x ИЛИ x = 40
- x ИЛИ x = 40
- НЕ – отрицание, обратное условие
- НЕ – отрицание, обратное условие
НЕ ( x 25 ) ???
- НЕ ( x 25 ) ???
равно
не равно
x

Сложные условия
Порядок выполнения (приоритет = старшинство )
- выражения в скобках
- выражения в скобках
- НЕ , =, =, И ИЛИ
- НЕ
- , =, =,
- И
- ИЛИ
Пример
2 1 6 3 5 4
если не (a 2 ) или c 5 и b то
…
все
- если не (a 2 ) или c 5 и b то … все
Сложные условия
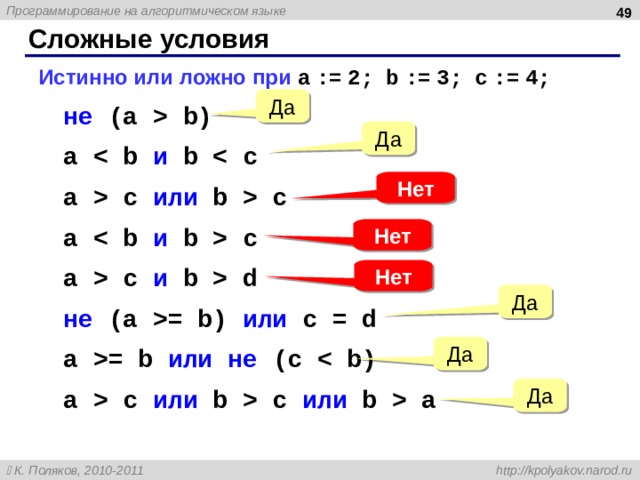
Истинно или ложно при a := 2; b := 3; c := 4;
не (a b)
- не (a b)
a и b
a c или b c
a и b c
a c и b d
- a и b a c или b c a и b c a c и b d
не (a = b) или c = d
- не (a = b) или c = d
a = b или не (c
a c или b c или b a
- a = b или не (c a c или b c или b a
Да
Да
Нет
Нет
Нет
Да
Да
Да

Сложные условия
Для каких значений x истинны условия:
x и x
x и x 10
x 6 и x
x 6 и x 10
x или x
x или x 10
x 6 или x
x 6 или x 10
- x и x x и x 10 x 6 и x x 6 и x 10 x или x x или x 10 x 6 или x x 6 или x 10
x
нет таких
6
x 10
x
все x
x 6
Задания
«3»: Ввести три числа и определить, верно ли, что они вводились в порядке возрастания.
Пример:
Введите три числа:
4 5 17
да
«4»: Ввести номер месяца и вывести название времени года.
Пример:
Введите номер месяца:
4
весна
Задания
«5»: Ввести возраст человека (от 1 до 150 лет) и вывести его вместе с последующим словом «год», «года» или «лет».
Пример:
Введите возраст: Введите возраст:
24 57
Вам 24 года Вам 57 лет
Программирование на алгоритмическом языке
Тема 4. Циклы
Циклы
Цикл – это многократное выполнение одинаковых действий.
- цикл с известным числом шагов цикл с неизвестным числом шагов (цикл с условием)
- цикл с известным числом шагов
- цикл с неизвестным числом шагов (цикл с условием)
Задача. Вывести на экран 5 раз слово «Привет».
Особенность: одинаковые действия выполняются 5 раз.
?
Можно ли решить известными методами ?
54
Циклы
алг Привет
нач
вывод «Привет» , нс
вывод «Привет» , нс
вывод «Привет» , нс
вывод «Привет» , нс
вывод «Привет» , нс
кон
?
Что плохо ?
55
Циклы
алг Привет
нач
нц 5 раз
вывод «Привет!» , нс
кц
кон
тело цикла
начало цикла
вывод «Привет!» , нс
конец цикла
?
Как выглядит блок-схема ?
56
Циклы
Блок-схема:
начало
да
конец
нет
тело цикла
Число шагов – переменная
Задача: ввести количество повторения с клавиатуры.
алг Привет
нач
цел N
вывод «Сколько раз?» , нс
ввод N
нц N раз
вывод «Привет!» , нс
кц
кон
Задания
«3»: Ввести натуральное число и вывести в строчку все числа от 1 до этого числа.
Пример:
Введите натуральное число:
4
Ответ: 1 2 3 4
«4»: Ввести два целых числа, найти их произведение, не используя операцию умножения.
Пример:
Введите два числа:
4 15
4*15=60
Задания
«5»: Ввести натуральное число N и найти сумму всех чисел от 1 до N ( 1+2+3+…+ N ).
Пример:
Введите число слагаемых:
100
Сумма чисел от 1 до 100 равна 5050
Циклы
алг Привет
нач
нц 5 раз
вывод «Привет!» , нс
кц
кон
?
Как отсчитать ровно 5 раз ?
?
Как запоминать, сколько раз уже сделали ?
N := N + 1
61
61
Блок-схема алгоритма
начало
еще не сделали ни одного раза
N := 0
проверить, все ли сделали
N = 5 ?
да
конец
цикл
нет
N := N + 1
считаем очередной шаг
61
Цикл с условием
алг Привет 2
нач
цел N
N:= 0
нц пока N 5
вывод «Привет!» , нс
N:= N + 1
кц
кон
Цикл с условием
Вместо знаков вопроса добавьте числа и операторы так, чтобы цикл выполнился ровно 5 раз:
алг Привет 3
нач
цел N
N: = 5
нц пока N ???
вывод «Привет!» , нс
???
кц
кон
0
N:= N — 1
Что получим?
алг Пример 1
нач
цел N
N:= 1
нц пока N
вывод N , нс
N:= N + 1
кц
кон
1
2
3
4
5
Что получим?
алг Пример 2
нач
цел N
N:= 1
нц пока N
вывод N , нс
N:= N + 2
кц
кон
1
3
5
Что получим?
алг Пример 3
нач
цел N
N:= 2
нц пока N 5
вывод N , нс
N:= N + 2
кц
кон
2
4
6
8
10
12
14
16
…
!
Условие цикла никогда не станет ложным – это зацикливание !
67
Что получим?
алг Пример 4
нач
цел N
N:= 1
нц пока N
вывод N * N*N , нс
N:= N + 1
кц
кон
1
8
27
64
125
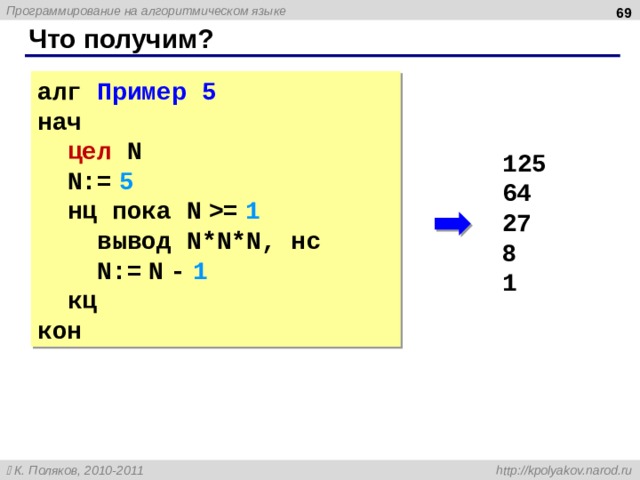
Что получим?
алг Пример 5
нач
цел N
N:= 5
нц пока N = 1
вывод N * N*N , нс
N:= N — 1
кц
кон
1 25
64
27
8
1
Задания
«3»: Ввести натуральное число вывести квадраты и кубы всех чисел от 1 до этого числа.
Пример:
Введите натуральное число:
3
1: 1 1
2: 4 8
3: 9 27
«4»: Ввести два целых числа a и b ( a ≤ b ) и вывести квадраты все чисел от a до b .
Пример:
Введите два числа:
4 5
4*4=16
5*5=25
Задания
«5»: Ввести два целых числа a и b ( a ≤ b ) и вывести сумму квадратов всех чисел от a до b .
Пример:
Введите два числа:
4 10
Сумма квадратов 371
Циклы с условием
Пример: Отпилить полено от бревна. Сколько раз надо сделать движения пилой?
Задача: Ввести целое число (
Идея решения: Отсекаем последовательно последнюю цифру, увеличиваем счетчик.
Проблема: Неизвестно, сколько шагов надо сделать.
Решение: Надо остановиться, когда n = 0 , т.е. надо делать «пока n 0 » .
n
123
count
12
0
1
1
0
2
3
Блок-схема алгоритма
начало
обнулить счетчик цифр
ввод n
count := 0
выполнять «пока n 0 »
n 0 ?
нет
да
вывод count
count := count + 1
n := div(n, 10 )
конец
Программа
алг Число цифр
нач
цел n, count
вывод «Введите целое число» , нс
ввод n
count : = 0
вывод «В числе » , n, » нашли » , c ount , » цифр»
кон
, n1
; n1:= n
нц пока n 0
count:= count + 1
n:= div (n, 10 )
кц
n1,
?
Что плохо ?
74
Цикл с условием
Особенности:
- можно использовать сложные условия: можно записывать в одну строчку, разделяя команды точкой с запятой:
- можно использовать сложные условия:
- можно записывать в одну строчку, разделяя команды точкой с запятой:
нц пока a 5
a:= a + 5 ; b:= b — 2
кц
a 5
нц пока a
;
75

Цикл с условием
Особенности:
- условие пересчитывается при каждом входе в цикл если условие на входе в цикл ложно, цикл не выполняется ни разу если условие никогда не станет ложным, программа зацикливается
- условие пересчитывается при каждом входе в цикл
- если условие на входе в цикл ложно, цикл не выполняется ни разу
- если условие никогда не станет ложным, программа зацикливается
a := 4 ; b := 6
нц пока a b ; a:= a – b кц
a:= 4 ; b:= 6
нц пока a
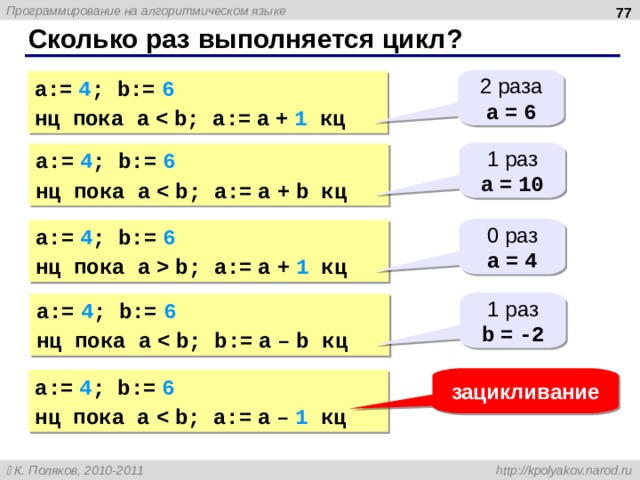
Сколько раз выполняется цикл ?
2 раза
a = 6
a:= 4 ; b:= 6
нц пока a
1 раз
a = 10
a:= 4 ; b:= 6
нц пока a
0 раз
a = 4
a:= 4 ; b:= 6
нц пока a b ; a:= a + 1 кц
1 раз
b = -2
a:= 4 ; b:= 6
нц пока a
зацикливание
a:= 4 ; b:= 6
нц пока a
Задания
«3»: Ввести целое число и определить, верно ли, что в нём ровно 3 цифры.
Пример:
Введите число: Введите число:
123 1234
Да. Нет.
«4»: Ввести целое число и найти сумму его цифр.
Пример:
Введите целое число:
1234
Сумма цифр числа 1234 равна 10.
Задания
«5»: Ввести целое число и определить, верно ли, что в его записи есть две одинаковые цифры , стоящие рядом .
Пример:
Введите целое число: Введите целое число:
1232 1224
Нет. Да.
«6»: Ввести целое число и определить, верно ли, что в его записи есть две одинаковые цифры , НЕ обязательно стоящие рядом.
Пример:
Введите целое число: Введите целое число:
1234 1242
Нет. Да.
Задания -2
«3»: Ввести целое число и определить, верно ли, что в нём ровно 1 цифра «9».
Пример:
Введите число: Введите число:
193 1994
Да. Нет.
«4»: Ввести целое число и определить, верно ли, что все его цифры четные.
Пример:
Введите число: Введите число:
2684 2994
Да. Нет.
Задания -2
«5»: Ввести целое число и определить, верно ли, что все его цифры расположены в порядке возрастания.
Пример:
Введите целое число: Введите целое число:
1238 1274
Да. Нет.
«6»: Ввести целое число и «перевернуть» его, так чтобы первая цифра стала последней и т.д.
Пример:
Введите целое число: Введите целое число:
1234 782
4321 287
Вычисление НОД
НОД = наибольший общий делитель двух натуральных чисел – это наибольшее число, на которое оба исходных числа делятся без остатка.
Перебор:
- Записать в переменную k минимальное из двух чисел.
- Если a и b без остатка делятся на k , то стоп.
- Уменьшить k на 1.
- Перейти к шагу 2.
это цикл с условием!
?
Где будет НОД?
?
Почему алгоритм обязательно закончится?
82
Алгоритм Евклида
Надо : вычислить наибольший общий делитель (НОД) чисел a и b .
Заменяем большее из двух чисел разностью большего и меньшего до тех пор, пока они не станут равны. Это и есть НОД.
НОД( a,b)= НОД( a-b, b)
= НОД( a, b-a)
Евклид
(365-300 до. н. э.)
Пример:
НОД (14 , 21 ) = НОД (14 , 21-14 ) = НОД (14 , 7 )
= НОД (7 , 7 ) = 7
много шагов при большой разнице чисел:
НОД (1998 , 2 ) = НОД (1996 , 2 ) = … = 2
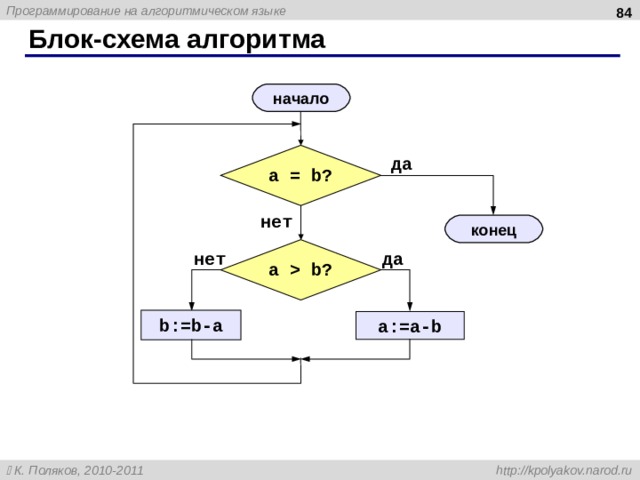
Блок-схема алгоритма
начало
a = b?
да
нет
конец
a b?
нет
да
b:=b-a
a:=a-b
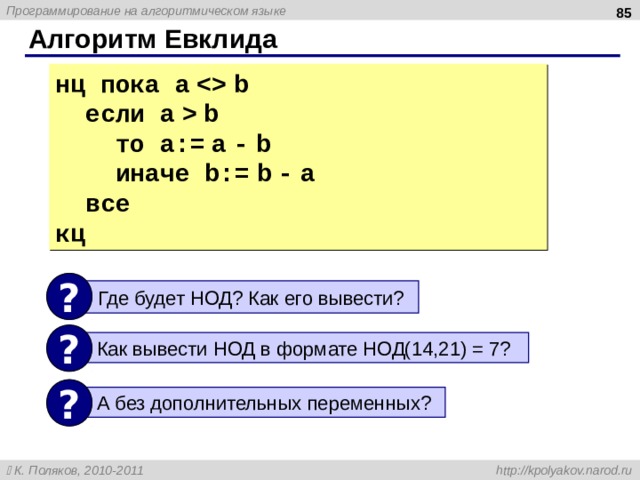
Алгоритм Евклида
нц пока a b
если a b
то a:= a — b
иначе b:= b — a
все
кц
?
Где будет НОД? Как его вывести?
?
Как вывести НОД в формате НОД(14,21) = 7?
?
А без дополнительных переменных?
85
Модифицированный алгоритм Евклида
Заменяем большее из двух чисел остатком от деления большего на меньшее до тех пор, пока меньшее не станет равно нулю. Тогда большее — это НОД.
НОД( a,b)= НОД( mod (a,b), b)
= НОД( a, mod (b,a))
Пример:
НОД (14 , 21 ) = НОД (14 , 7 ) = НОД (0 , 7 ) = 7
Еще один вариант:
НОД( 2 · a,2 · b)= 2 · НОД( a, b)
НОД( 2 · a,b)= НОД( a, b) | при нечетном b
Алгоритм Евклида
«3» : Составить программу для вычисления НОД с помощью алгоритма Евклида.
« 4 » : Составить программу для вычисления НОД с помощью модифицированного алгоритма Евклида и заполнить таблицу:
a
b
64168
НОД( a,b )
358853
82678
6365133
691042
11494962
17905514
23108855
549868978
298294835
Алгоритм Евклида
«5» : Выполнить задание на «4» и подсчитать число шагов алгоритма для каждого случая.
a
64168
b
82678
358853
НОД( a,b )
691042
шагов
6365133
11494962
17905514
23108855
549868978
298294835
Программирование на алгоритмическом языке
Тема 5. Циклы с переменной
Цикл с переменной
Задача: вывести кубы чисел от 1 до 8.
?
Можно ли решить известными способами ?
- Нужны ли переменные? Сколько?
- Как они должны изменяться?
- Нужен ли цикл?
90
Блок-схема алгоритма
начало
N := 1
N
нет
конец
да
куб N := N*N*N
вывод куб N
N := N + 1
91
Цикл с переменной
Задача: вывести кубы натуральных чисел от 1 до 8.
алг Кубы
нач
цел N, куб N
N:= 1
нц пока N
куб N:= N*N*N
вывод куб N, нс
N:= N + 1
кц
кон
3 действия с N
N:= 1
N
N:= N + 1
Цикл с переменной
Задача: вывести кубы натуральных чисел от 1 до 8.
алг Кубы
нач
цел N, куб N
кон
для 1,2,3,…,8
нц для N от 1 до 8
куб N:= N*N*N
вывод куб N, нс
кц
?
Как обойтись без переменной куб N ?
93
Цикл с переменной
Задача: вывести кубы чётных чисел от 2 до 8.
алг Кубы
нач
цел N, куб N
кон
для 2,4,6,8
нц для N от 2 до 8 шаг 2
куб N:= N*N*N
вывод куб N, нс
кц
только целые !
94
Сколько раз выполняется цикл?
a := 1
нц для i от 1 до 3 ; a:=a+ 1 кц
a = 4
a := 1
нц для i от 3 до 1 ; a:=a+ 1 кц
a = 1
a = 1
a := 1
нц для i от 1 до 3 шаг -1 ; a:=a+ 1 кц
a = 4
a := 1
нц для i от 3 до 1 шаг -1 ; a:=a+ 1 кц

Цикл с переменной
Особенности:
- переменная цикла может быть только целой ( цел ) начальное и конечное значения и шаг – целые можно записывать в одну строчку, разделяя команды точкой с запятой: если шаг 0 и конечное значение начального, цикл не выполняется ни разу
- переменная цикла может быть только целой ( цел )
- начальное и конечное значения и шаг – целые
- можно записывать в одну строчку, разделяя команды точкой с запятой:
- если шаг 0 и конечное значение
- если шаг начального, цикл не выполняется ни разу
нц для n от 1 до 4 вывод n кц
;
96

Замена одного вида цикла на другой
i:= 1
нц пока i
| тело цикла
i:= i + 1
кц
нц для i от 1 до 10
| тело цикла
кц
i:= a
нц пока i = b
| тело цикла
i:= i — 1
кц
нц для i от a до b шаг -1
| тело цикла
кц
Замена цикла для на пока возможна всегда .
Замена пока на для возможна только тогда, когда можно заранее вычислить число шагов цикла.
Задания
«3»: Ввести натуральное число N и вывести числа от N до 1 (через одно) в порядке убывания.
Пример:
Введите натуральное число:
8
Ответ: 8 6 4 2
Задания
«4»: Ввести два целых числа a и b ( a ≤ b ) и вывести кубы всех чисел от a до b .
Пример:
Введите два числа:
4 6
4*4*4=64
5*5*5=125
6*6*6=216
«5»: Ввести целое число a и вывести сумму квадратов всех чисел от 1 до a с шагом 0.1 .
Пример:
Введите последнее число:
3
Сумма 91.7
1 2 + 1.1 2 + 1.2 2 + … + a 2
Задания-2
«4»: Ввести a и b и вывести квадраты и кубы чисел от a до b .
Пример:
Введите границы интервала:
4 6
4 : 16 64
5 : 25 125
6 : 36 216
«5»: Вывести квадраты и кубы 10 чисел следующей последовательности: 1, 2, 4, 7, 11, 16, …
Пример:
1: 1 1
2: 4 8
4: 16 64
…
46: 2116 97336
Программирование на алгоритмическом языке
Тема 6. Графика
Система координат
X
(0,0)
y
( x , y )
x
Y
Исполнитель Рисователь
использовать Рисователь
алг
нач
| текст программы
кон
Линии
Цвет и толщина линий:
черный
белый
серый
фиолетовый
синий
голубой
зеленый
желтый
оранжевый
красный
толщина линии
перо ( 2 , «синий» )
(10, 15)
перо ( 1 , «зеленый» ) линия ( 10 , 1 5 , 90 , 80 )
(90, 80)
(5,5)
перо ( 1 , «красный“ )
в точку ( 5 , 5 )
линия в точку ( 50 , 5 )
линия в точку ( 70 , 50 )
линия в точку ( 30 , 80 )
линия в точку ( 5 , 60 )
(50,5)
(70, 50)
(5,60 )
(30,80)
104
104
Фигуры с заливкой
(0,0)
перо ( 1 , «синий» )
кисть ( «желтый» )
прямоугольник ( 0 , 0 , 80 , 40 )
(80, 40)
(0,0)
перо ( 1 , «красный» )
кисть ( «зеленый» )
эллипс ( 0 , 0 , 100 , 50 )
(100, 50)
?
кисть ( «» ) ; | отменить заливку
Как построить круг?
(70, 80)
кисть ( «фиолетовый» )
залить ( 70 , 80 )
105
105
Пример
использовать Рисователь
алг Домик
нач
перо ( 2 , «фиолетовый» )
кисть ( «синий» )
прямоугольник ( 100 , 100 , 300 , 200 )
в точку ( 100 , 100 )
линия в точку ( 200 , 50 )
линия в точку ( 300 , 100 )
кисть ( «желтый» )
залить ( 200 , 75 );
перо ( 2 , «белый» );
кисть ( «зеленый» );
эллипс ( 150 , 100 , 250 , 200 );
кон
(200, 50)
(100, 100)
(300, 200)
105
Задания
«3»: «Домик»
«4»: «Лягушка»
107
Задания
«5»: «Корона»
108
Штриховка
N линий ( N=5)
( x 1 , y 1 )
x
y 1
y 2
h
( x 2 , y 2 )
прямоугольник (x1, y1, x2, y2)
x:= x1 + h
линия (x, y1, x, y2)
x:= x + h
линия (x, y1, x, y2)
x:= x + h
…
цикл N раз
Штриховка (программа)
N
( x 1 , y 1 )
использовать Рисователь
алг Штриховка
нач
цел N = 5 | число линий
цел x1 = 100 , x2 = 300
цел y1 = 100 , y2 = 200
вещ h, x
h:=(x2 — x1)/(N + 1 )
прямоугольник ( x1, y1, x2, y2)
x:= x1 + h
нц N раз
линия ( int (x), y1, int (x), y2)
x:= x + h
кц
кон
вещ h, x
h
( x 2 , y 2 )
?
Почему?
целая часть
110
110
Штриховка
x 1
( x 1 , y 1 )
h x
( x , y )
h y
x:= x1 + hx ; y:= y1 + hy
линия (x1, int (y), int (x), int (y))
x:= x + hx; y:= y + hy
линия (x1, int (y), int (x), int (y))
x:= x + hx; y:= y + hy
…
( x 2 , y 2 )
цикл N раз
111
111
Штриховка
вещ hx, hy, x, y
hx:=(x2 — x1)/(N + 1 )
hy:=(y2 — y1)/(N + 1 )
в точку ( x1, y1)
линия в точку ( x1, y2)
линия в точку ( x2, y2)
линия в точку ( x1, y1)
x:= x1 + hx ; y:= y1 + hy
нц N раз
линия ( x1, int (y), int (x), int (y))
x:= x + hx
y:= y + hy
кц
( x 1 , y 1 )
h x
h y
( x 2 , y 2 )
Задания
« 3 »: Ввести с клавиатуры количество линий , построить фигуру и выполнить штриховку :
«4»: Ввести с клавиатуры количество линий , построить фигуру и выполнить штриховку :
или
113
113
Задания
«5»: Ввести с клавиатуры количество линий и построить фигуру:
Программирование на алгоритмическом языке
Тема 7. Вспомогательные алгоритмы
Задача
?
Можно ли решить известными методами ?
Особенность: три похожие фигуры.
общее : размеры, угол поворота
отличия : координаты, цвет
- общее : размеры, угол поворота отличия : координаты, цвет
?
Сколько координат надо задать ?
116
С чего начать?
- найти похожие действия (три фигуры) найти общее (размеры, форма, угол поворота) и отличия (координаты, цвет) отличия = параметры алгоритма (доп. данные)
- найти похожие действия (три фигуры)
- найти общее (размеры, форма, угол поворота) и отличия (координаты, цвет)
- отличия = параметры алгоритма (доп. данные)
цепочка символов
использовать Рисователь
алг Тр ( цел x, y, лит цвет)
нач
в точку (x, y)
линия в точку (x, y- 60 )
линия в точку (x+ 100 , y)
линия в точку (x, y)
кисть (цвет)
залить (x+ 20 , y- 20 )
кон
( x , y -60)
параметры
60
( x , y )
100
( x +100, y )
Если запустить?
(50,100)
Как использовать?
использовать Рисователь
алг Треугольники
нач
перо ( 1 , «черный» )
Тр ( 100 , 100 , «синий» )
Тр ( 200 , 100 , «зеленый» )
Тр ( 200 , 160 , «красный» )
кон
основной
алгоритм
60
( 100 , 100 )
100
вызовы алгоритма
алг Тр ( цел x, y, лит цвет)
нач
…
кон
вспомогательный
алгоритм
119
Вспомогательные алгоритмы
- расположены ниже основного в заголовке перечисляются формальные параметры, они обозначаются именами для каждого параметра указывают тип однотипные параметры перечисляются через запятую при вызове в скобках указывают фактические параметры в том же порядке
- расположены ниже основного
- в заголовке перечисляются формальные параметры, они обозначаются именами
- для каждого параметра указывают тип
- однотипные параметры перечисляются через запятую
- при вызове в скобках указывают фактические параметры в том же порядке
алг Тр ( цел x, y, лит цвет)
Тр ( 200 , 100 , «зеленый» )
x
цвет
y
Задания
« 3 »: Используя одну процедуру, построить фигуру.
« 4 »: Используя одну процедуру, построить фигуру.
121
Задания
«5»: Используя одну процедуру, построить фигуру.
122
Рекурсивные объекты
Сказка о поп é и собаке:
Примеры:
У попа была собака, он ее любил.
Она съела кусок мяса, он ее убил.
В ямку закопал, надпись написал:
- У попа была собака, он ее любил. Она съела кусок мяса, он ее убил. В ямку закопал, надпись написал:
Сказка о поп é и собаке
- Сказка о поп é и собаке
Рисунок с рекурсией:
Факториал:
если
если
Рекурсивный объект – это объект, определяемый через один или несколько таких же объектов.
123
Рекурсивная фигура
3 уровня:
?
Где рекурсия?
Фигура из N уровней – это
- окружность и
- 4 фигуры из N-1 уровней
N-1
N-1
N-1
N-1
Рекурсивная фигура: алгоритм
центр
радиус
уровней
( x , y-R )
алг РекОк ( цел x, y, R, N )
нач
если N
окружность (x, y, R)
РекОк (x, y-R, div (R, 2 ), N — 1 )
РекОк (x+R, y, div (R, 2 ), N — 1 )
РекОк (x, y+R, div (R, 2 ), N — 1 )
РекОк (x-R, y, div (R, 2 ), N — 1 )
кон
( x , y )
( x+R , y )
окончание рекурсии
( x-R , y )
( x , y+R )
рекурсивные вызовы
Рекурсивный алгоритм – это алгоритм, который вызывает сам себя (с другими параметрами!).
Рекурсивная фигура: программа
использовать Рисователь
алг Рекурсия
нач
РекОк (200, 200, 100, 3)
кон
алг РекОк ( цел x, y, R, N )
нач
…
кон
Рекурсивные алгоритмы
- вызывают сами себя прямо … или через другой алгоритм: должно быть условие окончания рекурсии (иначе?) рекурсия может стать бесконечной все задачи могут быть решены без рекурсии, но… часто рекурсивные алгоритмы проще и понятнее как правило, алгоритмы без рекурсии работают быстрее и требуют меньше памяти
- вызывают сами себя прямо
- … или через другой алгоритм:
- должно быть условие окончания рекурсии (иначе?)
- рекурсия может стать бесконечной
- все задачи могут быть решены без рекурсии, но…
- часто рекурсивные алгоритмы проще и понятнее
- как правило, алгоритмы без рекурсии работают быстрее и требуют меньше памяти
A
прямая рекурсия
A
B
косвенная рекурсия
Задания
« 3 » : Нарисовать рекурсивную фигуру, число уровней вводить с клавиатуры:
« 4 » : Нарисовать рекурсивную фигуру, число уровней вводить с клавиатуры:
128
Задания
«5» : Нарисовать рекурсивную фигуру, число уровней вводить с клавиатуры:
129
Программирование на алгоритмическом языке
Тема 8 . Анимация
Анимация
Анимация (англ. animation ) – оживление изображения на экране.
Задача : внутри синего квадрата 200 на 200 пикселей слева направо двигается желтый квадрат 20 на 20 пикселей. Программа останавливается, если нажата клавиша Esc или квадрат дошел до границы синей области.
Проблема : как изобразить перемещение объекта на экране?
Привязка: состояние объекта задается координатами ( x,y)
Принцип анимации:
- рисуем объект в точке ( x,y) задержка на несколько миллисекунд стираем объект изменяем координаты ( x,y) переходим к шагу 1
- рисуем объект в точке ( x,y)
- задержка на несколько миллисекунд
- стираем объект
- изменяем координаты ( x,y)
- переходим к шагу 1
131
Процедура (рисование и стирание)
- одна процедура рисует и стирает стереть = рисовать цветом фона границу квадрата отключить
- одна процедура рисует и стирает
- стереть = рисовать цветом фона
- границу квадрата отключить
( x , y )
( x +20, y +20)
рисуем: цвет кисти – желтый
стираем: цвет кисти – синий
алг Фигура ( цел x, y, лит цвет)
нач
кисть (цвет)
прямоугольник (x,y,x+ 20 ,y+ 20 )
кон
Полная программа
использовать Рисователь
алг Анимация
нач
цел x, y | текущие координаты
кисть ( «синий» )
перо (1, «» ) | отключить контур
прямоугольник ( 0 , 0 , 200 , 200 ) | синий фон
x:= 0 ; y:= 100 | начальные координаты
кон
нц пока x
Фигура (x, y, «желтый» )
delay (50)
Фигура (x, y, «синий» )
x:= x + 5
кц
пока не дошли до границы
алг Фигура ( цел x, y, лит цвет)
нач
…
кон
Задания
«3»: Квадрат двигается справа налево:
«4»: Два квадрата двигаются в противоположных направлениях:
134
Задания
«5»: Два квадрата двигаются в противоположных направлениях и отталкиваются от стенок синего квадрата:
Управление клавишами
Задача : жёлтый квадрат внутри синего квадрата управляется клавишами-стрелками. Коды клавиш:
влево – 16777234 вверх – 16777235
вправо – 16777236 вниз – 16777237
Проблема : как изменять направление движения?
Решение :
ждать нажатия на клавишу, записать ее код в переменную c
c:= клав
выбор
при c = 16777234 : x:= x – 5 | влево
при c = 16777235 : y:= y – 5 | вверх
при c = 16777236 : x:= x + 5 | вправо
при c = 16777237 : y:= y + 5 | вниз
все
?
Когда стирать фигуру?
136
Программа
использовать Рисователь
алг Управление клавишами
нач
цел x, y, c
| нарисовать синий квадрат
x:= 100; y:= 100 | начальная точка
нц пока x
Фигура (x, y, «желтый» ) | рисуем фигуру
c:= клав | ждем нажатия клавиши
Фигура (x, y, «синий» ) | стираем фигуру
выбор
при c = 16777234 : x:= x — 5
при c = 16777235 : y:= y — 5
при c = 16777236 : x:= x + 5
при c = 16777237 : y:= y + 5
все
кц
кон
Задания
« 3 »: Квадрат в самом начале стоит в правом нижнем углу, и двигается при нажатии стрелок только вверх или влево:
«4»: Квадрат двигается при нажатии стрелок, однако не может выйти за границы синего квадрата:
138
Задания
« 5 »: Два квадрата, один управляется стрелками, второй – любыми другими клавишами. Оба не могут выйти за границы синего поля.
139
Программирование на алгоритмическом языке
Тема 9 . Случайные числа
Случайность и ее моделирование
Случайно…
Случайный выбор:
- встретить друга на улице
- разбить тарелку
- найти 10 рублей
- выиграть в лотерею
- жеребьевка на соревнованиях
- выигравшие номера в лотерее
Как получить случайность?
142
Случайные числа на компьютере
Электронный генератор
- нужно специальное устройство
- нельзя воспроизвести результаты
Псевдослучайные числа – обладают свойствами случайных чисел, но каждое следующее число вычисляется по заданной формуле.
Метод середины квадрата (Дж. фон Нейман)
в квадрате
564321
- малый период (последовательность повторяется через 10 6 чисел)
458191
318458191041
209938992481
938992
142
143
Распределение случайных чисел
Модель : снежинки падают на отрезок [a,b]
распределение
равномерное
неравномерное
a
a
b
b
?
Сколько может быть разных распределений ?
143
144
Распределение случайных чисел
Особенности :
- распределение – это характеристика всей последовательности , а не одного числа равномерное распределение одно, компьютерные датчики случайных чисел дают равномерное распределение неравномерных – много любое неравномерное можно получить с помощью равномерного
- распределение – это характеристика всей последовательности , а не одного числа
- равномерное распределение одно, компьютерные датчики случайных чисел дают равномерное распределение
- неравномерных – много
- любое неравномерное можно получить с помощью равномерного
a
a
b
b
144
Генератор случайных чисел
Вещественные числа в интервале [0, 10 ) :
вещ X, Y
X:= r a nd ( 0 , 1 0 ) | интервал от 0 до 10 (
Y:= r a nd ( 0 , 1 0 ) | это уже другое число!
англ. random – случайный
Целые числа в интервале [0,10] :
цел K , L
K:= ira nd ( 0 , 1 0 ) | интервал от 0 до 10 (
L := ira nd ( 0 , 1 0 ) | это уже другое число!
англ. i nteger – целый
Случайные числа
Задача : заполнить прямоугольник 200 на 150 пикселей равномерно точками случайного цвета
Как получить случайные координаты пикселя?
Как добиться равномерности?
автоматически при использовании irand
цел X, Y
X:= ira nd ( 0 , 200 )
Y:= ir a nd ( 0 , 1 5 0 )
Цвет пикселя на мониторе
!
Красный, зелёный и синий лучи создают почти такое же ощущение, как луч «смешанного» цвета!
red : R
green : G
blue : B
Вывод: цвет можно разложить на составляющие (каждая кодируется числом от 0 до 255).
Модель RGB :
R G B
RGB( 255 ,0, 255 )
RGB(0,0,0)
RGB( 255 , 255 , 255 )
RGB( 255 , 255 ,0)
RGB( 255 ,0,0)
RGB( 0 , 255 , 255 )
RGB(0, 255 ,0)
RGB(0,0, 255 )
RGB( 10 0, 10 0, 10 0)
Случайный цвет пикселя
Случайные составляющие цвета:
цел r , g, b
r:= ira nd ( 0 , 255 )
g:= ir a nd ( 0 , 255 )
b:= ir a nd ( 0 , 255 )
это разные числа!
Управление цветом пикселя:
случайный цвет
пиксель ( X , Y, RGB (r,g,b) )
встроенные функции Рисователя
Программа
использовать Рисователь
алг Случайные точки
нач
цел x, y, r, g, b
нц пока да
x:= irand ( 0 , 200 )
y:= irand ( 0 , 100 )
r:= irand ( 0 , 255 )
g:= irand ( 0 , 255 )
b:= irand ( 0 , 255 )
пиксель ( x,y, RGB (r,g,b))
кц
кон
это бесконечный цикл:
нц пока да
…
кц
Задания
«3»: Заполнить квадрат точками случайного цвета. размер квадрата ввести с клавиатуры:
Пример:
Введите размер квадрата:
150
«4»: Заполнить область точками случайного цвета:
Задания
«5»: Заполнить область точками случайного цвета:
или
Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики высшей категории ,
ГОУ СОШ № 163, г. Санкт-Петербург
[email protected]




























































































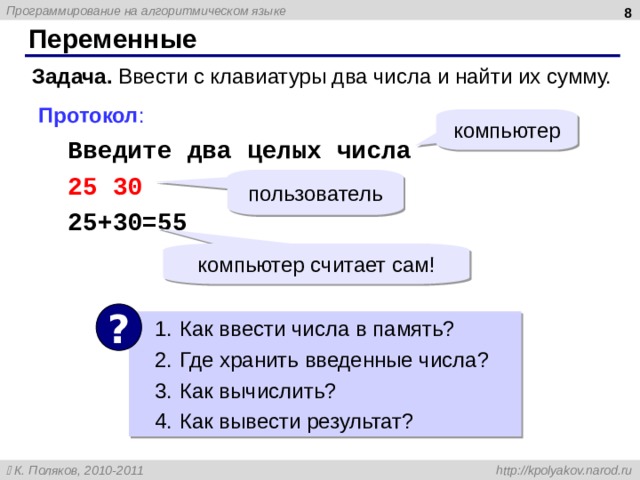
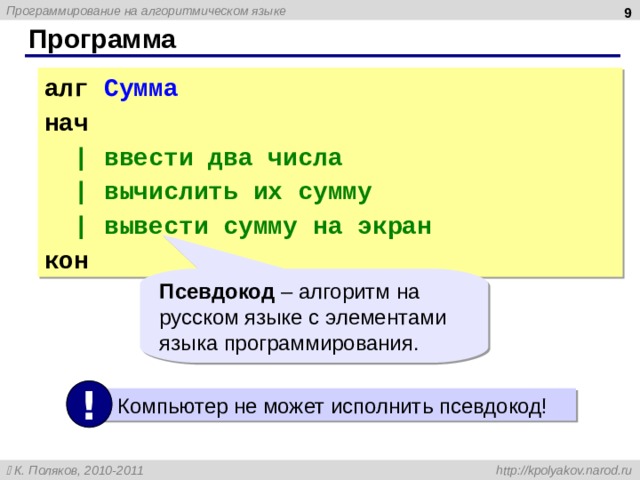
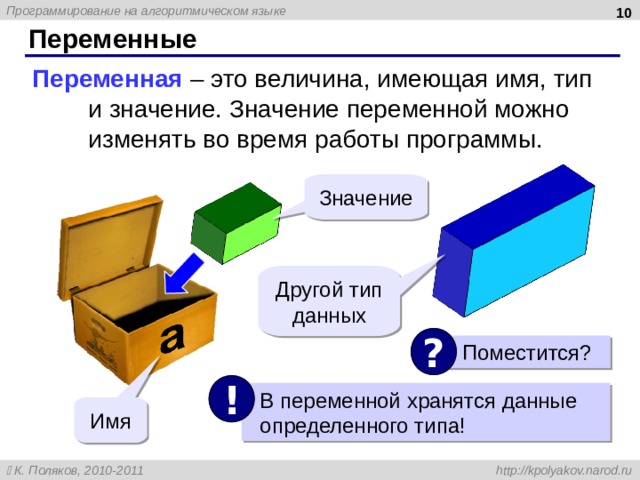
![Имена переменных МОЖНО использовать латинские буквы ( A-Z) , русские буквы (А-Я) цифры знак подчеркивания _ латинские буквы ( A-Z) , русские буквы (А-Я) цифры знак подчеркивания _ заглавные и строчные буквы различаются имя не может начинаться с цифры Какие имена правильные? AXby R&B 4Wheel Вася “PesBarbos” TU154 [QuQu] _ABBA A+B](https://fsd.videouroki.net/html/2021/04/01/v_60659c4fe052b/img10.jpg)
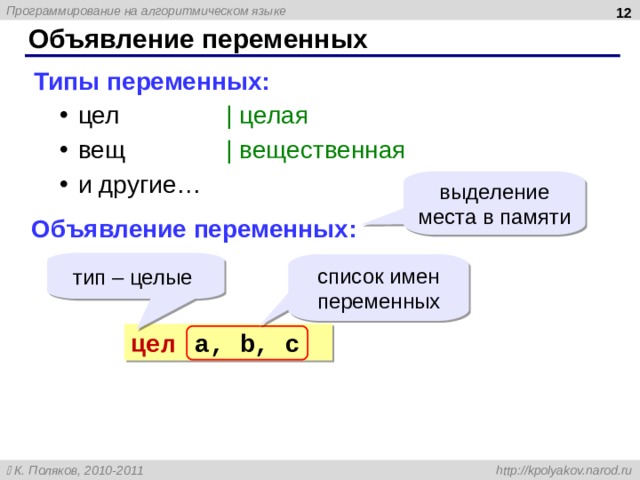

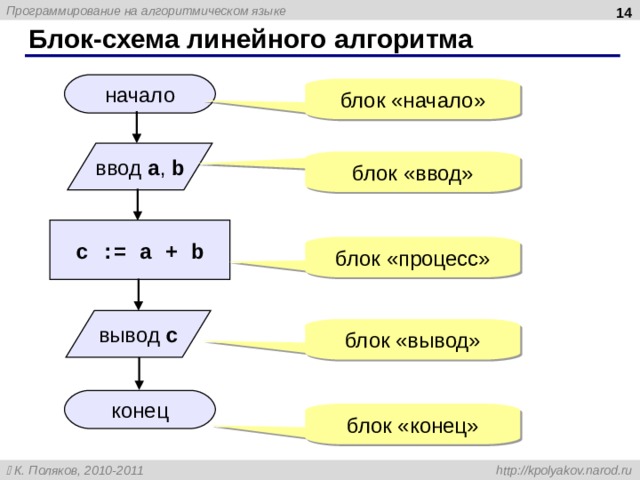
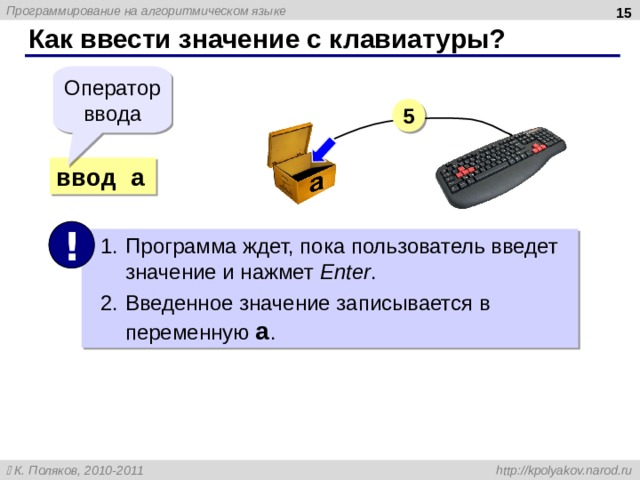

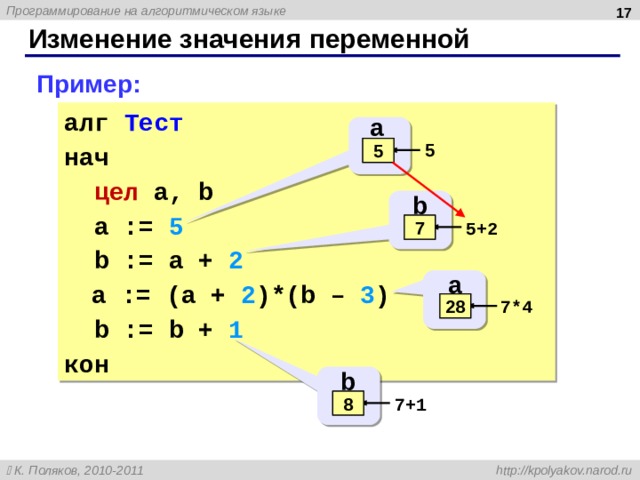



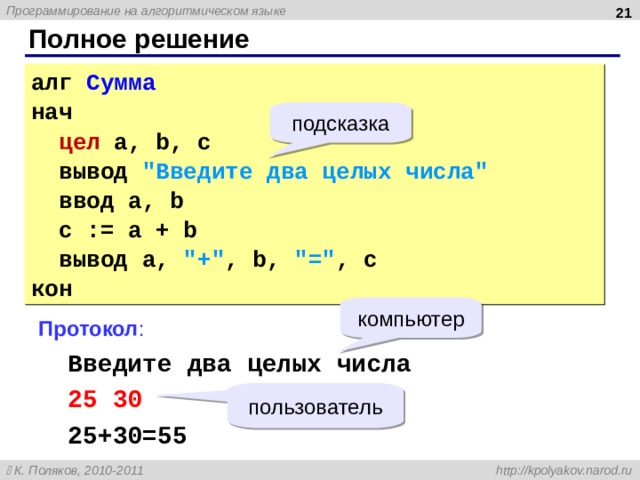

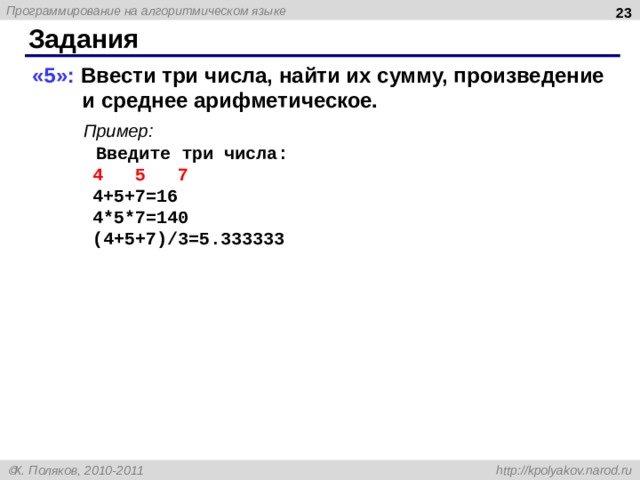
















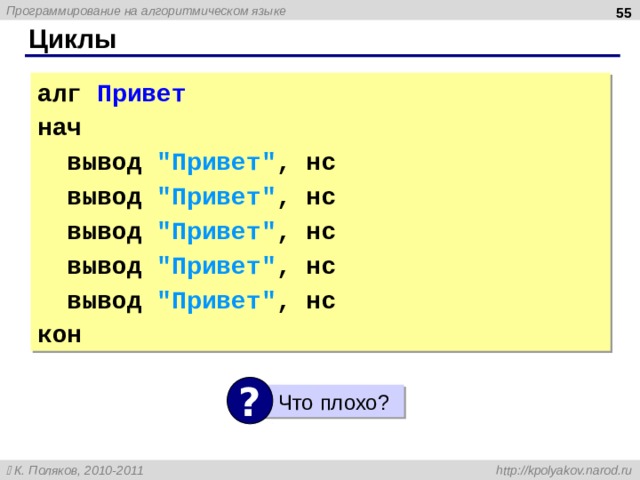

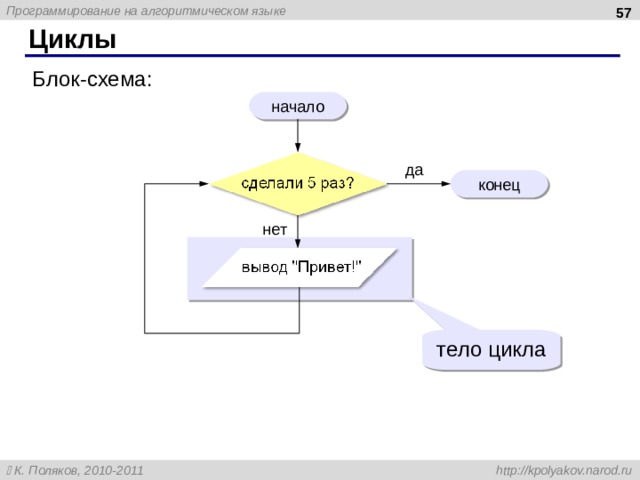




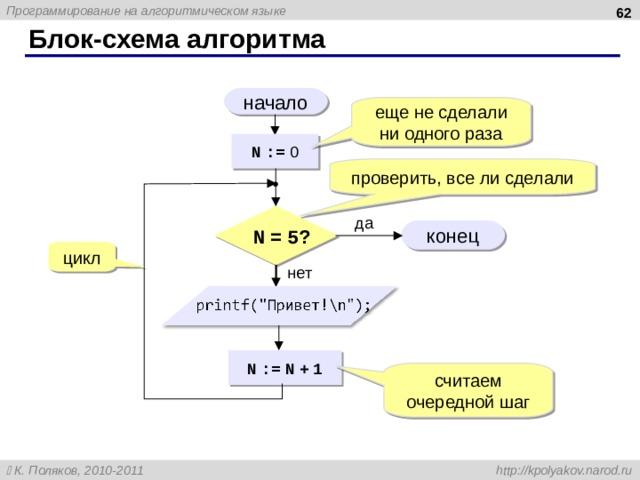


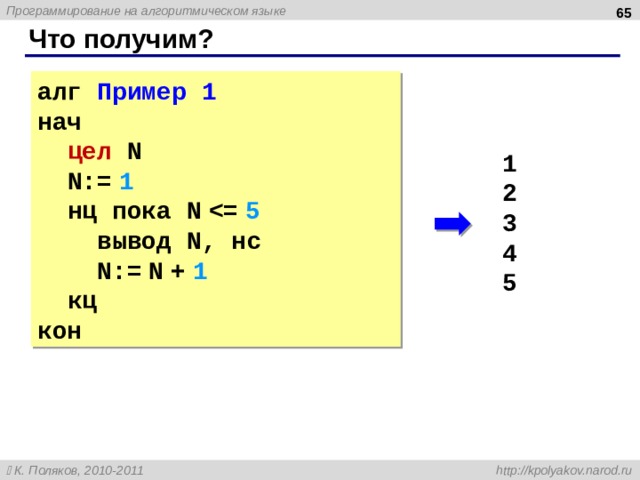
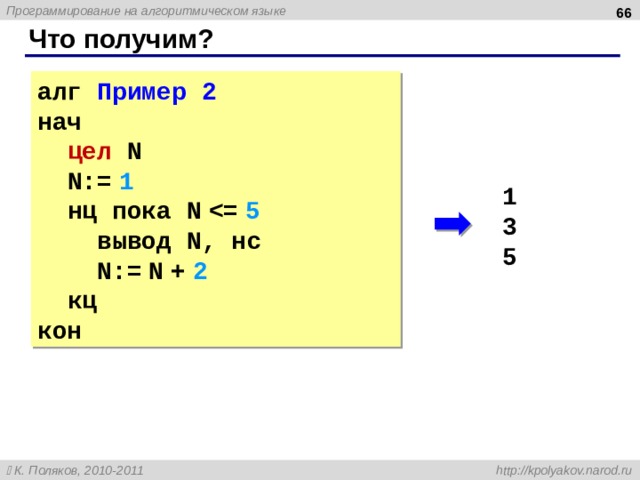

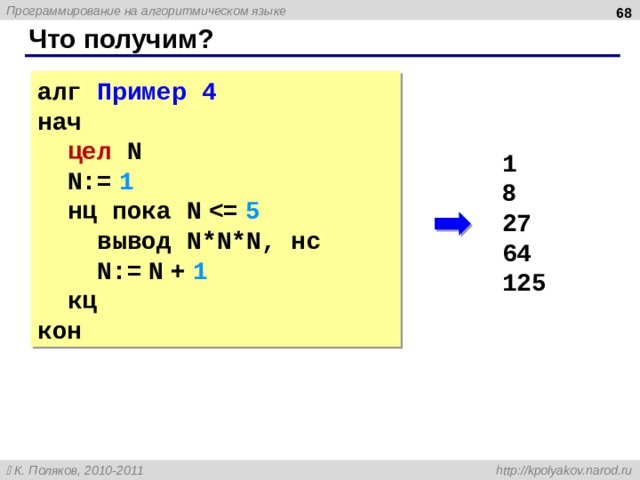



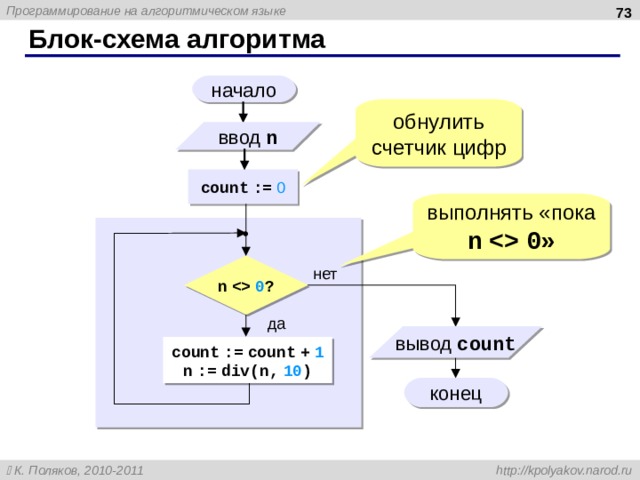


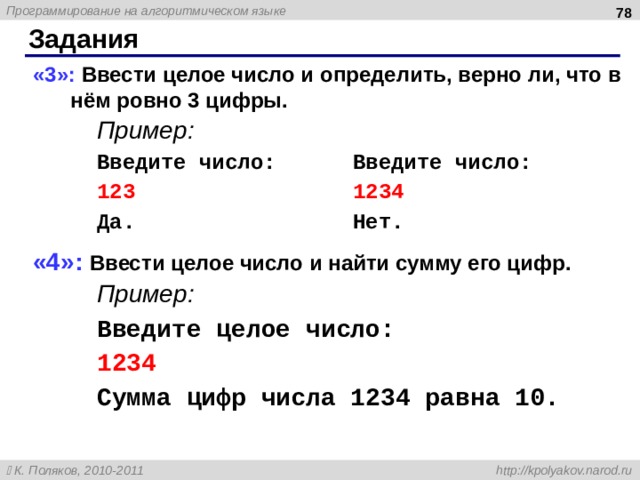






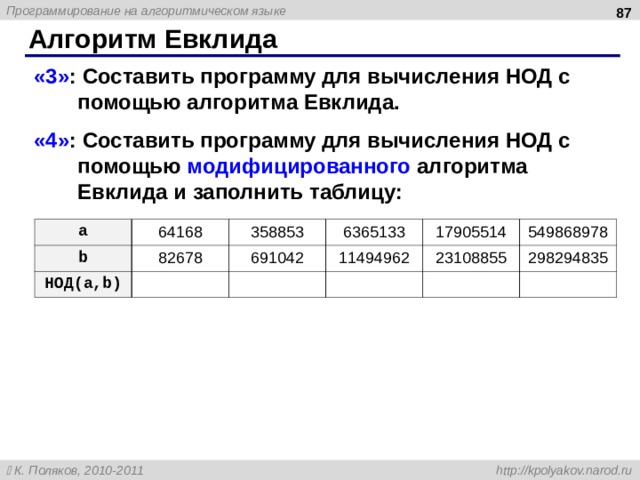
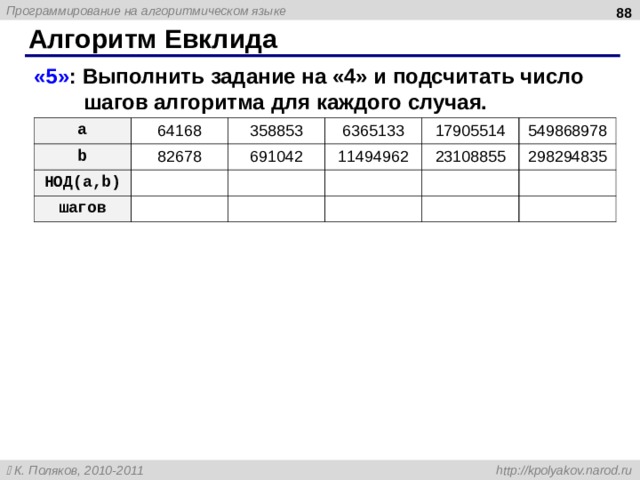

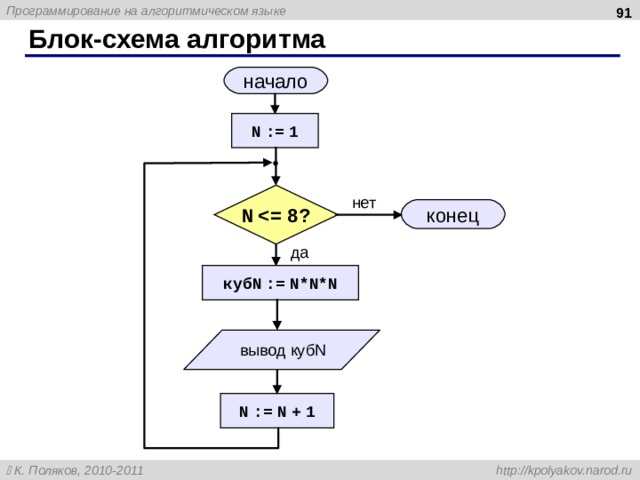






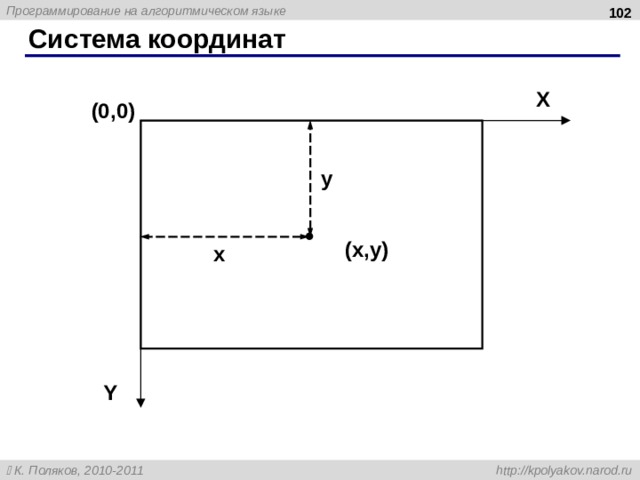
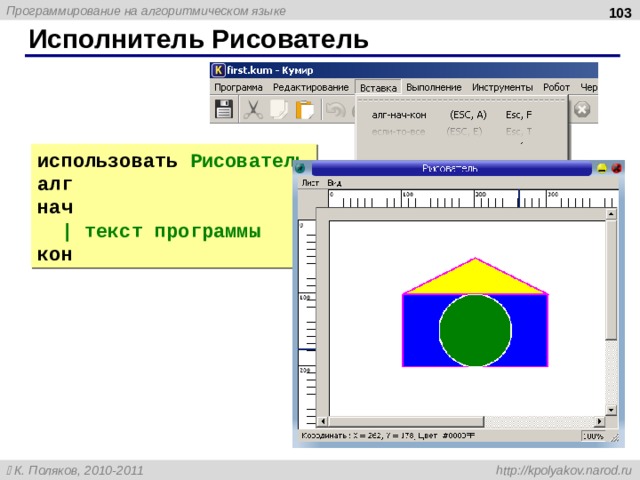

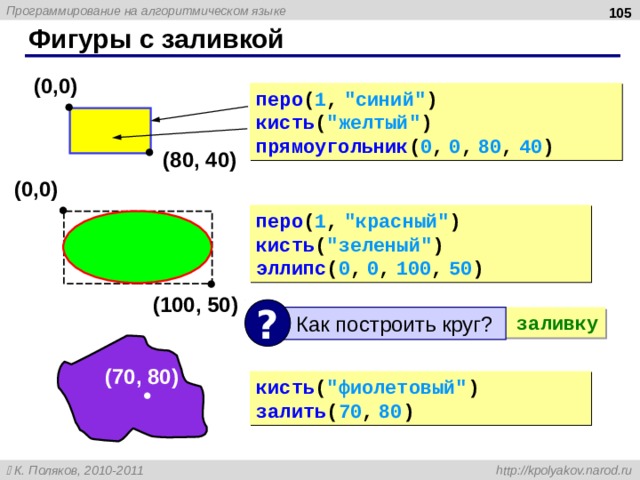
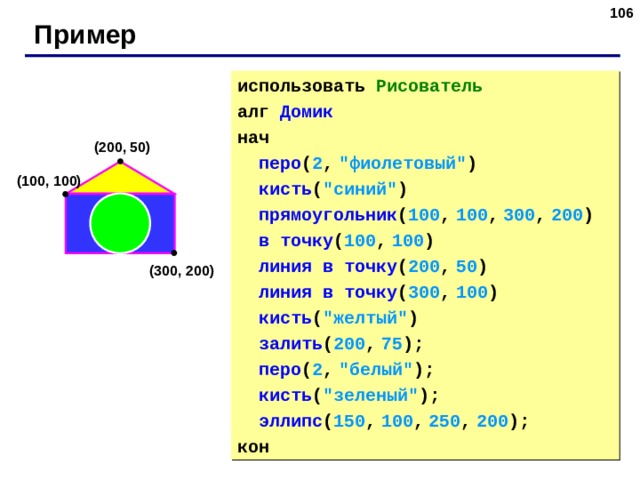
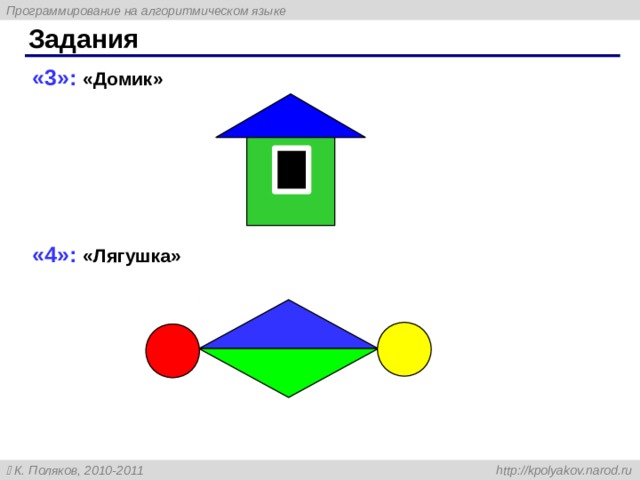
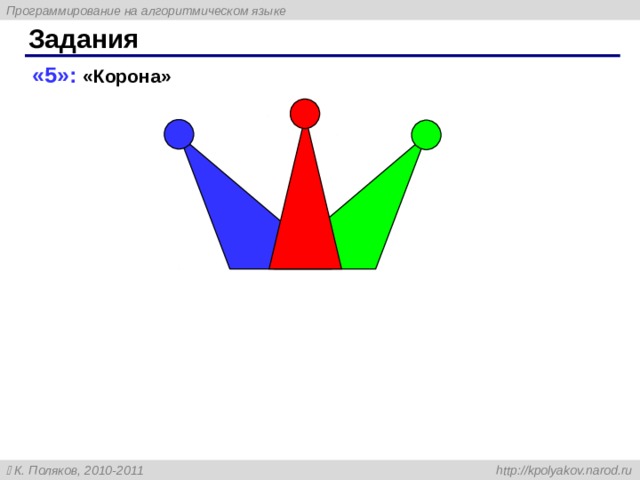
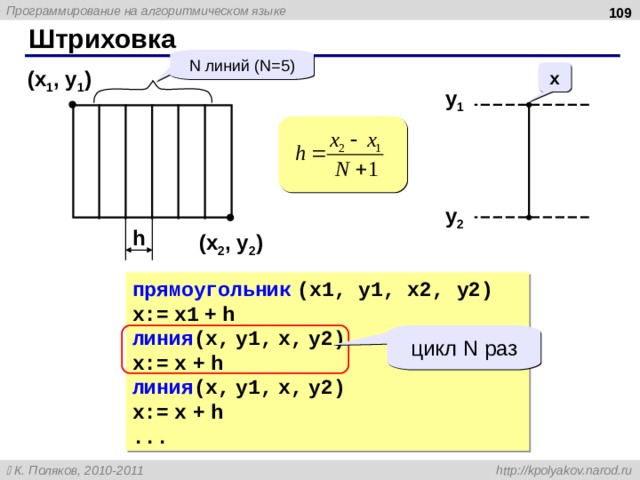

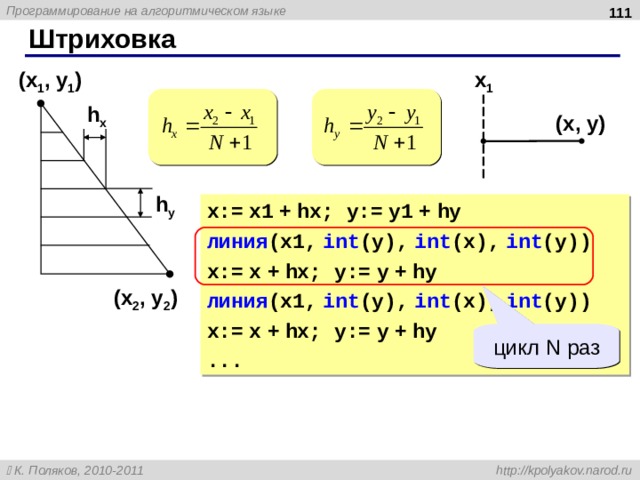

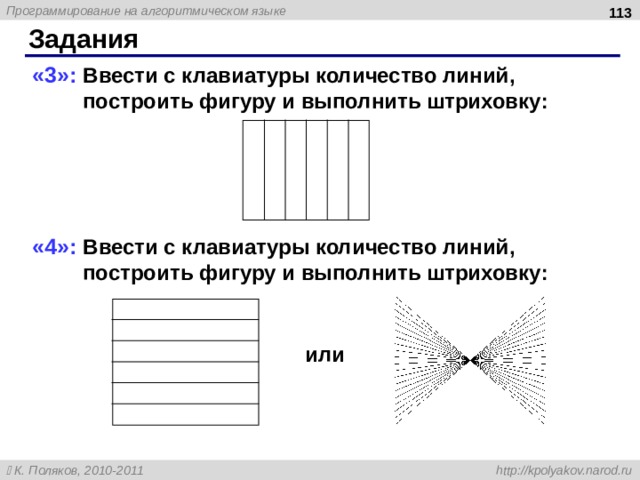
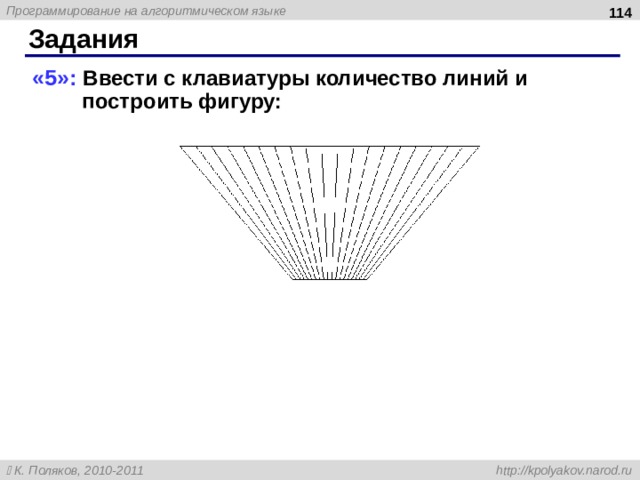



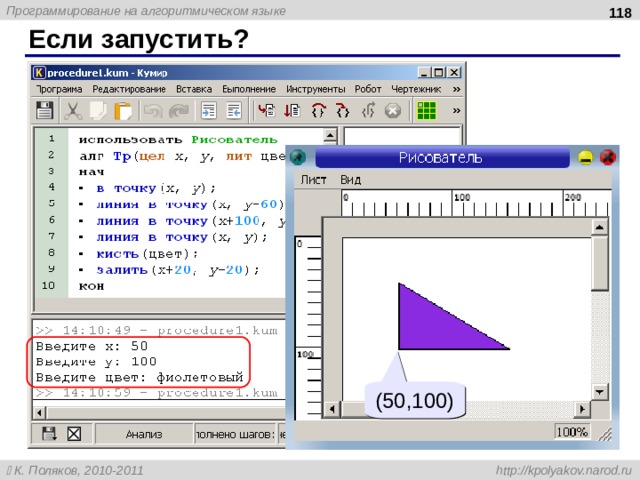
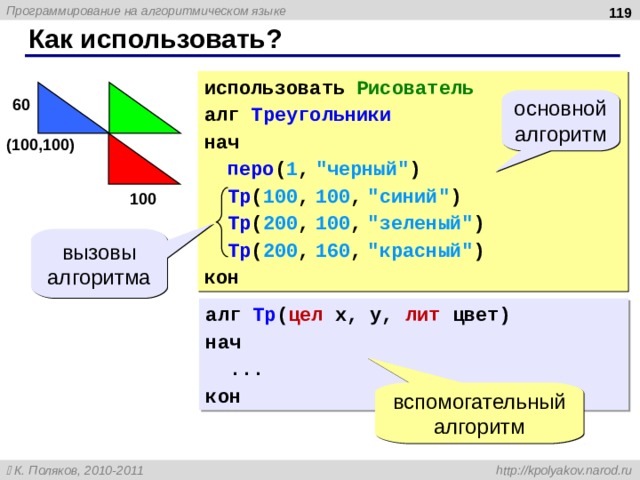

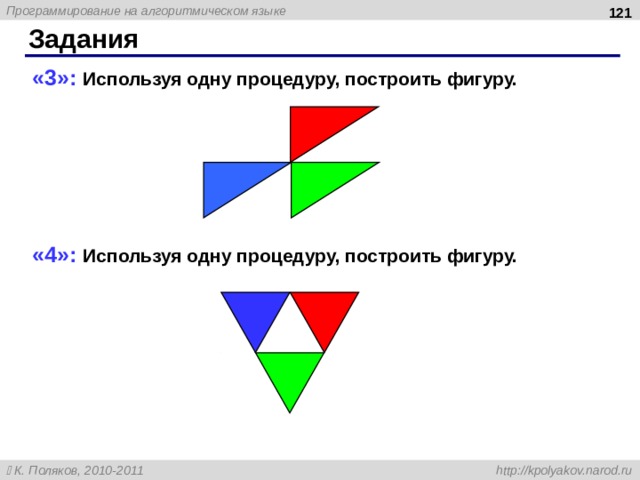
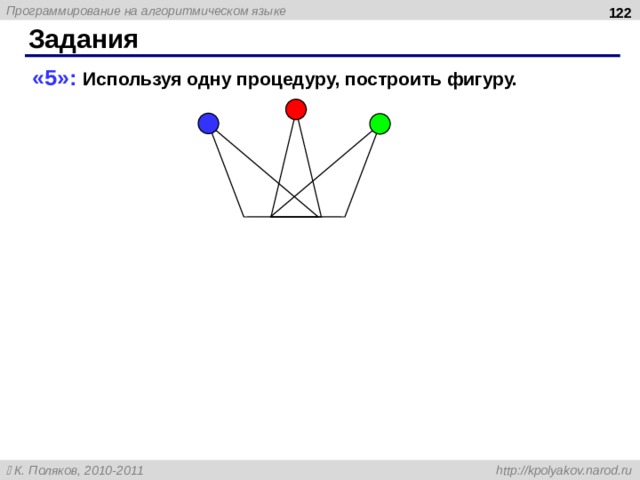

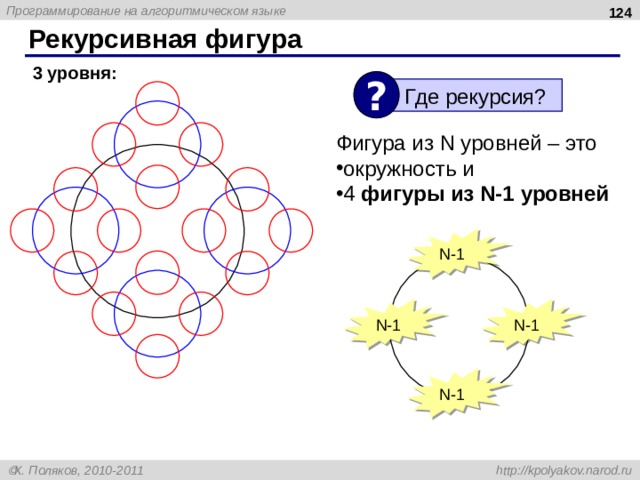



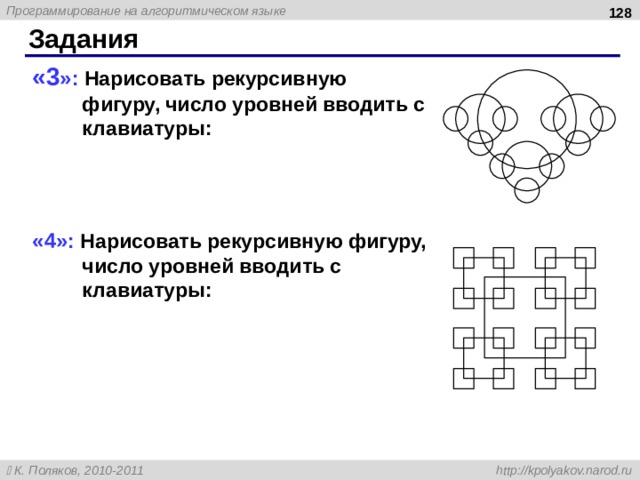


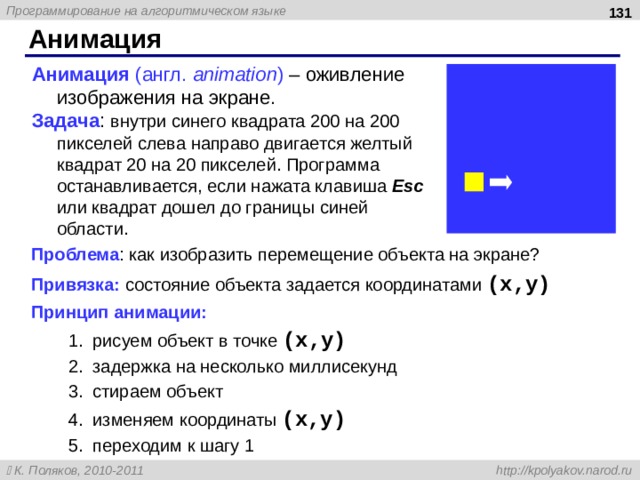



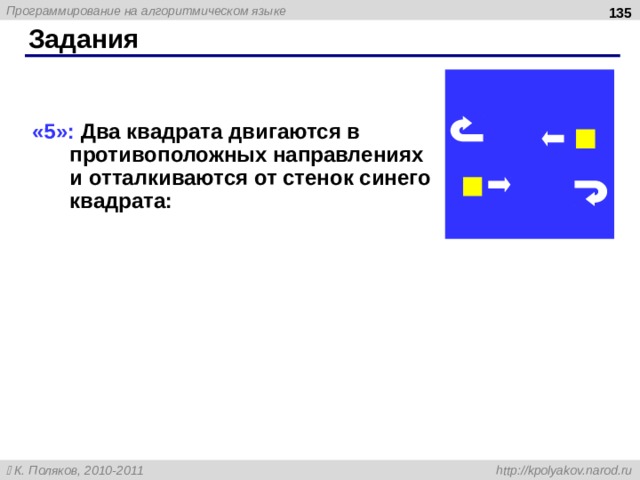

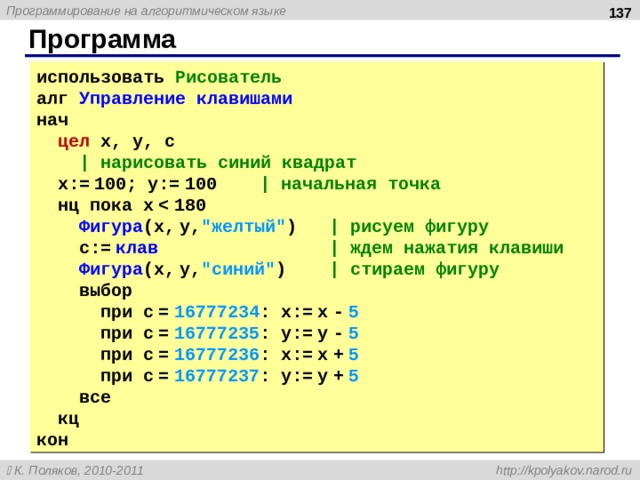
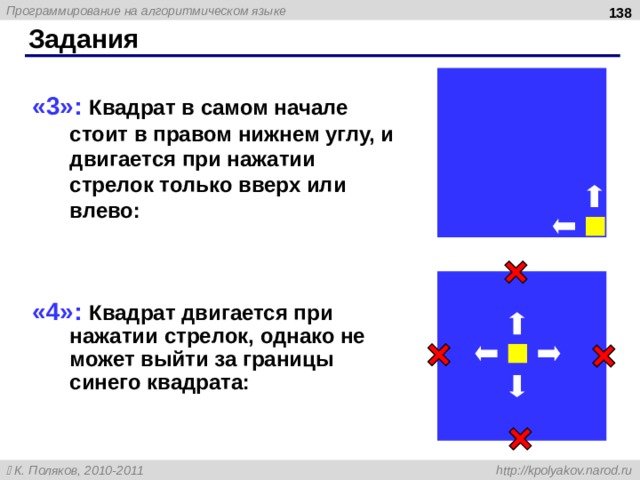
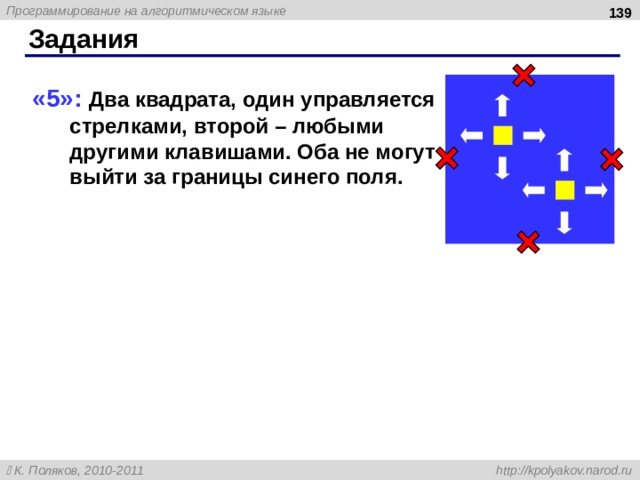



![143 Распределение случайных чисел Модель : снежинки падают на отрезок [a,b] распределение равномерное неравномерное a a b b ? Сколько может быть разных распределений ? 143](https://fsd.videouroki.net/html/2021/04/01/v_60659c4fe052b/img142.jpg)
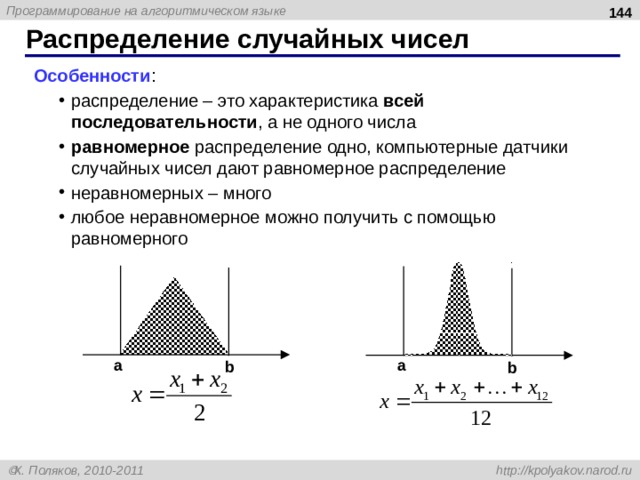
![Генератор случайных чисел Вещественные числа в интервале [0, 10 ) : вещ X, Y X:= r a nd ( 0 , 1 0 ) | интервал от 0 до 10 ( Y:= r a nd ( 0 , 1 0 ) | это уже другое число! англ. random – случайный Целые числа в интервале [0,10] : цел K , L K:= ira nd ( 0 , 1 0 ) | интервал от 0 до 10 ( L := ira nd ( 0 , 1 0 ) | это уже другое число! англ. i nteger – целый](https://fsd.videouroki.net/html/2021/04/01/v_60659c4fe052b/img144.jpg)