Как составить алгоритмический решение задач

Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.

Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.

При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.

В процессе разработки алгоритма решения задачи можно выделить следующие этапы:

• Этап 1 . Математическое описание решения задачи.
• Этап 2 . Определение входных и выходных данных.
• Этап 3 . Разработка алгоритма решения задачи.

Базовые алгоритмические конструкции

В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:

• следование (линейный алгоритм);
• ветвление (разветвляющийся алгоритм);
• цикл-пока (циклический алгоритм).

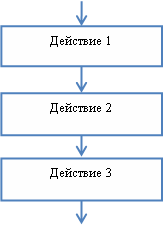
Линейные алгоритмы

Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.

Пример

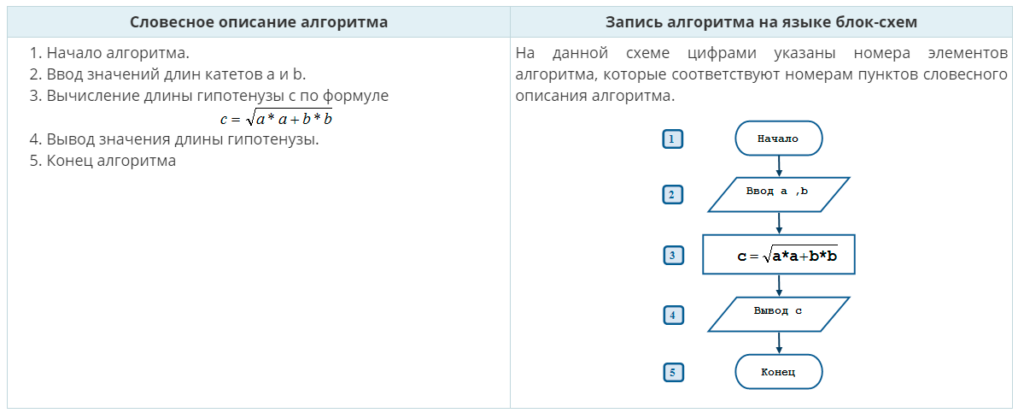
ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.

На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:

Этап 1. Математическое описание решения задачи.

Математическим решением задачи является известная формула:

,

где с-длина гипотенузы, a, b – длины катетов.

Этап 2. Определение входных и выходных данных.

Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.

Этап 3. Разработка алгоритма решения задачи.

Словесное описание алгоритма	Запись алгоритма на языке блок-схем
Начало алгоритма. Ввод значений длин катетов a и b. Вычисление длины гипотенузы с по формуле Вывод значения длины гипотенузы. Конец алгоритма	На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.

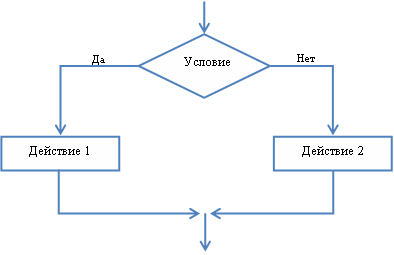
Разветвляющиеся алгоритмы

Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.

Пример

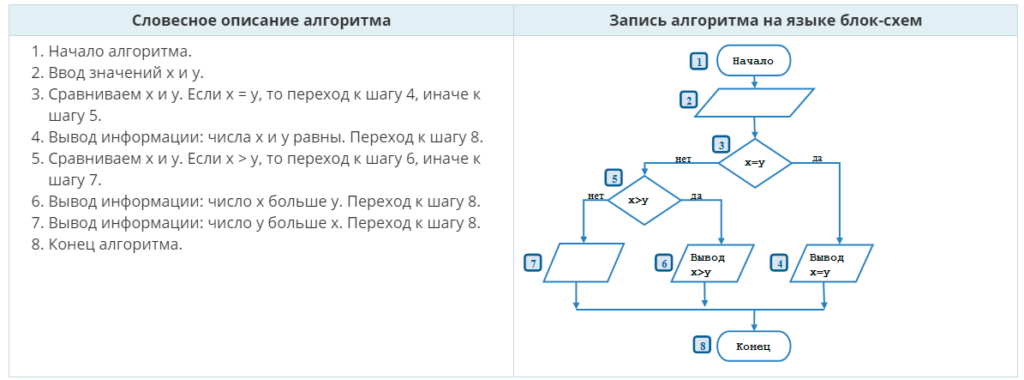
ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.

Этап 1. Математическое описание решения задачи.

Из курса математики известно, если x > y, то наибольшее число x, если x < y, то наибольшее число y, если x = y, то число x равно числу y.

Этап 2. Определение входных и выходных данных.

Входными данными являются значения чисел x и y. Выходным данными являются:

• наибольшее число
• любое из чисел, если числа равны

Для решения задачи нам необходимо знать значения x и y.

Этап 3. Разработка алгоритма решения задачи.

Словесное описание алгоритма	Запись алгоритма на языке блок-схем
Начало алгоритма. Ввод значений x и y. Сравниваем x и y. Если x = y, то переход к шагу 4, иначе к шагу 5. Вывод информации: числа x и y равны. Переход к шагу 8. Сравниваем x и y. Если x > y, то переход к шагу 6, иначе к шагу 7. Вывод информации: число x больше y. Переход к шагу 8. Вывод информации: число y больше x. Переход к шагу 8. Конец алгоритма.

В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма

В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:

• первая: это элементы 1, 2, 3, 4, 8.
• вторая: это элементы 1, 2, 3, 5, 6, 8
• третья: это элементы 1, 2, 3, 5, 7, 8.

Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.

Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.

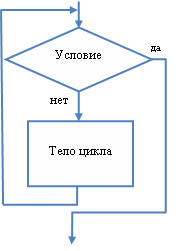
Циклические алгоритмы

Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.

Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.

При разработке алгоритма циклической структуры выделяют следующие понятия:

• параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
• начальное и конечное значения параметров цикла;
• шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.

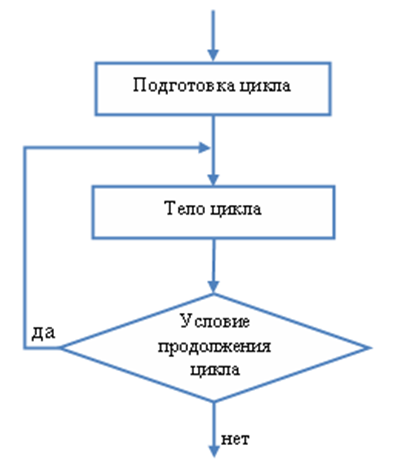
Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.

 

В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:

• начальные значения цикла;
• конечные значения цикла;
• шаг цикла.

В тело цикла входят:

• многократно повторяющиеся действия для вычисления искомых величин;
• подготовка следующего значения параметра цикла;
• подготовка других значений, необходимых для повторного выполнения действий в теле цикла.

В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.

 Пример

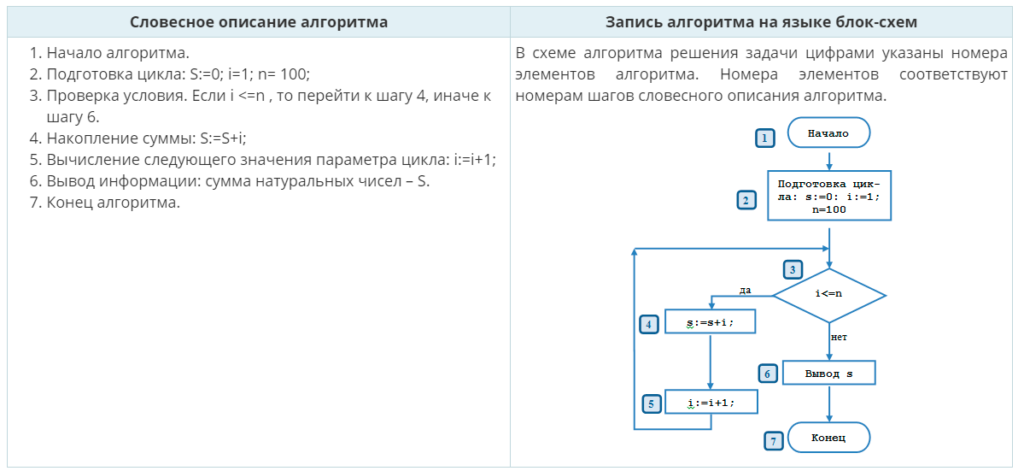
ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.

Этап 1. Математическое описание решения задачи.

Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:

где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.

Этап 2. Определение входных и выходных данных.

Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.

Выходные данные – значение суммы членов последовательности натуральных чисел.

Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.

Подготовка цикла заключается в задании начального и конечного значений параметра цикла.

• начальное значение параметра цикла равно 1,
• конечное значение параметра цикла равно n,
• шаг цикла равен 1.

Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.

Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:

S=S+i;              I=I+1;

Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.

Этап 3. Разработка алгоритма решения задачи.

Введем обозначения: S – сумма последовательности, i – значение натурального числа.

Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.

Словесное описание алгоритма	Запись алгоритма на языке блок-схем
Начало алгоритма. Подготовка цикла: S:=0; i=1; n= 100; Проверка условия. Если i <=n , то перейти к шагу 4, иначе к шагу 6. Накопление суммы: S:=S+i; Вычисление следующего значения параметра цикла: i:=i+1; Вывод информации: сумма натуральных чисел – S. Конец алгоритма.	В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма. Номера элементов соответствуют номерам шагов словесного описания алгоритма.

Мы уже рассказывали про алгоритмы, их виды и свойства. В этой статье поговорим о том, как составить алгоритм решения какой-нибудь задачи, что и в какой последовательности следует написать.

При решении задач на алгоритмы немаловажным является умение использовать язык блок-схем. Процесс решения одной и той же задачи можно реализовать посредством применения алгоритмов разных классов, поэтому результат может отличаться и по времени счета, и по объему вычислений, и по сложности. Записывая алгоритмическую последовательность с помощью составления блок-схем, вы сможете сравнить решения, выбрав самый лучший algorithm. Также появляется возможность упростить способ решения, найти и устранить ошибку.

Можно ли отказаться от языка блок-схем при описании алгоритма и сразу составить его на языке программирования? Можно, однако существует риск выбора неоптимального решения и существенных потерь времени. Именно поэтому при данной постановке вопроса рекомендуется сначала составлять способ решения задачи путем создания блок-схемы, а уже потом переводить алгоритм на нужный язык программирования.

Когда речь идет о задаче высокого класса сложности, не обойтись без пошаговой реализации. Сначала продумывают общую структуру алгоритмической последовательности, то есть детальная проработка отдельных частей здесь не требуется. Модули, которые далее потребуют более детального рассмотрения, обводят пунктиром, чтобы потом продумать и детализировать.

В решении задачи на алгоритмы выделяют ряд этапов:

1. Математическое описание.
2. Определение входных/выходных данных.
3. Разработка алгоритма по решению поставленной задачи.

Алгоритмические конструкции базовых классов

В теории программирования считают, что для того, чтобы составить запись любого, даже самого сложного алгори тма, хватит  3-х базовых структур. Речь идет о следующих алгоритмах:

• линейного класса;
• ветвления (речь идет о разветвляющихся алгоритмах);
• циклического класса.

Алгоритмы линейного класса

Образуются из последовательности действий, которые следуют одно за другим. К примеру, чтобы определить площадь прямоугольника, надо сначала задать длину 1-й стороны, потом — 2-й стороны, ну а в конце уже можно решать пример по формуле нахождения площади.

В качестве примера возьмем задание с разработкой алгоритма по вычислению гипотенузы прямоугольного треугольника, зная длины катетов a и b. Вспоминаем вышеописанные этапы разработки:

1. Математическое описание.

Математически задача решается по следующей формуле:

Здесь c является длиной гипотенузы, a, b – длинами катетов.

2. Определяем входные/выходные данные.

Входные данные — значения катетов a и b. Выходные — длина гипотенузы c.

3. Разработка алгоритма.

Алгоритмы ветвления

В таких алгоритмических последовательностях всегда существует какое-нибудь условие. В зависимости от того, соблюдается это условие либо нет, происходит выполнение той либо иной последовательности действий.

Для примера возьмем задание, постановка которого связана с разработкой алгоритма по вычислению наибольшего числа из 2-х чисел: x и y.

1. Математическое описание.

Из первых классов математики мы знаем, что когда x > y, то x больше y и наоборот, что является очевидными вещами. И если x = y, то числа равны.

2. Определяем входные/выходные данные.

Входные данные — это значения x и y. Выходными данными являются:

• самое большое число;
• любое из чисел в том случае, если они равны.

Таким образом, чтобы решить эту задачу на алгоритмы, надо знать значения переменных x и y.

3. Разработка.

В вышеуказанной схеме цифрами отмечены номера алгоритмических элементов, соответствующие номерам шагов словесного описания. Здесь есть 3 ветви решения:

• 1, 2, 3, 4, 8;
• 1, 2, 3, 5, 6, 8;
• 1, 2, 3, 5, 7, 8.

Алгоритмы циклического класса

В алгоритмах циклического класса некоторая часть действий из задания повторяется до тех пор, пока не нарушится заранее определенное условие. Выполнение условия проверяется в начале. Совокупность операций, которые выполняются многократно, — это тело цикла.

В алгоритмических последовательностях этого класса выделяют ряд понятий:

• параметр цикла (с изменением этой величины связано многократное выполнение цикла);
• начальное и конечное значения циклических параметров;
• шаг цикла (речь идет о значении, на которое меняется параметр при каждом повторе).

Работу циклов организуют по специальным правилам. Алгоритмическая последовательность циклического класса включает в себя и подготовку, и тело, и условия продолжения работы.

В подготовку входят действия, которые связаны с заданием исходных значений:

• начальные значения;
• конечные значения;
• шаг.

В тело цикла входят:

• многократно повторяющиеся операции по вычислению искомых величин;
• подготовка последующего значения параметра;
• подготовка иных значений, нужных для повторного выполнения действий непосредственно в теле.

В условии продолжения цикла определяют допустимость выполнения повторяемых операций. Когда циклический параметр равен либо превышает конечное значение, выполнение прекращается.

Рассмотрим задание, постановка которого связана с разработкой алгоритма вычисления суммы натуральных чисел в диапазоне от 1 до 100.

1. Математическое описание.

Сначала следует обозначить сумму натуральных чисел буквой S. В результате формулу вычисления суммы чисел от 1 до 100 можно записать следующим образом:

Здесь Xi является натуральным числом X c номером i. Этот номер меняется от 1 до n. А n=100 обозначает общее кол-во натуральных чисел.

2. Определяем входные/выходные данные.

Входные данные — это натуральные числа: 1, 2, 3, …, 99, 100.

Выходные данные представляют собой значение суммы членов последовательности натуральных чисел.

Относительно параметра цикла — речь идет о величине, определяющей число циклических повторений. В нашем задании i представляет собой номер натурального числа.

Подготовка цикла — задание начального и конечного значений циклического параметра. Тут надо пояснить следующее:

• начальное значение циклического параметра равняется единице,
• конечное значение — n,
• шаг равен 1.

Чтобы обеспечить корректность суммирования, надо, чтобы начальное значение суммы предварительно равнялось нулю.

Тело цикла. В теле станут выполняться как накопление значения суммы, так и вычисление последующего значения циклического параметра по формулам ниже:

• S=S+i;             
• I=I+1.

Циклическое повторение должно осуществляться до тех пор, пока не добавится последний член последовательности натуральных чисел, то есть до тех пор, пока циклический параметр будет меньше либо равен окончательному значению параметра.

3. Разработка.

Вводим следующие обозначения: S – это сумма последовательности, i – это значение натурального числа.

Начальное циклическое значение i=1, конечное — i =100, шаг равен 1.

По материалам: https://www.turbopro.ru/index.php/osnovy-programmirovaniya/6836-algoritmy-razrabotka-algoritma-resheniya-zadachi.

Алгоритмизация
понимается как выбор метода решения
математической модели и его оформление
в подетальном виде, понятном человеку
(алгоритмом).

Рассмотрим
выделенные элементы с увеличенной
степенью детализации.

1. Выбор метода решения

Выбор метода
решения– второй этап создания
программного продукта, определяющий
общие принципы реализации полученной
математической модели.

Полное название
этапа – выбор численного метода решения.

Выбор численного
метода решения обусловлен применением
цифровых ЭВМ, выполняющих только
арифметические и логические операции
над числами. Поэтому каждую используемую
в математическом описании аналитическую
зависимость (интеграл, дифференциал,
тригонометрическую или иную функцию)
необходимо заменить определённой
совокупностью арифметических действий.
Так, интеграл заменяется суммой,
дифференциал – конечной разностью,
тригонометрические функции – степенными
рядами или цепными дробями. Например,
показательная функция может быть
заменена степенным рядом:

Выбрать
метод решения – значит найти вариант
замены неарифметической функции
последовательностью арифметических
действий. Осуществить эту замену без
потерь невозможно. Таким образом, любой
численный метод позволяет получить
приближённое значение функции с нужной
степенью точности. Это иллюстрирует
приведённый степенной ряд, который
реально нельзя рассчитывать до
бесконечности. Следовательно, прекратив
суммирование при достаточно большом
n, придётся отбросить все расположенные
правее элементы ряда, доказав неспособность
получить истинное значение.

В
вычислительной математике разработано
множество численных методов для решения
различных инженерных и экономических
задач. Большинство из них реализовано
в виде библиотек подпрограмм в программном
обеспечении ЭВМ.

При
выборе численного метода решения задачи
вначале желательно выяснить, имеется
ли он в программном обеспечении ЭВМ и
как его использовать. Подпрограммы
вычисления большинства трансцендентных
функций постоянно хранятся в системных
библиотеках и требуют только вызова с
указанием аргумента.

Если
стандартные подпрограммы отсутствуют,
необходимо, используя литературу по
прикладной математике, выбрать из
нескольких возможных разновидностей
методов один, удовлетворяющий пользователя
по точности и, может быть, вначале самый
простой.

Возможны
задачи, в которых математическая
формулировка не требует выбора численного
метода решения или он используется как
вспомогательный из библиотек подпрограмм
ЭВМ. Для таких задач под выбором метода
решения будем понимать реализацию одной
из стандартных разновидностей простых
вычислительных процессов – линейного,
ветвящегося, циклического.

Так,
математическая модель задачи о картофеле
(пример 2.3) не содержит нестандартных
трансцендентных функций и для получения
результатов требует последовательного
однократного выполнения всех
запланированных в расчётных зависимостях
арифметических операций, т.е. использования
в качестве метода решения линейного
вычислительного процесса.

1. Составление алгоритма решения

Составление
алгоритма решения– завершающий
этап алгоритмизации, однозначно
определяющий, с учётом выбранного метода
решения, путь преобразования математической
модели задачи в результаты.

Составить
алгоритм – значит выбрать единственный
из всех возможных вариантов решения.

Алгоритм– совокупность предписаний, однозначно
и подетально определяющих последовательность
преобразования исходных данных в
конечные результаты.

Основные
свойства алгоритма:

• определённость;

• массовость;

• результативность;

• дискретность.

Определённостьозначает однозначность выполнения
запланированной последовательности
элементарных действий.

Определённость
исключает нарушения заданного порядка
вычислений и произвольность толкования
предписаний.

Массовость
определяет возможность применения
для различных задач одного класса.

Массовость
достигается реализацией в алгоритме
конкретной задачи её универсального
математического описания.

Результативность
характеризует неизбежность получения
конкретного результата при выполнении
алгоритма.

Результатом
могут быть выходные данные или сообщение
о невозможности решения задачи.

Дискретностьозначает представление в виде совокупности
фрагментов, элементарных действий.

Дискретность
определяет обязательную детализацию
алгоритма.

Основные
качества алгоритма:

• наглядность;

• информативность.

Наглядность– обеспечение простоты, доступности
восприятия алгоритма в целом.

Информативность– представление максимума детализированных
сведений о технологии решения задачи.

Алгоритм
составляется для человека, поэтому
должен быть относительно простым
(наглядным) и достаточно информативным.
Компромисс между этими требованиями
достигается выбором степени детализации.
Например, замена несложной формулы
несколькими простыми увеличивает
информативность, но делает алгоритм
громоздким, менее наглядным. Укрупнение
действий улучшает наглядность, но
ухудшает информативность.

Существуют
различные способы представления
алгоритмов, чаще используют два из них:

• словесное описание;

• графическое изображение
  (схема алгоритма).

Словесное
описание алгоритма– последовательность
конкретных указаний на разговорном
языке, приводящая к решению задачи.

Так, для задачи
о картофеле (пример 2.3) на основании
составленной математической модели и
выбранного численного метода решения
можно предложить следующее словесное
описание алгоритма:

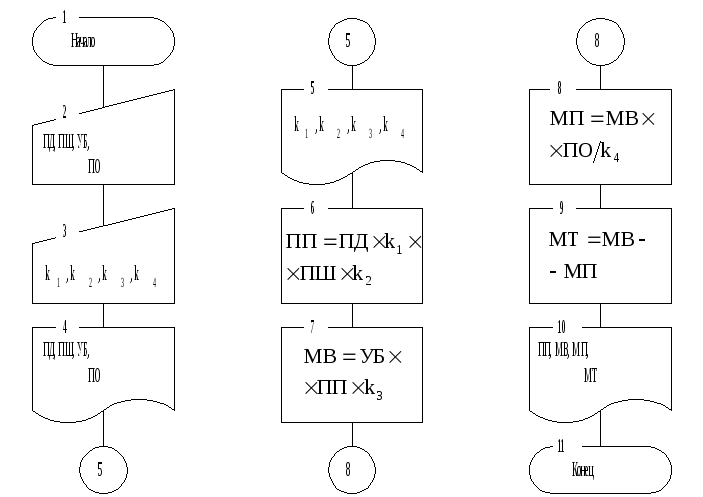
1. Начать решение.

2. Ввести исходные данные ПД,
   ПШ, УБ, ПО, k₁, k₂, k₃, k₄.

3. Вывести исходные данные
   ПД, ПШ, УБ, ПО, k₁, k₂, k₃,
   k₄.

4. Вычислить площадь поля
   .

5. Вычислить массу выращенного
   картофеля
   .

6. Вычислить массу потерь
   картофеля
   .

7. Вычислить товарную массу
   картофеля МТ = МВ – МП.

8. Вывести на печать результаты
   ПП, МВ, МП, МТ.

9. Закончить решение.

Вывод
исходных данных выполняется для контроля
правильности их ввода.

Основные
недостатки словесного способа –
громоздкость и отсутствие наглядности
при описании сложных алгоритмов. Поэтому
в большинстве случаев используется
способ представления алгоритма в виде
графической схемы.

Схема
алгоритма – совокупность
геометрических фигур (блоков), обозначающих
(определяющих) запланированный путь
решения задачи.

Блоки– элементы схемы, обозначающие стандартные
предписания (действия) в алгоритме.

Например,
ввод, вывод, вычисление по формулам,
проверка условий. В схеме блоки соединяются
линиями связи, определяющими
последовательность их выполнения.

Обозначения,
наименования и правила использования
блоков определяются ГОСТом (табл. 1.3).

Таблица 1.3

Наименование	Обозначение	Пояснение
Процесс		Обозначение вычислений по одной или нескольким формулам, записываемым внутри блока. Имеет один вход и один выход
Решение		Проверка записанного в блоке условия, в результате чего выбирается тот или иной путь решения задачи. Имеет один вход и 2 (несколько) выходов
Ручной ввод		Ввод данных, указанных в блоке. Имеет один вход и один выход

Продолжение табл. 1.3

Наименование	Обозначение	Пояснение
Документ		Вывод указанной в блоке информации на бумажный носитель. Имеет один вход и один выход
Дисплей		Вывод указанной в блоке информации на экран дисплея. Имеет один вход и один выход
Ввод, вывод		Общий вид операции ввода/вывода информации. Имеет один вход и один выход
Модификация		Начало цикла с параметрами, записанными внутри блока. Имеет два входа и два выхода
Предопре-делённый процесс		Переход к подпрограмме с возвратом из неё. Имеет один вход и один выход
Начало цикла		Общее обозначение начала цикла. Имеет один вход и один выход
Конец цикла		Общее обозначение окончания цикла. Имеет один вход и один выход

Окончание табл. 1.3

Наименование	Обозначение	Пояснение
Запоминающее устройство с прямым доступом		Запись (считывание) данных. Носитель данных – магнитный диск. Имеет один вход и один выход
Пуск, останов		Начало (конец) в основном алгоритме или вход (выход) в дополнительном
Соединитель		Обозначение разрывов соединительных линий алгоритма, расположенных на одной или разных страницах
Комментарий		Обозначение, примыкающее к блоку, содержимое которого требуется пояснить, расшифровать

В
качестве вертикального размера блоков
рекомендуется использовать значения
ряда 10, 15, 20 мм с допускаемым увеличением
на число, кратное 5.

Горизонтальный
размер b рекомендуется выбирать в полтора
раза большим, чем a().
При выполнении схем вручную допускается
соотношение.
В одной схеме возможно использование
блоков не более чем с двумя размерами
а.

В верхней
левой части блоков в разрыве контура
записываются их порядковые номера.
Основные направления построения схемы
– вниз и вправо. На линиях, соединяющих
блоки в схему, стрелки указываются на
направлениях, противоположных основным,
т.е. снизу вверх и справа налево.

Пересечение
линий связи нежелательно. Если этого
избежать нельзя, пересекающиеся линии
считаются не имеющими логической связи.
Соединение (состыковка) двух линий
возможна (табл. 1.4).

Таблица 1.4

Примеры пересечения линий
не соединяющиеся	соединяющиеся слева	соединяющиеся справа

При необходимости
изображения других вариантов соединяющихся
линий требуется руководствоваться
следующими примерами (табл. 1.5).

Таблица 1.5

Соединение	правильное	неправильное
с передачей управления вниз:
с передачей управления вверх:

Минимальное
расстояние между параллельными линиями
связи 3 мм, между блоками – 5 мм. При
разрыве линии связи на концах разрыва
размещаются соединители. Оба соединителя
имеют одинаковую маркировку, например,
номер блока, которому передаётся
управление. Если соединители расположены
на разных страницах, каждый дополняется
комментарием. Например:

С
учётом изложенного выполним простейшую
схему алгоритма задачи о картофеле
(пример 1.3) при выбранной в модели степени
детализации (рис. 1.4).

Рис. 1.4. Простейшая схема алгоритма
задачи о картофеле

Рекомендации
по эффективным методам составления
алгоритмов приведены в разделе 2.3.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Перед вами руководство, подготовленное сайтом proglib.io для того, чтобы вы могли научиться быстро и без труда решать алгоритмические задачи. Готовьтесь к собеседованиям правильно.

Для начала, если вы думаете, что изучения основ компьютерных наук хватит для того, чтобы вам посыпались предложения от разных компаний, вы можете закончить читать здесь. Это руководство предназначено для тех, кто хочет обеспечить себя необходимыми навыками для того, чтобы без проблем пройти собеседование с помощью LeetCode.

Оттачивать навыки написания кода на LeetCode — это не просто запоминать ответы. Вам нужно знать шаблоны решения задач и уметь их применять. Количество решённых задач — это только одна сторона знакомства с шаблонами, но изучение включает в себя не только числа.

Пункт 0: За пределами основ компьютерных наук

В этом руководстве предполагается, что вы по крайней мере слышали об основных вещах, таких как двойные указатели и манипулирование битами. Вам не нужно знать их в совершенстве, но хотя бы базовые знания о том, что это такое, помогут вам более эффективно практиковаться решать задачи на LeetCode. Если вы изучали только основы компьютерных наук, вам может понадобиться обратиться к некоторым книгам, чтобы немного подтянуться.

Легкие алгоритмические задачи на LeetCode

Легкие задачи призваны помочь вам ознакомиться с основными приёмами. Обычно у них есть грубые тривиальные решения. Вам нужно научиться применять эти приёмы, чтобы лёгкие задачи не вызывали у вас никаких проблем.

Пункт 1: Практика основных приёмов

Если случайно открывая несколько простых задач из структур данных или алгоритмов вы можете легко и быстро придумать оптимальное решение, после чего реализовать его, вы можете переходить к следующему пункту. Если же нет, то вам очевидно придётся задержаться и больше тренироваться решать лёгкие задачи.

Как тренироваться

1. Отсортируйте задачи по убыванию рейтинга принятия (англ. acceptance rate). Обычно задачи с более высоким рейтингом принятия немного легче.
2. Старайтесь решать лёгкие задачи без подсказок.
3. Как ни странно, злоупотреблять кнопкой «run» не очень полезно. Попробуйте написать решение лёгких задач так, чтобы они были приняты с первого раза. Такой подход имитирует ситуацию, когда вы пишете код на доске, что позволит вам научиться рассматривать все варианты сразу в голове.
4. Иногда следует приглядываться к решениям в топе на предмет применения каких-то интересных приёмов. Часто решения попадают в топ, когда они короткие и недостаточно документированы. Также читайте комментарии и не стесняйтесь просить пояснить какие-то моменты.
5. Как только вы чувствуете что изучили достаточно шаблонов решений простых задач, вернитесь к пункту 1 и решите, готовы ли вы двигаться дальше.

Средние алгоритмические задачи на LeetCode

Средние задачи предназначены для того, чтобы вы научились видеть суть. Чаще всего они представляют собой различные комбинации лёгких задач. Но решения «в лоб» часто могут привести к ошибке времени выполнения. Вам нужно уметь определять, какой именно шаблон решения требует та или иная задача.

Пункт 2: Распознавание шаблонов задач

Если случайно открывая несколько средних задач из структур данных или алгоритмов, вы можете определить, какой вид задач в них представлен, и реализовать близкое к оптимальному решение в течение получаса, то смело переходите к более высокому уровню.

Как тренироваться

1. Внимательно читайте сам текст задачи и ищите в нём подсказки по поводу реализации. Например, количество подзадач может указывать на динамическое программирование, строковое преобразование с помощью dictionary указывает на поиск в ширину, поиск в длину или префиксное дерево, поиск повторяющихся или уникальных элементов указывает на хеширование или манипулирование битами и т. д. Если вам требуется более полный список приёмов, то следует обратить внимание на книгу-руководство для программистов.
2. Когда есть приблизительное представление о решении — это уже полпути. Попытайтесь реализовать его, даже если оно не совсем оптимальное. Это нормально, ведь обычно люди тратят гораздо больше времени на оптимизацию, чем на само решение.
3. Когда вы реализовали своё неидеальное решение, посмотрите на топовые решения этой же задачи, чтобы посмотреть, как вы можете улучшить своё.
4. Затем попытайтесь хорошо понять основную мысль и реализовать более оптимальное решение, не используя подсказки.
5. Как только вы чувствуете, что можете больше, чем просто применять шаблоны, настало время перейти к сложным задачам.

Сложные алгоритмические задачи на LeetCode

Сложные задачи предназначены для того, чтобы заставить вас напрячься. Обычно 45 минут достаточно для того, чтобы вы могли придумать рабочее решение. Чтобы научиться их решать, нужно научиться видеть какие-то более изящные пути, чем тривиальное решение «в лоб».

Пункт 3: Последняя проверка

В сложных задачах обычно есть ограничения, которые не позволят вам получить решения, используя привычные шаблоны. Если вы можете модифицировать обычные приёмы для решения сложных задач, то ваша подготовка завершена. Время здесь не так важно, вы должны научиться видеть связь между привычными шаблонами решений и этими ограничениями.

Как тренироваться

1. В этом случае решение задачи важнее, чем нахождение оптимального решения. Если вы можете решить задачу «в лоб», жертвуя ограничениями по времени и/или месту, делайте это.
2. И только после нужно определить, как оптимизировать решение, чтобы оно соответствовало ограничениям.
3. Если у вас не получается оптимизировать решение, то самое время обратить внимание на топовые варианты реализации. Здесь очень важно понять ход решения. Вы должны научиться подбирать правильный алгоритм и использовать нужные структуры данных, а также уметь учитывать все случаи.
4. Как только вы научитесь находить решения одних сложных задач, переходите к другим видам задач и старайтесь делать ваши решения более оптимальными.

Спасибо, что прочитали. Надеемся, вы нашли для себя что-то полезное.

***
Подписывайтесь на наш канал в Telegram!