Аналитическая
и геометрическая модели
числового промежутка
Цели: ввести понятие числового
промежутка как геометрической модели числового неравенства; рассмотреть
различные виды числовых промежутков; формировать умения изображать на
координатной прямой числовой промежуток и множество чисел, удовлетворяющих
неравенству.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Назовите верное
неравенство, которое получится, если:
а) к обеим частям неравенства –1 < 3
прибавить число 4; число –2;
б) из обеих частей неравенства –15 < –2
вычесть число 3; число –5;
в) обе части неравенства 6 > –1 умножить на
8; на –5;
г) обе части неравенства 9 < 27 разделить на
9; на –3; на –1.
2. Заполните пустые квадратики:
а) 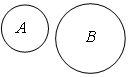
А В =
А
В =
А
В =
III. Объяснение нового материала.
1. А к т у а л и з а ц и я з н а н и й.
Напоминаем учащимся, что алгебра, в частности,
занимается тем, что описывает различные реальные ситуации на математическом
языке в виде математических моделей, а затем имеет дело уже не с реальными
ситуациями, а с этими моделями, используя разные правила, свойства, законы,
выработанные в алгебре.
Математические модели бывают не только алгебраические
(в виде числового равенства, уравнения, неравенства), но и словесные
(в виде словесного описания реальной ситуации), графические (в
виде схемы, графика, чертежа). Учащиеся уже знакомы со всеми этими видами
моделей. Напоминаем, что алгебраическую модель ещё называют аналитической,
а графическую – геометрической. Чтобы свободно оперировать любыми
видами математических моделей, нужно учиться переходить от одного из них к
другому.
Н а п р и м е р:
|
Словесная модель № 1 |
Аналитическая |
Геометрическая |
Словесная модель № 2 |
|
b больше а |
b > a |
|
Точка с координатой b |
2. В в е д е н и е н о в о г о п о н я
т и я.
Работаем с представленными выше моделями,
причём идём в обратном порядке: от словесной модели № 2 к словесной модели № 1.
Возьмём произвольную точку х на
координатной прямой, причём эта точка лежит между точками a и b.
Это означает, что ей соответствует число х, которое больше a и
меньше b, то есть a < x < b. Верно и
обратное: для любой точки, лежащей между точками a и b, будет
выполняться это неравенство.
О п р е д е л е н и е: Множество чисел,
удовлетворяющих условию
a < x < b, называют интервалом и
обозначают так: (a; b).
На рисунке (геометрическая модель) это множество
изображают в виде:
Светлые кружочки означают, что числа a и
b не принадлежат этому множеству.
Аналогично вводим определения отрезка,
полуинтервала, числового луча, открытого числового луча и числовой прямой.
О п р е д е л е н и е: Числовые отрезки,
интервалы, полуинтервалы, числовые лучи, открытые числовые лучи и числовая
прямая называются числовыми промежутками.
3. О п е р а ц и и с р а з л и ч н ы м
и м о д е л я м и.
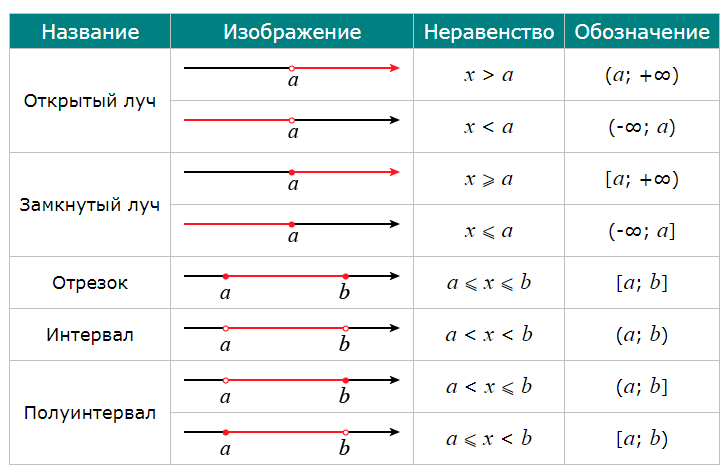
Рассматриваем на с. 173 учебника таблицу, в
которой представлены такие модели числовых промежутков, как:
– аналитическая (неравенство, задающее числовой
промежуток), например: a ≤ x ≤ b;
– словесная (обозначение и название числового
промежутка), например: [a; b] – числовой промежуток от a
до b;
– геометрическая (изображение
числового промежутка на координатной прямой), например:
IV. Формирование умений и навыков.
Все упражнения, решаемые на этом уроке,
можно разбить на т р и
г р у п п ы:
1) Изобразить на координатной прямой
числовой промежуток по его обозначению (создание геометрической модели).
2) Назвать числовой промежуток,
изображённый на координатной прямой, и обозначить его (создание словесной
модели).
3) Изобразить на координатной прямой
множество чисел, удовлетворяющих неравенству, и записать неравенство,
соответствующее изображенному или обозначенному числовому промежутку (переход
от аналитической к геометрической модели и наоборот).
О с о б о е в н и м а н и е уделяем:
– правильным формулировкам;
– верному использованию круглых и квадратных
скобок при обозначении числового промежутка;
– верному использованию светлых кружков
(«выколотых» точек) и тёмных при изображении числовых промежутков на
координатной прямой.
1. № 812 (а, б, д, е), № 813, № 814.
2. № 815 (а, г), № 816 (в, г).
Р е ш е н и е
№ 815.
а) х ≥ –2; ; [–2;
+∞).
г) х < –5; ; (–∞;
–5).
№ 816.
в) –5 ≤ х ≤
–3;
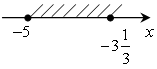
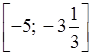
г) 2 < х ≤
6,1; ; (–2; 6,1].
3. № 817 (а) – устно, № 819 (а, в).
Р е ш е н и е
№ 819.
а) ≈
1,4, (1,5; 2,4).
в) ≈
2,2, (1,5; 2,4).
4. Задайте неравенством числовой промежуток:
а) 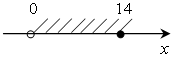
х [2;7,3];
б) 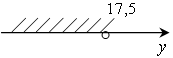
y (–∞; 100);
в) 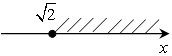
х (–8,3; 0];
г) 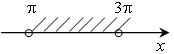
y (0; +∞);
д) 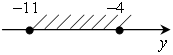
х (–15; –4);
е) 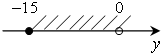
y [–60; 100).
Р е ш е н и е
а) 0 < x ≤ 14; ж)
2 ≤ х ≤ 7,3;
б) y < 17,5; з)
у < 100;
в) x ≥; и)
–8,3 < x ≤ 0;
г) π < x
< 3π; к) у > 0;
д) –11 ≤ у ≤ –4; л)
–15 < x < –4;
е) –15 ≤ у < 0; м)
–60 ≤ у < 100.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется числовым промежутком?
– Какие виды числовых промежутков существуют?
– Как выглядит геометрическая модель числового
промежутка?
– Как записать аналитическую модель числового
промежутка с помощью неравенства?
Домашнее задание: № 812
(в, г, ж, з), № 815 (б, в), № 816 (а, б), № 817 (б), № 819 (б, г).
Инфоурок
›
Алгебра
›Презентации›Презентация урока по алгебре «Числовые промежутки» (8 класс)
Скачать материал

Скачать материал


- Сейчас обучается 49 человек из 33 регионов


- Сейчас обучается 27 человек из 13 регионов




Описание презентации по отдельным слайдам:
-
1 слайд
Числовые промежутки
Тема урока: -
2 слайд
Сегодня мы узнаем:
Что такое числовые промежутки;
Виды числовых промежутков;
Как выглядит геометрическая модель числового промежутка;
Как записать аналитическую модель числового промежутка… -
3 слайд
Определение
Множество всех чисел, удовлетворяющих данному условию, называется числовым промежутком -
4 слайд
Таблица числовых промежутков
-
5 слайд
а ≤ x ≤ b
a b
Обозначение: [a; b] – отрезок
Читают: отрезок от а до b.
Числовой отрезок– множество всех чисел, удовлетворяющих условию -
6 слайд
а < x < b
a b
Обозначение: (a; b) – интервал
Читают: интервал от а до b.
Интервал – множество всех чисел, удовлетворяющих условию -
7 слайд
а ≤ x < b
a b
Обозначение: [a; b) – полуинтервал
Читают: полуинтервал
от а до b, включая а.
Полуинтервал – множество всех чисел, удовлетворяющих условию -
8 слайд
а < x ≤ b
a b
Обозначение: (a; b] – полуинтервал
Читают: полуинтервал
от а до b, включая b.
Полуинтервал – множество всех чисел, удовлетворяющих условию -
9 слайд
x ≥ а
a
Обозначение: [a; +∞) – числовой луч
Читают: числовой луч от а до плюс бесконечности.
Числовой луч – множество всех чисел, удовлетворяющих условию -
10 слайд
x > а
a
Обозначение: (a; +∞) – открытый
числовой луч
Читают: открытый числовой луч от а до плюс бесконечности.
Открытый числовой луч – множество всех чисел, удовлетворяющих условию -
11 слайд
x ≤ а
a
Обозначение: (-∞;а] – числовой луч
Читают: числовой луч от минус бесконечности до а.
Числовой луч – множество всех чисел, удовлетворяющих условию -
12 слайд
x < а
a
Обозначение: (-∞;а) – открытый
числовой луч
Читают: открытый числовой луч от минус бесконечности до а.
Числовой луч – множество всех чисел, удовлетворяющих условию -
13 слайд
Множество действительных чисел
(х -любое число)
(-∞;+∞) — интервал
Числовой промежуток от -∞ до +∞ -
14 слайд
Успех
Скобки
Круглые ( )
Квадратные [ ]
Формулировки:
-интервал
— Отрезок
— Полуинтервал
— Числовой луч
— Открытый числовой луч
Точки
«пустые»
«черные» -
-
16 слайд
Назовите промежутки, изображенные
на рисунке
— 3
12
— 8 1,8
-8,4 67 -
17 слайд
6
— 42
25 32
-2,3 0 -
18 слайд
Изобразите промежутки на координатной прямой
[ -3;7); [8;21]; (-1; 3)(2;+∞) (-∞; +∞)
(-∞; 12]; (4;+∞)
-
19 слайд
По данной аналитической модели назовите соответствующий числовой промежуток.
х>12
х
12
ВЕРНО!
Проверка
1
2
4
3
ОТКРЫТЫЙ ЛУЧ -
20 слайд
По данной аналитической модели назовите соответствующий числовой промежуток.
-1<х<8
х
-1
ВЕРНО!
Проверка
1
2
4
3
8
ИНТЕРВАЛ -
21 слайд
По данной аналитической модели назовите соответствующий числовой промежуток.
х≤-7
2
1
3
4
х
-7
ВЕРНО!
Проверка
ЛУЧ -
22 слайд
По данной геометрической модели назовите соответствующий числовой промежуток.
х
-3
ВЕРНО!
Проверка
1
2
4
3
ЛУЧ -
23 слайд
По данной геометрической модели назовите соответствующий числовой промежуток.
ВЕРНО!
Проверка
1
2
4
3
х
-26
-13
ПОЛУИНТЕРВАЛ -
24 слайд
2
1
3
4
х
17
ВЕРНО!
Проверка
По данной геометрической модели назовите соответствующий числовой промежуток.
ОТКРЫТЫЙ ЛУЧ -
25 слайд
По данному обозначению назовите соответствующую геометрическую модель.
ВЕРНО!
1
2
4
3
7
9
х
7
9
х
7
9
х
9
7
х
ПОЛУИНТЕРВАЛ -
26 слайд
ВЕРНО!
1
2
4
3
По данному обозначению назовите соответствующую геометрическую модель.
19
8
х
8
19
х
8
19
х
8
19
х
ОТРЕЗОК -
27 слайд
2
1
3
4
ВЕРНО!
По данному обозначению назовите соответствующую геометрическую модель.
-8
х
-8
х
-8
х
-8
х
ОТКРЫТЫЙ ЛУЧ -
28 слайд
Домашнее задание
п.33(таблица)
№№ 814,815, 816
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 268 686 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
Тема
34. Решение неравенств с одной переменной
Больше материалов по этой теме
Другие материалы
Рейтинг:
5 из 5
- 05.04.2017
- 1637
- 6
- 05.04.2017
- 1696
- 1
- 05.04.2017
- 3810
- 9
- 05.04.2017
- 592
- 0
- 05.04.2017
- 327
- 0
- 05.04.2017
- 705
- 4
- 05.04.2017
- 517
- 2
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
-
Курс повышения квалификации «Маркетинг в организации как средство привлечения новых клиентов»
-
Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Финансы предприятия: актуальные аспекты в оценке стоимости бизнеса»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Методы и инструменты современного моделирования»
-
Курс профессиональной переподготовки «Гражданско-правовые дисциплины: теория и методика преподавания в образовательной организации»
-
Скачать материал
-
05.04.2017
6006
-
PPTX
931.5 кбайт -
1133
скачивания -
Рейтинг:
3 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Рыжикова Марина Петровна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 6 месяцев
- Подписчики: 3
- Всего просмотров: 68270
-
Всего материалов:
36
Графический метод решения системы линейных уравнений
Расположение графиков и количество решений системы линейных уравнений
Рассмотрим систему двух уравнений: $ <left< begin 3x-y = 5 \ 3x+2y = 8end right.>$
Построим график каждого из уравнений и найдём точку пересечения.
Точка пересечения (2;1)
Подставим координаты точки пересечения в уравнение:
$ <left< begin3 cdot 2-1 ≡ 5\ 3cdot2+2cdot1 ≡ 8end right.> Rightarrow$ (2;1) — решение системы
Таким образом, точка пересечения графиков уравнений является решением системы.
Графики двух уравнений системы могут пересекаться, быть параллельными и совпадать. Получаем разное количество решений системы в зависимости от соотношения коэффициентов уравнений:
Как составить аналитическую модель системы линейных уравнений по графику
Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться , такую группу уравнений мы называем системой.
Объединяем уравнения в систему с помощью фигурной скобки:
Графический метод
Недаром ответ записывается так же, как координаты какой-нибудь точки.
Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.
Например, построим графики уравнений из предыдущего примера.
Пример 1
Для этого сперва выразим y y y в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно x x x ):
Для того чтобы графически решить систему уравнений с двумя переменными нужно:
1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);
Разберем это задание на примере.
Решить графически систему линейных уравнений.
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Пример 2
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:
а) иметь единственное решение;
б) не иметь решений;
в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Пример 3
Графическое решение системы
Пример 4
Решить графическим способом систему уравнений.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Пример 5
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.
Видео YouTube
Составьте аналитическую модель системы линейных уравнений, геометрическая иллюстрация которой представлена?
Алгебра | 5 — 9 классы
Составьте аналитическую модель системы линейных уравнений, геометрическая иллюстрация которой представлена.
См. прилагаыемый файл.
ЗДЕСЬ две прямые — каждая из которых выражается уравнением общего вида у = кх + в
определим эти «к» и «в»
Проходит через 4 и параллельна оси «Х», т.
)(. ) с координатами ( — 2 ; 4) и (0 ; 1)
подставляя в у = кх + в
получим 4 = к * ( — 2) + в и 1 = к * 0 + в = > ; из второго уравнения в = 1,
подставляя полученное в первое 4 = — 2к + 1
имеем к = — 3 / 2, или к = — 1, 5
след — но система
Система линейных уравнений?
Система линейных уравнений.
Дан луч с концом в точке 7?
Дан луч с концом в точке 7.
Запишите обозначения, аналитическую и геометрическую модели данного числового промежутка.
Сколько натуральных чисел принадлежит этому промежутку?
Дан отрезок от( — 1) до 8запишите обозначение аналитическую и геометрическую модели, данного числового промежутка?
Дан отрезок от( — 1) до 8
запишите обозначение аналитическую и геометрическую модели, данного числового промежутка.
Сколько натуральных чисел принадлежит этому промежутку?
Линейные уравнения и их системы?
Линейные уравнения и их системы.
Система из трёх линейных уравнений ?
Система из трёх линейных уравнений :
Помогите сделать?
На одной координатной прямой изобразите геометрические модели промежутков ( — бесконечность ; 1] и [ — 3 ; 5).
Запишите аналитическую модель общей части этих промежутков и найдите длину.
Как составить аналитическую модель прямой, параллельной х?
Как составить аналитическую модель прямой, параллельной х.
Составьте уравнение прямой MN, если M( — 1 ; — 2) и N(1 ; 7) Пожалуйста, системой линейных уравнений)?
Составьте уравнение прямой MN, если M( — 1 ; — 2) и N(1 ; 7) Пожалуйста, системой линейных уравнений).
За интервал от — 3 до 6?
За интервал от — 3 до 6.
Запишите обозначение, аналитическую и геометрическую модели данного числового промежутка.
Сколько целых чисел принадлежит промежутку?
Помогите завтро сдовать пожалуста?
Помогите завтро сдовать пожалуста.
А)Запешите обозначения, аналитическую и геометрическую модели числового промежутка : < ; Луч с началом в точке ( — 4)> ; .
Сколько отрицательных целых чисел принадлежит данному лучу.
Б) Запешите обозначение, аналитическую и геометрическую модели числового промежутка : < ; Открытый луч с началом в точке ( — 7)> ; .
Сколько отрицательных целых чисел принадлежит данному лучу.
На этой странице сайта, в категории Алгебра размещен ответ на вопрос Составьте аналитическую модель системы линейных уравнений, геометрическая иллюстрация которой представлена?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.
http://www.sites.google.com/site/7klassdistancionnoeobucenie/sistema-linejnyh-uravnenij-graficeskij-sposob-resenia
http://algebra.my-dict.ru/q/6165207_sostavte-analiticeskuu-model-sistemy-linejnyh-uravnenij/
23.11.2020г.
Математика
6 а/б класс. Ссылка на видеоурок https://youtu.be/qT5qXlDDd-s
Тема урока: Числовые промежутки. Понятие множества, элемента множества, подмножества. Пересечение и объединение множеств. Графическая и аналитическая модель числовых промежутков.
Открой тетрадь и запиши число на полях и «Классная работа».
Ниже запиши тему урока.
Запишите в тетрадь все определения, таблицу и примеры.
Числовые промежутки или просто промежутки — множества всех чисел, удовлетворяющих неравенству. По другому, это числовые множества, которые можно изобразить на координатной прямой.
Числовые промежутки – луч и открытый луч
Сегодня на уроке мы познакомимся с понятиями «луч», «открытый луч», «отрезок», «интервал», «числовые промежутки», а также научимся записывать по рисунку числовые промежутки и неравенства.

Для рассмотрения новых понятий воспользуемся рисунками, на которых изображена координатная прямая. Правда, без обозначенных на ней начала отсчета и единичного отрезка. Мы это сделали для того, чтобы не загромождать рисунок.
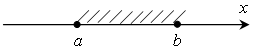
На координатной прямой отмечена точка a, штриховкой отмечены все точки прямой, которые лежат правее a,т.е. числа большие числаa.
Такое множество точек (чисел) называют открытым лучом и обозначают так:
Читают так: а плюс бесконечность или от а до плюс бесконечности.
Для любого числа х из этого множества верно неравенство х a.
Таким образом, открытый луч – это луч, начало которого ему не принадлежит.
Строгие и нестрогие неравенства

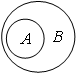
Рассмотрим еще один открытый луч:
На координатной прямой штриховкой отмечены точки, которые расположены слева от точки а. Эти числа меньше, чем а.
Данное множество точек (чисел) обозначается так:
И читается: от минус бесконечности до а.
Для любого числа х этого открытого луча верно неравенство

Обратите внимание, на рисунках, которые мы рассмотрели, точка, соответствующая числу а, обозначена незакрашенным кружочком.
Если закрасить кружок, то множество чисел изменится.
В этом случае число, обозначающее точку а, тоже принадлежит к заштрихованному множеству. Получается луч.
Данные множества записываются с помощью квадратной скобки:
Такие неравенства называют нестрогими.
Неравенства вида х a и х строгими.
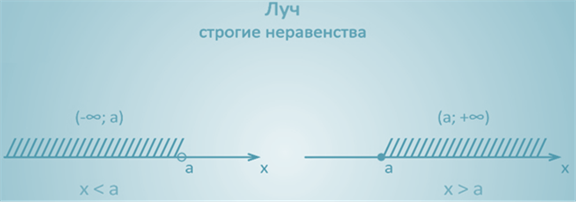
Числовые промежутки – интервал и отрезок
Рассмотрим еще два рисунка.
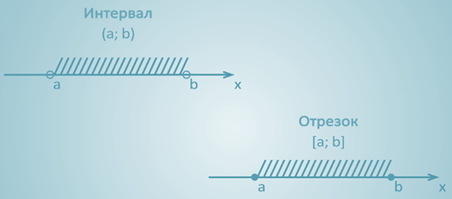
На обоих рисунках штриховкой обозначены точки (числа), которые находятся между точками a и b. В первом случае числа a и b не входят в множество – точки не закрашены, во втором входят – точки закрашены.
Первое множество называют интервалом и обозначают с помощью круглых скобок (a; b).
На втором рисунке изображен тот же интервал, но к нему присоединили его концы точки а и b, поэтому это уже не интервал, а отрезок, и записывается данное множество с помощью квадратных скобок [а; b].
Для всех точек интервала (a; b) верно двойное неравенство а
Для всех точек х, принадлежащих отрезку [а; b], верно двойное нестрогое неравенство а ≤ х ≤ b, (х больше или равен а, но меньше или равен b).
Запись числового промежутка и неравенства по рисунку
«Луч», «открытый луч», «отрезок», «интервал» – это всё числовые промежутки.
Часто при решении задачи мы рисуем схему по ее условию, а затем составляем уравнение. И схема и уравнение – это математические модели ситуации, описанной в задаче.
Схема – графическая модель, уравнение – аналитическая модель.
Аналогично дело обстоит и с числовыми промежутками.
Числовой промежуток – это все числа, соответствующие определенному условию.
Условие соответствует какой-либо математической ситуации. Можно построить как графическую, так и аналитическую модель, кроме того сделать еще и символическую запись.
Например, все числа меньшие 3.
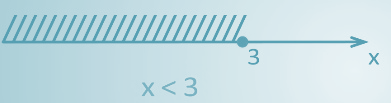
В данном случае числовым промежутком будет открытый луч, графическая модель будет такая:
Аналитической моделью является строгое неравенство х а символическая запись (-∞; 3).
Графическими моделями для числовых промежутков являются: луч, открытый луч, отрезок, интервал.
Аналитическими моделями: строгие, нестрогие неравенства, а так же двойные неравенства.
Обобщим полученную знания о числовых промежутках в следующей таблице.
Виды числовых промежутков: (перерисуйте в тетрадь данную таблицу)
В таблице a и b — это граничные точки, а x — переменная, которая может принимать координату любой точки, принадлежащей числовому промежутку.
Граничная точка — это точка, определяющая границу числового промежутка. Граничная точка может как принадлежать числовому промежутку, так и не принадлежать ему. На чертежах граничные точки, не принадлежащие рассматриваемому числовому промежутку, обозначают незакрашенным кругом, а принадлежащие — закрашенным кругом.
Сделай паузу. Выполни упражнения:

Теперь рассмотрим на конкретных примерах виды числовых промежутков.
Открытый луч
Рассмотрим множество точек координатной прямой, имеющих координату, большую 2, а, значит, расположенных правее точки 2:
Такое множество можно задать неравенством x 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности.
Множество, которому соответствует неравенство x
Замкнутый луч
Замкнутые числовые лучи задаются нестрогими неравенствами. Например, неравенства x ⩾ 2 и x ⩽ 2 можно изобразить так:
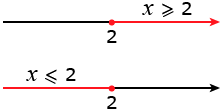
Обозначаются данные замкнутые лучи так: [2; +∞) и (-∞; 2], читается это так: числовой луч от двух до плюс бесконечности и числовой луч от минус бесконечности до двух. Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.
Отрезок
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх.
Интервал и полуинтервал
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:

Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 x
Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:
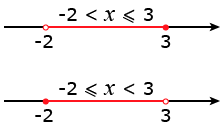
Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3, и полуинтервал от минус двух до трёх, включая минус два.
Теперь рассмотрим, какие операции можно производить с числовыми промежутками.
Пересечение и объединение числовых промежутков
Пересечение числовых промежутков
Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В. Промежуток [3;5] является пересечением промежутков [-1;5] и [3;7]. Это можно записать так: [-1;5]∩[3;7]=[3;5].

Промежутки [0;4] и [6;10] не имеют общих элементов. Если множество не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков [0;4]∩[6;10]=0.

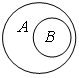
Объединение числовых промежутков
Каждое число из промежутка [1;7] принадлежит хотя бы одному из промежутков [1;5] и [3;7], то есть, либо промежутку [1;5], либо промежутку [3;7], либо им обоим.
Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают A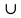
Промежуток [1;7] является объединением промежутков [1;5] и [3;7]. Это можно записать так:
Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество не является промежутком.
Теперь подведи итоги своей работе на уроке и устно ответь на вопросы:
-
Что такое числовой промежуток?
-
Какими скобками обозначается строгое неравенство?
-
Что называют пересечением множеств А∩В?
-
Что называют объединением множеств A
B?
Сделай в тетради все необходимы записи, разбери еще раз непонятные для тебя моменты, отдохни 15 минут.
Теперь открой файл «23.11.20 Практикум Числовые промежутки», рассмотри примеры решенных заданий, выполни упражнения самостоятельно, пришли на проверку свою работу.
Цели: ввести понятие числового промежутка как геометрической модели числового неравенства; рассмотреть различные виды числовых промежутков; формировать умение изображать на координатной прямой числовой промежуток и множество чисел, удовлетворяющих неравенству.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Назовите верное неравенство, которое получится, если:
а) к обеим частям неравенства -1 < 3 прибавить число 4; число -2;
б) из обеих частей неравенства -15 < -2 вычесть число 3; число -5;
в) обе части неравенства 6 > -1 умножить на 8; на -5;
г) обе части неравенства 9 < 27 разделить на 9; на -3; на -1.
2. Заполните пустые квадратики:
III. Объяснение нового материала.
1. Актуализация знаний.
Напоминаем учащимся, что алгебра, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке в виде математических моделей, а затем имеет дело уже не с реальными ситуациями, а с этими моделями, используя разные правила, свойства, законы, выработанные в алгебре.
Математические модели бывают не только алгебраические (в виде числового равенства, уравнения, неравенства), но и словесные (в виде словесного описания реальной ситуации), графические (в виде схемы, графика, чертежа). Учащиеся уже знакомы со всеми этими видами моделей. Напоминаем, что алгебраическую модель ещё называют аналитической, а графическую — геометрической. Чтобы свободно оперировать любыми видами математических моделей, нужно учиться переходить от одного из них к другому.
Например:
|
Словесная модель 1 |
Аналитическая модель |
Геометрическая модель |
Словесная модель 2 |
|
b больше а |
b > а |
|
Точка с координатой b лежит правее точки с координатой а |
2. Введение нового понятия.
Работаем с представленными выше моделями, причём идём в обратном порядке: от словесной модели 2 к словесной модели 1.
Возьмём произвольную точку x на координатной прямой, причём эта точка лежит между точками а и b. Это означает, что ей соответствует число x, которое больше а и меньше b, то есть а < х < b. Верно и обратное: для любой точки, лежащей между точками a и b, будет выполняться это неравенство.
Определение: множество чисел, удовлетворяющих условию а < х < b, называют интервалом и обозначают так: (а; b).
На рисунке (геометрическая модель) это множество изображают в виде:
Светлые кружочки означают, что числа а и b не принадлежат этому множеству.
Аналогично вводим определения отрезка, полуинтервала, числового луча, открытого числового луча и числовой прямой.
Определение: числовые отрезки, интервалы, полуинтервалы, числовые лучи, открытые числовые лучи и числовая прямая называются числовыми промежутками.
3. Операции с различными моделями.
Рассматриваем на с. 173 учебника таблицу, в которой представлены такие модели числовых промежутков, как:
— аналитическая (неравенство, задающее числовой промежуток), например а ≤ х ≤ b;
— словесная (обозначение и название числового промежутка), например [а; b] — числовой промежуток от а до b;
— геометрическая (изображение числового промежутка на координатной прямой), например:
IV. Формирование умений и навыков.
Все задания этого урока можно разбить на три группы:
1) Изобразить на координатной прямой числовой промежуток по его обозначению (создание геометрической модели).
2) Назвать числовой промежуток, изображённый на координатной прямой, и обозначить его (создание словесной модели).
3) Изобразить на координатной прямой множество чисел, удовлетворяющих неравенству, и записать неравенство, соответствующее изображенному или обозначенному числовому промежутку (переход от аналитической к геометрической модели и наоборот).
Особое внимание уделяем:
— правильным формулировкам;
— верному использованию круглых и квадратных скобок при обозначении числового промежутка;
— верному использованию светлых кружков (“выколотых” точек) и тёмных при изображении числовых промежутков на координатной прямой.
• № 812 (а, б, д, е), 813, 814,
• № 815 (а, г), 816 (в, г).
№ 815.
№ 816.
• № 817 (а) (устно), 819 (а, в)
№ 819.
— Задайте неравенством числовой промежуток:
Решение
V. Итоги урока.
— Что называется числовым промежутком?
— Какие виды числовых промежутков существуют?
— Как выглядит геометрическая модель числового промежутка?
— Как записать аналитическую модель числового промежутка с помощью неравенства?
Домашнее задание: № 812 (в, г, ж, з), 815 (б, в), 816 (а, б), 817 (б), 819 (б, г).

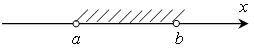









![x ≤ а aОбозначение: (-∞;а] – числовой лучЧитают: числовой луч от минус... x ≤ а aОбозначение: (-∞;а] – числовой лучЧитают: числовой луч от минус...](https://documents.infourok.ru/723eea3f-eb8f-4734-91ef-49c9bbdd405d/0/slide_11.jpg)


![УспехСкобки
Круглые ( )
Квадратные [ ] Формулировки:
-интервал
- Отре... УспехСкобки
Круглые ( )
Квадратные [ ] Формулировки:
-интервал
- Отре...](https://documents.infourok.ru/723eea3f-eb8f-4734-91ef-49c9bbdd405d/0/slide_14.jpg)



![Изобразите промежутки на координатной прямой[ -3;7); [8;21];... Изобразите промежутки на координатной прямой[ -3;7); [8;21];...](https://documents.infourok.ru/723eea3f-eb8f-4734-91ef-49c9bbdd405d/0/slide_18.jpg)