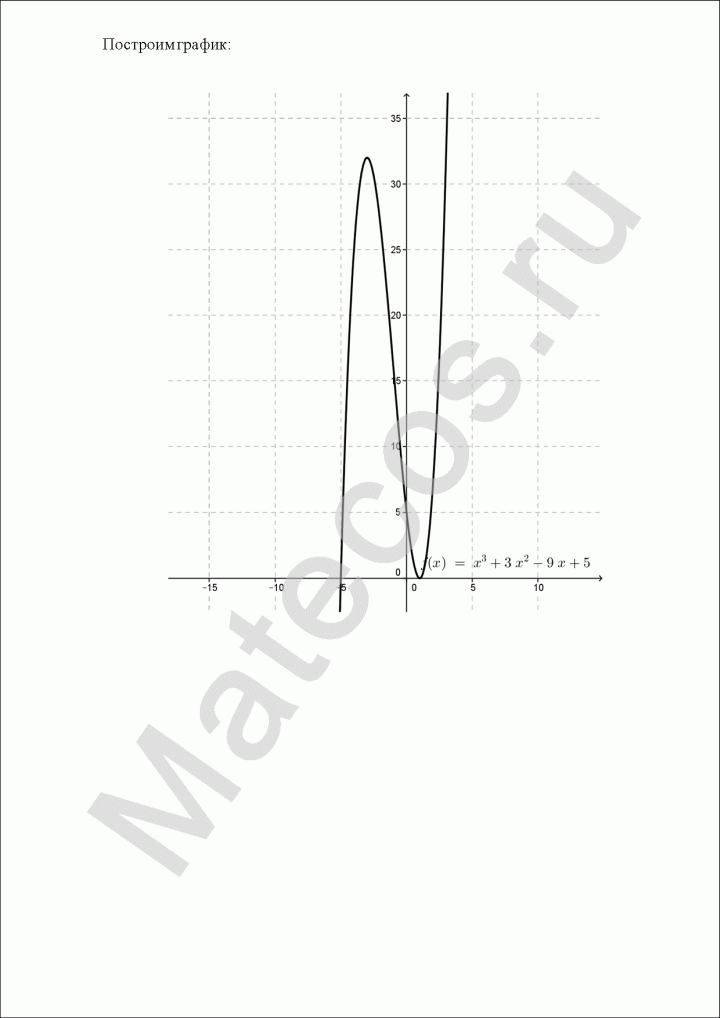
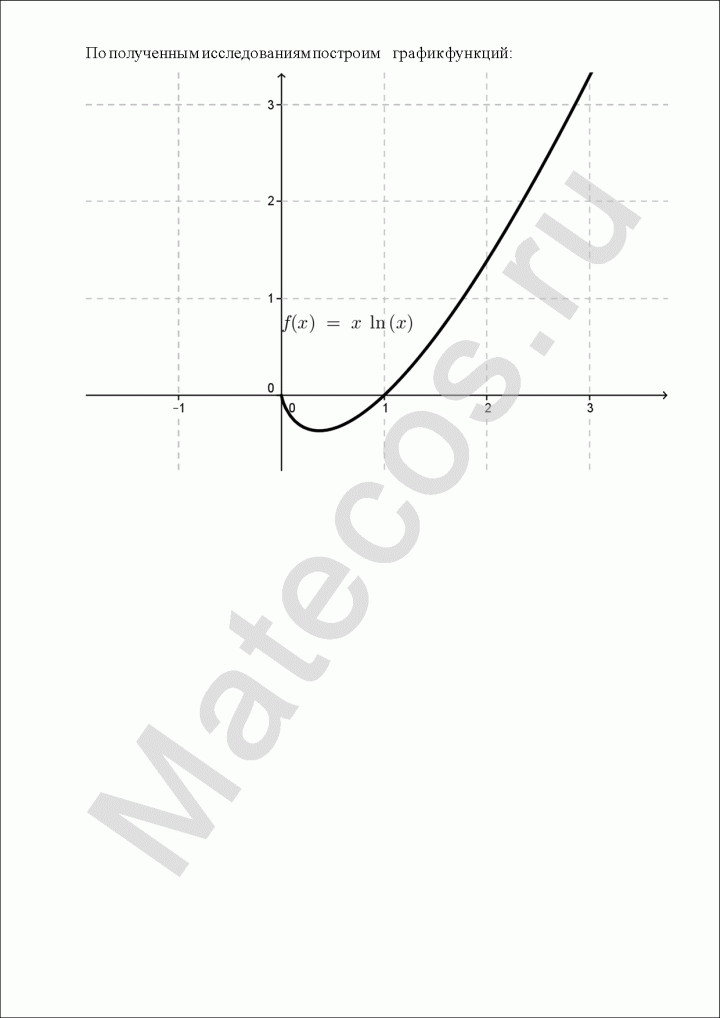
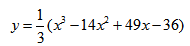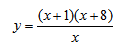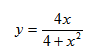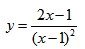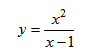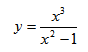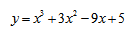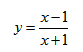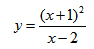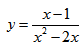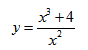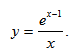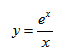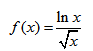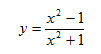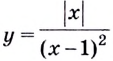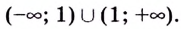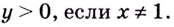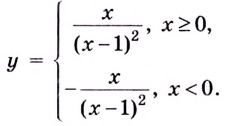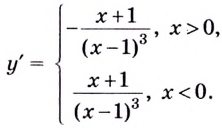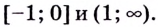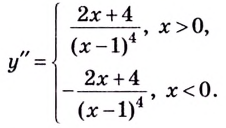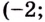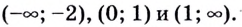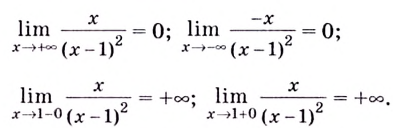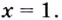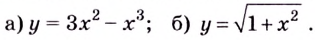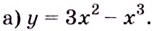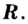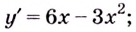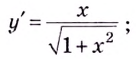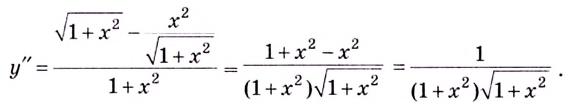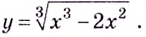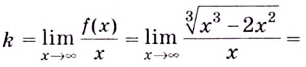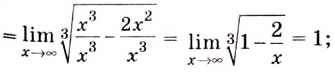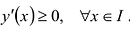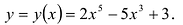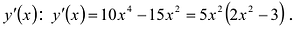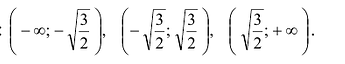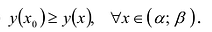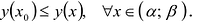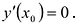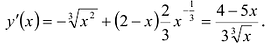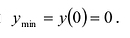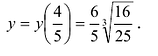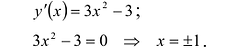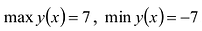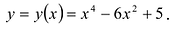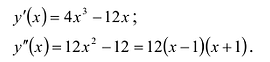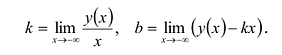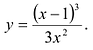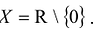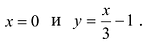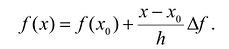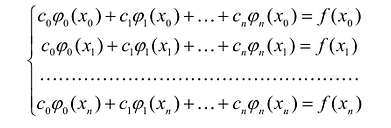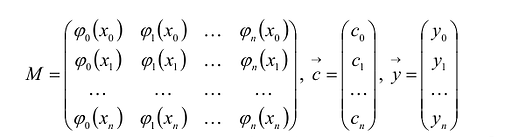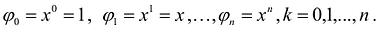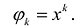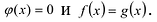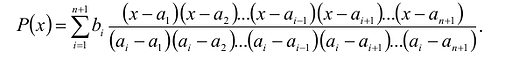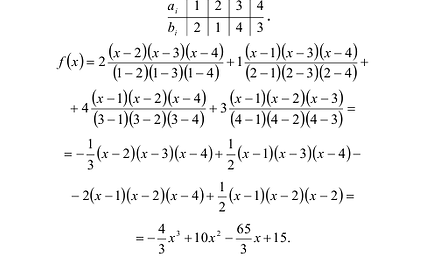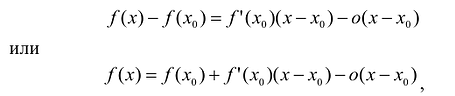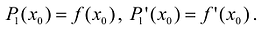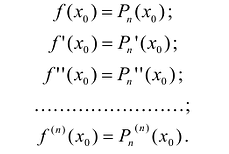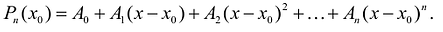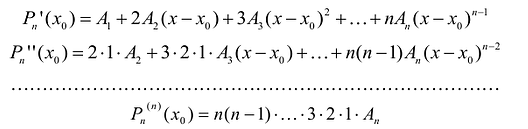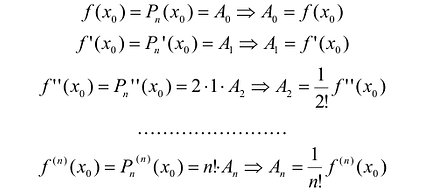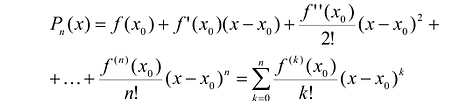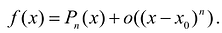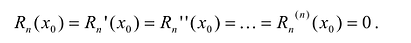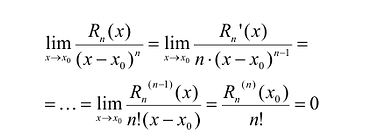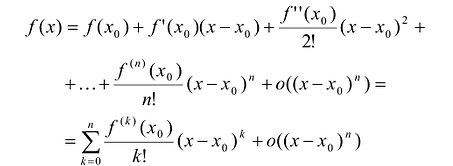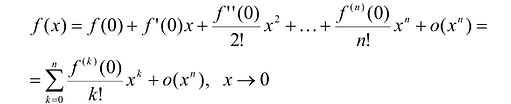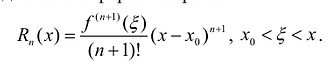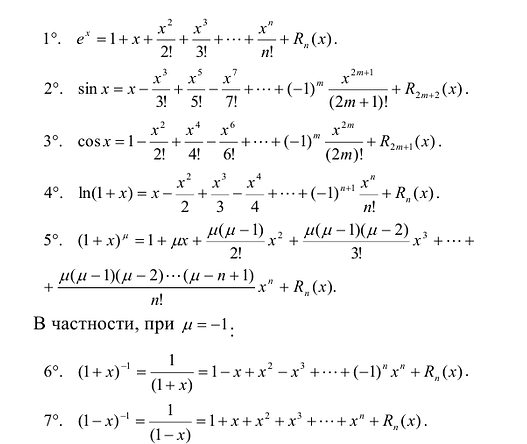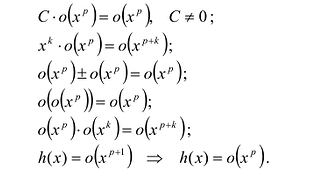Исследование функции и построение графика
На этой странице мы постарались собрать для вас наиболее полную информацию об исследовании функции. Больше не надо гуглить! Просто читайте, изучайте, скачивайте, переходите по отобранным ссылкам.
Что будет дальше?
Исследование функции и построение графика
Общая схема исследования
Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены «горбы» выпуклости, где не определены значения и т.п.
А уже на основании этих «особенностей» и строится макет графика — картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).
Начнем, конечно же, с плана. Исследование функции — объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.
Алгоритм
- Найти область определения. Выделить особые точки (точки разрыва).
- Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
- Найти точки пересечения с осями координат.
- Установить, является ли функция чётной или нечётной.
- Определить, является ли функция периодической или нет (только для тригонометрических функций).
- Найти точки экстремума и интервалы монотонности.
- Найти точки перегиба и интервалы выпуклости-вогнутости.
- Найти наклонные асимптоты. Исследовать поведение на бесконечности.
- Выбрать дополнительные точки и вычислить их координаты.
- Построить график и асимптоты.
В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.
Схема исследования в формате pdf: скачать.
Полный пример решения онлайн
Понравилось? Добавьте в закладки
Провести полное исследование и построить график функции
$$
y(x)=frac{x^2+8}{1-x}.
$$
1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, quad Rightarrow quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-infty; 1) cup (1;+infty).
$$
2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:
Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.
3) Определим точки пересечения графика функции с осями координат.
Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:
Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.
Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:
Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.
Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x in (-infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x in (1; +infty)$ функция $ylt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).
4) Функция не является ни четной, ни нечетной, так как:
5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.
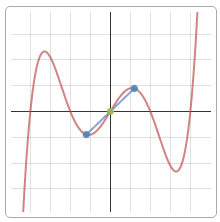
6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:
Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):
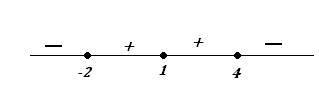
Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:
При $x in (-infty; -2), (4;+infty)$ производная $y’ lt 0$, поэтому функция убывает на данных промежутках.
При $x in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.
При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).
Найдем значения функции в этих точках:
Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.
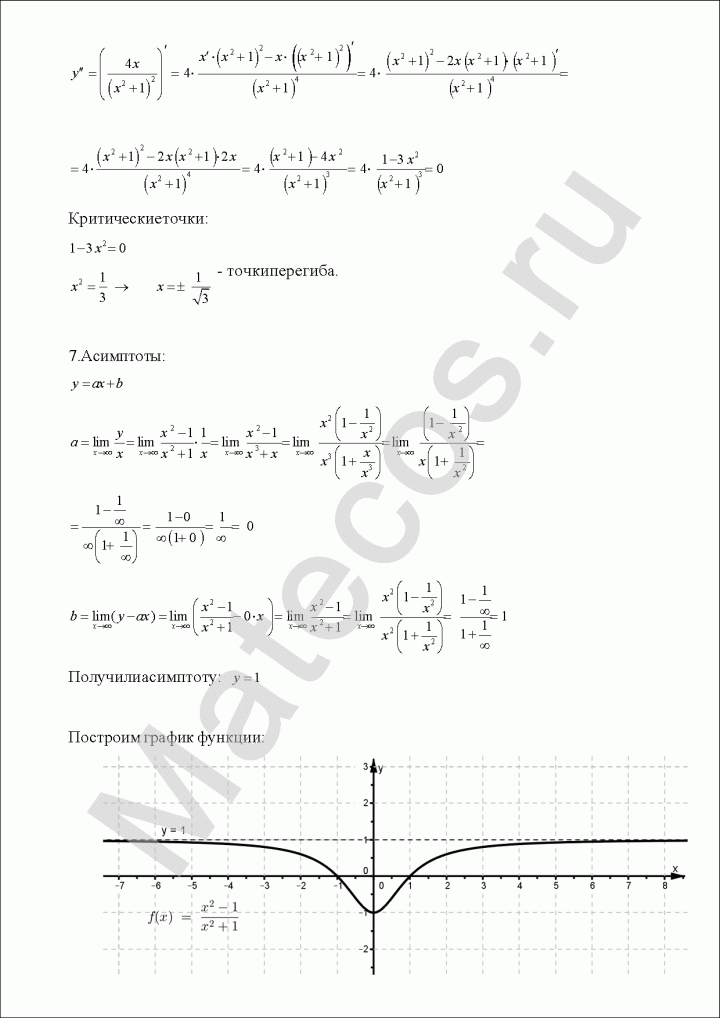
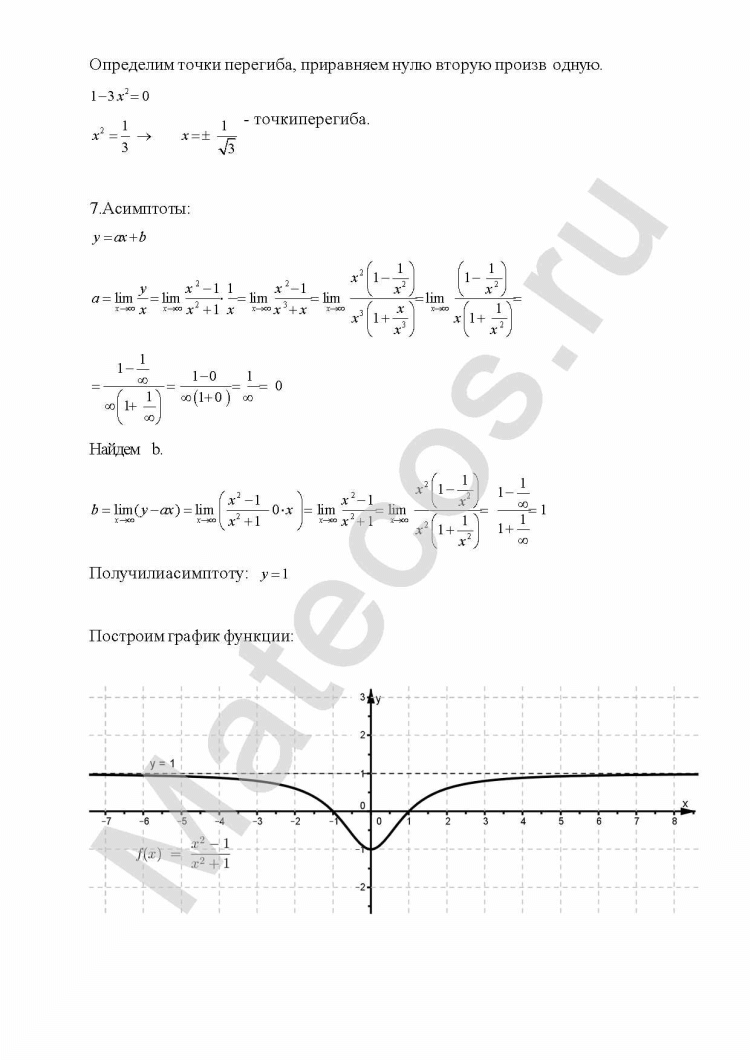
7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:
Приравняем вторую производную к нулю:
Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x in (-infty; 1)$ выполняется $y» gt 0$, то есть функция вогнутая, когда $x in (1;+infty)$ выполняется $y» lt 0$, то есть функция выпуклая.

.
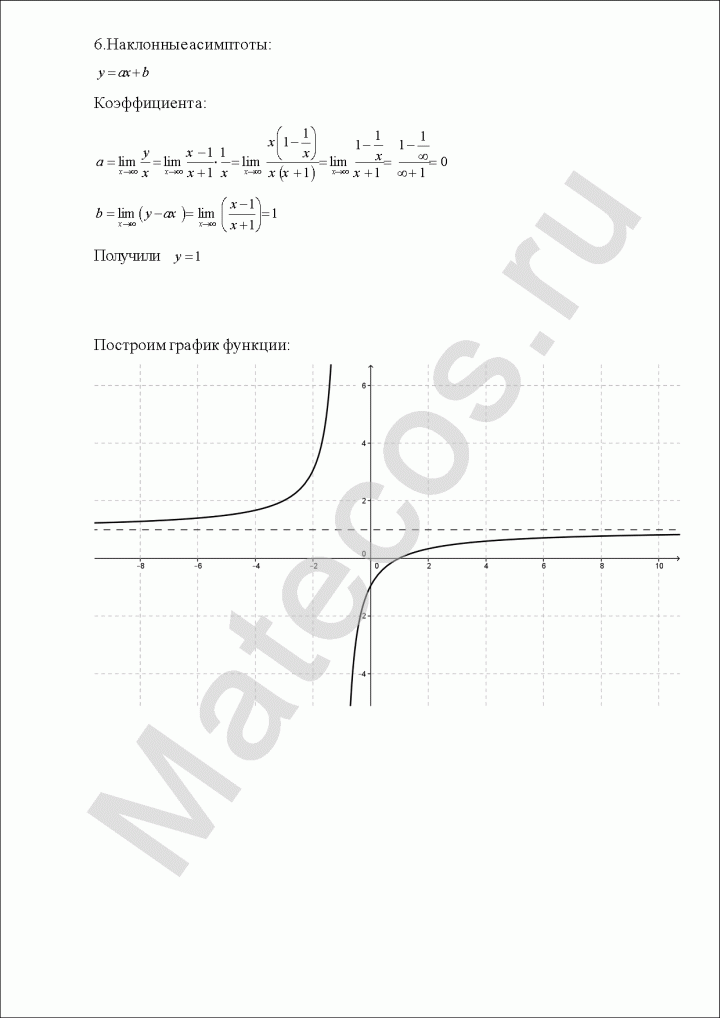
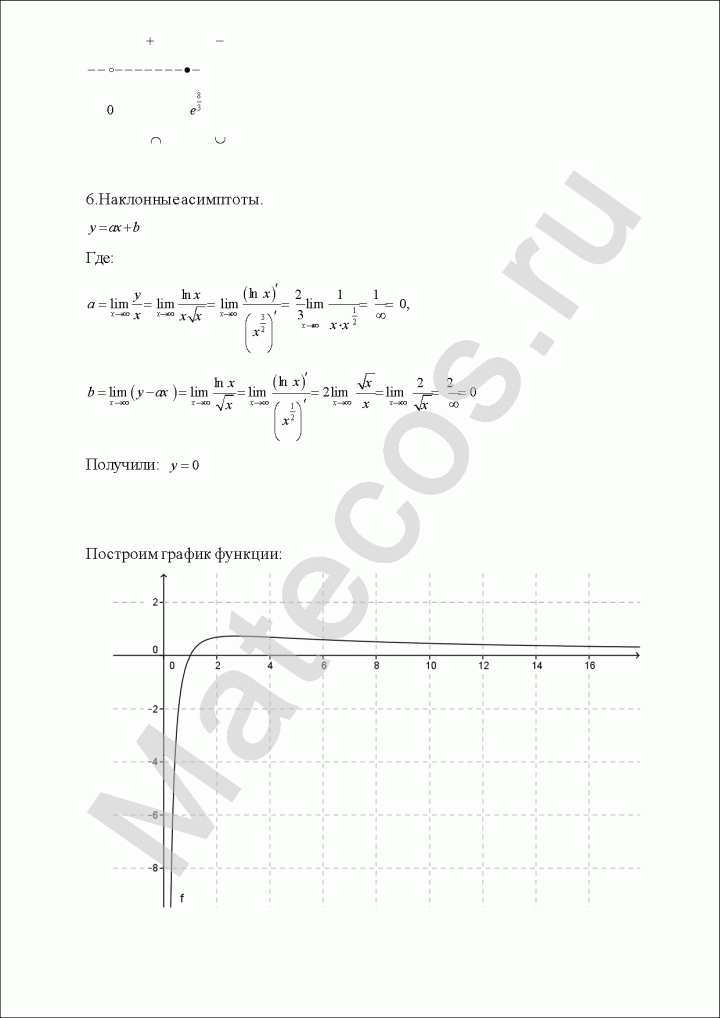
Так как пределы бесконечны, горизонтальных асимптот нет.
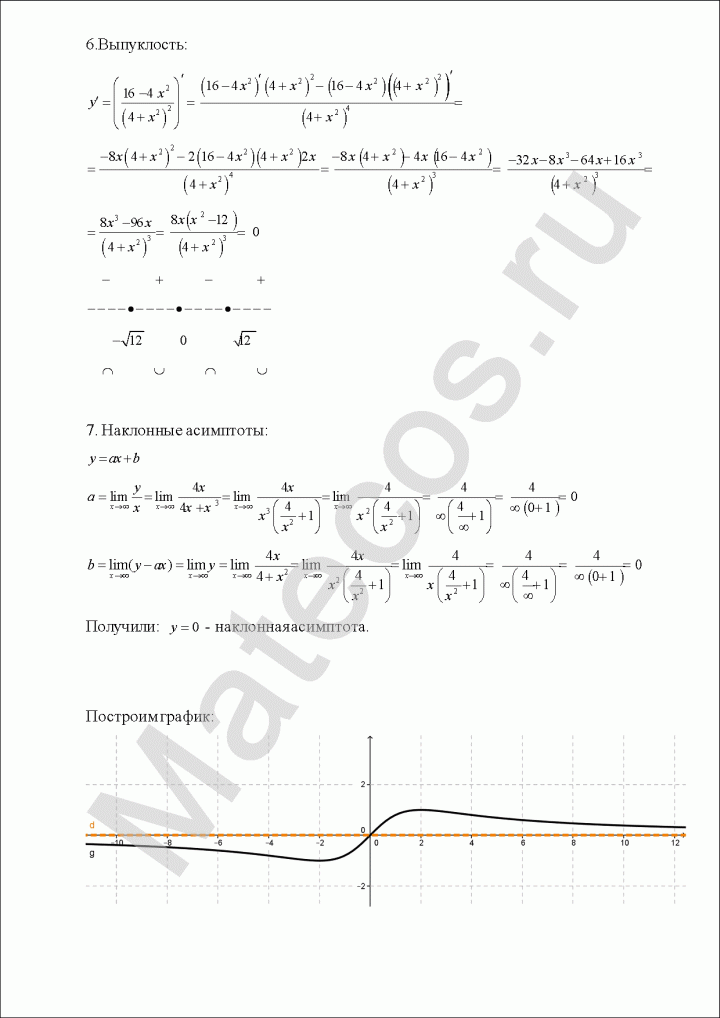
Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:
Получили, у что функции есть одна наклонная асимптота $y=-x-1$.
9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
$$
y(-5)=5.5; quad y(2)=-12; quad y(7)=-9.5.
$$
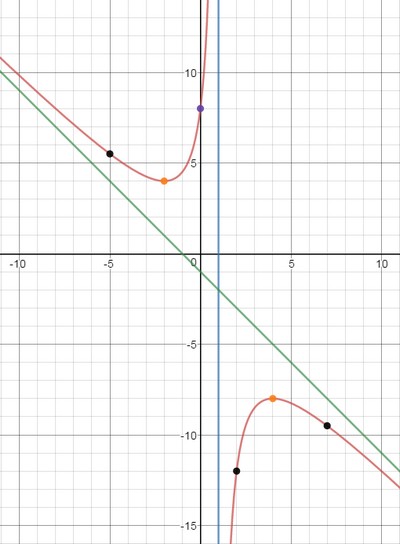
10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):
Примеры решений по исследованию функции
Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!
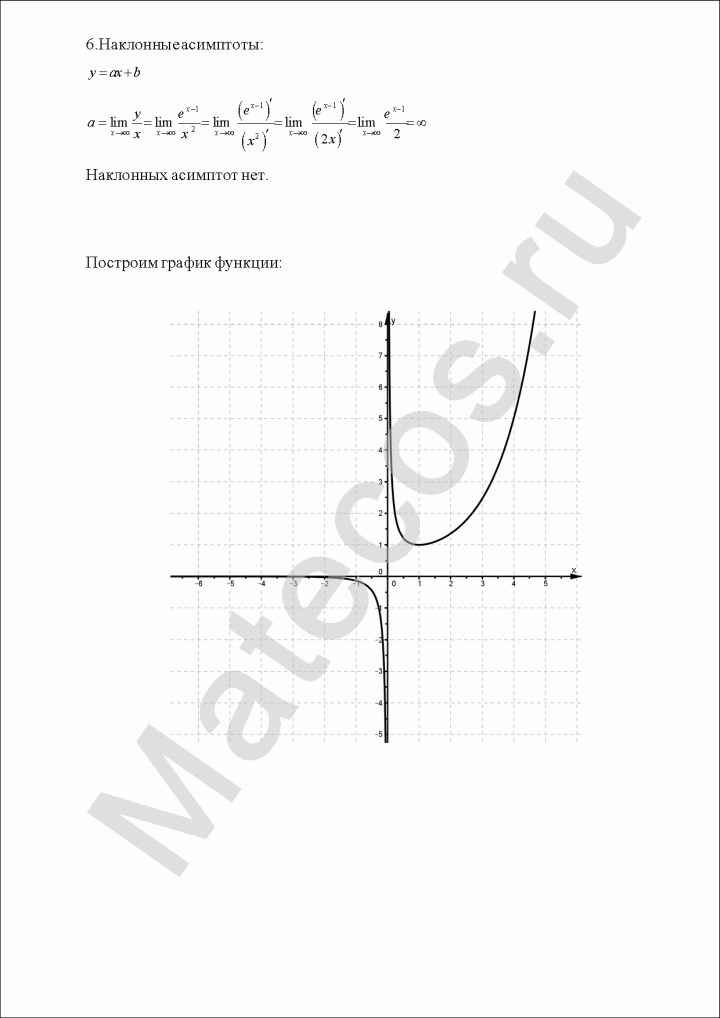
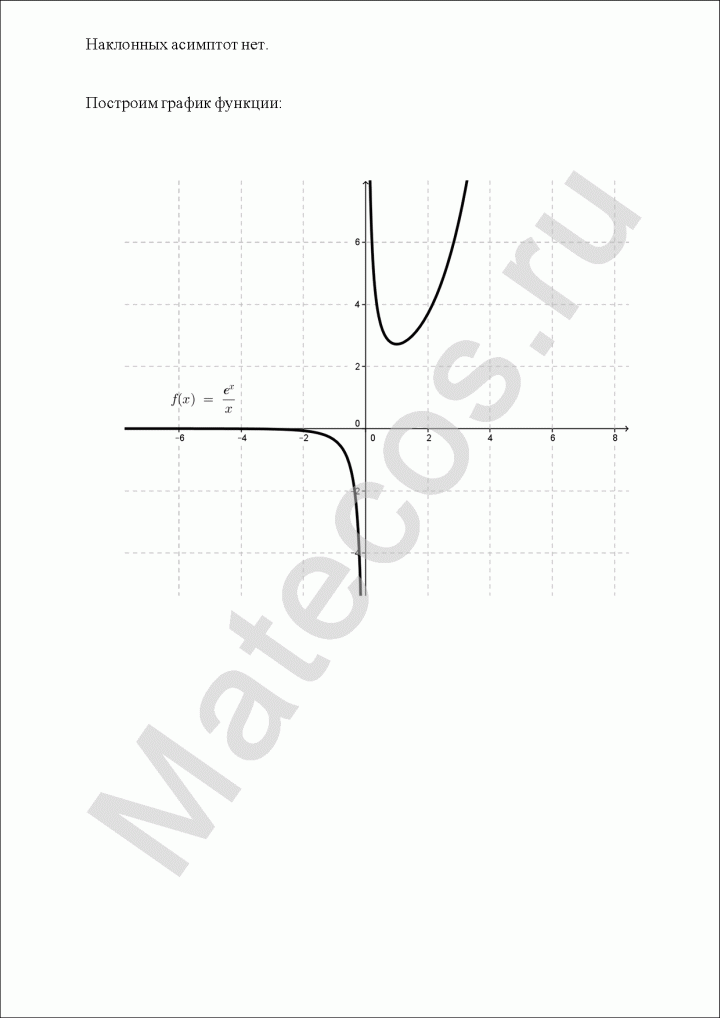
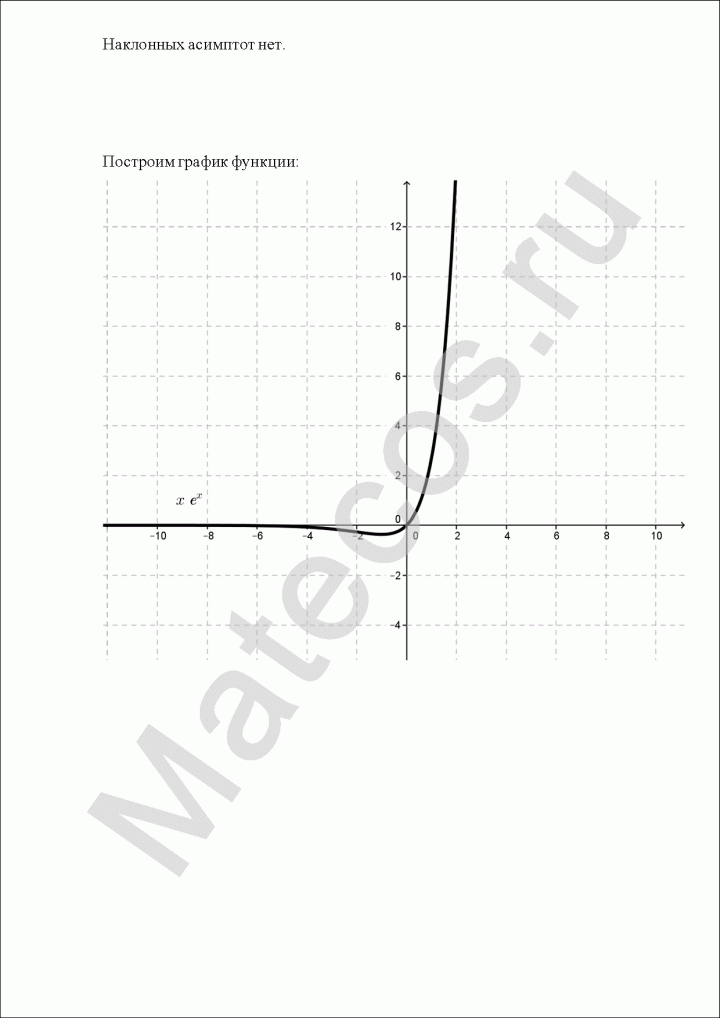
Задача 1. Исследовать функцию методами дифференциального исчисления и построить график.
$$y=frac{e^x}{x}.$$
Задача 2. Исследовать функцию и построить ее график.
$$y=-frac{1}{4}(x^3-3x^2+4).$$
Задача 3. Исследовать функцию с помощью производной и построить график.
$$y=ln frac{x+1}{x+2}.$$
Задача 4. Провести полное исследование функции и построить график.
$$y=frac{x}{sqrt{x^2+x}}.$$
Задача 5. Исследовать функцию методом дифференциального исчисления и построить график.
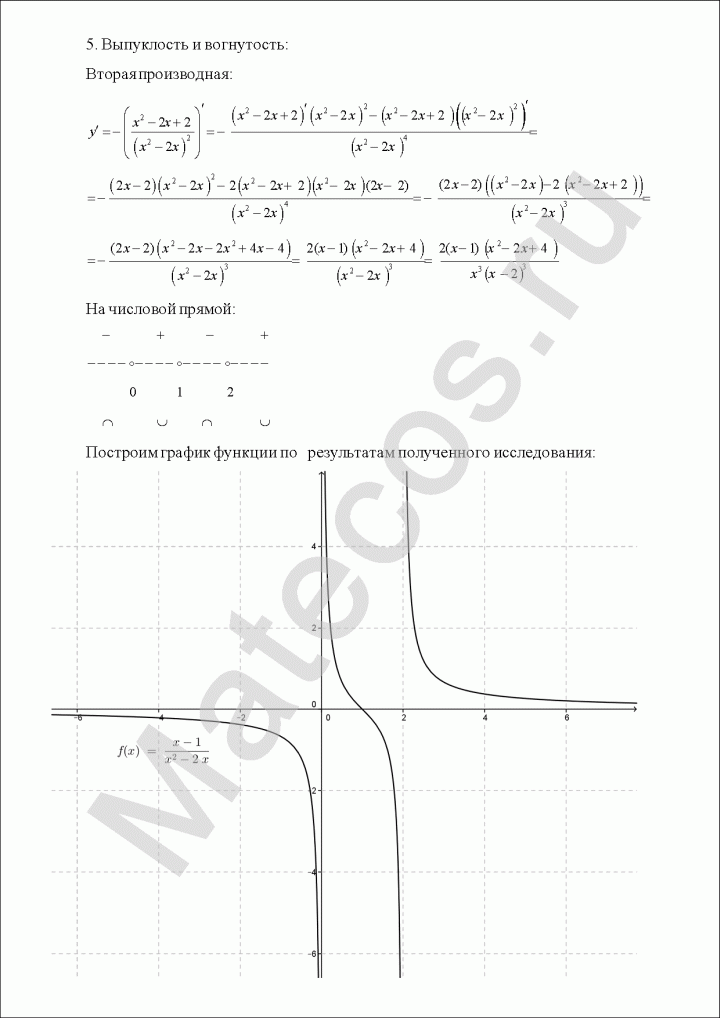
$$y=frac{x^3-1}{4x^2}.$$
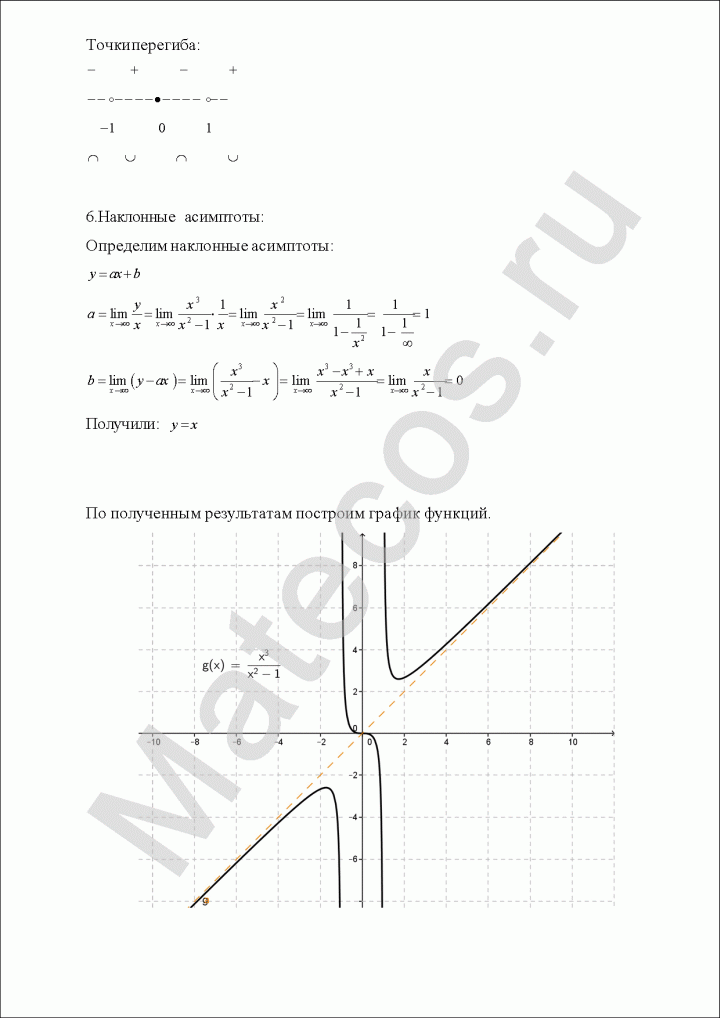
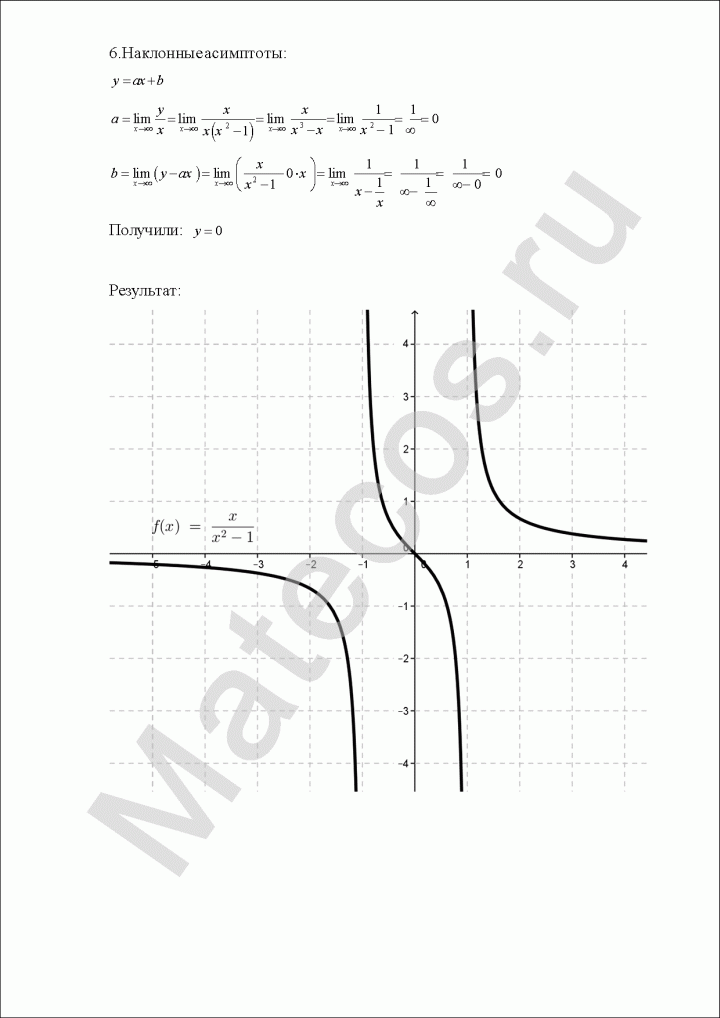
Задача 6. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.
$$y=frac{x^3}{x^2-1}.$$
Поможем с исследованием функции: быстро, подробно
Задача 7. Проведите исследование функции с построением графика.
$$y=frac{x^3}{2(x+5)^2}.$$
Задача 8. Построить график функции $y=y(x)$, заданной параметрически
$$x=frac{t^2}{t+1}, y=frac{1}{t}-frac{t^3}{3}.$$
Задача 9. Исследовать функцию и построить ее график $r=1+tg phi$.
Задача 10. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.
Задача 11. Провести полное исследование периодической функции
$y = cos 3x – 2 sin 6x$ и построить её график.
Задача 12. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.
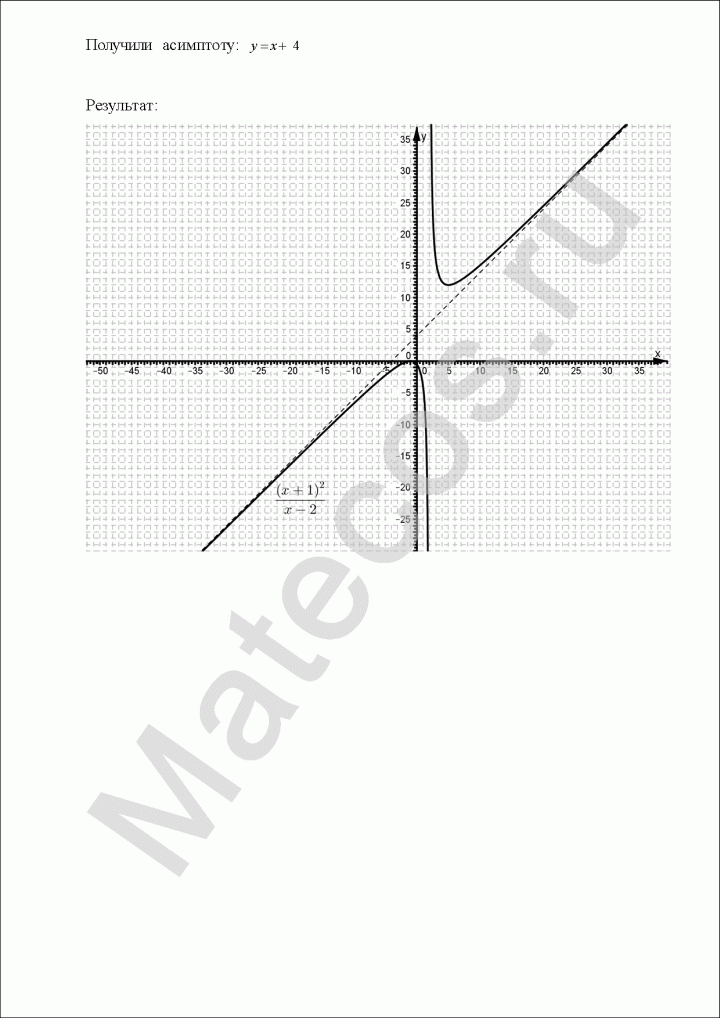
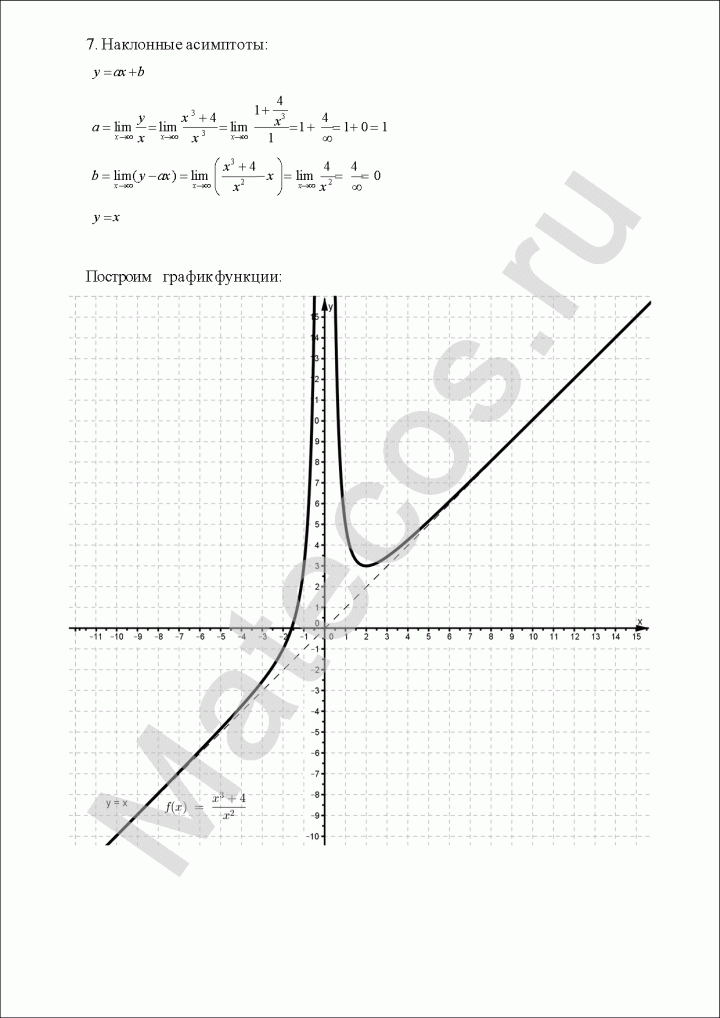
$$y=frac{4-x^3}{x^2}.$$
Задача 13. Провести полное исследование и построить график функции.
$$f(x)=frac{x}{2}-arccosfrac{2x}{1+x^2}.$$
Еще примеры исследования функции (контрольные работы)
Как построить график онлайн?
Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).
Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?
Графический калькулятор Desmos
Desmos.com
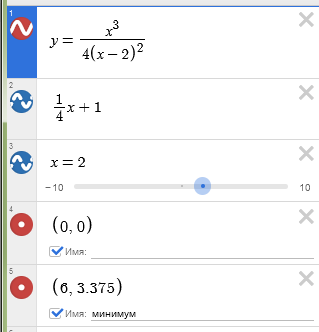
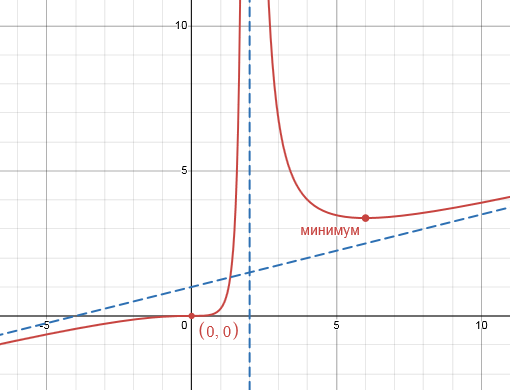
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=frac{x^3}{4(x-2)^2}$ буквально за минуту построены основной график и асимптоты, вот что получилось:
При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.
Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!
Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):
Сайт для построения графиков y(x).ru
y(x).ru
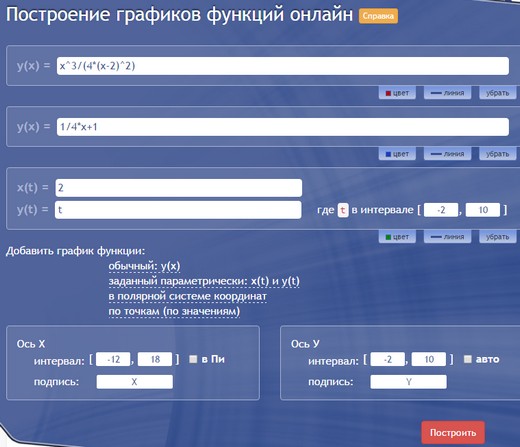
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:
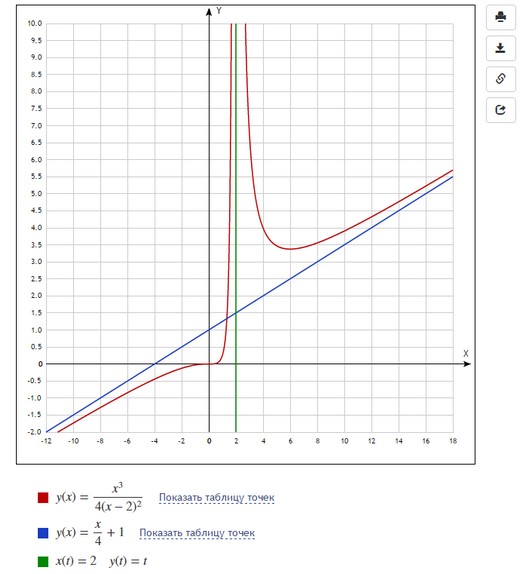
И такой график получается в итоге:
Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).
Другие сайты
Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:
- ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
- mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
- easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
- grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет
Больше знаний: теория и практика
Еще немного ссылок для тех, кто хочет углубиться в тему. Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень «съедобно» даже для полного чайника в математике: Исследование функций от Александра Емелина.
Вторая ссылка практическая, для тех, кто хочет научиться строить красивые графики в Desmos.com (см. выше описание): Полная инструкция по работе с Desmos. Эта инструкция довольно старая, с тех пор интерфейс сайта поменялся в лучшую сторону, но основы остались неизменными и помогут быстро разобраться с важными функциями сервиса.
Официальные инструкции, примеры и видео-инструкции на английском можно найти тут: Learn Desmos.
Решебник
Срочно нужна готовая задача? Более сотни разных функций с полным исследованием уже ждут вас. Подробное решение, быстрая оплата по SMS и низкая цена — около 50 рублей. Может, и ваша задача уже готова? Проверьте!
Полезные видео-ролики
Вебинар по работе с Desmos.com. Это уже полноценный обзор функций сайта, на целых 36 минут. К сожалению, он на английском языке, но базовых знаний языка и внимательности достаточно, чтобы понять большую часть.
Классный старый научно-популярный фильм «Математика. Функции и графики». Объяснения на пальцах в прямом смысле слова самых основ.
Закажите полное исследование функции в МатБюро
Полезная страница? Сохрани или расскажи друзьям
 |
Для того, чтобы построить график функции необходимо провести полное исследование заданной функции. Затем поэтапно, используя полученные результаты, построить график.Как построить график функции?После краткого описания пунктов исследования, приведем ряд примеров по теме построения графиков функции с полным предварительным исследованием. |
Приведем примерный алгоритм получения необходимых данных.
1.Нахождение области определения функции
Определение интервалов, на которых функция существует.
!!! Очень подробно об области определения функций и примеры нахождения области определения тут.
2.Нули функции
Для вычисления нулей функции, необходимо приравнять заданную функцию к нулю и решить полученное уравнение. На графике это точки пересечения с осью ОХ.
3.Четность, нечетность функции
Функция четная, если y(-x) = y(x). Функция нечетная, если y(-x) = -y(x). Если функция четная – график функции симметричен относительно оси ординат (OY). Если функция нечетная – график функции симметричен относительно начала координат.
4.Промежутки знакопостоянства
Расстановка знаков на каждом из интервалов области определения. Функция положительна на интервале — график расположен выше оси абсцисс. Функция отрицательна — график ниже оси абсцисс.
5. Промежутки возрастания и убывания функции.
Для определения вычисляем первую производную, приравниваем ее к нулю. Полученные нули и точки области определения выносим на числовую прямую. Для каждого интервала определяем знак производной. Производная положительна — график функции возрастает, отрицательна — убывает.
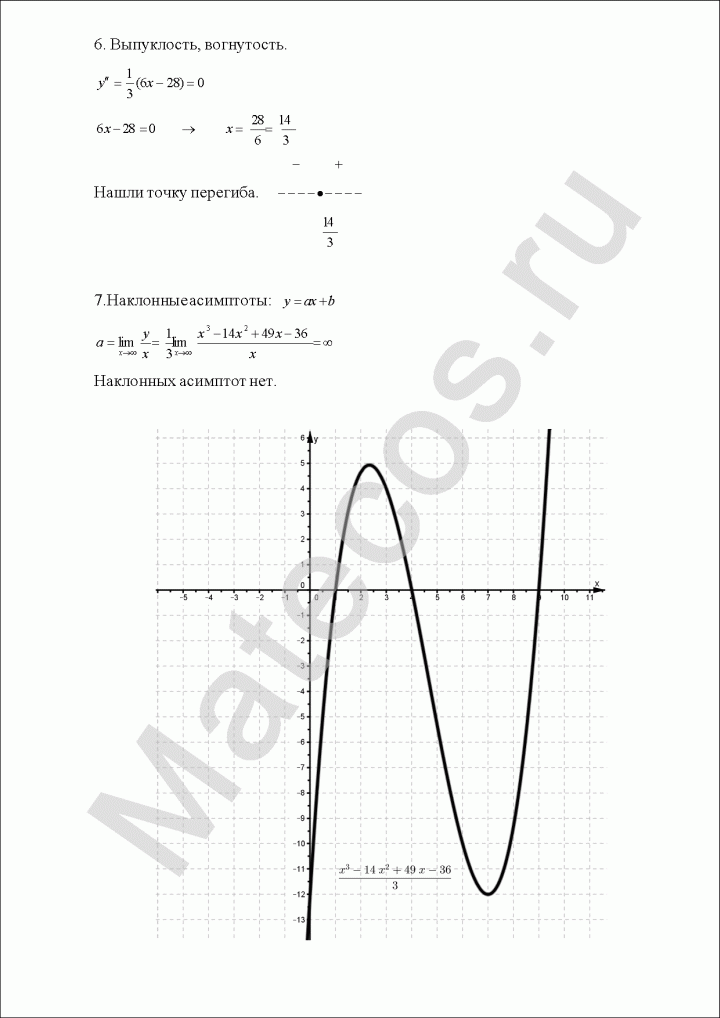
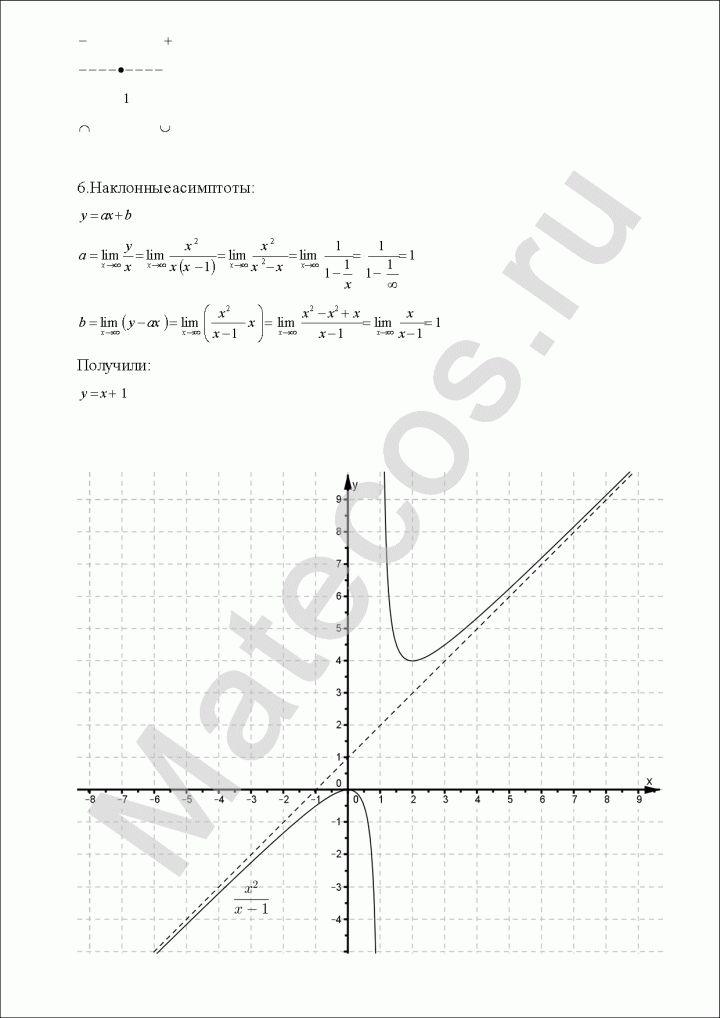
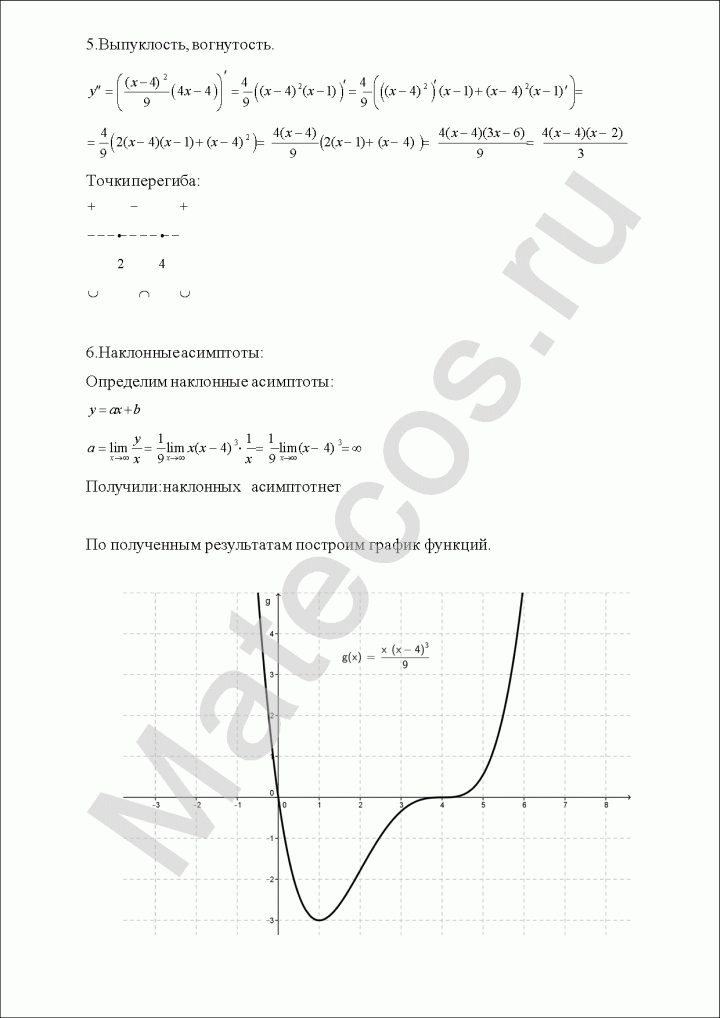
6. Выпуклость, вогнутость.
Вычисляем вторую производную. Находим значения, в которых вторая производная равна нулю или не существует. Вторая производная положительна — график функции выпукл вверх. Отрицательна — график функции выпукл вниз.
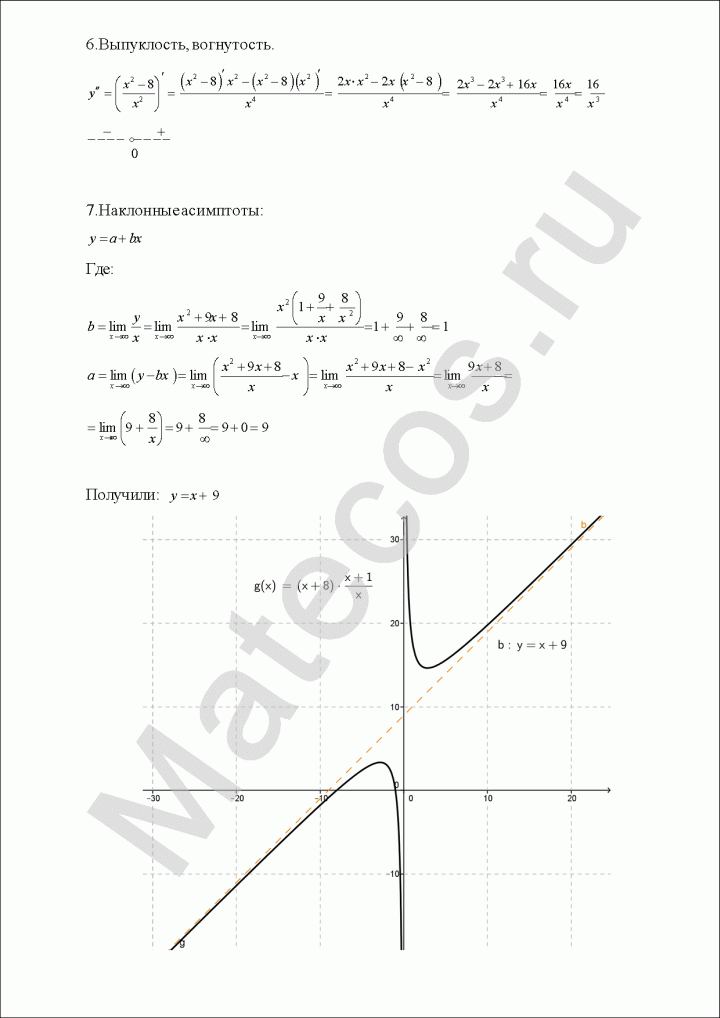
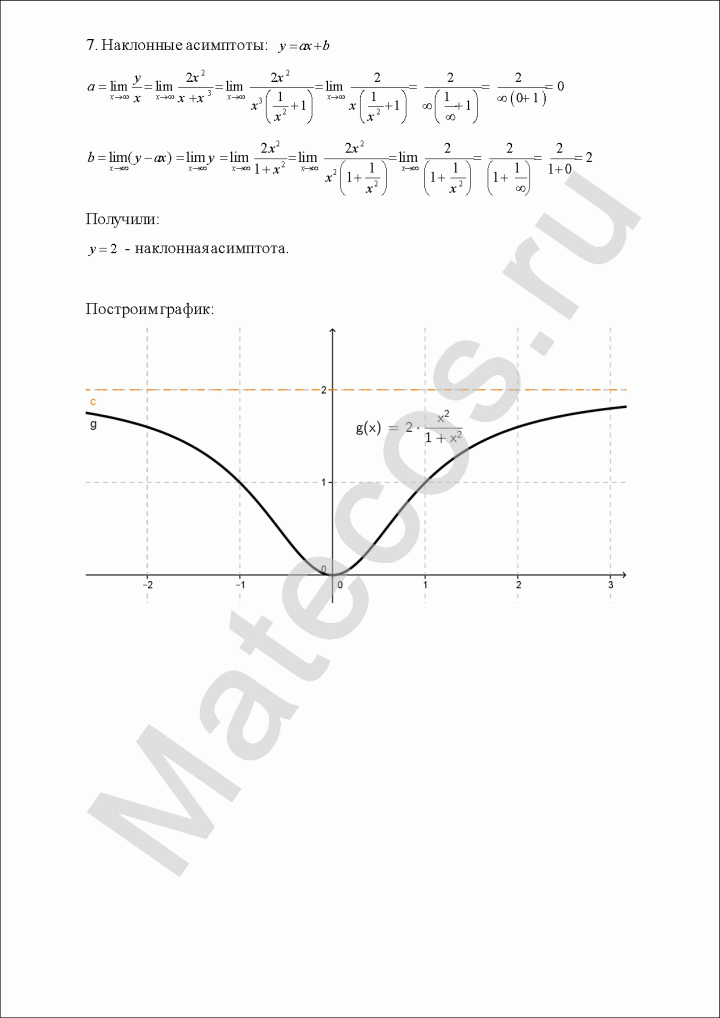
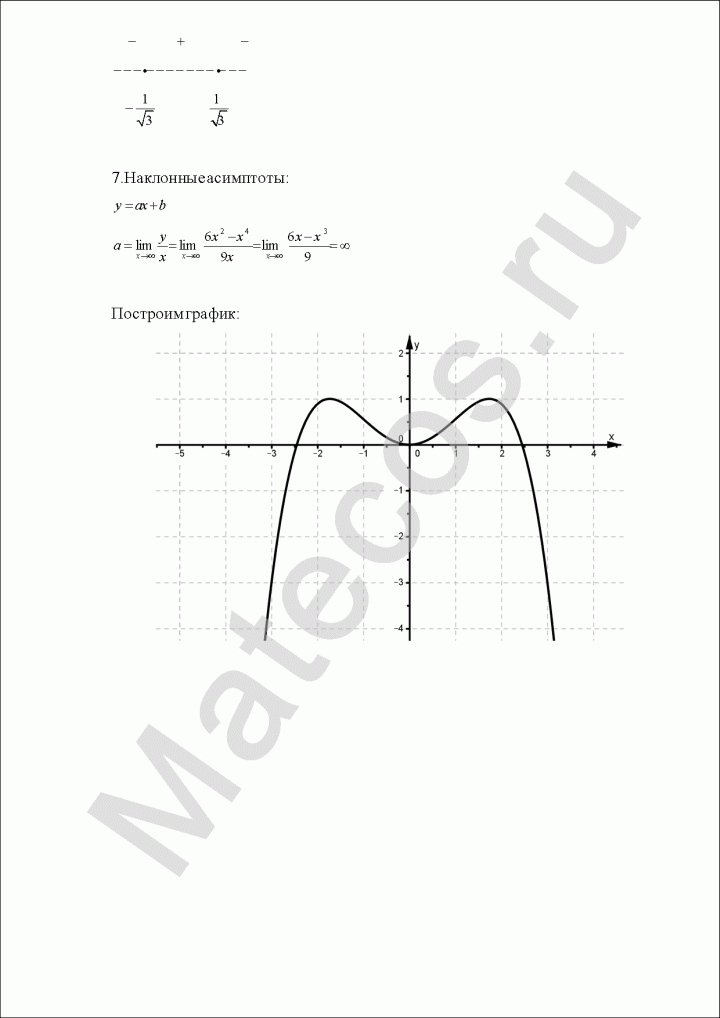
7. Наклонные асимптоты.
Пример исследования функции и построения графика №1
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №2
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №3
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №4
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №5
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №6
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №7
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №8
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №9
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №10
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №11
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №12
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №13
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №14
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №15
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №16
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №17
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №18
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №19
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №20
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №21
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №22
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №23
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №24
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №25
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №26
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.
Пример исследования функции и построения графика №27
Исследовать функцию средствами дифференциального исчисления и построить ее график. Скачать файл решения можно в конце данной статьи.

п.1. Алгоритм исследования и построения графика функции
1. Найти область определения функции, классифицировать точки разрыва
2. Исследовать функцию на четность и периодичность
3. Провести анализ асимптотического поведения функции (наличие вертикальных, горизонтальных и наклонных асимптот) (см. §41 данного справочника)
4. Взять первую производную. Определить критические точки, интервалы монотонности, точки экстремума
5. Взять вторую производную. Определить критические точки 2-го порядка, интервалы выпуклости и точки перегиба
6. Найти точки пересечения функции с осями координат (если уравнение (f(x)=0) не имеет аналитического решения, указать количество точек пересечения с осью OX)
7. Построить график функции
п.2. Примеры
Пример 1. Постройте график функции (y=2x^3-6x^2-18x+7)
1) Область определения (xinmathbb{R})
Точек разрыва нет
2) Четность begin{gather*} f(-x)=2(-x)^3-6(-x)^2-18(-x)+7ne left[ begin{array}{l} f(x)\ -f(x) end{array} right. end{gather*} Функция ни четная, ни нечетная.
Периодичность: функция не периодическая
3) Асимптоты
1. Вертикальных асимптот нет, т.к. нет точек разрыва 2-го рода
2. Горизонтальные асимптоты: begin{gather*} b_1=lim_{xrightarrow -infty}2x^3-6x^2-18x+7=-infty\ b_2=lim_{xrightarrow +infty}2x^3-6x^2-18x+7=+infty\ end{gather*} Пределы бесконечны, горизонтальных асимптот нет.
3. Наклонные асимптоты: begin{gather*} k_1=lim_{xrightarrow -infty}frac{2x^3-6x^2-18x+7}{x}=+infty\ k_2=lim_{xrightarrow +infty}frac{2x^3-6x^2-18x+7}{x}=+infty\ end{gather*} Пределы бесконечны, наклонных асимптот нет.
4) Первая производная begin{gather*} f'(x)=2cdot 3x^2-6cdot 2x-18cdot 1+0=6x^2-12x-18=6(x^2-2x-3)=\ =6(x-3)(x+1)\ f'(x)=0 text{при} left[ begin{array}{l} x=3\ x=-1 end{array} right. end{gather*} Критические точки: (x=-1) и (x=3)
Составляем таблицу:
| (x) | ((-infty;-1)) | -1 | (-1;3) | 3 | ((3;+infty)) |
| (f'(x)) | >0 | 0 | <0 | 0 | >0 |
| (f(x)) | (nearrow) | max | (searrow) | min | (nearrow) |
Функция возрастает при (xin(-infty;-1)cup(3;+infty))
Функция убывает при (xin(-1;3))
Точка максимума (x=-1; y_{max}=f(-1)=-2-6+18+7=17)
Точка минимума (x=3; y_{min}=f(3)=54-54-54+7=-47)
5) Вторая производная: begin{gather*} f»(x)=(6x^2-12x-18)’=6cdot 2x-12cdot 1-0=12x-12=12(x-1)\ f»(x)=0 text{при} x=1 end{gather*} Критическая точка 2-го порядка: (x=1)
Составляем таблицу:
| (x) | ((-infty;1)) | 1 | ((1;+infty)) |
| (f»(x)) | <0 | 0 | >0 |
| (f(x)) | (cap) | перегиб | (cup) |
Функция выпуклая вверх при (xin(-infty;1))
Функция выпуклая вниз при (xin(1;+infty))
Точка перегиба (x=1; f(1)=2-6-18+7=-15)
6) Точки пересечения с осями координат
Пересечение с осью OY: (x=0, y=7)
Пересечение с осью OX: $$ 2x^3-6x^2-18x+7=0 $$ У кубической параболы точка максимума (-1;17), точка минимума (3;-47).
Т.к. (y_{max}gt 0, y_{min}lt 0) кубическая парабола пересекает ось OX в трех точках: $$ x_1lt -1, -1lt x_2lt 3, x_3gt 3 $$
7) График
Пример 2. Постройте график функции (y=frac3x+frac x3)
1) Область определения
ОДЗ: (xne 0)
(x=0) — точка разрыва. Исследуем односторонние пределы: begin{gather*} lim_{xrightarrow -0}left(frac 3x+frac x3right)=frac{3}{-0}+0=-infty, lim_{xrightarrow +0}left(frac 3x+frac x3right)=frac{3}{+0}+0=+infty end{gather*} Пределы не равны и бесконечны. (x=0) — точка разрыва 2-го рода.
2) Четность $$ f(-x)=frac{3}{-x}+frac{-x}{3}=-left(frac 3x+frac x3right)=-f(x) $$ Функция нечётная.
Периодов нет. Функция не периодическая.
3) Асимптоты
1. Вертикальная асимптота (x=0) – точка разрыва 2-го рода
2. Горизонтальные асимптоты begin{gather*} b_1=lim_{xrightarrow -infty}left(frac 3x+frac x3right)=0+(-infty)=-infty\ b_2=lim_{xrightarrow +infty}left(frac 3x+frac x3right)=0+(+infty)=+infty end{gather*} Пределы бесконечны, горизонтальных асимптот нет.
3. Наклонные асимптоты: begin{gather*} k_1=frac1x lim_{xrightarrow -infty}left(frac 3x+frac x3right)=lim_{xrightarrow -infty}left({3}{x^2}+frac13right)=0+frac13=frac13\ k_1=frac1x lim_{xrightarrow +infty}left(frac 3x+frac x3right)=lim_{xrightarrow +infty}left({3}{x^2}+frac13right)=0+frac13=frac13\ k=k_1=k_2=frac13 end{gather*} Ищем b: $$ b=lim_{xrightarrow infty}(y-kx)=lim_{xrightarrow infty}left(frac3x+frac x3-frac x3right)=lim_{xrightarrow infty}frac 3x=0 $$ Есть одна наклонная асимптота (y=frac 3x)
Кривая стремится к ней на минус и плюс бесконечности.
4) Первая производная: begin{gather*} f'(x)=-frac{3}{x^2}+frac13=frac{x^2-9}{3x^2}=frac{(x+3)(x-3)}{3x^2}\ f'(x)=0 text{при} x=pm 3 end{gather*} Критические точки: (x=left{0;pm 3right})
Составляем таблицу:
| (x) | ((-infty;-3)) | -3 | (-3;0) | 0 | ((0;3)) | 3 | ((3+infty)) |
| (f'(x)) | >0 | 0 | <0 | (varnothing) | <0 | 0 | >0 |
| (f(x)) | (nearrow) | max | (searrow) | (varnothing) | (searrow) | min | (nearrow) |
Функция возрастает при (xin(-infty;-3)cup(-3;+infty))
Функция убывает при (xin(-3;0)cup(0;3))
Точка максимума (x=-3; y_{max}=f(-3)=-1-1=-2)
Точка минимума (x=3; y_{min}=f(3)=1+1=2)
5) Вторая производная: begin{gather*} f»(x)=frac13left(1-frac{9}{x^2}right)’=frac13left(0+frac{9cdot 2}{x^3}right)=frac{6}{x^3} end{gather*} Вторая производная нулей не имеет.
Критическая точка 2-го порядка: (x=0)
Составляем таблицу:
| (x) | ((-infty;0)) | 0 | ((0;+infty)) |
| (f»(x)) | <0 | (varnothing) | >0 |
| (f(x)) | (cap) | (varnothing) | (cup) |
Функция выпуклая вверх при (xin(-infty;0))
Функция выпуклая вниз при (xin(0;+infty))
Точек перегиба нет.
6) Точки пересечения с осями
Пересечение с осью OY: (x=0notin D) — не входит в ОДЗ, пересечений с OY нет
Пересечение с осью OX:
(frac3x+frac x3=0Rightarrow frac{9+x^2}{3x}=0Rightarrow xin varnothing) — решений нет, пересечений с OX нет
7) График
Пример 3*. Постройте график функции (y=frac{x^3-4}{(x-1)^3})
Сколько корней имеет уравнение (frac{x^3-4}{(x-1)^3}=a)?
1) Область определения
ОДЗ: (xne 1)
(x=1) — точка разрыва. Исследуем односторонние пределы: begin{gather*} lim_{xrightarrow 1-0}frac{x^3-4}{(x-1)^3}=frac{1-4}{(1-0-1)^3}=frac{-3}{-0}=+infty\ lim_{xrightarrow 1+0}frac{x^3-4}{(x-1)^3}=frac{1-4}{(1+0-1)^3}=frac{-3}{+0}=-infty end{gather*} Пределы не равны и бесконечны. (x=1) — точка разрыва 2-го рода.
2) Четность $$ f(-x)=frac{(-x)^3-4}{(-x-1)^3}ne left[ begin{array}{l} f(x)\ -f(x) end{array} right. $$ Функция ни четная, ни нечетная.
Периодичность: функция не периодическая
3) Асимптоты
1. Вертикальная асимптота (x=1) – точка разрыва 2-го рода
2. Горизонтальные асимптоты begin{gather*} b_1=lim_{xrightarrow -infty}frac{x^3-4}{(x-1)^3}=left[frac{infty}{infty}right]=lim_{xrightarrow -infty}frac{x^3left(1-frac{4}{x^3}right)}{x^3left(1-frac{1}{x^3}^3right)}=frac{1-0}{(1-0)^3}=1\ b_2=lim_{xrightarrow +infty}frac{x^3-4}{(x-1)^3}=left[frac{infty}{infty}right]=lim_{xrightarrow +infty}frac{x^3left(1-frac{4}{x^3}right)}{x^3left(1-frac{1}{x^3}^3right)}=frac{1-0}{(1-0)^3}=1\ b=b_1=b_2=1 end{gather*} Одна горизонтальная асимптота: (y=1)
Функция стремится к ней на минус и плюс бесконечности.
3. Наклонные асимптоты: begin{gather*} k_1=lim_{xrightarrow infty}frac{x^3-4}{x(x-1)^3}=left[frac{infty}{infty}right]=lim_{xrightarrow infty}frac{x^4left(frac1x-frac{4}{x^4}right)}{x^4left(1-frac{1}{x^3}^3right)}=frac{0-0}{(1-0)^3}=0 end{gather*} Угловой коэффициент (k=0). Наклонных асимптот нет.
4) Первая производная: begin{gather*} f'(x)=left(frac{x^3-4}{(x-1)^3}right)’=frac{3x^2(x-1)^3-(x^3-4)cdot 3(x-1)^2}{(x-1)^6}=frac{3x^2(x-1)-3(x^3-4)}{(x-1)^4}=\ =frac{3x^3-3x^2-3x^3+12}{(x-1)^4}=frac{-3(x^2-4)}{(x-1)^4}=frac{-3(x-2)(x+2)}{(x-1)^4}\ f'(x)=0 text{при} x=pm 2 end{gather*} Критические точки: (x=left{1;pm 2right})
Составляем таблицу:
| (x) | ((-infty;-2)) | -2 | (-2;1) | 1 | ((1;2)) | 2 | ((2+infty)) |
| (f'(x)) | <0 | 0 | >0 | (varnothing) | >0 | 0 | <0 |
| (f(x)) | (searrow) | min | (nearrow) | (varnothing) | (nearrow) | max | (searrow) |
Функция возрастает при (xin(-2;1)cup(1;2))
Функция убывает при (xin(-infty;-2)cup(2;+infty))
Точка максимума (x=2; y_{max}=f(2)=frac{2^3-4}{(2-1)^3}=4)
Точка минимума (x=-2; y_{min}=f(-2)=frac{(-2)^3-4}{(-2-1)^3}=frac{-12}{-27}=frac49)
5) Вторая производная: begin{gather*} f»(x)=left(frac{-3(x^2-4)}{(x-1)^4}right)’=-3left(frac{2x(x-1)^4-(x^2-4)cdot 4(x-1)^3}{(x-1)^8}right)=\ =-3left(frac{2x(x-1)-4(x^2-4)}{(x-1)^5}right)=-3left(frac{2x^2-2x-4x^2+16}{(x-1)^5}right)=\ =-3left(frac{-2x^2-2x+16}{(x-1)^5}right)=frac{6(x^2+x-8)}{(x-1)^5}=frac{6(x-x_1)(x-x_2)}{(x-1)^5}\ D=1^2-4cdot (-8)=33, x_{1,2}=frac{-1pm sqrt{33}}{2}= left[ begin{array}{l} approx -3,37\ approx 2,37 end{array} right.\ f»(x)=0, text{при} x=x_{1,2} end{gather*} Критические точки 2-го порядка: (x=left{1;frac{-1pm sqrt{33}}{2}right})
| (x) | ((-infty;x_1)) | (x_1) | ((x_1;1)) | 1 | ((1;x_2)) | (x_2) | ((x_2;+infty)) |
| (f»(x)) | <0 | 0 | >0 | (varnothing) | <0 | 0 | >0 |
| (f(x)) | (cap) | перегиб | (cup) | (varnothing) | (cap) | перегиб | (cup) |
Функция выпуклая вверх при (xin(-infty;x_1)cup(1;x_2))
Функция выпуклая вниз при (xin(x_1;1)cup (x_2;++infty))
Точки перегиба: $$ begin{cases} x=frac{-1-sqrt{33}}{2}approx -3,37\ yapprox 0,51 end{cases}, begin{cases} x=frac{-1+sqrt{33}}{2}approx 2,37\ yapprox 3,62 end{cases} $$
6) Точки пересечения с осями
Пересечение с OY: (x=0, y=frac{0^3-4}{(0-1)^3}=4)
Пересечение с осью OX:
(frac{x^3-4}{(x-1)^3}=0Rightarrow x=sqrt[3]{4}, y=0)
7) График
Чтобы узнать количество корней уравнения (frac{x^3-4}{(x-1)^3}=a), нужно снизу вверх двигать горизонталь (y=a) и считать количество точек её пересечения с графиком функции.
Последовательно, получаем:
(altfrac{12}{27}) — один корень
(a=frac49) – два корня
(frac49lt alt 1) — три корня
(a=1) – два корня
(1lt alt 4) – три корня
(a=4) — два корня
(agt 4) — один корень
Ответ:
(altfrac49cup agt 4), один корень
(a=left{frac49;1;4right}), два корня
(frac{12}{27}lt 1lt 1cup 1lt alt 4), три корня
Пример 4*. Постройте график функции (y=sin^4x+cos^4x), используя правила преобразования тригонометрических функций и с помощью стандартной процедуры исследования функции
1) Область определения (xinmathbb{R})
2) Четность $$ f(-x)=sin^4(-x)+cos^4(-x)=sin^4x+cos^4x=f(x) $$ Функция четная.
Чтобы найти период, преобразуем тригонометрическое выражение, применяя формулы понижения степени (см. §15 данного справочника): begin{gather*} sin^4x+cos^4x=left(frac{1-cos2x}{2}right)^2+left(frac{1+cos2x}{2}right)^2=\ =frac14(1-2cos2x+cos^2 2x+1+2cos2x+cos^2 2x)=frac{1+cos^2 2x}{2}=\ =frac12left(1+frac{1+cos4x}{2}right)=frac{3+cos4x}{4} end{gather*} Функция периодическая с периодом (T=frac{2pi}{4}=frac pi 2)
Исходя из полученного выражения и применяя правила преобразования графиков тригонометрических функций (см. §8 данного справочника), можно сразу получить результат. $$ y=frac{3+cos4x}{4}=frac34+frac14 cos4x $$ Цепочка преобразований: $$ x xrightarrow1 4xxrightarrow2 cos4x xrightarrow3 frac14xrightarrow4 frac34+frac14 cos4x $$ Пошагово получаем:
1. Умножение аргумента на 4 приводит к уменьшению периода в 4 раза (T=fracpi 2)
2. Косинус – функция четная, при (x=0, cos4x=1), остальные единицы будут через период: (x=frac{pi k}{2}, cos4x=1). Соответственно: (x=fracpi 4+frac{pi k}{2}0 ,cos4x=-1).
Нули функции: (x=fracpi 8+frac{pi k}{4}, cos4x=0).
3. Умножение на (frac14) уменьшает амплитуду косинусоиды в 4 раза: (-frac14leqfrac14 cos4xleq frac14)
4. Прибавление (frac34) перемещает график на (frac34) вверх: (frac12leqfrac34+frac14 cos4xleq 1)
Получаем график:
Продолжим стандартное исследование функции.
3) Асимптоты
1. Вертикальных асимптот нет, т.к. нет точек разрыва 2-го рода.
2. Горизонтальных асимптот нет, т.к. нет пределов на бесконечности.
3. Наклонных асимптот нет, т.к. на бесконечности отношение ограниченной тригонометрической функции к бесконечному x дает (k=0).
4) Первая производная:
Исследуем промежуток, равный одному периоду (T=fracpi 2, 0leq xleqfracpi 2) begin{gather*} f'(x)=(sin^4 x+cos^4 x)’=left(frac{3+cos4x}{4}right)’=0-frac14cdot 4cdot sin4x=-sin4x\ sin4x=0Rightarrow 4x=pi kRightarrow x=frac{pi k}{4} end{gather*} Критические точки: (x=frac{pi k}{4}). На периоде (T=fracpi 2) получаем три точки (x=left{0;fracpi 4;fracpi 2right})
| (x) | 0 | (left(0;fracpi 4right)) | (fracpi 4) | (left(fracpi 4;fracpi 2right)) | (fracpi 2) |
| (f'(x)) | 0 | <0 | 0 | >0 | 0 |
| (f(x)) | 1 max |
(searrow) | (frac12) min |
(nearrow) | 1 max |
Функция убывает при (xinleft(frac{pi k}{2};fracpi 4+frac{pi k}{2}right))
Функция возрастает при (xinleft(fracpi 4+frac{pi k}{2};fracpi 2+frac{pi k}{2}right))
Точки минимума (x=fracpi 4+frac{pi k}{2}; y_{min}=frac12)
Точки максимума (x=frac{pi k}{2}; y_{max}=1)
5) Вторая производная: begin{gather*} f»(x)=(-sin4x)’=-4cos4x\ cos4x=0Rightarrow 4x=fracpi 2+pi kRightarrow x=fracpi 8+frac{pi k}{4} end{gather*} Критические точки 2-го порядка: (x=fracpi 8+frac{pi k}{4}).
На периоде (T=fracpi 2) получаем две точки (x=left{fracpi 8;frac{3pi}{8}right})
| (x) | (left(0;fracpi 8right)) | (fracpi  |
(left(fracpi 8;frac{3pi}{8}right)) | (frac{3pi}{8}) | (left(frac{3pi}{8};fracpi 2right)) |
| (f»(x)) | <0 | 0 | >0 | 0 | <0 |
| (f(x)) | (cap) | перегиб | (cup) | перегиб | (cap) |
Функция выпуклая вниз при (xinleft(fracpi 8+frac{pi k}{2};frac{3pi}{8}+frac{pi k}{2}right))
Функция выпуклая вверх при (xinleft(-fracpi 8+frac{pi k}{2};fracpi 8+frac{pi k}{2}right))
Точки перегиба: ( x=fracpi 8+frac{pi k}{4}, y=frac{3+cos4cdot left(fracpi 8+frac{pi k}{4}right)}{4}=frac{3+0}{4}=frac34 )
6) Точки пересечения с осями
Пересечение с OY: (x=0, y_{max}=1)
Пересечение с осью OX: т.к. функция ограничена (frac12leq yleq 1), пересечений с OX нет.
7) График
График тот же, что и полученный с помощью правил преобразований графиков тригонометрических функций. Добавились только точки перегиба.
Содержание:
Полная схема исследования функции:
- Найти область определения функции.
- Исследовать функцию на чётность и периодичность.
- Найти точки пересечения графика функции с осями координат.
- Найти интервалы знакопостоянства.
- Найти первую производную, промежутки возрастания и убывания, точки экстремума и экстремумы функции.
- Найти вторую производную. Определить интервалы выпуклости графика функции и точки перегиба.
- Исследовать поведение функции на концах промежутков определения.
- Найти асимптоты графика функции.
- Построить график функции.
Пример:
Исследуйте функцию
Решение:
1) Область определения функции:
2) Функция ни чётная, ни нечётная, ни периодическая.
3) 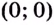
4)
5) Чтобы найти производную функции, запишем её в виде
Поскольку в точке 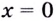
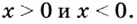
Функция имеет две критические точки:
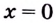
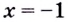
Составим и заполним таблицу для первой производной
Из таблицы видно, что функция возрастает на промежутках 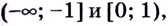
Первая производная при переходе через точку 
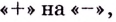
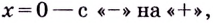
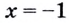
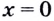
6) Найдём вторую производную:
Функция имеет две критические точки второго рода: 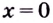

Составим и заполним таблицу для второй производной
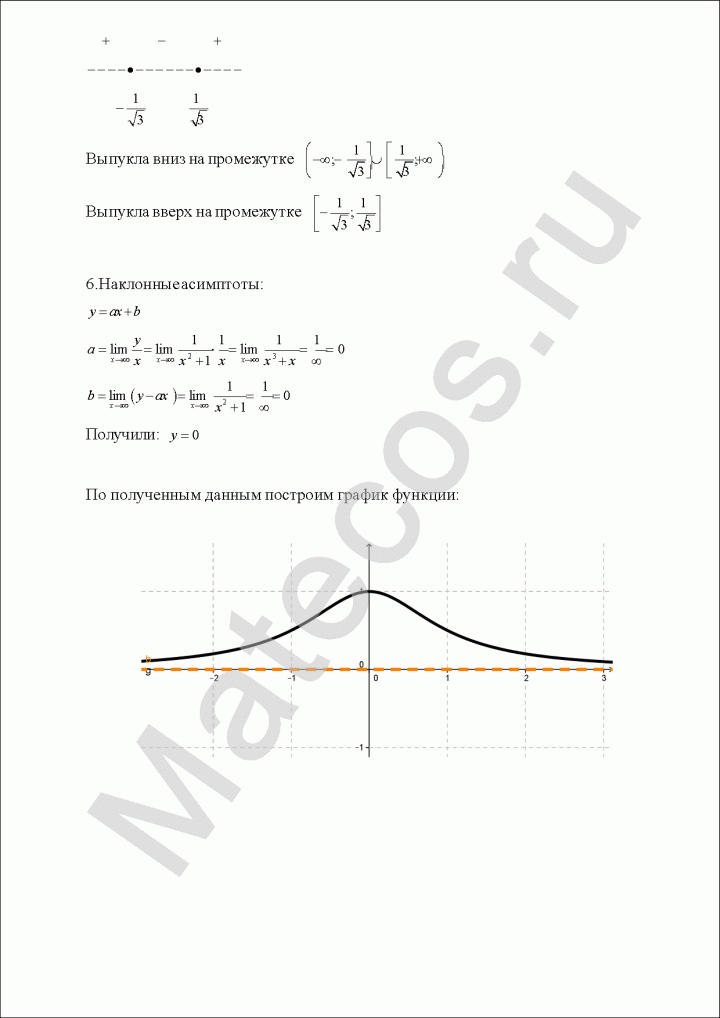
Как видим из таблицы, кривая выпуклая на промежутке 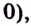
Вторая производная при переходе через точку 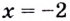
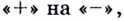

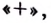
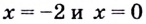
7) Исследуем поведение заданной функции на концах промежутков определения:

Поскольку 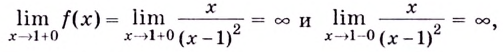
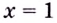
Поскольку 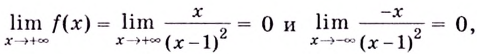
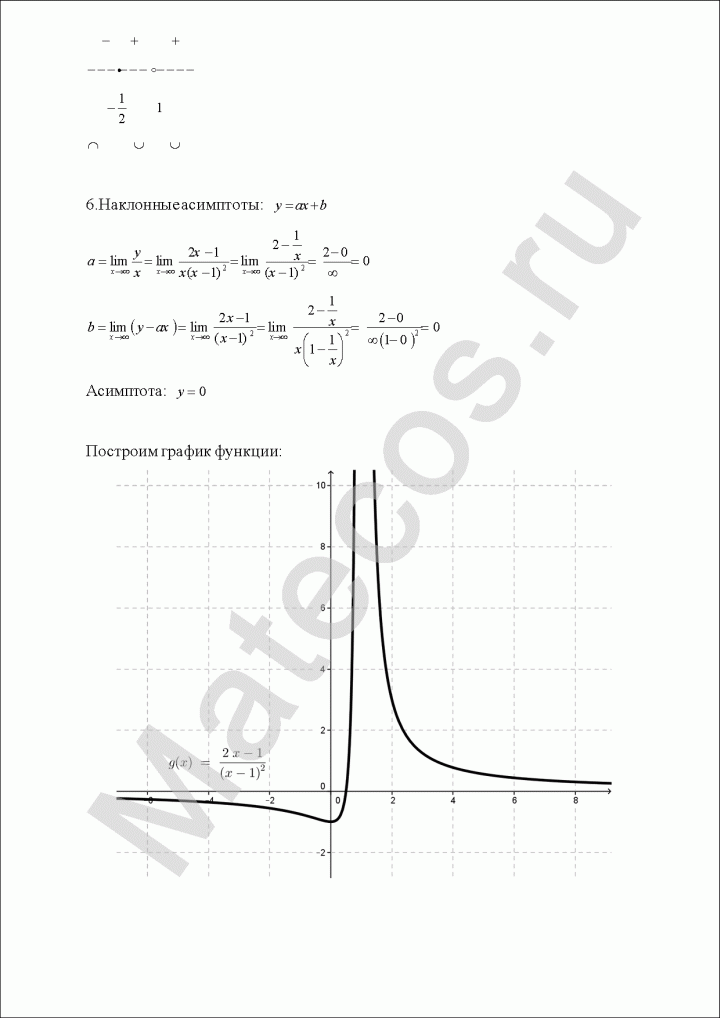
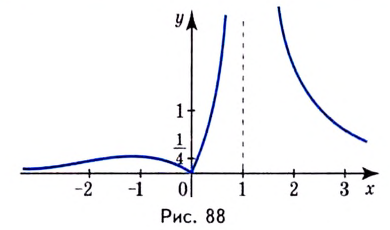
9) Используя полученные данные, построим график функции {рис. 88).
Пример:
Найдите интервалы выпуклости, вогнутости и точки перегиба кривых:
Решение:
1) Область определения функции —
2) Найдём первую и вторую производные. Имеем: 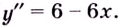
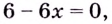
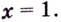
3) Определим знак второй производной на каждом из интервалов 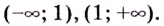
Если 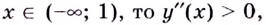
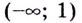
Если 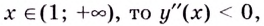
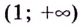
Точка 
Следовательно, 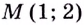
1) Область определения функции—
2) Найдём критические точки второго рода:
Как видим, вторая производная существует на множестве всех действительных чисел и ни в одной точке в ноль не превращается. А потому критических точек второго рода нет. Следовательно, нет и точек перегиба. На всей области определения 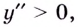
Пример:
Найдите асимптоты кривой
Решение:
Область определения функции — 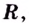
Найдем наклонную асимптоту:
Следовательно, прямая 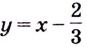
Исследование функций
Процесс управления требует от менеджера компактного представления разносторонних знаний из разных областей хозяйственной, управленческой, налоговой, коммерческой и других видов деятельности в виде разнообразных функциональных зависимостей.
В процессе такой деятельности перед менеджером возникают задачи тактического и стратегического планирования, оценки возможностей предприятия и конкурентов, оптимального распределения ресурсов, разумного реагирования на налоговую политику, выбора ценовой и инвестиционной политики и др.
Важную роль при этом играет исследование функций, используемых при построении математической модели рассматриваемой проблемы. Такое исследование проводится с учетом свойств конкретных функций и позволяет уточнить сформулированную математическую задачу, решая которую (с учетом выбранного метода решения), рассчитывают получить определенный результат, требующий в дальнейшем интерпретации в терминах исследуемой проблемы.
Все это связано с выявлением таких свойств функций, используемых в модели, как характер изменения (монотонность), наличие точек с особыми свойствами (стационарные точки, экстремумы), геометрические свойства (выпуклость графика функции) и другие.
Настоящий раздел посвящен исследованию функций методами дифференциального исчисления и использованию полученных навыков для решения задач.
Монотонность функции
Функция y = y (x) называется возрастающей на промежутке l, если 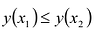
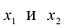
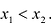
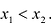
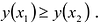
Теорема. Если функция у = f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b), то для того, чтобы f(x) была возрастающей (убывающей) необходимо и достаточно, чтобы 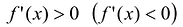
Дифференцируемая функция является возрастающей на промежутке l тогда и только тогда, когда
Пример:
Найти промежутки возрастания и убывания функции
Вычислим:
Точки 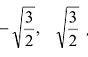
Производная 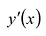
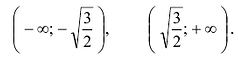
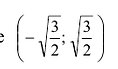
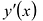
Локальный экстремум
Точка 
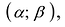

Точка 
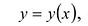
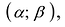

Точки локального минимума и локального максимума называются точками локального экстремума.
Необходимым условием локального экстремума дифференцируемой функции является выполнение равенства 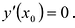
Решения этого уравнения называют стационарными точками.
Исследование стационарных точек
I правило. Если при возрастании .v при переходе через стационарную точку х0 производная у'(х) меняет знак с + на — , то 
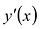

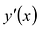

II правило. Если вторая производная 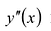


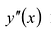


Точками локального экстремума функции могут быть такие точки, в которых производная не существует или обращается в бесконечность. Исследовать такие точки можно по I правилу. Экстремум в такой точке называется острым экстремумом.
Пример:
Найти экстремум функции 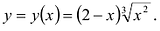
Функция имеет стационарную точку 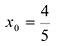
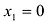
Поскольку 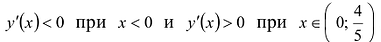
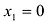
Это будет острый минимум.
При переходе через стационарную точку 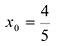
Глобальный экстремум
Непрерывная на отрезке [a;b] функция у = y(x) принимает свое наибольшее значение 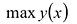
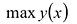
Это и будут 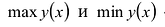
Пример:
Найти наибольшее и наименьшее значения функции 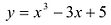
Вычисляем 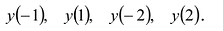
Выпуклость и перегибы графика функции
Графиком функции у = у(х), заданной на множестве X, называют множество точек плоскости с координатами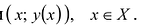
Если на промежутке l вторая производная у'(х) положительна, то график является выпуклым вниз на этом промежутке. Если .у «(x) < 0 на промежутке l, то график является выпуклым вверх на промежутке l.
Точка М(с;у{с)) может быть точкой перегиба только в том случае, когда у'(x) = 0, либо у»(x) не существует — необходимое условие перегиба. Однако равенство нулю или не существование второй производной в точке с не означает еще, что в точке 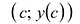
Пример:
Найти промежутки выпуклости и точки перегиба графика функции
Вычислим вторую производную .
Точки -1 и 1 разбивают числовую прямую на три промежутка: 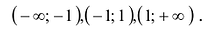
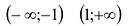
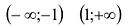
В точках 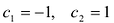
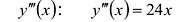
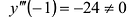
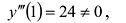
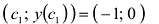
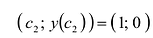
Исследование функции и построение графика
График функции у = у(х)у заданной на множестве X, т.е. множество точек плоскости с координатами 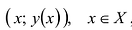
Для построения графика функции у = у{х) выясняют особенности поведения функции. Существенную роль при этом играют характерные точки: концевые точки промежутков задания функции, точки разрыва, стационарные точки и точки недифференцируемости функции и се производной и т.д. По этим точкам выделяются участки однообразного поведения функции, а именно: промежутки ее непрерывности; промежутки, на которых у'(х) и y»(x) сохраняют знак, что позволяет изучить характер монотонности функции и направление ее выпуклости.
Построение графика функции может быть осуществлено по следующему плану.
Если функция задана аналитическими выражениями, то выясняют естественную область определения функции, т.е. множество значений аргумента х, при которых y(x) имеет смысл.
Если функция периодическая, то находят ее период, т.е. число 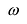
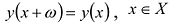
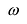
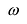
Для четной функции: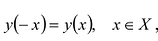
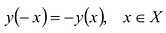
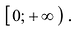
Используя симметричное отражение относительно оси Oy для четной функции и относительно точки О — для нечетной функции.
Находят точки разрыва и промежутки, на которых она непрерывна. Выясняют характер точек разрыва. Вычисляют предельные значения функции в граничных точках множества X (если таковые имеются). Находят вертикальные асимптоты (в точках бесконечного скачка). Если X ограничено, то вычисляют пределы функции при 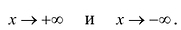
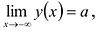
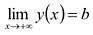
Аналогично находят коэффициенты правосторонней асимптоты (нужно вычислить пределы при 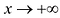
Вычисляют производную 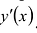
Вычисляют вторую производную . Находят критические точки производной 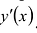
Исследуя стационарные точки функции у(х), находят точки локального экстремума и локальные экстремальные значения функции. Для этого можно изучить поведение производной 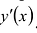
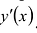
Опираясь на характерные точки функции, строят таблицу, в которую вносят все особенности функции.
На координатную плоскость в выбранном масштабе наносят характерные точки функции, асимптоты и строят график, руководствуясь п. 1-6. Если нужно, строят дополнительно несколько точек графика
Пример:
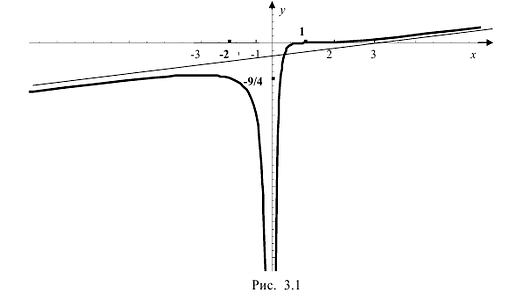
Построить график функции
I. Область определения
Функция не является периодической, четной, нечетной.
II. Поскольку 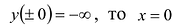
Так как 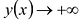
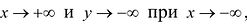
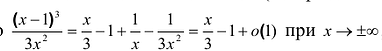
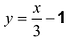
3. 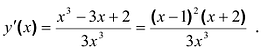
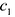
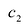
IV. 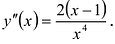
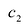
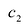
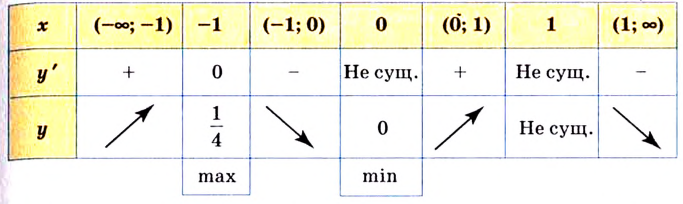
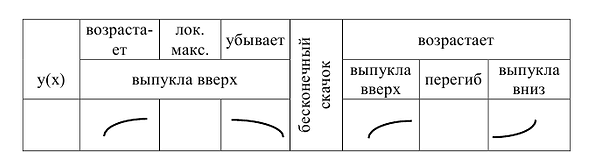
V. Строим таблицу, в которой выделены промежутки однообразного поведения функции и ее характерные точки.
VI. На координатной плоскости отмечаем точки локального максимума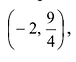
Строим схематично график функции с учетом выясненных ранее особенностей ее поведения.
Интерполяция и аппроксимация функций
При табличной форме задания функции часто возникает ситуация, когда аргумент функции задан с большей точностью, чем позволяет таблица. В этом случае приходится прибегнуть к интерполяции (или интерполированию) — приближенному нахождению неизвестных значений функций по известным ее значениям в заданных точках.
Наиболее простым является линейное интерполирование, при котором допускается, что приращение функции пропорционально приращению аргумента. Если заданное значение д: лежит между приведенными в таблице значениями 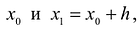
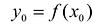
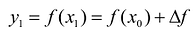
Если по заданным значениям функции необходимо найти приближенное значение аргумента, то такая операция называется обратным интерполированием.
В общем виде интерполяционная задача состоит в построении обобщенного многочлена Р(х), принимающего значения исследуемой функции у = f(x) на конечном множестве 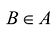
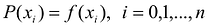
В частности, если A = [a,b] а множество 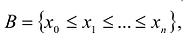
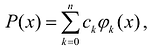
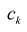
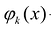
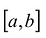
Условия интерполирования 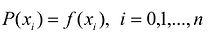
К системе можно применить векторно-матричную форму записи 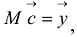
Если семейство функций 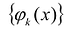
- Заказать решение задач по высшей математике
Интерполяционный полином Лагранжа
Примером наипростейшей базисной системы функций можно считать систему
Утверждение 1. Если два многочлена степени 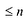
Пусть многочлены P(x) и Q(x) степени n, 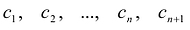
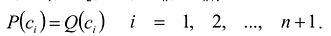
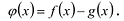
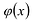
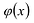
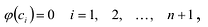
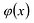
Это утверждение позволяет доказать следующую теорему.
Теорема. Для каждого натурального числа n существует один и только один многочлен степени 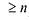
Пусть 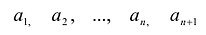
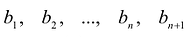
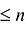
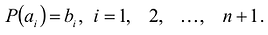
Степень 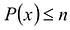
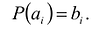
Пример. Построить интерполяционный многочлен Лагранжа по заданной таблице значений:
Формула Тейлора
Задача аппроксимации (приближенного вычисления) функции в окрестности данной точки, которую часто называют рабочей точкой, является одной из основных задач математического анализа. Для дифференцируемых функций эта задача решается с помощью формулы Тейлора.
Поскольку функция дифференцируема, то ее приращение представимо в виде:
т.е. существует многочлен первой степени 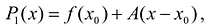
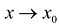
В более общем виде задачу можно сформулировать следующим образом. Пусть функция определена в некоторой окрестности точки 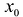
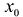
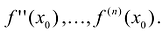
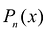
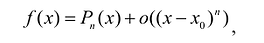
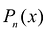
Предположим, что искомый аппроксимационный многочлен имеет вид:
Тогда:
Тогда, с учетом условий (5), можно получить:
Таким образом, если в аппроксимационый полином подставить полученные значения коэффициентов, то полином можно записать следующим образом:
Этот многочлен называется многочленом Тейлора функции f. Можно показать, что он удовлетворяет условию
Рассмотрим функцию 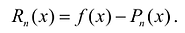
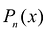
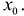
Для того, чтобы убедиться, что 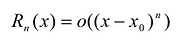
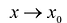
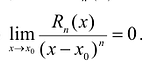
Полученные выводы можно сформулировать в виде теоремы.
Теорема. Пусть функция f определена в некоторой окрестности точки 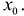
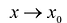
Полученный многочлен называется формулой Тейлора n -го порядка с остаточным членом в форме Пеано.
Если 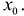
Для остаточного члена формулы Тейлора существуют и другие представления. Так, если функция f имеет производную n-го порядка в окрестности точки 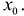
Основные разложения
Используя основные разложения можно получать формулы Тейлора для других функций. При этом используют то, что:
Понятие об эмпирических формулах
На практике часто возникает задача аппроксимации данных о зависимости между двумя переменными у их, полученных опытным путем и представленных в табличной форме. Это могут быть результаты опыта, наблюдений, статистической обработки результатов и т.д. При этом необходимо зависимость между этими переменными представить в виде аналитического выражения функции у = f(x) так, чтобы эта формула наилучшим образом отражала общую тенденцию зависимости у от fx, исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений.
Формулы, служащие для аналитического представления опытных данных, называются эмпирическими. Задача нахождения эмпирических формул выполняется в два этапа:
- Установление вида зависимости у = f(x);
- Определение неизвестных параметров этой функции.
При определении вида эмпирической функции у-f{x)
обычно предполагается, что это наиболее гладкая кривая, согласованная с экспериментальными данными. Кроме того, для выбора этой функции привлекаются дополнительные соображения, как правило, не математического характера (теоретические модели, опыт предшествующих исследований, и т.п.).
Эта задача может быть решена в ходе регрессионного анализа, который изучается в курсе теории вероятностей, но решить ее можно и математическими методами. Согласно наиболее распространенному и теоретически обоснованному методу наименьших квадратов, в качестве неизвестных параметров функции у = f (х) выбираются такие значения, которые соответствуют минимальному значению суммы квадратов отклонений эмпирических значений у. от значений функции 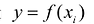
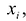
Разность 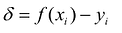
В ходе решения задачи отыскания оптимальных параметров аппроксимационной функции y = f(x) возникает необходимость поиска экстремума функции нескольких переменных, поэтому, прежде чем решать эту задачу для конкретных эмпирический функций, необходимо рассмотреть свойства функций нескольких переменных.
- Пространство R»
- Неопределённый интеграл
- Методы интегрирования неопределенного интеграла
- Определённый интеграл
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной