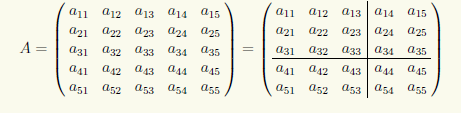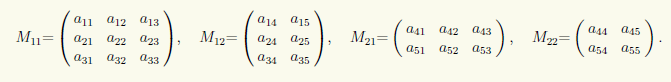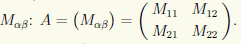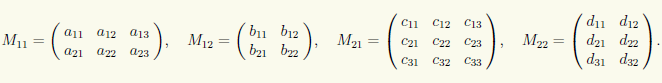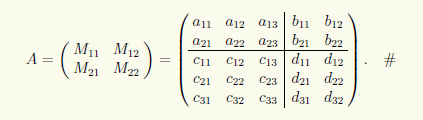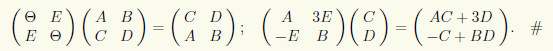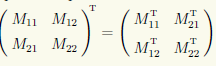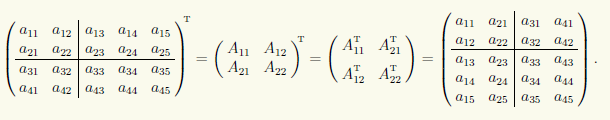Блочные матрицы и кронекеровские произведение и сумма матриц
Блочные (клеточные) матрицы и операции над ними
Числовая матрица размеров
, разделенная горизонтальными и вертикальными линиями на блоки (клетки), которые представляют собой матрицы, называется блочной (клеточной) матрицей. Элементами блочной матрицы
являются матрицы
размеров
,
, причем
и
.
Операции с блочными матрицами выполняются по тем же правилам, что и с числовыми матрицами. Если числовые матрицы и
равных размеров одинаково разбиты на блоки
и
, то их сумму
можно аналогичным образом разбить на блоки
, причем для каждого блока
. Если блочную матрицу
умножить на число
, то получим матрицу
. При транспонировании блочной матрицы транспонированию подлежит блочная структура и все ее блоки, например
Пример 1.25. Даны блочные матрицы
Найти матрицы .
Решение. Матрицы и
имеют блоки одинаковых размеров: блоки
и
имеют размеры
; блоки
и
—
; блоки
и
—
; блоки
и
—
. Матрица
будет иметь такие же по размерам блоки
. Для каждого блока находим
Следовательно, матрица будет следующая
Матрица будет иметь блоки тех же размеров, что и
:
Поэтому матрица будет иметь вид
Используя правило транспонирования блочных матриц, получаем
Умножение блочных матриц
Рассмотрим теперь операцию умножения блочных матриц и
. Блочные матрицы
и
называются согласованными, если разбиение матрицы
на блоки по столбцам совпадает с разбиением матрицы
по строкам, т.е. блоки
имеют размеры
, а блоки
—
. У согласованных блочных матриц блоки
и
являются согласованными матрицами.
Произведением согласованных блочных матриц
и
называется блочная матрица
, блоки которой вычисляются по следующей формуле
Это означает, что блочные матрицы, разделенные на блоки надлежащим образом, можно перемножать обычным способом. Чтобы получить блок произведения, надо выделить i-ю строку блоков матрицы
и j-й столбец блоков матрицы
. Затем найти сумму попарных произведений соответствующих блоков: первый блок i-й строки блоков умножается на первый блок j-го столбца блоков, второй блок i-й строки блоков умножается на второй блок j-го столбца и т.д., а результаты умножений складываются.
Пример 1.26. Даны блочные матрицы
Найти произведение блочных матриц .
Решение. Матрица разбита на блоки:
размеров
—
—
—
. Матрица
разбита на блоки:
размеров
—
—
—
. Блочные матрицы
и
согласованы. Матрица
разбита по столбцам на два и один (считая слева), матрица
разбита по строкам на две и одну (считая сверху). Поэтому произведение
определено. Матрица
будет иметь блоки
. Для каждого блока находим
Следовательно, матрица будет иметь вид
Замечания 1.7
1. Операции сложения, умножения на число и произведения блочных матриц выполняются по тем же правилам, что и для обычных матриц, только вместо элементов в формулах используются блоки.
2. Выполняя операции над блочными матрицами, всегда можно их рассматривать как числовые, и проводить указанные операции по обычным правилам для числовых матриц. При этом результат операций (числовая матрица) будет один и тот же. Действия с блочными матрицами предпочтительнее, чем с числовыми, в том случае, когда в результате вычислений требуется искать не всю матрицу, а только ее часть — блок.
3. Матрица, у которой большинство элементов отличны от нуля, называется плотной матрицей. Матрица, большинство элементов которой -нули, называется разреженной матрицей. Для разреженных матриц, подавляющее количество элементов которых равно нулю, полезно выделять нулевые блоки с целью уменьшения вычислительных операций.
Пример 1.27. Найти произведение матриц четвёртого порядка
Решение. Разобьем данные матрицы на блоки размеров
где — единичная,
— нулевая. Запишем сначала произведение блочных матриц
Следовательно, вместо умножения матриц и
достаточно определить только один блок, сложив матрицы
и
Осталось записать результат
Кронекеровские произведение и сумма матриц
Пусть даны матрицы и
размеров
и
соответственно. Числовая матрица размеров
, составленная из блоков
называется правым кронекеровским произведением матриц и
(или правым прямым произведением матриц).
Пусть и
квадратные матрицы n-го и m-го порядков соответственно. Кронекеровскои суммой матриц
и
называется квадратная матрица mn-го порядка
где — единичные матрицы соответствующих порядков.
Пример 1.28. Даны матрицы
Найти кронекеровское произведение и кронекеровскую сумму
.
Решение. По определению находим
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
From Wikipedia, the free encyclopedia
In mathematics, a block matrix or a partitioned matrix is a matrix that is interpreted as having been broken into sections called blocks or submatrices.[1] Intuitively, a matrix interpreted as a block matrix can be visualized as the original matrix with a collection of horizontal and vertical lines, which break it up, or partition it, into a collection of smaller matrices.[2] Any matrix may be interpreted as a block matrix in one or more ways, with each interpretation defined by how its rows and columns are partitioned.
This notion can be made more precise for an 











Block matrix algebra arises in general from biproducts in categories of matrices.[3]
Example[edit]
A 168×168 element block matrix with 12×12, 12×24, 24×12, and 24×24 sub-matrices. Non-zero elements are in blue, zero elements are grayed.
The matrix
can be partitioned into four 2×2 blocks
The partitioned matrix can then be written as
Block matrix multiplication[edit]
It is possible to use a block partitioned matrix product that involves only algebra on submatrices of the factors. The partitioning of the factors is not arbitrary, however, and requires «conformable partitions»[4] between two matrices 





and a 



that are compatible with the partitions of 
can be performed blockwise, yielding 




Or, using the Einstein notation that implicitly sums over repeated indices:
Block matrix inversion[edit]
For more details and derivation using block LDU decomposition, see Schur complement.
If a matrix is partitioned into four blocks, it can be inverted blockwise as follows:
where A and D are square blocks of arbitrary size, and B and C are conformable with them for partitioning. Furthermore, A and the Schur complement of A in P: P/A = D − CA−1B must be invertible.[6]
Equivalently, by permuting the blocks:
Here, D and the Schur complement of D in P: P/D = A − BD−1C must be invertible.
If A and D are both invertible, then:
By the Weinstein–Aronszajn identity, one of the two matrices in the block-diagonal matrix is invertible exactly when the other is.
Block matrix determinant[edit]
The formula for the determinant of a 

If 

If 


If the blocks are square matrices of the same size further formulas hold. For example, if 


[8]
This formula has been generalized to matrices composed of more than 
For 



Block diagonal matrices [edit]
A block diagonal matrix is a block matrix that is a square matrix such that the main-diagonal blocks are square matrices and all off-diagonal blocks are zero matrices. That is, a block diagonal matrix A has the form
where Ak is a square matrix for all k = 1, …, n. In other words, matrix A is the direct sum of A1, …, An. It can also be indicated as A1 ⊕ A2 ⊕ … ⊕ An or diag(A1, A2, …, An) (the latter being the same formalism used for a diagonal matrix). Any square matrix can trivially be considered a block diagonal matrix with only one block.
For the determinant and trace, the following properties hold
A block diagonal matrix is invertible if and only if each of its main-diagonal blocks are invertible, and in this case its inverse is another block diagonal matrix given by
The eigenvalues and eigenvectors of 

Block tridiagonal matrices[edit]
A block tridiagonal matrix is another special block matrix, which is just like the block diagonal matrix a square matrix, having square matrices (blocks) in the lower diagonal, main diagonal and upper diagonal, with all other blocks being zero matrices. It is essentially a tridiagonal matrix but has submatrices in places of scalars. A block tridiagonal matrix A has the form
where Ak, Bk and Ck are square sub-matrices of the lower, main and upper diagonal respectively.
Block tridiagonal matrices are often encountered in numerical solutions of engineering problems (e.g., computational fluid dynamics). Optimized numerical methods for LU factorization are available and hence efficient solution algorithms for equation systems with a block tridiagonal matrix as coefficient matrix. The Thomas algorithm, used for efficient solution of equation systems involving a tridiagonal matrix can also be applied using matrix operations to block tridiagonal matrices (see also Block LU decomposition).
Block Toeplitz matrices[edit]
A block Toeplitz matrix is another special block matrix, which contains blocks that are repeated down the diagonals of the matrix, as a Toeplitz matrix has elements repeated down the diagonal.
A block Toeplitz matrix A has the form
Block transpose[edit]
A special form of matrix transpose can also be defined for block matrices, where individual blocks are reordered but not transposed. Let 








As with the conventional trace operator, the block transpose is a linear mapping such that 



Direct sum[edit]
For any arbitrary matrices A (of size m × n) and B (of size p × q), we have the direct sum of A and B, denoted by A 
For instance,
This operation generalizes naturally to arbitrary dimensioned arrays (provided that A and B have the same number of dimensions).
Note that any element in the direct sum of two vector spaces of matrices could be represented as a direct sum of two matrices.
Application[edit]
In linear algebra terms, the use of a block matrix corresponds to having a linear mapping thought of in terms of corresponding ‘bunches’ of basis vectors. That again matches the idea of having distinguished direct sum decompositions of the domain and range. It is always particularly significant if a block is the zero matrix; that carries the information that a summand maps into a sub-sum.
Given the interpretation via linear mappings and direct sums, there is a special type of block matrix that occurs for square matrices (the case m = n). For those we can assume an interpretation as an endomorphism of an n-dimensional space V; the block structure in which the bunching of rows and columns is the same is of importance because it corresponds to having a single direct sum decomposition on V (rather than two). In that case, for example, the diagonal blocks in the obvious sense are all square. This type of structure is required to describe the Jordan normal form.
This technique is used to cut down calculations of matrices, column-row expansions, and many computer science applications, including VLSI chip design. An example is the Strassen algorithm for fast matrix multiplication, as well as the Hamming(7,4) encoding for error detection and recovery in data transmissions.
The technique can also be used where the elements of the A,B,C, and D matrices do not all require the same field for their elements. For example, The matrix A can be over the field of complex numbers, while the matrix D can be over the field of real numbers. This can lead to valid operations involving the matrices, while simplifying the operations within one of the matrices. For example, if D has only real elements finding its inverse takes less calculations than if complex elements must be considered. But the reals is a subfield of the complex numbers (further it can be considered a projection), so the matrices operations can be well defined.
See also[edit]
- Kronecker product (matrix direct product resulting in a block matrix)
Notes[edit]
- ^ Eves, Howard (1980). Elementary Matrix Theory (reprint ed.). New York: Dover. p. 37. ISBN 0-486-63946-0. Retrieved 24 April 2013.
We shall find that it is sometimes convenient to subdivide a matrix into rectangular blocks of elements. This leads us to consider so-called partitioned, or block, matrices.
- ^ Anton, Howard (1994). Elementary Linear Algebra (7th ed.). New York: John Wiley. p. 30. ISBN 0-471-58742-7.
A matrix can be subdivided or partitioned into smaller matrices by inserting horizontal and vertical rules between selected rows and columns.
- ^ Macedo, H.D.; Oliveira, J.N. (2013). «Typing linear algebra: A biproduct-oriented approach». Science of Computer Programming. 78 (11): 2160–2191. arXiv:1312.4818. doi:10.1016/j.scico.2012.07.012.
- ^ Eves, Howard (1980). Elementary Matrix Theory (reprint ed.). New York: Dover. p. 37. ISBN 0-486-63946-0. Retrieved 24 April 2013.
A partitioning as in Theorem 1.9.4 is called a conformable partition of A and B.
- ^ Anton, Howard (1994). Elementary Linear Algebra (7th ed.). New York: John Wiley. p. 36. ISBN 0-471-58742-7.
…provided the sizes of the submatrices of A and B are such that the indicated operations can be performed.
- ^
Bernstein, Dennis (2005). Matrix Mathematics. Princeton University Press. p. 44. ISBN 0-691-11802-7. - ^ Taboga, Marco (2021). «Determinant of a block matrix», Lectures on matrix algebra.
- ^ Silvester, J. R. (2000). «Determinants of Block Matrices» (PDF). Math. Gazette. 84 (501): 460–467. doi:10.2307/3620776. JSTOR 3620776. Archived from the original (PDF) on 2015-03-18. Retrieved 2021-06-25.
- ^ Sothanaphan, Nat (January 2017). «Determinants of block matrices with noncommuting blocks». Linear Algebra and Its Applications. 512: 202–218. arXiv:1805.06027. doi:10.1016/j.laa.2016.10.004. S2CID 119272194.
- ^ Mackey, D. Steven (2006). Structured linearizations for matrix polynomials (PDF) (Thesis). University of Manchester. ISSN 1749-9097. OCLC 930686781.
References[edit]
- Strang, Gilbert (1999). «Lecture 3: Multiplication and inverse matrices». MIT Open Course ware. 18:30–21:10.

6.1.Работасблочнымиматрицами
Блочные матрицы – это матрицы, составленные из непересекающихся подматриц (блоков). Соответствующие размеры блоков должны совпадать.
6.1.1. Конструированиеблочныхматриц
Введите матрицы
|
−1 |
4 |
, |
2 |
0 |
, |
3 |
−3 |
, |
8 |
9 |
||||||||
|
А = |
В = |
С = |
D = |
|||||||||||||||
|
−1 |
4 |
0 |
5 |
−3 |
3 |
1 |
10 |
|||||||||||
и создайте из них блочную матрицу
|
A |
| |
B |
||
|
− − |
+ |
, |
||
|
K = |
− − |
|||
|
C |
| |
|||
|
D |
учитывая, что матрица К состоит из двух строк: в первой строке матрицы А и В, а во второй – С и D:
>> K = [A B; C D] K =
|
–1 |
4 |
2 |
0 |
|
–1 |
4 |
0 |
5 |
|
3 |
-3 |
8 |
9 |
|
-3 |
3 |
1 |
10 |
Блочная матрица получена. Можно было поступить и по-другому, например, считать, что матрица К состоит из двух столбцов: в первом – матрицы А и С, а во втором – В и D. Тогда команду для создания блочной матрицы следовало бы записать так:
>> K = [[A; C] [B; D]]
Рассмотрим еще один пример для проверки знаний о работе с массивами в MatLab. Требуется составить блочную матрицу
|
Математическое программное обеспечение. Учебное пособие |
-56- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.1.Работа с блочными матрицами
|
S |
| |
a |
|||
|
−− |
+ |
−− |
, |
||
|
M = |
|||||
|
b |
| |
2.5 |
|||
где
|
2 |
0 |
, |
4 |
, b = (−9 9). |
||||
|
S = |
a = |
|||||||
|
0 |
3 |
5 |
||||||
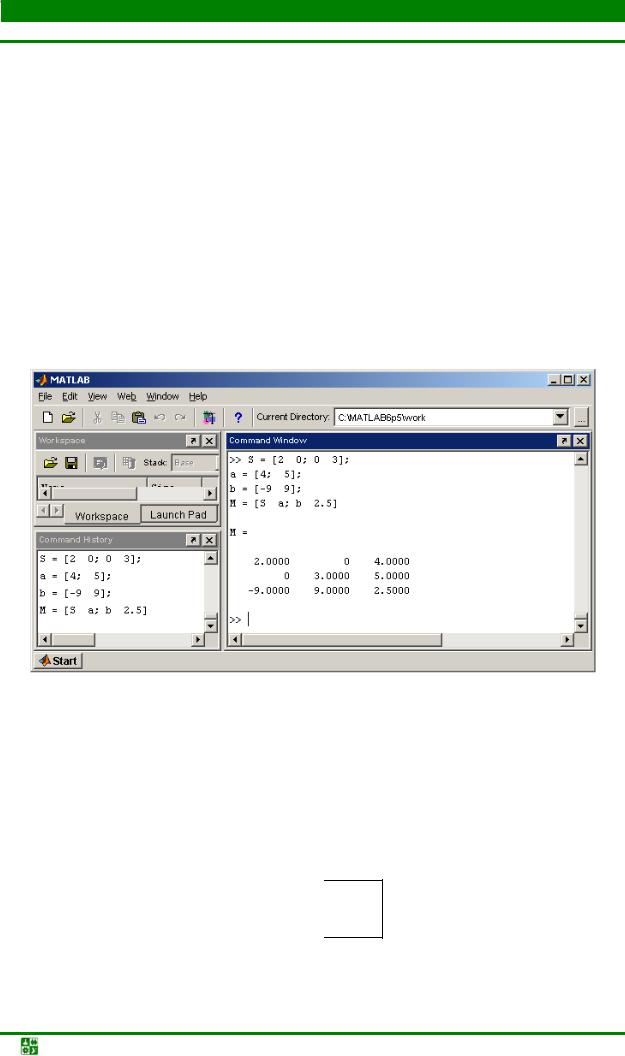
Решение этой задачи показано на рис. 6.1.
Последний оператор можно заменить на эквивалентный М = [[S; b] [a; 2.5]].
Обратной задачей к конструированию блочных матриц является выделение блоков.
Рис. 6.1
6.1.2. Выделениеблоков
Выделение блоков матриц осуществляется индексацией при помощи двоеточия, которая уже использовалась ранее для выделения блоков из векторов. Введите матрицу
|
1 |
2 |
0 |
2 |
||||
|
4 |
10 |
12 |
5 |
||||
|
, |
|||||||
|
P = |
0 |
11 |
10 |
5 |
|||
|
9 |
2 |
3 |
5 |
||||
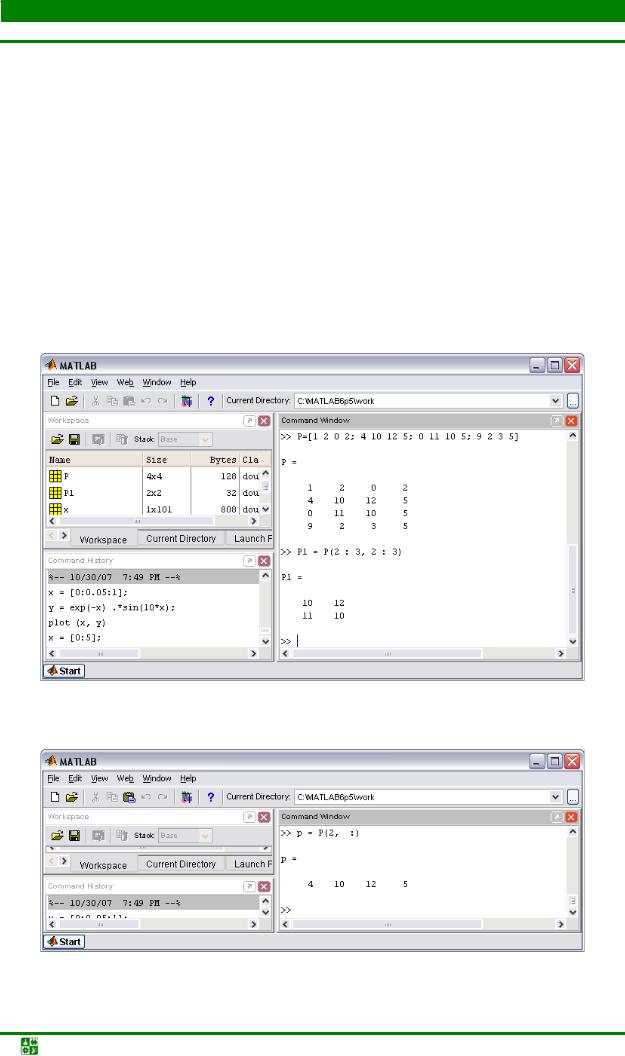
затем выделите очерченный блок, задав номера строк и столбцов при помо-
|
Математическое программное обеспечение. Учебное пособие |
-57- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.1.Работа с блочными матрицами
щи двоеточия – см. рис. 6.2.
Для выделения из матрицы столбца или строки (т. е. массива, у которого один из размеров равен единице) следует в качестве одного из индексов использовать номер столбца или строки матрицы, а другой индекс заменить на двоеточие без указания пределов. Например, запишите вторую строку P в вектор p – см. рис. 6.3.
При выделении блока до конца матрицы можно не указывать ее размеры, а использовать элемент end:
>> p = P(2, 2:end) p =
10 12 5
Рис. 6.2
Рис. 6.3
|
Математическое программное обеспечение. Учебное пособие |
-58- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.1.Работа с блочными матрицами
6.1.3.Удалениестрокистолбцов
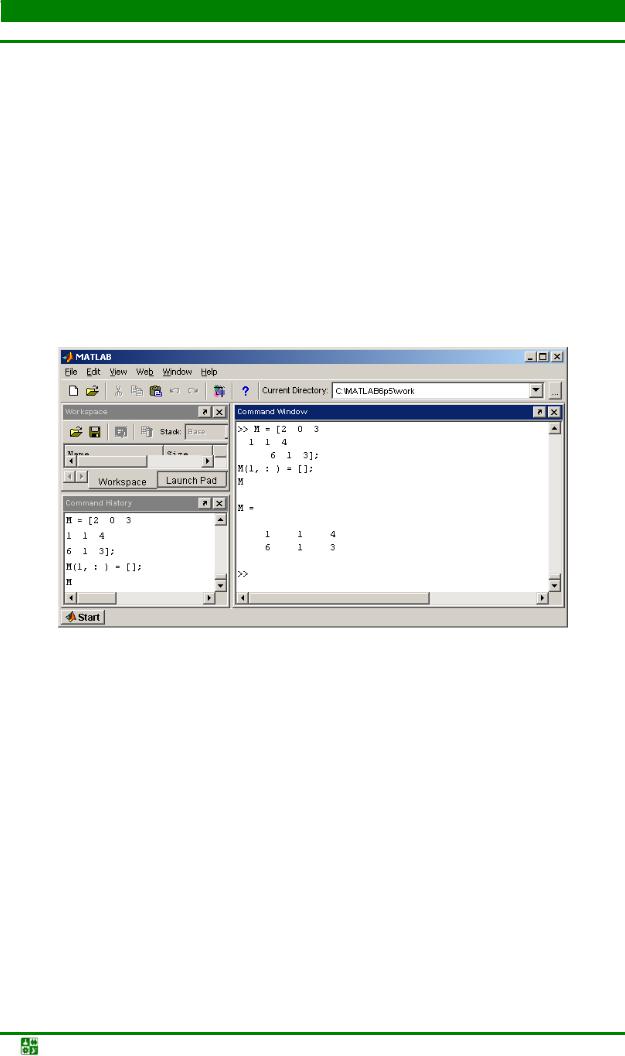
ВMatLab парные квадратные скобки [ ] обозначают пустой массив, который, в частности, позволяет удалять строки и столбцы матрицы. Для удаления строки следует присвоить ей пустой массив. Удалите, например, первую строку квадратной матрицы – см. рис. 6.4.
Обратите внимание на соответствующее изменение размеров массива,
которое можно проверить при помощи size:
>> size(M) ans =
2 3
Рис. 6.4
Аналогичным образом удаляются и столбцы. Для удаления нескольких идущих подряд столбцов (или строк) им нужно присвоить пустой массив. Удалите второй и третий столбец в массиве M – см. рис. 6.5.
|
Математическое программное обеспечение. Учебное пособие |
-59- |

6.БЛОЧНЫЕ МАТРИЦЫ
6.1.Работа с блочными матрицами
Рис. 6.5
Индексация существенно экономит время при вводе матриц, имеющих определенную структуру.
6.2. Заполнениематрицприпомощииндексации
Выше было описано несколько способов ввода матриц в MatLab, в том числе и считывание из файла. Однако бывает проще сгенерировать матрицу, чем вводить ее, особенно если она обладает простой структурой. Рассмотрим пример такой матрицы:
|
1 |
1 |
1 |
1 |
1 |
||
|
0 |
0 |
0 |
0 |
0 |
||
|
T = |
0 |
0 |
0 |
0 |
0 |
. |
|
0 |
0 |
0 |
0 |
0 |
||
|
0 |
0 |
−1 |
−1 |
|||
|
−1 |
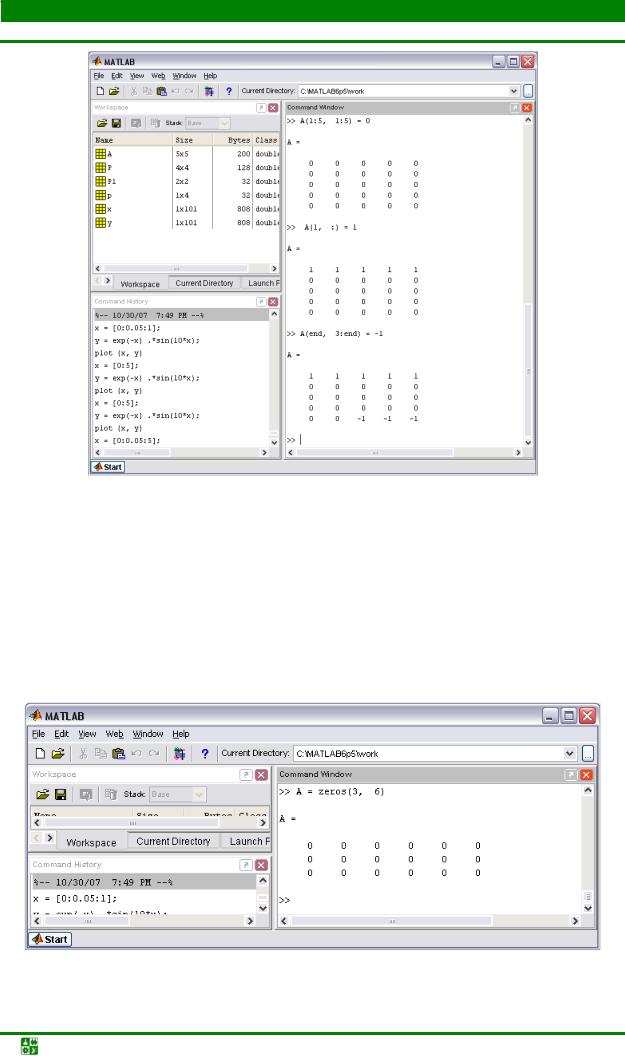
Генерация матрицы Т осуществляется в три этапа:
1.Создание массива T размера пять на пять, состоящего из нулей.
2.Заполнение первой строки единицами.
3.Заполнение части последней строки минус единицами до последнего элемента.
Соответствующие команды MatLab приведены ниже (они записаны в три колонки с целью экономии места, но набирать их надо последовательно).
Команды не завершаются точкой с запятой для вывода промежуточных результатов в командное окно с целью слежения за процессом формирования матрицы
|
Математическое программное обеспечение. Учебное пособие |
-60- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.2.Заполнение матриц при помощи индексации
Рис. 6.6
Создание некоторых специальных матриц в MatLab осуществляется при помощи встроенных функций.
6.3. Созданиематрицспециальноговида
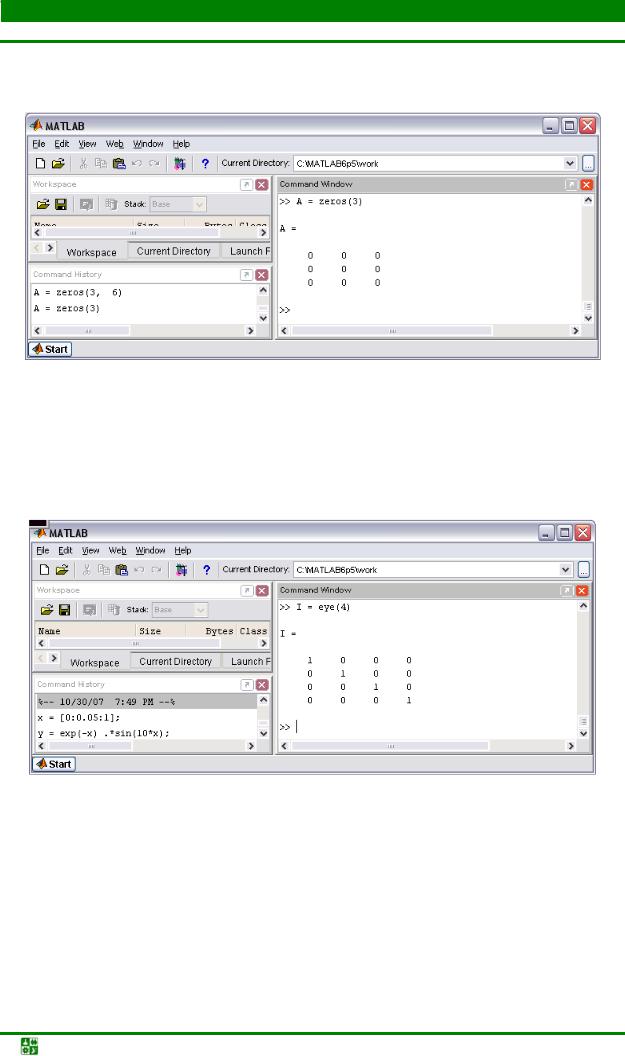
Заполнение прямоугольной матрицы нулями производится встроенной функцией zeros, аргументами которой являются число строк и столбцов матрицы, показанной на рис. 6.7.
Рис. 6.7
Один аргумент функции zeros приводит к образованию квадратной
|
Математическое программное обеспечение. Учебное пособие |
-61- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.3.Создание матриц специального вида
матрицы заданного размера – см. рис. 6.8.
Рис. 6.8
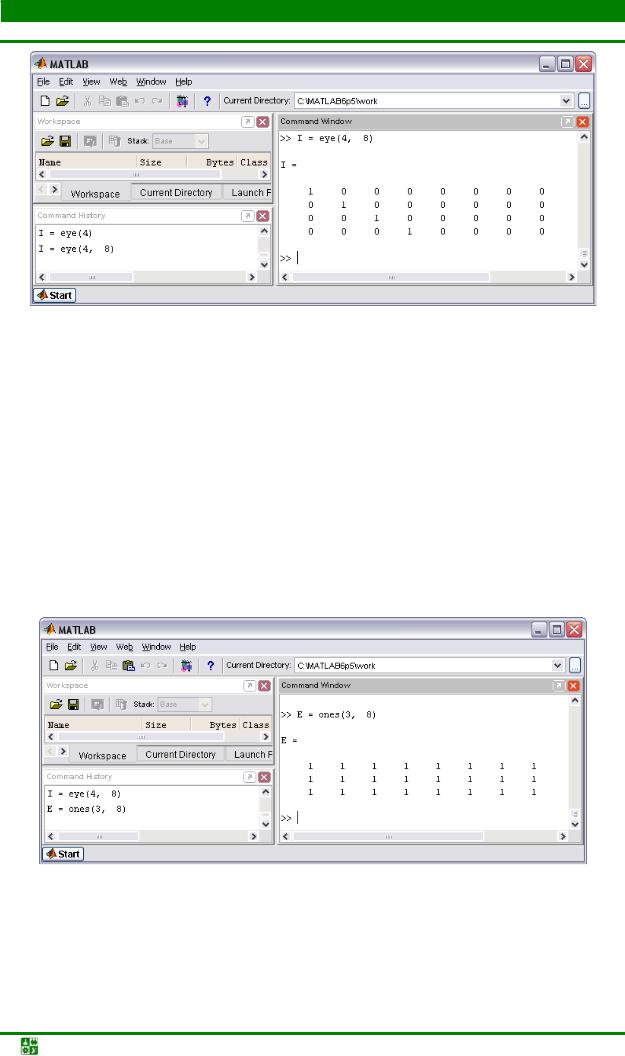
Единичная матрица инициализируется при помощи функции eye – см.
рис. 6.9.
Рис. 6.9
Функция eye с двумя аргументами создает прямоугольную матрицу, у
которой на главной диагонали стоят единицы, а остальные элементы равны нулю – см. рис. 6.10.
|
Математическое программное обеспечение. Учебное пособие |
-62- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.3.Создание матриц специального вида
Рис. 6.10
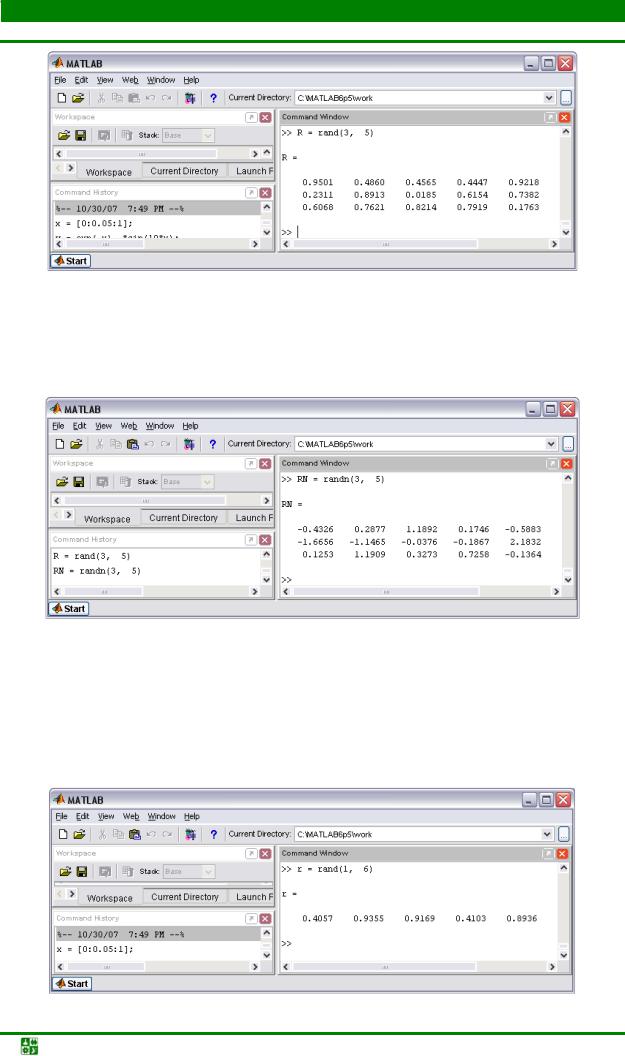
Матрица, состоящая из единиц, образуется в результате вызова функции ones – см. рис. 6.11.
Использование одного аргумента в ones приводит к созданию квадрат-
ной матрицы, состоящей из единиц.
MatLab предоставляет возможность заполнения матриц случайными элементами. Результатом функции rand является матрица чисел, распреде-
ленных случайным образом между нулем и единицей, а функции randn – матрица чисел, распределенных по нормальному закону, – см. рис. 6.12.
Рис. 6.11
|
Математическое программное обеспечение. Учебное пособие |
-63- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.3.Создание матриц специального вида
Рис. 6.12
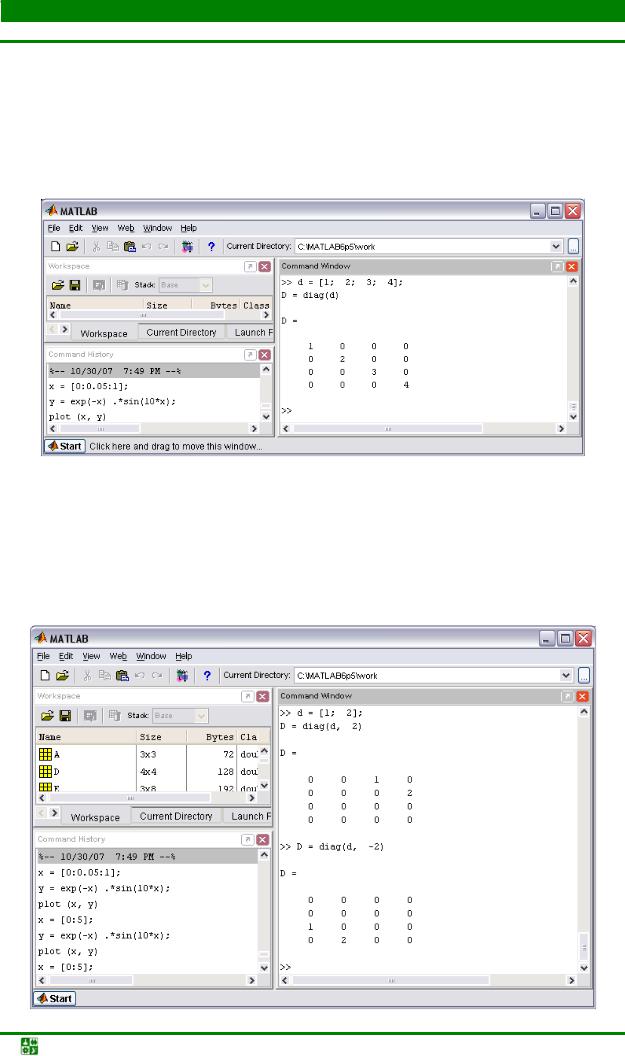
Один аргумент функций rand и randn приводит к формированию квадратных матриц – см. рис. 6.13.
Рис. 6.13
Вопрос об автоматическом заполнении векторов или вектор-строк не должен поставить нас в тупик, поскольку мы знаем что вектор или векторстрока в MatLab являются матрицей, у которой один из размеров равен единице. Заполните вектор-строку случайными числами.
Проверьте себя, выполнив следующий пример, – см. рис. 6.14.
|
Математическое программное обеспечение. Учебное пособие |
-64- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.3.Создание матриц специального вида
Рис. 6.14
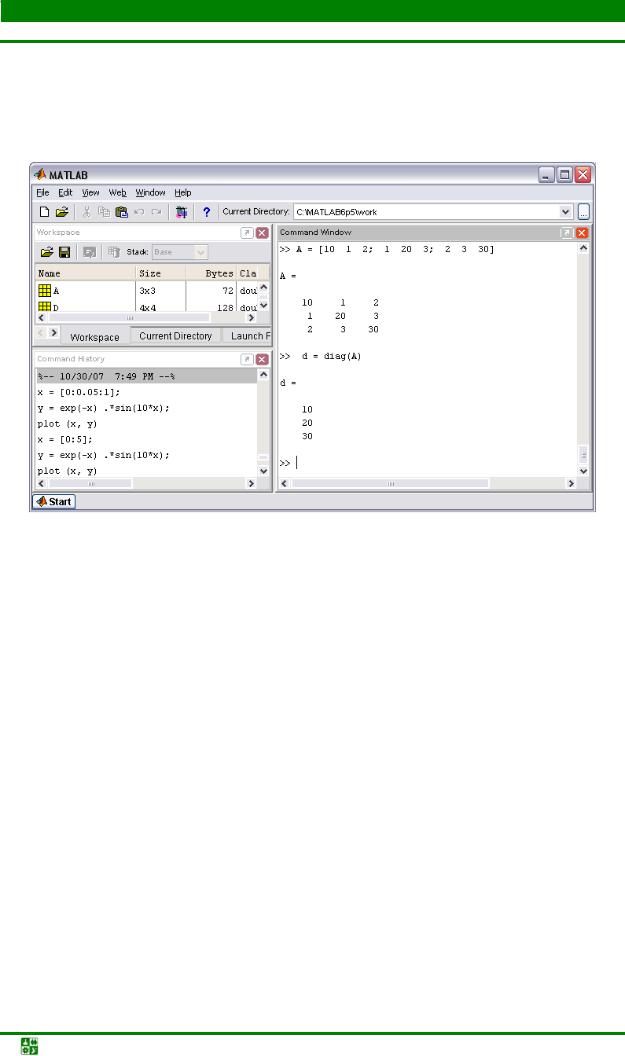
Часто возникает необходимость создания диагональных матриц, т. е. матриц, у которых все внедиагональные элементы равны нулю. Функция diag
формирует диагональную матрицу из вектора или вектор-строки, располагая их элементы по диагонали матрицы, – см. рис. 6.15.
Рис. 6.15
Для заполнения не главной, а побочной диагонали предусмотрена возможность вызова функцииdiag с двумя аргументами. В этом случае второй аргумент
означает, насколько побочная диагональ отстоит от главной, а его знак указывает на направление: плюс– вверх, минус – вниз от главной диагонали (рис. 6.16).
|
Математическое программное обеспечение. Учебное пособие |
-65- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.3.Создание матриц специального вида
Рис. 6.16
Функция diag служит и для выделения диагонали матрицы в вектор – см. рис. 6.17.
Рис. 6.17
Проделайте следующее упражнение для того, чтобы убедиться, что вы освоили автоматическое заполнение матриц, работу с блочными матрицами и запись данных в файл. Заполните и запишите в файлы матрицы следующее:
|
1 |
0 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
||||||||||||
|
0 |
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
||||||||||||
|
2 |
1 |
0 |
0 |
0 |
0 |
0 |
|||||||||||||||
|
0 |
0 |
1 |
0 |
0 |
2 |
2 |
2 |
2 |
2 |
||||||||||||
|
1 |
2 |
1 |
0 |
0 |
0 |
0 |
|||||||||||||||
|
0 |
0 |
0 |
1 |
0 |
2 |
2 |
2 |
2 |
2 |
0 |
1 |
2 |
1 |
0 |
0 |
0 |
|||||
|
M = |
0 |
0 |
0 |
0 |
1 |
2 |
2 |
2 |
2 |
2 |
, |
0 |
0 |
1 |
2 |
1 |
0 |
0 |
|||
|
G = |
. |
||||||||||||||||||||
|
3 |
3 |
3 |
3 |
3 |
− 4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
1 |
0 |
|||||
|
3 3 3 3 3 0 |
− 4 0 |
0 |
0 |
||||||||||||||||||
|
0 |
0 |
0 |
0 |
1 |
2 |
1 |
|||||||||||||||
|
3 |
3 |
3 |
3 |
3 |
0 |
0 |
− 4 0 |
0 |
|||||||||||||
|
3 |
3 |
3 |
3 |
3 |
0 |
0 |
0 |
− 4 0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
||||||
|
3 |
3 |
3 |
3 |
3 |
0 |
0 |
0 |
0 |
− 4 |
||||||||||||
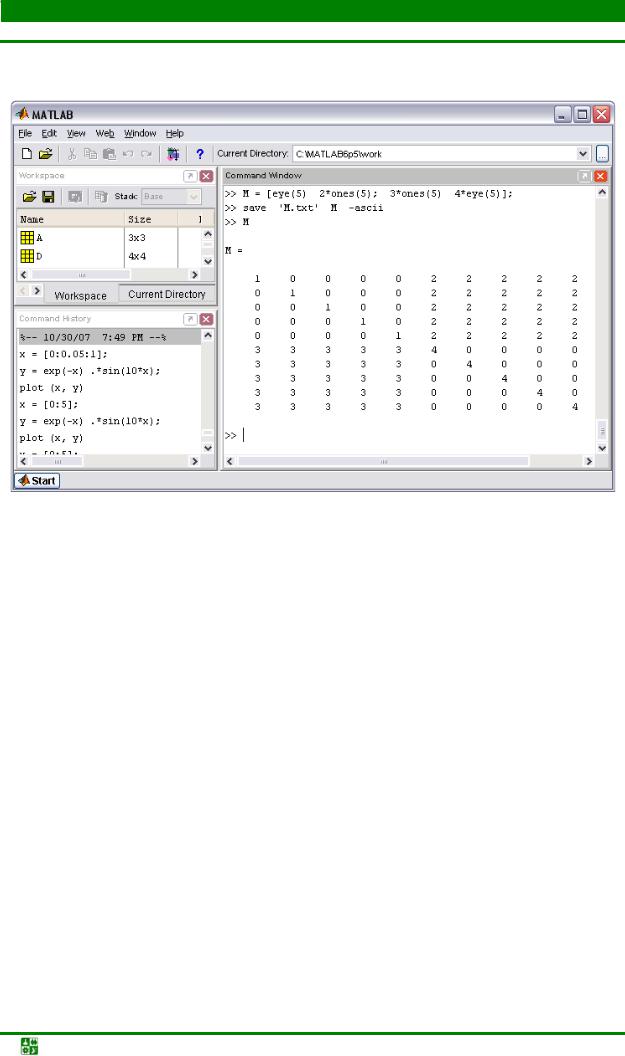
Матрицу М можно представить в виде блочной матрицы из четырех квадратных блоков размера пять, диагональные блоки формируются при помо-
|
Математическое программное обеспечение. Учебное пособие |
-66- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.3.Создание матриц специального вида
щи функцииeye, а внедиагональные – с использованиемones – см. рис. 6.18.
Рис. 6.18
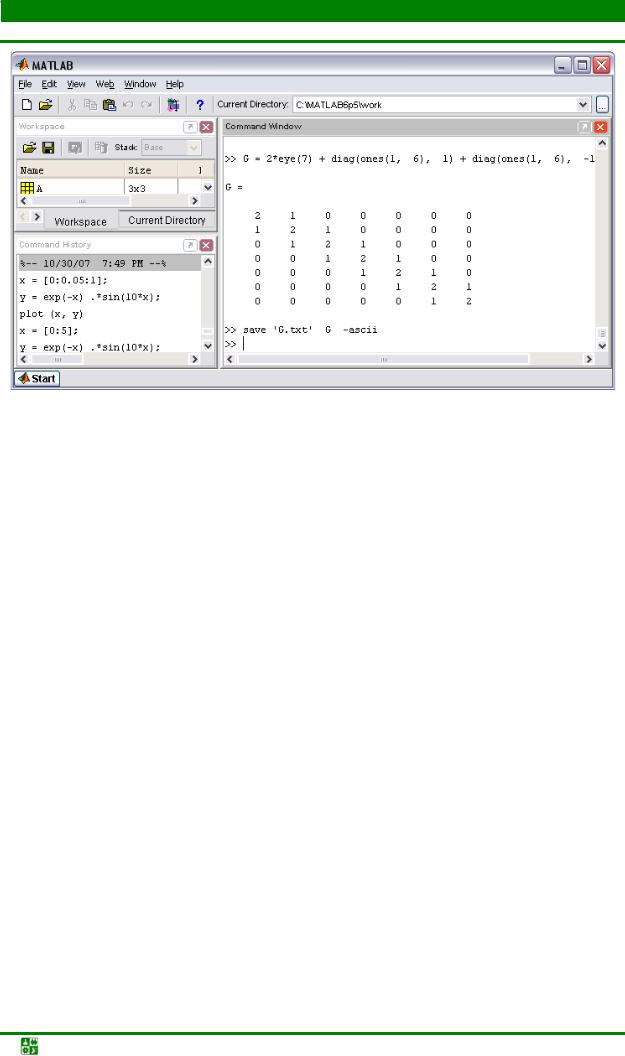
Квадратная матрица G размера семь является трехдиагональной. Заполняя эту матрицу, можно использовать то обстоятельство, что G является суммой диагональной матрицы и двух матриц с шестью ненулевыми элементами над и под главной диагональю (рис. 6.19).
|
Математическое программное обеспечение. Учебное пособие |
-67- |
6.БЛОЧНЫЕ МАТРИЦЫ
6.3.Создание матриц специального вида
Рис. 6.19
Посмотрите содержание полученных файлов (они должны находиться в подкаталоге work основного каталога MatLab). При больших размерах матриц бывает удобно получить ее представление в наглядном виде. В MatLab это можно проделать при помощи визуализации матриц. В следующем разделе разобраны простейшие способы визуализации матричных данных.
|
Математическое программное обеспечение. Учебное пособие |
-68- |
Соседние файлы в папке 3324_KT
- #
- #
- #
- #
Если разделить некоторую матрицу А на части вертикальными и горизонтальными прямыми, то получаются прямоугольные ячейки, являющиеся сами по себе матрицами. Эти ячейки называют блоками матрицы. Сама матрица А может рассматриваться как таблица, элементами которой являются более мелкие матрицы Mαβ: А = (Mαβ). При таком построении матрица А составляется из блоков, и поэтому ее называют блочной. Например, матрицу А разобьем на блоки
и обозначим их
Тогда матрицу А можно записать в виде блочной матрицы, элементами которой будут эти матрицы
Для составления блочной матрицы из серии матриц Mαβ необходимо, чтобы подмножества матриц из серии с одинаковым значением индекса α имели одинаковое количество строк, а под-множества матриц с одинаковым значением индекса β — одинаковое количество столбцов. Эти подмножества образуют соответственно » блочные » строки и » блочные » столбцы (соответству-ющие нескольким строкам или столбцам обычной записи матрицы).
Пример 10.11. Указанным требованиям удовлетворяют следующие четыре матрицы:
Поэтому из них можно составить блочную матрицу
Основное свойство блочных матриц состоит в том, что операции над блочными матрицами совершаются по тем же правилам, что и операции над обычными матрицами. В самом деле, это в достаточной степени очевидно для суммы матриц и произведения матрицы на число. Однако относительно суммы это можно утверждать лишь в том случае, когда размеры слагаемых блочных матриц, равно как и размеры отдельных блоков с равными индексами у слагаемых, совпадают.
Подробнее рассмотрим ситуацию с умножением блочных матриц. Пусть блочные матрицы А = (Аαβ) и В = (Bβγ) удовлетворяют двум условиям.
1. Число «блочных» столбцов матрицы А совпадает с числом «блочных » строк матрицы B (т.е. индекс β для А и B изменяется в одинаковых пределах).
2. Для любых индексов α, β, γ число столбцов у матрицы Aαβ совпадает с числом строк у матрицы Bβγ.
Тогда AB = (Cαγ), Cαγ = ΣβАαβВβγ. Для доказательства этого равенства достаточно
расписать обе его части через элементы матриц.
Указанные два условия довольно сложны, но все упрощается, если блоки матриц — это квадратные матрицы одного порядка. В этом случае условия близки к обычным: число » блочных » столбцов множимого должно совпадать с числом » блочных » строк множителя.
Представление матриц в блочном виде часто оказывается удобным при нахождении суммы и произведения, если матрицы имеют достаточно большие размеры, а их согласованные разбиения на блоки содержат нулевые, единичные, диагональные, треугольные матрицы.
Пример 10.12. Найдем произведения следующих блочных матриц предполагая, что все операции определены:
При транспонировании блочной матрицы транспонированию подлежат и ее элементы. Например,
Пример 10.13. Транспонируем блочную матрицу:
В математике , А матричный блок или распределяли матрица представляет собой матрицу , которая интерпретируется как будто они были разбиты на секции , называемые блоки или подматрицы . Интуитивно матрица, интерпретируемая как блочная матрица, может быть визуализирована как исходная матрица с набором горизонтальных и вертикальных линий, которые разбивают ее или разбивают на набор более мелких матриц. Любая матрица может быть интерпретирована как блочная матрица одним или несколькими способами, причем каждая интерпретация определяется тем, как ее строки и столбцы разделены.
Это понятие может быть более точным для по матрице путем разделения в коллекцию , а затем секционирования в коллекцию . Исходная матрица затем рассматривается как «сумма» этих групп в том смысле, что элемент исходной матрицы соответствует 1 к 1 некоторому смещению элемента some , где и .

Алгебра блочных матриц возникает, как правило, из двойных произведений в категориях матриц.
Пример
Блочная матрица размером 168 × 168 элементов с субматрицами 12 × 12, 12 × 24, 24 × 12 и 24 × 24. Ненулевые элементы выделены синим цветом, нулевые элементы — серым.
Матрица
можно разбить на четыре блока 2 × 2
Тогда разделенная матрица может быть записана как
Блочное умножение матриц
Можно использовать блочно-разбитое матричное произведение, которое включает только алгебру на подматрицах факторов. Однако разделение факторов не является произвольным и требует «согласованных разделов» между двумя матрицами и таким образом, чтобы были определены все продукты подматриц, которые будут использоваться. Учитывая матрицу с разделами строк и столбцов
и матрица с разделами строк и столбцов
совместимые с разбиениями , матричное произведение
может быть сформировано покадрово, получая в качестве матрицы с перегородками строк и разделами столбцов. Матрицы в итоговой матрице вычисляются путем умножения:
Или, используя нотацию Эйнштейна, которая неявно суммирует повторяющиеся индексы:
Обращение блочной матрицы
Для получения дополнительных сведений и вывода с использованием блочной декомпозиции LDU см. Дополнение Шура .
Если матрица разбита на четыре блока, ее можно поблочно инвертировать следующим образом:
где и D является квадратом произвольного размера, а В и С являются созвучны для разделения. Кроме того, A и дополнение Шура к A в P : P / A = D — CA −1 B должны быть обратимы.
Эквивалентно, переставляя блоки:
Здесь D и дополнение Шура к D в P : P / D = A — BD −1 C должны быть обратимы.
Если A и D оба обратимы, то:
Согласно тождеству Вайнштейна – Ароншайна одна из двух матриц в блочно-диагональной матрице обратима в точности тогда, когда другая обратима.
Определитель блочной матрицы
Приведенная выше формула для определителя -матрицы продолжает оставаться верной при соответствующих дополнительных предположениях для матрицы, состоящей из четырех подматриц . Самая простая такая формула, которую можно доказать с помощью формулы Лейбница или факторизации с использованием дополнения Шура , — это
Если это обратимый (и аналогично , если обратим), один имеет
Если — матрица, это упрощается до .
Если блоки представляют собой квадратные матрицы одинакового размера, дальнейшие формулы остаются в силе. Например, если и коммутируют (т. Е. ), То выполняется

Эта формула была обобщена для матриц, состоящих из более чем блоков, опять же при соответствующих условиях коммутативности между отдельными блоками.
Для и имеет место следующая формула (даже если и и B не коммутируют)
Блочно-диагональные матрицы
Блок — диагональная матрица представляет собой блок — матрица , которая представляет собой квадратную матрицу таким образом, что основные диагональных блоки квадратные матриц и все недиагональные блоки нулевых матриц. То есть блочно-диагональная матрица A имеет вид
где A k — квадратная матрица для всех k = 1, …, n . Другими словами, матрица является прямой суммой из A 1 , …, А п . Его также можно обозначить как A 1 ⊕ A 2 ⊕ … ⊕ A n или diag ( A 1 , A 2 , …, A n ) (последний — тот же формализм, который используется для диагональной матрицы ). Любую квадратную матрицу можно тривиально рассматривать как блочно-диагональную матрицу только с одним блоком.
Для определителя и следа выполняются следующие свойства
Блочно-диагональная матрица обратима тогда и только тогда, когда каждый из ее главных диагональных блоков обратим, и в этом случае ее обратная матрица является другой блочно-диагональной матрицей, заданной формулой
Собственные значения и собственные векторы просто те и и … и в сочетании.
Блочные трехдиагональные матрицы
Блок трехдиагональная матрица является еще специальный блок матрицы, который так же , как блок диагональной матрицы квадратной матрицы , имеющей квадратные матрицы (блоки) в нижней диагонали, главной диагонали и верхней диагонали, причем все остальные блоки быть нулевые матрицы. По сути, это трехдиагональная матрица, но вместо скаляров есть подматрицы. Блочная трехдиагональная матрица A имеет вид
где A k , B k и C k — квадратные подматрицы нижней, главной и верхней диагонали соответственно.
Блочные трехдиагональные матрицы часто встречаются при численном решении инженерных задач (например, вычислительной гидродинамики ). Доступны оптимизированные численные методы факторизации LU и, следовательно, эффективные алгоритмы решения для систем уравнений с блочной трехдиагональной матрицей в качестве матрицы коэффициентов. Алгоритм Томаса , используемый для эффективного решения систем уравнений , включающих трехдиагональную матрицу , также может быть применен с помощью матричных операций , чтобы блокировать трехдиагональные (смотрите также разложение Блока LU ).
Блочные матрицы Теплица
Блок Теплица матрица является еще специальным блоком матрицей, которая содержит блоки, которые повторяются вниз по диагонали матрицы, в качестве матрицы Теплицы имеет элементы повторяются вниз по диагонали. Отдельные элементы блочной матрицы Aij также должны быть тёплицевой матрицей.
Блочная теплицева матрица A имеет вид
Блокировать транспонирование
Специальная форма транспонирования матрицы также может быть определена для блочных матриц, когда отдельные блоки переупорядочиваются, но не транспонируются. Пусть будет блочная матрица с блоками , блок транспонированная является блок — матрица с блоками .
Как и в случае с обычным оператором трассировки, транспонирование блока представляет собой линейное отображение, такое что . Однако, как правило, это свойство не сохраняется, если только блоки и коммутируют.
Прямая сумма
Для любых произвольных матриц (размера м × п ) и B (размера р × д ), мы имеем прямую сумму в A и B , обозначаемое A B и определяются как

Например,
Эта операция естественным образом обобщается на массивы произвольных размеров (при условии, что A и B имеют одинаковое количество измерений).
Обратите внимание, что любой элемент в прямой сумме двух векторных пространств матриц может быть представлен как прямая сумма двух матриц.
Заявление
В терминах линейной алгебры использование блочной матрицы соответствует линейному отображению, которое мыслится в терминах соответствующих «пучков» базисных векторов . Это снова совпадает с идеей различения разложений на прямую сумму области и диапазона . Это всегда особенно важно, если блоком является нулевая матрица ; который несет информацию, которую слагаемое отображает в подсумму.
Учитывая интерпретацию с помощью линейных отображений и прямых сумм, существует специальный тип блочной матрицы, который встречается для квадратных матриц (случай m = n ). Для тех , мы можем предположить , интерпретацию как эндоморфизму в качестве п — мерного пространства V ; блочная структура, в которой группировка строк и столбцов одинакова, важна, потому что она соответствует наличию единственного разложения прямой суммы на V (а не двух). В этом случае, например, все диагональные блоки в очевидном смысле квадратные. Такая структура требуется для описания жордановой нормальной формы .
Этот метод используется для сокращения вычислений матриц, разложения столбцов на строки и многих приложений информатики , включая проектирование микросхем СБИС . Примером может служить алгоритм Штрассена для быстрого умножения матриц , а также кодирование Хэмминга (7,4) для обнаружения ошибок и восстановления при передаче данных.
Смотрите также
- Произведение Кронекера (матричное прямое произведение, приводящее к блочной матрице)
Заметки
Рекомендации
- Стрэнг, Гилберт (1999). «Лекция 3: Умножение и обратные матрицы» . Посуда открытого курса MIT. 18: 30–21: 10.