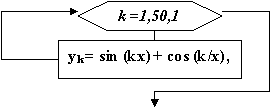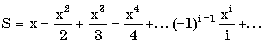При вычислении
суммы или произведения ряда чисел
пользуются соответствующими формулами.
ФОРМУЛА
СУММЫ
Si=Si-1+xi
Сумма равна
предыдущей сумме плюс аргумент. Начальная
сумма равна нулю. При нахождении
количества аргумент равен одному.
ФОРМУЛА
ПРОИЗВЕДЕНИЯ
Pi=Pi-1*xi
Произведение равно
предыдущему произведению, умноженному
на аргумент. Начальное произведение
всегда равно единице.
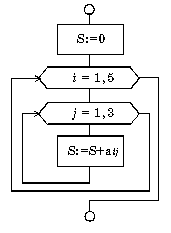
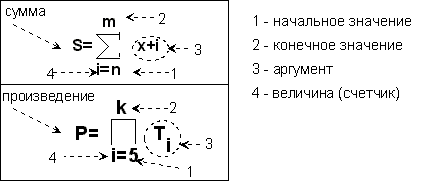
Математически
данные формулы записываются так (рис.
9.14).
Если в аргументе
около имени какой-нибудь величины стоит
индекс
счетчика,
то внутри цикла необходимо поставить
блок ввода этой величины.
Рис.
9. 14. Формулы для вычисления суммы и
произведения
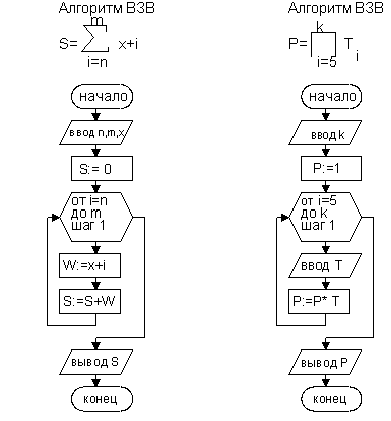
В качестве примера
рассмотрим блок-схемы алгоритмов для
приведенных на рис. 9.14 примеров.
9.3.1.4. Вложенные циклы
Возможны случаи,
когда внутри тела цикла необходимо
повторять некоторую последовательность
операторов, т. е. организовать внутренний
цикл. Такая структура получила название
цикла
в цикле
или вложенных
циклов.
Глубина вложения циклов (то есть
количество вложенных друг в друга
циклов) может быть различной.
Рис.
9. 15. Блок-схемы алгоритмов вычисления
суммы и произведения
При использовании
такой структуры для экономии машинного
времени необходимо выносить из внутреннего
цикла во внешний все операторы, которые
не зависят от параметра внутреннего
цикла.
Рассмотрим два
примера вычисления вложенных циклов.
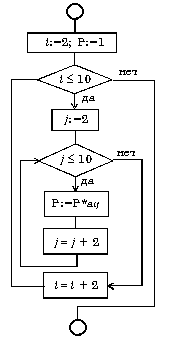
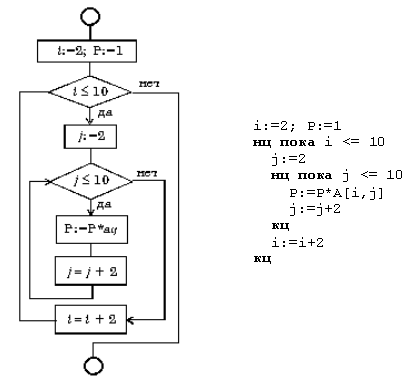
Рис.
9. 16. Вложенный цикл «до»
Вложенный
цикл «до»
Пример
Вычислите
произведение тех элементов заданной
матрицы A(10,10),
которые расположены на пересечении
четных строк и четных столбцов (рис.
9.16).
Вложенный
цикл «пока»
Рис.
9. 17. Вложенный цикл «пока»
Пример
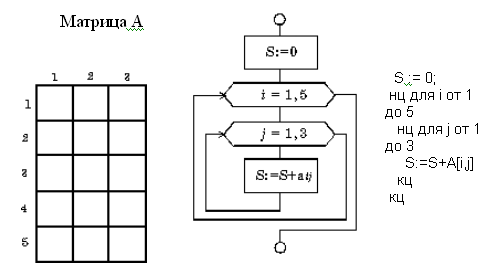
Вычислите сумму
элементов заданной матрицы А(5,3)
– рис. 9.17.
9.4. Языки программирования
9.4.1. Программный способ записи алгоритмов. Уровни языка программирования
При записи алгоритма
в словесной форме, в виде блок-схемы или
на псевдокоде допускается некоторый
произвол при изображении команд. Вместе
с тем такая запись точна настолько, что
позволяет человеку понять суть дела и
исполнить алгоритм.
Однако на практике
в качестве исполнителей алгоритмов
используются специальные автоматы —
компьютеры. Поэтому алгоритм,
предназначенный для исполнения на
компьютере, должен быть записан на
понятном ему языке. И здесь на первый
план выдвигается необходимость точной
записи команд, не оставляющей места для
произвольного толкования их исполнителем.
Следовательно,
язык для
записи алгоритмов должен быть формализован.
Такой язык принято называть языком
программирования,
а запись алгоритма на этом языке —
программой
для компьютера.
В настоящее время
в мире существует несколько сотен
реально используемых языков
программирования. Для каждого есть своя
область применения.
Любой алгоритм
есть последовательность предписаний,
выполнив которые можно за конечное
число шагов перейти от исходных данных
к результату. В зависимости от степени
детализации предписаний обычно
определяется уровень языка программирования
— чем меньше детализация, тем выше
уровень языка.
По этому критерию
можно выделить следующие уровни языков
программирования:
-
машинные;
-
машинно-оpиентиpованные
(ассемблеpы); -
машинно-независимые
(языки высокого уровня).
Машинные языки
и машинно-ориентированные языки —
это языки низкого
уровня,
требующие указания мелких деталей
процесса обработки данных. Языки же
высокого
уровня
имитируют естественные языки, используя
некоторые слова разговорного языка и
общепринятые математические символы.
Эти языки более удобны для человека.
Языки высокого
уровня делятся на:
-
Процедурные
(алгоритмические)
(Basic, Pascal, C и др.), которые предназначены
для однозначного описания алгоритмов;
для решения задачи процедурные языки
требуют в той или иной форме явно
записать процедуру ее решения. -
Логические
(Prolog, Lisp и др.), которые ориентированы
не на разработку алгоритма решения
задачи, а на систематическое и
формализованное описание задачи с тем,
чтобы решение следовало из составленного
описания. -
Объектно-ориентированные
(Object Pascal, C++, Java и др.), в основе которых
лежит понятие
объекта, сочетающего в себе данные и
действия над нами.
Программа на объектно-ориентированном
языке, решая некоторую задачу, по сути,
описывает часть мира, относящуюся к
этой задаче. Описание действительности
в форме системы взаимодействующих
объектов естественнее, чем в форме
взаимодействующих процедур.
При программировании
на машинном
языке программист может держать под
своим контролем каждую команду и каждую
ячейку памяти, использовать все
возможности имеющихся машинных операций.
Но процесс написания
программы на машинном языке очень
трудоемкий
и утомительный.
Программа получается громоздкой,
труднообозримой, ее трудно отлаживать,
изменять и развивать.
Поэтому в случае,
когда нужно
иметь эффективную программу,
в максимальной степени учитывающую
специфику конкретного компьютера,
вместо машинных языков используют
близкие к ним машинно-ориентированные
языки (ассемблеры)
или языки
высокого уровня.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Видеоурок 1: Разбор заданий ЕГЭ на алгоритмы
Видеоурок 2: Разбор задания ЕГЭ на циклы
Лекция: Построение алгоритмов и практические вычисления

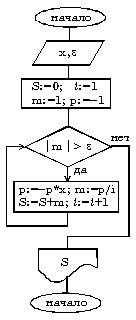
Составим блок-схему алгоритма вычисления суммы знакопеременного ряда:
с заданной точностью ε.
Необходимо представить алгоритм в виде псевдокода.
Для решения данной задачи используем обозначения:
S — частичная сумма ряда (стартовое значение равно 0);
ε — точность вычисления;
i — номер очередного слагаемого;
m — значение очередного слагаемого;
p — числитель очередного слагаемого.
Требуемая точность вычисления будет достигнута в случае, когда очередное слагаемое станет по абсолютной величине меньше ε. Составим блок-схему алгоритма:
На псевдокоде запись алгоритма будет выглядеть следующим образом:
алг Сумма (арг вещ х, ε рез вещ S)
дано l 0<х<1
надо l S=x-x2/2+x3/3+x4/4+…
нач цел i, вещ m, p
вводх, ε
S := 0; i :=1
m :=1; p := -1
нц покаabc(m)>ε
Р := -p*x
m := p/i
S := S+m
i := i+1
кц
вывод S
кон

Массивы – это множество элементов, значение которых относится к одному типу.
Все значения массива являются упорядоченными и имеют свой индекс.
Индекс позволяет присвоить элементу массива свое место.
Именно поэтому найти некий элемент в массиве можно с помощью его имени и индекса.
Максимальное количество элементов данного массива – это его размерность.
Если массив состоит из некоторого ряда элементов, то он называется векторным или одномерным, если же он состоит из нескольких рядов, то он называется матричным или многомерным массивом.
. В массиве а каждый элемент равен 0 или 1. Заменить все нули единицами и наоборот.
Решение. Достаточно одного оператора присваивания в теле цикла:
a[i] := 1 — a[i]
. В массиве каждый элемент равен 0,1 или 2. Переставить элементы массива так, чтобы сначала располагались все 0, затем все 1 и, наконец, все 2. Дополнительный массив не использовать.
Решение. Можно не переставлять элементы массива, а подсчитать количество 0,1,2 и заново заполнить массив требуемым образом.
алг Сумма (арг цел n, рез арг вещ таб А[1:n] )
дано l массив А содержит нули, единицы и двойки
надо l упорядочить массив по возрастанию
нач цел i, k1, k2
k1 := 0; k2 :=0
нц дляi от 1 до n
если А[i] =0
то k1 := k1+1; всё
если А[i] =1
то k2 := k2+1; всё
кц
нц дляi от 1 до k1
А[i] =0
кц
нц для i от k1+1 до k2+2
А[i] =1
кц
нц для i от k1+k2 до n
А[i] =2
кц
кон
. Даны два n-элементных массива x и Y одного типа. Поменять местами все xi и Yi, (i=1…n) не используя промежуточные величины.
Решение. Обмен можно выполнить в цикле для всех i от 1 до n с помощью серии из трех операторов присваивания:
x[i] := x[i] + y[i]
y[i] := x[i] — y[i]
x[i] := x[i] — y[i]
. Найти сумму элементов одномерного массива А(n).
Решение. Для суммирования положительных элементов массива вместо оператора S := S+А[i] необходимо записать:
если А[i]>0
то S := S+А[i]
всё
На псевдокоде алгоритм расчета суммы выглядит следующим образом:
алг Сумма (арг цел n, арг вещ таб А[1:n], рез вещ S )
дано l массив А
надо l найти сумму элементов массива
нач
цел i
S := 0
нц для i от 1 до n
S := S+А[i]
кц
кон
Действия над массивом
Данные в массиве можно искать или же сортировать.
Основным действием, которое производится над массивом, называется поиск.
Именно он лежит в основе множества других возможных манипуляций с массивами. В зависимости от того упорядочен массив или нет, поиск выполняется различным образом.
Если массив не упорядочен, то для поиска определенного элемента необходимо просмотреть каждое значение, имеющееся в массиве. Такой вид поиска называется линейным. Если же массив упорядочен, то используют метод половинного деления или бинарный.
Сортировка – это действие, которое приводит к изменению положения элементов в заданном массиве, согласно поставленным условиям.
Сортировка производится перед поиском для более быстрого его завершения.
Существует большое разнообразие способов сортировки. Давайте рассмотрим некоторые из них:
1. Сортировка с помощью обмена
Данный способ сортировки предусматривает сравнение элемента с соседними и в случае необходимости смена их местами. Подобные перемещения элементов массива относительно друг друга производятся до тех пор, пока массив не будет упорядочен. В литературе данный метод можно так же встретить под названием «метод пузырьков» или «пузырьковая сортировка». Элементы в массиве передвигаются на свое место подобно пузырькам, которые поднимается на высоту, согласно собственному размеру.
Пример сортировки массива с помощью псевдокода:
алг Обменная_сортировка (арг цел n, арг рез вещ таб А[1:n] )
дано l А — массив размерности n
надо l упорядочить массив по возрастанию
нач
цел i, j
вещ Tmp
нц дляiот2доn
нц дляjотnдо1
еслиА[j]<А[j-1]
тоTmp :=А[j]; А[j] :=А[j-1];
А[j-1] :=Tmp
всё
кц
кц
кон
2. Метод сортировки прямым включением
В данном случае все элементы делятся на два массива – один уже отсортированный, а второй произвольный. Постепенно из неотсортированного массива берется элемент и вставляется на свое место в отсортированный массив. То есть программа ищет позицию необходимого элемента и вставляет его. Следует помнить, что это приводит к сдвигу всех остальных элементов.
Пример алгоритма методом сортировки прямым включением:
алг Сортировка_вставкой (арг цел n, арг рез вещ таб А[1:n] )
дано l А — массив размерности n
надо l упорядочить массив по возрастанию
нач
цел i, j
вещ Tmp
нц дляiот2доn
Tmp :=А[j]; j :=i-1;
нц покаj>= 1 и А[j]>Tmp
А[j+1] :=А[j]
j :=i-1
кц
А[j+1] :=Tmp
кц
кон
3. Метод сортировки прямым выбором
Данный способ заключается в поиске элемента, который будет самым большим (меньшим), после чего он ставится в начало массива. И так до тех пор, пока сортировка не будет выполнена полностью.
Пример алгоритма сортировки методом прямого выбора:
алг Сортировка_выбором (арг цел n, арг рез вещ таб А[1:n] )
дано l А — массив размерности n
надо l упорядочить массив по возрастанию
нач
цел i, k
вещ Min
нц дляiот1доn-1
Min :=А[j]; k :=i
нц дляj от i+1 до n
еслиMin > А[j]
тоMin :=А[j]; k :=j
всё
кц
А[k] :=А[i]; А[i] :=Min
кц
кон

Подпрограмма – это готовый алгоритм, который можно использовать многократно в различных программах.
Подпрограммы включают в основной алгоритм более сложной программы. Они делятся на функции и процедуры.
Функция — выражение, используемое для вычислений, которому присваивается идентификатор функции.
Процедура – это некое действие, которое не позволяет вернуть исходное значение переменных.
Подпрограммы делятся на стандартные и пользовательские.
Стандартные программы изначально встроены в язык программирования, который вы используете. Их еще называют встроенными.
Любой язык программирования имеет библиотеки, в которых изначально забиты стандартные программы, пользоваться которыми можно с помощью идентификатора.
Если же некая стандартная программа была написана вами, и вы сохраняете её в библиотеку, то она называется пользовательской.
2.1 Разработка алгоритма.
2.2 Блок-схема.
2.3 Структуры алгоритмов.
2.1 Разработка алгоритма.
Алгоритм — это
a. описание последовательности действий для решения задачи или достижения поставленной цели;
b. правила выполнения основных операций обработки данных;
c. описание вычислений по математическим формулам.
Перед началом разработки алгоритма необходимо четко уяснить задачу: что требуется получить в качестве результата, какие исходные данные необходимы и какие имеются в наличии, какие существуют ограничения на эти данные. Далее требуется записать, какие действия необходимо предпринять для получения из исходных данных требуемого результата.
На практике наиболее распространены следующие формы представления алгоритмов:




Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.
Пример. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел.
Алгоритм может быть следующим:
1. задать два числа;
2. если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
3. определить большее из чисел;
4. заменить большее из чисел разностью большего и меньшего из чисел;
5. повторить алгоритм с шага 2.
Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Убедитесь в этом самостоятельно, определив с помощью этого алгоритма наибольший общий делитель чисел 125 и 75.
Словесный способ не имеет широкого распространения по следующим причинам:



Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой.
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.
Он занимает промежуточное место между естественным и формальным языками.
С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.
2.2 Блок-схема.
Блок-схемой называют графическое представление алгоритма, в котором он изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.
Приведем наиболее часто употребляемые символы.
| Название символа | Обозначение и пример заполнения | Пояснение |
| Процесс | Вычислительное действие или последовательность действий | |
| Решение |  |
Проверка условий |
| Модификация | 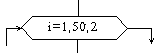 |
Начало цикла |
| Предопределенный процесс |  |
Вычисления по подпрограмме, стандартной подпрограмме |
| Ввод-вывод | 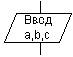 |
Ввод-вывод в общем виде |
| Пуск-останов |  |
Начало, конец алгоритма, вход и выход в подпрограмму |
| Документ |  |
Вывод результатов на печать |
Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Блок «решение» используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок «модификация» используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок «предопределенный процесс» используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
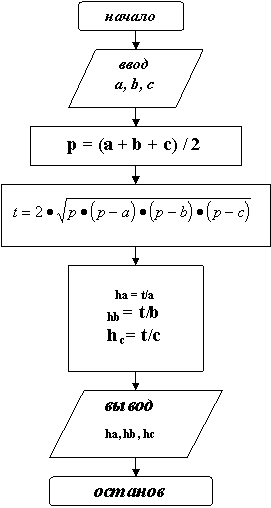
Пример. Составить блок-схему алгоритма определения высот ha, hb, hc треугольника со сторонами a, b, c, если
где p = (a + b + c) / 2.
Решение. Введем обозначение 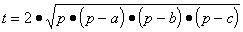
2.3 Структуры алгоритмов.
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых (т.е. основных) элементов. Естественно, что при таком подходе к алгоритмам изучение основных принципов их конструирования должно начинаться с изучения этих базовых элементов
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.
Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.
1. Базовая структура следование. Образуется из последовательности действий, следующих одно за другим:
2. Базовая структура ветвление. Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.
Структура ветвление существует в четырех основных вариантах:




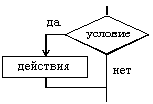
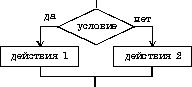
1) если-то если условие то действия конец если2) если-то-иначе если условие то действия 1 иначе действия 2 конец если
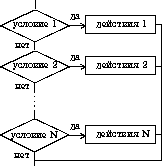
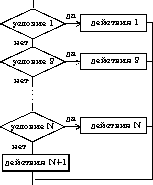
3) выбор выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N конец выбора
4) выбор-иначе выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N иначе действия N+1 конец выбора

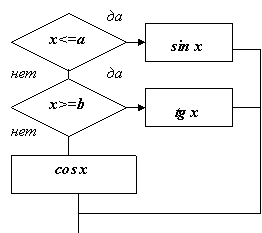
Пример. Составить блок-схему алгоритма вычисления функции
Базовая структура цикл. Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.
Структура цикл существует в трех основных вариантах:
Цикл типа для.
Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне.
Цикл типа пока.
Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока.
Цикл типа делать — пока.
Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока. Условие проверяется после выполнения тела цикла.
Заметим, что циклы для и пока называют также циклами с предпроверкой условия а циклы делать — пока — циклами с постпроверкой условия. Иными словами, тела циклов для и пока могут не выполниться ни разу, если условие окончания цикла изначально не верно. Тело цикла делать — пока выполнится как минимум один раз, даже если условие окончания цикла изначально не верно.
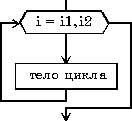
цикл для i от i1 до i2 шаг i3 тело цикла (последовательность действий) конец циклацикл пока условие тело цикла (последовательность действий) конец цикла
цикл делать тело цикла (последовательность действий) пока условие конец цикла

Пример. Составить блок-схему алгоритма вычисления функции
yk = sin (kx) + cos (k/x), k = 1, 2, …, 50
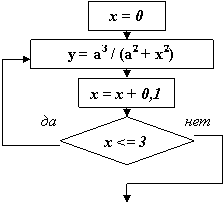
Пример. Составить блок-схему вычисления функции
y = a3 / (a2 + x2)
при x, изменяющимся от x = 0 до x = 3 с шагом Dx = 0,1
Итерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия.
На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата.
Пример. Составить алгоритм вычисления суммы ряда
с заданной точностью (для данного знакочередующегося степенного ряда требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше).
Вычисление сумм — типичная циклическая задача. Особенностью же нашей конкретной задачи является то, что число слагаемых (а, следовательно, и число повторений тела цикла) заранее неизвестно. Поэтому выполнение цикла должно завершиться в момент достижения требуемой точности.
При составлении алгоритма нужно учесть, что знаки слагаемых чередуются и степень числа х в числителях слагаемых возрастает.
Решая эту задачу «в лоб» путем вычисления на каждом i-ом шаге частичной суммы
S:=S+(-1)**(i-1)*x**i/i ,
мы получим очень неэффективный алгоритм, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления следующим образом: если обозначить числитель какого-либо слагаемого буквой р, то у следующего слагаемого числитель будет равен -р*х (знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m
будет равно p/i, где i — номер слагаемого.
Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т.е. не будет выполняться основное свойство алгоритма — результативность.
Вложенные циклы.
Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.
При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.
Пример вложенных циклов для. Вычислить сумму элементов заданной матрицы А(5,3).
Пример вложенных циклов пока. Вычислить произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов.
«Универсальная» блок-схема и 3 типовых алгоритма 
Дважды за день заходила речь об одном и том же, да и жаль выкидывать пару картинок, могут ещё понадобиться. Речь шла об изображении базовых типовых алгоритмов, связанных с расчётом какой-либо элементарной характеристики последовательности (массива) — суммы, количества, произведения, максимума, минимума и т.п.
В картинках не показаны «начало» и «конец», только содержательная часть.
ГОСТовские «перевёртыши» на практике крайне неудобны, классическое изображение с помощью «ромбика» часто сбивает начинающих с толку похожестью на обычное ветвление (плюс они забывают делать шаг в конце тела цикла),
а вот значок «цикла с параметром», если отказаться от паскалевского шага, непременно равного единице, удобен и нормально воспринимается.
I Алгоритм табулирования (составление списка или таблицы)
Алгоритм табулирования (составление списка или таблицы)
Что писать в фигурках вместо цифр?
1. Примем, что управляющая переменная цикла называется x, а здесь зададим её начальное (x1) и конечное (x2) значения, а также шаг изменения dx. Это можно записать присваиванием x1=0,x2=1,dx=0.1 или поставить вместо прямоугольника параллелограмм (оператор ввода) с подписью «ввод x1,x2,dx«;
2. Обычно внутри значка «цикл с параметром» (цикл, пределы изменения и шаг управляющей переменной которого известны) пишут что-то вроде псевдокода: «для x от x1 до x2 шаг dx» или то же самое в форме x=x1,x1+dx..x2 или просто x=x1,x2,dx ;
3. Для очередного x вычислить y=f(x). Этот шаг может включать несколько действий и предполагать вставку дополнительных блоков «расчёт» или условных операторов;
4. Вывести строку таблицы: вывод x, f(x)
II. Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности
Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности
Вместо цифр в элементах блок-схему указываем:
1. Для каждой искомой величины задать по переменной и присвоить ей начальные значения: сумме s=0, количеству k=0, произведению p=1 (на самом деле, это не совсем корректно, но для обсуждаемого уровня сойдёт);
2. Выполняется как в задаче I;
3. Считаем очередной элемент последовательности y=f(x), с тем же замечанием, что к задаче I;
4-5. Если y отвечает условию задачи (проверка на шаге 4), сумма на шаге 5 ищется в виде s=s+f(x), количество в виде k=k+1, произведение в виде p=p*f(x). При нескольких искомых величинах блок вида 4-5 может повторяться несколько раз;
6. По выходе из цикла выводим найденную величину или величины.
III. Алгоритм поиска максимума или минимума
Блок схема задачи II годится и для этого случая.
1. Для каждого максимума или минимума задать по переменной (примем, что минимум обозначен min, а максимум — max) и присвоить каждой переменной начальные значения: максимуму – заведомо малое значение (например, -1030, оператор будет иметь вид Max=-1030) или первый элемент последовательности (массива); минимуму присвоить заведомо большое значение (например, 1030) или первый элемент последовательности;
2-3. Выполняются как в задачах I-II, с теми же замечаниями.
4-5. Для поиска максимума проверяется условие 4 f(x)>max, выполняется действие 5 вида max=f(x), дли минимума проверяется условие 4 f(x)<min и выполняется действие 5 вида min=f(x). С чем сравнивали max или min, то им и присваиваем.Могут понадобиться дополнительные условия, связанные логической операцией «И» либо «ИЛИ» с основным, например, поиск максимального из отрицательных элементов предполагает проверку y<0 and y>max;
6. По выходе из цикла выводим найденную величину или величины.
Несмотря на обилие средств для рисования блок-схем, удобнее простого Paint из Win7 и выше для этой цели ничего пока не придумали 
IV. Схема ввода и обработки элементов одномерного массива
Как правило, ввод, обработка или вывод одномерного массива (вектора, списка) выполняется поэлементно с помощью цикла с параметром (цикла «for»). Счётчиком цикла служит номер элемента в массиве (обычно применяется нумерация с единицы). Ниже показаны ввод и обработка массива x из 6 элементов.
Схема ввода и обработки элементов одномерного массива
V. Реализация алгоритма в кратных (вложенных) циклах
Основное отличие – все действия над матрицей (таблицей) выполняются поэлементно в двойном цикле следующего вида:
Блок-схема двойного цикла с параметром
Здесь показан ввод матрицы A из 6 строк и 4 столбцов, а счётчиками внешнего и внутреннего цикла с параметром служат номера строки (i) и столбца (j) в матрице. Обработка и вывод элементов матрицы могут быть реализованы аналогичными конструкциями, часто, если элементы обрабатываются последовательно и независимо друг от друга, ввод и обработку или обработку и вывод можно объединить.
31.10.2016, 21:46 [10922 просмотра]
Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.
Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.
При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.
В процессе разработки алгоритма решения задачи можно выделить следующие этапы:
- Этап 1 . Математическое описание решения задачи.
- Этап 2 . Определение входных и выходных данных.
- Этап 3 . Разработка алгоритма решения задачи.
Базовые алгоритмические конструкции
В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:
- следование (линейный алгоритм);
- ветвление (разветвляющийся алгоритм);
- цикл-пока (циклический алгоритм).
Линейные алгоритмы
Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.
Пример
ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.
На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:
Этап 1. Математическое описание решения задачи.
Математическим решением задачи является известная формула:
,
где с-длина гипотенузы, a, b – длины катетов.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.
Этап 3. Разработка алгоритма решения задачи.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма. |
Разветвляющиеся алгоритмы
Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.
Пример
ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.
Этап 1. Математическое описание решения задачи.
Из курса математики известно, если x > y, то наибольшее число x, если x < y, то наибольшее число y, если x = y, то число x равно числу y.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения чисел x и y. Выходным данными являются:
- наибольшее число
- любое из чисел, если числа равны
Для решения задачи нам необходимо знать значения x и y.
Этап 3. Разработка алгоритма решения задачи.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
|
В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма
В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:
- первая: это элементы 1, 2, 3, 4, 8.
- вторая: это элементы 1, 2, 3, 5, 6, 8
- третья: это элементы 1, 2, 3, 5, 7, 8.
Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.
Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.
Циклические алгоритмы
Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.
Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.
При разработке алгоритма циклической структуры выделяют следующие понятия:
- параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
- начальное и конечное значения параметров цикла;
- шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.
Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.
В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:
- начальные значения цикла;
- конечные значения цикла;
- шаг цикла.
В тело цикла входят:
- многократно повторяющиеся действия для вычисления искомых величин;
- подготовка следующего значения параметра цикла;
- подготовка других значений, необходимых для повторного выполнения действий в теле цикла.
В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.
Пример
ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.
Этап 1. Математическое описание решения задачи.
Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:
где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.
Этап 2. Определение входных и выходных данных.
Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.
Выходные данные – значение суммы членов последовательности натуральных чисел.
Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.
Подготовка цикла заключается в задании начального и конечного значений параметра цикла.
- начальное значение параметра цикла равно 1,
- конечное значение параметра цикла равно n,
- шаг цикла равен 1.
Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.
Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:
S=S+i; I=I+1;
Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.
Этап 3. Разработка алгоритма решения задачи.
Введем обозначения: S – сумма последовательности, i – значение натурального числа.
Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма. Номера элементов соответствуют номерам шагов словесного описания алгоритма. |



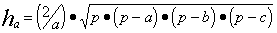
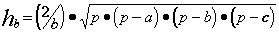
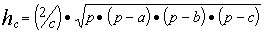

 2) если-то-иначе
если условие
то действия 1
иначе действия 2
конец если
2) если-то-иначе
если условие
то действия 1
иначе действия 2
конец если
 3) выбор
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
конец выбора
3) выбор
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
конец выбора
 4) выбор-иначе
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
иначе действия N+1
конец выбора
4) выбор-иначе
выбор
при условие 1: действия 1
при условие 2: действия 2
. . . . . . . . . . . .
при условие N: действия N
иначе действия N+1
конец выбора

 цикл пока условие
тело цикла (последовательность действий)
конец цикла
цикл пока условие
тело цикла (последовательность действий)
конец цикла
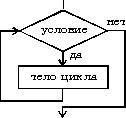 цикл делать
тело цикла (последовательность действий)
пока условие
конец цикла
цикл делать
тело цикла (последовательность действий)
пока условие
конец цикла