Часто при решении задач приходится повторять выполнение операций по одним и тем же зависимостям при различных значениях входящих в них переменных и производить многократный проход по одним и тем же участкам алгоритма. Такие участки называются циклами. Алгоритмы, содержащие циклы, называется циклическими. Использование циклов существенно сокращает объем алгоритма.
Различают циклы с наперед известным и наперед неизвестным количеством проходов.
Пример 1. Рассмотрим пример алгоритма с циклом, имеющим наперед неизвестное количество проходов. Для этого решим следующую задачу. Указать наименьшее количество членов ряда натуральных чисел 1, 2, 3, …, сумма которых больше числа К.
Блок-схема алгоритма решения этой задачи приведена на рисунке 1. Она состоит из восьми блоков.
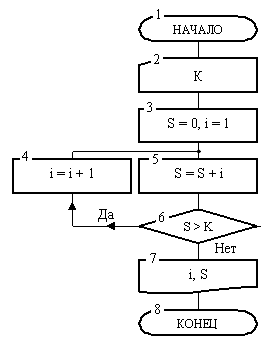
После начала работы в блоке 2 вводится значение числа К. Далее в блоке 3 переменная i получает значение 1, т. е. значение, с которого начнется отсчет натуральных чисел. Переменная S, предназначенная для накопления сумма этих чисел, перед началом суммирования получает значение 0. После этого управление передается блоку 5.
В нем при выполнении команды S = S + i производится сложение содержимого ячеек S и i, а результат записывается в ячейку S. Поскольку до операции сложения было S = 0, i = 1, то после операции будет S = 1. При записи нового значения старое содержимое ячейки S (нуль) стирается, а на его место записывается число 1.
Нужно обратить внимание на то, что если бы до этой операции в блоке 3 не была выполнена команда S = 0 (записать нуль в ячейку S ), то при нахождении суммы S + 1 возникла бы ошибка, поскольку из ячейки S была бы извлечена константа, которая оказалась там после распределения памяти.
После суммирования первого члена последовательности в блоке 6 выполняется проверка условия о превышении суммы S заданного числа К.
Если условие 6 не выполнится, то производится переход к блоку 4, где при выполнении операции значение переменной увеличивается на 1 и становится равным 2. Теперь алгоритм вновь вернется к блоку 5 и к старому значении суммы добавит новый член 2. После этого сумма станет равной 3. В блоке б вновь проверяется условие получения требуемой суммы и т. д. Цепочка блоков 5-4 будет обрабатываться вновь и вновь до того момента, когда однажды при определенном значении переменной i, наконец, выполнится условие S > К, т. е. когда накапливаемая в таком цикле сумма впервые превысит заданное значение К. Переменная i, значение которой при очередном проходе цепочки этих блоков увеличивается на 1, играет роль счетчика этого цикла.
Далее производится переход к блоку 7, где отпечатается значение количества членов ряда (извлечено и отпечатано число из ячейки i, которое там хранится в момент выполнения условия), суммы S и в блоке 8 алгоритм закончит работу.
Пример 2. Теперь приведем пример алгоритма, содержащего цикл с наперед известным количеством проходов (повторений). Алгоритм решает задачу накопления суммы положительных элементов одномерного массива Z длины N ( под длиной массива понимается количество его элементов ). Блок-схема алгоритма дана на рисунке 2.
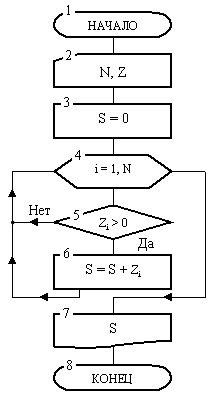
Вначале в блоке 2 производится ввод двух переменных N и Z. Первая из них представляет одну ячейку. В нее записывается одна константа – число, равное количеству элементов массива Z. Именно такое количество ячеек объединяет другая переменная – Z.
Следует подчеркнуть, что если бы ввод этих переменных в блоке 2 производился в противоположном порядке, то это привело бы к ошибке. Действительно, невозможно заполнить N ячеек массива Z, когда самое N еще не известно (оно будет введено позже Z). Далее в блоке 3 переменной S присвоено начальное значение 0. Это сделано для того, чтобы приготовить ячейку к дальнейшему накоплению необходимой суммы.
Блоки 4-6 представляет собой сам цикл, в котором накапливается сумма.
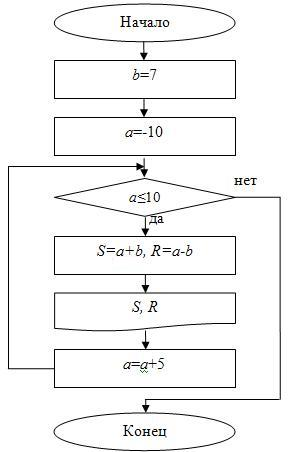
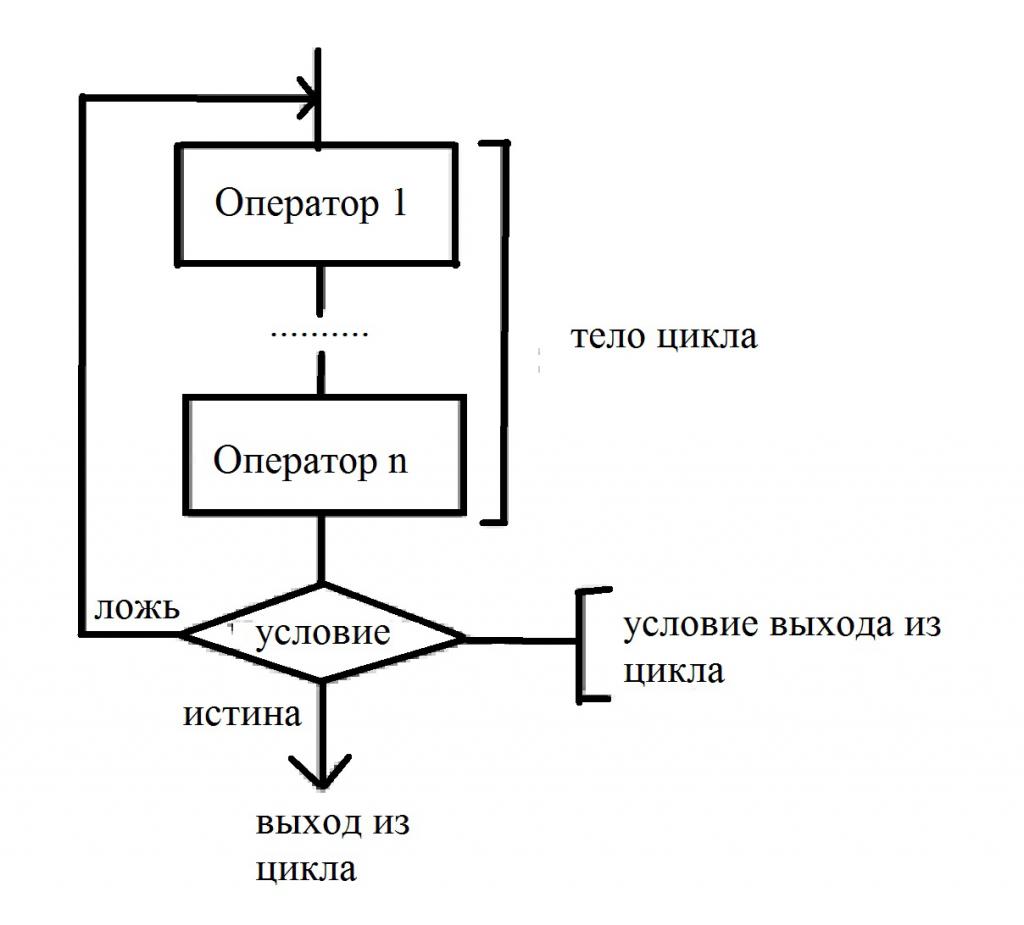
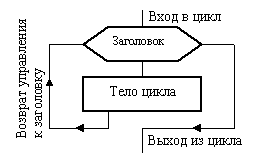
Для того чтобы понять, как функционирует не только этот, а и любой другой цикл, обратимся к рисункам 3 и 4. На них показана общая структура цикла и его важнейшие параметры.
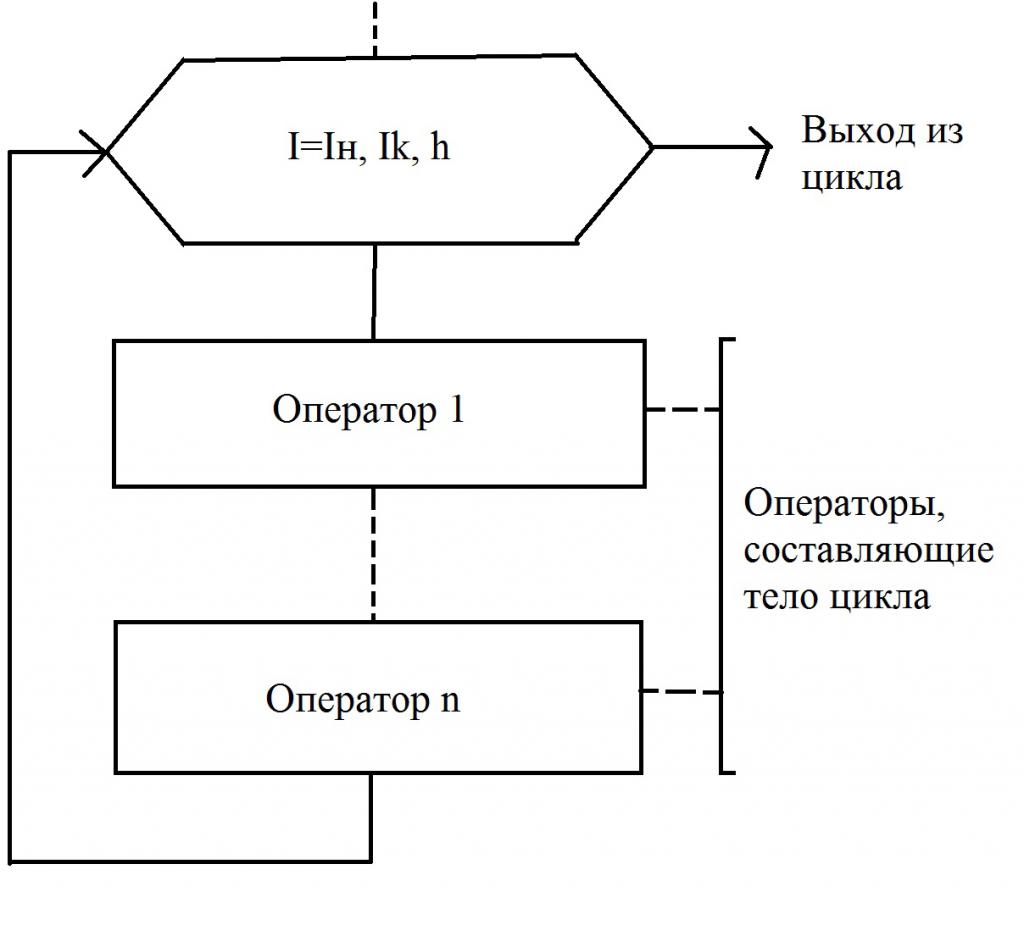
Как видно из рисунка 3, цикл состоит из заголовка и тела. Всякий цикл обязательно имеет свой счетчик.
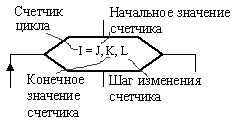
На рисунке 4, где показана структура и параметры заголовка цикла, роль такого счетчика выполняет переменная i.
Внутри заголовка после счетчика и символа «=» через запятую указывает начальное и конечное значения счетчика и шаг его изменения (на рисунке 4 их роль выполняют переменные j, k, l соответственно). Если значение шага l = l, то его можно не указывать.
Сначала производится вход в цикл. После этого начинается его выполнение.
Внутри заголовка счетчику первоначально присваивается значение i = j. Затем выполняется блоки, образующие тело цикла. Обработка блоков внутри цикла производится по часовой стрелке. В результате после первого выполнения тела цикла управление вновь передается заголовку. Здесь к текущему значению счетчика добавится шаг. Теперь, если новое значение счетчика не вышло за свои пределы (т. е. не стало больше своего конечного значения при положительном шаге или меньше конечного значения – при отрицательном шаге), то снова выполняется тело цикла, вновь после возврата к заголовку к счетчику добавляется шаг. Так цикл будет выполняться до тех пор, пока значение счетчика однажды не выйдет за предписанный предел. Как только такой предел будет преодолен, произойдет выход из цикла и управление будет передано блоку, который следует сразу за циклом.
Вернемся к блок-схеме рис. 2. Заголовок ее цикла представлен блоком 4. Роль счетчика цикла играет переменная i, которая должна в цикле изменяться от 1 до N. Поскольку шаг явно не указан, то по умолчанию он подразумевается равным 1. Тело цикла образуют блоки 5 и 6.
Сразу после входа в цикл переменная i примет начальное значение i = 1. Далее в блоке 5 выполняется проверка положительности первого элемента массива Z (т. к. i = 1). Если этот элемент действительно положителен, то в блоке б он будет добавлен к переменной S, после чего выполняется возврат к заголовку цикла. Если этот элемент не положителен (т. е. нуль или отрицательный), то будет выполнен переход сразу к заголовку цикла, минуя блок суммирования 6.
На втором круге цикла счетчик i в заголовке увеличится на 1 и станет равным 2. Теперь, при новом выполнении тела цикла, в блоке 5 проверяется на положительность второй элемент массива Z и, если он положителен, то добавляется в сумму и т. д. Последний раз тело цикла выполнится при i = N. При этом значении счетчика проверяется последний элемент массива. Наконец, в заголовке цикла i примет значение N+1. Это значение выходит за предписанный предел, следовательно, произойдет выход из цикла и управление перейдет блоку 7. В этом блоке выводится накопленная сумма и алгоритм закончит работу.
Занятие 4. Графическая реализация циклического алгоритма
В рассмотрении циклического алгоритма следует выделить несколько понятий.
Тело цикла – это набор инструкций, предназначенный для многократного выполнения.
Итерация – это единичное выполнение тела цикла.
Переменная цикла – это величина, изменяющаяся на каждой итерации цикла.
Каждый цикл должен содержать следующие необходимые элементы:
- первоначальное задание переменной цикла,
- проверку условия,
- выполнение тела цикла,
- изменение переменной цикла.
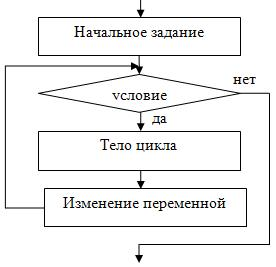
Циклы бывают двух видов – с предусловием и с постусловием. В цикле с предусловием сначала проверяется условие входа в цикл, а затем выполняется тело цикла, если условие верно. Цикл с предусловием представлен на рис. 2.9. Цикл с предусловием также может быть задан с помощью счетчика. Это удобно в тех случаях, когда точно известно количество итераций. В общем виде блок-схема, реализующая цикл с предусловием, представлена ниже. Сначала задается начальное значение переменной цикла, затем условие входа в цикл, тело цикла и изменение переменной цикла. Выход из цикла осуществляется в момент проверки условия входа в цикл, когда оно не выполняется, т.е. условие ложно. Цикл с предусловием может ни разу не выполниться, если при первой проверке условия входа в цикл оно оказывается ложным.
Рис.
2.9.
Циклический алгоритм с предусловием в общем виде
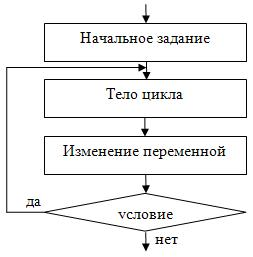
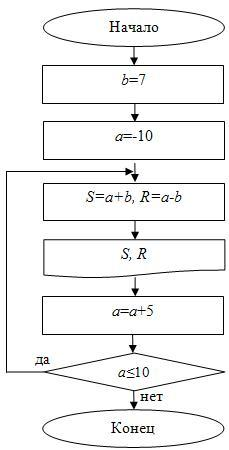
В цикле с постусловием сначала выполняется тело цикла, а потом проверяется условие. Циклический алгоритм с постусловием представлен на рис. 2.10.
Рис.
2.10.
Циклический алгоритм с постусловием в общем виде
Если условие верно, то итерация повторяется, если же неверно, то осуществляется выход из цикла. В отличие от цикла с предусловием, любой цикл с постусловием всегда выполнится хоть раз.
Примечание. Как видно из представленных блок-схем для циклов с предусловием и постусловием, условие записывается внутри блока условия (формы ромба), как и в разветвляющемся алгоритме. Принципиальная разница между разветвляющимся и циклическим алгоритмами при графической реализации состоит в том, что в циклическом алгоритме в обязательном порядке присутствует стрелка, идущая наверх. Именно эта стрелка обеспечивает многократный повтор тела цикла.
Приведем простейшие примеры, соответствующие циклическому алгоритму.
Пример 7. Вася звонит Пете, но у Пети может быть занята линия. Составить блок-схему действий Васи в этом случае.
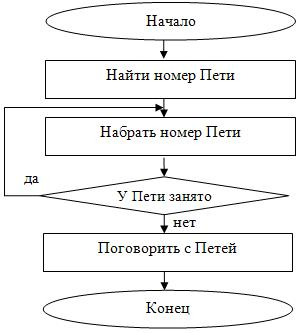
Решение. Когда телефонная линия занята, то необходимо снова и снова набирать номер, пока Петя не закончит предыдущий разговор, и телефонная линия не окажется вновь свободной. Блок-схема представлена на рис. 2.11.
Рис.
2.11.
Блок-схема для примера 7
Здесь тело цикла состоит из одного действия «Набрать номер Пети», т.к. именно это действие следует повторять, пока линия будет занята. Под итерацией цикла понимается очередная попытка дозвониться до Пети. Как таковой переменной цикла здесь нет, т.к. ситуация взята из жизни. Выход из цикла происходит в тот момент, когда условие «У Пети занято» стало неверным, т.е. телефонная линия свободна – действительно, нет необходимости больше набирать номер Пети. В данном примере применен цикл с постусловием, т.к. сначала необходимо набрать номер Пети, ведь иначе мы не можем ответить на вопрос – занята ли линия у Пети.
Пример 8. Ученику требуется купить учебник. Составить блок-схему, описывающую действия ученика в случае, если учебника нет в ряде магазинов.
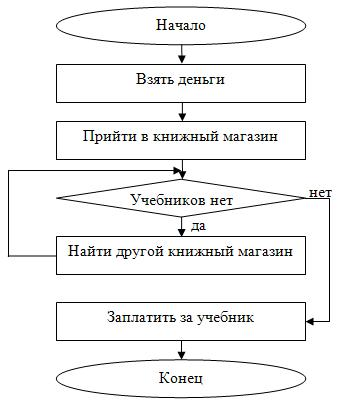
Решение. Действия ученика в данном примере очевидны: когда он приходит в первый и любой последующий магазины, то возможны два варианта – учебник имеется в наличии или учебника нет в продаже. Если учебника нет в продаже, то ученику следует пойти в другой книжный магазин и спросить данный учебник, и т.д. пока учебник не будет куплен, т.к. перед учеником стоит конечная цель – купить учебник. Мы будем использовать цикл с предусловием, т.к. сначала требуется найти магазин, имеющий в наличии данный учебник. Цикл будет выполняться, пока условие «В данном магазине нет учебника» будет верным, а выход из цикла осуществится, когда условие станет ложным, т.е. когда ученик придет в магазин, в котором есть данный учебник. Действительно, в этом случае ученик купит нужный ему учебник и не будет больше искать книжные магазины. Результат блок-схемы представлен на рис. 2.12.
Рис.
2.12.
Блок-схема для примера 8
Здесь тело цикла состоит из одного действия «Найти другой книжный магазин». Переменной цикла в явном виде нет, но можно подразумевать номер магазина, в который пришел ученик в очередной раз. Как любой другой цикл с предусловием, данный цикл может ни разу не выполниться (не иметь итераций), если в первом же магазине окажется нужный учебник.
Примечание. Если в данную задачу добавить условие выбора учебника в жесткой или мягкой обложке, как в примере 5, то оно появится после выхода из цикла. На реализацию циклического алгоритма данное условие не повлияет.
Пример 9. Даны числа 

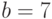






Решение. В отличие от примеров 3 и 6 здесь число 






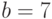
Рис.
2.13.
Блок-схема для примера 9 (с предусловием)
Тело цикла состоит из нескольких действий: вычисление суммы, вычисление разности и вывод полученных данных на экран. Таким образом, у нас получится несколько значений сумм и разностей, т.к. 

Данная задача может быть сделана и с циклом с предусловием, и с постусловием. В этом случае тело цикла, условие и изменение переменной цикла будут такими же, как и в цикле с предусловием, но сначала необходимо выполнить тело цикла, а потом проверить условие для выполнения следующей итерации.
Приведем блок-схему, использующую цикл с постусловием, на рис. 2.14.
Рис.
2.14.
Блок-схема для примера 9 (с постусловием)
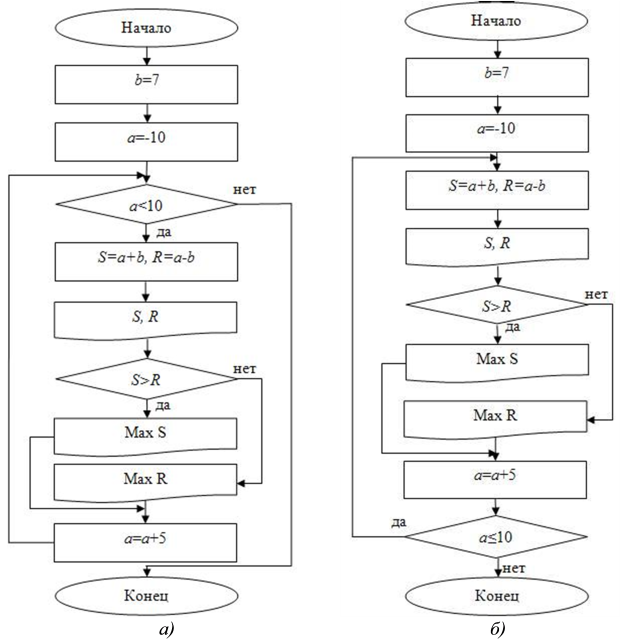
В данной задаче также могут быть соединены циклический и разветвляющийся алгоритмы, если по условию задачи требуется сравнить полученные значения суммы и разности, как в примере 6. В этом случае цикл можно реализовать как с предусловием, так и с постусловием, а сравнение суммы и разности добавится внутрь тела цикла, т.к. следует сравнить между собой все полученные суммы и разности. Организация самого цикла останется прежней. Приведем на рис. 2.15а блок-схему с предусловием, а на рис. 2.15б блок-схему с постусловием.
Рис.
2.15.
Блок-схема с ветвлением для примера 9: а) с предусловием, б) с постусловием
В этой статье будут рассмотрены примеры блок-схем, которые могут встретиться вам в учебниках по информатике и другой литературе. Блок-схема представляет собой алгоритм, по которому решается какая-либо задача, поставленная перед разработчиком. Сначала нужно ответить на вопрос, что такое алгоритм, как он представляется графически, а самое главное – как его решить, зная определенные параметры. Нужно сразу отметить, что алгоритмы бывают нескольких видов.
Что такое алгоритм?
Это слово ввел в обиход математик Мухаммед аль-Хорезми, который жил в период 763-850 года. Именно он является человеком, который создал правила выполнения арифметических действий (а их всего четыре). А вот ГОСТ от 1974 года, который гласит, что:
Алгоритм – это точное предписание, которое определяет вычислительный процесс. Причем имеется несколько переменных с заданными значениями, которые приводят расчеты к искомому результату.
Алгоритм позволяет четко указать исполнителю выполнять строгую последовательность действий, чтобы решить поставленную задачу и получить результат. Разработка алгоритма – это разбивание одной большой задачи на некую последовательность шагов. Причем разработчик алгоритма обязан знать все особенности и правила его составления.
Особенности алгоритма
Всего можно выделить восемь особенностей алгоритма (независимо от его вида):
- Присутствует функция ввода изначальных данных.
- Есть вывод некоего результата после завершения алгоритма. Нужно помнить, что алгоритм нужен для того, чтобы достичь определенной цели, а именно – получить результат, который имеет прямое отношение к исходным данным.
- У алгоритма должна быть структура дискретного типа. Он должен представляться последовательными шагами. Причем каждый следующий шаг может начаться только после завершения предыдущего.
- Алгоритм должен быть однозначным. Каждый шаг четко определяется и не допускает произвольной трактовки.
- Алгоритм должен быть конечным – необходимо, чтобы он выполнялся за строго определенное количество шагов.
- Алгоритм должен быть корректным – задавать исключительно верное решение поставленной задачи.
- Общность (или массовость) – он должен работать с различными исходными данными.
- Время, которое дается на решение алгоритма, должно быть минимальным. Это определяет эффективность решения поставленной задачи.
А теперь, зная, какие существуют блок-схемы алгоритмов, можно приступить к рассмотрению способов их записи. А их не очень много.
Словесная запись
Такая форма, как правило, применяется при описании порядка действий для человека: «Пойди туда, не знаю куда. Принеси то, не знаю что».
Конечно, это шуточная форма, но суть понятна. В качестве примера можно привести еще, например, привычную запись на стеклах автобусов:«При аварии выдернуть шнур, выдавить стекло».
Здесь четко ставится условие, при котором нужно выполнить два действия в строгой последовательности. Но это самые простые алгоритмы, существуют и более сложные. Иногда используются формулы, спецобозначения, но при обязательном условии – исполнитель должен все понимать.
Допускается изменять порядок действий, если необходимо вернуться, например, к предыдущей операции либо обойти какую-то команду при определенном условии. При этом команды желательно нумеровать и обязательно указывается команда, к которой происходит переход: «Закончив все манипуляции, повторяете пункты с 3 по 5».
Запись в графической форме
В этой записи участвуют элементы блок-схем. Все элементы стандартизированы, у каждой команды имеется определенная графическая запись. А конкретная команда должна записываться внутри каждого из блоков обычным языком или математическими формулами. Все блоки должны соединяться линиями – они показывают, какой именно порядок у выполняемых команд. Собственно, этот тип алгоритма более подходит для использования в программном коде, нежели словесный.
Запись на языках программирования
В том случае, если алгоритм необходим для того, чтобы задачу решала программа, установленная на ПК, то нужно его записывать специальным кодом. Для этого существует множество языков программирования. И алгоритм в этом случае называется программой.
Блок-схемы
Блок-схема – это представление алгоритма в графической форме. Все команды и действия представлены геометрическими фигурами (блоками). Внутри каждой фигуры вписывается вся информация о тех действиях, которые нужно выполнить. Связи изображены в виде обычных линий со стрелками (при необходимости).
Для оформления блок-схем алгоритмов имеется ГОСТ 19.701-90. Он описывает порядок и правила создания их в графической форме, а также основные методы решения. В этой статье приведены основные элементы блок-схем, которые используются при решении задач, например, по информатике. А теперь давайте рассмотрим правила построения.
Основные правила составления блок-схемы
Можно выделить такие особенности, которые должны быть у любой блок-схемы:
- Обязательно должно присутствовать два блока – «Начало» и «Конец». Причем в единичном экземпляре.
- От начального блока до конечного должны быть проведены линии связи.
- Из всех блоков, кроме конечного, должны выходить линии потока.
- Обязательно должна присутствовать нумерация всех блоков: сверху вниз, слева направо. Порядковый номер нужно проставлять в левом верхнем углу, делая разрыв начертания.
- Все блоки должны быть связаны друг с другом линиями. Именно они должны определять последовательность, с которой выполняются действия. Если поток движется снизу вверх или справа налево (другими словами, в обратном порядке), то обязательно рисуются стрелки.
- Линии делятся на выходящие и входящие. При этом нужно отметить, что одна линия является для одного блока выходящей, а для другого входящей.
- От начального блока в схеме линия потока только выходит, так как он является самым первым.
- А вот у конечного блока имеется только вход. Это наглядно показано на примерах блок-схем, которые имеются в статье.
- Чтобы проще было читать блок-схемы, входящие линии изображаются сверху, а исходящие снизу.
- Допускается наличие разрывов в линиях потока. Обязательно они помечаются специальными соединителями.
- Для облегчения блок-схемы разрешается всю информацию прописывать в комментариях.
Графические элементы блок-схем для решения алгоритмов представлены в таблице:
Линейный тип алгоритмов
Это самый простой вид, который состоит из определенной последовательности действий, они не зависят от того, какие данные вписаны изначально. Есть несколько команд, которые выполняются однократно и только после того, как будет сделана предшествующая. Линейная блок-схема выглядит таким образом:
Причем связи могут идти как сверху вниз, так и слева направо. Используется такая блок-схема для записи алгоритмов вычислений по простым формулам, у которых не имеется ограничений на значения переменных, входящих в формулы для расчета. Линейный алгоритм – это составная часть сложных процессов вычисления.
Разветвляющиеся алгоритмы
Блок-схемы, построенные по таким алгоритмам, являются более сложными, нежели линейные. Но суть не меняется. Разветвляющийся алгоритм – это процесс, в котором дальнейшее действие зависит от того, как выполняется условие и какое получается решение. Каждое направление действия – это ветвь.
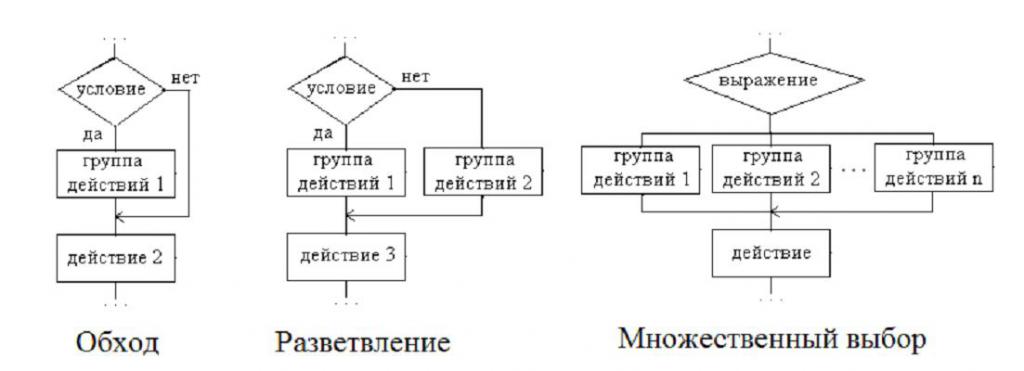
На схемах изображаются блоки, которые называются «Решение». У него имеется два выхода, а внутри прописывается логическое условие. Именно от того, как оно будет выполнено, зависит дальнейшее движение по схеме алгоритма. Можно разделить разветвляющиеся алгоритмы на три группы:
- «Обход» – при этом одна из веток не имеет операторов. Другими словами, происходит обход нескольких действий другой ветки.
- «Разветвление» – каждая ветка имеет определенный набор выполняемых действий.
- «Множественный выбор» – это разветвление, в котором есть несколько веток и каждая содержит в себе определенный набор выполняемых действий. Причем есть одна особенность – выбор направления напрямую зависит от того, какие заданы значения выражений, входящих в алгоритм.
Это простые алгоритмы, которые решаются очень просто. Теперь давайте перейдем к более сложным.
Циклический алгоритм
Здесь все предельно понятно – циклическая блок-схема представляет алгоритм, в котором многократно повторяются однотипные вычисления. По определению, цикл – это определенная последовательность каких-либо действий, выполняемая многократно (более, чем один раз). И можно выделить несколько типов циклов:
- У которых известно число повторений действий (их еще называют циклами со счетчиком).
- У которых число повторений неизвестно – с постусловием и предусловием.
Независимо от того, какой тип цикла используется для решения алгоритма, у него обязательно должна присутствовать переменная, при помощи которой происходит выход. Именно она определяет количество повторений цикла. Рабочая часть (тело) цикла – это определенная последовательность действий, которая выполняется на каждом шаге. А теперь более детально рассмотрим все типы циклов, которые могут встретиться при составлении алгоритмов и решении задач по информатике.
Циклы со счетчиками
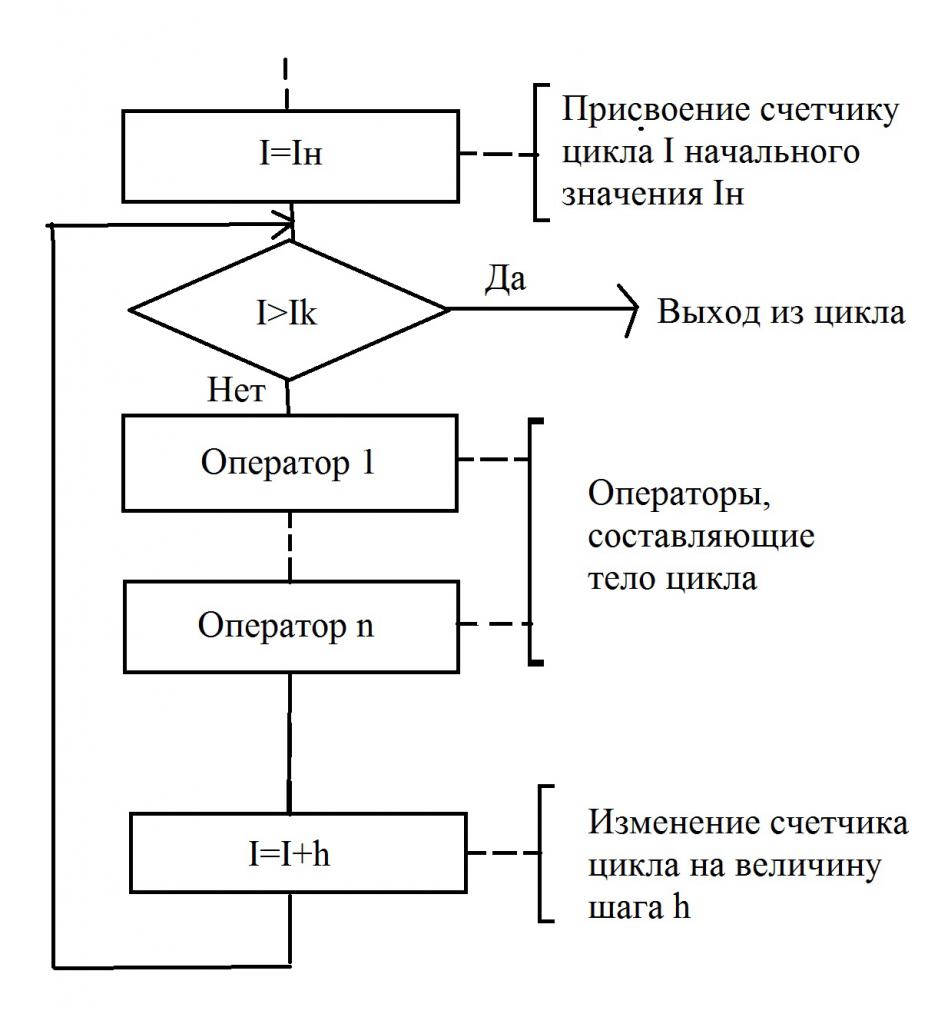
На рисунке изображена простая блок-схема, в которой имеется цикл со счетчиком. Такой тип алгоритмов показывает, что заранее известно количество повторений данного цикла. И это число фиксировано. При этом переменная, считающая число шагов (повторений), так и называется – счетчик. Иногда в учебниках можно встретить иные определения – параметр цикла, управляющая переменная.
Блок-схема очень наглядно иллюстрирует, как работает цикл со счетчиком. Прежде чем приступить к выполнению первого шага, нужно присвоить начальное значение счетчику – это может быть любое число, оно зависит от конкретного алгоритма. В том случае, когда конечное значение меньше величины счетчика, начнет выполняться определенная группа команд, которые составляют тело цикла.
После того, как тело будет выполнено, счетчик меняется на величину шага счетчика, обозначенную буквой h. В том случае, если значение, которое получится, будет меньше конечного, цикл будет продолжаться. И закончится он лишь в тогда, когда конечное значение будет меньше, чем счетчик цикла. Только в этом случае произойдет выполнение того действия, которое следует за циклом.
Обычно в обозначениях блок-схем используется блок, который называется «Подготовка». В нем прописывается счетчик, а затем указываются такие данные: начальное и конечное значения, шаг изменения. На блок-схеме это параметры I н, Ik и h, соответственно. В том случае, когда h=1, величину шага не записывают. В остальных случаях делать это обязательно. Необходимо придерживаться простого правила – линия потока должна входить сверху. А линия потока, которая выходит снизу (или справа, в зависимости от конкретного алгоритма), должна показывать переход к последующему оператору.
Теперь вы полностью изучили описание блок-схемы, изображенной на рисунке. Можно перейти к дальнейшему изучению. Когда используется цикл со счетчиком, требуется соблюдать определенные условия:
- В теле не разрешается изменять (принудительно) значение счетчика.
- Запрещено передавать управление извне оператору тела. Другими словами, войти в цикл можно только из его начала.
Циклы с предусловием
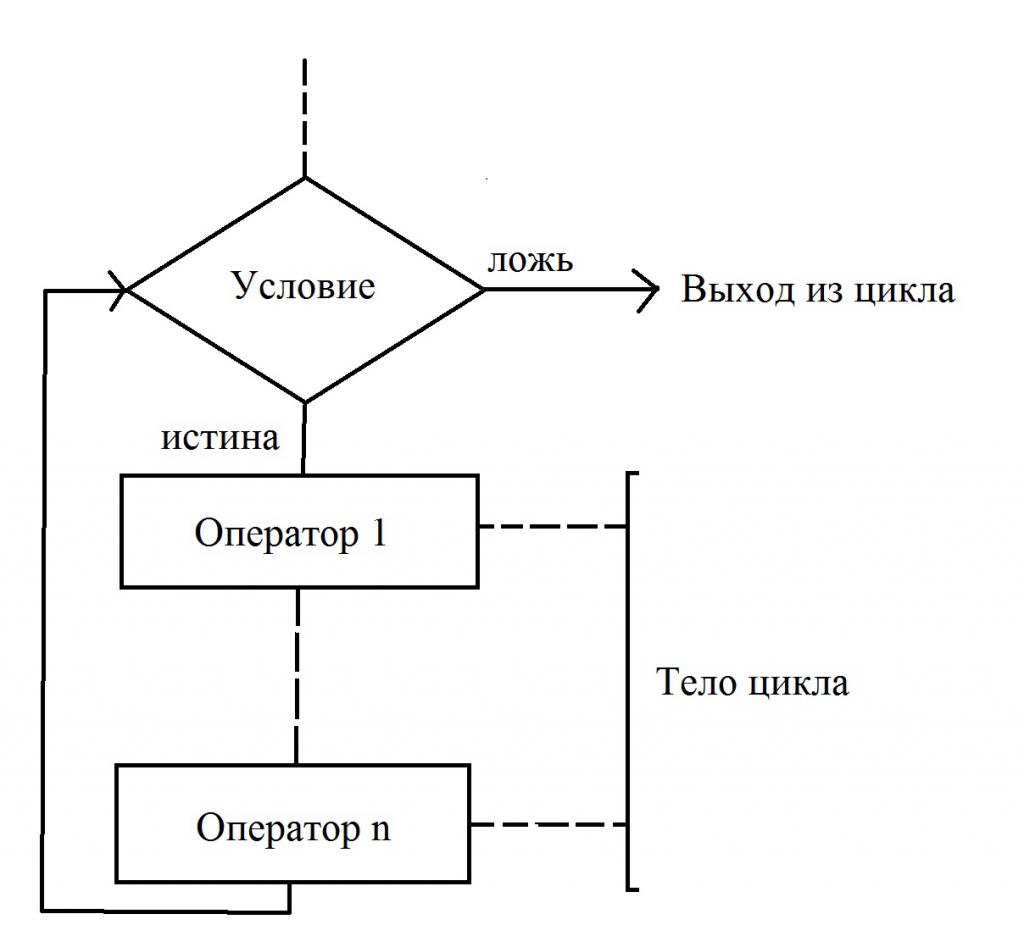
Этот тип циклов применяется в тех случаях, когда количество повторений заранее неизвестно. Цикл с предусловием – это тип алгоритма, в котором непосредственно перед началом выполнения тела осуществляется проверка условия, при котором допускается переход к следующему действию. Обратите внимание на то, как изображаются элементы блок-схемы.
В том случае, когда условие выполняется (утверждение истинно), происходит переход к началу тела цикла. Непосредственно в нем изменяется значение хотя бы одной переменной, влияющей на значение поставленного условия. Если не придерживаться этого правила, получим «зацикливание». В том случае, если после следующей проверки условия выполнения тела цикла оказывается, что оно ложное, то происходит выход.
В блок-схемах алгоритмов допускается осуществлять проверку не истинности, а ложности начального условия. При этом из цикла произойдет выход только в том случае, если значение условия окажется истинным. Оба варианта правильные, их использование зависит от того, какой конкретно удобнее использовать для решения той или иной задачи. Такой тип цикла имеет одну особенность – тело может не выполниться в случае, когда условие ложно или истинно (в зависимости от варианта, который применяется для решения алгоритма).
Ниже приведена блок-схема, которая описывает все эти действия:
Что такое цикл с постусловием?
Если внимательно присмотреться, то этот вид циклов чем-то похож на предыдущий. Самостоятельно построить блок-схему, описывающую этот цикл, мы сейчас и попробуем. Особенность заключается в том, что неизвестно заранее число повторений. А условие задается уже после того, как произошел выход из тела. Отсюда видно, что тело, независимо от решения, будет выполняться как минимум один раз. Для наглядности взгляните на блок-схему, описывающую выполнение условия и операторов:
Ничего сложного в построении алгоритмов с циклами нет, достаточно в них только один раз разобраться. А теперь перейдем к более сложным конструкциям.
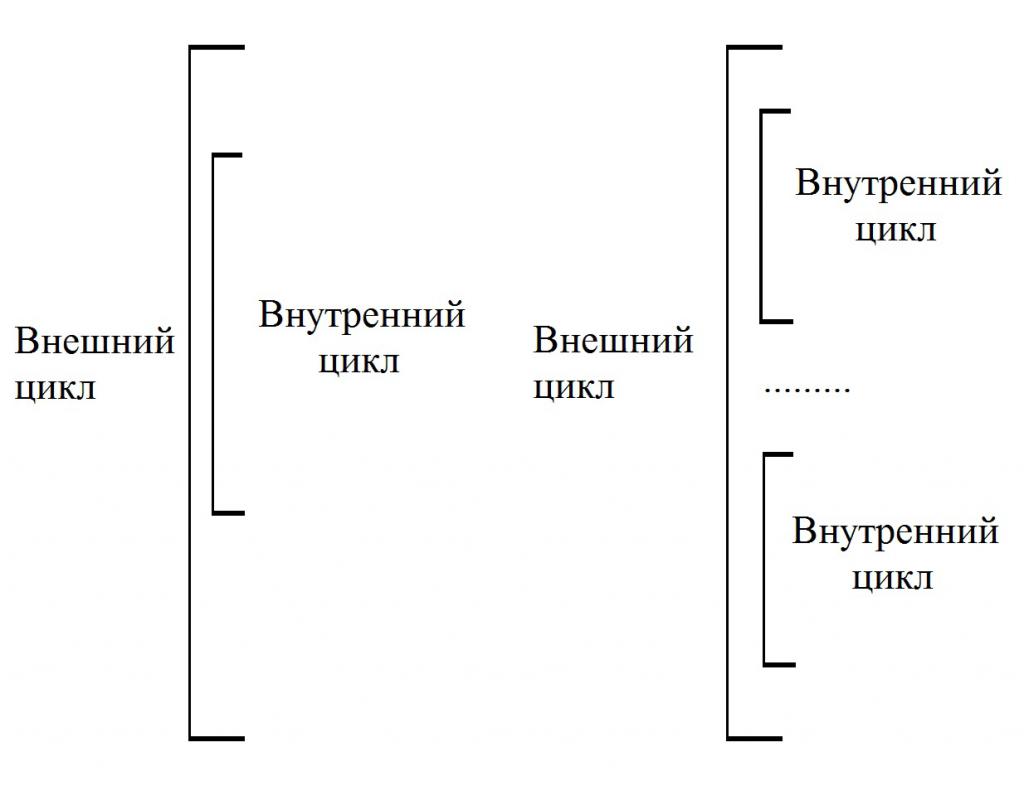
Сложные циклы
Сложные – это такие конструкции, внутри которых есть один или больше простых циклов. Иногда их называют вложенными. При этом те конструкции, которые охватывают иные циклы, называют «внешними». А те, которые входят в конструкцию внешних – внутренними. При выполнении каждого шага внешнего цикла происходит полная прокрутка внутреннего, как представлено на рисунке:
Вот и все, вы рассмотрели основные особенности построения блок-схем для решения алгоритмов, знаете принципы и правила. Теперь можно рассмотреть конкретные примеры блок-схем из жизни. Например, в психологии такие конструкции используются для того, чтобы человек решил какой-то вопрос:
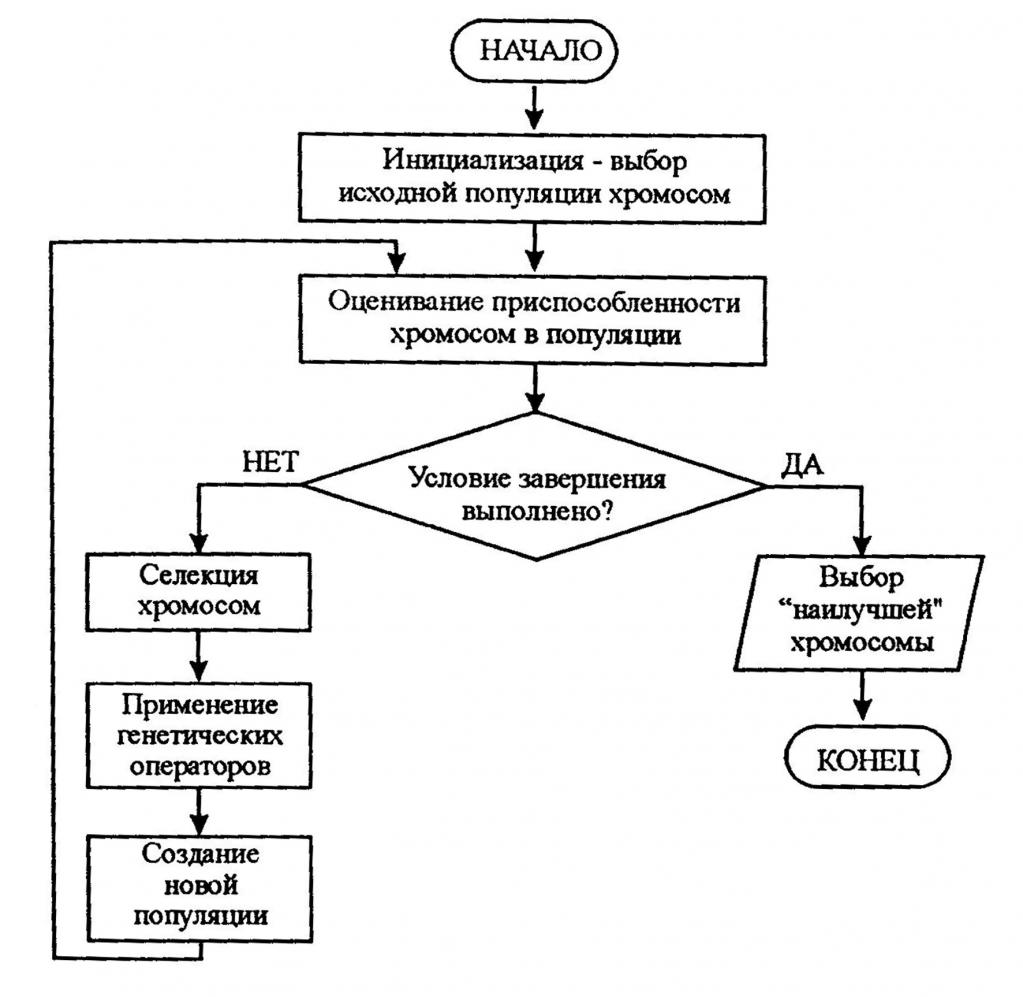
Или пример из биологии для решения поставленной задачи:
Решение задач с блок-схемами
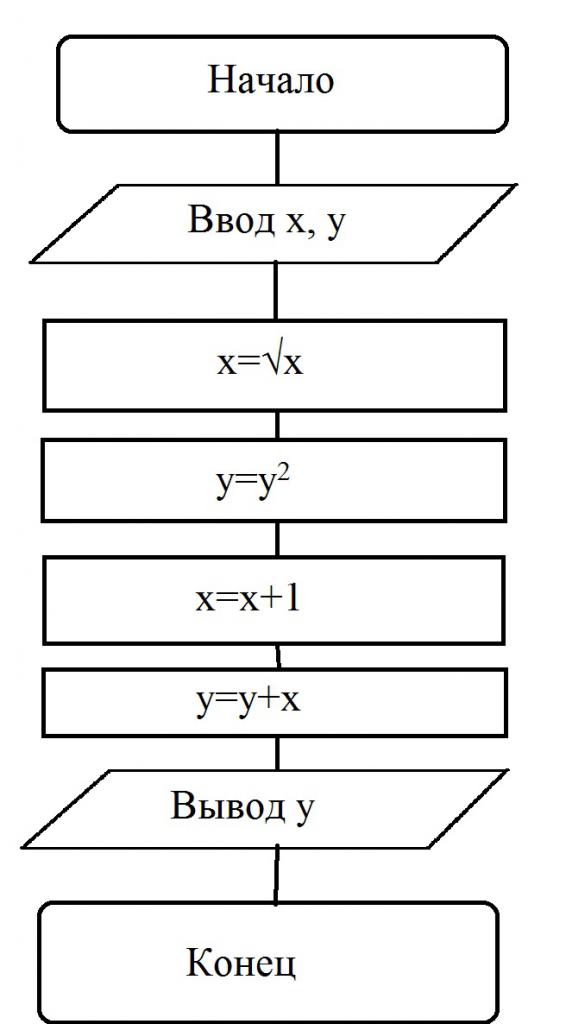
А теперь рассмотрим примеры задач с блок-схемами, которые могут попасться в учебниках информатики. Например, задана блок-схема, по которой решается какой-то алгоритм:
При этом пользователь самостоятельно вводит значения переменных. Допустим, х=16, а у=2. Процесс выполнения такой:
- Производится ввод значений х и у.
- Выполняется операция преобразования: х=√16=4.
- Выполняется условие: у=у2=4.
- Производится вычисление: х=(х+1)=(4+1)=5.
- Дальше вычисляется следующая переменная: у=(у+х)=(5+4)=9.
- Выводится решение: у=9.
На этом примере блок-схемы по информатике хорошо видно, как происходит решение алгоритма. Нужно обратить внимание на то, что значения х и у задаются на начальном этапе и они могут быть любыми.
Схема — это абстракция какого-либо процесса или системы, наглядно отображающая наиболее значимые части. Схемы широко применяются с древних времен до настоящего времени — чертежи древних пирамид, карты земель, принципиальные электрические схемы. Очевидно, древние мореплаватели хотели обмениваться картами и поэтому выработали единую систему обозначений и правил их выполнения. Аналогичные соглашения выработаны для изображения схем-алгоритмов и закреплены ГОСТ и международными стандартами.
На территории Российской Федерации действует единая система программной документации (ЕСПД), частью которой является Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем» [1]. Не смотря на то, что описанные в стандарте обозначения могут использоваться для изображения схем ресурсов системы, схем взаимодействия программ и т.п., в настоящей статье описана лишь разработка схем алгоритмов программ.
Рассматриваемый ГОСТ практически полностью соответствует международному стандарту ISO 5807:1985.
Содержание:
- Элементы блок-схем алгоритмов
- Примеры блок-схем
- Нужны ли блок-схемы? Альтернативы
Элементы блок-схем алгоритмов
Блок-схема представляет собой совокупность символов, соответствующих этапам работы алгоритма и соединяющих их линий. Пунктирная линия используется для соединения символа с комментарием. Сплошная линия отражает зависимости по управлению между символами и может снабжаться стрелкой. Стрелку можно не указывать при направлении дуги слева направо и сверху вниз. Согласно п. 4.2.4, линии должны подходить к символу слева, либо сверху, а исходить снизу, либо справа.
Есть и другие типы линий, используемые, например, для изображения блок-схем параллельных алгоритмов, но в текущей статье они, как и ряд специфических символов, не рассматриваются. Рассмотрены лишь основные символы, которых всегда достаточно студентам.
 |
Терминатором начинается и заканчивается любая функция. Тип возвращаемого значения и аргументов функции обычно указывается в комментариях к блоку терминатора. |
 |
В ГОСТ определено множество символов ввода/вывода, например вывод на магнитные ленты, дисплеи и т.п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях. |
 |
В блоке операций обычно размещают одно или несколько (ГОСТ не запрещает) операций присваивания, не требующих вызова внешних функций. |
 |
Блок в виде ромба имеет один вход и несколько подписанных выходов. В случае, если блок имеет 2 выхода (соответствует оператору ветвления), на них подписывается результат сравнения — «да/нет». Если из блока выходит большее число линий (оператор выбора), внутри него записывается имя переменной, а на выходящих дугах — значения этой переменной. |
 |
Вызов внешних процедур и функций помещается в прямоугольник с дополнительными вертикальными линиями. |
 |
Символы начала и конца цикла содержат имя и условие. Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while). |
 |
Символ «подготовка данных» в произвольной форме (в ГОСТ нет ни пояснений, ни примеров), задает входные значения. Используется обычно для задания циклов со счетчиком. |
 |
В случае, если блок-схема не умещается на лист, используется символ соединителя, отражающий переход потока управления между листами. Символ может использоваться и на одном листе, если по каким-либо причинам тянуть линию не удобно. |
 |
Комментарий может быть соединен как с одним блоком, так и группой. Группа блоков выделяется на схеме пунктирной линией. |
Примеры блок-схем
В качестве примеров, построены блок-схемы очень простых алгоритмов сортировки, при этом акцент сделан на различные реализации циклов, т.к. у студенты делают наибольшее число ошибок именно в этой части.
Сортировка вставками
Массив в алгоритме сортировки вставками разделяется на отсортированную и еще не обработанную части. Изначально отсортированная часть состоит из одного элемента, и постепенно увеличивается.
На каждом шаге алгоритма выбирается первый элемент необработанной части массива и вставляется в отсортированную так, чтобы в ней сохранялся требуемый порядок следования элементов. Вставка может выполняться как в конец массива, так и в середину. При вставке в середину необходимо сдвинуть все элементы, расположенные «правее» позиции вставки на один элемент вправо. В алгоритме используется два цикла — в первом выбираются элементы необработанной части, а во втором осуществляется вставка.
В приведенной блок-схеме для организации цикла используется символ ветвления. В главном цикле (i < n) перебираются элементы необработанной части массива. Если все элементы обработаны — алгоритм завершает работу, в противном случае выполняется поиск позиции для вставки i-того элемента. Искомая позиция будет сохранена в переменной j в результате выполнения внутреннего цикла, осуществляющем сдвиг элементов до тех пор, пока не будет найден элемент, значение которого меньше i-того.
На блок-схеме показано каким образом может использоваться символ перехода — его можно использовать не только для соединения частей схем, размещенных на разных листах, но и для сокращения количества линий. В ряде случаев это позволяет избежать пересечения линий и упрощает восприятие алгоритма.
Сортировка пузырьком
Сортировка пузырьком, как и сортировка вставками, использует два цикла. Во вложенном цикле выполняется попарное сравнение элементов и, в случае нарушения порядка их следования, перестановка. В результате выполнения одной итерации внутреннего цикла, максимальный элемент гарантированно будет смещен в конец массива. Внешний цикл выполняется до тех пор, пока весь массив не будет отсортирован.
На блок-схеме показано использование символов начала и конца цикла. Условие внешнего цикла (А) проверяется в конце (с постусловием), он работает до тех пор, пока переменная hasSwapped имеет значение true. Внутренний цикл использует предусловие для перебора пар сравниваемых элементов. В случае, если элементы расположены в неправильном порядке, выполняется их перестановка посредством вызова внешней процедуры (swap). Для того, чтобы было понятно назначение внешней процедуры и порядок следования ее аргументов, необходимо писать комментарии. В случае, если функция возвращает значение, комментарий может быть написан к символу терминатору конца.
Сортировка выбором
В сортировке выбором массив разделяется на отсортированную и необработанную части. Изначально отсортированная часть пустая, но постепенно она увеличивается. Алгоритм производит поиск минимального элемента необработанной части и меняет его местами с первым элементом той же части, после чего считается, что первый элемент обработан (отсортированная часть увеличивается).
На блок-схеме приведен пример использования блока «подготовка», а также показано, что в ряде случаев можно описывать алгоритм более «укрупнённо» (не вдаваясь в детали). К сортировке выбором не имеют отношения детали реализации поиска индекса минимального элемента массива, поэтому они могут быть описаны символом вызова внешней процедуры. Если блок-схема алгоритма внешней процедуры отсутствует, не помешает написать к символу вызова комментарий, исключением могут быть функции с говорящими названиями типа swap, sort, … .
На блоге можно найти другие примеры блок-схем:
- блок-схема проверки правильности расстановки скобок арифметического выражения [2];
- блок-схемы алгоритмов быстрой сортировки и сортировки слиянием [3].
Часть студентов традиционно пытается рисовать блок-схемы в Microsoft Word, но это оказывается сложно и не удобно. Например, в MS Word нет стандартного блока для терминатора начала и конца алгоритма (прямоугольник со скругленными краями, а не овал). Наиболее удобными, на мой взгляд, являются утилиты MS Visio и yEd [5], обе они позволяют гораздо больше, чем строить блок-схемы (например рисовать диаграммы UML), но первая является платной и работает только под Windows, вторая бесплатная и кроссплатфомренная. Все блок-схемы в этой статье выполнены с использованием yEd.
Частные конторы никакие блок-схемы не используют, в книжках по алгоритмам [6] вместо них применяют словесное описание (псевдокод) как более краткую форму. Возможно блок-схемы применяют на государственных предприятиях, которые должны оформлять документацию согласно требованиям ЕСПД, но есть сомнения — даже для регистрации программы в Государственном реестре программ для ЭВМ никаких блок-схем не требуется.
Тем не менее, рисовать блок-схемы заставляют школьников (примеры из учебников ГОСТ не соответствуют) — выносят вопросы на государственные экзамены (ГИА и ЕГЭ), студентов — перед защитой диплом сдается на нормоконтроль, где проверяется соответствие схем стандартам.
Разработка блок-схем выполняется на этапах проектирования и документирования, согласно каскадной модели разработки ПО, которая сейчас почти не применяется, т.к. сопровождается большими рисками, связанными с ошибками на этапах проектирования.
Появляются подозрения, что система образования прогнила и отстала лет на 20, однако аналогичная проблема наблюдается и за рубежом. Международный стандарт ISO 5807:1985 мало чем отличается от ГОСТ 19.701-90, более нового стандарта за рубежом нет. Там же производится множество программ для выполнения этих самых схем — Dia, MS Visio, yEd, …, а значит списывать их не собираются. Вместо блок-схем иногда применяют диаграммы деятельности UML [6], однако удобнее они оказываются, разве что при изображении параллельных алгоритмов.
Периодически поднимается вопрос о том, что ни блок-схемы, ни UML не нужны, да и документация тоже не нужна. Об этом твердят программисты, придерживающиеся методологии экстремального программирования (XP) [7], ходя даже в их кругу нет единого мнения.
В ряде случаев, программирование невозможно без рисования блок-схем, т.к. это один процесс — существуют визуальные языки программирования, такие как ДРАКОН [8], кроме того, блок-схемы используются для верификации алгоритмов (формального доказательства их корректности) методом индуктивных утверждений Флойда [9].
В общем, единого мнения нет. Очевидно, есть области, в которых без чего-то типа блок-схем обойтись нельзя, но более гибкой альтернативы нет. Для формальной верификации необходимо рисовать подробные блок-схемы, но для проектирования и документирования такие схемы не нужны — я считаю разумным утверждение экстремальных программистов о том, что нужно рисовать лишь те схемы, которые помогают в работе и не требуют больших усилий для поддержания в актуальном состоянии [10].
Список использованных источников:
- ГОСТ 19.701–90 (ИСО 5807–85) «Единая система программной документации».
- Алгоритм. Свойства алгоритма https://pro-prof.com/archives/578
- Алгоритмы сортировки слиянием и быстрой сортировки https://pro-prof.com/archives/813
- yEd Graph Editor https://www.yworks.com/products/yed
- Книги: алгоритмы https://pro-prof.com/books-algorithms
- Рамбо Дж., Якобсон А., Буч Г. UML: специальный справочник. -СПб.: Питер, 2002. -656 с.
- Кент Бек Экстремальное программирование: разработка через тестирование – СПб.: Питер – 2003
- Визуальный язык ДРАКОН https://drakon.su/
- Шилов Н.В. Верификация шаблонов алгоритмов для метода отката и метода ветвей и границ. Моделирование и анализ информационных систем, ISSN 1818 – 1015, т.18, №4, 2011
- Брукс Ф., Мифический человеко — месяц или как создаются программные системы. СПб. Символ Плюс, 1999 — 304 с. ил.
Построение блок-схем алгоритмов циклических вычислительных процессов
В большинстве
задач, встречающихся на практике,
необходимо вычисления по некоторой
группе формул осуществлять многократно.
Этот многократно повторяющийся участок
вычислительного процесса называют
циклом. Цикл, не содержащий в себя другие
циклы, называют простым. Цикл называется
сложным, если он содержит внутри себя
другие циклы или разветвления. Обычно
при каждом повторении цикла вычисления
осуществляются с новыми значениями
переменных. В любом циклическом процессе
в ходе вычислений необходимо решать
вопрос: повторять вычисления или нет?
Ответ на этот вопрос получают в результате
анализа значений одной или нескольких
переменных, т.е. анализ некоторого
условия. Анализируемую переменную
называют параметром цикла. Из
вышеизложенного следует, что циклический
процесс является разветвляющимся
вычислительным процессом с двумя
ветвями, из которых одна возвращается
на предыдущие блоки, т.е. реализует цикл.
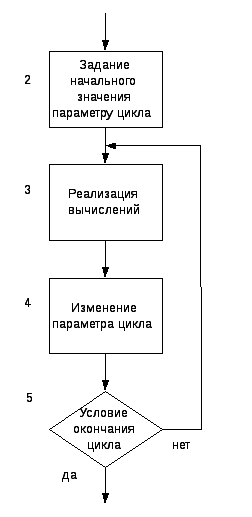
Блок-схема циклического процесса,
независимо от многообразия сводящихся
к нему задач, должна содержать блок
задания начального значения параметру
цикла (2), блок реализации необходимых
вычислений (3), блок изменения параметра
цикла (4) и блок проверки условия окончания
цикла (5)(рис.5.)
Рисунок 5. Блок-схема
циклического процесса
При каждом
выполнении цикла выполняются по формулам
вычисления (3), изменяются параметры
цикла (4), и в зависимости от результата
проверки цикл повторяется, начиная с
блока 3, или заканчивается.
Пример: составить
блок-схему нахождения суммы чисел от 1
до 15 (рис.6).
Рисунок 6. Блок-схема
алгоритма нахождения суммы чисел
Используя символы
для изображения циклов, эту блок-схему
алгоритма можно представить в следующем
виде (рис.7).

Рисунок 7. Блок-схема
циклического процесса
Построение блок-схем алгоритмов итерационных процессов
Итерационным
вычислительным процессом называется
такой циклический процесс, который
продолжается до тех пор, пока разность
между соседними, уточняемыми на каждом
шаге цикла (итерации) значениями, не
окажется меньше или равной некоторой
заданной величине. Характерной
особенностью итерационного процесса
является то, что в нем количество
повторений вычислений заранее неизвестно
и становится определенным только после
окончания вычислений. Решение об
окончании вычислений принимается тогда,
когда результаты счета (значение функции,
искомые величины на очередной отличаются
от предыдущих или эталонных не более,
чем на некоторую, наперед заданную
величину, т.е. найдены с заданной
точностью.
Второй особенностью
итерационного процесса является то,
что результаты вычислений очередного
выполнения цикла используются как
исходные данные при следующем выполнении
цикла, т.е. решение находится
последовательными приближениями, путем
уточнения на каждом шаге цикла.
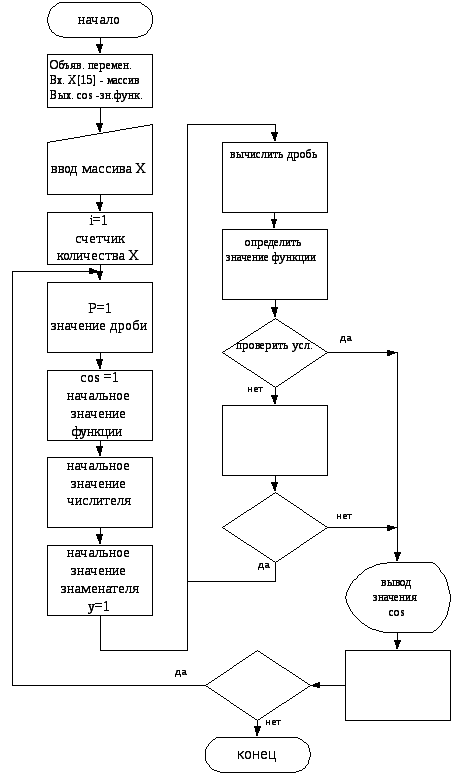
Пример: для 15
значений переменной Х вычислить функцию
cosx,
используя формулу Тейлора.
cos
x=1-+
—
+
—
…
Вычисления
ряда необходимо прекратить, как только
очередной учитываемый член ряда окажется
по абсолютной величине не больше
заданного числа
(но в разложении ряда не должно быть
более 50 членов). Знаменатель очередного
члена ряда рекомендуется вычислить
используя значения предыдущего
знаменателя и умножая его на очередные
два числа натурального ряда чисел.
Числитель каждого последующего члена
получается из предыдущего умножением
на –x2
. Это
одновременно позволит изменять знак
каждого очередного члена (рис.8).
Рисунок 8. Блок-схема
алгоритма итерационного вычислительного
процесса.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #