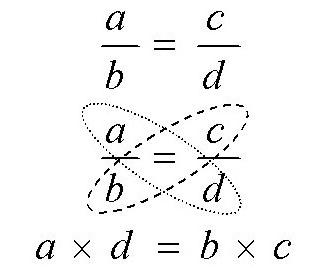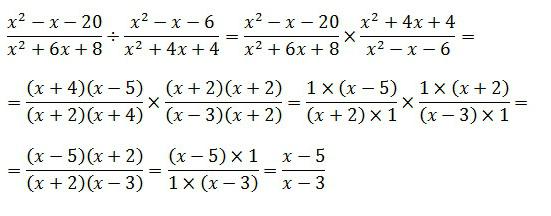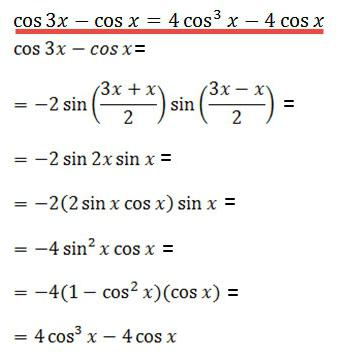Как составить больше равенства

2 ответа:

Читайте также

Если вам необходимо получить ответ на вопрос Напиши как можно больше верных равенств используя только эти числа 9 3 6?, относящийся
к уровню подготовки учащихся 1 — 4 классов, вы открыли нужную страницу.
В категории Математика вы также найдете ответы на похожие вопросы по
интересующей теме, с помощью автоматического «умного» поиска. Если после
ознакомления со всеми вариантами ответа у вас остались сомнения, или
полученная информация не полностью освещает тематику, создайте свой вопрос с
помощью кнопки, которая находится вверху страницы, или обсудите вопрос с
посетителями этой страницы.

Числовые равенства, свойства числовых равенств

После получения общих сведений о равенствах в математике переходим к более узким темам. Материал этой статьи даст представление о свойствах числовых равенств.

Что такое числовое равенство

Первый раз мы сталкиваемся с числовыми равенствами еще в начальной школе, когда происходит знакомство с числами и понятием «столько же». Т.е. самые примитивные числовые равенства это: 2 = 2 , 5 = 5 и т.д. И на том уровне изучения мы называли их просто равенствами, без уточнения «числовые», и закладывали в них количественный или порядковый смысл (который несут натуральные числа). Например, равенство 2 = 2 будет соответствовать изображению, на котором – два цветка и на каждом сидит по две шмеля. Или, к примеру, две очереди, где вторыми по порядку стоят Вася и Ваня.

По мере появления знаний об арифметических действиях числовые равенства становятся сложнее: 5 + 7 = 12 ; 6 — 1 = 5 ; 2 · 1 = 2 ; 21 : 7 = 3 и т.п. Затем начинают встречаться равенства, в записи которых участвуют числовые выражения разного рода. Например, ( 2 + 2 ) + 5 = 2 + ( 5 + 2 ) ; 4 · ( 4 − ( 1 + 2 ) ) + 12 : 4 − 1 = 4 · 1 + 3 − 1 и т.п. Дальше мы знакомимся с прочими видами чисел, и числовые равенства приобретают все более и более интересный и разнообразный вид.

Числовое равенство – это равенство, обе части которого состоят из чисел и/или числовых выражений.

Свойства числовых равенств

Сложно переоценить значимость свойств числовых равенств в математике: они являются опорой многому, определяют принцип работы с числовыми равенствами, методы решений, правила работы с формулами и многое другое.Очевидно, что существует необходимость детального изучения свойств числовых равенств.

Свойства числовых равенств абсолютно согласованы с тем, как определяются действия с числами, а также с определением равных чисел через разность: число a равно числу b только в тех случаях, когда разность a − b есть нуль. Далее в описании каждого свойства мы проследим эту связь.

Основные свойства числовых равенств

Изучать свойства числовых равенств начнем с трех базовых свойств, которые присущи всем равенствам. Перечислим основные свойства числовых равенств:

• свойство рефлексивности: a = a ;
• свойство симметричности: если a = b , то b = a ;
• свойство транзитивности: если a = b и b = c , то a = c ,где a , b и c – произвольные числа.

Определение 2

Свойство рефлексивности обозначает факт равенства числа самому себе: к примеру, 6 = 6 , − 3 = − 3 , 4 3 7 = 4 3 7 и т.п.

Нетрудно продемонстрировать справедливость равенства a − a = 0 для любого числа a : разность a − a можно записать как сумму a + ( − a ) , а свойство сложения чисел дает нам возможность утверждать, что любому числу a соответствует единственное противоположное число − a , и сумма их есть нуль.

Согласно свойству симметричности числовых равенств: если число a равно числу b ,
то число b равно числу a . К примеру, 4 3 = 64 , тогда 64 = 4 3 .

Обосновать данное свойство можно через разность чисел. Условию a = b соответствует равенство a − b = 0 . Докажем, что b − a = 0 .

Запишем разность b − a в виде − ( a − b ) , опираясь на правило раскрытия скобок, перед которыми стоит знак минус. Новая запись выражения равна — 0 , а число, противоположное нулю, это нуль. Таким образом, b − a = 0 , следовательно: b = a .

Свойство транзитивности числовых равенств гласит, что два числа равны друг другу в случае их одновременного равенства третьему числу. К примеру, если 81 = 9 и 9 = 3 2 , то 81 = 3 2 .

Свойству транзитивности также отвечает определение равных чисел через разность и свойства действий с числами. Равенствам a = b и b = c соответствуют равенства a − b = 0 и b − c = 0 .

Докажем справедливость равенства a − c = 0 , из чего последует равенство чисел a и c . Посколькусложение числа с нулем не меняет само число, то a − c запишем в виде a + 0 − c . Вместо нуля подставим сумму противоположных чисел − b и b , тогда крайнее выражение станет таким: a + ( − b + b ) − c . Выполним группировку слагаемых: ( a − b ) + ( b − c ) . Разности в скобках равны нулю, тогда и сумма ( a − b ) + ( b − c ) есть нуль. Это доказывает, что, когда a − b = 0 и b − c = 0 , верно равенство a − c = 0 , откуда a = c .

Прочие важные свойства числовых равенств

Основные свойства числовых равенств, рассмотренные выше, являются базисом для ряда дополнительных свойств, довольно ценных в разрезе практики. Перечислим их:

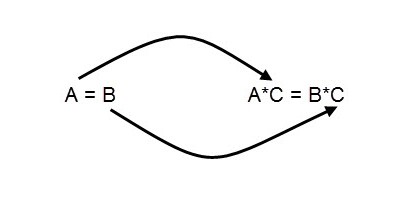
Прибавив к (или убавив от) обеим частям числового равенства, являющегося верным, одно и то же число, получим верное числовое равенство. Запишем буквенно: если a = b , где a и b – некоторые числа, то a + c = b + c при любом c .

В качестве обоснования запишем разность ( a + c ) − ( b + c ) .
Это выражение легко преобразуется в вид ( a − b ) + ( c − c ) .
Из a = b по условию следует, что a − b = 0 и c − c = 0 , тогда ( a − b ) + ( c − c ) = 0 + 0 = 0 . Это доказывает, что ( a + c ) − ( b + c ) = 0 , следовательно, a + c = b + c ;

Если обе части верного числового равенства перемножить с любым числом или разделить на число, не равное нулю, тогда получим верное числовое равенство.
Запишем буквенно: когда a = b , то a · c = b · c при любом числе c . Если c ≠ 0 , тогда и a : c = b : c .

Равенство верно: a · c − b · c = ( a − b ) · c = 0 · c = 0 , и из него следует равенство произведений a · c и b · c . А деление на отличное от нуля число c возможно записать как умножение на обратное число 1 c ;

При a и b , отличных от нуля и равных между собой, обратные им числа также равны.
Запишем: когда a ≠ 0 , b ≠ 0 и a = b , то 1 a = 1 b . Крайнее равенство нетрудно доказать: с этой целью разделим обе части равенства a = b на число, равное произведению a · b и не равное нулю.

Укажем еще на пару свойств, которые позволяют осуществлять сложение и умножение соответствующих частей верных числовых равенств:

При почленном сложении верных числовых равенств получается верное равенство. Запись этого свойства такова: если a = b и c = d , то a + c = b + d для любых чисел a , b , c и d .

Обосновать это полезное свойство возможно, опираясь на указанные ранее свойства. Мы знаем, что к обеим частям верного равенства возможно прибавить любое число.
К равенству a = b прибавим число c , а к равенству c = d — число b , итогом станут верные числовые равенства: a + c = b + c и c + b = d + b . Крайнее запишем в виде: b + c = b + d . Из равенств a + c = b + c и b + c = b + d согласно свойству транзитивности следует равенство a + c = b + d . Что и нужно было доказать.

Необходимо уточнить, что почленно можно сложить не только два верных числовых равенства, но и три, и более;

Наконец, опишем такое свойство: почленное перемножение двух верных числовых равенств дает верное равенство. Запишем при помощи букв: если a = b и c = d , то a · c = b · d .

Доказательство этого свойства подобно доказательству предыдущего. Умножим обе части равенства на любое число, умножим a = b на c , а c = d на b , получим верные числовые равенства a · c = b · c и c · b = d · b . Крайнее запишем как b · c = b · d . Свойство транзитивности дает возможность из равенства a · c = b · c и b · c = b · d вывести равенство a · c = b · d , которое нам необходимо было доказать.

И вновь уточним, что данное свойство применимо для двух, трех и более числовых равенств.
Так, можно записать: если a = b , то a n = b n для любых чисел a и b , и любого натурального числа n .

Завершим данную статью, собрав для наглядности все рассмотренные свойства:

Если a = b , то b = a .

Если a = b и b = c , то a = c .

Если a = b , то a + c = b + c .

Если a = b , то a · c = b · c .

Если a = b и с ≠ 0 , то a : c = b : c .

Если a = b , a = b , a ≠ 0 и b ≠ 0 , то 1 a = 1 b .

Источник

Что такое равенство? Первый признак и принципы равенства

«Равенство» — это тема, которую ученики проходят еще в начальной школе. Сопутствует ей также ей «Неравенства». Эти два понятия тесно взаимосвязаны. Кроме того, с ними связывают такие термины, как уравнения, тождества. Итак, что такое равенство?

Понятие равенства

Под этим термином понимают высказывания, в записи которых есть знак «=». Равенства разделяются на верные и неверные. Если в записи вместо = стоит , тогда речь идет о неравенствах. Кстати, первый признак равенства говорит о том, что обе части выражения идентичны по своему результату или записи.

Кроме понятия равенства, в школе изучают также тему «Числовое равенство». Под этим высказыванием понимают два числовых выражения, которые стоят по обе стороны от знака =. К примеру, 2*5+7=17. Обе части записи равны между собой.

В числовых выражениях подобного типа могут использоваться скобки, влияющие на порядок действий. Итак, существует 4 правила, которые следует учесть при вычислении результатов числовых выражений.

1. Если в записи нет скобок, тогда действия выполняются с высшей ступени: III→II→I. Если есть несколько действий одной категории, тогда они выполняются слева направо.
2. Если в записи есть скобки, тогда действие выполняется в скобках, а затем с учетом ступеней. Возможно, в скобках будет несколько действий.
3. Если выражение представлено в виде дроби, тогда вычислять нужно сначала числитель, потом знаменатель, затем числитель делится на знаменатель.
4. Если в записи есть вложенные скобки, тогда вычисляется сначала выражение во внутренних скобках.

Итак, теперь понятно, что такое равенство. В дальнейшем будут рассмотрены понятия уравнения, тождества и способы их вычисления.

Свойства числовых равенств

Что такое равенство? Изучение этого понятия требует знания свойств числовых тождеств. Приведенные ниже текстовые формулы позволяют лучше изучить данную тему. Конечно, эти свойства больше подходят для изучения математики в старших классах.

1. Числовое равенство не будет нарушено, если в обеих его частях прибавить одно и то же число к существующему выражению.

А = В ↔ А + 5 = В + 5

2. Не будет нарушено уравнение, если обе его части умножить или разделить на одно и то же число или выражение, которые отличны от нуля.

Р = О ↔ Р ∙ 5 = О ∙ 5

Р = О ↔ Р : 5 = О : 5

3. Прибавив к обеим частям тождества одинаковую функцию, которая имеет смысл при любых допустимых значениях переменной, мы получим новое равенство, равносильное первоначальному.

F(X) = Ψ(X) ↔ F(X) + R(X) = Ψ(X) + R(X)

4. Любое слагаемое или выражение можно перенести по другую сторону знака равенства, при этом нужно поменять знаки на противоположные.

Х + 5 = У – 20 ↔ Х = У – 20 – 5 ↔ Х = У – 25

5. Умножив или разделив обе части уравнения на одну и ту же функцию, отличную от нуля и имеющую смысл для каждого значения Х из ОДЗ, мы получим новое уравнение, равносильное первоначальному.

F(X) = Ψ(X) ↔ F(X) ∙ R(X) = Ψ(X) ∙ R(X)

F(X) = Ψ(X) ↔ F(X) : G(X) = Ψ(X) : G(X)

Приведенные правила в явной степени указывают на принцип равенства, который существует при определенных условиях.

Понятие пропорции

В математике существует такое понятие, как равенство отношений. В этом случае подразумевается определение пропорции. Если разделить А на В, то результатом будет отношение числа А к числу В. Пропорцией называют равенство двух отношений:

Иногда пропорция записывается следующим образом: A : B = C : D. Отсюда вытекает основное свойство пропорции: A * D = D * C, где A и D – крайние члены пропорции, а В и С – средние.

Тождества

Тождеством называют равенство, которое будет верно при всех допустимых значениях тех переменных, которые входят в задание. Тождества могут быть представлены как буквенные или числовые равенства.

Тождественно равными называются выражения, содержащие в обеих частях равенства неизвестную переменную, которая способна приравнять две части одного целого.

Если проводить замены одного выражения другим, которое будет равно ему, тогда речь идет о тождественном преобразовании. В этом случае можно воспользоваться формулами сокращенного умножения, законами арифметики и прочими тождествами.

Чтобы сократить дробь, нужно провести тождественные преобразования. К примеру, дана дробь. Чтобы получить результат, следует воспользоваться формулами сокращенного умножения, разложением на множители, упрощением выражений и сокращением дробей.

При этом стоит учесть, что данное выражение будет тождественным тогда, когда знаменатель не будет равен 3.

5 способов доказать тождество

Чтобы доказать равенство тождественное, нужно провести преобразование выражений.

I способ

Необходимо провести равносильные преобразования в левой части. В результате получается правая часть, и можно говорить о том, что тождество доказано.

II способ

Все действия по преобразованию выражения происходят в правой части. Итогом проделанных манипуляций является левая часть. Если обе части идентичны, то тождество доказано.

III способ

«Трансформации» происходят в обеих частях выражения. Если в результате получатся две идентичные части, тождество доказано.

IV способ

Из левой части вычитается правая. В результате равносильных преобразований должен получиться нуль. Тогда можно говорить о тождественности выражения.

V способ

Из правой части вычитается левая. Все равносильные преобразования сводятся к тому, чтобы в ответе стоял нуль. Только в таком случае можно говорить о тождественности равенства.

Основные свойства тождеств

В математике зачастую используют свойства равенств, чтобы ускорить процесс вычисления. Благодаря основным алгебраическим тождествам процесс вычисления некоторых выражений займет считанные минуты вместо долгих часов.

• Х + У = У + Х
• Х + (У + С) = (Х + У) + С
• Х + 0 = Х
• Х + (-Х) = 0
• Х ∙ (У + С) = Х∙У + Х∙С
• Х ∙ (У – С) = Х∙У – Х∙С
• (Х + У) ∙ (С + Е) = Х∙С + Х∙Е + У∙С + У∙Е
• Х + (У + С) = Х + У + С
• Х + (У – С) = Х + У – С
• Х – (У + С) = Х – У – С
• Х – (У – С) = Х – У + С
• Х ∙ У = У ∙ Х
• Х ∙ (У ∙ С) = (Х ∙ У) ∙ С
• Х ∙ 1 = Х
• Х ∙ 1/Х = 1, где Х ≠ 0

Формулы сокращенного умножения

По своей сути формулы сокращенного умножения являются равенствами. Они помогают решить множество задач в математике благодаря своей простоте и легкости в обращении.

• (А + В) 2 = А 2 + 2∙А∙В + В 2 – квадрат суммы пары чисел;

• (А – В) 2 = А 2 – 2∙А∙В + В 2 – квадрат разности пары чисел;

• (С + В) ∙ (С – В) = С 2 – В 2 – разность квадратов;

• (А + В) 3 = А 3 + 3∙А 2 ∙В + 3∙А∙В 2 + В 3 – куб суммы;

• (А – В) 3 = А 3 – 3∙А 2 ∙В + 3∙А∙В 2 – В 3 – куб разности;

• (Р + В) ∙ (Р 2 – Р∙В + В 2 ) = Р 3 + В 3 – сумма кубов;

• (Р – В) ∙ (Р 2 + Р∙В + В 2 ) = Р 3 – В 3 – разность кубов.

Формулы сокращенного умножения зачастую применяются, если необходимо привести многочлен к привычному виду, упростив его всеми возможными способами. Представленные формулы доказываются просто: достаточно раскрыть скобки и привести подобные слагаемые.

Уравнения

После изучения вопроса, что такое равенство, можно приступать к следующему пункту: что такое уравнение. Под уравнением понимается равенство, в котором присутствуют неизвестные величины. Решением уравнения называют нахождение всех значений переменной, при которых обе части всего выражения будут равны. Также встречаются задания, в которых нахождение решений уравнения невозможно. В таком случае говорят, что корней нет.

Как правило, равенства с неизвестными в качестве решения выдают целые числа. Однако возможны случаи, когда корнем являются вектор, функция и другие объекты.

Уравнение является одним из важнейших понятий в математике. Большинство научных и практических задач не позволяют измерить или вычислить какую-либо величину. Поэтому необходимо составлять соотношение, которое удовлетворит все условия поставленной задачи. В процессе составления такого соотношения появляется уравнение или система уравнений.

Обычно решение равенства с неизвестным сводится к преобразованию сложного уравнения и сведению его к простым формам. Необходимо помнить, что преобразования нужно проводить относительно обеих частей, в противном случае на выходе получится неверный результат.

4 способа решить уравнение

Под решением уравнения понимают замену заданного равенства другим, которое равносильно первому. Подобная подмена известна как тождественное преобразование. Чтобы решить уравнение, необходимо воспользоваться одним из способов.

1. Одно выражение заменяется другим, которое в обязательном порядке будет тождественно первому. Пример: (3∙х+3) 2 =15∙х+10. Это выражение можно преобразовать в 9∙х 2 +18∙х+9=15∙х+10.

2. Перенесение членов равенства с неизвестным из одной стороны в другую. В таком случае необходимо правильно менять знаки. Малейшая ошибка сгубит всю проделанную работу. В качестве примера возьмем предыдущий «образец».

9∙х 2 + 12∙х + 4 = 15∙х + 10

9∙х 2 + 12∙х + 4 – 15∙х – 10 = 0

Дальше уравнение решается с помощью дискриминанта.

3. Перемножение обеих частей равенства на равное число или выражение, которые не равняются 0. Однако стоит напомнить, что если новое уравнение не будет равносильным равенству до преобразований, тогда количество корней может существенно измениться.

4. Возведение в квадрат обеих частей уравнения. Этот способ просто замечательный, особенно когда в равенстве есть иррациональные выражения, то есть квадратный корень и выражение под ним. Тут есть один нюанс: если возвести уравнение в четную степень, тогда могут появиться посторонние корни, которые исказят суть задания. И если неправильно извлечь корень, тогда смысл вопроса в задаче будет неясен. Пример: │7∙х│=35 → 1) 7∙х = 35 и 2) – 7∙х = 35 → уравнение будет решено верно.

Итак, в этой статье упоминаются такие термины, как то уравнения и тождества. Все они происходят от понятия «равенство». Благодаря различного рода равносильным выражениям решение некоторых задач в значительной мере облегчено.

Источник

Что означают понятия «равенство» и «неравенство» в математике? Приведите примеры. Запись, в которой используется знак «равно» (=), который стоит между математическими объектами, называется «равенством». Такой знак может разделять два числа, несколько чисел или выражения. Правая и левая части выражений, стоящие перед и после знака «=», всегда имеют одно и то же значение. Примеры: 5 ∙ 4 = 20; 3 + 6 = 9; 21 : 7 = 3. Бывают случаи, когда выражения имеют совершенно разные значения, в этом случае знак «равно» между ними не ставится. Имеется специальный знак, которым можно отметить, что выражения отличаются между собой: «≠». Примеры: 15 ≠ 20 — 2; 14 ≠ 6 + 4; 2 ∙ 5 ≠ 12. Неравенство — это понятие, которое связано со сравнением двух математических объектов, но составляются они с использованием знаков «≠», «>» (больше) и «<« (меньше). Обычно значения справа и слева от этих знаков имеют разные числовые значения. Примеры: 8 < 10; 3 ∙ 4 > 2 ∙ 5; 81 : 9 < 7 ∙ 8. автор вопроса выбрал этот ответ лучшим Annag­ne [103K] 3 года назад  Понятие равенства или неравенства в математике происходит от сравнения либо чисел, либо выражений. Знак равенства обозначается двумя параллельными прямыми одинаковой длины «=», причём применяться в математике этот знак стал только с конца 16 века, а до этого момента он обозначался в буквенном выражении. Пример равенства : 7=7 или 2+6=8 или a+b=b+a . Неравенство обозначается знаками больше и меньше. Как правило, и само понятие, и знак равенства легко понимается и запоминается, а вот со знаками больше и меньше у многих детей возникают сложности в запоминании и я, в своё время, не была исключением. Помню, как нас учили запоминать эти знаки в советской школе : если подставить птичку к знаку с право и её клювик открыт — значит это знак больше, а если закрыт — то знак меньше. Например : Читаем мы слева на право и данные примеры звучат так : четыре больше единицы; два меньше шести. Правда, в математике есть и ещё понятия верное и неверное, и относятся они как к равенству, так и к неравенству. wildc­at [140K] 4 года назад  Равенство — это когда что-то равно другому. Когда мы имеем по пять пальцев на каждой руке, но два глаза, по одному носу. В математике равенство обозначается двумя короткими параллельными полосками: =. Они означают, что без разницы куда идти и что брать, везде все одинаково. 5=5, 6=6, 7=7. Пять пальцев на одной руке равны пяти пальцам на другой и так было всегда. А вот неравенство, это отсутствие совпадения. Это если у тебя пять пальцев на руке, а у Егора четыре, потому что он был дурак и один палец ему оторвало. Получается, что у тебя пальцев больше: 5>4 Это знак «больше». Он находится над буквой Ю на клавиатуре и чтобы его извлечь следует использовать английский алфавит. Рядом и знак меньше: <, и тоже доступен он в английской раскладке. 4<5 и это действительно так. Попробуйте поднять четыре килограмма, а потом возьмите пять. Чувствуете разницу? Autho­r [788K] 5 лет назад  Для данного употребляется знак равно (и ещё его именуют знаком равенства), какой имеет вид =. Пример При записи различных равенств вносят равные объекты, а также между ними и ставят знак =. К примеру сказать, запись равных чисел 6 и 6 будет начертано следующим образом 6=6, и ее можно прочесть как «шесть равно шести» А если письменно нам потребуется отметить неравенство 2 объектов, тогда применяется знак не равно ≠. Знак представляет собой просто перечеркнутый знак равно. Например, запись 3+5≠7. Можно прочесть так: «Сумма тройки и пятерки не равна семи». Еще используются знаки «<«, «>». Меньше, больше. Когда мы говорим про числовое равенство, мы используем знак «=». При этом одно числовое выражение, которые стоит справа, равно числовому выражению, которое находится слева. Числовые равенства обладают несколькими свойствами: Свойство рефлексивности. Например: х=х; 2=2. Свойство симметричности. Например: 3+1=2+2, тогда 2+2=3+1. Свойство транзитивности. Например: х=у, у=z, тогда х=z. Также, если мы проделываем с обоими частями равенства некие одинаковые манипуляции, то равенство не меняет. Например, умножение, сложение (кроме манипуляций с 0), деление и вычитание. 3+1=2+2. Прибавляем к каждой из частей еще 1. И получаем 3+1+1=2+2+1. 5=5. Равенство не нарушено. 3+1=2+2. Умножаем на 2 обе части. 2(3+1)=2(2+2), 6+2=4+4, 8=8. Равенство не нарушено. Когда мы говорим про числовые неравенства, то подразумеваем, что она часть выражения больше или меньше другой. Тогда знак равенства не используется, берутся знаки «<» или «>», «≤» или «≥». Они также обладают рядом свойств. И могут быть верными и неверными. Например: 3+5>6 — это верное неравенство; 3+5<6 — это неверное неравенство. Равенство или неравенство — вытекает из сравнения чисел или выражений. Что то одинаковое при сравнении можно назвать равенством. Например 2+5 будет 7 и 3+4 даст в сумме 7 эти два выражения 2+5 и 3+4 между собой равны и записать можно так: 2+5=3+4 Неравенством, соответственно будет выражение, в котором сумма в правой части будет отличаться от суммы в левой части выражения. Например: 2+6 не равно 3+4, а больше по значению. Неравенство записывают знаками больше или меньше или перечеркнутым знаком равенства. Maria Muzja [66K] 5 лет назад  Эти понятия (равенство/неравенст­во) в математике, очень взаимосвязаны между собой. Равенство — это понятие, которое проходят еще в начальной школе, и под этим термином, надо понимать «высказывание», к которому можно применить знак «=», что-то равное и идентичное. Бывают и числовые равенства. Бываеют равенства неверные и верные. А «неравенство» — это такое математическое утверждение, показывающее, на сколько одно число, отличается от другого. Dilya­ra K [5K] 5 лет назад  Равенством называют такие математические выражения, когда значения слева и справа от знака «=» равны. Равенство, примеры: 18 — 6*2 = 6 23 — (13 + 3) = 7 Если значения слева и справа различны, то вместо знака равенства ставятся знаки неравенства «<«, «>», в зависимости от того, какая сторона неравенства больше. Неравенство, примеры: 7 — 9 < 5 17 > 21 — 19 [поль­зоват­ель забло­киров­ан] [3.9K] 5 лет назад  В алгебре существует понятие «математическое выражение». Если совсем просто это, набор всевозможных математических действий и преобразований. Результатом «выражения» является его значение. Если значения двух выражений одинаковы, значит присутствует «равенство», если значения отличаются, это «неравенство» Алиса в Стран­е [364K] 4 года назад  Равенство в математике — это математическое выражение, между частями которого стоит знак «ровно». Например: 7 + 5 = 12 lg (x + 3) = 3 + 2 lg 5 Неравенство же это когда в математическом выражении между его частями стоит не знак «равно», а знак «меньше» или знак «больше». Например: 4 — 2 < 5 4 (х – 2)∙(х + 2) > 0. Иногда между частями выражения ставится вот такой вот знак (перечеркнутый знак «равно»: ≠, тогда это выражение тоже можно назвать неравенством: 20 + 5 ≠ 19 √ n(х) ≠ √ m(х) isa-isa [73.9K] 4 года назад  «Равенством» в математике называются примеры, в которых между числами или произведениями чисел стоит знак «равно» =. Например: 2х2=4, либо 2х2=1+3, это верное равенство. Бывают неверные равенства, когда пример решен неверно. Неравенство, это когда между числами стоят знаки больше или меньше. Как же как и равенства, неравенства бывают неверными. 31-26 < 7 2х2 < 5 100 > 68-7 Знаете ответ?