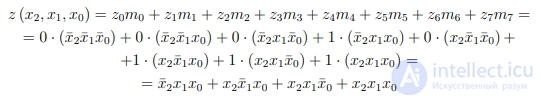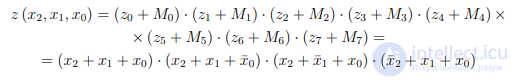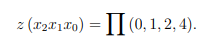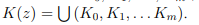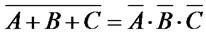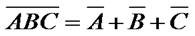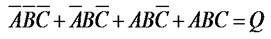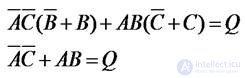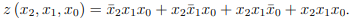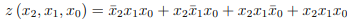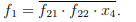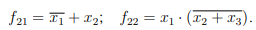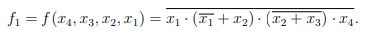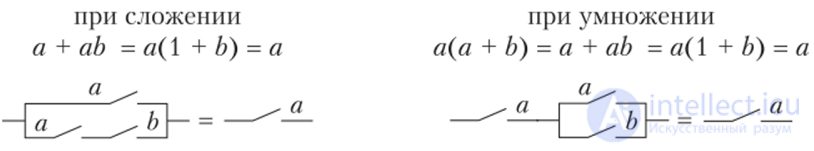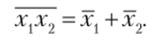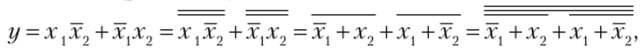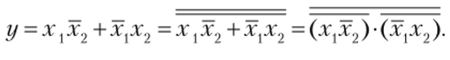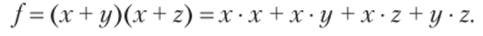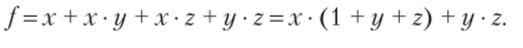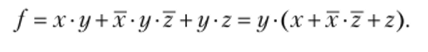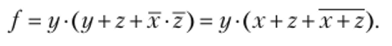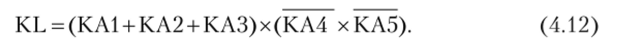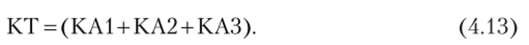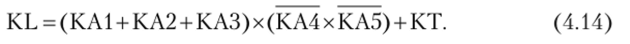Как составить булеву функцию по логической схеме - Исправление недочетов и поиск решений вместе с Examum.ru

Редактор схемы логических элементов

Сервис представляет собой ряд калькуляторов: создание схемы из логических элементов, построение таблицы истинности по булевой функции (с помощью него можно будет также упростить эту функцию) и редактор карт Карно.

С помощью первой программы можно онлайн создать схему логических элементов. По построенной схеме находятся СКНФ, СДНФ, полином Жегалкина. Имеется возможность минимизировать булеву функцию.

Если схему необходимо построить по заданной таблице истинности, то используйте этот калькулятор (иногда задается просто строка, например, f=10001011).

Ввод данных
Параметры схемы
Решение
Видеоинструкция
Оформление Word

Количество переменных
Стандарт изображений элементов
Инверсные входы

INV

AND

NAND

NOR

XOR

MOD

Размеры графического полотна

Ширина
Высота

Созданную логическую схему можно сохранить в форматах docx и png (меню Действия).

По логической схеме можно построить СКНФ, СДНФ, полином Жегалкина, карты Вейча-Карно, а также минимизировать булеву функцию.

Здесь будет показано решение

Инструкция к сервису

Для добавления логического элемента необходимо выделить его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле.

Чтобы соединить элементы, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить. Для соединения с переменной x_i нажмите на соответствующее ей название.

Построенную схему можно сохранить в формате docx или png.

Булевы функции

С помощью этого калькулятора по булевой функции строится таблица истинности, определяются свойства функции и другие параметры (см. вкладку Параметры решения). При этом вводится только само логическое выражение без префикса. Например, при f(x,y,z) = x → y!z, ввести необходимо только x → y!z.

Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр Упростить выражение).

(...) — ввод скобок, x -отрицание (NOT, !, ¬), & — логическое И, AND, ∧, *, v — логическое ИЛИ, OR, ∨, = — эквивалентность, ˜, ≡, ↔, ⊕ — сумма по модулю 2, | — штрих Шеффера, И-НЕ, AND-NOT, ↓ — стрелка Пирса, ИЛИ-НЕ, OR-NOT, ← — обратная импликация.

Для вложенного отрицания необходимо использовать знак !. Например, x v y = !(x v y) или x v y = x v !y

По найденной таблице истинности можно определить логические значения высказываний, например, при x=0, y=0, z=1

Чтобы проверить высказывание на истинность или ложность, функцию необходимо вводить без знака равно (=). Например, A+B→A&B=1, необходимо ввести A+B→A&B. Если в результате преобразований получится, что f=1, то высказывание истинно, если f=0 — ложно.

Логические (функциональные) элементы {v,&, ¬} являются наиболее распространенными: в силу полноты системы любую булеву функцию (БФ) можно представить в виде суперпозиции дизъюнкции, конъюнкции и отрицания. В качестве функциональных элементов (ФЭ) можно рассматривать любые булевы функции, при этом их можно соединять друг с другом, подавая выходы одних элементов на входы других (суперпозиция БФ).

Область определения БФ E – конечное множество, поэтому БФ можно задать с помощью таблицы истинности, содержащей |E|=2ⁿ строк. Столбец значений БФ при этом представляет собой двоичное слово длиной 2ⁿ. Поэтому количество различных БФ n переменных равно 2^2ⁿ.

Отрицание, ¬

x f

0 1

1 0
Конъюнкция, &

x y f

0 0 0

0 1 0

1 0 0

1 1 1
Дизъюнкция, v

x y f

0 0 0

0 1 1

1 0 1

1 1 1
Сумма по модулю 2, x⊕y

x y f

0 0 0

0 1 1

1 0 1

1 1 0
Стрелка Пирса, x↓y

x y f

0 0 1

0 1 0

1 0 0

1 1 0
Эквивалентность, x↔y

x y f

0 0 1

0 1 0

1 0 0

1 1 1
Импликация, x→y

x y f

0 0 1

0 1 1

1 0 0

1 1 1
Штрих Шеффера, x|y

x y f

0 0 1

0 1 1

1 0 1

1 1 0

Другие БФ строятся из элементарных с помощью суперпозиций функций.

Основные равносильности логики высказываний

Название	Формула
Закон исключенного третьего	X v !X ≡ И
Закон противоречия	X & !X ≡ Л
Закон коммутативности	X & Y ≡ Y & X X v Y ≡ Y v X
Закон ассоциативности	(X & Y)&Z ≡ X&(Y&Z) (X v Y) v Z ≡ X v (Y v Z)
Закон дистрибутивности	X&(Y v Z) ≡ X&Y v X&Z X v Y&Z ≡ (X v Y)&(X v Z)
Закон двойного отрицания	!!X ≡ X
Закон идемпотентности	X&X ≡ X, X v X ≡ X
Законы де Моргана	!(X v Y) ≡ !X & !Y !(X & Y) ≡ !X v !Y
Закон поглощения	X v X&Y ≡ X X&(X v Y) ≡ X
Законы склеивания	(X & Y)v(X & !Y) ≡ X (X v Y)&(X v !Y) ≡ X
Замена импликации	X → Y ≡ !X v Y
Замена эквиваленции	X = Y ≡ X&Y v !X&!Y

Пример. Упростите выражение: (x˅y˅z)→(x˅y)*(x˅z)

Упростим функцию, используя основные законы логики высказываний.

Замена импликации: A → B = !A v B

Для нашей функции:

(x v y v z)→((x v y) (x v z)) = x v y v z v (x v y) (x v z)

Упростим функцию, используя законы де Моргана: !(A v B) = !A & !B

Для нашей функции:

x v y v z = x y z

По закону дистрибутивности:

(x v y) (x v z) = x v x z v y x v y z

получаем:

f = x y z v x v x z v y x v y z

После элементарных преобразований получаем:

f = x y z v x v x z v y x v y z = x y z v x v y z

f = y z v y z v x

Минимизация булевых функций

В данном сервисе для минимизации булевых функций используются метод Квайна и карт Карно-Вейча. После получения минимальной формы имеется возможность заново построить логическую схему. Если исходная схема понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).

Сократить БФ можно, применяя некоторые равносильности логики высказываний:

Kx v K ≡ K — тождество поглощения;
Kx v Kx ≡ K — тождество склеивания;
Kx v Ky ≡ K(xvy) — дистрибутивный закон,

где K— элементарная конъюнкция. Большинство методов минимизации БФ основываются на первых двух тождествах. А третье – дистрибутивный закон – уменьшает количество букв в формуле, но выводит формулу из класса ДНФ.
При минимизации БФ используют различные термины (и обозначения) для полных элементарных конъюнкций (ПЭК). Наиболее часто используются термины «минтерм» и «конституента единицы». (Для полных элементарных дизъюнкций (ПЭД) используются термины «макстерм» и «конституента нуля»). Слово «конституента» означает «составляющая», а название «минтерм» исходит из определения конъюнкции, как минимального значения ее операндов. При этом используются обозначения m_i — для минтерма и M_i — для макстерма. Номер i соответствует двоичной записи той оценки переменных, для которой m_i=1.

Метод карт Карно

Склеить можно как целиком всю карту, либо только выделенные единицы (меню Операции).

Количество переменных
Сетка

После минимизации можно получить логическую схему функции и построить таблицу истинности (кнопка Далее)

Этот метод используется для БФ не более, чем с шестью аргументами и основан на тождестве склеивания: Kx v Kx ≡ K — две элементарные конъюнкции (ЭК) склеиваются, если они отличаются только знаком инверсии одного аргумента. Чтобы облегчить нахождение таких пар (четверок, восьмерок,…) склеивающихся ЭК, используют специальное представление БФ в виде таблицы – карты Карно (другое название — диаграмма Вейча). Чтобы заполнить карту Карно необходимо щелкнуть левой кнопкой мышки на соответствующую ячейку.

Карта Карно обладает той особенностью, что две ПЭК, соответствующие соседним клеткам карты, отличаются знаком инверсии только одного аргумента, т.е. их можно склеивать. Причем соседними являются не только клетки, например, с номерами 1 и 3, но и клетки с номерами 12 и 8, 12 и 4, т.е. карту можно «сворачивать» в цилиндр, соединяя горизонтальные (вертикальные) ее границы.

Две единицы «склеиваются» каждый раз, когда они стоят рядом в строке или столбце (карту можно свернуть в цилиндр). В результате склеивания число букв, входящих в ПЭК, уменьшается на единицу.

Минимизая функции через равносильные преобразования

см. таблицу равносильных преобразований

Алгоритм минимизии логической функции

Замена импликации и эквиваленции.
Упрощение функции через законы де Моргана.
Раскрытие скобок, используя законы поглощения, исключенного третьего, противоречия.
Минимизация через закон дистрибутивности.

Алгоритм Куайна построения сокращенной ДНФ

Получить СДНФ функции.
Провести все операции неполного склеивания.
Провести все операции поглощения.

Построение логической схемы по таблице истинности

По заданной СДНФ (по таблице истинности) определяются существенные и фиктивные переменные, полином Жегалкина и принадлежность классам T0,T1, S, M, L. Также можно создать новую логическую схему (если не выбран пункт Строить новую схему при минимизации булевой функции). Если вычисления происходят по исходной схеме и она понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).

Название переменных можно изменить. Для этого их необходимо выбрать (первая строка таблицы).

Количество переменных
Ввести как вектор значений (в виде строки)

a	b	c	f
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

Для установки параметров решения, необходимо нажать Далее.

Пример. Найдите СДНФ(А) и СКНФ(А) с помощью равносильных преобразований и таблицы истинности, если A = xvyv(x→y)&x

Таблица истинности

x	y	x	y	xvy	xvy	x→y	(x→y)&x	xvyv(x→y)&x
0	0	1	1	1	0	1	0	0
0	1	1	0	1	0	1	0	0
1	0	0	1	1	0	0	0	0
1	1	0	0	0	1	1	1	1

Упростим функцию, используя основные законы логики высказываний.

Замена импликации

A → B = !A v B

Для нашей функции:

x→y = x v y

f = x v y v (x v y) x

Упростим функцию, используя законы де Моргана онлайн.

!(A v B) = !A & !B

!(A & B) = !A v !B

Для нашей функции:

x v y = x y

f = x y v (x v y) x

По закону дистрибутивности:

x x = 0

(x v y) x = y x

x y v (x v y) x = x y v y x

f = x y

Используя равносильные преобразования, найдем СДНФ(А).

СДНФ(А) = x y

Используя равносильные преобразования, найдем СДНФ(А).

1. Для получения элементарных дизъюнкций используем закон дистрибутивности XvYZ=(XvY)(XvZ).

2. Закон исключенного третьего Xv!X=1. При этом элементарную дизъюнкцию можно отбросить (в силу равносильности C & 1 = C).

3. По закону поглощения XvXYZ = X

A = x y

Из КНФ А путем равносильных преобразований получаем СКНФ А, последовательно добиваясь выполнения четырех свойств СКНФ А.

1. Если элементарная дизъюнкция В, входящая в КНФ А, не содержит переменную x_i, тогда заменяем В на Bv(x_i & !x_i) = (B v x_i)(B v !x_i)

2. Если в некоторую элементарную дизъюнкцию В переменная x_i входит дважды, то лишнюю переменную нужно отбросить, так как x_i v x_i = x_i.

3. Если КНФ А содержит две одинаковых элементарных дизъюнкций, то одну можно отбросить, так как B & B = B

4. Если в элементарную дизъюнкцию входит пара x_i v !x_i, то ее можно отбросить так как x_i v !x_i=1, а истинное высказывание из конъюнкции можно выбросить (в силу равносильности C & 1 = C).

A = (x v y y) (y v x x) = (x v y) (x v y) (y v x) (y v x)

A = (x v y) (x v y) (y v x) (y v x)

СКНФ(А) = (x v y) (x v y) (x v y)

Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:

1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x₁,x₂,…x_n).

2. Все логические слагаемые формулы различны.

3. Ни одно логическое слагаемое не содержит переменную и её отрицание.

4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.

F = x y

Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:

1. Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x₁,x₂,…x_n).

2. Все элементарные дизъюнкции различны.

3. Каждая элементарная дизъюнкция содержит переменную один раз.

4. Ни одна элементарная дизъюнкция не содержит переменную и её отрицание

F = (x v y) (x v y) (x v y)

Список литературы

Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.,1992.
Бауэр Ф.Л., Гооз Г. Информатика. Вводный курс: Часть 2, М.: Мир, 1990.
Горбатов В.А. Основы дискретной математики. – М.: Высш. школа, 1986. – 312 с.

Количество входов

Текст

РазмерЦвет

Линия

ТолщинаЦвет

пунктирная — — — —

Размеры в px и фон

Номер входа

Текст

РазмерЦвет

Линия

ТолщинаЦвет

пунктирная — — —

Введите название переменных

Количество входов у элемента

Источник

В цифровой технике
часто задача формулируется в форме
таблицы истинности, в которой для всех
возможных наборов входных переменных
определяют их выходные значения.

Пример таблицы
истинности для трех переменных представлен
таблицей 10.5.

Таблица
10.5. Пример таблицы истинности для трех
переменных

Строка

х₁

х₂

х₃

При переходе к
функциональным схемам для таблицы
истинности ищут соответствующую
логическую функцию таким образом, чтобы
она правильно определяла соответствие
между ее значением и всеми наборами
аргументов. На следующем этапе эту
функцию преобразуют в простейшую форму,
которую потом реализуют с помощью
соответствующей комбинации базовых
логических схем. Как правило, логические
функции записывают в так называемой
дизъюнктивной нормальной форме, которую
получают следующим образом:

1. В таблице
истинности выделяют строки, в которых
выходная переменная имеет значение 1.

2.
Для каждой выделенной в п.1 строки
составляют конъюнкцию всех входных
переменных, причем записывают сомножитель
x_i,
если рассматриваемая переменная
принимает значение 1, в противном случае
записывают
.
Таким образом, составляют столько
произведений, сколько имеется строк с
у = 1.

3. Записывается
конечная сумма всех найденных произведений,
которая и представляет собой искомую
функцию.

В
соответствии с рассмотренным методом
рассмотрим построение функциональной
схемы устройства реализующего логическую
функцию, определенную таблицей 10.5.

В этой таблице
переменная У принимает значение 1 для
трех строк: 3, 5 и 7.

Составляем
конъюнкцию по этим строкам:

Строка
3:
;

Строка
5:
;

Строка
7:
.

Искомая функция
записывается в виде логической суммы
этих произведений.

(10.1)

Эта запись называется
дизъюнктивной нормальной формой
рассматриваемой логической функции.

Используя условные
обозначения элементов, реализующих
электронные наборы логических функций
(рис.10.3), легко построить соответствующую
функциональную схему, представленную
на рис. 10.4.

Как и в классической
алгебре, в булевой алгебре существуют
соответствующие законы, тождества,
допустимые наборы операций, с помощью
которых можно производить различные
преобразования булевых функций, включая
их упрощение, называемое минимизацией.

Рис.10.4. Функциональная
схема реализации логического выражения
(10.1).

Например, имеется
набор следующих простых тождеств:

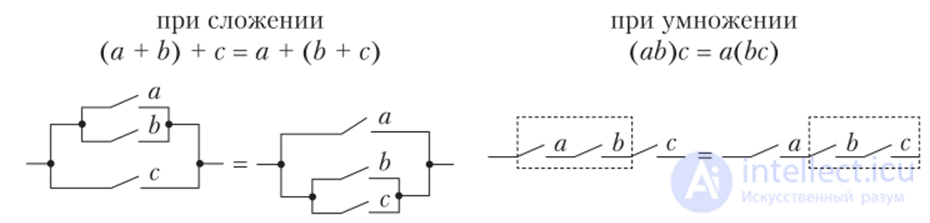
х₁х₂= х₂х₁;

х₁(х₂+ х₃)
= х₁х₂+ х₁х₃;

х₁(х₂х₃)
= (х₁х₂)х₃;

; (10.2)

х + х = х;

х₁+ х₂х₃= (х₁+ х₂)(х₁+ х₃);

;

и т.д.

Рассмотрим вариант
минимизации выражения (10.1) с помощью
тождеств (10.2). С учетом второго тождества
10.2 имеем:

Используя
последнее тождество (10.2) и с учетом того,
что х1=х
получаем:

откуда с учетом
шестого тождества 10.2 получаем:

откуда получаем
конечный результат:

Схемная реализация
последнего выражения представлена на
рис. 10.5.

Рис.10.5. Функциональная схема реализации
выражения 10.1 после его минимизации.

Простое сравнение
рис. 10.4 и 10.5 позволяет сделать вывод,
что использование процедуры минимизации
может значительно сократить затраты
на техническую реализацию цифровых
систем.

Известно большое
число методов минимизации булевых
функций, которые описаны в соответствующей
литературе, однако «ручная» минимизация
сейчас заменена соответствующими
пакетами прикладных программ.

Соседние файлы в папке Учебник по Электронике.

Источник

Логические схемы и таблицы истинности

Логические схемы создаются для реализации в цифровых устройствах булевых функций (функций алгебры логики).

В цифровой схемотехнике цифровой сигнал — это сигнал, который может принимать два значения, рассматриваемые как логическая «1» и логический «0».

Логические схемы могут содержать до 100 миллионов входов и такие гигантские схемы существуют. Представьте себе, что булева функция (уравнение) такой схемы была потеряна. Как восстановить её с наименьшими потерями времени и без ошибок? Наиболее продуктивный способ — разбить схему на ярусы. При таком способе записывается выходная функция каждого элемента в предыдущем ярусе и подставляется на соответствующий вход на следующем ярусе. Этот способ анализа логических схем со всеми нюансами мы сегодня и рассмотрим.

Логические схемы реализуются на логических элементах: «НЕ», «И», «ИЛИ», «И-НЕ», «ИЛИ-НЕ», «Исключающее ИЛИ» и «Эквивалентность». Первые три логических элемента позволяют реализовать любую, сколь угодно сложную логическую функцию в булевом базисе. Мы будем решать задачи на логические схемы, реализованные именно в булевом базисе.

Для обозначения логических элементов используется несколько стандартов. Наиболее распространёнными являются американский (ANSI), европейский (DIN), международный (IEC) и российский (ГОСТ). На рисунке ниже приведены обозначения логических элементов в этих стандартах (для увеличения можно нажать на рисунок левой кнопкой мыши).

На этом уроке будем решать задачи на логические схемы, на которых логические элементы обозначены в стандарте ГОСТ.

Задачи на логические схемы бывают двух видов: задача синтеза логических схемы и задачи анализа логических схем. Мы начнём с задачи второго типа, так как в таком порядке удаётся быстрее научиться читать логические схемы.

Чаще всего в связи с построением логических схем рассматриваются функции алгебры логики:

трёх переменных (будут рассмотрены в задачах анализа и в одной задаче синтеза);
четырёх переменных (в задачах синтеза, то есть в двух последних параграфах).

Рассмотрим построение (синтез) логических схем

в булевом базисе «И», «ИЛИ», «НЕ» (в предпоследнем параграфе);
в также распространённых базисах «И-НЕ» и «ИЛИ-НЕ» (в последнем параграфе).

На основе логических выражений и функций строятся логические схемы. Бывает, что изначально составленная функция является излишне сложной, из-за чего её схемная или программная реализация оказывается избыточной. Способам и приёмам минимизации логических функций посвящены отдельные материалы сайта — минимизация логических функций: общие сведения и минимизация логических функций: метод непосредственных преобразований.

Задача анализа логических схем

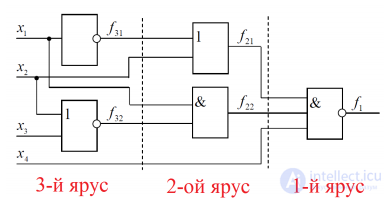
Задача анализа заключается в определении функции f , реализуемой заданной логической схемой. При решении такой задачи удобно придерживаться следующей последовательности действий.

Логическая схема разбивается на ярусы. Ярусам присваиваются последовательные номера.
Выводы каждого логического элемента обозначаются названием искомой функции, снабжённым цифровым индексом, где первая цифра — номер яруса, а остальные цифры — порядковый номер элемента в ярусе.
Для каждого элемента записывается аналитическое выражение, связывающее его выходную функцию с входными переменными. Выражение определяется логической функцией, реализуемой данным логическим элементом.
Производится подстановка одних выходных функций через другие, пока не получится булева функция, выраженная через входные переменные.

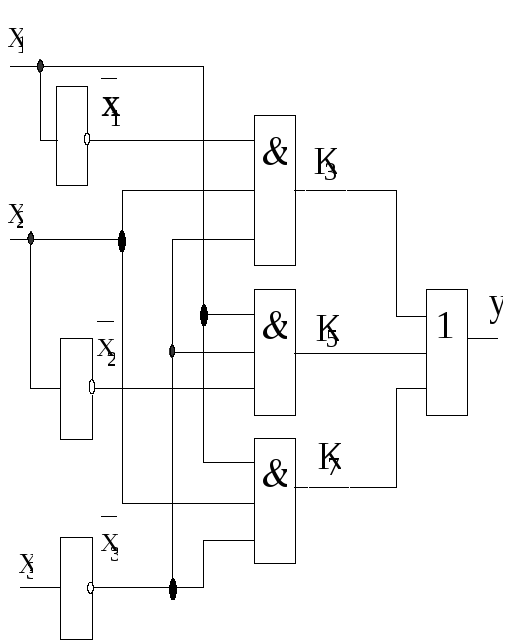
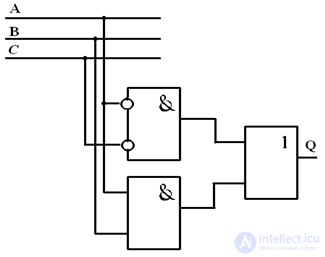
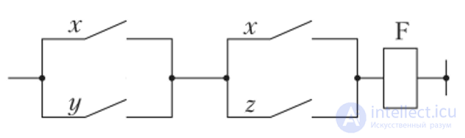
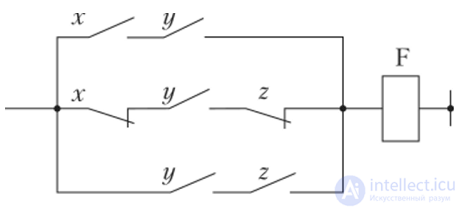
Пример 1. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы, что уже показано на рисунке. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z :

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z					f
1	1	1	0	1	1	1	1
1	1	0	0	0	0	1	0
1	0	1	0	0	0	1	0
1	0	0	0	0	0	1	0
0	1	1	0	0	0	1	0
0	1	0	0	0	0	1	0
0	0	1	0	0	0	1	0
0	0	0	1	0	1	0	0

Найти булеву функцию логической схемы самостоятельно, а затем посмотреть решение

Пример 2. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Пример 3. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Продолжаем искать булеву функцию логической схемы вместе

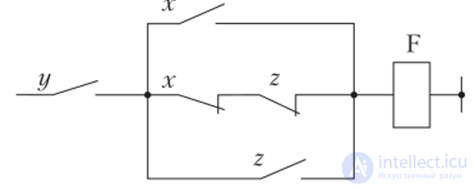
Пример 4. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z :

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	0	1	1
1	1	0	0	1	1
1	0	1	1	0	1
1	0	0	0	0	0
0	1	1	0	1	1
0	1	0	0	1	1
0	0	1	0	1	1
0	0	0	0	1	1

Пример 5. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы. Структура данной логической схемы, в отличие от предыдущих примеров, имеет 5 ярусов, а не 4. Но одна входная переменная — самая нижняя — пробегает все ярусы и напрямую входит в логический элемент в первом ярусе. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z :

В итоге получим функцию, которую реализует на выходе логическая схема:

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	1	1	1
1	1	0	1	1	1
1	0	1	1	0	1
1	0	0	1	0	1
0	1	1	1	1	1
0	1	0	1	1	1
0	0	1	1	0	1
0	0	0	1	0	1

Задача синтеза логических схем в булевом базисе

Разработка логической схемы по её аналитическому описанию имеет название задачи синтеза логической схемы.

Каждой дизъюнкции (логической сумме) соответствует элемент «ИЛИ», число входов которого определяется количеством переменных в дизъюнкции. Каждой конъюнкции (логическому произведению) соответствует элемент «И», число входов которого определяется количеством переменных в конъюнкции. Каждому отрицанию (инверсии) соответствует элемент «НЕ».

Часто разработка логической схемы начинается с определения логической функции, которую должна реализовать логическая схемы. В этом случае дана только таблица истинности логической схемы. Мы разберём именно такой пример, то есть, решим задачу, полностью обратную рассмотренной выше задаче анализа логических схем.

Пример 6. Построить логическую схему, реализующую функцию с данной таблицей истинности:

x	y	f
1	1	0
1	0	0
0	1	1
0	0	0

Решение. Разбираем таблицу истинности для логической схемы. Определяем функцию, которая получится на выходе схемы и промежуточные функции, которые на входе принимают аргументы x и y . В первой строке результатом реализации выходной функции при том, что значения входных переменных равны единицам, должен быть логический «0», во второй строке — при разных значениях входных переменных на выходе тоже должен быть логический «0». Поэтому нужно, чтобы выходная функция была конъюнкцией (логическим произведением).

Теперь подбираем промежуточные функции. Получаем следующую таблицу для промежуточных функций и выходной функции — конъюнкции промежуточных функций:


0	0	0
0	1	0
1	1	1
0	1	0

Для построения логической схемы необходимо элементы, реализующие логические операции, указанные в выходной функции, располагать в порядке, заданной этой функцией. Из выражения видно, что понадобятся 3 схемы «НЕ», две двухвходовых схемы «И» и одна двухвходовая схема «ИЛИ». В соответствии с выходной функцией получаем следующую логическую схему:

А теперь очередь дошла до функций алгебры логики четырёх переменных. Сначала выполним синтез логической схемы в булевом базисе.

Пример 7. Построить в булевом базисе логическую схему, реализующую функцию алгебры логики

Решение. Для построения логической схемы потребуются 4 схемы «НЕ», одна трёхвходовая схема «И», 2 двухвходовые схемы «И» и одна трёхвходовая схема «ИЛИ». В соответствии с этим получаем следующую логическую схему:

Задача синтеза логических схем в базисах «И-НЕ» и «ИЛИ-НЕ»

Часто для сокращения числа микросхем используют элементы «И-НЕ» или/и «ИЛИ-НЕ». Рассмтрим примеры, как построить схему, реализующую ту же функцию, что в предыдущем примере, но, сначала в базисе «И-НЕ», а затем в базисе «ИЛИ-НЕ».

Пример 8. Построить в базисе «И-НЕ» логическую схему, реализующую функцию алгебры логики .

Решение. Логическая функция должна быть приведена к виду, содержащему только операции логического умножения (конъюнкции) и инвертирования (отрицания). Это делается при помощи двойного инвертирования исходного выражения функции и применения закона де Моргана:

Для построения логической схемы потребуются 8 схем «И-НЕ». Получаем следующую логическую схему:

Пример 9. Построить в базисе «ИЛИ-НЕ» логическую схему, реализующую функцию алгебры логики .

Построение логических схем

Цели урока:

Образовательные:

закрепить у учащихся представление об устройствах элементной базы компьютера;
закрепить навыки построения логических схем.

Развивающие:

формировать развитие алгоритмического мышления;
развить конструкторские умения;
продолжать способствовать развитию ИКТ — компетентности;

Воспитательные:

продолжить формирование познавательного интереса к предмету информатика;
воспитывать личностные качества:
активность,
самостоятельность,
аккуратность в работе;

Требования к знаниям и умениям:

Учащиеся должны знать:

основные базовые элементы логических схем;
правила составления логических схем.

Учащиеся должны уметь:

составлять логические схемы.

Тип урока: урок закрепления изученного материала

Вид урока: комбинированный

Методы организации учебной деятельности:

фронтальная;
индивидуальная;

Программно-дидактическое обеспечение:

ПК, SMART Board, карточки с индивидуальным домашним заданием.

Урок разработан с помощью программы Macromedia Flash.

Ход урока

I. Постановка целей урока.

Сегодня мы продолжаем изучение темы «Построение логических схем».

Приготовьте раздаточный материал «Логические основы ЭВМ. Построение логических схем» Приложение 1

Вопрос учителя. Назовите основные логические элементы. Какой логический элемент соответствует логической операции И, ИЛИ, НЕ?

Ответ учащихся. Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию. Основные логические элементы конъюнктор (соответствует логическому умножению), дизъюнктор (соответствует логическому сложению), инвертор (соответствует логическому отрицанию).

Вопрос учителя. По каким правилам логические элементы преобразуют входные сигналы. Рассмотрим элемент И. В каком случае на выходе будет ток (сигнал равный 1).

Ответ учащихся. На первом входе есть ток (1, истина), на втором есть (1, истина), на выходе ток идет (1, истина).

Вопрос учителя. На первом входе есть ток, на втором нет, однако на выходе ток идет. На входах тока нет и на выходе нет. Какую логическую операцию реализует данный элемент?

Ответ учащихся. Элемент ИЛИ — дизъюнктор.

Вопрос учителя. Рассмотрим логический элемент НЕ. В каком случае на выходе не будет тока (сигнал равный 0)?

Ответ учащихся. На входе есть ток, сигнал равен 1.

Вопрос учителя. В чем отличие логической схемы от логического элемента?

Ответ учащихся. Логические схемы состоят из логических элементов, осуществляющих логические операции.

Проанализируем схему и определим сигнал на выходе.

II. Закрепление изученного материала.

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом), становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.

Дома вам необходимо было построить логические схемы, соответствующие логическим выражениям.

Вопрос учителя. Каков алгоритм построение логических схем?

Ответ учащихся. Алгоритм построение логических схем:

Определить число логических переменных.

Определить количество базовых логических операций и их порядок.

Изобразить для каждой логической операции соответствующий ей элемент (вентиль).

Соединить вентили в порядке выполнения логических операций.

Проверка домашнего задания Приложение 1. Домашнее задание. Часть 1

Построить логическую схему для логического выражения: .

Две переменные — А и В.
Две логические операции: &,
Строим схему.

Построить логическую схему для логического выражения:

Вычислить значение данного выражения для А=1, В=0.

III. Пропедевтика (законы логики)

Выполним задачу обратную данной. Составим логическое выражение по заданной логической схеме:

Данное логическое выражение можно упростить.

Операция И — логическое умножение, ИЛИ — сложение. Запишем выражение, заменяя знаки & и U на * и + соответственно.

F= (A*B+B*С) Упростим F= (B*(А+С)), затем запишем и тогда логическая схема примет вид:

Вывод: Логические схемы, содержащие минимальное количество элементов, обеспечивают большую скорость работы и увеличивают надёжность устройства.

Алгебра логики дала конструкторам мощное средство разработки, анализа и совершенствования логических схем. Проще, и быстрее изучать свойства и доказывать правильность работы схемы с помощью выражающей её формулы, чем создавать реальное техническое устройство.

Таким образом, цель нашего следующего урока — изучить законы алгебры логики.

IV. Домашнее задание. Часть 2

V. Практическая работа.

Программа — тренажер «Построение логических схем»

Схемотехника. Минимизация логических функций

Зачем это нужно?

Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.

К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.

В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.

Минимизация логических функций при помощи карт Карно

Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.

В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

Возможность поглощения следует из очевидных равенств

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.

Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

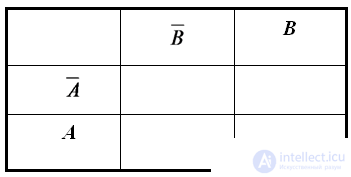
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:

В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.

Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.

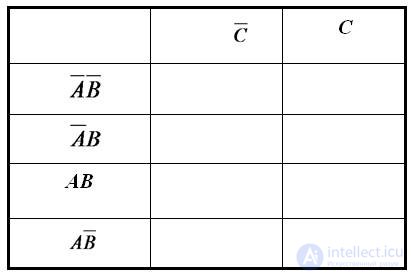
Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):

Объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2 n (n целое число = 0…) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
Область должна быть как можно больше, а кол-во областей как можно меньше;
Области могут пересекаться;
Возможно несколько вариантов накрытия.

Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):

источники:

http://urok.1sept.ru/articles/613002

http://habr.com/ru/post/93296/

Источник

Сразу хочу сказать, что здесь никакой воды про синтез логических схем, и только нужная информация. Для того чтобы лучше понимать что такое
синтез логических схем, анализ логических схем , настоятельно рекомендую прочитать все из категории Электроника, Микроэлектроника , Элементная база.

Содержание

Способы записи функций алгебры логики
анализ логических схем
синтез логических схем
Синтез логического устройства
Переход от логической схемы к логической функции

Методы минимизации логических функций.

Способы записи функций алгебры логики

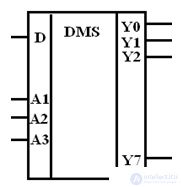
Рассмотрим некоторое логическое устройство, на входе которого присутствует некоторый n–разрядный двоичный код xn−1, . . . , x1, x0, на выходе соответственно m–разрядный двоичный код zm−1, . . . , z1, z0, (рис. 2.1).

Для того, чтобы описать поведение этой схемы, необходимо определить зависимость каждой из m выходных переменных zi от входного двоичного кода xn−1, . . . , x1, x0.

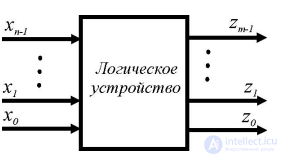
Рис. 2.1. Обобщенная схема логического устройства

Зависимость выходных переменных zi , выраженная через совокупность входных переменных xn−1, . . . , x1, x0 с помощью операций алгебры–логики, носит название функции алгебры логики (ФАЛ). Иногда данную зависимость также называют переключательной функцией. Задать ФАЛ — это значит определить значения zi для всех возможных комбинаций переменных xn−1, . . . , x1, x0. Очевидно, что для n-разрядного двоичного кода xn−1, . . . , x1, x0 существует 2n различных значений zixn−1, . . . , x1, x0. Функция называется полностью определенной, если заданы 2 n ее значений. Если часть значений функции не задана, то она называется частично определенной или недоопределенной. Иногда известно, что по условиям работы устройства появление некоторых входных кодов невозможно, и поэтому значения ФАЛ на этих кодах не задаются. При этом возникают так называемые факультативные или необязательные значения функции, которые могут задаваться произвольными значениями. Входные коды, для которых ФАЛ имеет факультативные значения, называются запрещенными. Устройства, поведение которых описывается при помощи ФАЛ, называют логическими.

Для описания ФАЛ могут быть использованы различные способы.

Основными из них являются:

описание функции в словесной форме,
в виде таблиц истинности,
алгебраических выражений,
последовательностей десятичных чисел и т. д.

1 Словесное описание ФАЛ
Данный вид описания наиболее часто применяется для первоначального, исходного описания поведения логического устройства. Проиллюстрируем словесное описание ФАЛ на примере.

Пример 2.1 Логическая функция трех переменных равна единице, если хотя бы две входные переменные равны единице.

2 Описание ФАЛ в виде таблицы истинности
Таблица, содержащая все возможные комбинации входных переменных xn−1, . . . , x1, x0 и соответствующие им значения выходных переменных zi
, называется таблицей истинности, или комбинационной таблицей. В общем случае таблица истинности содержит 2n строк и m + n столбцов. Проиллюстрируем построение таблицы истинности на примере.

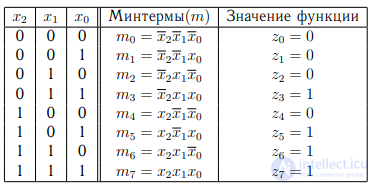
Пример 2.2 Составить таблицу истинности для ФАЛ из примера 2.1.
Решение. Количество входных переменных n = 3, т. о. строк будет — 2 3 = 8. Количество выходных переменных m = 1, т. е. количество столбцов — m + n = 1 + 3 = 4. Составим таблицу истинности (см. таблицу 2.4).
Таблица 2.4. Таблица истинности для ФАЛ трех переменных

3 Описание ФАЛ в виде алгебраического выражения
При описании ФАЛ алгебраическим выражением используются две стандартные формы ее представления.

1. Дизъюнктивная нормальная форма (ДНФ). ДНФ называется логическая сумма элементарных логических произведений, в каждое из которых аргумент или его
инверсия входят один раз. Получена ДНФ может быть из таблицы истинности с использованием следующего алгоритма:

для каждого набора переменных, на котором ФАЛ равна единице, записываются элементарные логические произведения входных переменных, причем переменные, равные нулю, записываются с инверсией. Полученные произведения называют конституентами единицы, или минтермами (m);
логически суммируются все конституенты единицы (минтермы).

Пример 2.3 Записать ДНФ для ФАЛ, заданной в примере 2.2.
Решение. Составим таблицу конституент единицы (минтермов) для ФАЛ, заданной в примере 2.2.
Согласно приведенному выше алгоритму, используя минтермы из таблицы 2.5 и
основные аксиомы (тождества) алгебры-логики (табл. 2.2), получим:

Дизъюнктивную нормальную форму, полученную суммированием конституент единицы (минтермов), называют совершенной дизъюнктивной нормальной формой
(СДНФ).

Таблица 2.5. Минтермы ФАЛ z(x2, x1, x0)

2. Конъюнктивная нормальная форма (КНФ). КНФ называется логическое произведение элементарных логических сумм, в каждую из которых аргумент или его
инверсия входят один раз. Получена КНФ может быть из таблицы истинности с использованием следующего алгоритма:

для каждого набора переменных, на котором ФАЛ равна нулю, записывают элементарные логические суммы входных переменных, причем переменные, значения которых равны единице, записывают с инверсией. Полученные суммы называют конституентой нуля, или макстермами;
логически перемножают все конституенты нуля (макстермы).

Пример 2.4 Записать KНФ для ФАЛ, заданной в примере 2.2.
Решение. Составим таблицу конституент нуля (макстермов) для ФАЛ, заданной в примере 2.2.

Таблица 2.6. Макстермы ФАЛ z(x2, x1, x0)

Согласно приведенному выше алгоритму, используя макстермы из таблицы 2.6 и основные аксиомы (тождества) алгебры-логики (табл. 2.2), получим:

Конъюнктивную нормальную форму, полученную суммированием конституент нуля (макстермов), также называют совершенной конъюнктивной нормальной формой (СКНФ).

Рассмотренные методики позволяют получить математическую форму записи для самой функции. Иногда удобнее применять не саму ФАЛ, а ее инверсию. В этом случае при использовании вышеописанных методик для записи СДНФ необходимо выбирать
нулевые, а для записи СКНФ — единичные значения функции.

Пример 2.5 Для ФАЛ из примера 2.2 записать СДНФ и СКНФ инверсной функцией.
Решение. Воспользовавшись таблицей 2.4, запишем

4 Описание ФАЛ в виде последовательности десятичных чисел
Иногда для сокращения записи ФАЛ представляют в виде последовательности десятичных чисел. При этом последовательно записывают десятичные эквиваленты двоичных кодов соответствующих конституент единицы и нуля (минтермов и макстермов).

Пример 2.6 Записать в виде последовательности десятичных чисел ФАЛ из примеров 2.3 и 2.4
Решение. В СДНФ из примера 2.3 первая конституента единицы (минтерм — x2x1x0) соответствует двоичному коду 011 (табл. 2.5). Десятичный эквивалент этого кода равен 3. Аналогично записываются все остальные конституенты:

В СКНФ из примера 2.4 первая конституента нуля (макстерм — x2 + x1 + x0) соответствует двоичному коду 000 (табл. 2.6).

Десятичный эквивалент этого кода равен 0.
Аналогично записывают все остальные конституенты:

5 Кубические комплексы
В последнее время широкое распространение получило так называемое кубическое представление ФАЛ. Такое представление использует ограниченное число символов и поэтому применяется при автоматизации процессов логического проектирования цифровых интегральных схем (ИС).
Основой кубической формы является представление каждого набора входных переменных в качестве n–мерного вектора. Вершины этих векторов геометрически могут быть представлены как вершины n-мерного куба. Отмечая точками вершины векторов, для которых ФАЛ равна единице, получаем геометрическое представление функции куба.

Пример 2.7 Задана 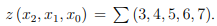. Дать геометрическое представление в виде куба.

Решение. Графическое решение задачи проиллюстрировано на рисунке 2.2.

Очевидно, что наборы переменных, расположенные на концах ребер куба, отличаются только одной переменной. Такие наборы (коды) принято называть соседними.
Каждую функцию куба, в которой функция принимает единичное значение, называют нулевым кубом (0–кубом). Записывается 0–куб последовательностью образовавших его входных переменных, т.е. кодом, соответствующим конституенте единицы.
Множество нулевых кубов образуют нулевой кубический комплекс K0 ФАЛ.

Если два нулевых куба комплекса K0 отличаются только по одной координате (переменной), т.е. два набора переменных, для которых ФАЛ равна единице, являются
соседними, то они образуют единичный куб (1–куб). Геометрически это соответствует ребру исходного n–мерного куба (рис 2.3), 1–куб записывается последовательностью общих элементов образовавших его 0–кубов с прочерком несовпадающих элементов.
Множество единичных кубов образует единичный кубический комплекс K1.
Аналогично, если два единичных куба комплекса K1 отличаются только по одной координате (переменной), то эти единичные кубы образуют двоичный куб (2-куб).
Геометрически это соответствует грани исходного n-мерного куба (рис. 2.4). 2-куб также записывается последовательностью общих элементов образовавших его 1-кубов с прочерком несовпадающих элементов, а множество двоичных кубов образуют двоичный кубический комплекс K2. И так далее.

Пример 2.8 Для ФАЛ из примера 2.7 записать кубические комплексы.
Решение. Нулевой кубический комплекс содержит пять членов по числу конституент единицы ФАЛ. K₀ = (011, 100, 101, 110, 111).
Сравнивая записанные 0-кубы, можно увидеть, что 1–й и 5–й кубы отличаются только первым членом . Об этом говорит сайт https://intellect.icu . Поэтому они образуют 1–куб вида ˘11. Аналогично, 2-ой и 3-й
0–кубы образуют 1–куб вида 10− и т.д. Единичный кубический комплекс заданной
ФАЛ будет иметь вид: K1 = (−11, 10−, 11−, 1 − 1).
Аналогично может быть получен и двоичный кубический комплекс, состоящий из
одного 2–куба: K2 = (1 − −).
Из сказанного следует, что размерность куба (его ранг) определяется числом несовпадающих координат, т. е. числом прочерков в его записи.
Объединение кубических комплексов K0, K1, . . . , Km для ФАЛ n-переменных образует ее кубический комплекс

Анализ логических схем

Анализом логических схем называется составление по логической схеме таблицы истинности.
Таблица истинности сложного элемента может быть составлена по таблицам истинности отдельных простейших элементов.

Пример анализа логического устройства

Составляем таблицу истинности

Синтез логических схем

Синтез логических схем – составление логических схем по заданной таблицы истинности.

Правила синтеза

1. По выходной величине Q определяются количество «0» и «1», если «0»<«1», то синтез осуществляется по строкам, где Q=0 (если «1»<«0», то, где Q=1)

2. Каждая строка реализуется одним элементом «И» с соответствующими элементами «НЕ» на входах.

3. Устройство «ИЛИ», если синтезируем по «1» «ИЛИ-НЕ», если синтезируем по «0» осуществляет преобразование сигналов в выходную величину Q.

Минимизация с помощью карт Карно или с помощью совершенной дизъюнктивной нормальной форме (СДНФ)
• Составляется структурная формула
• Составляется карта Карно для двух, трех, четырех и т.д. переменных
для двух переменных

для трех переменных

Набор правил Булевой алгебры

Теоремы Де Моргана
Дополнение суммы равно произведению дополнений переменных

Дополнение произведения равно сумме дополнений переменных

Пример
Дано: синтезировать функцию представленную структурной формулой

Запишем уравнение в совершенной дизъюнктивной нормальной форме (СДНФ)

Итоговая схема

Различают комбинационные и последовательностные логические устройства.

Комбинационные логические устройства — это устройства, у которых значения выходных сигналов зависят только от комбинации входных сигналов в данный момент времени.

Последовательностные логические устройства — это устройства, выходные сигналы которых зависят от значений входных сигналов не только в данный момент времени, но и в предыдущие моменты времени. В состав этих устройств обязательно входят элементы памяти — триггеры. Различают несколько видов триггеров в зависимости от того, какую элементарную функцию памяти они реализуют.

При разработке логического устройства сначала формулируют словесное описание его алгоритма действия. Затем составляют удовлетворяющую этому описанию логическую функцию (абстрактный синтез) и далее разрабатывают структурную логическую схему устройства (структурный синтез).

В процессе абстрактного синтеза осуществляется переход от словесного описания ТП (его нормальный ход и аварийные ситуации) к составлению алгоритма функционирования в виде таблицы, циклограммы, графика и т.п. Циклограмма представляет собой ряд горизонтальных строк, равных числу входов и выходов логического устройства. Для составления логического алгоритма управления технологическим оборудованием необходимо иметь полную информацию о ТП каждой технологической операции и применяемом оборудовании. На этой стадии уточняют последовательность операций и необходимые временные задержки для всех режимов работы объекта управления, определяют параметры, подлежащие контролю и учету в ходе процесса; формулируют требования управляемого объекта к логическому устройству. Эти требования представляют в виде значений двоичных сигналов, которые должны быть поданы на исполнительные устройства системы управления в зависимости от состояния управляемого объекта.

В процессе структурного синтеза происходит переход от логической функции, описывающей алгоритм функционирования, к структурной схеме логического устройства.

Однако прежде чем приступить к разработке схемы, необходимо попытаться преобразовать исходную логическую функцию к максимально простому виду. На основе структурной схемы логического устройства разрабатывают его принципиальную схему с использованием конкретной элементной базы, например в базисе ИЛИ-HE или И-НЕ. Завершающий этап создания схемы логического устройства — разработка и согласование узлов связи устройства с оператором и управляемым объектом, защита от помех и т.п.

Исторически первыми устройствами, для описания действий которых использовали логические функции, были устройства, выполненные на релейно-контактных элементах. Для проектирования таких устройств была разработана теория релейно-контактных схем (ТРКС). Затем появились бесконтактные устройства, предназначенные только для логических преобразований сигналов и представляющие собой конструктивно оформленные изделия.

Устройства автоматики, действие которых описывается элементарными логическими функциями, обычно называют в соответствии с реализуемой ими логической операцией элементами НЕ, И, ИЛИ, И-НЕ, ИЛИ-HE (см. табл. 4.1).

Имея необходимые элементы, по логической функции можно синтезировать логическое устройство любой сложности. Однако построенная схема может оказаться неоправданно сложной, требующей использования большого числа логических элементов, что может повлиять на стоимость и надежность устройства. Во многих случаях удается так упростить логическую функцию, что соответствующая ей схема устройства оказывается существенно более простой и выполняющей поставленную задачу.

Синтез логического устройства

Для построения логической схемы необходимо логические элементы (ЛЭ), предназначенные для выполнения логических операций, указанных в ФАЛ, располагать от входа в порядке, определенном булевым выражением.

Пример 1

Построить структурную схему логического устройства по ФАЛ из примера 2.1, т. е. определенную ФАЛ вида:

Решение.

Для реализации заданной ФАЛ в виде структурной логической схемы нам понадобятся три ЛЭ, реализующих операцию НЕ, т. к. исходная ФАЛ формируется тремя переменными (x2, x1, x0), которые входят в нее как в прямом, так и в инверсном виде. Операция дизъюнкции должна быть выполнена четыре раза над тремя переменными, таким образом, для ее реализации нам понадобятся четыре ЛЭ, реализующих 29 операцию 3И. Последней выполняется операция конъюнкции над четырьмя выражениями, для реализации которой потребуется ЛЭ, реализующий операцию 4ИЛИ. Пример структурной логической схемы, реализующей заданную ФАЛ, приведен на рис. 3.1.

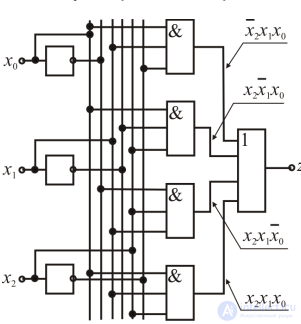
Рис. 3.1. Структурная схема логического устройства, реализующая ФАЛ вида

Переход от логической схемы к логической функции

Можно решить обратную задачу, т. е. по схеме логического устройсва перейти к логической функции. Обратная задача решается в несколько этапов:

заданная схема разбивается по ярусам;

начиная с последнего, выходы каждого элемента обозначаются проиндексированными функциями в зависимости от яруса, к которому относится элемент;
записываются выходные функции каждого элемента в виде формул в соответствии с выбранными обозначениями логических операций;
производится подстановка одних выходных функций через другие, используя входные переменные;
записывается получившаяся булева функция через входные переменные;

Пример 3.2 По заданной логической схеме (рис. 3.2) составить булеву функцию.

Рис. 3.2. Пример логической схемы устройства

Решение. Согласно приведенному выше алгоритму разобьем схему на ярусы, пронумеруем получившиеся ярусы, произведем индексирование выходных функций для каждого элемента (рис. 3.2). Запишем все функции, начиная с 1-го яруса:

1-й ярус :
2-ой ярус :
3-й ярус :

Запишем все функции, подставляя входные переменные x1, x2, x3 и x4:

Окончательно получим:

Методы минимизации логических функций.

Методы упрощения комбинационных устройств называют методами минимизации логических функций. Метод минимизации основан на применении законов алгебры логики, или булевой алгебры, которые приведены ниже для минимального числа переменных. Эквивалентность левой и правой части уравнений обозначена знаком равенства. Одновременно изображены релейные эквиваленты рассматриваемых законов алгебры логики.

Переместительный закон. Для логической суммы и произведения порядок расположения переменных безразличен:

Сочетательный закон. Результат последовательного сложения переменных или умножения их не зависит от порядка этих действий:

Закон поглощения. Сложение переменной с этой же переменной, умноженной на другую переменную, или умножение переменной на сумму этой же переменной и другой переменной равно первой переменной:

Распределительный закон. Общий множитель можно выносить за скобки, как в обычной алгебре:

Закон склеивания. Сумма произведений первой и второй переменных и второй переменной и инверсии первой переменной равна второй переменной. Произведение суммы двух переменных и суммы инверсии первой переменной со второй переменной равно второй переменной:

Закон инверсии (закон Моргана — Шеннона). Отрицание логического сложения равносильно произведению отрицаний слагаемых, и, наоборот, отрицание логического умножения равносильно сумме отрицаний сомножителей:

Инверсия произвольной комбинации двоичных переменных, соединенных знаком «плюс» или «умножение», эквивалентна замене в ней значений перемен-

ных их инверсиями при одновременном изменении знака «плюс» на знак «умножение» и наоборот. Например, xtx2+x3x4 =(xlx2)(x3x4) = (xl +х2)(х3+х4). Закон инверсии встречается только в алгебре логики.

Таким образом, закон инверсии позволяет заменить операцию ИЛИ операцией И, а при необходимости — наоборот. Это особенно важно, поскольку при широком использовании интегральных логических элементов в построении логических устройств наиболее часто используют элементы базисов И-НЕ, ИЛИ-НЕ.

Преобразования логических функций, выполняемые с применением распределительного закона, являются основным методом упрощений, так как вынесение общего множителя за скобки сокращает общее число переменных выражения, следовательно, позволяет сократить число элементов в схемах логических устройств.

Выполняя минимизацию, пользуются также следствиями законов алгебры логики, основные из которых следующие:

Последнее тождество для минимизации получено путем двойной инверсии упрощаемого выражения. Первая инверсия дает

Вторая инверсия дает

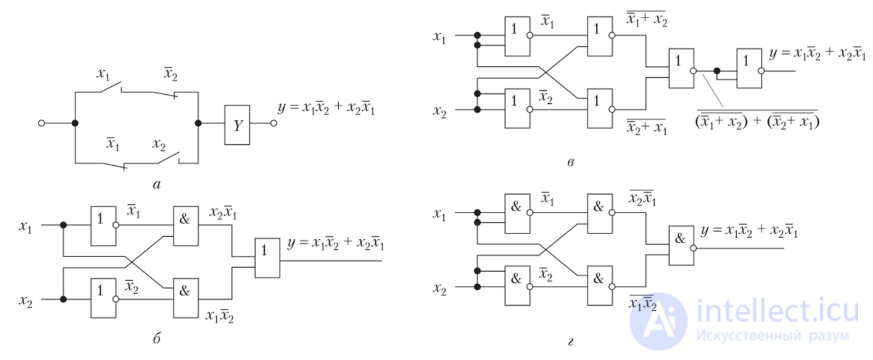
Для перехода из базиса И, ИЛИ, НЕ в базис ИЛИ-HE, а также в базис И-НЕ также выполняется преобразование логической формулы с использованием двойного отрицания. Рассмотрим пример перехода для релейной схемы на рис. 4.5, а, реализованной в базисе И, ИЛИ, НЕ (рис. 4.5, б), в базис ИЛИ-HE (рис. 4.5, в):

и в базис И-НЕ (рис. 4.5, г):

Количество черточек сверху формул равно количеству элементов отрицания, т.е. элементов ИЛИ-HE и И-НЕ. В первой формуле шесть отрицаний, и соответственно схема на рис. 4.5, в содержит шесть элементов ИЛИ-HE. Во второй формуле пять отрицаний, и соответственно схема на рис. 4.5, г содержит пять элементов И-НЕ.

Рис. 45. Реализация структурной формулы логического элемента:

а — на релейных элементах; б — на элементах ИЛИ, И, НЕ; в — на элементах

ИЛИ-HE; г-на элементах И-НЕ

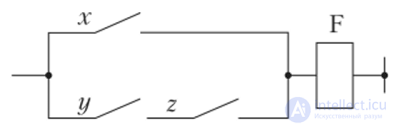
Пример 4.1

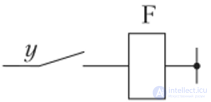
Упростите выражение/ = (х + у)(х + z) и начертите релейный эквивалент до упрощения и после него. Здесь/ — выходной сигнал (состояние замыкающего контакта) релейного элемента F.

Решение

До упрощения релейный эквивалент в соответствии с заданным выражением выглядит следующим образом:

Упростим заданное выражение в соответствии с законами алгебры логики:

Учитывая, что х • х = х, запишем

Учитывая, что 1 + у + z = 1, окончательно запишем /= х + у • z. После упрощения релейный эквивалент выглядит следующим образом:

Упростите выражение f = х-у + х y-z +y-z и начертите релейный эквивалент до упрощения и после него.

Решение

До упрощения релейный эквивалент в соответствии с заданным выражением выглядит следующим образом:

Упростим заданное выражение в соответствии с законами алгебры логики, вынося общий множитель за скобки:

Релейно-контактная схема этого выражения примет вид

Далее преобразуем полученное выражение:

Здесь учтено, что x-z =x + z иа + а = 1, или x+z+x+z = 1, где a = x + z; а = x+z. Поэтому после преобразования упрощенное выражение примет вид

После упрощения выражения релейный эквивалент выглядит так:

Проверим правильность преобразования с помощью таблицы состояния (табл. 4.2), в которой показаны все возможные комбинации двух переменных х и 2, и убедимся, что выражение х + г + х-г всегда равно единице.

Таблица 4.2

Таблица состояния

X	2	X + Z + X-Z
0	0	1
1	0	1
0	1	1
1	1	1

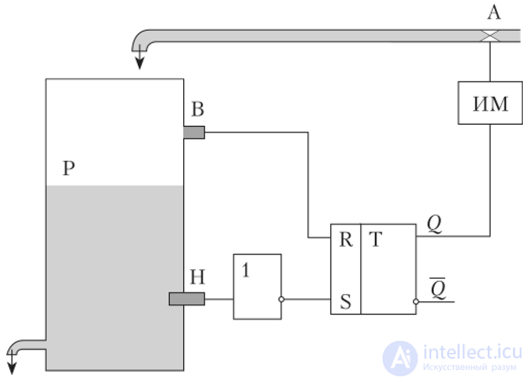
Рассмотрим пример применения алгебры логики для создания системы автоматического регулирования уровня воды в резервуаре Р (рис. 4.6). Исполнительный механизм ИМ осуществляет подачу воды в резервуар путем полного открытия или закрытия подающего вентиля А. В резервуаре имеются два датчика уровня воды: датчик верхнего уровня В и датчик нижнего уровня Н. Когда уровень воды достигнет или превысит положение датчика, сигнал его становится равным единице. Если уровень воды опустится ниже уровня датчика, сигнал на его выходе становится равным нулю.

Рис. 4.6. Релейная система автоматического регулирования уровня воды в резервуаре

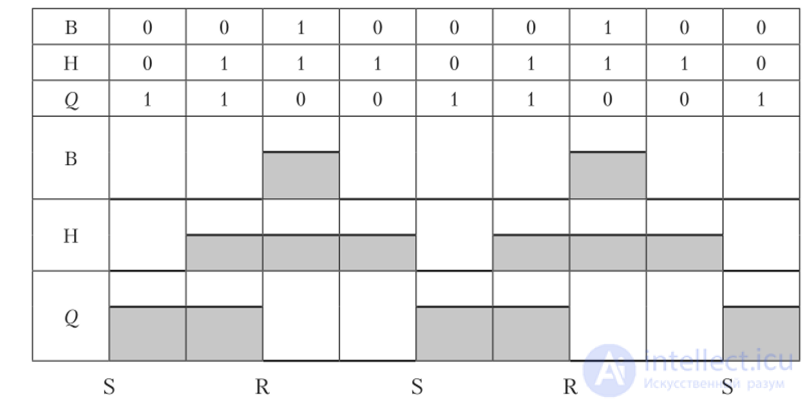
Проанализируем условия работы автоматической системы. Если уровень воды достигнет нижнего уровня Н, то необходимо включить подачу. Если уровень воды достигнет верхнего уровня В, то подачу необходимо отключить. Если уровень воды занимает промежуточное положение между В и Н, то подача должна остаться включенной, если она была включена от датчика Н. Если же подача была выключена датчиком В, то она должна оставаться выключенной. Временная диаграмма сигналов с выхода датчиков и управляющего сигнала Q приведена на рис. 4.7.

Рис. 4.7. Временные диаграммы сигналов в релейной САР, показанной

на рис. 4.6

Условия работы, т.е. все комбинации входных сигналов и сигнала управления, переведены на язык алгебры логики и представлены на рис. 4.7 в верхней таблице в виде единиц и нулей. В таблице указано, при каких соотношениях входных сигналов имеется или отсутствует сигнал Q на выходе релейной САР. Сигнал на выходе является результатом логических операций над входными сигналами.

Если по данным таблицы мы попытаемся записать условия работы в виде логических функций, то обнаружим, что включенному сигналу управления соответствуют два различных соотношения входных сигналов. То же относится и к выключенному сигналу управления. Получается неоднозначность выходного сигнала в зависимости от сочетания входных сигналов. При В = 0 и Н = 1 есть положение, когда Q = 0 и есть положение, когда Q=l. Это значит, что в схеме должен быть элемент памяти, в качестве которого можно использовать уже знакомый нам RS-триггер Т. Для включения триггера используем появление нулевого сигнала на выходе 11 (II = 0). Этот сигнал инвертируется и подается на устанавливающий вход S триггера Т. Поскольку сигнал В не изменяется, то его не будем учитывать и запишем условие для включения S = Н. Условия для сброса триггера и снятия сигнала управления записываем как R = В.

По этому же принципу строятся системы для регулирования температуры при охлаждении электрических машин и трансформаторов, а также силовых установок автомобилей и тракторов с помощью вентиляторов. Схема может использоваться и для автоматического поддержания температуры за счет подогрева в жилых и животноводческих помещениях.

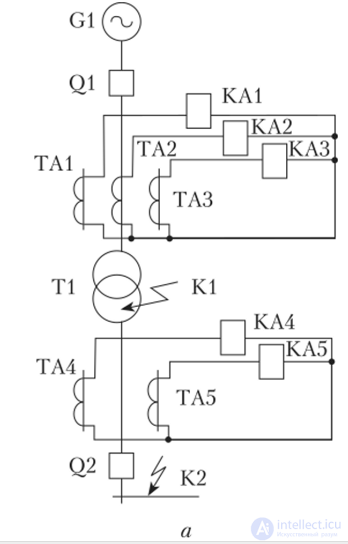
Рассмотрим еще один пример применения алгебры логики для создания логических релейных защит электротехнических объектов на примере релейной защиты силового трансформатора, приведенной на рис. 4.8.

Правила устройства электроустановок [20] предусматривают для ответственных объектов основную и резервную защиту. Основная защита должна отключать объект без выдержки времени, а резервная — с выдержкой времени.

Рис. 4.8. Принципиальная схема максимальной токовой защиты трансформатора с временной селективностью:

а — силовая схема; б — схема цепей защиты

Основной защитой трансформатора Т1 при коротком замыкании в трансформаторе (КЗ в точке К1) служит дифференциальная релейная защита (на схеме она не показана). Резервной защитой при коротком замыкании на отходящих шинах подстанции за выключателем Q2 (КЗ в точке К2) служит максимальная токовая защита, действующая при срабатывании токовых реле КЛ1—К АЗ. Короткое замыкание в трансформаторе Т1 должно отключаться выключателем Q1 от действия резервной защиты без выдержки времени, т.е. «мгновенно». Короткое замыкание в точке К2 должно без выдержки времени отключаться выключателем Q2 (защита выключателя Q2 на схеме не показана). Если по каким-либо причинам защита, воздействующая на выключатель Q2 или сам выключатель Q2, не сработает, то от резервной защиты с выдержкой времени должен отключиться выключатель Q1.

Рассмотрим, как можно повысить быстродействие рассматриваемой резервной защиты, если КЗ произошло в трансформаторе и основная защита не сработала. Для этого измерительные органы ставят на входе и выходе трансформатора Т1. Они выполняют функцию определения места КЗ: на защищаемом объекте или на участке внешней сети. При КЗ на защищаемом объекте (КЗ в основной зоне) они разрешают работу резервной защиты без выдержки времени, а при внешнем КЗ они блокируют цепь мгновенного отключения, и защита работает как резервная с выдержкой времени.

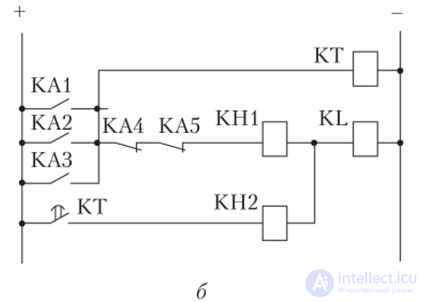
Определение места КЗ выполняется следующим образом. При КЗ в Т1 (точка К1) трансформаторы тока ТА 1—ТАЗ обтекаются током КЗ, и срабатывают реле тока КА1—КАЗ. Трансформаторы тока ТА4—ТА5 на выходе трансформатора Т1 не обтекаются током КЗ. Реле тока КА4 и КА5 не срабатывают, их размыкающие контакты замкнуты. В такой ситуации защита должна сработать без выдержки времени. Промежуточное реле KL подает сигнал на отключение выключателя Q1.

Условия работы промежуточного реле KL для отключения без выдержки времени словесно можно сформулировать так: реле KL сработает, если сработает реле КЛ1, ИЛИ сработает реле КА2 ИЛИ, сработает реле КАЗ И НЕ сработают реле КА4 И реле КА5.

В символах математической логики условие срабатывания реле KL записывается так:

В выражении (4.12) и далее логические переменные в целях наглядности записаны прописными буквами в соответствии с обозначениями на схеме.

При КЗ на участке внешней сети (точка К2) трансформаторы тока ТА4 и ТА5 обтекаются током КЗ, что приводит к срабатыванию реле тока КА4 и КА5 и размыканию их размыкающих контактов в цепи релейной защиты без выдержки времени. Таким образом, работа защиты без выдержки времени блокируется. Резервная защита при КЗ в точке К2 работает с выдержкой времени.

Условие срабатывания реле времени резервной защиты формулируется словесно так: реле времени КТ сработает, если сработает реле КА1, ИЛИ сработает реле КА2, ИЛИ сработает реле КАЗ.

В символах математической логики условие срабатывания реле времени записывается как

Полностью условие срабатывания промежуточного реле KL, отключающего выключатель Q1 без выдержки времени и с выдержкой времени, записывается так:

Схема на рис. 4.8, б построена в соответствии с уравнениями (4.13) и (4.14). Срабатывание защиты без выдержки времени (логической защиты) фиксируется указательным реле КН1. Срабатывание защиты с выдержкой времени фиксируется указательным реле КН2.

Вау!! 😲 Ты еще не читал? Это зря!

карты Карно
СДНФ
СКНФ
теория автоматов

Статью про синтез логических схем я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое синтез логических схем, анализ логических схем
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Электроника, Микроэлектроника , Элементная база

Источник

Примеры решения задач «Логические основы работы компьютера»

Теория по этой теме по этой теме Пройти тестирование по этой теме Контрольная по этой теме

№1.

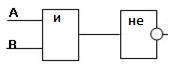
Дана логическая функция: F(А,В) = ¬ (А / В). Постройте соответствующую ей функциональную схему.

Решение:

Функциональная схема будет содержать 2 входа А и В. Рассмотрим логическое выражение и определим порядок действий в нем:

1) первым выполняется логическое умножение А / В, следовательно, сигналы с входов А и В подаются на конъюнктор;

2) далее выполняется логическое отрицание ¬(А / В), следовательно, сигнал, полученный на выходе из конъюнктора должен быть инвертирован, т.е. подан на инвертор.

Выход инвертора является выходом функциональной схемы.

Изобразим схему, следуя данным действиям:

№2.

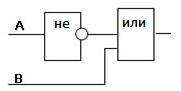
Определите логическую функцию, соответствующую заданной функциональной схеме:

Решение:

Функциональная схема содержит 2 входа А и В. Вход А инвертирован и его выход является входом дизъюнктора. Вход В подает сигнал на дизъюнктор. Выход дизъюнктора является выходом функциональной схемы.

Итак, последовательность действий:

1) ¬A — сигнал входа А инвертирован;

2) ¬A / B — на дизъюнктор подают инвертированный сигнал входа А и нормальный входа В.

Выход дизъюнктора является выходом функциональной схемы. Следовательно, логическая функция F –это функция двух переменных А и В и имеет вид:

F(A, B) = ¬A / B

Ответ: F(A, B) = ¬A / B

№3.

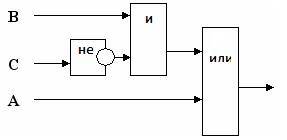
Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F=A/B/ ¬C, если А=1, В=1, С=1.

Решение:

Значение логического выражения — 1

№4.

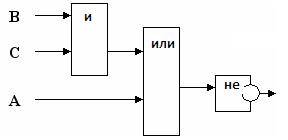
Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F= ¬(A/B/C),если А=0, В=1, С=1.

Решение:

Значение логического выражения — 1

Источник

x	y	z					f
1	1	1	0	1	1	1	1
1	1	0	0	0	0	1	0
1	0	1	0	0	0	1	0
1	0	0	0	0	0	1	0
0	1	1	0	0	0	1	0
0	1	0	0	0	0	1	0
0	0	1	0	0	0	1	0
0	0	0	1	0	1	0	0

x	y	z					f
1	1	1	0	1	1	1	1
1	1	0	0	0	0	1	0
1	0	1	0	0	0	1	0
1	0	0	0	0	0	1	0
0	1	1	0	0	0	1	0
0	1	0	0	0	0	1	0
0	0	1	0	0	0	1	0
0	0	0	1	0	1	0	0

Редактор схемы логических элементов

Размеры графического полотна

Инструкция к сервису

Булевы функции

Отрицание, ¬

Конъюнкция, &

Дизъюнкция, v

Сумма по модулю 2, x⊕y

Стрелка Пирса, x↓y

Эквивалентность, x↔y

Импликация, x→y

Штрих Шеффера, x|y

Основные равносильности логики высказываний

Минимизация булевых функций

Метод карт Карно

Минимизая функции через равносильные преобразования

Алгоритм минимизии логической функции

Алгоритм Куайна построения сокращенной ДНФ

Построение логической схемы по таблице истинности

Список литературы

Логические схемы и таблицы истинности

Задача анализа логических схем

Найти булеву функцию логической схемы самостоятельно, а затем посмотреть решение

Продолжаем искать булеву функцию логической схемы вместе

Задача синтеза логических схем в булевом базисе

Задача синтеза логических схем в базисах «И-НЕ» и «ИЛИ-НЕ»

Построение логических схем

Схемотехника. Минимизация логических функций

Зачем это нужно?

Минимизация логических функций при помощи карт Карно

Содержание

Способы записи функций алгебры логики

Анализ логических схем

Синтез логических схем

Синтез логического устройства

Переход от логической схемы к логической функции

Методы минимизации логических функций.

Вау!! 😲 Ты еще не читал? Это зря!

Примеры решения задач «Логические основы работы компьютера»

x	y	z					f
1	1	1	0	1	1	1	1
1	1	0	0	0	0	1	0
1	0	1	0	0	0	1	0
1	0	0	0	0	0	1	0
0	1	1	0	0	0	1	0
0	1	0	0	0	0	1	0
0	0	1	0	0	0	1	0
0	0	0	1	0	1	0	0