До сих пор мы рассматривали структуры данных, данные в которых располагаются линейно. В связном списке — от первого узла к единственному последнему. В динамическом массиве — в виде непрерывного блока.
В этой части мы рассмотрим совершенно новую структуру данных — дерево. А точнее, двоичное (бинарное) дерево поиска (binary search tree). Бинарное дерево поиска имеет структуру дерева, но элементы в нем расположены по определенным правилам.
Также смотрите другие материалы этой серии: стеки и очереди, динамический массив, связный список, оценка сложности алгоритма, сортировка и множества.
Для начала мы рассмотрим обычное дерево.
Деревья
Дерево — это структура, в которой у каждого узла может быть ноль или более подузлов — «детей». Например, дерево может выглядеть так:
Структура организации
Это дерево показывает структуру компании. Узлы представляют людей или подразделения, линии — связи и отношения. Дерево — это самый эффективный способ представления и хранения такой информации.
Дерево на картинке выше очень простое. Оно отражает только отношение родства категорий, но не накладывает никаких ограничений на свою структуру. У генерального директора может быть как один непосредственный подчиненный, так и несколько или ни одного. На рисунке отдел продаж находится левее отдела маркетинга, но порядок на самом деле не имеет значения. Единственное ограничение дерева — каждый узел может иметь не более одного родителя. Самый верхний узел (совет директоров, в нашем случае) родителя не имеет. Этот узел называется «корневым», или «корнем».
Вопросы о деревьях задают даже на собеседовании в Apple.
Двоичное дерево поиска
Двоичное дерево поиска похоже на дерево из примера выше, но строится по определенным правилам:
- У каждого узла не более двух детей.
- Любое значение меньше значения узла становится левым ребенком или ребенком левого ребенка.
- Любое значение больше или равное значению узла становится правым ребенком или ребенком правого ребенка.
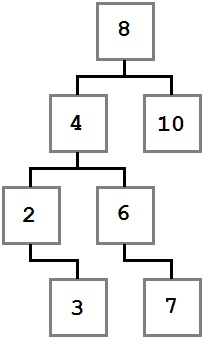
Давайте посмотрим на дерево, построенное по этим правилам:
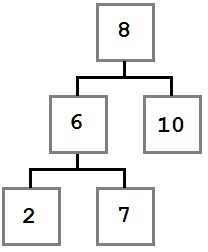
Двоичное дерево поиска
Обратите внимание, как указанные ограничения влияют на структуру дерева. Каждое значение слева от корня (8) меньше восьми, каждое значение справа — больше либо равно корню. Это правило применимо к любому узлу дерева.
Учитывая это, давайте представим, как можно построить такое дерево. Поскольку вначале дерево было пустым, первое добавленное значение — восьмерка — стало его корнем.
Мы не знаем точно, в каком порядке добавлялись остальные значения, но можем представить один из возможных путей. Узлы добавляются методом Add, который принимает добавляемое значение.
BinaryTree tree = new BinaryTree();
tree.Add(8);
tree.Add(4);
tree.Add(2);
tree.Add(3);
tree.Add(10);
tree.Add(6);
tree.Add(7);Рассмотрим подробнее первые шаги.
В первую очередь добавляется 8. Это значение становится корнем дерева. Затем мы добавляем 4. Поскольку 4 меньше 8, мы кладем ее в левого ребенка, согласно правилу 2. Поскольку у узла с восьмеркой нет детей слева, 4 становится единственным левым ребенком.
После этого мы добавляем 2. 2 меньше 8, поэтому идем налево. Так как слева уже есть значение, сравниваем его со вставляемым. 2 меньше 4, а у четверки нет детей слева, поэтому 2 становится левым ребенком 4.
Затем мы добавляем тройку. Она идет левее 8 и 4. Но так как 3 больше, чем 2, она становится правым ребенком 2, согласно третьему правилу.
Последовательное сравнение вставляемого значения с потенциальным родителем продолжается до тех пор, пока не будет найдено место для вставки, и повторяется для каждого вставляемого значения до тех пор, пока не будет построено все дерево целиком.
Класс BinaryTreeNode
Класс BinaryTreeNode представляет один узел двоичного дерева. Он содержит ссылки на левое и правое поддеревья (если поддерева нет, ссылка имеет значение null), данные узла и метод IComparable.CompareTo для сравнения узлов. Он пригодится для определения, в какое поддерево должен идти данный узел. Как видите, класс BinaryTreeNode очень простой:
class BinaryTreeNode : IComparable
where TNode : IComparable
{
public BinaryTreeNode(TNode value)
{
Value = value;
}
public BinaryTreeNode Left { get; set; }
public BinaryTreeNode Right { get; set; }
public TNode Value { get; private set; }
///
/// Сравнивает текущий узел с данным.
///
/// Сравнение производится по полю Value.
/// Метод возвращает 1, если значение текущего узла больше,
/// чем переданного методу, -1, если меньше и 0, если они равны
public int CompareTo(TNode other)
{
return Value.CompareTo(other);
}
}Класс BinaryTree
Класс BinaryTree предоставляет основные методы для манипуляций с данными: вставка элемента (Add), удаление (Remove), метод Contains для проверки, есть ли такое значение в дереве, несколько методов для обхода дерева различными способами, метод Count и Clear.
Кроме того, в классе есть ссылка на корневой узел дерева и поле с общим количеством узлов.
public class BinaryTree : IEnumerable
where T : IComparable
{
private BinaryTreeNode _head;
private int _count;
public void Add(T value)
{
throw new NotImplementedException();
}
public bool Contains(T value)
{
throw new NotImplementedException();
}
public bool Remove(T value)
{
throw new NotImplementedException();
}
public void PreOrderTraversal(Action action)
{
throw new NotImplementedException();
}
public void PostOrderTraversal(Action action)
{
throw new NotImplementedException();
}
public void InOrderTraversal(Action action)
{
throw new NotImplementedException();
}
public IEnumerator GetEnumerator()
{
throw new NotImplementedException();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
throw new NotImplementedException();
}
public void Clear()
{
throw new NotImplementedException();
}
public int Count
{
get;
}
}Метод Add
- Поведение: Добавляет элемент в дерево на корректную позицию.
- Сложность: O(log n) в среднем; O(n) в худшем случае.
Добавление узла не представляет особой сложности. Оно становится еще проще, если решать эту задачу рекурсивно. Есть всего два случая, которые надо учесть:
- Дерево пустое.
- Дерево не пустое.
Если дерево пустое, мы просто создаем новый узел и добавляем его в дерево. Во втором случае мы сравниваем переданное значение со значением в узле, начиная от корня. Если добавляемое значение меньше значения рассматриваемого узла, повторяем ту же процедуру для левого поддерева. В противном случае — для правого.
public void Add(T value)
{
//Случай 1: Если дерево пустое, просто создаем корневой узел.
if (_head == null)
{
_head = new BinaryTreeNode(value);
}
//Случай 2: Дерево не пустое =>
//ищем правильное место для вставки.
else
{
AddTo(_head, value);
}
_count++;
}
//Рекурсивная ставка.
private void AddTo(BinaryTreeNode node, T value)
{
//Случай 1: Вставляемое значение меньше значения узла
if (value.CompareTo(node.Value) < 0)
{
//Если нет левого поддерева, добавляем значение в левого ребенка,
if (node.Left == null)
{
node.Left = new BinaryTreeNode(value);
}
else
{
//в противном случае повторяем для левого поддерева.
AddTo(node.Left, value);
}
}
//Случай 2: Вставляемое значение больше или равно значению узла.
else
{
//Если нет правого поддерева, добавляем значение в правого ребенка,
if (node.Right == null)
{
node.Right = new BinaryTreeNode(value);
}
else
{
//в противном случае повторяем для правого поддерева.
AddTo(node.Right, value);
}
}
}Метод Remove
- Поведение: Удаляет первый узел с заданным значением.
- Сложность: O(log n) в среднем; O(n) в худшем случае.
Удаление узла из дерева — одна из тех операций, которые кажутся простыми, но на самом деле таят в себе немало подводных камней.
В целом, алгоритм удаления элемента выглядит так:
- Найти узел, который надо удалить.
- Удалить его.
Первый шаг достаточно простой. Мы рассмотрим поиск узла в методе Contains ниже. После того, как мы нашли узел, который необходимо удалить, у нас возможны три случая.
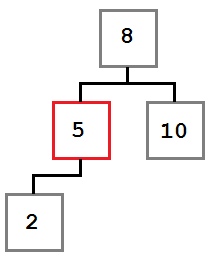
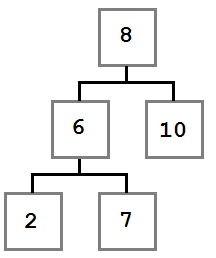
Случай 1: У удаляемого узла нет правого ребенка.
В этом случае мы просто перемещаем левого ребенка (при его наличии) на место удаляемого узла. В результате дерево будет выглядеть так:
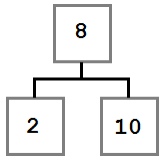
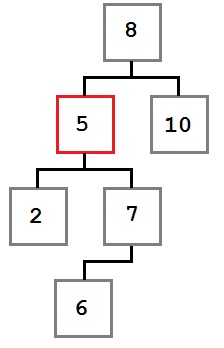
Случай 2: У удаляемого узла есть только правый ребенок, у которого, в свою очередь нет левого ребенка.
В этом случае нам надо переместить правого ребенка удаляемого узла (6) на его место. После удаления дерево будет выглядеть так:
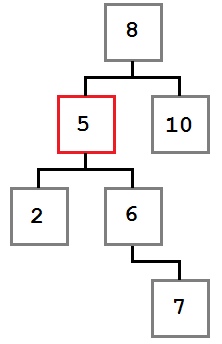
Случай 3: У удаляемого узла есть первый ребенок, у которого есть левый ребенок.
В этом случае место удаляемого узла занимает крайний левый ребенок правого ребенка удаляемого узла.
Давайте посмотрим, почему это так. Мы знаем о поддереве, начинающемся с удаляемого узла следующее:
- Все значения справа от него больше или равны значению самого узла.
- Наименьшее значение правого поддерева — крайнее левое.
Мы дожны поместить на место удаляемого узел со значением, меньшим или равным любому узлу справа от него. Для этого нам необходимо найти наименьшее значение в правом поддереве. Поэтому мы берем крайний левый узел правого поддерева.
После удаления узла дерево будет выглядеть так:
Теперь, когда мы знаем, как удалять узлы, посмотрим на код, который реализует этот алгоритм.
Отметим, что метод FindWithParent (см. метод Contains) возвращает найденный узел и его родителя, поскольку мы должны заменить левого или правого ребенка родителя удаляемого узла.
Мы, конечно, можем избежать этого, если будем хранить ссылку на родителя в каждом узле, но это увеличит расход памяти и сложность всех алгоритмов, несмотря на то, что ссылка на родительский узел используется только в одном.
public bool Remove(T value)
{
BinaryTreeNode current, parent;
// Находим удаляемый узел.
current = FindWithParent(value, out parent);
if (current == null)
{
return false;
}
_count--;
//Случай 1: Если нет детей справа,
//левый ребенок встает на место удаляемого.
if (current.Right == null)
{
if (parent == null)
{
_head = current.Left;
}
else
{
int result = parent.CompareTo(current.Value);
if (result > 0)
{
//Если значение родителя больше текущего,
//левый ребенок текущего узла становится левым ребенком родителя.
parent.Left = current.Left;
}
else if (result < 0) {
//Если значение родителя меньше текущего,
// левый ребенок текущего узла становится правым ребенком родителя.
parent.Right = current.Left;
}
}
}
//Случай 2: Если у правого ребенка нет детей слева
//то он занимает место удаляемого узла.
else if (current.Right.Left == null) {
current.Right.Left = current.Left;
if (parent == null) {
_head = current.Right;
} else {
int result = parent.CompareTo(current.Value);
if (result > 0)
{
//Если значение родителя больше текущего,
//правый ребенок текущего узла становится левым ребенком родителя.
parent.Left = current.Right;
}
else if (result < 0) {
//Если значение родителя меньше текущего,
// правый ребенок текущего узла становится правым ребенком родителя.
parent.Right = current.Right;
}
}
}
//Случай 3: Если у правого ребенка есть дети слева,
//крайний левый ребенок
//из правого поддерева заменяет удаляемый узел.
else {
//Найдем крайний левый узел.
BinaryTreeNode leftmost = current.Right.Left;
BinaryTreeNode leftmostParent = current.Right;
while (leftmost.Left != null) {
leftmostParent = leftmost; leftmost = leftmost.Left;
}
//Левое поддерево родителя становится правым поддеревом
//крайнего левого узла.
leftmostParent.Left = leftmost.Right;
//Левый и правый ребенок текущего узла становится левым
//и правым ребенком крайнего левого. leftmost.
Left = current.Left;
leftmost.Right = current.Right;
if (parent == null) {
_head = leftmost;
} else {
int result = parent.CompareTo(current.Value);
if (result > 0)
{
//Если значение родителя больше текущего,
//крайний левый узел становится левым ребенком родителя.
parent.Left = leftmost;
}
else if (result < 0)
{
//Если значение родителя меньше текущего,
//крайний левый узел становится правым ребенком родителя.
parent.Right = leftmost;
}
}
}
return true;
}Метод Contains
- Поведение: Возвращает
trueесли значение содержится в дереве. В противном случает возвращаетfalse. - Сложность: O(log n) в среднем; O(n) в худшем случае.
Метод Contains выполняется с помощью метода FindWithParent, который проходит по дереву, выполняя в каждом узле следующие шаги:
- Если текущий узел
null, вернутьnull. - Если значение текущего узла равно искомому, вернуть текущий узел.
- Если искомое значение меньше значения текущего узла, установить левого ребенка текущим узлом и перейти к шагу 1.
- В противном случае, установить правого ребенка текущим узлом и перейти к шагу 1.
Поскольку Contains возвращает булево значение, оно определяется сравнением результата выполнения FindWithParent с null. Если FindWithParent вернул непустой узел, Contains возвращает true.
Метод FindWithParent также используется в методе Remove.
public bool Contains(T value)
{
//Поиск узла осуществляется другим методом.
BinaryTreeNode parent;
return FindWithParent(value, out parent) != null;
}
//Находит и возвращает первый узел с заданным значением.
//Если значение не найдено, возвращает null.
//Также возвращает родителя найденного узла (или null)
//для использования в методе Remove.
private BinaryTreeNode FindWithParent(T value,
out BinaryTreeNode parent)
{
//Попробуем найти значение в дереве.
BinaryTreeNode current = _head;
parent = null;
//До тех пор, пока не нашли...
while (current != null)
{
int result = current.CompareTo(value);
if (result > 0)
{
//Если искомое значение меньше, идем налево.
parent = current;
current = current.Left;
}
else if (result < 0)
{
//Если искомое значение больше, идем направо.
parent = current;
current = current.Right;
}
else
{
//Если равны, то останавливаемся
break;
}
}
return current;
}Метод Count
- Поведение: Возвращает количество узлов дерева или 0, если дерево пустое.
- Сложность: O(1)
Это поле инкрементируется методом Add и декрементируется методом Remove.
>public int Count
{
get
{
return _count;
}
}Метод Clear
- Поведение: Удаляет все узлы дерева.
- Сложность: O(1)
public void Clear()
{
_head = null;
_count = 0;
}Обход деревьев
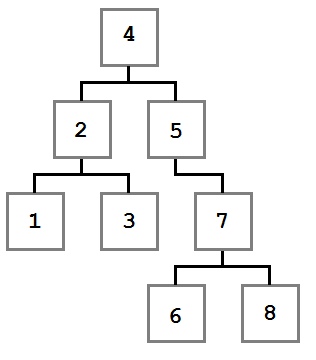
Обходы дерева — это семейство алгоритмов, которые позволяют обработать каждый узел в определенном порядке. Для всех алгоритмов обхода ниже в качестве примера будет использоваться следующее дерево:
Пример дерева для обхода
Методы обхода в примерах будут принимать параметр Action<T>, который определяет действие, поизводимое над каждым узлом.
Также, кроме описания поведения и алгоритмической сложности метода будет указываться порядок значений, полученный при обходе.
Метод Preorder (или префиксный обход)
- Поведение: Обходит дерево в префиксном порядке, выполняя указанное действие над каждым узлом.
- Сложность: O(n)
- Порядок обхода: 4, 2, 1, 3, 5, 7, 6, 8
При префиксном обходе алгоритм получает значение текущего узла перед тем, как перейти сначала в левое поддерево, а затем в правое. Начиная от корня, сначала мы получим значение 4. Затем таким же образом обходятся левый ребенок и его дети, затем правый ребенок и все его дети.
Префиксный обход обычно применяется для копирования дерева с сохранением его структуры.
public void PreOrderTraversal(Action action)
{
PreOrderTraversal(action, _head);
}
private void PreOrderTraversal(Action action, BinaryTreeNode node)
{
if (node != null)
{
action(node.Value);
PreOrderTraversal(action, node.Left);
PreOrderTraversal(action, node.Right);
}
}Метод Postorder (или постфиксный обход)
- Поведение: Обходит дерево в постфиксном порядке, выполняя указанное действие над каждым узлом.
- Сложность: O(n)
- Порядок обхода: 1, 3, 2, 6, 8, 7, 5, 4
При постфиксном обходе мы посещаем левое поддерево, правое поддерево, а потом, после обхода всех детей, переходим к самому узлу.
Постфиксный обход часто используется для полного удаления дерева, так как в некоторых языках программирования необходимо убирать из памяти все узлы явно, или для удаления поддерева. Поскольку корень в данном случае обрабатывается последним, мы, таким образом, уменьшаем работу, необходимую для удаления узлов.
public void PostOrderTraversal(Action action)
{
PostOrderTraversal(action, _head);
}
private void PostOrderTraversal(Action action, BinaryTreeNode node)
{
if (node != null)
{
PostOrderTraversal(action, node.Left);
PostOrderTraversal(action, node.Right);
action(node.Value);
}
}Метод Inorder (или инфиксный обход)
- Поведение: Обходит дерево в инфиксном порядке, выполняя указанное действие над каждым узлом.
- Сложность: O(n)
- Порядок обхода: 1, 2, 3, 4, 5, 6, 7, 8
Инфиксный обход используется тогда, когда нам надо обойти дерево в порядке, соответствующем значениям узлов. В примере выше в дереве находятся числовые значения, поэтому мы обходим их от самого маленького до самого большого. То есть от левых поддеревьев к правым через корень.
В примере ниже показаны два способа инфиксного обхода. Первый — рекурсивный. Он выполняет указанное действие с каждым узлом. Второй использует стек и возвращает итератор для непосредственного перебора.
Public void InOrderTraversal(Action action)
{
InOrderTraversal(action, _head);
}
private void InOrderTraversal(Action action, BinaryTreeNode node)
{
if (node != null)
{
InOrderTraversal(action, node.Left);
action(node.Value);
InOrderTraversal(action, node.Right);
}
}
public IEnumerator InOrderTraversal()
{
// Это нерекурсивный алгоритм.
// Он использует стек для того, чтобы избежать рекурсии.
if (_head != null)
{
// Стек для сохранения пропущенных узлов.
Stack stack = new Stack();
BinaryTreeNode current = _head;
// Когда мы избавляемся от рекурсии, нам необходимо
// запоминать, в какую стороны мы должны двигаться.
bool goLeftNext = true;
// Кладем в стек корень.
stack.Push(current);
while (stack.Count > 0)
{
// Если мы идем налево...
if (goLeftNext)
{
// Кладем все, кроме самого левого узла на стек.
// Крайний левый узел мы вернем с помощю yield.
while (current.Left != null)
{
stack.Push(current);
current = current.Left;
}
}
// Префиксный порядок: left->yield->right.
yield return current.Value;
// Если мы можем пойти направо, идем.
if (current.Right != null)
{
current = current.Right;
// После того, как мы пошли направо один раз,
// мы должным снова пойти налево.
goLeftNext = true;
}
else
{
// Если мы не можем пойти направо, мы должны достать родительский узел
// со стека, обработать его и идти в его правого ребенка.
current = stack.Pop();
goLeftNext = false;
}
}
}
}Метод GetEnumerator
- Поведение: Возвращает итератор для обхода дерева инфиксным способом.
- Сложность: Получение итератора — O(1). Обход дерева — O(n).
public IEnumerator GetEnumerator()
{
return InOrderTraversal();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
return GetEnumerator();
}Продолжение следует
На этом мы заканчивает пятую часть руководства по алгоритмам и структурам данных. В следующей статье мы рассмотрим множества (Set).
Перевод статьи «The Binary Search Tree»
При решении задач на двоичное кодирование используют «двоичное дерево».
Двоичное дерево — это схема, по которой можно определить, сколько вариантов кодов можно получить исходя из длины цепочки символов.
Каждый уровень в данном дереве — это разряд кода.
|
|
|
|
| Рис. (1). Один уровень двоичного дерева | Рис. (2). Два уровня двоичного дерева | Рис. (3). Три уровня двоичного дерева |
На рис. (1) один уровень, и получаем два кода: (0) и (1). На рис. (2) два уровня, и получаем четыре кода (читаем сверху вниз): (11), (10), (01), (00).
Задача (1). С помощью двоичного дерева составь двоичные коды для букв А, Б, В, Г.
Решение.
Кодом длиной в один знак можно закодировать только две буквы:
Рис. (4). Кодирование двух букв
А — (0).
Б — (1).
А нам нужно закодировать (4) буквы, значит, надо построить дерево в два уровня, т. е. длина цепочки будет в два знака.
Рис. (5). Кодирование четырёх букв
Коды для А — (00), Б — (01), В — (10), Г — (11).
Источники:
Рис. 1. Один уровень двоичного дерева. © ЯКласс.
Рис. 2. Два уровня двоичного дерева. © ЯКласс.
Рис. 3. Три уровня двоичного дерева. © ЯКласс.
Рис. 4. Кодирование двух букв. © ЯКласс.
Рис. 5. Кодирование четырёх букв. © ЯКласс.
Перепечатка, пожалуйста, укажите источник, часть материалов цитируетсяблог бананана
——————————————————————————————————————————————
Не говори, что не знаешь, что такое дерево ╮(─▽─)╭(Помочь вам Baidu)
Предварительные знания: дерево сегментов dfs order
——————————————————————————————————————————————
Давайте сначала рассмотрим два вопроса:
1. Добавьте z ко всем узлам на кратчайшем пути дерева от x до y
Это также шаблонный вопрос: мы можем легко думать, что различие в дереве может решить эту проблему с превосходной сложностью O (n + m).
2. Найти сумму значений всех узлов на кратчайшем пути дерева от узлов x до y
Поскольку мы имеем дело с большой проблемой с водой, dfs O (n) предварительно обрабатывает dis каждого узла (т. е. кратчайший путь до корневого узла).
Затем для каждого запроса найдите lca в двух точках x и y и используйте свойства lca distance (x, y) = dis (x) + dis (y) -2 * dis (lca), чтобы найти результат
Временная сложность O (mlogn + n)
Теперь подумай об одномbug:
Что если два вопроса, которые были объединены, были двумя операциями, которые стали одной проблемой?
Предыдущий метод явно недостаточно хорош (вы должны запускать dfs для обновления dis перед каждым запросом)
——————————————————————————————————————————————
Дебютная цепочка дебютирует великолепно
Разделение дерева — это разбиение дерева на несколько цепочек с помощью разделения по легким и тяжелым краям, а затем использование структур данных для поддержки этих цепочек (по сути, это оптимизация).
Сначала уточнить понятие:
Тяжелый сын: узел с наибольшим числом узлов нейтронного дерева (наибольший размер) среди всех сыновей узла-отца;
Легкий сын: сын, кроме тяжелого сына в узле отца;
Двойной край: край, образованный отцовским узлом и тяжелым сыном;
Светлый край: край, образованный отцовским узлом и легким сыном;
Тяжелая цепь: путь, образованный соединением нескольких тяжелых краев;
Легкая цепь: путь, составленный из нескольких легких краев;
Например, на рисунке выше узлы, соединенные черными линиями, являются тяжелыми узлами, а остальные — легкими узлами.
2-11 — тяжелая цепь, 2-5 — легкая цепь, а красная точка — начальная точка тяжелой цепи, где расположен узел, который является верхним узлом, упомянутым ниже.
Кроме того, значение каждого ребра фактически является номером выполнения при выполнении dfs.
Объявление переменной:
const int maxn=1e5+10;
struct edge{
int next,to;
}e[2*maxn];
struct Node{
int sum,lazy,l,r,ls,rs;
}node[2*maxn];
int rt,n,m,r,a[maxn],cnt,head[maxn],f[maxn],d[maxn],size[maxn],son[maxn],rk[maxn],top[maxn],id[maxn];
| имя | объяснение |
|---|---|
| f[u] | Сохранить родительский узел узла u |
| d[u] | Сохранить значение глубины узла u |
| size[u] | Сохраните количество узлов поддерева, укорененных в u |
| son[u] | Спаси тяжелого сына |
| rk[u] | Сохраните узел, соответствующий текущей метке DFS в дереве |
| top[u] | Сохранить верхний узел цепочки текущего узла |
| id[u] | Сохраните новый номер после разделения каждого узла в дереве (порядок выполнения DFS) |
Все, что нам нужно сделать, это (реализация разбиения цепочки деревьев):
1. Для точки, мы сначала находим размер поддерева, в котором оно находится, и находим его тяжелого сына (то есть обрабатываем размер, массив сына),
Пояснение: скажем, пункт 1, у него есть три сына 2, 3, 4
Размер поддерева 2 составляет 5
Размер поддерева 3 равен 2
Размер поддерева 4 равен 6
Тогда сыну 1 4 года
ps: если поддеревья множества сыновей точки равны по размеру и наибольшему
Тогда просто найди одного из его лучших сыновей.
Листовые узлы не имеют тяжелых сыновей, не листовые узлы имеют только одного тяжелого сына
2. В процессе dfs запишите отца и глубину (то есть обработайте массив f, d). Операции 1, 2 могут быть снова выполнены dfs
void dfs1 (int u, int fa, int deep) // Текущий узел, родительский узел и глубина слоя
{
f[u]=fa;
d[u]=depth;
size [u] = 1; // сама точка size = 1
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v==fa)
continue;
dfs1 (v, u, глубина + 1); // уровень глубины + 1
size [u] + = size [v]; // Размер дочернего узла обработан, используйте его для обновления размера родительского узла
if(size[v]>size[son[u]])
son [u] = v; // Выберите самый большой размер как тяжелый сын
}
}
// ввод
dfs1(root,0,1);
dfs1, вероятно, так, вы можете смоделировать его вручную
3. Передайте dfs второй раз, затем подключите тяжелую цепочку и отметьте порядок dfs каждого узла в одно и то же время. Чтобы поддерживать тяжелую цепочку со структурой данных, мы гарантируем, что порядок dfs каждого узла в тяжелой цепочке является непрерывным (то есть обрабатывает массив). top, id, rk)
void dfs2 (int u, int t) // Текущий узел, вершина тяжелой цепи
{
top[u]=t;
id [u] = ++ cnt; // Пометить порядок в dfs
rk [cnt] = u; // последовательность cnt соответствует узлу u
if(!son[u])
return;
dfs2(son[u],t);
/ * Мы решили сначала ввести тяжелого сына, чтобы убедиться, что порядок dfs каждого узла в тяжелой цепи непрерывен.
Точка находится на той же тяжелой цепи, что и ее тяжелый сын, поэтому вершина тяжелой цепи, где находится тяжелый сын, по-прежнему обозначена * /
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v!=son[u]&&v!=f[u])
dfs2 (v, v); // Точка находится внизу легкой цепи, поэтому ее вершина должна быть самой
}
}
DFS1, вероятно, так, вы можете смоделировать его вручную
4. Двойной проход dfs является основной обработкой разбиения цепочки деревьев. Благодаря dfs мы обеспечили непрерывность dfs каждого узла в тяжелой цепочке. Тогда мы можем думать, что мы можем поддерживать тяжелую цепочку через структуру данных (в качестве примера рассмотрим дерево строк) информация
Возвращаясь к предыдущему разделу, принципы модификации и работы с запросами аналогичны: на примере операции запроса это фактически LCA, но top используется здесь для ускорения, поскольку top может напрямую переходить к началу тяжелой цепочки. Точка, у легкой цепи нет стартового узла, их вершина — это они сами. Следует отметить, что каждый цикл может прыгать только один раз, и позволить тому, у которого самый глубокий узел, переместиться в положение вершины, чтобы избежать двух одновременных пропусков и прохождения.
int sum(int x,int y)
{
int ans=0,fx=top[x],fy=top[y];
while (fx! = fy) // Две точки не в одной тяжелой цепи
{
if(d[fx]>=d[fy])
{
ans + = query (id [fx], id [x], rt); // Сумма сегментов дерева и обработка вклада этой тяжелой цепочки
x = f [fx], fx = top [x]; // Установить x в качестве родительского узла исходной головки цепи, взять светлую сторону и продолжить цикл
}
else
{
ans+=query(id[fy],id[y],rt);
y=f[fy],fy=top[y];
}
}
// Конец цикла, две точки находятся в одной и той же тяжелой цепи, но эти две точки не обязательно являются одной и той же точкой, поэтому мы также должны посчитать вклады между двумя точками
if(id[x]<=id[y])
ans+=query(id[x],id[y],rt);
else
ans+=query(id[y],id[x],rt);
return ans;
}
Если вы понимаете разделение древовидной цепочки, у вас также должна быть возможность учиться у других (у меня нет так или иначе), и модификация и LCA будут предоставлены каждому для завершения.
5. Временная сложность расщепления цепочки деревьев
Два свойства расщепления цепочки деревьев:
1, если (u, v) — светлый край, то size (v) <size (u) / 2;
2. Количество легких и тяжелых цепей, которые дорога проходит от корневого узла к любому узлу, должно быть меньше logn;
Можно доказать, что временная сложность расщепления цепочки деревьев равна O (nlog ^ 2n)
Несколько примеров вопросов:
1,Шаблон расщепления цепочки деревьев
это то, что я только что сказал
В коде:
#include<iostream>
#include<cstdio>
#define int long long
using namespace std;
const int maxn=1e5+10;
struct edge{
int next,to;
}e[maxn*2];
struct node{
int l,r,ls,rs,sum,lazy;
}a[maxn*2];
int n,m,r,rt,mod,v[maxn],head[maxn],cnt,f[maxn],d[maxn],son[maxn],size[maxn],top[maxn],id[maxn],rk[maxn];
void add(int x,int y)
{
e[++cnt].next=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void dfs1(int x)
{
size[x]=1,d[x]=d[f[x]]+1;
for(int v,i=head[x];i;i=e[i].next)
if((v=e[i].to)!=f[x])
{
f[v]=x,dfs1(v),size[x]+=size[v];
if(size[son[x]]<size[v])
son[x]=v;
}
}
void dfs2(int x,int tp)
{
top[x]=tp,id[x]=++cnt,rk[cnt]=x;
if(son[x])
dfs2(son[x],tp);
for(int v,i=head[x];i;i=e[i].next)
if((v=e[i].to)!=f[x]&&v!=son[x])
dfs2(v,v);
}
inline void pushup(int x)
{
a[x].sum=(a[a[x].ls].sum+a[a[x].rs].sum)%mod;
}
void build(int l,int r,int x)
{
if(l==r)
{
a[x].sum=v[rk[l]],a[x].l=a[x].r=l;
return;
}
int mid=l+r>>1;
a[x].ls=cnt++,a[x].rs=cnt++;
build(l,mid,a[x].ls),build(mid+1,r,a[x].rs);
a[x].l=a[a[x].ls].l,a[x].r=a[a[x].rs].r;
pushup(x);
}
inline int len(int x)
{
return a[x].r-a[x].l+1;
}
inline void pushdown(int x)
{
if(a[x].lazy)
{
int ls=a[x].ls,rs=a[x].rs,lz=a[x].lazy;
(a[ls].lazy+=lz)%=mod,(a[rs].lazy+=lz)%=mod;
(a[ls].sum+=lz*len(ls))%=mod,(a[rs].sum+=lz*len(rs))%=mod;
a[x].lazy=0;
}
}
void update(int l,int r,int c,int x)
{
if(a[x].l>=l&&a[x].r<=r)
{
(a[x].lazy+=c)%=mod,(a[x].sum+=len(x)*c)%=mod;
return;
}
pushdown(x);
int mid=a[x].l+a[x].r>>1;
if(mid>=l)
update(l,r,c,a[x].ls);
if(mid<r)
update(l,r,c,a[x].rs);
pushup(x);
}
int query(int l,int r,int x)
{
if(a[x].l>=l&&a[x].r<=r)
return a[x].sum;
pushdown(x);
int mid=a[x].l+a[x].r>>1,tot=0;
if(mid>=l)
tot+=query(l,r,a[x].ls);
if(mid<r)
tot+=query(l,r,a[x].rs);
return tot%mod;
}
inline int sum(int x,int y)
{
int ret=0;
while(top[x]!=top[y])
{
if(d[top[x]]<d[top[y]])
swap(x,y);
(ret+=query(id[top[x]],id[x],rt))%=mod;
x=f[top[x]];
}
if(id[x]>id[y])
swap(x,y);
return (ret+query(id[x],id[y],rt))%mod;
}
inline void updates(int x,int y,int c)
{
while(top[x]!=top[y])
{
if(d[top[x]]<d[top[y]])
swap(x,y);
update(id[top[x]],id[x],c,rt);
x=f[top[x]];
}
if(id[x]>id[y])
swap(x,y);
update(id[x],id[y],c,rt);
}
signed main()
{
scanf("%lld%lld%lld%lld",&n,&m,&r,&mod);
for(int i=1;i<=n;i++)
scanf("%lld",&v[i]);
for(int x,y,i=1;i<n;i++)
{
scanf("%lld%lld",&x,&y);
add(x,y),add(y,x);
}
cnt=0,dfs1(r),dfs2(r,r);
cnt=0,build(1,n,rt=cnt++);
for(int op,x,y,k,i=1;i<=m;i++)
{
scanf("%lld",&op);
if(op==1)
{
scanf("%lld%lld%lld",&x,&y,&k);
updates(x,y,k);
}
else if(op==2)
{
scanf("%lld%lld",&x,&y);
printf("%lldn",sum(x,y));
}
else if(op==3)
{
scanf("%lld%lld",&x,&y);
update(id[x],id[x]+size[x]-1,y,rt);
}
else
{
scanf("%lld",&x);
printf("%lldn",query(id[x],id[x]+size[x]-1,rt));
}
}
return 0;
}
2, [NOI2015] менеджер пакетов
Заметил, что заголовок требует поддержки двух операций
1, установить х: указывает на установку пакета х
2, удалить х: удалить пакет х
Для первой операции мы можем подсчитать количество пакетов, которые не установлены от x до корневого узла, а затем изменить интервал, который нужно установить.
Для второй операции мы можем подсчитать количество установленных пакетов в поддереве, где находится x, и затем изменить поддерево, чтобы оно не было установлено.
В коде:
#include<iostream>
#include<cstdio>
#define int long long
using namespace std;
const int maxn=1e5+10;
struct edge{
int next,to;
}e[2*maxn];
struct Node{
int l,r,ls,rs,sum,lazy;
}node[2*maxn];
int rt,n,m,cnt,head[maxn];
int f[maxn],d[maxn],size[maxn],son[maxn],rk[maxn],top[maxn],tid[maxn];
int readn()
{
int x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
ch=getchar();
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+ch-'0';
ch=getchar();
}
return x;
}
void add_edge(int x,int y)
{
e[++cnt].next=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void dfs1(int u,int fa,int depth)
{
f[u]=fa;
d[u]=depth;
size[u]=1;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v==fa)
continue;
dfs1(v,u,depth+1);
size[u]+=size[v];
if(size[v]>size[son[u]]||!son[u])
son[u]=v;
}
}
void dfs2(int u,int t)
{
top[u]=t;
tid[u]=++cnt;
rk[cnt]=u;
if(!son[u])
return;
dfs2(son[u],t);
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(v!=son[u]&&v!=f[u])
dfs2(v,v);
}
}
void pushup(int x)
{
int lson=node[x].ls,rson=node[x].rs;
node[x].sum=node[lson].sum+node[rson].sum;
node[x].l=node[lson].l;
node[x].r=node[rson].r;
}
void build(int li,int ri,int cur)
{
if(li==ri)
{
node[cur].ls=node[cur].rs=node[cur].lazy=-1;
node[cur].l=node[cur].r=li;
return;
}
int mid=(li+ri)>>1;
node[cur].ls=cnt++;
node[cur].rs=cnt++;
build(li,mid,node[cur].ls);
build(mid+1,ri,node[cur].rs);
pushup(cur);
}
void pushdown(int x)
{
int lson=node[x].ls,rson=node[x].rs;
node[lson].sum=node[x].lazy*(node[lson].r-node[lson].l+1);
node[rson].sum=node[x].lazy*(node[rson].r-node[rson].l+1);
node[lson].lazy=node[x].lazy;
node[rson].lazy=node[x].lazy;
node[x].lazy=-1;
}
void update(int li,int ri,int c,int cur)
{
if(li<=node[cur].l&&node[cur].r<=ri)
{
node[cur].sum=c*(node[cur].r-node[cur].l+1);
node[cur].lazy=c;
return;
}
if(node[cur].lazy!=-1)
pushdown(cur);
int mid=(node[cur].l+node[cur].r)>>1;
if(li<=mid)
update(li,ri,c,node[cur].ls);
if(mid<ri)
update(li,ri,c,node[cur].rs);
pushup(cur);
}
int query(int li,int ri,int cur)
{
if(li<=node[cur].l&&node[cur].r<=ri)
return node[cur].sum;
if(node[cur].lazy!=-1)
pushdown(cur);
int tot=0;
int mid=(node[cur].l+node[cur].r)>>1;
if(li<=mid)
tot+=query(li,ri,node[cur].ls);
if(mid<ri)
tot+=query(li,ri,node[cur].rs);
return tot;
}
int sum(int x)
{
int ans=0;
int fx=top[x];
while(fx)
{
ans+=tid[x]-tid[fx]-query(tid[fx],tid[x],rt)+1;
update(tid[fx],tid[x],1,rt);
x=f[fx];
fx=top[x];
}
ans+=tid[x]-tid[0]-query(tid[0],tid[x],rt)+1;
update(tid[0],tid[x],1,rt);
return ans;
}
signed main()
{
n=readn();
for(int i=1;i<n;i++)
{
int x=readn();
add_edge(x,i);
add_edge(i,x);
}
cnt=0;
dfs1(0,-1,1);
dfs2(0,0);
cnt=0;
rt=cnt++;
build(1,n,rt);
m=readn();
for(int i=1;i<=m;i++)
{
int x;
string op;
cin>>op;
x=readn();
if(op=="install")
printf("%lldn",sum(x));
else if(op=="uninstall")
{
printf("%lldn",query(tid[x],tid[x]+size[x]-1,rt));
update(tid[x],tid[x]+size[x]-1,0,rt);
}
}
return 0;
}
3, [SDOI2011] окрашивание
Есть несколько вопросов о содержании мышления
Невозможно просто добавить между регионами при подсчете количества цветовых сегментов
Дерево сегментов также должно поддерживать самый левый цвет интервала и самый правый цвет интервала
При слиянии
Если правый конец S (l, k) совпадает с левым концом S (k + 1, r), то S (l, r) = S (l, k) + S (k + 1, r) -1 Повторить один)
В противном случае S (l, r) = S (l, k) + S (k + 1, r)
Вот и все, спасибо за сообщения в блоге от двух dalaus!
orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz orz
На уроках истории дети изучают династию Романовых. Согласитесь, не самое увлекательное занятие: она прекратила существовать в далеком 1917 году. Исследовать родословную своей семьи интереснее, ведь она продолжает разрастаться по сей день. В этой статье вы узнаете, как сделать фамильное древо семьи своими руками.
Что такое генеалогическое древо
Схема родственных связей в виде дерева. Чтобы понять, зачем она нужна, вернемся к Романовым. За время правления сменилось несколько поколений. Кто за кем следовал? Можно прочитать учебник от корки до корки, и ничего не запомнить. Генеалогическое дерево семьи — «шпаргалка», где можно отобразить порядок и типы связей между родственниками.
Виды древа
Всего их 4. Выбор будет зависеть от количества имеющейся информации и того, сколько времени вы согласны потратить на работу.
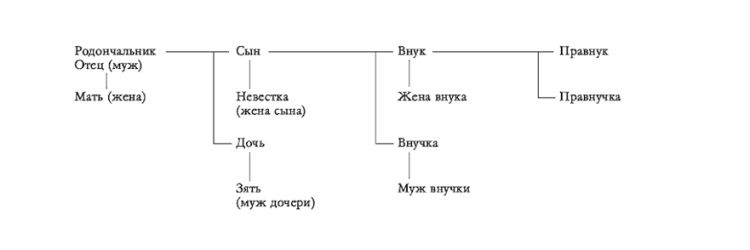
Нисходящее
Цепочка родословной строится сверху вниз: от предка к потомкам. Указываются все кровные связи, поэтому от вас требуется тщательная подготовка. Может объединять сотни людей.
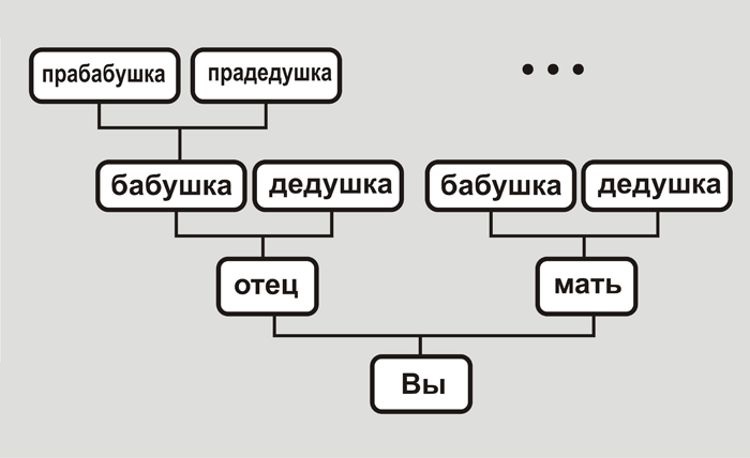
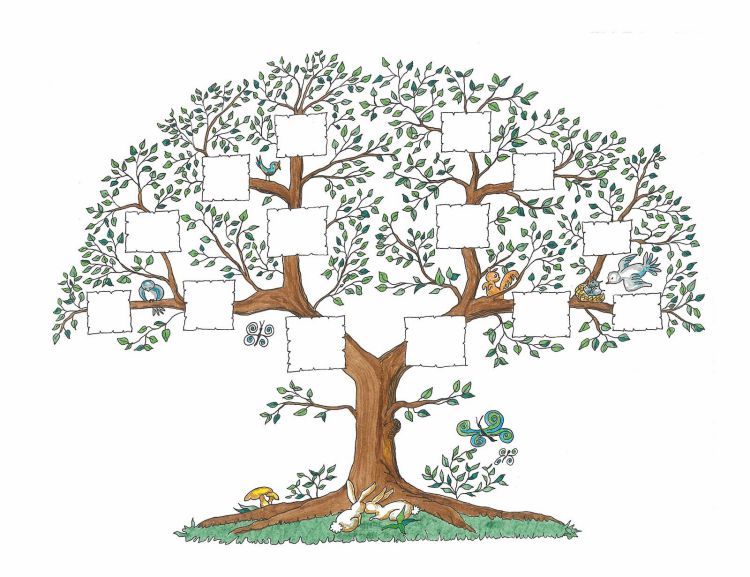
Восходящее
Схема растет вверх. Потомок находится у подножия, а предков «рассаживают» по ветвям. Соответственно, крону дерева венчает старший из них. Оптимальный вариант, если материалов не хватает: достаточно изучить прямые связи. Братья и сестры не указываются.
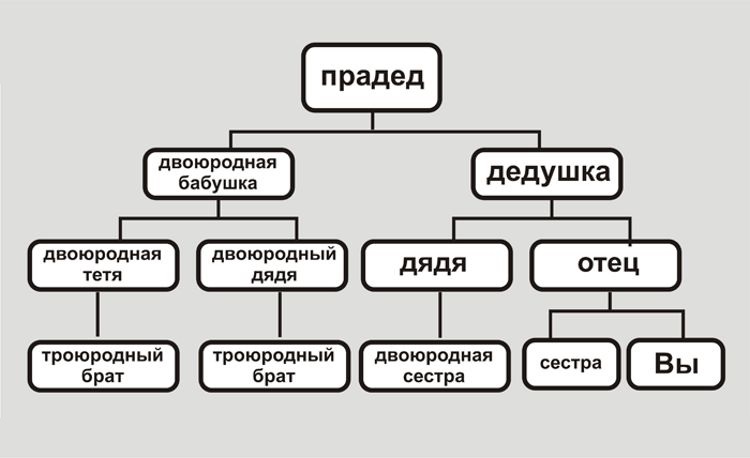
Горизонтальное
Заполняется слева направо, по старшинству. Этот вид наиболее распространен в европейских странах. Может включать как прямые, так и косвенные связи.
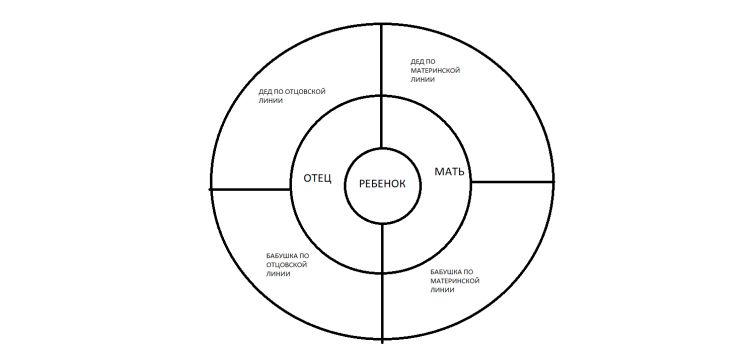
Круговая схема
Родословная изображается в форме круга или полукруга. В центре располагают ребенка. Следующий круг делится на 2 части (для мамы и папы), третий — на 4 и т.д.
Как составить родословную
Перед тем, как составить генеалогическое древо семьи, нужно провести тщательное исследование. Сделать это в одиночку достаточно сложно. Вам помогут:
Старшие родственники
Ваша бабуля наверняка знает, как зовут мужа троюродной сестры тети Лены из Владивостока, и будет рада поболтать на эту тему. Подготовьте вопросы и запаситесь снимками из семейного архива. Так вы сможете узнать не только сухие факты, но и забавные случаи из жизни.
Фотоальбомы
Решили пересмотреть старые альбомы и нашли кого-то незнакомого? Используйте дедукцию. По качеству пленки, одежде и макияжу легко понять, где и когда была сделана фотография.
В 70-е девушки носили полосатые брюки-клеш, а в 90-е — мини-юбки и яркие олимпийки. Эти зацепки натолкнут вас на правильный ответ.
На обратной стороне фото можно найти подпись, поэтому не забывайте заглядывать и туда.
Уцелевшие документы
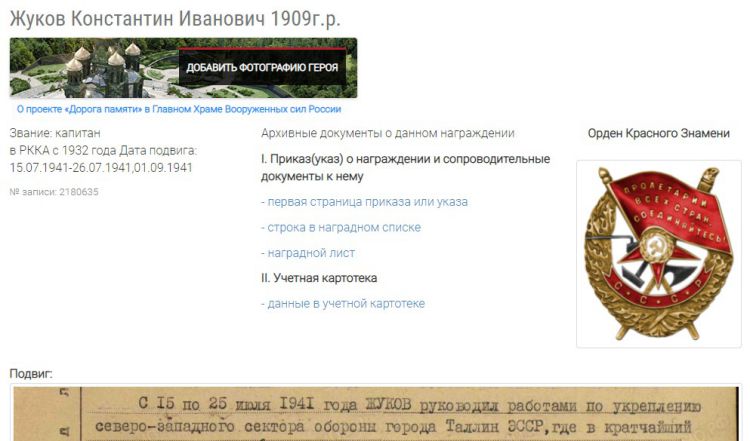
Старшее поколение бережно хранит письма, грамоты, дипломы и прочие документы. Настолько, что медаль прадеда, которую тот получил за оборону Ленинграда, выглядит как новенькая. При ней есть наградной лист, с указанием имени, даты и подвига. Это ценный материал для школьного доклада и еще один повод гордиться своими корнями.
Сюда же относятся пресса. Вдруг при жизни он стал героем репортажа? Посетите местную библиотеку: там могли остаться старые выпуски газет.
Интернет
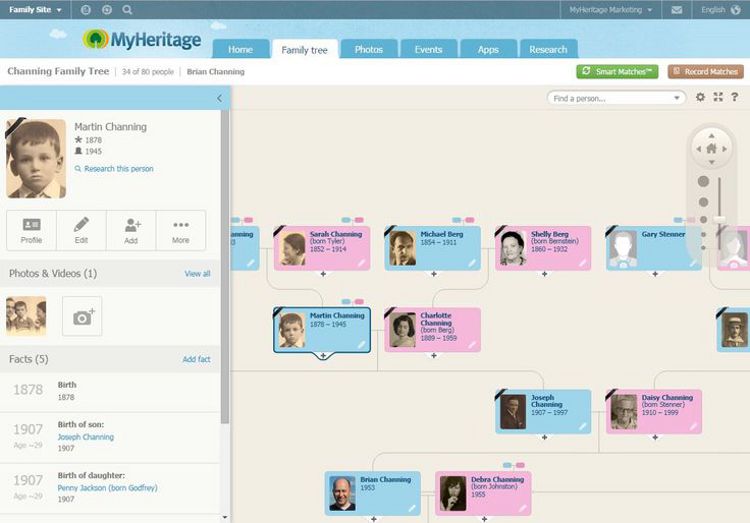
Если все вышеперечисленное хранится на даче, а она глубоко в Сибири, поможет интернет. Существуют специальные платформы (например, MyHeritage) для поиска людей по определенным критериям. Его результативность зависит от объема имеющихся данных.
Великая Отечественная война занимает в истории России особое место. Для сбора информации об участниках боевых действий воспользуйтесь сайтами Подвиг народа или Память народа. Они предоставляют сведения о звании, награждениях, дате призыва и т.д.
Государственный архив
Долгий, но наиболее эффективный способ. Чтобы собрать данные о родственнике из Хабаровска, нужно ехать в Хабаровск. Городские или районные архивы хранят документы
о тех, кто родился или проживал на их территории.
Можно обратиться в ЗАГС. Если у вас есть документ, подтверждающий генетическое родство
с прабабушкой, работники с радостью посодействуют созданию древа. Вам выдадут ее свидетельство о рождении, заключении брака, смерти.
Профессионалы
Стоимость генеалогического исследования начинается от 30 000 рублей. Специалисты найдут информацию о ваших предках, проверят факты на достоверность и оформят родословную в виде книги. В среднем поиск сведений о 3-5 поколениях занимает 2-3 недели работы.
Как оформить древо
Есть несколько способов. Логично предположить, что какой-то из них занимает меньше времени. Это не совсем так. Чтобы нарисовать дерево, уйдет несколько часов. Можно воспользоваться компьютером, но тогда фотографии необходимо отсканировать и обработать. Сделать это на пару минут тоже не получится.
Нарисовать
Если речь идет о школьном задании, оптимальный вариант. Здесь не требуется изучать историю рода до эпохи царствования Ивана Грозного. Понадобятся цветные карандаши, ластик, клей, фотокарточки (или их копии) и бумага.
Нарисуйте ствол и ветви дерева, пышную крону. По ней нужно разбросать несколько ячеек, внутри которых будут портреты. Подпишем их ниже: можно изобразить раскрытый папирус
с загнутыми краями или обычные полосочки. Когда черновой вариант вас удовлетворит, приступайте к раскрашиванию и заполните крону.
Почему этот способ не подойдет для всех? Если данных много, составление дерева продлится долго. При этом никто не застрахован от ошибок: они могут обнаружиться после окончания работы. Тогда встает вопрос, как ее исправить. В компьютерной программе это займет пару минут. На бумаге так не получится — придется начинать все с начала.
Создать на компьютере
Как составить родословную на ПК? Ранее мы рассказывали, почему данный способ гораздо удобнее. Посмотрим, что вам понадобится.
Подготовить фото
Нужно прошерстить старые альбомы, выбрать портреты и сделать цифровые копии. Если нет ничего подходящего, используйте групповые фото. Обрезать других людей можно в редакторе.
Иногда снимкам необходимо восстановление: сказываются неправильные условия хранения, дефекты пленки. Убрать царапины, пятна и заломы поможет софт для реставрации. Некоторые программы умеют раскрашивать черно-белые кадры.
Найти шаблон
В интернете полно макетов с пустыми ячейками на 3-4 поколения. При выборе обращайте внимание на разрешение картинки: чем оно выше, тем лучше. Найти красивые шаблоны можно на платном стоке (Depositphotos или Shutterstock) и на генеалогических сайтах. Например, тут.
Программы для создания древа
Приступаем к оформлению. Для этого нужен фоторедактор или узкопрофильный софт для построения родословных. У него больше возможностей, но на их изучение потребуется время.
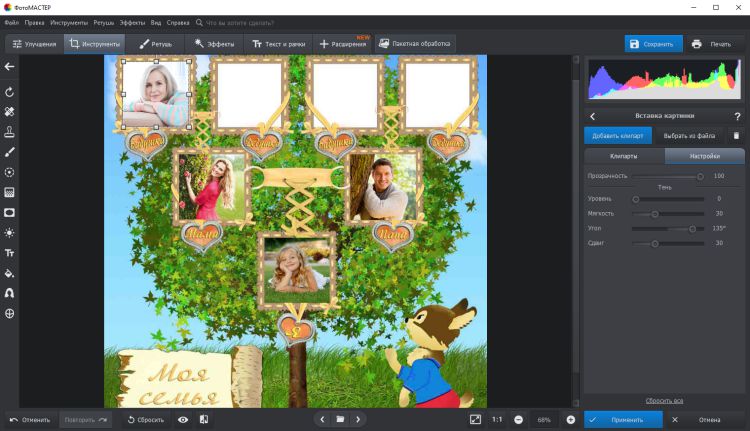
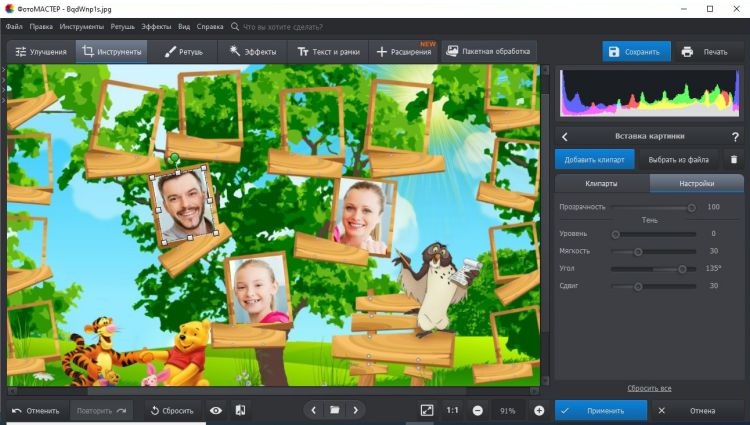
ФотоМАСТЕР
Стоимость: от 690 рублей.
Удобное приложение для обработки изображений, где можно создать фамильное дерево по шаблону. Загрузите фотографии и сделайте надписи. Чтобы добавить изюминки, используйте яркий клипарт. Готовую картинку можно распечатать или сохранить на компьютер.
Преимущества:
- куча функций для улучшения качества снимка;
- крупная библиотека шрифтов;
- 100+ фильтров для стилизации;
- простое управление.
Как оформить генеалогическое древо: краткая инструкция
- Запустите редактор и кликните «Открыть фото». Найдите нужный шаблон.
- Начнем с фотографий. Перейдите в «Инструменты» и щелкните по кнопке «Вставка картинки» -> «Наложить изображение из файла». Чтобы параметры фото соответствовали размеру окошка, понятие за края рамки. Вы можете повернуть снимок, зажав зеленый кружочек. Также на панели слева можно изменить прозрачность и сделать тень.
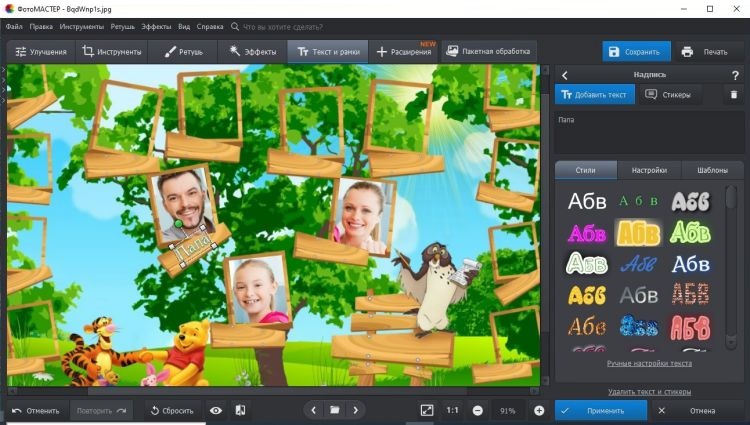
- Добавить надпись можно во вкладке «Текст и рамки». Там вас ждут 150+ дизайнерских шрифтов. Выберите понравившийся или создайте уникальный стиль в «Настройках». После этого переместите надпись, куда требуется.
- Когда работа будет окончена, нажмите «Сохранить». Теперь остается установить нужное качество и определить формат экспорта. Готово!
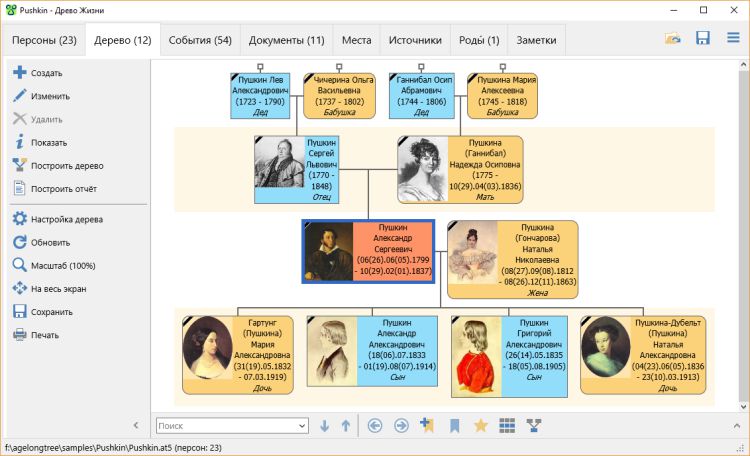
Древо Жизни
Стоимость: от 1 200 рублей.
Программа для построения генеалогических деревьев. Автоматически устанавливает степени родства и располагает членов семьи согласно их статусу. Позволяет прикреплять фото, аудио и видеоматериалы, документы. Поддерживает экспорт в PNG и SVG-форматы.
Преимущества:
- вычисляет статистику: средняя продолжительность жизни, количество женщин и т.д.;
- отображает памятные даты, место жительства, профессии;
- широкий выбор фонов.
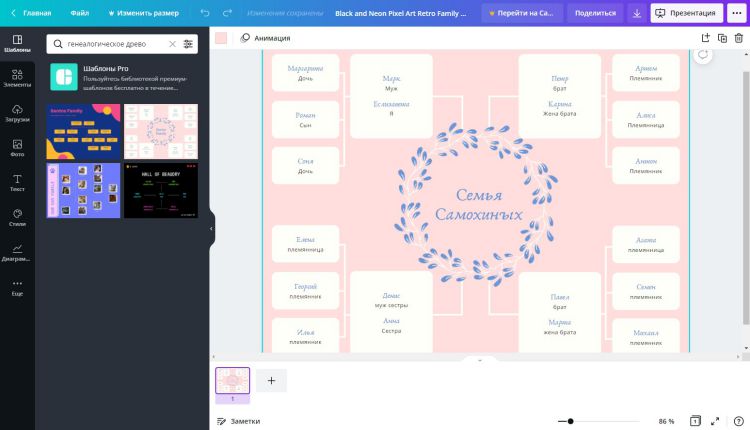
Canva
Стоимость: 499 рублей/месяц.
Онлайн-редактор Canva предлагает неплохие шаблоны. Вы можете поэкспериментировать
с различными образцами или построить схему самостоятельно, а после добавить графические элементы. К примеру, разместить сердечко между супругами. Готовый проект можно сохранить как обычное изображение, видео, GIF или PDF-файл.
Преимущества:
- коллекция рамок;
- инструменты для создания анимации;
- возможна настройка совместного доступа;
- 5 ГБ облачного хранилища.
MyHeritage
Стоимость: 89$/год.
Эта платформа пользуется большой популярностью. После регистрации MyHeritage автоматически начнет поиск совпадений. Если ветви вашего дерева пересекаются с проектом другого пользователя, на почту придет уведомление.
Преимущества:
- собственная база данных;
- технология Deep Nostalgia: «оживите» старые фото за пару кликов;
- дерево может объединять несколько тысяч человек.
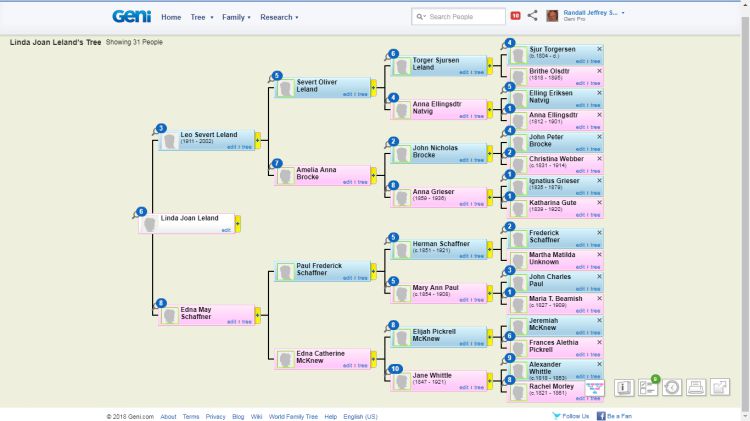
Geni
Стоимость: 120$/год.
Geni содержит свыше десятка инструментов для исследований. Если кто-то из родственников уже пользуется этим сервисом, Geni правильно объединит ваши ветви. При заполнении карточки персоны можно указать место учебы, работы, любопытные факты из биографии.
Преимущества:
- понятный интерфейс;
- внутренняя социальная сеть: общайтесь с другими пользователями,
вступайте в сообщества по интересам; - создание семейной статистики.
Заключение
Как составить семейное древо самому? Мы рассмотрели все возможные варианты. Компьютерные программы и онлайн-платформы подходят тем, кто хочет систематизировать информацию. Если же вы уверены в своих навыках рисования и хотите получить красивый результат, изобразите дерево на бумаге. Впрочем, какой бы способ вы ни выбрали, приготовьтесь к увлекательному путешествие в прошлое.
Эти статьи могут вам понравиться:
Лесов на нашей планете множество и их даже разделяют на несколько природных зон. Например это зона тайги, смешанных лесов, широколиственных лесов.
Для каждого из этих лесов характерен свой видовой состав растений и животных и свои цепи питания.
Рассмотрим модель цепи питания тайги, в которой растут только хвойные деревья:
Кедровые орехи — Белка — Куница — Рысь.
А вот модель цепи питания смешанного леса, в которых есть и хвойные и лиственные деревья:
Ягоды — Мышь — Лиса — Волк.
И наконец схема, модель питания широколиственного леса, в котором растут теплолюбивые лиственные деревья:
Желуди — Кабан
Желуди — Сойка — Беркут.
Графически эти схемы питания можно изобразить следующим образом: