Как составить цифровое выражение

Конспект урока

Алгебра

7 класс

Урок № 13

Числовые выражения

Перечень рассматриваемых вопросов:

Числовые выражения;
Значение числового выражения;
Текстовые задачи на составление числового выражения.

Тезаурус:

Числовое выражение – это выражение, состоящее из чисел, знаков математических действий и скобок.

Значение числового выражения – результат выполненных арифметических действий в числовом выражении.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

«Числа не управляют миром, но показывают, как управляется мир» – однажды сказал немецкий писатель Иоганн Гёте. Сегодня пойдёт речь именно о числах и арифметических операциях с ними.

Мы уже неоднократно решали задачи, в которых над заданными числовыми значениями приходится выполнять арифметические действия, такие как сложение, вычитание, умножение и деление. Иногда в том или ином задании все перечисленные действия встречаются одновременно, поэтому чтобы верно вычислить значение того или иного выражения или решить задачу, нужно сначала задать правильный порядок действий.

Порядок арифметических действий.

Арифметические действия выполняются слева направо:

1) действие в скобках;

2) операции умножения или деления;

3) сложения или вычитания.

Таким образом, мы подошли к определению понятия числового выражения.

Числовое выражение – это выражение, состоящее из чисел, знаков математических действий и скобок.

Например, числовые выражения могут выглядеть так:

25 – 67 : 2 + 17 = 8,5

245 – (25 : 0,5) = 195

Если в данных выражениях выполнить все действия, т.е. получить ответ в виде действительного числа, то говорят, что получено значение числового выражения. Например, в этих числовых выражениях значения соответственно равны 8,5 и 195.

Но всегда ли можно получить значение числового выражения?

Рассмотрим следующее выражение:

245 : (25 – 12,5 : 0,5).

В данном случае выражение не имеет смысла, т.к. на некотором этапе вычисления требуется делить на ноль, но на ноль делить нельзя. Таким образом, числовое выражение имеет смысл при условии что делитель (если таковой есть) не равен нулю.

Стоит отметить, что числовое выражение может состоять только из числа.

Например, 45 и 1/2 – тоже числовые выражения.

Как уже отмечалось ранее, числовые выражения иногда используют и для решения задач.

Решим такую задачу:

Автомобиль двигался по трассе 20 км со скоростью 100 км/ч, а затем ещё 30 км со скоростью 90 км/ч. Какова средняя скорость автомобиля на всём участке?

Для решения задачи нужно вспомнить, что средняя скорость – это отношение всего пути, пройденного телом ко времени прохождения всего пути.

Решение:

V ср =

Исходя из этого, составим числовые выражения, необходимые для решения задачи.

Сначала найдём путь, который преодолел автомобиль.

20 +30 = 50 (км) – весь путь автомобиля.

Далее найдём все потраченное автомобилем время на прохождение трассы.

+ = (ч) – время движения автомобиля по всей трассе.

Остаётся определить среднюю скорость автомобиля при движении по трассе:

50: = 93,75 (км/ч) – средняя скорость движения автомобиля по трассе.

Ответ: 93,75 км/ч

Это и есть искомый ответ к данной задаче.

Эту же задачу можно решить, используя следующую таблицу.

участки	путь	скорость	время
1	20 км	100км/ч	? 20 : 100 ч
2	30 км	90км/ч	? 30 : 90 ч
весь	? 20 + 30 = 50 км	Средняя скорость ? 50 : (20 : 100 + 30 : 90) км/ч = 93,75 км/ч	? 20 : 100 + 30 : 90 = ч

Запишем все числовые данные, известные нам по условию задачи. Отметим вопросительным знаком, что неизвестно. Далее, используя формулу скорости, составляем числовые выражения и находим недостающие элементы:

– сначала время на первом, втором участках и всё время движения

– затем составляем числовое выражение для всего пути

– наконец, составляем числовое выражение для вычисления значения средней скорости.

Итак, сегодня мы получили представление о числовом выражении и его применении при решении задач.

Переходим к выполнению заданий.

Решим задачу.

В лаборатории было два куска сплава 500г и 700г, которые содержали 20% и 50% меди соответственно. Каково процентное содержание меди в сплаве, полученном из этих кусков?

Для решения данной задачи составим следующую таблицу.

сплавы	Масса сплава	% меди в сплаве	Масса меди в сплаве
1	500 г	20% : 100% = 0,2	? 500 г · 0,2 = 100г
2	700 г	50% : 100% = 0,5	? 700 г · 0,5 = 350г
3	? 500 г + 700 г = 1200г	? (450 г : 1200 г) · 100% = 37,5 %	? 100 г + 350 г = 450 г

Будем заполнять её, исходя из условия задачи. Нам известна масса 1 и 2 сплавов и процентное содержание меди в них, подставим их в таблицу. Остальные клеточки нам неизвестны. Будем находить неизвестные табличные данные, составляя числовые выражения.

Для начала переведём проценты в число, для этого составим числовые выражения:

1) 20% : 100% = 0,2 – первый сплав,

2) 50% : 100% = 0,5 – второй сплав.

Далее определим массу меди в 1и 2 сплаве:

3) 500 г · 0,2 = 100 г – масса меди в 1 сплаве,

4)700 г · 0,5 = 350 г – масса меди во 2 сплаве.

Теперь найдём массы меди в 3 сплаве:

5)100 г + 350 г = 450 г.

Найдём массу всего сплава:

6)500 г + 700 г = 1200 г.

Остаётся найти процентное содержание меди в 3 сплаве, для этого составим числовое выражение:

7)(450 г : 1200 г) · 100% = 37,5 %.

Ответ: 37,5%ю

Тренировочные задания.

1) Какое из числовых выражений соответствует следующей записи – утроенное число 9?

Варианты ответа:

9³

9 · 3

3⁹

Решение:

Для решения задачи, нужно вспомнить, что утроенное число – это значит число, умноженное на 3. Следовательно, правильный ответ – 9·3.

2) Продавец в магазине получает зарплату 30000 руб. Через некоторое время происходит повышение зарплаты на 10%, а ещё через некоторое время её увеличивают на 5%. Какова новая зарплата продавца?

Решение: Для решения задачи сначала нужно составить числовое выражение для вычисления зарплаты после повышения ее на 10%. Для этого переведём 10% в число.

1) 10% : 100% = 0,1

Далее найдём 10 % от 30000 руб.

2) 30000 · 0,1 = 3000 (руб.) – 1 повышение.

Далее найдём зарплату после первого повышения:

3) 30000 + 3000 = 33000 (руб.)

Далее переведём 5% в число:

4) 5% : 100% = 0,05

Далее найдём 5 % от 33000 руб:

5) 33000 · 0,05 = 1650 (руб.) – 2 повышение.

Остаётся найти новую зарплату продавца:

6)33000 + 1650 = 34650 (руб.).

Ответ: 34650 руб. новая зарплата.

Источник

Главная
Справочники
Справочник по математике для начальной школы
Числовые и буквенные выражения

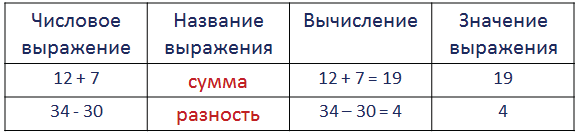
Числовые выражения

В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.

Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.

Например, 44 + 32

Значение выражения — это результат выполненных действий.

Например, в записи 44 + 32 = 76, значение выражения — это 76.

Чтение числовых выражений

12 + 9 — сумма

49 — 20 — разность

34 — (8 + 21) — из 34 вычесть сумму чисел 8 и 21

13 + (26 — — к 13 прибавить разность чисел 26 и 8

Решение числовых выражений

45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13

Сравнение значений числовых выражений

Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.

Давай сравним значения двух выражений: 14 — 6 и 18 — 9.

Для этого найдем значения каждого из них:

14 — 6 = 8

18 — 9 = 9

8 < 9, значит,

14 — 6 < 18 — 9

Буквенные выражения

Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.

В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением.

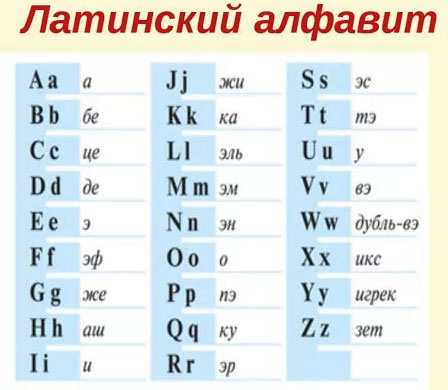
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.

Чаще всего используются буквы:

a, b, c, d, x, y, k, m, n

Алгоритм решения буквенного выражения

Алгоритм — значит, порядок, план выполнения команд.

1. Прочитать буквенное выражение

2. Записать буквенное выражение

3. Подставить значение неизвестного в выражении

4. Вычислить результат

Например, 28 – с

Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с

Подставим вместо неизвестного «с» число 4.

У нас получается выражение: 28 – 4

Вычисляем результат:

28 – 4 = 24

Переменные

Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.

Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства

c = 2, x = 3

Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:

2 + 3 + 2

Теперь мы можем найти значение этого выражения:

с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7

Советуем посмотреть:

Уравнения

Правило встречается в следующих упражнениях:

1 класс

Страница 8. Урок 5,
Петерсон, Учебник, часть 2

Страница 10. Урок 6,
Петерсон, Учебник, часть 2

Страница 49. Урок 25,
Петерсон, Учебник, часть 2

Страница 51. Урок 26,
Петерсон, Учебник, часть 2

Страница 22. Урок 12,
Петерсон, Учебник, часть 3

Страница 29. Урок 15,
Петерсон, Учебник, часть 3

Страница 31. Урок 16,
Петерсон, Учебник, часть 3

Страница 35. Урок 18,
Петерсон, Учебник, часть 3

Страница 44. Урок 23,
Петерсон, Учебник, часть 3

Страница 88. Урок 35,
Петерсон, Учебник, часть 3

2 класс

Страница 40,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 45,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 23. ПР 4-5. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 104,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 4. Урок 1,
Петерсон, Учебник, часть 2

Страница 41. Урок 16,
Петерсон, Учебник, часть 2

Страница 99. Повторение,
Петерсон, Учебник, часть 3

3 класс

Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 110,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 18. ПР 4. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 43,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 33. Урок 12,
Петерсон, Учебник, часть 1

Страница 57. Урок 23,
Петерсон, Учебник, часть 2

Страница 81. Урок 35,
Петерсон, Учебник, часть 2

Страница 44. Урок 20,
Петерсон, Учебник, часть 3

Страница 72. Повторение,
Петерсон, Учебник, часть 3

4 класс

Страница 7,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 68,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 4,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 74,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 30. Урок 10,
Петерсон, Учебник, часть 1

5 класс

Задание 429,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1291,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1319,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1803,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 255,
Мерзляк, Полонский, Якир, Учебник

Номер 389,
Мерзляк, Полонский, Якир, Учебник

Номер 948,
Мерзляк, Полонский, Якир, Учебник

Номер 1,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 33,
Мерзляк, Полонский, Якир, Учебник

Номер 400,
Мерзляк, Полонский, Якир, Учебник

Номер 1007,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

Номер 1,
Мерзляк, Полонский, Якир, Учебник

Задание 698,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 705,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1083,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1118,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1153,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 259,
Мерзляк, Полонский, Якир, Учебник

Номер 315,
Мерзляк, Полонский, Якир, Учебник

Номер 316,
Мерзляк, Полонский, Якир, Учебник

Номер 480,
Мерзляк, Полонский, Якир, Учебник

Номер 906,
Мерзляк, Полонский, Якир, Учебник

Номер 1040,
Мерзляк, Полонский, Якир, Учебник

Номер 1071,
Мерзляк, Полонский, Якир, Учебник

Номер 1139,
Мерзляк, Полонский, Якир, Учебник

Номер 1,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Номер 3,
Мерзляк, Полонский, Якир, Учебник

Номер 4,
Мерзляк, Полонский, Якир, Учебник

Номер 46,
Мерзляк, Полонский, Якир, Учебник

Номер 47,
Мерзляк, Полонский, Якир, Учебник

Номер 229,
Мерзляк, Полонский, Якир, Учебник

Номер 391,
Мерзляк, Полонский, Якир, Учебник

Номер 392,
Мерзляк, Полонский, Якир, Учебник

Источник

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №4 имени С.П.Королева»

Урок: Математика.

Класс: 2

Тема: «Составление числовых выражений».

Дата: 18.04.2022 г.

Цель: учить составлять числовые выражения из чисел и знаков действий; совершенствовать умения решать составные задачи; продолжить формирование вычислительных навыков; развивать умение анализировать и делать выводы.

УУД:

Предметные: читать и записывать цифрами числа; уметь читать простые выражения, находить значение числового выражения; уметь выполнять сложение и вычитание чисел в пределах 100; с использованием письменных и устных приемов вычислений; воспроизводить по памяти результаты табличного умножения однозначных чисел; результаты табличных случаев деления; знать свойства натурального ряда чисел; уметь сравнивать числа, располагать их в порядке увеличения; знать названия компонентов и результаты арифметических действий; знать порядок действий в числовых выражениях содержащие скобки.

Личностные: устанавливают значимость познавательной деятельности, оценивают усвоение содержания материала.

Метапредметные:

Регулятивные: уметь определять и формулировать цель на уроке с помощью учителя; уметь высказывать своё предположение на основе работы с учебным материалом; уметь работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной оценки; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; планировать своё действие в соответствии с поставленной задачей.

Познавательные: уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.

Коммуникативные: уметь оформлять свои мысли в устной форме; слушать и понимать речь других; учиться работать в группе, формулировать собственное мнение и позицию.

Тип урока: изучение нового материала.

Оборудование: учебник.

Ход урока:

№ п/п

Этапы работы

Содержание урока

Деятельность учителя

Деятельность учащихся

Организационный момент.

– Здравствуйте, ребята. Я желаю вам хорошего настроения. Повернитесь друг к другу, улыбнитесь и пожелайте хорошего настроения на уроке.

– Проверьте все ли у вас готово к уроку?

Приветствуют учителя, проверяют готовность к уроку.

Актуализация знаний.

1.Устный счет.

Математический диктант.

а) Назовите число, девятая часть которого равна: 2, 4, 6, 9.

б) Сумма двух чисел равна 20. Назовите несколько пар таких чисел.

в) Произведение двух чисел равно 12. Какие это числа?

2. Задача.

У Ксюши было 56 рублей. После того как она купила ручку и альбом, у нее осталось 30 р. Сколько стоил альбом, если ручка стоила 7 р.?

3. Поставьте знаки «+» или «–».

— 18, 36, 54, 81.

— 10 + 10, 1 + 19, 2 + 18, 3 + 17, 4 + 16, 5+15, и т.д.

— 6 · 2, 4 ·3.

— 56 – 30 – 7 = 19 (р)

8 – (5 + 2) =1

16 – (3 + 4) = 9

13 – (9 – 2) = 6

40 – 25 + 5 =20

65 + 10 – 30 = 45

50 + (43 – 10) = 83

Постановка темы и цели занятия.

— Откройте рабочие тетради. А сейчас мы поработаем в группах. Давайте назначим командира в каждой группе. Каждый несет ответственность за результат работы группы. Ребята, соревнования наши продолжаются.

В письме ещё есть задания.

— Эта запись является числовым выражением?

— Почему? Давайте сделаем эту запись числовым выражением.

— Какие мы можем поставить задачи на урок?

На доске:

22 6 19 11 = 2 (1 группа)

22 6 19 11 = 20

22 6 19 11 = 24 (2 группа)

22 6 19 _ 11 = 58

— Нет.

— Нет знаков действий.

Вставляют знаки действий.

(22 — 6) : ( 19-11)=2

22 + 6 – 19 + 11= 20

(22 – 6) + ( 19 -11)=24

22 + 6 + (19 + 11) = 58

— Разность чисел 22 и 2 разделить на разность чисел 19 и 11. Частное разности 22 и 6 и разности 19 и 11. Несколько действий.

— Научиться составлять числовые выражения, определять порядок действий и называть значение выражения.

Изучение новой темы.

– Рассмотрите в учебнике, как составлено выражение:

Учитель приглашает к доске двоих учеников: один будет исполнять роль Зайца, а другой – Волка. Каждому из них учитель дает заранее подготовленные карточки с такими же записями.

– Сейчас я прочитаю сложное выражение, а вы должны объяснить, как оно составлено. В этом вам помогут Волк и Заяц.

Выражение 9 – (3 + 4) можно прочитать так: «Из числа «девять» вычесть сумму трех и четырех».

– Из чего составлено это выражение? Заяц, покажи карточку с числом. Это первая часть выражения.

– Волк, покажи свою карточку. Что на ней написано?

– Это вторая часть выражения. Каким знаком соединены эти две части? Заяц, покажи карточку со знаком и назови его.

– Я запишу это выражение на доске и выделю в нем две части, вот так:

9 – (3 + 4).

– Как вы думаете, какое действие надо выполнить первым: вычитание или сложение? А почему?

— На это указывают скобки.

– Рассмотрим в учебнике следующий рисунок: Волк пригласил Зайку к доске и велел ему выполнить действия, указанные в выражении, то есть найти значение этого выражения. Как Заяц справился с заданием? Прочитайте, что он написал на доске.

А теперь мы будем учиться читать сложные выражения. Назовите в выражении 9 – (3 + 4) первую часть (9), вторую часть (3 + 4). Что представляет собой сложное выражение: сумму или разность? Как это определить? Обычно выражение называют по последнему действию; здесь последним действием выполняется вычитание. Поэтому само выражение называется разностью. Послушайте, как я прочитаю это выражение: «Разность девяти и суммы трех и четырех». А теперь прочитаем текст в рамке (на с. 100).

Сложное выражение может называться суммой, разностью, произведением или частным. Это зависит от того, какое из этих действий выполняется при нахождении значения выражения последним.

Давайте потренируемся составлять сложные выражения и читать их. Лера, подойди к доске. Сейчас мы с Лерой составим выражение. Как только я буду произносить слова «сумма», «разность», «произведение» или «частное», Лера будет открывать скобки.

Итак, слушаем. Надо составить выражение из разности… Лера, что ты делаешь?

…тридцати пяти и двадцати шести… Оля, что ты запишешь? (35 – 26.) Закрывай скобки. Продолжаем: знака «плюс» и частного…

…сорока пяти и девяти. Закрываем скобки. Получилась запись: (35 – 26) + (45 : 9). Прочитаем ее.

— Прочитаем это выражение по-другому. Сколько частей в этом выражении?

— Какое действие выполняется последним?

— Как же называется выражение?

— Как его можно прочитать? Я начну, а вы продолжайте: «Сумма…».

Задание № 2 (с. 101).

Цель данного задания – научить составлять числовые выражения в 2–3 действия из частей (чисел, знаков арифметических действий, скобок).

Когда выражение будет составлено, учитель дополнительно может спросить:

– В каком порядке надо выполнять действия?

– Какое действие последнее?

– Как называется это выражение?

– Чему равно значение выражения?

Запись:

(6 · 4) : 6 = 4.

(56 : – (14 – 9) = 2.

(3 + 6) · (4 + 5) = 81.

(40 – 5) + (24 : 6) = 39.

Физкультминутка

—

— «Три плюс четыре» или «Сумма трех и четырех».

— Минус.

— Потому что, прежде чем из 9 вычитать сумму, надо ее вычислить, то есть сложить 3 и 4.

— Открываю скобки.

— Открываем скобки.

— К разности 35 и 26 прибавить частное 45 и 9.

— Две: 35 – 26 и 45 : 5.

— Сложение.

— Суммой.

— Сумма разности тридцати пяти и двадцати шести и частного сорока пяти и девяти.

Учащиеся должны понимать, что если при составлении выражения они столкнутся со словами «сумма», «разность», «произведение» и «частное», то нужно использовать скобки.

Повторение пройденного материала.

1. Работа по учебнику.

Задание № 7 (с. 101).

Учащиеся читают задание и выполняют схемы-«машины».

Задание № 10 (с. 102).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите кратко условие этой задачи.

Запись:

Решение:

1) Сколько было грузовых машин?

24 : 6 = 4 (м.).

2) Сколько было автобусов?

4 · 2 = 8 (м.).

Ответ: 8 машин.

2. Работа в печатной тетради № 2.

Задание № ___.

Учащиеся впервые сталкиваются с ситуацией, когда по решению надо восстановить текст задачи.

Скорее всего, сопоставляя запись решения с текстом, дети предложат следующую формулировку задачи: «Школьники посадили 4 ряда яблонь по 8 яблонь в каждом ряду и 3 ряда слив по 9 слив в каждом ряду. Сколько всего деревьев посадили школьники?»

Обязательно обратите внимание второклассников на то, что сформулировать задачу можно по-другому, например:

1. Школьники посадили 3 ряда яблонь по 9 яблонь в каждом ряду и 4 ряда слив по 8 слив в каждом ряду. Сколько всего деревьев посадили школьники?

2. Школьники посадили 8 рядов яблонь по 4 яблони в каждом ряду и 9 рядов слив по 3 сливы в каждом ряду. Сколько всего деревьев посадили школьники?

Домашнее задание.

Учебник с. 102, № 8; с. 104, № 19.

Записывают задание в дневник.

Итог урока.

Рефлексия.

— Какую учебную задачу поставили перед собой на уроке? Мы достигли её?

— Чему мы научились?

— Кому было трудно?

— Что не получилось? Что нужно сделать, чтобы в дальнейшем избежать ошибок?

— Где вам пригодятся эти знания?

— Оцените свою работу на уроке. Встаньте те, кто считает, что он работал вот так:

— Все получилось;

— были затруднения;

— ничего не получилось.

— Почему вы так думаете?

— Да, вы молодцы. Я с вами полностью согласна.

— Спасибо за урок.

Источник

Эта информация доступна зарегистрированным пользователям

Любые математические задачи и примеры записываются с помощью математического языка.

Математический язык- это язык, не требующий перевода, универсальный и понятный всем, имеющий четкую структуру и грамматику.

Верная математическая запись всегда точна, логична, компактна, удобна для понимания, однозначно отражает действие, операцию, понятие.

Определенная осмысленная последовательность знаков (чисел, букв), связанных между собой знаками арифметических операций, называют математическим выражением.

Математические выражения делят на числовые и буквенные.

На этом уроке вы познакомитесь с числовыми и буквенными выражениями.

Узнаете, какое выражение называют числовым, а какое буквенным.

Научитесь составлять числовые и буквенные выражения к задачам.

Эта информация доступна зарегистрированным пользователям

Выясните, как правильно записывать, читать и находить значение математических выражений.

Числовые выражения вам уже хорошо знакомы.

В начальных классах на уроках математики, решая задачи и примеры, вы составляли и записывали числовые выражения и находили значения этих выражений.

Числовое выражение- это запись, состоящая из чисел, арифметических операций, скобок и иных специальных математических символов.

Эта информация доступна зарегистрированным пользователям

Числовым выражением можно назвать только такую запись, которая является осмысленной и составлена согласно математическим правилам.

Рассмотрим примеры числовых выражений.

4 — является числовым выражением.

2 + 17 — является числовым выражением.

247 + 13 — 3 — является числовым выражением.

84 + (273 — 16) — является числовым выражением.

Не каждую математическую запись из символов и знаков можно считать числовым выражением.

Числовое выражение всегда ориентировано на то, чтобы операции, входящие в него, могли быть выполнены.

Если числовое выражение невозможно вычислить, то оно не имеет смысла.

Пример.

45 + ( — + 1 — не является числовым выражением, данная запись представляет собой бессмысленный набор символов и знаков.

Существуют такие математические записи, которые на первый взгляд можно принять за числовые выражения, но вычислить их невозможно.

Пример.

15 : (37 — 22 — 15)

Число 15 необходимо разделить на результат операции в скобках, а он равен нулю.

Так как деление на нуль в математике запрещено, данную математическую операцию совершить невозможно, следовательно, запись 15 : (37 — 22 — 15) не вычислить, она не является числовым выражением.

Математические равенства и неравенства выражениями не являются, но равенства и неравенства состоят из математических выражений.

Два числовых выражения, соединенные знаком равно «=», называют числовым равенством.

Два числовых выражения, соединенные знаками больше «>» или меньше «<», называют неравенством.

Несмотря на то, что в записи равенств и неравенств присутствуют математически верно построенные комбинации из чисел и арифметических операций, они не являются математическими выражениями.

Например,

Запись вида 26 — 5 > 4 не является числовым выражением, это неравенство.

Запись вида 24 — 6 = 18 также не является числовым выражением, данная запись является равенством.

Смысл решения любой задачи, любого примера заключается в том, чтобы найти значение выражения, которое превращает его в верное равенство.

Число, которое получается после выполнения всех арифметических операций, называют значением числового выражения.

Следовательно, чтобы найти значение числового выражения, необходимо выполнить в определенном порядке все арифметические операции, указанные в выражении.

У числового выражения значение только одно.

Например, значение числового выражения (45 — 3) + (12 + 2) всегда равно 56, и только это значение является единственно верным.

Эта информация доступна зарегистрированным пользователям

Важно уметь не только верно записывать числовые выражения, но и уметь их правильно читать.

Чтобы прочитать числовое выражение нужно определить, какая арифметическая операция является последней при вычислении значения этого выражения.

Так, например, если последнее по порядку действие было сложение, то выражение называют «суммой».

Если последним действием является вычитание, то выражение называют «разностью».

Следовательно, если последним действием является умножение, то выражение называют «произведением», если деление- «частным».

Например, выражение (10 — 3) + (6 — 4) читается так: «Сумма разности чисел 10 и 3 и разности чисел 6 и 4».

Выражение (10 — 3)∙(6 — 4) читается так: «Произведение разности чисел 10 и 3 и разности чисел 6 и 4».

Умение составлять математические выражения и находить их значение используют при решении как простых, так и составных задач.

Рассмотрим пример решения составной задачи и выясним особенности процесса составления числовых выражений.

Известно, что любая составная задача содержит несколько простых.

Существуют различные способы оформления решения текстовых задач.

Чаще всего используют такие формы записи решения задач:

1. По действиям с пояснениями.

2. Выражением.

При решении составных задач важно выделить главное, сделать краткую запись, разделить задачу на простые, составить план решения.

Задача 1.

В первый день собрали 12 кг клубники, а во второй день на 2 кг больше.

Сколько килограммов клубники собрали за эти два дня?

Эта информация доступна зарегистрированным пользователям

Решение:

Запишем кратко условие задачи:

В I день — 12 кг клубники.

Во II день — на 2 кг больше, чем в I день.

Общее количество клубники в I и во II день- ?

Изобразим к задаче рисунок в виде схемы.

Эта информация доступна зарегистрированным пользователям

Чтобы определить, сколько собрали клубники за два дня, необходимо знать, какое количество клубники было собрано в первый и во второй день.

Из условия задачи известно количество клубники, собранной в первый день.

Неизвестно количество клубники, собранной во второй день.

Когда будет известно сколько собрали клубники во второй день, можно узнать какое количество ягод собрали за два дня.

Задачу решаем в два действия (каждое действие поясним).

1. Выясним сколько килограммов ягод собрали во второй день.

Известно, что в первый день собрали 12 кг клубники. Так как во второй день собрали на 2 кг больше, то во второй день собрали столько же, как в первый, и еще 2 кг.

Выполним сложение чисел 12 и 2, получим выражение 12 + 2.

Найдем значение данного числового выражения:

12 + 2 = 14 (кг) клубники собрали во второй день.

2. Вторым действием определим общее количество ягод, собранных за два дня.

Необходимо сложить все ягоды, который собрали в первый и во второй день, получим следующее выражение: 12 + 14.

Найдем значение данного числового выражения:

12 + 14 = 26 (кг) клубники собрали за два дня.

Ответ: 26 кг.

Как нам уже известно, решение задачи можно записать не только по действиям, но и в форме выражения.

Запись решения составной задачи с помощью составления по ней итогового числового выражения позволяет увидеть ход решения в целом, и такая запись сокращает время оформления задачи.

Составим числовое выражение для решения нашей задачи.

Согласно рассуждениям, изложенным выше, имеем следующие данные:

12 кг — клубники собрали в первый день.

12 + 2 кг — клубники собрали во второй день.

Определим общее количество ягод, собранных за два дня.

Сложив все ягоды, собранные в первый и во второй день, получим следующее числовое выражение:

12 + (12 + 2).

Вычислим значение данного выражения, выполнив последовательно все действия в нем.

Тогда запись решения задачи будет выглядеть так:

12 + (12 + 2) = 12 + 14 = 26 (кг) клубники собрали за два дня.

Ответ: 26 кг.

Попробуем решить вторую задачу.

Задача 2.

В первый день собрали 12 кг клубники, а во второй день на 5 кг больше.

Сколько килограммов клубники собрали за эти два дня?

Скорее всего вы заметили, что первая и вторая задачи отличаются только одним числом, а именно число 2 заменено на число 5.

Остальные условия задачи остались прежние.

Все логические рассуждения во второй задаче аналогичны рассуждениям первой.

Таким образом, имеем следующие данные:

12 кг — клубники собрали в первый день.

12 + 5 кг — клубники собрали во второй день.

Определим общее количество ягод, собранных за два дня.

Сложив все ягоды, собранные в первый и во второй день, получим следующее выражение:

12 + (12 + 5).

Вычислим значение данного выражения, выполнив последовательно все действия в нем.

Тогда запись решения задачи будет выглядеть так:

12 + (12 + 5) = 12 + 17 = 29 (кг) клубники собрали за два дня.

Ответ: 29 кг.

Эта информация доступна зарегистрированным пользователям

Рассмотрим еще одну такую же задачу, как первая и вторая, рассмотренные выше, но число, которое менялось в первой и во второй задаче заменим на ☐ пустое окошко, в которое можно вписать любое значение.

Тогда получим следующую задачу:

В первый день собрали 12 кг клубники, а во второй день на ☐ кг больше.

Сколько килограммов клубники собрали за эти два дня?

В математике принято обозначать переменное число не пустым окошком, а буквой.

Для нашей задачи вместо пустого окошка поставим латинскую букву «а».

По аналогии с уже решенными задачами математическое выражение для данной задачи будет следующее: 12 + (12 + а).

Если вместо буквы а подставлять различные числа, то каждый раз будем получать различные числовые выражения и, как следствие, различные значения.

Числовое выражение, в котором числа обозначены цифрами и буквами, называют буквенным выражением.

Соответственно, буквенное выражение отличается от числового тем, что содержит букву.

Буквы, которые содержатся в буквенных выражениях, называются переменными.

Для обозначения чисел буквами используют строчные буквы латинского алфавита.

Эта информация доступна зарегистрированным пользователям

Например, в выражении а + 3 — b буквы а и b являются переменными.

Буквенные выражения должны быть составлены согласно математическим правилам и по такому же принципу, как числовые выражения.

Буквенные выражения является таковым, если в их записи отсутствуют знаки больше «>», меньше «<», равно «=».

Приведем примеры нескольких буквенных выражений:

а + b + с — является буквенным выражением.

4а — 5а — является буквенным выражением.

(15 — а) + 26 — является буквенным выражением.

12 + (3 — 1) — не является буквенным выражением, это числовое выражение (в составе выражения нет букв).

3 + d = 19 — не является буквенным выражением, это равенство (равенство, в записи которого есть буква, называется уравнением).

Буквенное выражение должно содержать хотя бы одну букву.

Эта информация доступна зарегистрированным пользователям

Из приведенных выше примеров можно заметить, что буквенное выражение может содержать несколько одинаковых и (или) разных букв, может состоять только из одних букв.

Разные числа в выражении обозначаются разными буквами.

Если в выражении упоминается одна и та же буква несколько раз, то во всех случаях она имеет одно и то же значение.

Числа, которые заменяют буквы в буквенном выражении, называют значением этих букв.

Вычисления в буквенных выражениях выполняют после подстановки вместо букв их численных значений.

Для буквенного выражения характерно не просто значение выражения, а значение выражения при заданном значении переменной.

Рассмотрим алгоритм решения буквенного выражения.

Эта информация доступна зарегистрированным пользователям

Пример.

1. Пусть число а = 5, число b = 6.

Найдем значение буквенного выражения а + b.

Решение:

Подставим вместо а и b соответствующие им числовые значения.

Получим числовое выражение 5 + 6.

Найдем значение числового выражения: 5 + 6 = 11.

Ответ: 11.

2. Пусть число а = 5, число d = 10.

Найдем значение буквенного выражения (а + а) — (d — а).

Подставим вместо а и d соответствующие им числовые значения.

Получим числовое выражение (5 + 5) — (10 — 5).

Найдем значение числового выражения: (5 + 5) — (10 — 5) = 10 — 7 = 3.

Ответ: 3.

Буквенное выражение, в отличие от числового, может иметь много значений, так как вместо буквы можно подставить любое число.

Пример.

Определите значение выражение 218 — b, если b = 28, b = 13, b = 5.

1. Подставим вместо b число 28.

Получим числовое выражение 218 — 28.

Найдем значение полученного числового выражения: 218 — 28 = 190.

2. Подставим вместо b число 13.

Получим числовое выражение 218 — 13.

Найдем значение полученного числового выражения: 218 — 13 = 205.

3. Подставим вместо b число 5.

Получим числовое выражение 218 — 5.

Найдем значение полученного числового выражения: 218 — 5 = 213.

Ответ: 190, 205, 213.

Эта информация доступна зарегистрированным пользователям

Числовые выражения

Чтение числовых выражений

Решение числовых выражений

Сравнение значений числовых выражений

Буквенные выражения

Алгоритм решения буквенного выражения

Переменные

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Читайте также

Порядок действий в выражении, не содержащем скобки

Порядок действий в выражении, содержащем скобки

Буквенные выражения. Числовое значение буквенного выражения.