Введение
В этой главе мы рассмотрим ещё одно семейство моделей машинного обучения — решающие деревья (decision trees).
Решающее дерево предсказывает значение целевой переменной с помощью применения последовательности простых решающих правил (которые называются предикатами). Этот процесс в некотором смысле согласуется с естественным для человека процессом принятия решений.
Хотя обобщающая способность решающих деревьев невысока, их предсказания вычисляются довольно просто, из-за чего решающие деревья часто используют как кирпичики для построения ансамблей — моделей, делающих предсказания на основе агрегации предсказаний других моделей. О них мы поговорим в следующей главе.
Пример решающего дерева
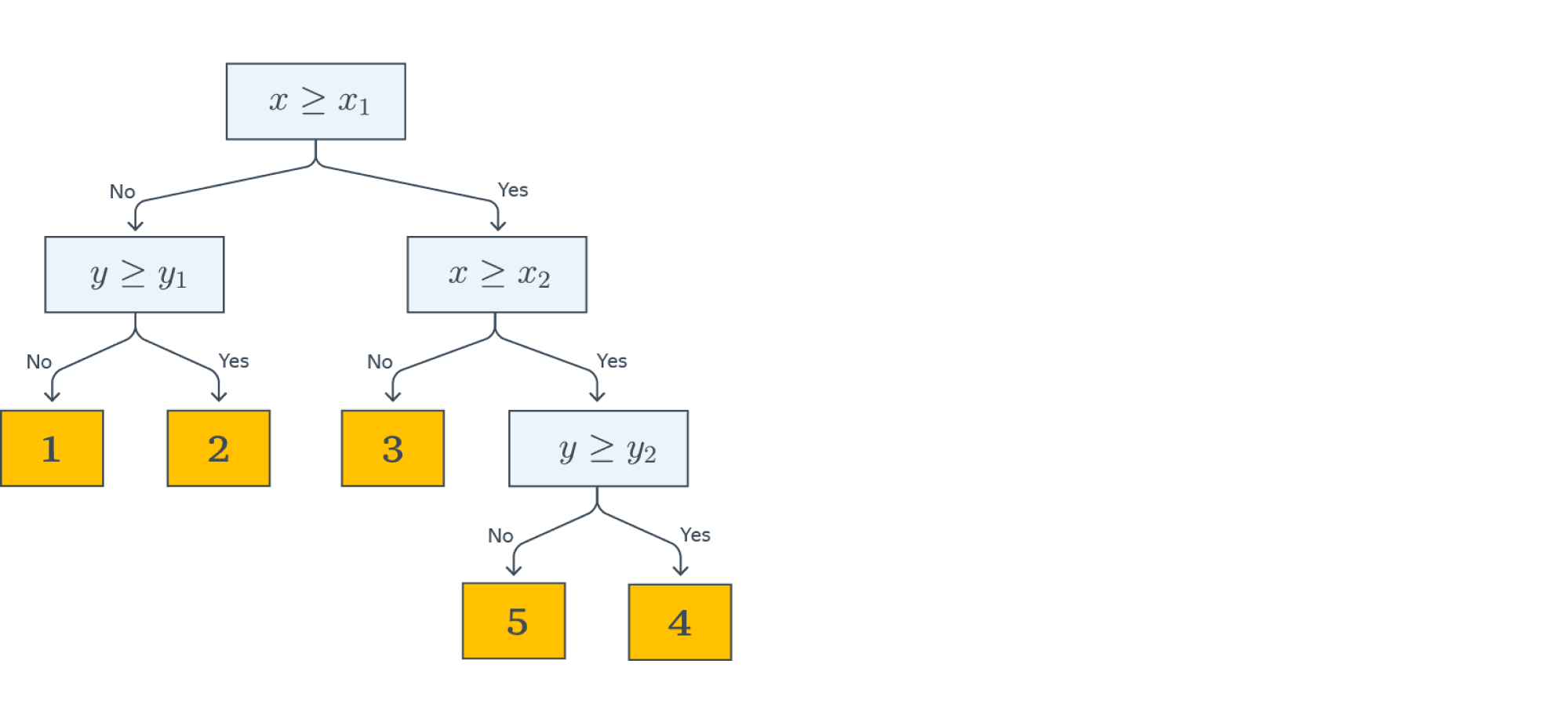
Начнём с небольшого примера. На картинке ниже изображено дерево, построенное для задачи классификации на пять классов:
Объекты в этом примере имеют два признака с вещественными значениями: $X$ и $Y$. Решение о том, к какому классу будет отнесён текущий объект выборки, будет приниматься с помощью прохода от корня дерева к некоторому листу.
В каждом узле этого дерева находится предикат. Если предикат верен для текущего примера из выборки, мы переходим в правого потомка, если нет — в левого. В данном примере все предикаты — это просто взятие порога по значению какого-то признака:
$$
B(x, j, t) = [ x_j le t ]
$$
В листьях записаны предсказания (например, метки классов). Как только мы дошли до листа, мы присваиваем объекту ответ, записанный в вершине.
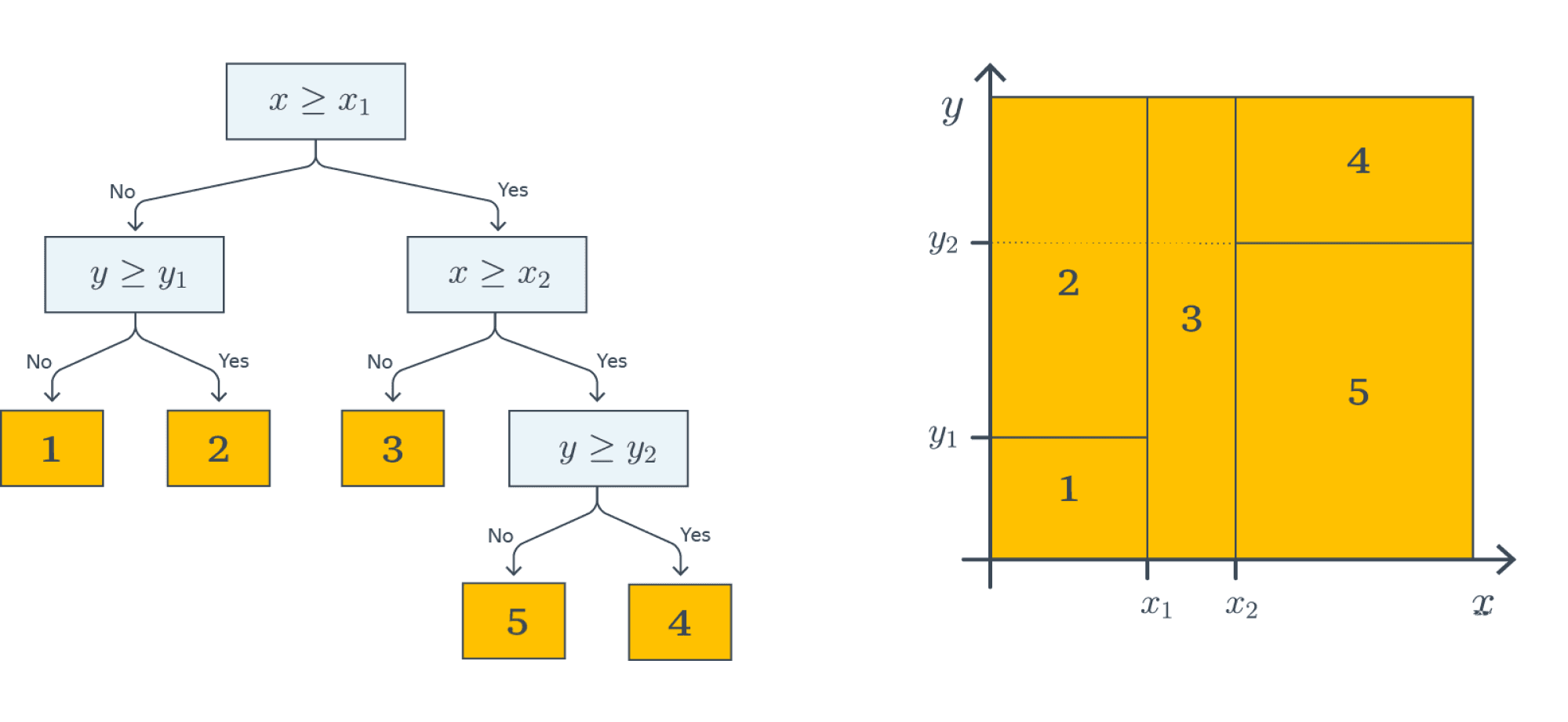
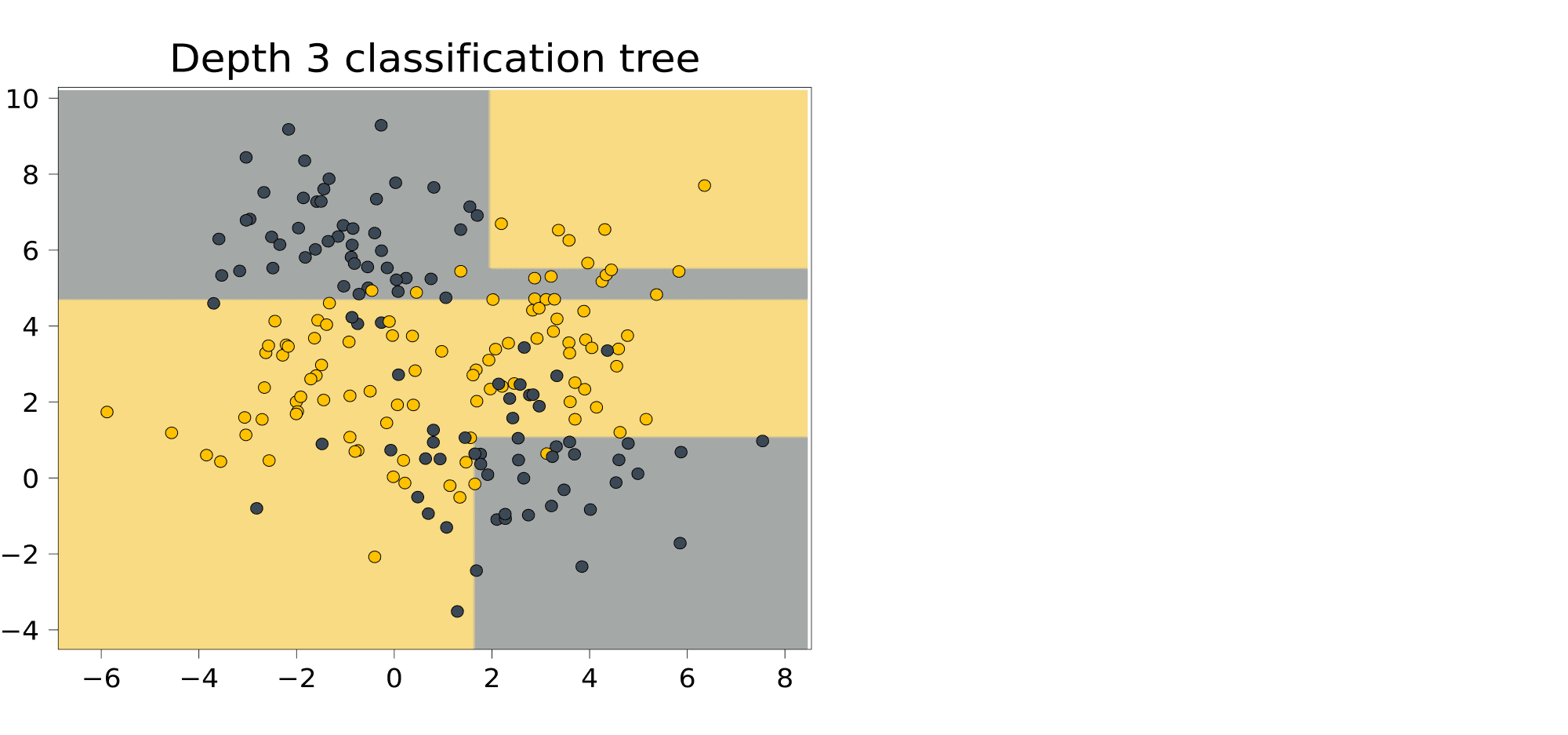
На картинке ниже визуализирован процесс построения решающих поверхностей, порождаемых деревом (правая часть картинки):
Каждый предикат порождает разделение текущего подмножества пространства признаков на две части. На первом этапе, когда происходило деление по $[ X le X_1 ]$, вся плоскость была поделена на две соответствующие части. На следующем уровне часть плоскости, для которой выполняется $X le X_1$, была поделена на две части по значению второго признака $Y le Y_1$ — так образовались области 1 и 2. То же самое повторяется для правой части дерева — и так далее до листовых вершин: получится пять областей на плоскости. Теперь любому объекту выборки будет присваиваться один из пяти классов в зависимости от того, в какую из образовавшихся областей он попадает.
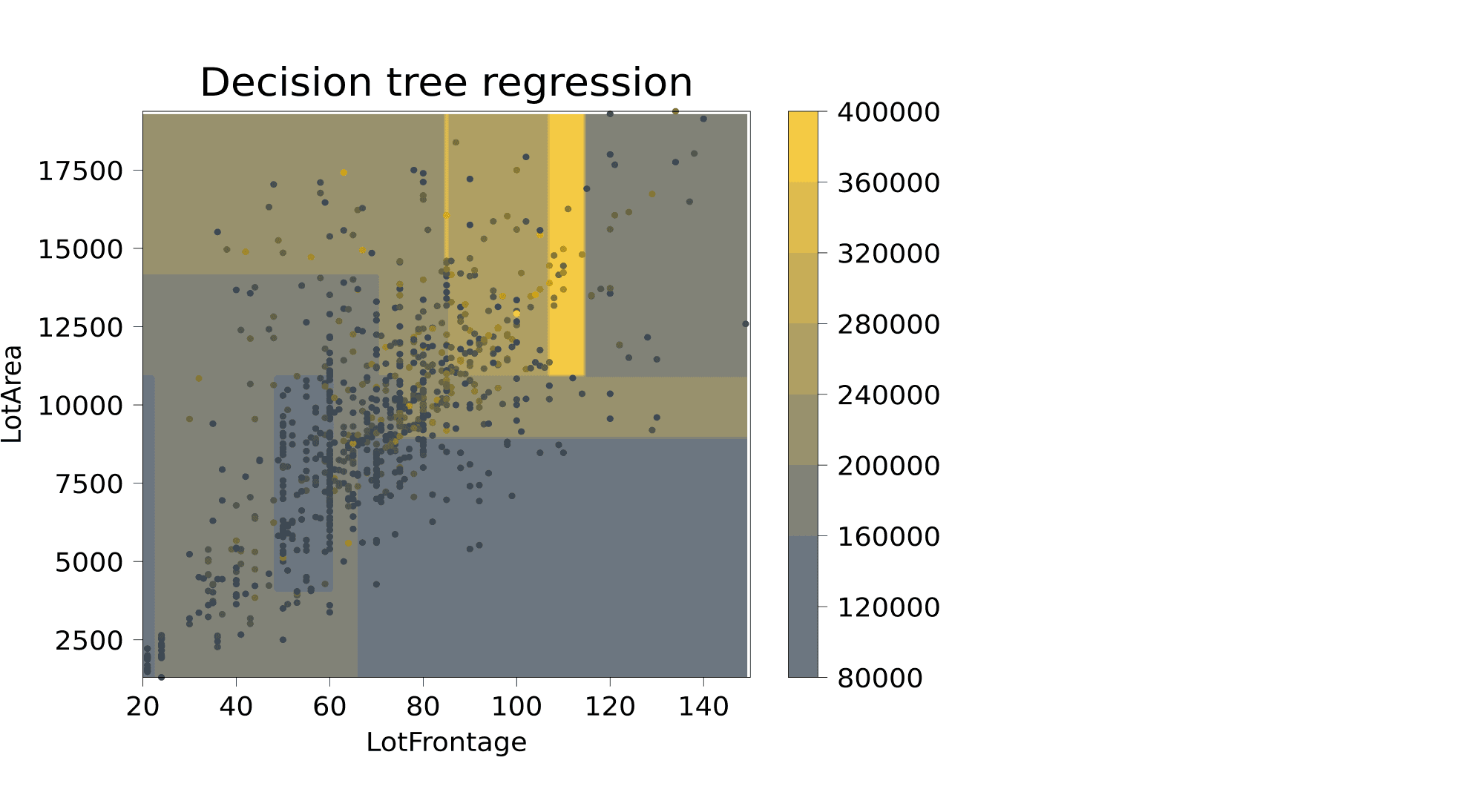
Этот пример хорошо демонстрирует, в частности, то, что дерево осуществляет кусочно-постоянную аппроксимацию целевой зависимости. Ниже приведён пример визуализации решающей поверхности, которая соответствует дереву глубины 4, построенному для объектов данных из Ames Hounsing Dataset, где из всех признаков, описывающих объекты недвижимости, были выбраны ширина фасада (Lot_Frontage) и площадь (Lot_Area), а предсказать нужно стоимость. Для более понятной визуализации перед построением дерева из датасета были выкинуты объекты с Lot_Frontage > 150 и с Lot_Area > 20000.
В каждой из прямоугольных областей предсказывается одна и та же стоимость.
Определение решающего дерева
Разобравшись с приведёнными выше примерами, мы можем дать определение решающего дерева. Пусть задано бинарное дерево, в котором:
- каждой внутренней вершине $v$ приписан предикат $B_v: mathbb{X} to {0,1}$;
- каждой листовой вершине $v$ приписан прогноз $c_v in mathbb{Y}$, где $mathbb{Y}$ — область значений целевой переменной (в случае классификации листу может быть также приписан вектор вероятностей классов).
В ходе предсказания осуществляется проход по этому дереву к некоторому листу. Для каждого объекта выборки $x$ движение начинается из корня. В очередной внутренней вершине $v$ проход продолжится вправо, если $B_v(x) = 1$, и влево, если $B_v(x) = 0$. Проход продолжается до момента, пока не будет достигнут некоторый лист, и ответом алгоритма на объекте $x$ считается прогноз $c_v$, приписанный этому листу.
Предикат $B_v$ может иметь, вообще говоря, произвольную структуру, но, как правило, на практике используют просто сравнение с порогом $t in mathbb{R}$ по какому-то $j$-му признаку:
$$
B_v(x, j, t) = [ x_j le t ]
$$
При проходе через узел дерева с данным предикатом объекты будут отправлены в правое поддерево, если значение $j$-го признака у них меньше либо равно $t$, и в левое — если больше. В дальнейшем рассказе мы будем по умолчанию использовать именно такие предикаты.
Из структуры дерева решений следует несколько интересных свойств:
- выученная функция является кусочно-постоянной, из-за чего производная равна нулю везде, где задана. Следовательно, о градиентных методах при поиске оптимального решения можно забыть;
- дерево решений (в отличие от, например, линейной модели) не сможет экстраполировать зависимости за границы области значений обучающей выборки;
- дерево решений способно идеально приблизить обучающую выборку и ничего не выучить (то есть такой классификатор будет обладать низкой обобщающей способностью): для этого достаточно построить такое дерево, в каждый лист которого будет попадать только один объект. Следовательно, при обучении нам надо не просто приближать обучающую выборку как можно лучше, но и стремиться оставлять дерево как можно более простым, чтобы результат обладал хорошей обобщающей способностью.
Иллюстрации
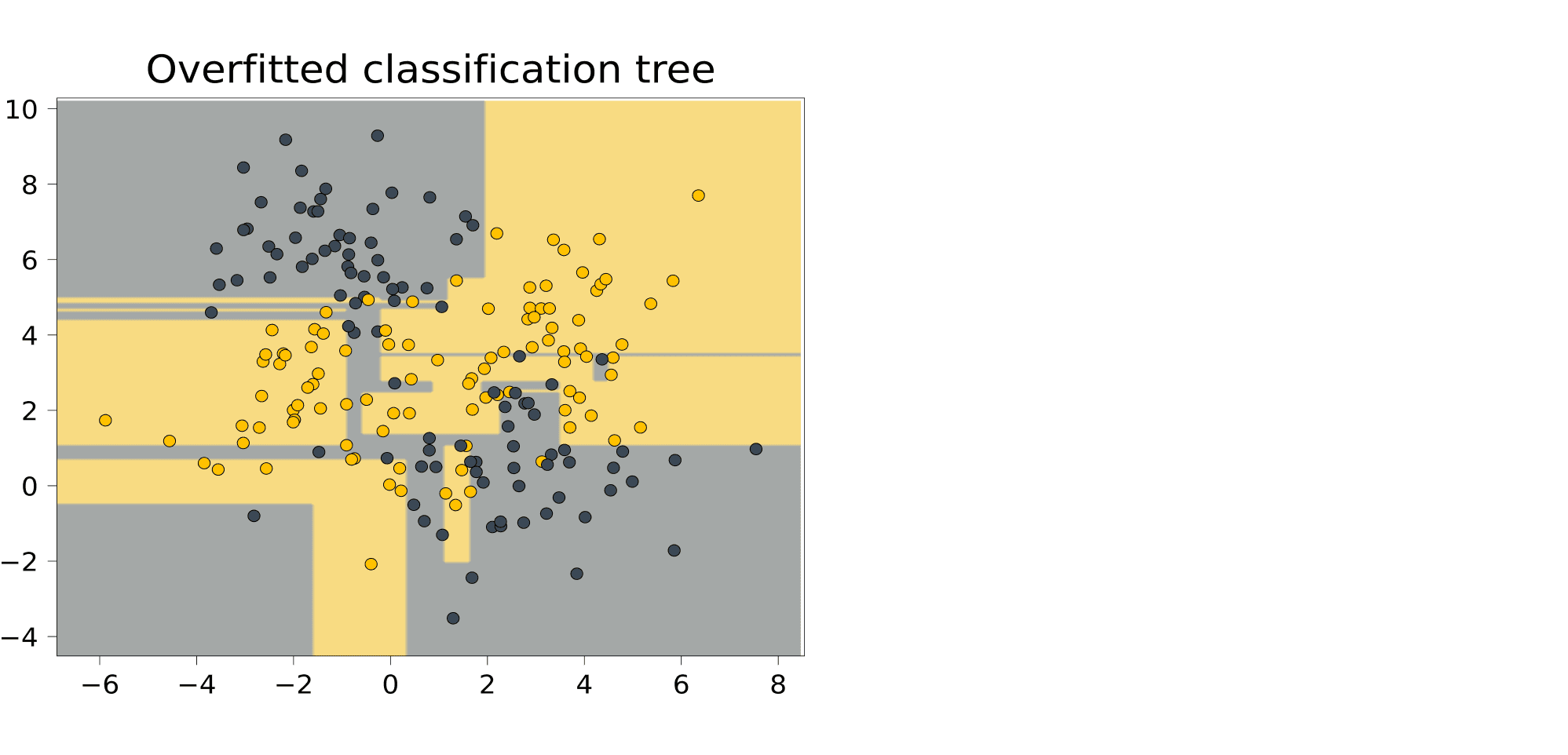
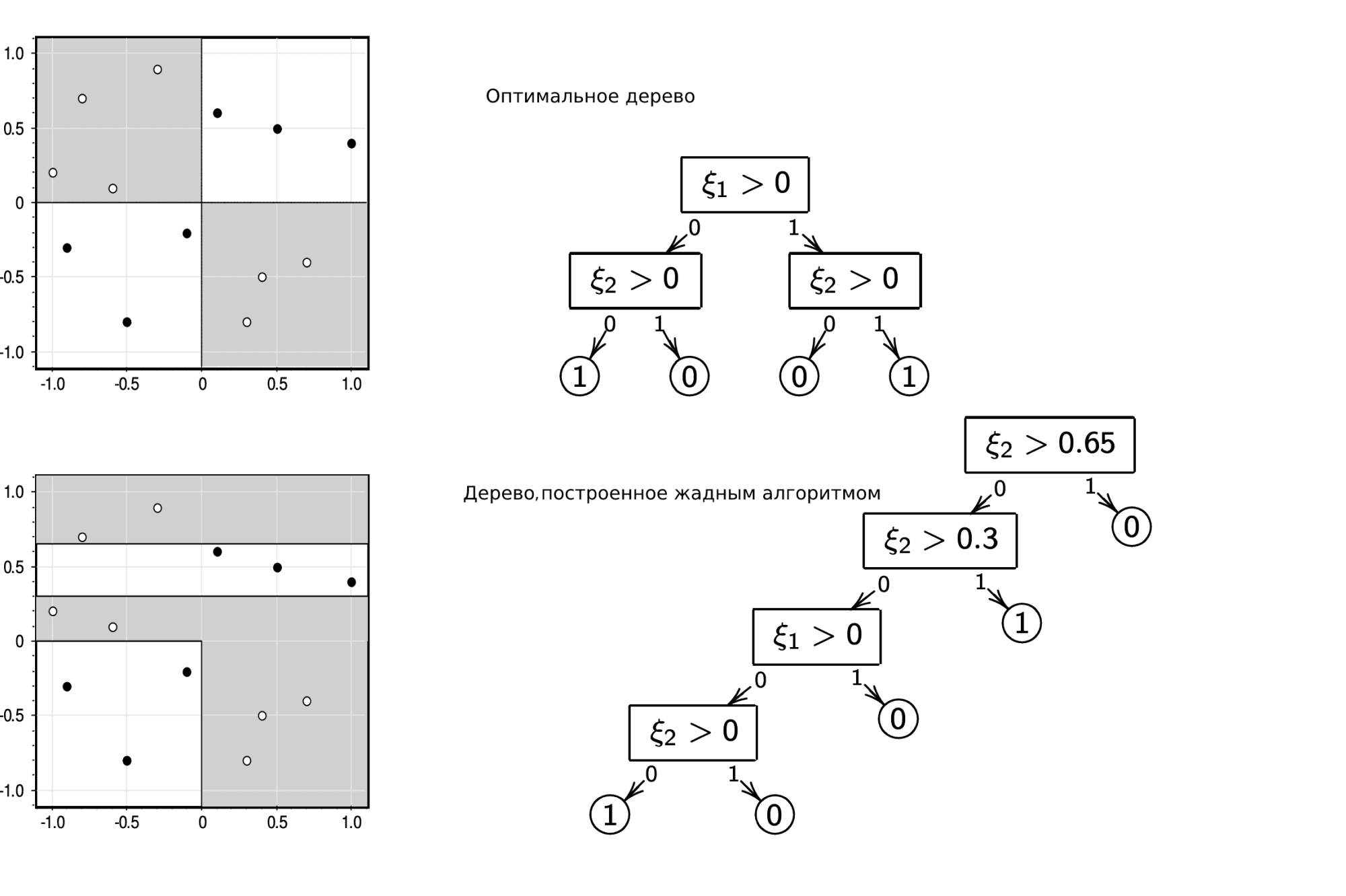
Сгенерируем для начала небольшой синтетический датасет для задачи классификации и обучим на нём решающее дерево, не ограничивая его потенциальную высоту.
Выученная закономерность очень сложная; иногда она выделяет прямоугольником одну точку. И действительно, как мы увидим дальше, деревья умеют идеально подстраиваться под обучающую выборку. Это чемпионы переобучения. Помешать этому может лишь ограничение на высоту дерева. Вот как будет выглядеть дерево высоты 3, построенное на том же датасете:
Не всё идеально, но уже гораздо менее безумный классификатор.
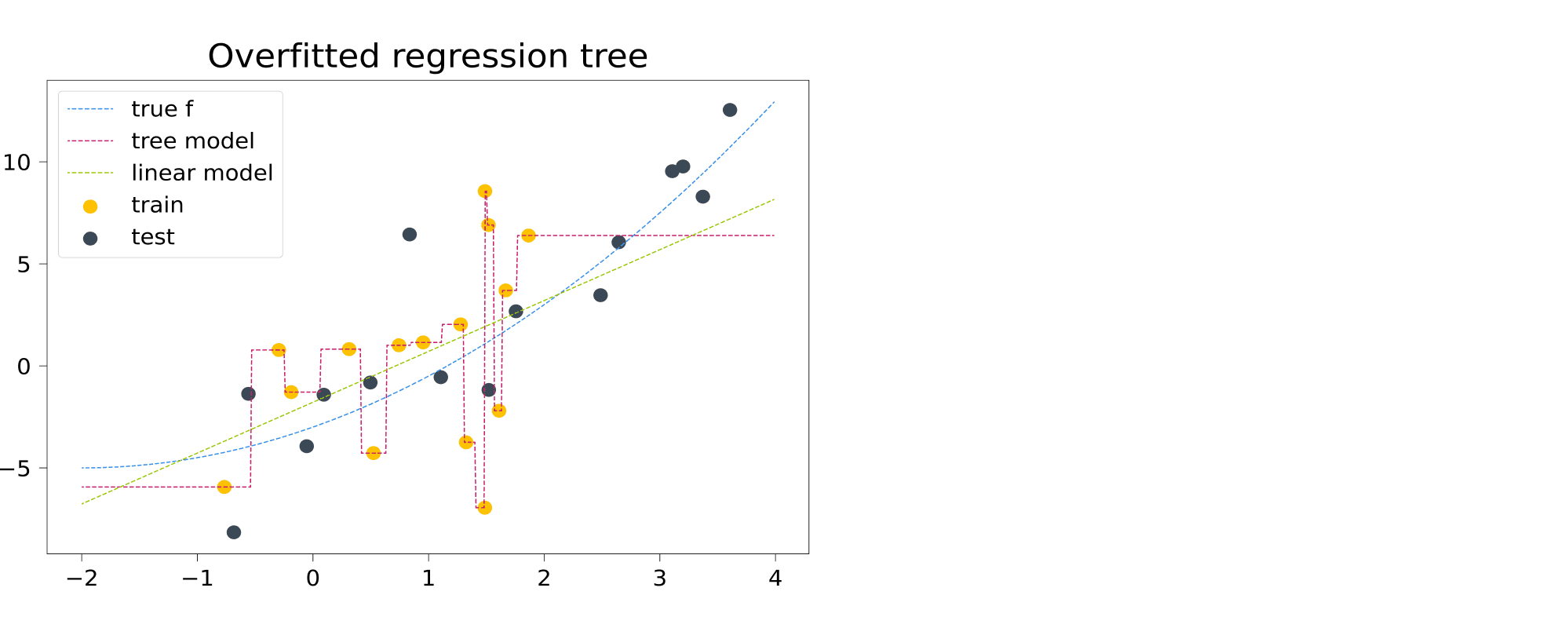
Теперь обратимся к задаче регрессии. Обучим решающее дерево, не ограничивая его высоту.
Восстановленная деревом зависимость (фиолетовая ступенчатая пунктирная линия) мечется между точками, идеально следуя за обучающей выборкой. Кроме того (и это не лечится ограничением глубины дерева) за пределами обучающей выборки дерево делает константные предсказания. Это и имеют в виду, когда говорят, что древесные модели неспособны к экстраполяции.
Почему построение оптимального решающего дерева — сложная задача?
Пусть, как обычно, у нас задан датасет $(X, y)$, где $y={y_i}_{i=1}^N subset mathbb{R}^N$ — вектор таргетов, а $X={x_i}_{i = 1}^N in mathbb{R}^{N times D}, x_i in mathbb{R}^D$ — матрица признаков, в которой $i$-я строка — это вектор признаков $i$-го объекта выборки. Пусть у нас также задана функция потерь $L(f, X, y)$, которую мы бы хотели минимизировать.
Наша задача — построить решающее дерево, наилучшим образом предсказывающее целевую зависимость. Однако, как уже было замечено выше, оптимизировать структуру дерева с помощью градиентного спуска не представляется возможным. Как ещё можно было бы решить эту задачу? Давайте начнём с простого — научимся строить решающие пни, то есть решающие деревья глубины 1.
Как и раньше, мы будем рассматривать только самые простые предикаты:
$$
B_{j, t}(x_i) = [ x_{ij} le t ]
$$
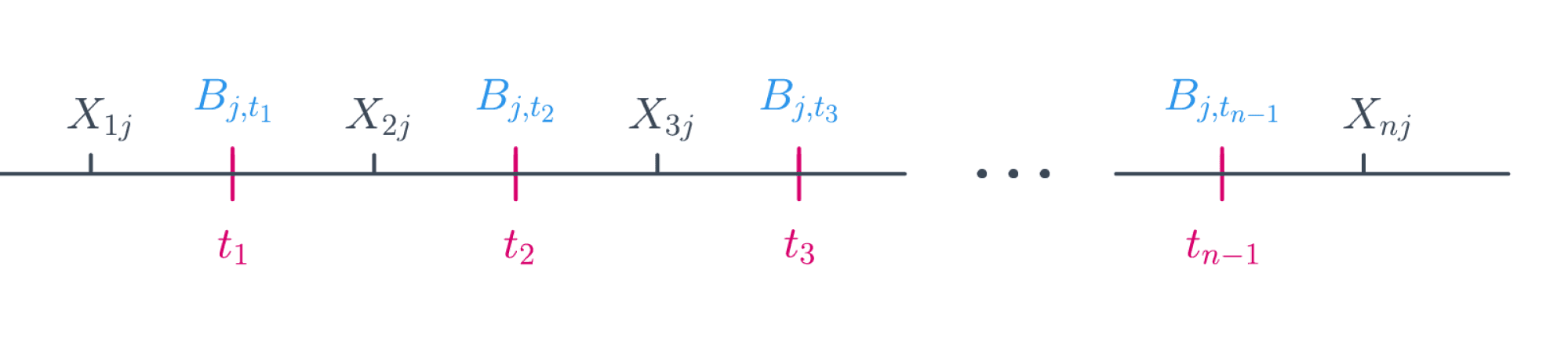
Ясно, что задачу можно решить полным перебором: существует не более $(N — 1) D$ предикатов такого вида. Действительно, индекс $j$ (номер признака) пробегает значения от $1$ до $D$, а всего значений порога $t$, при которых меняется значение предиката, может быть не более $N — 1$:
Решение, которое мы ищем, будет иметь вид:
$$
(j_{opt}, t_{opt}) = arg min_{j, t} L(B_{j, t}, X, y)
$$
Для каждого из предикатов $B_{j, t}$ нам нужно посчитать значение функции потерь на всей выборке, что, в свою очередь, тоже занимает $O(N)$. Следовательно, полный алгоритм выглядит так:
min_loss = inf
optimal_border = None
for j in range(D):
for t in X[:, j]: # Можно брать сами значения признаков в качестве порогов
loss = calculate_loss(t, j, X, y)
if loss < min_loss:
min_loss, optimal_border = loss, (j, t)
Сложность алгоритма — $O(N^2 D)$. Это не заоблачная сложность, хотя, конечно, не идеальная. Но это была схема возможного алгоритма поиска оптимального дерева высоты 1.
Как обобщить алгоритм для дерева произвольной глубины? Мы можем сделать наш алгоритм поиска решающего пня рекурсивным и в теле цикла вызывать исходную функцию для всех возможных разбиений. Как мы упоминали выше, так можно построить дерево, идеально запоминающее всю выборку, однако на тестовых данных такой алгоритм вряд ли покажет высокое качество. Можно поставить другую задачу: построить оптимальное с точки зрения качества на обучающей выборке дерево минимальной глубины (чтобы снизить переобучение). Проблема в том, что поиск такого дерева является NP-полной задачей, то есть человечеству пока неизвестны способы решить её за полиномиальное время.
Как быть? Идеального ответа на этот вопрос нет, но до некоторой степени ситуацию можно улучшить двумя не исключающими друг друга способами:
- Разрешить себе искать не оптимальное решение, а просто достаточно хорошее. Начать можно с того, чтобы строить дерево с помощью жадного алгоритма, то есть не искать всю структуру сразу, а строить дерево этаж за этажом. Тогда в каждой внутренней вершине дерева будет решаться задача, схожая с задачей построения решающего пня. Для того чтобы этот подход хоть как-то работал, его придётся прокачать внушительным набором эвристик.
- Заняться оптимизацией с точки зрения computer science — наивную версию алгоритма (перебор наборов возможных предикатов и порогов) можно ускорить и асимптотически, и в константу раз.
Эти две идеи мы и будем обсуждать в дальнейшем. Сначала попытаемся подробно разобраться с первой — использованием жадного алгоритма.
Жадный алгоритм построения решающего дерева
Пусть $X$ — исходное множество объектов обучающей выборки, а $X_m$ — множество объектов, попавших в текущий лист (в самом начале $X_m = X$). Тогда жадный алгоритм можно верхнеуровнево описать следующим образом:
- Создаём вершину $v$.
- Если выполнен критерий остановки $Stop(X_m)$, то останавливаемся, объявляем эту вершину листом и ставим ей в соответствие ответ $Ans(X_m)$, после чего возвращаем её.
- Иначе: находим предикат (иногда ещё говорят сплит) $B_{j, t}$, который определит наилучшее разбиение текущего множества объектов $X_m$ на две подвыборки $X_{ell}$ и $X_r$, максимизируя критерий ветвления $Branch(X_m, j, t)$.
- Для $X_ell$ и $X_r$ рекурсивно повторим процедуру.
Данный алгоритм содержит в себе несколько вспомогательных функций, которые надо выбрать так, чтобы итоговое дерево было способно минимизировать $L$:
- $Ans(X_m)$, вычисляющая ответ для листа по попавшим в него объектам из обучающей выборки, может быть, например:
- в случае задачи классификации — меткой самого частого класса или оценкой дискретного распределения вероятностей классов для объектов, попавших в этот лист;
- в случае задачи регрессии — средним, медианой или другой статистикой;
- простой моделью. К примеру, листы в дереве, задающем регрессию, могут быть линейными функциями или синусоидами, обученными на данных, попавших в лист. Впрочем, везде ниже мы будем предполагать, что в каждом листе просто предсказывается константа.
- Критерий остановки $Stop(X_m)$ — функция, которая решает, нужно ли продолжать ветвление или пора остановиться.
Это может быть какое-то тривиальное правило: например, остановиться только в тот момент, когда объекты в листе получились достаточно однородными и/или их не слишком много. Более детально мы поговорим о критериях остановки в параграфе про регуляризацию деревьев.
- Критерий ветвления $Branch(X_m, feature, value)$ — пожалуй, самая интересная компонента алгоритма. Это функция, измеряющая, насколько хорош предлагаемый сплит. Чаще всего эта функция оценивает, насколько улучшится некоторая финальная метрика качества дерева в случае, если получившиеся два листа будут терминальными, по сравнению с ситуацией, когда сама исходная вершина является листом. Выбирается такой сплит, который даёт наиболее существенное улучшение. Впрочем, есть и другие подходы.
При этом строгой теории, которая бы связывала оптимальность выбора разных вариантов этих функций и разных метрик классификации и регрессии, в общем случае не существует. Однако есть набор интуитивных и хорошо себя зарекомендовавших соображений, с которыми мы вас сейчас познакомим.
Критерии ветвления: общая идея
Давайте теперь по очереди посмотрим на популярные постановки задач ML и под каждую подберём свой критерий.
Ответы дерева будем кодировать так: $c in mathbb{R}$ — для ответов регрессии и меток класса; для случаев, когда надо ответить дискретным распределением на классах, $c in mathbb{R}^K$ будет вектором вероятностей:
$$ c = (c_1, ldots, c_K), quad sum_{i = 1}^K c_i = 1 $$
Предположим также, что задана некоторая функция потерь $L(y_i, c)$. О том, что это может быть за функция, мы поговорим ниже.
В момент, когда мы ищем оптимальный сплит $X_m = X_lsqcup X_r$, мы можем вычислить для объектов из $X_m$ тот константный таргет $c$, которые предсказало бы дерево, будь текущая вершина терминальной, и связанное с ними значение исходного функционала качества $L$. А именно — константа $c$ должна минимизировать среднее значение функции потерь:
$$
frac{1}{vert X_mvert}sumlimits_{(x_i, y_i) in X_m} L(y_i, c)
$$
Оптимальное значение этой величины
$$
H(X_m) = minlimits_{c in Y} frac{1}{vert X_mvert}sumlimits_{(x_i, y_i) in X_m} L(y_i, c)
$$
обычно называют информативностью, или impurity. Чем она ниже, тем лучше объекты в листе можно приблизить константным значением.
Похожим образом можно определить информативность решающего пня. Пусть, как и выше, $X_l$ — множество объектов, попавших в левую вершину, а $X_r$ — в правую; пусть также $c_l$ и $c_r$ — константы, которые предсказываются в этих вершинах. Тогда функция потерь для всего пня в целом будет равна
$$
frac1{|X_m|}left(sum_{x_iin X_l}L(y_i, c_l) + sum_{x_iin X_r}L(y_i, c_r)right) =
$$
Вопрос на подумать. Как информативность решающего пня связана с информативностью его двух листьев?
Ответ (не открывайте сразу; сначала подумайте сами!)
Преобразуем выражение:
$$
frac1{|X_m|}left(sum_{x_iin X_l}L(y_i, c_l) + sum_{x_iin X_r}L(y_i, c_r)right) =
$$
$$
= frac1{|X_m|}left(|X_l|cdotfrac{1}{|X_l|}sum_{x_iin X_l}L(y_i, c_l) + |X_r|cdotfrac1{|X_r|}sum_{x_iin X_r}L(y_i, c_r)right)
$$
Эта сумма будет минимальна при оптимальном выборе констант $c_l$ и $c_r$, и информативность пня будет равна
$$frac{|X_l|}{|X_m|}H(X_l) + frac{|X_r|}{|X_m|}H(X_r)$$
Теперь для того чтобы принять решение о разделении, мы можем сравнить значение информативности для исходного листа и для получившегося после разделения решающего пня.
Разность информативности исходной вершины и решающего пня равна
$$H(X_m) — frac{|X_l|}{|X_m|}H(X_l) — frac{|X_r|}{|X_m|}H(X_r)$$
Для симметрии её приятно умножить на $vert X_mvert$; тогда получится следующий критерий ветвления:
$$color{#348FEA}{Branch (X_m, j, t) = |X_m| cdot H(X_m) — |X_l| cdot H(X_l) — |X_r| cdot H(X_r)}$$
Получившаяся величина неотрицательна: ведь, разделив объекты на две кучки и подобрав ответ для каждой, мы точно не сделаем хуже. Кроме того, она тем больше, чем лучше предлагаемый сплит.
Теперь посмотрим, какими будут критерии ветвления для типичных задач.
Информативность в задаче регрессии: MSE
Посмотрим на простой пример — регрессию с минимизацией среднеквадратичной ошибки:
$$
L(y_i, c) = (y_i -c)^2
$$
Информативность листа будет выглядеть следующим образом:
$$
H(X_m) = frac{1}{vert X_mvert} minlimits_{c in Y} sumlimits_{(x_i, y_i) in X_m} (y_i — c)^2
$$
Как мы уже знаем, оптимальным предсказанием константного классификатора для задачи минимизации MSE является среднее значение, то есть
$$
c = frac{sum y_i}{|X_m|}
$$
Подставив в формулу информативности сплита, получаем:
$$
color{#348FEA}{H(X_m) = sumlimits_{(x_i, y_i) in X_m}frac{left(y_i — overline{y} right)^2}{|X_m|}, ~ text{где} ~ overline{y} = frac{1}{vert X_m vert} sum_i y_i}
$$
То есть при жадной минимизации MSE информативность — это оценка дисперсии таргетов для объектов, попавших в лист. Получается очень стройная картинка: оценка значения в каждом листе — это среднее, а выбирать сплиты надо так, чтобы сумма дисперсий в листьях была как можно меньше.
Информативность в задаче регрессии: MAE
$$
L(y_i, c) = |y_i -c|
$$
Случай средней абсолютной ошибки так же прост: в листе надо предсказывать медиану, ведь именно медиана таргетов для обучающих примеров минимизирует MAE констатного предсказателя (мы это обсуждали в главе про линейные модели).
В качестве информативности выступает абсолютное отклонение от медианы:
$$
H(X_m) = sumlimits_{(x_i, y_i) in X_m}frac{|y_i — MEDIAN(Y)|}{|X_m|}
$$
Критерий информативности в задаче классификации: misclassification error
Пусть в нашей задаче $K$ классов, а $p_k$ — доля объектов класса $k$ в текущей вершине $X_m$:
$$
p_k = frac{1}{|X_m|} sum_{(x_i, y_i) in X_m} mathbb{I}[ y_i = k ]
$$
Допустим, мы заботимся о доле верно угаданных классов, то есть функция потерь — это индикатор ошибки:
$$
L(y_i, c) = mathbb{I}[y_i ne c]
$$
Пусть также предсказание модели в листе — один какой-то класс. Информативность для такой функции потерь выглядит так:
$$
H(X_m) = min_{c in Y} frac{1}{|X_m|} sum_{(x_i, y_i) in X_m} mathbb{I}[y_i ne c]
$$
Ясно, что оптимальным предсказанием в листе будет наиболее частотный класс $k_{ast}$, а выражение для информативности упростится следующим образом:
$$
H(X_m) = frac{1}{|X_m|} sum_{(x_i, y_i) in X_m} mathbb{I}[y_i ne k_{ast}] = 1 — p_{k_{ast}}
$$
Информативность в задаче классификации: энтропия
Если же мы собрались предсказывать вероятностное распределение классов $(c_1, ldots, c_K)$, то к этому вопросу можно подойти так же, как мы поступали при выводе логистической регрессии: через максимизацию логарифма правдоподобия (= минимизацию минус логарифма) распределения Бернулли. А именно, пусть в вершине дерева предсказывается фиксированное распределение $c$ (не зависящее от $x_i$), тогда правдоподобие имеет вид
$$
P(yvert x, c) = P(yvert c) = prodlimits_{(x_i, y_i) in X_m}P(y_ivert c) = prodlimits_{(x_i, y_i) in X_m}
prodlimits_{k = 1}^K c_k^{mathbb{I}[ y_i = k ]},
$$
откуда
$$
H(X_m) = minlimits_{sumlimits_{k} c_k = 1}
left(
-frac{1}{|X_m|} sumlimits_{(x_i, y_i) in X_m} sumlimits_{k = 1}^K mathbb{I}[ y_i = k ] log c_k
right)
$$
То, что оценка вероятностей в листе $c_k$, минимизирующая $H(X_m)$, должна быть равна $p_k$, то есть доле попавших в лист объектов этого класса, до некоторой степени очевидно, но это можно вывести и строго.
Доказательство для любопытных
Из-за наличия условия на $sum_k c_k = 1$ нам придётся минимизировать лагранжиан
$$
L(c, lambda) = min_{c, lambda} left(
left(
-frac{1}{|X_m|} sumlimits_{(x_i, y_i) in X_m} sumlimits_{k = 1}^K mathbb{I}[ y_i = k ] log c_k
right) + lambda sumlimits_{k = 1}^K c_k right)
$$
Как обычно, возьмём частную производную и решим уравнение:
$$
0 = frac{partial }{partial c_j}L(c, lambda) =
$$
$$
= frac{partial }{partial c_j} left(
left(
-frac{1}{|X_m|} sumlimits_{(x_i, y_i) in X_m} sumlimits_{k = 1}^K mathbb{I}[ y_i = k ] log c_k
right) + lambda sumlimits_{k = 1}^K c_k right) =
$$
$$
= left(
left(
-frac{1}{|X_m|} sumlimits_{(x_i, y_i) in X_m} mathbb{I}[ y_i = j ] frac{1}{c_j}
right) + lambda right) = — frac{p_j}{c_j} + lambda,
$$
откуда выражаем $c_j = frac{p_j}{lambda}$. Суммируя эти равенства, получим:
$$
1 = sum_{k = 1}^K c_k = frac{1}{lambda} sum_{k = 1}^K p_k = frac{1}{lambda},
$$
откуда $lambda = 1$, а значит, $c_k = p_k$.
Подставляя вектор $c = (p_1,ldots,p_K)$ в выражение выше, мы в качестве информативности получим энтропию распределения классов:
$$
color{#348FEA}{H(X_m) = -sum_{k = 1}^K p_k log p_k}
$$
Немного подробнее об энтропии
Величина
$$
H(X_m) = -sum_k p_k log p_k
$$
называется информационной энтропией Шеннона и измеряет непредсказуемость реализации случайной величины. В оригинальном определении, правда, речь шла не о значениях случайной величины, а о символах (первичного) алфавита, так как Шеннон придумал эту величину, занимаясь вопросами кодирования строк. Для данной задачи энтропия имеет вполне практический смысл — среднее количество битов, которое необходимо для кодирования одного символа сообщения при заданной частоте символов алфавита.
Так как $p_kin[0,1]$, энтропия неотрицательна. Если случайная величина принимает только одно значение, то она абсолютно предсказуема и её энтропия равна $ — 1 log(1) = 0$.
Наибольшего значения энтропия достигает для равномерно распределённой случайной величины — и это отражает тот факт, что среди всех величин с данной областью значений она наиболее «непредсказуема». Для равномерно распределённой на множестве ${1,ldots,K}$ случайной величины значение энтропии будет равно:
$$-sum_{k = 1}^K frac{1}{K}logfrac{1}{K} = log K$$
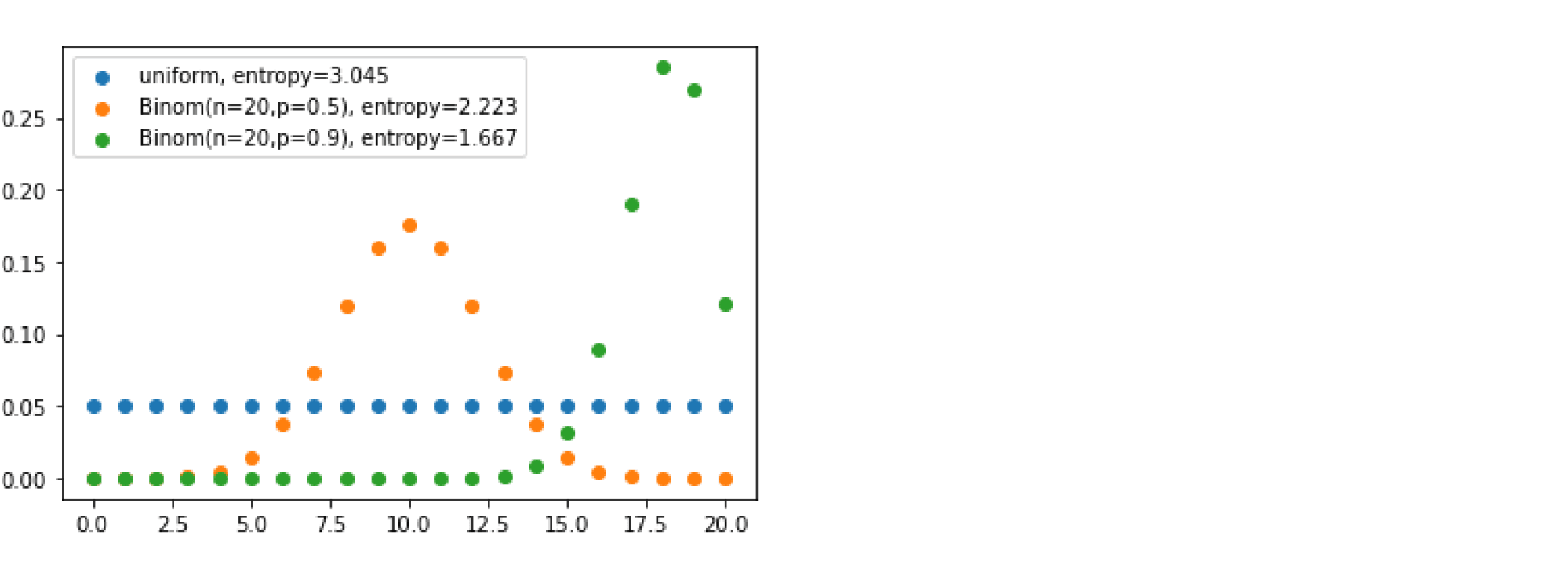
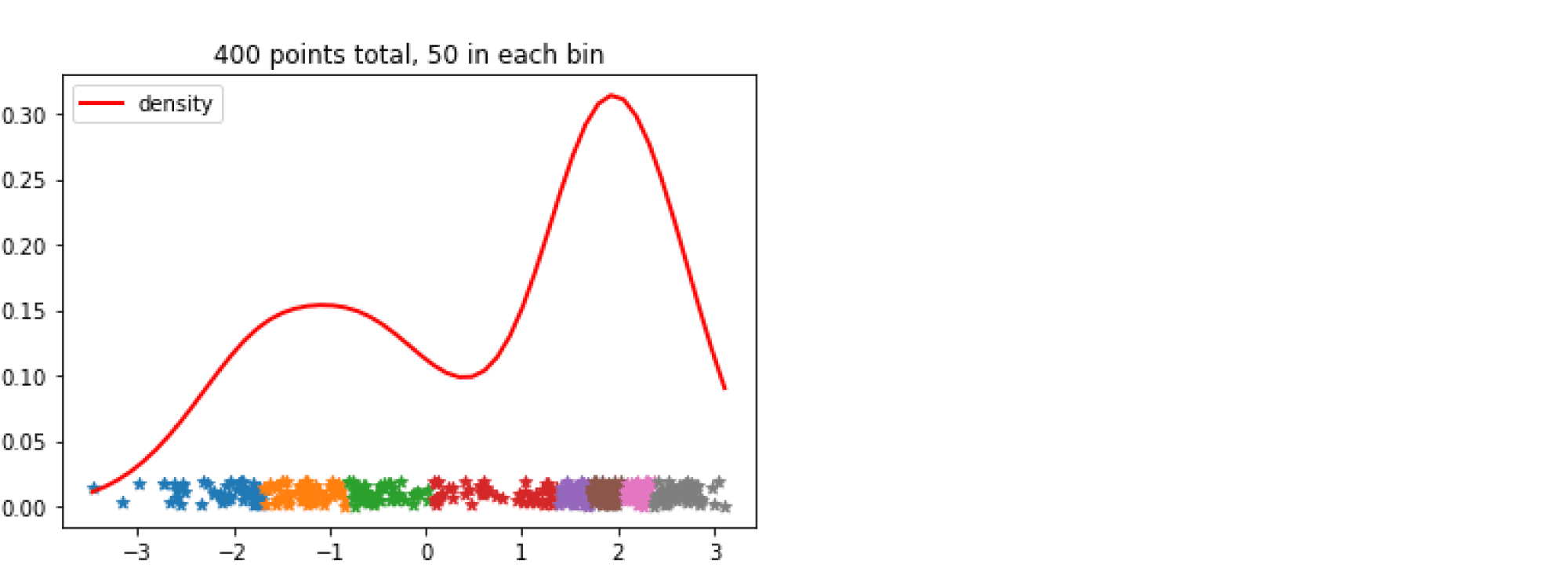
На следующем графике приведены три дискретных распределения на множестве $ {0, 1, ldots, 20} $ с их энтропиями. Как и указано выше, максимальную энтропию будет иметь равномерное распределение; у двух других проявляются пики разной степени остроты — и тем самым реализации этих величин обладают меньшей неопределённостью: мы можем с большей уверенностью говорить, что будет сгенерировано.
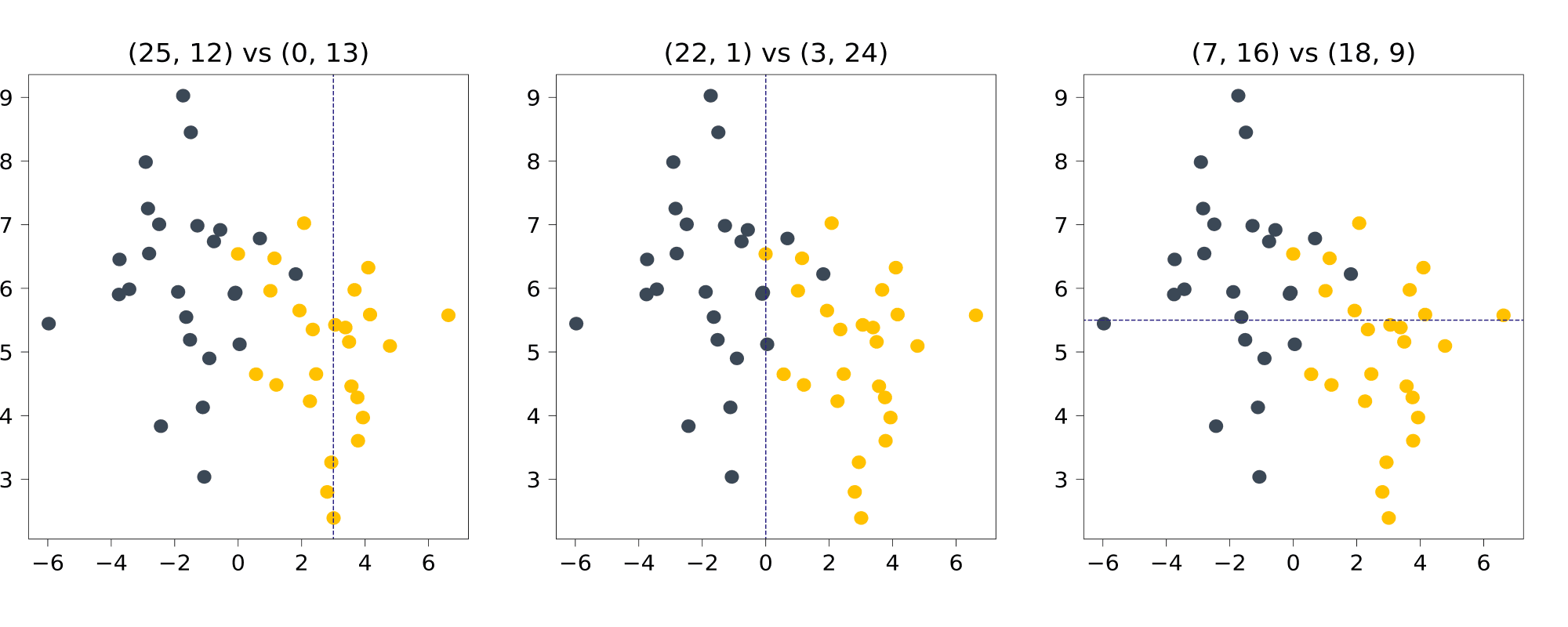
Разберём на примере игрушечной задачи классификации то, как энтропия может выступать в роли impurity. Рассмотрим три разбиения синтетического датасета и посмотрим, какие значения энтропии они дают. В подписях указано, каким становится соотношение классов в половинках.
В изначальном датасете по 25 точек каждого класса; энтропия состояния равна
$$S_0 = -frac{25}{50}log_2{frac{25}{50}}-frac{25}{50}log_2{frac{25}{50}} = 1$$
Для первого разбиения, по $[X_1 leqslant 3]$ в левую часть попадают $25$ точек класса 0 и $12$ точек класса 1, а в правую — $0$ точек класса 0 и $13$ точек класса 1. Энтропия левой группы равна
$$S_l = -frac{25}{37}log_2{frac{25}{37}}-frac{12}{37}log_2{frac{12}{37}}approx 0.9$$
Энтропия правой группы, строго говоря, не определена (под логарифмом ноль), но если заменить несуществующее значение на $lim_{trightarrow 0+}tlog_2{t} = 0$, то получится
$$S_r = — 0 — 1log_2{1}=0$$
Что, в принципе, логично: с вероятностью 1 выпадает единица, мы всегда уверены в результате, и энтропия у такого, вырожденного распределения тоже минимальная, равная нулю.
Как можно заметить, энтропия в обеих группах уменьшилась по сравнению с изначальной. Получается, что, разделив шарики по значению координаты, равному 12, мы уменьшили общую неопределённость системы. Но какое из разбиений даёт самое радикальное уменьшение? После несложных вычислений, мы получаем для нарисованных выше разбиений:
$$Branch^{(1)} approx 16.4$$
$$Branch^{(2)} approx 30.5$$
$$Branch^{(3)} approx 7$$
Ожидаемо, не так ли? Второе разбиение практически идеально разделяет классы, делая из исходного, почти равномерного распределения, два почти вырожденных. При остальных разбиениях в каждой из половинок неопределённость тоже падает, но не так сильно.
Кстати, Шеннон изначально собирался назвать информационную энтропию или «информацией», или «неопределённостью», но в итоге выбрал название «энтропия», потому что концепция со схожим смыслом в статистической механике уже была названа энтропией. Употребление термина из другой научной области выглядело убедительным преимуществом при ведении научных споров.
Информативность в задаче классификации: критерий Джини
Пусть предсказание модели — это распределение вероятностей классов $(c_1, ldots, c_k)$. Вместо логарифма правдоподобия в качестве критерия можно выбрать, например, метрику Бриера (за которой стоит всего лишь идея посчитать MSE от вероятностей). Тогда информативность получится равной
$$
H(X_m) = min_{sum_k c_k = 1} frac{1}{|X_m|} sum_{(x_i, y_i) in X_m} sum_{k = 1}^K (c_k — mathbb{I}[ y_i = k ] )^2
$$
Можно показать, что оптимальное значение этой метрики, как и в случае энтропии, достигается на векторе $c$, состоящем из выборочных оценок частот классов $(p_1, ldots, p_k)$, $p_i = frac{1}{vert X_mvert}sum_i mathbb{I}[ y_i = k ]$. Если подставить $(p_1, ldots, p_k)$ в выражение выше и упростить его, получится критерий Джини:
$$
color{#348FEA}{H(X_m) = sum_{k = 1}^K p_k (1 — p_k)}
$$
Критерий Джини допускает и следующую интерпретацию: $H(X_m)$ равно математическому ожиданию числа неправильно классифицированных объектов в случае, если мы будем приписывать им случайные метки из дискретного распределения, заданного вероятностями $(p_1, ldots, p_k)$.
Неоптимальность полученных критериев
Казалось бы, мы вывели критерии информативности для всех популярных задач, и они довольно логично следуют из их постановок, но получилось ли у нас обмануть NP-полноту и научиться строить оптимальные деревья легко и быстро?
Конечно, нет. Простейший пример — решение задачи XOR с помощью жадного алгоритма и любого критерия, который мы построили выше:
(источник картинки)
Вне зависимости от того, что вы оптимизируете, жадный алгоритм не даст оптимального решения задачи XOR. Но этим примером проблемы не исчерпываются. Скажем, бывают ситуации, когда оптимальное с точки зрения выбранной метрики дерево вы получите с критерием ветвления, построенным по другой метрике (например, MSE-критерий для MAE-задачи или Джини для misclassification error).
Особенности данных
Категориальные признаки
На первый взгляд, деревья прекрасно могут работать с категориальными переменными. А именно, если признак $x^i$ принимает значения из множества $C = {c_1,ldots,c_M}$, то при очередном разбиении мы можем рассматривать по этому признаку произвольные сплиты вида $C = C_lsqcup C_r$ (предикат будет иметь вид $[x^iin C_r]$). Это очень логично и естественно; проблема в том, что при больших $M$ у нас будет $2^{M-1}-1$ сплитов, и перебирать их будет слишком долго. Было бы здорово уметь каким-то образом упорядочивать значения $c_m$, чтобы работать с ними так же, как с обычными числами: разделяя на значения, «не превосходящие» и «большие» определённого порога.
Оказывается, что для некоторых задач такое упорядочение можно построить вполне естественным образом.
Так, для задачи бинарной классификации значения $c_m$ можно упорядочить по неубыванию доли объектов класса 1 с $x^i = c_m$, после чего работать с ними, как со значениями вещественного признака. Показано, что в случае, если мы выбираем таким образом сплит, оптимальный с точки зрения энтропийного критерия или критерия Джини, то он будет оптимальным среди всех $2^{M-1}-1$ сплитов.
Для задачи регрессии с функцией потерь MSE значения $c_m$ можно упорядочивать по среднему значению таргета на подмножестве ${Xmid x^i = c_m}$. Полученный таким образом сплит тоже будет оптимальным.
Работа с пропусками
Одна из приятных особенностей деревьев — это способность обрабатывать пропуски в данных. Разберёмся, что при этом происходит на этапе обучения и на этапе применения дерева.
Пусть у нас есть некоторый признак $x^i$, значение которого пропущено у некоторых объектов. Как обычно, обозначим через $X_m$ множество объектов, пришедших в рассматриваемую вершину, а через $V_m$ — подмножество $X_m$, состоящее из объектов с пропущенным значением $x^i$. В момент выбора сплитов по этому признаку мы будет просто игнорировать объекты из $V_m$, а когда сплит выбран, мы отправим их в оба поддерева. При этом логично присвоить им веса: $frac{vert X_lvert}{vert X_mvert}$ для левого поддерева и $frac{vert X_rvert}{vert X_mvert}$ для правого. Веса будут учитываться как коэффициенты при $L(y_i, c)$ в формуле информативности.
Вопрос на подумать. Во всех критериях ветвления участвуют мощности множеств $X_m$, $X_l$ и $X_r$. Нужно ли уменьшение размера выборки учитывать в формулах для информативности? Если нужно, то как?
Ответ (не открывайте сразу; сначала подумайте сами!)
Чтобы ответить на этот вопрос, вспомним, как работают критерии ветвления. Их суть в сравнении информативности $H(X_m)$ для исходной вершины с информативностью для решающего пня, порождённого рассматриваемым сплитом. Величина $H(X_m)$ никак не меняется; надо понять, что будет с пнём. Для него можно посчитать информативность так, словно объектов с пропущенными значениями нет:
$$frac1{|X_msetminus V_m|}left(sum_{x_iin X_lsetminus V_m}L(y_i, c_l) + sum_{x_iin X_rsetminus V_m}L(y_i, c_r)right)$$
Тогда в критерии ветвления нужно поменять коэффициенты, иначе мы не будем адекватным образом сравнивать такой сплит со сплитами по другим признакам:
$$Branch = |X_msetminus V_m|cdot H(X_m) — |X_lsetminus V_m|cdot H(X_lsetminus V_m) — |X_rsetminus V_m|cdot H(X_rsetminus V_m)$$
Если же мы предполагаем, что объекты из $V_m$ отправляются в новые листья с весами, как описано выше, то формула оказывается другой, и коэффициенты можно не менять:
$$frac1{|X_m|}left(underbrace{sum_{x_iin X_lsetminus V_m}L(y_i, c_l) + frac{|X_l|}{|X_m|}sum_{x_iin V_m}L(y_i, c_l)}_{text{Левый лист}} + underbrace{sum_{x_iin X_rsetminus V_m}L(y_i, c_r) + frac{|X_r|}{|X_m|}sum_{x_iin V_m}L(y_i, c_r)}_{text{Правый лист}}right)$$
Теперь рассмотрим этап применения дерева. Допустим, в вершину, где сплит идёт по $i$-му признаку, пришёл объект $x_0$ с пропущенным значением этого признака. Предлагается отправить его в каждую из дальнейших веток и получить по ним предсказания $widehat{y}_l$ и $widehat{y}_r$. Эти предсказания мы усредним с весами $frac{vert X_lvert}{vert X_mvert}$ и $frac{vert X_rvert}{vert X_mvert}$ (которые мы запомнили в ходе обучения):
$$widehat{y} = frac{vert X_lvert}{vert X_mvert}widehat{y}_l + frac{vert X_rvert}{vert X_mvert}widehat{y}_r$$
Для задачи регрессии это сразу даст нам таргет, а в задаче бинарной классификации — оценку вероятности класса 1.
Замечание. Если речь идёт о категориальном признаке, может оказаться хорошей идеей ввести дополнительное значение «пропущено» для категориального признака и дальше работать с пропусками, как с обычным значением. Особенно это актуально в ситуациях, когда пропуски имеют системный характер и их наличие несёт в себе определённую информацию.
Методы регуляризации решающих деревьев
Мы уже упоминали выше, что деревья легко переобучаются и процесс ветвления надо в какой-то момент останавливать.
Для этого есть разные критерии, обычно используются все сразу:
- ограничение по максимальной глубине дерева;
- ограничение на минимальное количество объектов в листе;
- ограничение на максимальное количество листьев в дереве;
- требование, чтобы функционал качества $Branch$ при делении текущей подвыборки на две улучшался не менее чем на $s$ процентов.
Делать это можно на разных этапах работы алгоритма, что не меняет сути, но имеет разные устоявшиеся названия:
- можно проверять критерии прямо во время построения дерева, такой способ называется pre-pruning или early stopping;
- а можно построить дерево жадно без ограничений, а затем провести стрижку (pruning), то есть удалить некоторые вершины из дерева так, чтобы итоговое качество упало не сильно, но дерево начало подходить под условия регуляризации. При этом качество стоит измерять на отдельной, отложенной выборке.
Алгоритмические трюки
Теперь временно снимем шапочку ML-аналитика, наденем шапочку разработчика и специалиста по computer science и посмотрим, как можно сделать полученный алгоритм более вычислительно эффективным.
В базовом алгоритме мы в каждой вершине дерева для всех возможных значений сплитов вычисляем информативность. Если в вершину пришло $q$ объектов, то мы рассматриваем $qD$ сплитов и для каждого тратим $O(q)$ операций на подсчёт информативности. Отметим, что в разных вершинах, находящихся в нашем дереве на одном уровне, оказываются разные объекты, то есть сумма этих $q$ по всем вершинам заданного уровня не превосходит $N$, а значит, выбор сплитов во всех вершинах уровня потребует $O(N^2 D)$ операций. Таким образом, общая сложность построения дерева — $O(hN^2 D)$ (где $h$ — высота дерева), и доминирует в ней перебор всех возможных предикатов на каждом уровне построения дерева. Посмотрим, что с этим можно сделать.
Динамическое программирование
Постараемся оптимизировать процесс выбора сплита в одной конкретной вершине.
Вместо того чтобы рассматривать все $O(ND)$ возможных сплитов, для каждого тратя $O(N)$ на вычисление информативности, можно использовать одномерную динамику. Для этого заметим, что если отсортировать объекты по какому-то признаку, то, проходя по отсортированному массиву, можно одновременно и перебирать все значения предикатов, и поддерживать все необходимые статистики для пересчёта значений информативности за $O(1)$ для каждого следующего варианта сплита (против изначальных $O(N)$).
Давайте разберём, как это работает, на примере построения дерева для MSE. Чтобы оценить информативность для листа, нам нужно знать несколько вещей:
- дисперсию и среднее значение таргета в текущем листе;
- дисперсию и среднее значение таргета в обоих потомках для каждого потенциального значения сплита.
Дисперсию и среднее текущего листа легко посчитать за $O(n)$.
С дисперсией и средним для всех значений сплитов чуть сложнее, но помогут следующие оценки математического ожидания и дисперсии:
$$overline{Y} = frac1Nsum y_i,$$
$$sigma^2 (Y) = overline{Y^2} — (overline{Y})^2 = frac1Nsum y_i^2 — frac{1}{N^2}(sum y_i)^2 $$
Следовательно, нам необходимо и достаточно для каждого потенциального значения сплита знать количество элементов в правом и левом поддеревьях, их сумму и сумму их квадратов (на самом деле всё это необходимо знать только для одной из половинок сплита, а для второй это можно получить, вычитая значения для первой из полных сумм). Это можно сделать за один проход по массиву, просто накапливая значения частичных сумм.
Если в вершину дерева пришло $q$ объектов, сложность построения одного сплита складывается из $D$ сортировок каждая по $O(qlog q)$ и одного линейного прохода с динамикой, всего $O(qDlog q + qD) = O(qDlog q)$, что лучше исходного $O(q^2D)$. Итоговая сложность алгоритма построения дерева — $O(hNDlog N)$ (где $h$ – высота дерева) против $hN^2D$ в наивной его версии.
Какие именно статистики накапливать (средние, медианы, частоты), зависит от критерия, который вы используете.
Гистограммный метод
Если бы мощность множества значений признаков была ограничена какой-то разумной константой $b ll N$, то сортировку в предыдущем способе можно было бы заменить сортировкой подсчётом и за счёт этого существенно ускорить алгоритм: ведь сложность такой сортировки — $O(N)$.
Чтобы провернуть это с любой выборкой, мы можем искусственно дискретизировать значения всех признаков. Это приведёт к локально менее оптимальным значениям сплитов, но, учитывая, что наш алгоритм и без этого был весьма приблизительным, это не ухудшит ничего драматически, а вот ускорение получается очень неплохое.
Самый популярный и простой способ дискретизации основан на частотах значений признаков: отрезок между максимальным и минимальным значением признака разбивается на $b$ подотрезков, длины которых выбираются так, чтобы в каждый попадало примерно равное число обучающих примеров. После чего значения признака заменяются на номера отрезков, на которые они попали.
Аналогичная процедура проводится для всех признаков выборки. Полная сложность предобработки — $O(DNlog N)$ (сортировка за $O(Nlog N)$ для каждого из $D$ признаков).
Теперь в процедуре динамического алгоритма поиска оптимального сплита нам надо перебирать не все $N$ объектов выборки, а всего лишь $b$ подготовленных заранее границ подотрезков. Частичные суммы статистик тоже придётся поддерживать не для исходного массива данных, а для списка из $b$ возможных сплитов. А для того чтобы делать это эффективно, необходим объект, называемый гистограммой: упорядоченный словарь, сопоставляющий каждому значению дискретизированного признака сумму необходимой статистики от таргета на отрезке [B[i-1], B[i]].
Финальный вид алгоритма таков:
- Дискретизируем каждый из признаков на $b$ значений. Сложность $O(DNlog N)$.
- Создаём корневую вершину
root. - Вызываем
build_tree_recursive(root, data).
Функция build_tree_recursive выглядит следующим образом:
- Проверяем, не пора ли остановиться. Если пора — считаем значение в листе.
- Теперь мы снова используем динамический алгоритм, но объекты будем сортировать не по исходным значениям признаков, а по их дискретизированным версиям, упорядочивая их с помощью сортировки подсчётом (для вершины, в которую попало $q$ объектов, сложность будет равна $O(qD)$ против $O(qlog qcdot D)$ в стандартной динамике).
- Находим оптимальный сплит за $O(qD)$.
- Делим данные, запускаем процедуру рекурсивно для обоих поддеревьев.
Общая сложность: $O(DNlog N + hND)$
Гистограммный метод на примере
Давайте посчитаем информативность сплита для MSE на данных с одним признаком, по которому мы уже отсортировали данные:
| x | -3 | -2 | -0.05 | 1 | 1 | 2 | 6 | 8 |
|---|---|---|---|---|---|---|---|---|
| y | 0 | 0.5 | -1 | 0 | 1 | 2 | 1 | 4 |
Дискретизируем на три отрезка с границами $B = [-1, 1.5]$
| discretized_x | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 |
|---|---|---|---|---|---|---|---|---|
| y | 0 | 0.5 | -1 | 0 | 1 | 2 | 1 | 4 |
Строим гистограмму частичных сумм, сумм квадратов и количества объектов для двух отрезков (для третьего можно посчитать, используя общую сумму):
| b | 0 | 1 |
|---|---|---|
| cnt | 2 | 3 |
| sum_y | 0.5 | 0 |
| sum_y_sq | 0.25 | 2 |
Всего объектов восемь, сумма таргетов — $text{sum_total} = 7.5$, сумма квадратов — $text{sum_sq_total} = 23.25$.
Информативность текущего листа:
$$
D[X_d] = frac{text{sum_sq_total}}{text{cnt_total}} — left(frac{text{sum_total}}{text {cnt_total}}right)^2 =
$$ $$
= frac{23.25}{8} — left( frac{7.5}{8} right)^{2} = 2.0273
$$
Посчитаем значение критерия ветвления для $b=-1$. Информативность левого листа, то есть дисперсия в нём, равна:
$$
D[X_l] = E[X_l^2] — E^2[X_l] = \
$$
$$
= frac{text{sum_y_sq}[0]}{text{cnt}[0]} — left(frac{text{sum_y}}{text{cnt}[0]}right)^2 = \
$$
$$
= 0.125 — 0.25 ^ 2 = 0.0625
$$
Информативность правого листа, то есть дисперсия в нём, равна:
$$
D[X_r] = E[X_r^2] — E^2[X_r] = \
$$
$$
= frac{text{sum_sq_total} — text{sum_y_sq}[0]}{text{cnt_total} — text{cnt}[0]} — left(frac{text{sum_total} — text{sum_y}}{text{cnt_total} — text{cnt}[0]}right)^2 \
approx 2.47
$$
Полное значение критерия для разбиения по $b=-1$:
$$
Branch(b = -1) = 8 cdot D[X_d] — 2 cdot D[X_l] — 6 cdot D[X_r] =
$$ $$
= 6.555
$$
Mixed integer optimization
Если вам действительно хочется построить оптимальное (или хотя бы очень близкое к оптимальному) дерево, то на сегодня для решения этой проблемы не нужно придумывать кучу эвристик самостоятельно, а можно воспользоваться специальными солверами, которые решают NP-полные задачи приближённо, но всё-таки почти точно. Так что единственной (и вполне решаемой) проблемой будет представить исходную задачу в понятном для солвера виде. Пример построения оптимального дерева с помощью решения задачи целочисленного программирования.
Историческая справка
Как вы, может быть, уже заметили, решающие деревья — это одна большая эвристика для решения NP-полной задачи, практически лишённая какой-либо стройной теоретической подоплёки. В 1970–1990-e годы интерес к ним был весьма велик как в индустрии, где был полезен хорошо интерпретируемый классификатор, так и в науке, где учёные интересовались способами приближённого решения NP-полных задач.
В связи с этим сложилось много хорошо работающих наборов эвристик, у которых даже были имена: например, ID3 был первой реализацией дерева, минимизирующего энтропию, а CART — первым деревом для регрессии. Некоторые из них были запатентованы и распространялись коммерчески.
На сегодня это всё потеряло актуальность в связи с тем, что существуют хорошо написанные библиотеки (например, sklearn, в которой реализована оптимизированная версия CART).
Бинарные деревья поиска и рекурсия – это просто
Время на прочтение
8 мин
Количество просмотров 525K
Существует множество книг и статей по данной теме. В этой статье я попробую понятно рассказать самое основное.
Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями.
Рис. 1 Бинарное дерево
Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом, если равно, то значение найдено и поиск прекращается.
Рис. 2 Бинарное дерево поиска
Сбалансированное бинарное дерево поиска — это бинарное дерево поиска с логарифмической высотой. Данное определение скорее идейное, чем строгое. Строгое определение оперирует разницей глубины самого глубокого и самого неглубокого листа (в AVL-деревьях) или отношением глубины самого глубокого и самого неглубокого листа (в красно-черных деревьях). В сбалансированном бинарном дереве поиска операции поиска, вставки и удаления выполняются за логарифмическое время (так как путь к любому листу от корня не более логарифма). В вырожденном случае несбалансированного бинарного дерева поиска, например, когда в пустое дерево вставлялась отсортированная последовательность, дерево превратится в линейный список, и операции поиска, вставки и удаления будут выполняться за линейное время. Поэтому балансировка дерева крайне важна. Технически балансировка осуществляется поворотами частей дерева при вставке нового элемента, если вставка данного элемента нарушила условие сбалансированности.
Рис. 3 Сбалансированное бинарное дерево поиска
Сбалансированное бинарное дерево поиска применяется, когда необходимо осуществлять быстрый поиск элементов, чередующийся со вставками новых элементов и удалениями существующих. В случае, если набор элементов, хранящийся в структуре данных фиксирован и нет новых вставок и удалений, то массив предпочтительнее. Потому что поиск можно осуществлять алгоритмом бинарного поиска за то же логарифмическое время, но отсутствуют дополнительные издержки по хранению и использованию указателей. Например, в С++ ассоциативные контейнеры set и map представляют собой сбалансированное бинарное дерево поиска.
Рис. 4 Экстремально несбалансированное бинарное дерево поиска
Теперь кратко обсудим рекурсию. Рекурсия в программировании – это вызов функцией самой себя с другими аргументами. В принципе, рекурсивная функция может вызывать сама себя и с теми же самыми аргументами, но в этом случае будет бесконечный цикл рекурсии, который закончится переполнением стека. Внутри любой рекурсивной функции должен быть базовый случай, при котором происходит выход из функции, а также вызов или вызовы самой себя с другими аргументами. Аргументы не просто должны быть другими, а должны приближать вызов функции к базовому случаю. Например, вызов внутри рекурсивной функции расчета факториала должен идти с меньшим по значению аргументом, а вызовы внутри рекурсивной функции обхода дерева должны идти с узлами, находящимися дальше от корня, ближе к листьям. Рекурсия может быть не только прямой (вызов непосредственно себя), но и косвенной. Например А вызывает Б, а Б вызывает А. С помощью рекурсии можно эмулировать итеративный цикл, а также работу структуры данных стек (LIFO).
int factorial(int n)
{
if(n <= 1) // Базовый случай
{
return 1;
}
return n * factorial(n - 1); //рекурсивеый вызов с другим аргументом
}
// factorial(1): return 1
// factorial(2): return 2 * factorial(1) (return 2 * 1)
// factorial(3): return 3 * factorial(2) (return 3 * 2 * 1)
// factorial(4): return 4 * factorial(3) (return 4 * 3 * 2 * 1)
// Вычисляет факториал числа n (n должно быть небольшим из-за типа int
// возвращаемого значения. На практике можно сделать long long и вообще
// заменить рекурсию циклом. Если важна скорость рассчетов и не жалко память, то
// можно совсем избавиться от функции и использовать массив с предварительно
// посчитанными факториалами).
void reverseBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
cout << n%2;
reverseBinary(n/2); //рекурсивеый вызов с другим аргументом
}
// Печатает бинарное представление числа в обратном порядке
void forvardBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
forvardBinary(n/2); //рекурсивеый вызов с другим аргументом
cout << n%2;
}
// Поменяли местами две последние инструкции
// Печатает бинарное представление числа в прямом порядке
// Функция является примером эмуляции стека
void ReverseForvardBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
cout << n%2; // печатает в обратном порядке
ReverseForvardBinary(n/2); //рекурсивеый вызов с другим аргументом
cout << n%2; // печатает в прямом порядке
}
// Функция печатает сначала бинарное представление в обратном порядке,
// а затем в прямом порядке
int product(int x, int y)
{
if (y == 0) // Базовый случай
{
return 0;
}
return (x + product(x, y-1)); //рекурсивеый вызов с другим аргументом
}
// Функция вычисляет произведение x * y ( складывает x y раз)
// Функция абсурдна с точки зрения практики,
// приведена для лучшего понимания рекурсии
Кратко обсудим деревья с точки зрения теории графов. Граф – это множество вершин и ребер. Ребро – это связь между двумя вершинами. Количество возможных ребер в графе квадратично зависит от количества вершин (для понимания можно представить турнирную таблицу сыгранных матчей). Дерево – это связный граф без циклов. Связность означает, что из любой вершины в любую другую существует путь по ребрам. Отсутствие циклов означает, что данный путь – единственный. Обход графа – это систематическое посещение всех его вершин по одному разу каждой. Существует два вида обхода графа: 1) поиск в глубину; 2) поиск в ширину.
Поиск в ширину (BFS) идет из начальной вершины, посещает сначала все вершины находящиеся на расстоянии одного ребра от начальной, потом посещает все вершины на расстоянии два ребра от начальной и так далее. Алгоритм поиска в ширину является по своей природе нерекурсивным (итеративным). Для его реализации применяется структура данных очередь (FIFO).
Поиск в глубину (DFS) идет из начальной вершины, посещая еще не посещенные вершины без оглядки на удаленность от начальной вершины. Алгоритм поиска в глубину по своей природе является рекурсивным. Для эмуляции рекурсии в итеративном варианте алгоритма применяется структура данных стек.
С формальной точки зрения можно сделать как рекурсивную, так и итеративную версию как поиска в ширину, так и поиска в глубину. Для обхода в ширину в обоих случаях необходима очередь. Рекурсия в рекурсивной реализации обхода в ширину всего лишь эмулирует цикл. Для обхода в глубину существует рекурсивная реализация без стека, рекурсивная реализация со стеком и итеративная реализация со стеком. Итеративная реализация обхода в глубину без стека невозможна.
Асимптотическая сложность обхода и в ширину и в глубину O(V + E), где V – количество вершин, E – количество ребер. То есть является линейной по количеству вершин и ребер. Записи O(V + E) с содержательной точки зрения эквивалентна запись O(max(V,E)), но последняя не принята. То есть, сложность будет определятся максимальным из двух значений. Несмотря на то, что количество ребер квадратично зависит от количества вершин, мы не можем записать сложность как O(E), так как если граф сильно разреженный, то это будет ошибкой.
DFS применяется в алгоритме нахождения компонентов сильной связности в ориентированном графе. BFS применяется для нахождения кратчайшего пути в графе, в алгоритмах рассылки сообщений по сети, в сборщиках мусора, в программе индексирования – пауке поискового движка. И DFS и BFS применяются в алгоритме поиска минимального покрывающего дерева, при проверке циклов в графе, для проверки двудольности.
Обходу в ширину в графе соответствует обход по уровням бинарного дерева. При данном обходе идет посещение узлов по принципу сверху вниз и слева направо. Обходу в глубину в графе соответствуют три вида обходов бинарного дерева: прямой (pre-order), симметричный (in-order) и обратный (post-order).
Прямой обход идет в следующем порядке: корень, левый потомок, правый потомок. Симметричный — левый потомок, корень, правый потомок. Обратный – левый потомок, правый потомок, корень. В коде рекурсивной функции соответствующего обхода сохраняется соответствующий порядок вызовов (порядок строк кода), где вместо корня идет вызов данной рекурсивной функции.
Если нам дано изображение дерева, и нужно найти его обходы, то может помочь следующая техника (см. рис. 5). Обводим дерево огибающей замкнутой кривой (начинаем идти слева вниз и замыкаем справа вверх). Прямому обходу будет соответствовать порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами слева. Для симметричного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами снизу. Для обратного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами справа. В коде рекурсивного вызова прямого обхода идет: вызов, левый, правый. Симметричного – левый, вызов, правый. Обратного – левый правый, вызов.
Рис. 5 Вспомогательный рисунок для обходов
Для бинарных деревьев поиска симметричный обход проходит все узлы в отсортированном порядке. Если мы хотим посетить узлы в обратно отсортированном порядке, то в коде рекурсивной функции симметричного обхода следует поменять местами правого и левого потомка.
struct TreeNode
{
double data; // ключ/данные
TreeNode *left; // указатель на левого потомка
TreeNode *right; // указатель на правого потомка
};
void levelOrderPrint(TreeNode *root) {
if (root == NULL)
{
return;
}
queue<TreeNode *> q; // Создаем очередь
q.push(root); // Вставляем корень в очередь
while (!q.empty() ) // пока очередь не пуста
{
TreeNode* temp = q.front(); // Берем первый элемент в очереди
q.pop(); // Удаляем первый элемент в очереди
cout << temp->data << " "; // Печатаем значение первого элемента в очереди
if ( temp->left != NULL )
q.push(temp->left); // Вставляем в очередь левого потомка
if ( temp->right != NULL )
q.push(temp->right); // Вставляем в очередь правого потомка
}
}
void preorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
cout << root->data << " ";
preorderPrint(root->left); //рекурсивный вызов левого поддерева
preorderPrint(root->right); //рекурсивный вызов правого поддерева
}
// Функция печатает значения бинарного дерева поиска в прямом порядке.
// Вместо печати первой инструкцией функции может быть любое действие
// с данным узлом
void inorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->left); //рекурсивный вызов левого поддерева
cout << root->data << " ";
preorderPrint(root->right); //рекурсивный вызов правого поддерева
}
// Функция печатает значения бинарного дерева поиска в симметричном порядке.
// То есть в отсортированном порядке
void postorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->left); //рекурсивный вызов левого поддерева
preorderPrint(root->right); //рекурсивный вызов правого поддерева
cout << root->data << " ";
}
// Функция печатает значения бинарного дерева поиска в обратном порядке.
// Не путайте обратный и обратноотсортированный (обратный симметричный).
void reverseInorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->right); //рекурсивный вызов правого поддерева
cout << root->data << " ";
preorderPrint(root->left); //рекурсивный вызов левого поддерева
}
// Функция печатает значения бинарного дерева поиска в обратном симметричном порядке.
// То есть в обратном отсортированном порядке
void iterativePreorder(TreeNode *root)
{
if (root == NULL)
{
return;
}
stack<TreeNode *> s; // Создаем стек
s.push(root); // Вставляем корень в стек
/* Извлекаем из стека один за другим все элементы.
Для каждого извлеченного делаем следующее
1) печатаем его
2) вставляем в стек правого! потомка
(Внимание! стек поменяет порядок выполнения на противоположный!)
3) вставляем в стек левого! потомка */
while (s.empty() == false)
{
// Извлекаем вершину стека и печатаем
TreeNode *temp = s.top();
s.pop();
cout << temp->data << " ";
if (temp->right)
s.push(temp->right); // Вставляем в стек правого потомка
if (temp->left)
s.push(temp->left); // Вставляем в стек левого потомка
}
}
// В симметричном и обратном итеративном обходах просто меняем инструкции
// местами по аналогии с рекурсивными функциями.
Надеюсь Вы не уснули, и статья была полезна. Скоро надеюсь последует продолжение
банкета
статьи.
Скачать материал

Скачать материал


- Сейчас обучается 1159 человек из 83 регионов


- Сейчас обучается 28 человек из 10 регионов


- Сейчас обучается 81 человек из 38 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Комбинаторные задачи:
дерево возможных вариантов -
2 слайд
Имя урока: Комбинаторика
Девиз урока: «Услышал – забыл,
Увидел – запомнил,
Сделал – понял»
Китайская поговорка -
3 слайд
В странных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне:
Вперёд поедешь – голову сложишь.
Налево поедешь – меча лишишься.
А дальше говорится, как он выходит из того положения, в которое попал в результате выбора.
Направо поедешь – коня потеряешь.Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации.
-
4 слайд
Что такое КОМБИНАТОРИКА?
Задачи, в которых требуется осуществить перебор всех возможных вариантов, или, как обычно говорят в таких случаях, всех возможных комбинаций, называют комбинаторными.
Область математики, изучающая комбинаторные задачи, называется комбинаторикой.
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить. -
5 слайд
Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2.
1 2
1
1
2
2
1
1
1
1
2
2
2
2
Ответ: 111, 112, 121, 122, 211, 212, 221, 222 – восемь чисел.
Такой метод решения комбинаторных задач называется деревом выбора(дерево возможных вариантов) -
6 слайд
Задача №2
Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7. -
7 слайд
Задача 3
В 5 «А» классе в среду 4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду?
Решение: построим картину-схему.
Для удобства закодируем названия предметов:
математика – м,
информатика – и,
русский язык – р,
английский язык – а. -
8 слайд
Решение задачи 3
Расписание1 урок м и р а
2 урок и р а м р а м и а м и р
3 урок р а и а и р р а м а м р и а м а м и и р м р м и
4 урок а р а и р и а р а м р м а и а м и м р и р м и м
Ответ: 24 варианта: мира, миар, мриа, мраи, маир, мари, имра, имар, ирма, ирам, иамр, иарм, рмиа, рмаи, рима, риам, рами, раим, амир, амри, аимр, аирм, арми, арим.
-
9 слайд
Построенная схема напоминает перевернутое дерево: от ствола («расписание») отходят ветки, сначала четыре (м, и, р, а), от каждой из четырех веток – еще по три, затем еще по две и еще по одной. Видимо поэтому такую схему называют деревом возможных вариантов.
Дерево возможных вариантов можно считать геометрической моделью рассматриваемой ситуации. -
10 слайд
Задача №4
В правление фирмы входят 5 человек. Из своего состава правления должно выбрать президента и вице-президента. Сколькими способами это можно сделать?
Президент
1Вице – президент
2 3 4 5
2
1 3 4 5
3
1 2 4 54
1 2 3 4
5
1 2 3 5
Такой метод решения комбинаторных задач называется правилом умножения.
Выбрать президента можно пятью способами, а для каждого выбранного президента четырьмя способами можно выбрать вице-президента . Следовательно, общее число способов выбрать президента и вице-президента фирмы равно: 5*4=20. -
11 слайд
Можно решить Задачу 3 короче, если применить правило умножения. Существует 4 варианта выбора первого урока. Для выбора второго урока есть только три варианта, так как один из четырех уроков мы уже выбрали. Тогда для третьего урока существует два варианта, а для четвертого только один. Применив правило умножения, получим
4 ∙ 3 ∙ 2 ∙1= 24
Ответ: 24 варианта. -
12 слайд
Задача №5
В классе 15 мальчиков и 10 девочек. Сколькими способами можно выбрать двух дежурных(одну девочку и одного мальчика)? -
13 слайд
Задача 2.
В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура.
а) Сколько имеется вариантов расписания при условии, что физкультура – последний урок?
б) Сколько имеется вариантов расписания при условии, что физкультура – последний урок, а математика – первый?
-
14 слайд
Задача 2 (продолжение).
В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура.в) Сколько всего можно составить вариантов расписания на четверг?
г) Сколько времени потратит завуч на запись всех вариантов, если известно, что на запись одного варианта у него уходит 30 секунд?
-
-
-
17 слайд
Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7.
Задача №2
Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7? Нарисуйте дерево выбора на альбомном листе.
Задача №3
Составьте комбинаторную задачу, которая решается с помощью правила умножения. Сделайте к ней рисунок.
Задача № 4
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4, причем цифры в числе
могут повторяться. Сколько чисел может составить Филя?
Задача № 5
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4 так, чтобы цифры в числе
не повторялись. Сколько чисел может составить Филя?
Домашнее задание
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 266 073 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 24.04.2017
- 1096
- 0
- 24.04.2017
- 626
- 0
- 24.04.2017
- 1132
- 0
Рейтинг:
4 из 5
- 24.04.2017
- 32754
- 272
- 24.04.2017
- 2577
- 2
- 24.04.2017
- 7022
- 11
- 24.04.2017
- 847
- 3
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
вариантов
Задача перебора вариантов и модель дерева решений
Задача оптимального выбора (задача о рюкзаке)
Метод полного перебора двоичного дерева
Метод ветвей и границ
Эвристические методы
Задача перебора вариантов и модель дерева решений
Решение многих прикладных задач (особенно задач искусственного интеллекта) сводится к перебору большого числа возможных вариантов с целью нахождения наиболее приемлемого из них по заданному критерию.
В этом случае для наглядной интерпретации перебора вариантов удобно использовать модель в виде дерева решений.
Например, для задачи моделирования игры в крестики-нолики всевозможные ситуации можно представить в виде следующего дерева решений

Игра в крестики-нолики
|
Корень (начало игры) |
|||||||||||||||||||||||||||||
|
О |
|||||||||||||||||||||||||||||
|
Первый ход |
. . . |
. . . |
|||||||||||||||||||||||||||
|
О |
О |
О |
О |
О |
|||||||||||||||||||||||||
|
О |
||||||
|
О |
О |
О |
лист |
О |
(конец |
|
|
О |
О |
игры) |
||||
Описание модели
Каждый узел в дереве интерпретируется как результат выполнения некоторой последовательности шагов решения задачи перебора вариантов.
Ветвь в дереве при этом соответствует принятию очередного решения (шагу), которое ведет к более полному решению. В игровых деревьях, например, каждая ветвь соответствует ходу игрока.
Листы (узлы у которых нет выходящих ветвей) представляют собой окончательные варианты решений.
Цель состоит в том, чтобы из всех возможных вариантов решений найти наилучший по заданному критерию путь от корня до листа при выполнении некоторых условий-ограничений.
Форма дерева, критерий оптимальности и условия-ограничения
|
определяются конкретной задачей. |
4 |
|
02.07.19 |

Задача о почтальоне |
Дерево решений |
1
3 4
2 4 2 3
4 2 3 2
1 1 1 1
Почтальон выходит из пункта 1 Он должен обойти все пункты и возвратиться обратно
Формализация задачи
•Предположим, что на каждом i-том ходу возможен выбор из ki вариантов (ai1..aiki ) хода. Т.е. задана матрица возможных кандидатов на каждом ходу, например такая:
начало
|
a |
a |
|||||
|
11 |
12 |
|||||
|
a22 |
a23 |
|||||
|
A a21 |
a |
i-й ход (i=1..n) |
||||
|
a |
a |
a |
33 |
34 |
||
|
31 |
32 |
|||||
|
a41 |
a42 |
a43 |
J – вариант хода
Один из путей S=(a11, a22, a34, a42) Целевая функция
02.07.19
F(S)= a11+ a22+a34+a42
Попытайтесь
запрограммировать перебор вариантов с помощью операторов цикла и найти максимальный
6
Рекурсивная программа полного перебора
• Var S:array[1..n]of тип <кандидатов a11..ankn>;
•n,j:word;
•Procedure Vbr(i:word);
|
• |
Begin |
j:=0; |
|
• |
Repeat |
j:=j+1; |
•//выбор и запоминание j-го кандидата на i-том ходу
|
• |
S[i]:= a[i,j]; |
|
|
• |
if i<n then |
Vbr(i+1) |
|
• |
else begin |
|
|
• |
{лист решения сформирован в S[1..n], здесь возможна проверка |
|
|
приемлемости и оптимальности, печать или отображение |
||
|
варианта }; |
end; |
•until j=ki ;
•// список кандидатов на i – м ходу исчерпан; end;//Vbr
•Обращение к процедуре:
|
• |
Read(n); |
For i:=1 to n do S[i]:=0; |
|
|
• |
02.07.19 |
Vbr(1); |
7 |
Пример (сколькими способами можно укомплектовать рюкзак тремя вещами)
|
Матрица имеет двух |
Программа выдаст следующие 8 |
|||||||
|
кандидатов на каждом |
вариантов массива S |
|||||||
|
шагу |
1 |
2 |
3 |
|||||
|
1 |
0 |
1 |
2 |
0 |
||||
|
0 |
||||||||
|
1 |
3 |
|||||||
|
0 |
||||||||
|
A 2 |
0 |
0 |
||||||
|
1 |
||||||||
|
3 |
0 |
0 |
2 |
3 |
||||
|
0 |
2 |
0 |
||||||
|
На основе такого алгоритма создаются |
||||||||
|
0 |
3 |
|||||||
|
программы игры в шахматы, карты, а также |
0 |
|||||||
|
решается множество задач искусственного |
0 |
0 |
||||||
|
интеллекта |
8 |
|||||||
|
02.07.19 |
0 |
|
• |
Procedure Vbr(i:word); |
|
|
• |
Begin |
j:=0; |
|
• |
Repeat |
j:=j+1; |
|
• |
S[i]:= a[i,j]; |
•if i<n
•else
•begin {печать S[1..n],} end;
•until j=2 ;
•end;
•n=3; Vbr(1);
02.07.19
i=1 j=1 s[1]=a[11]
i=2 j=1 s[2]= a[21] i=3 j=1 s[3]= a[31]
Печать (1,2,3)
|
i=3 |
j=2 |
s[3]= a[32] |
||
|
Печать |
(1,2,0) |
|||
|
i=2 |
j=2 |
s[2]= a[22] |
||
|
i=3 |
j=1 |
s[3]= a[31] |
||
|
Печать |
(1,0,3) |
|||
|
i=3 |
j=2 |
s[3]= a[32] |
||
|
Печать |
(1,0,0) |
|||
|
i=1 j=2 s[1]=a[12] |
||||
|
i=2 j=1 s[2]=a[21] |
||||
|
i=3 j=1 s[3]=a[31] |
||||
|
Печать |
(0,2,3) |
и т.д. |
9 |
Задача оптимального выбора (о рюкзаке)
Имеется n элементов a1…an
Каждый элемент ai характеризуется определенными
свойствами, например вес wi и цена ci
(это могут быть размер и время, объем инвестиций и ожидаемый доход, и т.д.).
Требуется найти оптимальную выборку ai1 …aik
k n
т.е. такую для которой, при заданном ограничении на
|
суммарный вес достигается максимальная стоимость . |
||
|
k |
k |
|
|
wij |
Wmax |
max ci j |
|
j 1 |
j 1 |
|
|
02.07.19 |
10 |
Соседние файлы в папке Презентации 2часть
- #
- #
- #
- #
- #
- #
- #
- #
- #
До сих пор мы рассматривали структуры данных, данные в которых располагаются линейно. В связном списке — от первого узла к единственному последнему. В динамическом массиве — в виде непрерывного блока.
В этой части мы рассмотрим совершенно новую структуру данных — дерево. А точнее, двоичное (бинарное) дерево поиска (binary search tree). Бинарное дерево поиска имеет структуру дерева, но элементы в нем расположены по определенным правилам.
Также смотрите другие материалы этой серии: стеки и очереди, динамический массив, связный список, оценка сложности алгоритма, сортировка и множества.
Для начала мы рассмотрим обычное дерево.
Деревья
Дерево — это структура, в которой у каждого узла может быть ноль или более подузлов — «детей». Например, дерево может выглядеть так:
Структура организации
Это дерево показывает структуру компании. Узлы представляют людей или подразделения, линии — связи и отношения. Дерево — это самый эффективный способ представления и хранения такой информации.
Дерево на картинке выше очень простое. Оно отражает только отношение родства категорий, но не накладывает никаких ограничений на свою структуру. У генерального директора может быть как один непосредственный подчиненный, так и несколько или ни одного. На рисунке отдел продаж находится левее отдела маркетинга, но порядок на самом деле не имеет значения. Единственное ограничение дерева — каждый узел может иметь не более одного родителя. Самый верхний узел (совет директоров, в нашем случае) родителя не имеет. Этот узел называется «корневым», или «корнем».
Вопросы о деревьях задают даже на собеседовании в Apple.
Двоичное дерево поиска
Двоичное дерево поиска похоже на дерево из примера выше, но строится по определенным правилам:
- У каждого узла не более двух детей.
- Любое значение меньше значения узла становится левым ребенком или ребенком левого ребенка.
- Любое значение больше или равное значению узла становится правым ребенком или ребенком правого ребенка.
Давайте посмотрим на дерево, построенное по этим правилам:
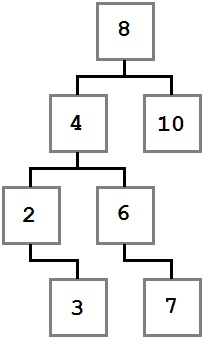
Двоичное дерево поиска
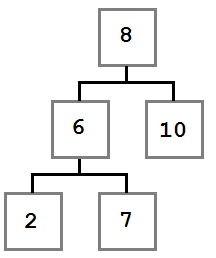
Обратите внимание, как указанные ограничения влияют на структуру дерева. Каждое значение слева от корня (8) меньше восьми, каждое значение справа — больше либо равно корню. Это правило применимо к любому узлу дерева.
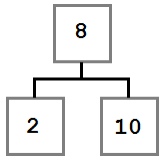
Учитывая это, давайте представим, как можно построить такое дерево. Поскольку вначале дерево было пустым, первое добавленное значение — восьмерка — стало его корнем.
Мы не знаем точно, в каком порядке добавлялись остальные значения, но можем представить один из возможных путей. Узлы добавляются методом Add, который принимает добавляемое значение.
BinaryTree tree = new BinaryTree();
tree.Add(8);
tree.Add(4);
tree.Add(2);
tree.Add(3);
tree.Add(10);
tree.Add(6);
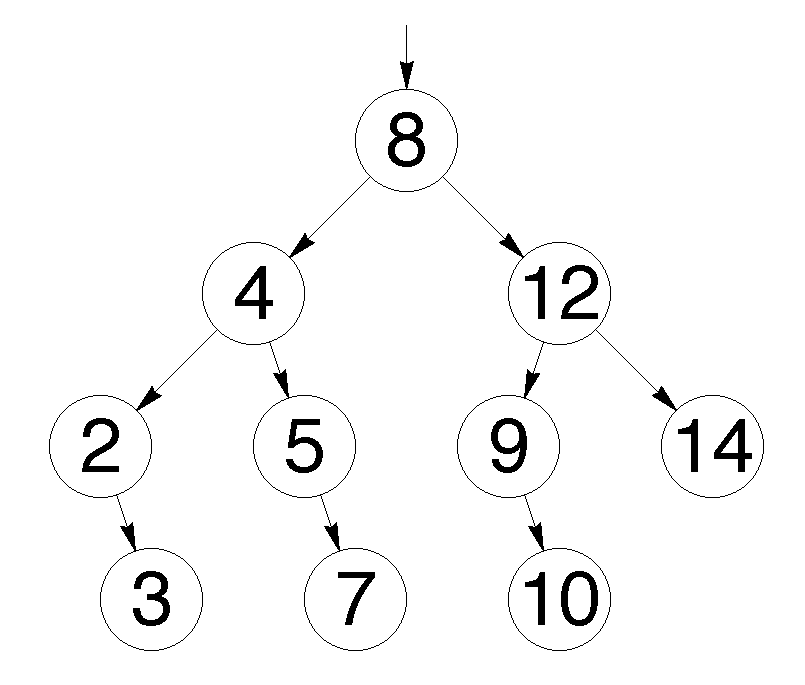
tree.Add(7);Рассмотрим подробнее первые шаги.
В первую очередь добавляется 8. Это значение становится корнем дерева. Затем мы добавляем 4. Поскольку 4 меньше 8, мы кладем ее в левого ребенка, согласно правилу 2. Поскольку у узла с восьмеркой нет детей слева, 4 становится единственным левым ребенком.
После этого мы добавляем 2. 2 меньше 8, поэтому идем налево. Так как слева уже есть значение, сравниваем его со вставляемым. 2 меньше 4, а у четверки нет детей слева, поэтому 2 становится левым ребенком 4.
Затем мы добавляем тройку. Она идет левее 8 и 4. Но так как 3 больше, чем 2, она становится правым ребенком 2, согласно третьему правилу.
Последовательное сравнение вставляемого значения с потенциальным родителем продолжается до тех пор, пока не будет найдено место для вставки, и повторяется для каждого вставляемого значения до тех пор, пока не будет построено все дерево целиком.
Класс BinaryTreeNode
Класс BinaryTreeNode представляет один узел двоичного дерева. Он содержит ссылки на левое и правое поддеревья (если поддерева нет, ссылка имеет значение null), данные узла и метод IComparable.CompareTo для сравнения узлов. Он пригодится для определения, в какое поддерево должен идти данный узел. Как видите, класс BinaryTreeNode очень простой:
class BinaryTreeNode : IComparable
where TNode : IComparable
{
public BinaryTreeNode(TNode value)
{
Value = value;
}
public BinaryTreeNode Left { get; set; }
public BinaryTreeNode Right { get; set; }
public TNode Value { get; private set; }
///
/// Сравнивает текущий узел с данным.
///
/// Сравнение производится по полю Value.
/// Метод возвращает 1, если значение текущего узла больше,
/// чем переданного методу, -1, если меньше и 0, если они равны
public int CompareTo(TNode other)
{
return Value.CompareTo(other);
}
}Класс BinaryTree
Класс BinaryTree предоставляет основные методы для манипуляций с данными: вставка элемента (Add), удаление (Remove), метод Contains для проверки, есть ли такое значение в дереве, несколько методов для обхода дерева различными способами, метод Count и Clear.
Кроме того, в классе есть ссылка на корневой узел дерева и поле с общим количеством узлов.
public class BinaryTree : IEnumerable
where T : IComparable
{
private BinaryTreeNode _head;
private int _count;
public void Add(T value)
{
throw new NotImplementedException();
}
public bool Contains(T value)
{
throw new NotImplementedException();
}
public bool Remove(T value)
{
throw new NotImplementedException();
}
public void PreOrderTraversal(Action action)
{
throw new NotImplementedException();
}
public void PostOrderTraversal(Action action)
{
throw new NotImplementedException();
}
public void InOrderTraversal(Action action)
{
throw new NotImplementedException();
}
public IEnumerator GetEnumerator()
{
throw new NotImplementedException();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
throw new NotImplementedException();
}
public void Clear()
{
throw new NotImplementedException();
}
public int Count
{
get;
}
}Метод Add
- Поведение: Добавляет элемент в дерево на корректную позицию.
- Сложность: O(log n) в среднем; O(n) в худшем случае.
Добавление узла не представляет особой сложности. Оно становится еще проще, если решать эту задачу рекурсивно. Есть всего два случая, которые надо учесть:
- Дерево пустое.
- Дерево не пустое.
Если дерево пустое, мы просто создаем новый узел и добавляем его в дерево. Во втором случае мы сравниваем переданное значение со значением в узле, начиная от корня. Если добавляемое значение меньше значения рассматриваемого узла, повторяем ту же процедуру для левого поддерева. В противном случае — для правого.
public void Add(T value)
{
//Случай 1: Если дерево пустое, просто создаем корневой узел.
if (_head == null)
{
_head = new BinaryTreeNode(value);
}
//Случай 2: Дерево не пустое =>
//ищем правильное место для вставки.
else
{
AddTo(_head, value);
}
_count++;
}
//Рекурсивная ставка.
private void AddTo(BinaryTreeNode node, T value)
{
//Случай 1: Вставляемое значение меньше значения узла
if (value.CompareTo(node.Value) < 0)
{
//Если нет левого поддерева, добавляем значение в левого ребенка,
if (node.Left == null)
{
node.Left = new BinaryTreeNode(value);
}
else
{
//в противном случае повторяем для левого поддерева.
AddTo(node.Left, value);
}
}
//Случай 2: Вставляемое значение больше или равно значению узла.
else
{
//Если нет правого поддерева, добавляем значение в правого ребенка,
if (node.Right == null)
{
node.Right = new BinaryTreeNode(value);
}
else
{
//в противном случае повторяем для правого поддерева.
AddTo(node.Right, value);
}
}
}Метод Remove
- Поведение: Удаляет первый узел с заданным значением.
- Сложность: O(log n) в среднем; O(n) в худшем случае.
Удаление узла из дерева — одна из тех операций, которые кажутся простыми, но на самом деле таят в себе немало подводных камней.
В целом, алгоритм удаления элемента выглядит так:
- Найти узел, который надо удалить.
- Удалить его.
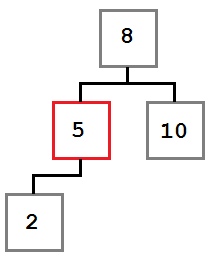
Первый шаг достаточно простой. Мы рассмотрим поиск узла в методе Contains ниже. После того, как мы нашли узел, который необходимо удалить, у нас возможны три случая.
Случай 1: У удаляемого узла нет правого ребенка.
В этом случае мы просто перемещаем левого ребенка (при его наличии) на место удаляемого узла. В результате дерево будет выглядеть так:
Случай 2: У удаляемого узла есть только правый ребенок, у которого, в свою очередь нет левого ребенка.
В этом случае нам надо переместить правого ребенка удаляемого узла (6) на его место. После удаления дерево будет выглядеть так:
Случай 3: У удаляемого узла есть первый ребенок, у которого есть левый ребенок.
В этом случае место удаляемого узла занимает крайний левый ребенок правого ребенка удаляемого узла.
Давайте посмотрим, почему это так. Мы знаем о поддереве, начинающемся с удаляемого узла следующее:
- Все значения справа от него больше или равны значению самого узла.
- Наименьшее значение правого поддерева — крайнее левое.
Мы дожны поместить на место удаляемого узел со значением, меньшим или равным любому узлу справа от него. Для этого нам необходимо найти наименьшее значение в правом поддереве. Поэтому мы берем крайний левый узел правого поддерева.
После удаления узла дерево будет выглядеть так:
Теперь, когда мы знаем, как удалять узлы, посмотрим на код, который реализует этот алгоритм.
Отметим, что метод FindWithParent (см. метод Contains) возвращает найденный узел и его родителя, поскольку мы должны заменить левого или правого ребенка родителя удаляемого узла.
Мы, конечно, можем избежать этого, если будем хранить ссылку на родителя в каждом узле, но это увеличит расход памяти и сложность всех алгоритмов, несмотря на то, что ссылка на родительский узел используется только в одном.
public bool Remove(T value)
{
BinaryTreeNode current, parent;
// Находим удаляемый узел.
current = FindWithParent(value, out parent);
if (current == null)
{
return false;
}
_count--;
//Случай 1: Если нет детей справа,
//левый ребенок встает на место удаляемого.
if (current.Right == null)
{
if (parent == null)
{
_head = current.Left;
}
else
{
int result = parent.CompareTo(current.Value);
if (result > 0)
{
//Если значение родителя больше текущего,
//левый ребенок текущего узла становится левым ребенком родителя.
parent.Left = current.Left;
}
else if (result < 0) {
//Если значение родителя меньше текущего,
// левый ребенок текущего узла становится правым ребенком родителя.
parent.Right = current.Left;
}
}
}
//Случай 2: Если у правого ребенка нет детей слева
//то он занимает место удаляемого узла.
else if (current.Right.Left == null) {
current.Right.Left = current.Left;
if (parent == null) {
_head = current.Right;
} else {
int result = parent.CompareTo(current.Value);
if (result > 0)
{
//Если значение родителя больше текущего,
//правый ребенок текущего узла становится левым ребенком родителя.
parent.Left = current.Right;
}
else if (result < 0) {
//Если значение родителя меньше текущего,
// правый ребенок текущего узла становится правым ребенком родителя.
parent.Right = current.Right;
}
}
}
//Случай 3: Если у правого ребенка есть дети слева,
//крайний левый ребенок
//из правого поддерева заменяет удаляемый узел.
else {
//Найдем крайний левый узел.
BinaryTreeNode leftmost = current.Right.Left;
BinaryTreeNode leftmostParent = current.Right;
while (leftmost.Left != null) {
leftmostParent = leftmost; leftmost = leftmost.Left;
}
//Левое поддерево родителя становится правым поддеревом
//крайнего левого узла.
leftmostParent.Left = leftmost.Right;
//Левый и правый ребенок текущего узла становится левым
//и правым ребенком крайнего левого. leftmost.
Left = current.Left;
leftmost.Right = current.Right;
if (parent == null) {
_head = leftmost;
} else {
int result = parent.CompareTo(current.Value);
if (result > 0)
{
//Если значение родителя больше текущего,
//крайний левый узел становится левым ребенком родителя.
parent.Left = leftmost;
}
else if (result < 0)
{
//Если значение родителя меньше текущего,
//крайний левый узел становится правым ребенком родителя.
parent.Right = leftmost;
}
}
}
return true;
}Метод Contains
- Поведение: Возвращает
trueесли значение содержится в дереве. В противном случает возвращаетfalse. - Сложность: O(log n) в среднем; O(n) в худшем случае.
Метод Contains выполняется с помощью метода FindWithParent, который проходит по дереву, выполняя в каждом узле следующие шаги:
- Если текущий узел
null, вернутьnull. - Если значение текущего узла равно искомому, вернуть текущий узел.
- Если искомое значение меньше значения текущего узла, установить левого ребенка текущим узлом и перейти к шагу 1.
- В противном случае, установить правого ребенка текущим узлом и перейти к шагу 1.
Поскольку Contains возвращает булево значение, оно определяется сравнением результата выполнения FindWithParent с null. Если FindWithParent вернул непустой узел, Contains возвращает true.
Метод FindWithParent также используется в методе Remove.
public bool Contains(T value)
{
//Поиск узла осуществляется другим методом.
BinaryTreeNode parent;
return FindWithParent(value, out parent) != null;
}
//Находит и возвращает первый узел с заданным значением.
//Если значение не найдено, возвращает null.
//Также возвращает родителя найденного узла (или null)
//для использования в методе Remove.
private BinaryTreeNode FindWithParent(T value,
out BinaryTreeNode parent)
{
//Попробуем найти значение в дереве.
BinaryTreeNode current = _head;
parent = null;
//До тех пор, пока не нашли...
while (current != null)
{
int result = current.CompareTo(value);
if (result > 0)
{
//Если искомое значение меньше, идем налево.
parent = current;
current = current.Left;
}
else if (result < 0)
{
//Если искомое значение больше, идем направо.
parent = current;
current = current.Right;
}
else
{
//Если равны, то останавливаемся
break;
}
}
return current;
}Метод Count
- Поведение: Возвращает количество узлов дерева или 0, если дерево пустое.
- Сложность: O(1)
Это поле инкрементируется методом Add и декрементируется методом Remove.
>public int Count
{
get
{
return _count;
}
}Метод Clear
- Поведение: Удаляет все узлы дерева.
- Сложность: O(1)
public void Clear()
{
_head = null;
_count = 0;
}Обход деревьев
Обходы дерева — это семейство алгоритмов, которые позволяют обработать каждый узел в определенном порядке. Для всех алгоритмов обхода ниже в качестве примера будет использоваться следующее дерево:
Пример дерева для обхода
Методы обхода в примерах будут принимать параметр Action<T>, который определяет действие, поизводимое над каждым узлом.
Также, кроме описания поведения и алгоритмической сложности метода будет указываться порядок значений, полученный при обходе.
Метод Preorder (или префиксный обход)
- Поведение: Обходит дерево в префиксном порядке, выполняя указанное действие над каждым узлом.
- Сложность: O(n)
- Порядок обхода: 4, 2, 1, 3, 5, 7, 6, 8
При префиксном обходе алгоритм получает значение текущего узла перед тем, как перейти сначала в левое поддерево, а затем в правое. Начиная от корня, сначала мы получим значение 4. Затем таким же образом обходятся левый ребенок и его дети, затем правый ребенок и все его дети.
Префиксный обход обычно применяется для копирования дерева с сохранением его структуры.
public void PreOrderTraversal(Action action)
{
PreOrderTraversal(action, _head);
}
private void PreOrderTraversal(Action action, BinaryTreeNode node)
{
if (node != null)
{
action(node.Value);
PreOrderTraversal(action, node.Left);
PreOrderTraversal(action, node.Right);
}
}Метод Postorder (или постфиксный обход)
- Поведение: Обходит дерево в постфиксном порядке, выполняя указанное действие над каждым узлом.
- Сложность: O(n)
- Порядок обхода: 1, 3, 2, 6, 8, 7, 5, 4
При постфиксном обходе мы посещаем левое поддерево, правое поддерево, а потом, после обхода всех детей, переходим к самому узлу.
Постфиксный обход часто используется для полного удаления дерева, так как в некоторых языках программирования необходимо убирать из памяти все узлы явно, или для удаления поддерева. Поскольку корень в данном случае обрабатывается последним, мы, таким образом, уменьшаем работу, необходимую для удаления узлов.
public void PostOrderTraversal(Action action)
{
PostOrderTraversal(action, _head);
}
private void PostOrderTraversal(Action action, BinaryTreeNode node)
{
if (node != null)
{
PostOrderTraversal(action, node.Left);
PostOrderTraversal(action, node.Right);
action(node.Value);
}
}Метод Inorder (или инфиксный обход)
- Поведение: Обходит дерево в инфиксном порядке, выполняя указанное действие над каждым узлом.
- Сложность: O(n)
- Порядок обхода: 1, 2, 3, 4, 5, 6, 7, 8
Инфиксный обход используется тогда, когда нам надо обойти дерево в порядке, соответствующем значениям узлов. В примере выше в дереве находятся числовые значения, поэтому мы обходим их от самого маленького до самого большого. То есть от левых поддеревьев к правым через корень.
В примере ниже показаны два способа инфиксного обхода. Первый — рекурсивный. Он выполняет указанное действие с каждым узлом. Второй использует стек и возвращает итератор для непосредственного перебора.
Public void InOrderTraversal(Action action)
{
InOrderTraversal(action, _head);
}
private void InOrderTraversal(Action action, BinaryTreeNode node)
{
if (node != null)
{
InOrderTraversal(action, node.Left);
action(node.Value);
InOrderTraversal(action, node.Right);
}
}
public IEnumerator InOrderTraversal()
{
// Это нерекурсивный алгоритм.
// Он использует стек для того, чтобы избежать рекурсии.
if (_head != null)
{
// Стек для сохранения пропущенных узлов.
Stack stack = new Stack();
BinaryTreeNode current = _head;
// Когда мы избавляемся от рекурсии, нам необходимо
// запоминать, в какую стороны мы должны двигаться.
bool goLeftNext = true;
// Кладем в стек корень.
stack.Push(current);
while (stack.Count > 0)
{
// Если мы идем налево...
if (goLeftNext)
{
// Кладем все, кроме самого левого узла на стек.
// Крайний левый узел мы вернем с помощю yield.
while (current.Left != null)
{
stack.Push(current);
current = current.Left;
}
}
// Префиксный порядок: left->yield->right.
yield return current.Value;
// Если мы можем пойти направо, идем.
if (current.Right != null)
{
current = current.Right;
// После того, как мы пошли направо один раз,
// мы должным снова пойти налево.
goLeftNext = true;
}
else
{
// Если мы не можем пойти направо, мы должны достать родительский узел
// со стека, обработать его и идти в его правого ребенка.
current = stack.Pop();
goLeftNext = false;
}
}
}
}Метод GetEnumerator
- Поведение: Возвращает итератор для обхода дерева инфиксным способом.
- Сложность: Получение итератора — O(1). Обход дерева — O(n).
public IEnumerator GetEnumerator()
{
return InOrderTraversal();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
return GetEnumerator();
}Продолжение следует
На этом мы заканчивает пятую часть руководства по алгоритмам и структурам данных. В следующей статье мы рассмотрим множества (Set).
Перевод статьи «The Binary Search Tree»