Как составить доверительный интервал

Была ли эта статья полезной?

Как написать заключение о доверительном интервале (шаг за шагом)

Доверительный интервал

Доверительный
интервал – это отрезок на оси значений
оцениваемой характеристики случайной
величины (например, математического
ожидания), который с заданной вероятностью
накрывает неизвестное значение
оцениваемой характеристики.

Доверительная
вероятность
– это вероятность того, что неизвестное
значение оцениваемой характеристики
окажется внутри доверительного интервала.

Точки на оси,
ограничивающие доверительный интервал,
называются доверительными
границами.

Чем шире доверительный
интервал, тем больше доверительная
вероятность.

Для того чтобы по
заданной доверительной вероятности
установить границы доверительного
интервала необходимо иметь плотность
распределения или закон распределения
статистики, применяемой для оценивания
неизвестного значения характеристики
случайной величины.

Однако известно,
что при объёме выборки большем 25
распределение любой статистики очень
близко к нормальному распределению.

Границы доверительного
интервала устанавливают так, чтобы в
его пределах оказались значения
оцениваемой характеристики, наиболее
близкие к среднему значению плотности
распределения или закона распределения,
а «хвосты», содержащие достаточно
удалённые и, как правило, маловероятные
значения, оказались вне границ. Причём
суммы вероятностей значений в каждом
из «хвостов» должны быть равными друг
другу.

Если оценка среднего


имеет нормальное или близкое к нормальному
распределение, то границы доверительного
интервала могут быть определены прямо
через величину среднеквадратической
ошибки оценки
,
на основании свойств нормального
распределения. Делается это следующим
образом.

Пусть вычислены
оценка среднего

и её среднеквадратическая ошибка
.
Истинное неизвестное математическое
ожидание случайной величины будет
находиться в доверительном интервале
от
–до
+с доверительной вероятностью 0,682 .

Если выбрать
доверительный интервал вдвое шире, т.е.
по двукратной
ошибке,
его границами будут значения от
–2до
+2.
Доверительная вероятность при таком
интервале составляет 0,955, т.е. больше,
чем при предыдущем интервале, определённом
пооднократной
ошибке.

Доверительная
вероятность в пределах трёхкратной
ошибки,
т.е. от
–3до
+3,
будет 0,997 , а значит, практически все
выборочные данные, 99,7 %, попадут в
этот интервал. Это свойство нормального
распределения носит название «правило
трёх сигм».

Чем больше
доверительная вероятность, тем выше
надёжность результата. Однако при этом
увеличивается и доверительный интервал,
который желательно иметь как можно уже.

Помимо
задания доверительного интервала по
одно-, двух- и трёхкратной ошибке
существует ещё один способ задания: по
доверительной вероятности. Обычно
используются следующие значения
доверительной вероятности: 0,90 ,
0,95 и 0,99. Ширины доверительного
интервала в этом случае составляют
соответственно  1,65, 1,96и 2,58от выборочного среднего
.
А вероятности ошибки: 0,10 , 0,05 и 0,01 (10 %,
5 % и 1 %).

Результатом
оценивания является:

1. либо значение
   оценки неизвестной характеристики
   случайной величины (например, её
   математического ожидания) и
   среднеквадратическая ошибка оценки
   ;

2. либо две границы
   доверительного интервала, накрывающего
   неизвестное значение интересующей
   характеристики случайной величины с
   заданной (указываемой) доверительной
   вероятностью.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.

Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.

Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.

Определение доверительного интервала.

Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 — alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.

Этот интервал часто упоминается как (100 (1 — alpha)% ) доверительный интервал для параметра.

Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).

В этом чтении, мы имеем дело только с двусторонними доверительными интервалами — доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.

Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.

При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.

При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.

Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.

Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.

На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.

Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.

Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.

Построение доверительных интервалов.

Доверительный интервал (100 (1 — alpha)% ) для параметра имеет следующую структуру.

Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.

Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.

Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.

Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).

Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).

Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.

Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.

В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.

---

Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 — alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.

Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:

( sigma_{overline X} = 20 Big / sqrt{100} = 2 )

Доверительный интервал, таким образом, имеет нижний предел:

( overline X — 1.96 sigma_{overline X} ) = 25 — 1.96(2) = 25 — 3.92 = 21.08.

Верхний предел доверительного интервала равен:

( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92

95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.

Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).

Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:

( Large dst overline X pm z_{alpha /2}{sigma over sqrt n}  ) (Формула 4)

Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.

Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.

Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:

Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.

«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»

см. Freund и Williams (1977), стр. 266.

На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.

Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.

---

Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).

Распределение статистики (t) называется t-распределением Стьюдента (англ. «Student’s t-distribution») из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.

В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.

Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, — это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).

В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).

Доверительные интервалы для среднего по совокупности — z-альтернатива (большая выборка, дисперсия совокупности неизвестна).

Доверительный интервал (100 (1 — alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:

( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)

Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.

Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.

Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.

[см. также: CFA — Коэффициент Шарпа]

Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.

Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.

---

Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).

Доверительный интервал будет равен:

( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495   end{aligned} )

Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.

В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.

Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.

Концепция степеней свободы.

Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.

Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.

Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.

t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.

Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.

Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n — 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.

Мы также используем ( n — 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.

---

Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?

При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.

Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n — 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.

Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.

t-распределение Стьюдента.

Предположим, что мы делаем выборку из нормального распределения.

Коэффициент (z = (overline X — mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X — mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n — 1) степеней свободы.

Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.

Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.

На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.

Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.

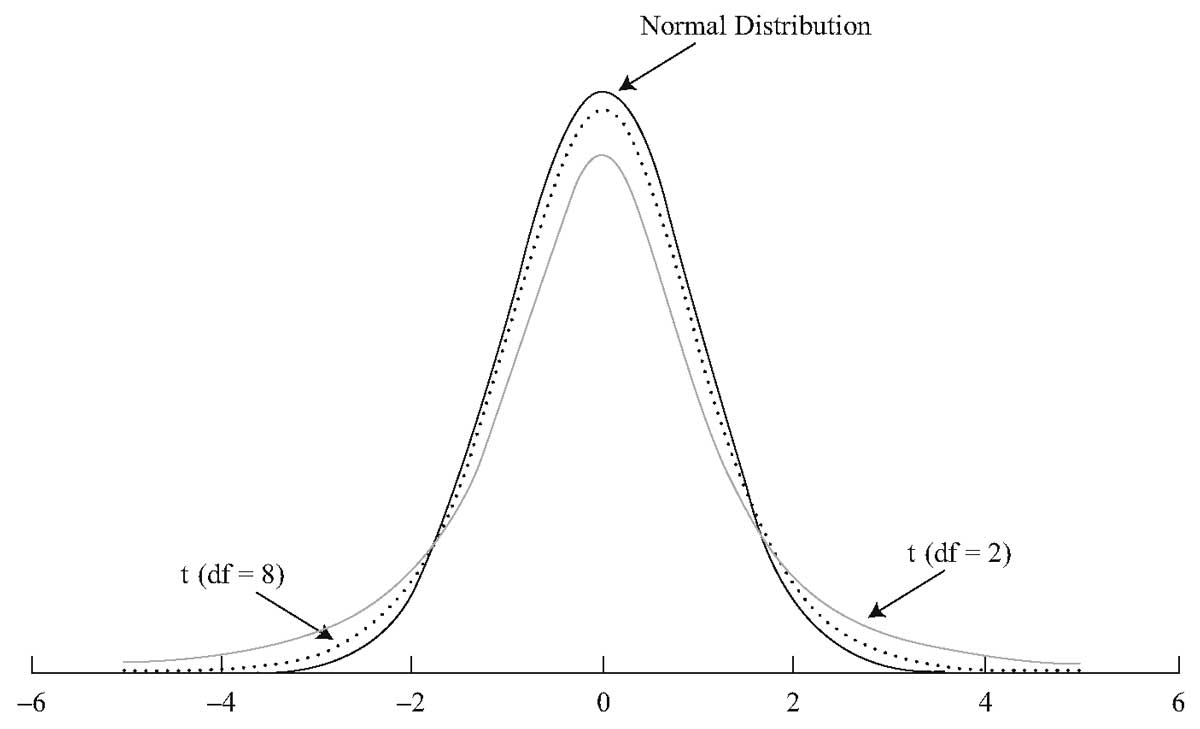
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.

По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.

Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.

t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.

Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.

Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.

Например,

Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.

Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) — t-распределение.

Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:

• выборка является большой, или
• выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,

то доверительный интервал (100 (1 — alpha)% ) для среднего совокупности ( mu ) задается формулой:

Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.

Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.

Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.

Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение — 0.30.

Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.

Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.

Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.

Доверительный интервал будет:

( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \  &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498   end{aligned} )

Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.

В Таблице 3 приведены различные факторы надежности, которые мы использовали.

Таблица 3. Основы для расчета факторов надежности.

Выборка из:	Статистика для выборки малого размера	Статистика для выборки большого размера
Нормальное распределение с известной дисперсией	(z)	(z)
Нормальное распределение с неизвестной дисперсией	(t)	(t)*
Ненормальное распределение с известной дисперсией	недоступно	(z)
Ненормальное распределение с неизвестной дисперсией	недоступно	(t)*

* Использование (z) также приемлемо.