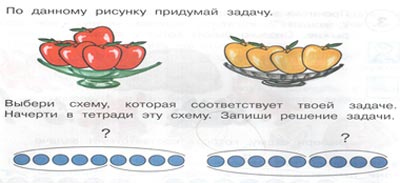
Найди верный ответ на вопрос ✅ «Как составить дуговую схему к уравнению х-591=254 …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по математике
1.Создание
психологического комфорта
Просыпаемся
с утра — нам считать уже пора.
Открываем мы тетрадь —
снова хочется считать.
1, 2, 3, 4, 5 — я иду
тебя искать!
Математика, приди и всему
нас научи!
2. Создание ситуации
успеха
Повторение
сторон:
Положьте 4 палочки
справа и 3 палочки слева.
Над 4 палочками
положьте палочек меньше
Под 3 палочками
положите больше палочек
Из палочек постройте
замкнутую линию, у которой будет столько вершин. (показываю цифру 4)
Постройте незамкнутую
линию, у которой будет столько звеньев (5)
3. Физминутка
Хомка
4. Постановка учебной
цели
Сегодня у нас очень
важная тема – она пригодится вам решать задачи в будущем.
5. Решение учебной
задачи
посмотрите, прочтите
и скажите сколько будет? 3+2
Откуда вы узнали?
Что означает число 3?
Не заметил ли ты на
рисунке другой знак, обозначающий это же число зайчат?
Что обозначает знак 2?
Не заметил ли ты на
рисунке другой знак, обозначающий это же число?
Кто объяснит смысл
знака +?
Не заметил ли ты
другой знак, обозначающий общее число?
Давайте обозначим
рисунок кружочками.
Сколько кружочков мы
нарисуем сначала вместо зайчат?
Сколько кружочков мы
нарисуем вместо котят?
Сколько всего животных?
А мы видим сколько
было зайчат и сколько было котят?
Что нужно сделать?
Кто это сделает?
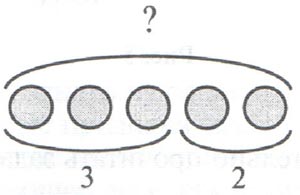
Это называется дуговая
схема .
6. Этап первичного
закрепления. Работа по учебнику с.59.
-№ 3
-№7
7. Работа в тетрадях.
-№6 стр.60
-№7 стр. 60
7 Рефлексия
Что нового узнали
на уроке?
Понравилась ли тебе
твоя работа на уроке?
Что тебе понравилось
и не понравилось?
Чья работа тебе
понравилась?
Урок окончен, спасибо
за урок!
Выполняют на партах
Хомка, хомка, хомячок,
полосатенький бочок.
Хомка раненько встаёт,
щёчки моет, шейку трёт,
Подметает хомка хатку
и выходит на зарядку.
Раз, два ,три, четыре,
пять-хомка хочет сильным встать!
Это число зайчат
Это же число зайчат
обозначено дугой.
Цифра 2 обозначает
число котят.
На рисунке обозначено
это же число маленькой дугой.
Н ахождение
общего числа животных
На рисунке общее число
обозначено большой дугой
3
2
5
Нет
Начертить дуги
(О о о) ( о о)
Составление рассказа
по картине, по данной математической записи
1+2
Работа парами.
Выполнение сложения с
помощью схем
К записи 3+1 построить
дуговую схему
К рассказу о лягушках
построить дуговую схему
В соответствии с Концепцией развития математического образования одним из основных направлений её реализации в начальном общем образовании является: обеспечение широкого спектра математической активности (занятий) обучающихся как на уроках, так и во внеурочной деятельности, которое реализуется, в том числе, и через решение арифметических задач.
Вопросы решения текстовых арифметических задач в курсе математики всегда занимали центральное место. Это особое положение определяется тем, что эта линия математики имеет прикладную направленность, которая выражается в умении применять полученные знания на практике.
В процессе решения арифметических тестовых задач широко применяется метод графического моделирования, суть которого состоит в упрощении сюжета решаемой задачи.
Для успешного использования метода моделирования у учащихся должны быть сформированы знаково-символические универсальные учебные действия:
- кодирование/замещение (использование знаков и символов как условных заместителей реальных объектов и предметов);
- декодирование/считывание информации;
- умение использовать наглядные модели (схемы, чертежи, таблицы), отражающие отношения между предметами или их частями для решения задач;
- умение строить схемы, модели и т.п.
При решении задач используются различные способы построения моделей. На начальном этапе обучения (при решении задач) учащиеся опираются на иллюстрированное моделирование, а потом, усложняя, переходят к графическому или схематическому.
При работе с моделями важно соблюдать алгоритм действия:
- построение модели
- исследование модели
- выбор пути решения
- перевод результата решения в исходный
В программе по математике УМК «ПНШ» (автор Александр Леонидович Чекин) систематическая работа по обучению решению текстовых задач начинается со второго полугодия первого класса и осуществляется в следующей последовательности:
1-й класс — Иллюстрация, простейшая графическая схема.
2-й класс — Краткая запись, схема (круговая, дуговая)
3 класс — Числовая диаграмма, таблица.
4 класс — Графическая схема, построенная на основе отрезка.
На первом уроке знакомства с задачей и её основными элементами используются иллюстрации. (условие и требование). А уже на 2 уроке уч-ся учатся сопоставлять формулировку задачи ( условие и требование) с данной к ней схемой, при этом рассматривается смысловая нагрузка каждого элемента схемы и устанавливается взаимосвязь.
При выполнении этого задания смысл каждого элемента схемы-модели определяется в условиях парной работы самостоятельно с последующей демонстрацией на классной доске.
Учебник предлагает: Расскажи условие и покажи на схеме дуги, которые его обозначают. Твой сосед по парте пусть расскажет требование задачи и покажет на схеме соответствующую дугу. Какой знак на схеме стоит рядом с дугой, обозначающей требование задачи? (показывают дуги и дополняют)
Затем при решении задач используются различные задания со схемами-моделями:
- дополнение схем данными и искомыми,
- составление задач по рисунку и заданной схеме,
- выбор нужной схемы из нескольких данных,
- самостоятельное построение схем к задачам,чтение схем.
- решение задач с использованием готовой схемы.
Данные виды деятельности при работе с задачами выполняются в течение всего 2 полугодия. Это приводит к тому, что учащиеся начинают легко справляться при помощи моделей-схем с выбором действия при решении простых задач.
При работе со схемами большей самостоятельностью отличается построение модели самими учащимися.
Во 2-м классе учащиеся начинают работать с большими числами, использовать круги становится неудобным и не всегда возможным, вследствие этого вводятся дуговые схемы. Сначала схемы даются готовыми (полностью соответствуют тексту задачи). Они имеются только в рабочих тетрадях.
Затем при решении задач выполняются различные задания на
а) дополнение схем ( частичное и полное);
б) составление краткой записи к задаче, формулировка задачи по краткой записи текста;
в) построение схем к задачам.
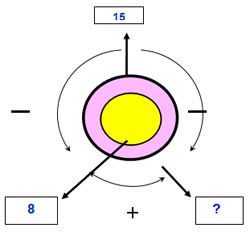
Следующий шаг (новое для второклассников) – введение круговых схем, для решения текстовых задач.
В этих схемах для анализа и поиска решения задач данные обозначаются в виде геометрических фигур: объекты — квадраты; отношения между состояниями объектов — линии, стрелки на которых указывают направленность отношений; отношения между величинами состояния объекта — круги. Заданные числовые значения величин объекта и отношений между величинами указываются соответствующими числами, знак при которых фиксирует характер отношения величин.
Знакомству с круговой схемой посвящен отдельный урок, на котором рассматриваются все элементы данной схемы: объекты, отношения между величинами объектов, характер отношений, как они фиксируются, знакомство осуществляется при решении простой задачи через систему вопросов.
На следующем этапе работы с круговыми схемами сопоставляются дуговая и круговая схемы, что помогает быстрее понять и легче освоить круговую схему.
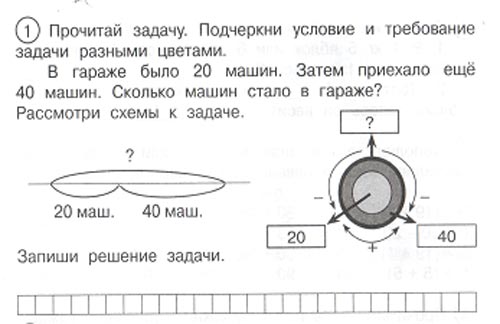
Рассмотрите дуговую схему, расскажите, что означают на ней верхняя и нижние дуги? (две нижние дуги – сколько было машин и сколько приехало, верхняя дуга – сколько стало машин.)
Рассматриваем круговую схему и предлагаем рассказать, что означают числа в квадратиках. Какой знак стоит около стрелки, соединяющей квадраты с данными из условия задачи числами? (знак +)
Какое действие надо выполнить, чтобы удовлетворить требование задачи (действие сложения) Тетрадь с.12 №1.
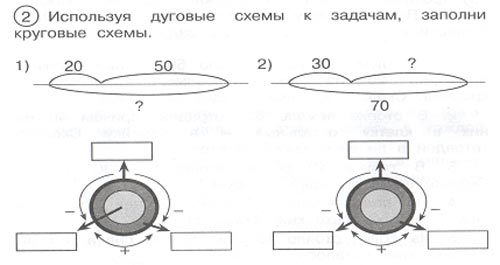
Далее, используя дуговые схемы к задачам, учим заполнять круговые схемы. №1 Разбираем зависимость, существующую между обозначениями одной схемы и другой: 2 верхние дуги и 2 нижних квадрата — сколько было (машин) и сколько приехало; нижняя дуга и верхний квадрат – сколько стало (машин).
№2 Разбираем зависимость, существующую между обозначениями одной схемы и другой: левая верхняя дуга и левый нижний квадрат — сколько было (машин); правая верхняя дуга и правый нижний квадрат — сколько приехало; нижняя дуга и верхний квадрат – сколько всего (машин). Затем уч-ся заполняют нижнюю схему.
Последовательность работы с круговыми схемами та же.
Сначала работают с готовыми схемами:
а) составление задач по готовой схеме;
б) нахождение значений выражений по готовой схеме;
в) решение задач по готовой схеме;
г) соотнесение схем и условий задач;
г) выбор нужной схемы из ряда других схем, соответствующих содержанию задачи.
В рабочих тетрадях также предлагаются задания, которые помогают найти решение:
а) дополнение схем;
б) заполнение круговых схем к задаче;
в) построение круговых схем.
Т.о. выбор действия при решении задачи осуществляется через анализ данных с помощью графической схемы. При этом формируем умение чертить и читать готовые схемы, составленные на основе диаграмм Эйлера-Венна.
Опыт показывает, что схемы (и дуговые, и круговые ) незаменимы при усвоении конкретного смысла умножения, при работе с задачами в косвенной форме и обратными задачами (когда нужно выполнить проверку решения задачи).
Во 2 полугодии второклассники знакомятся с задачами, которые имеют одно условие и несколько требований. С такими задачами авторы учебника предлагают работать во 2 классе только с использованием дуговых схем.
Виды заданий и последовательность работы со схемами при наличии дополнительных требований:
- объяснение готовых схем (коллективно);
- дополнение частично заполненных схем (коллективно);
- соотнесение готовой схемы и готового решения задачи;
- самостоятельное составление схемы (в групповой работе) и формулирование дополнительного требования;
- самостоятельное построение схемы (индивидуально);
- решение задачи с помощью готовой схемы.
В заключение нужно отметить, очень важно, чтобы предметное и графическое моделирование математической ситуации в процессе решения текстовых задач применялось в школьной практике системно и последовательно.
Список литературы
1. Давыдов В.В. Психическое развитие в младшем школьном возрасте // Возрастная и педагогическая психология. – М., 1973.
2. Далингер В.А. Методика реализации внутри предметных связей при обучении математике. – М.: «Просвещение», 1991.
3. Истомина Н.Б. Методика обучения математике в начальных классах. Уч.пособие. – М.: «ACADEMA».
4. Концепция математического образования в Российской федерации (утверждена распоряжением Правительства РФ от 24 декабря 2013 года № 2506).
5. Чекин А.Л. Математика: Методическое пособие для учителя. В 2-х ч. – М.: Академкнига/Учебник.
6. Хеннер Е.К., Шестаков А.П. Математическое моделирование. Пособие для учителя. – Пермь, 1995. – 158 с.
Как составить дуговую схему к уравнению х — 591 = 254.
Вы перешли к вопросу Как составить дуговую схему к уравнению х — 591 = 254?. Он относится к категории Математика,
для 1 — 4 классов. Здесь размещен ответ по заданным параметрам. Если этот
вариант ответа не полностью вас удовлетворяет, то с помощью автоматического
умного поиска можно найти другие вопросы по этой же теме, в категории
Математика. В случае если ответы на похожие вопросы не раскрывают в полном
объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части
сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете
ознакомиться с вариантами ответов пользователей.
minesedlsedi998
Вопрос по математике:
Как выполнить дуговую схему уровнения
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
hangainlori776
Каждая часть уравнения обозначается отрезком. По рисунку видно, что является целым, а что частью.
(подробнее смотри на рисунке)
А потом выводятся два основных правила:
-чтобы найти целое, надо известные части сложить;
-чтобы найти неизвестную часть, надо из целого вычесть известную часть.

Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.