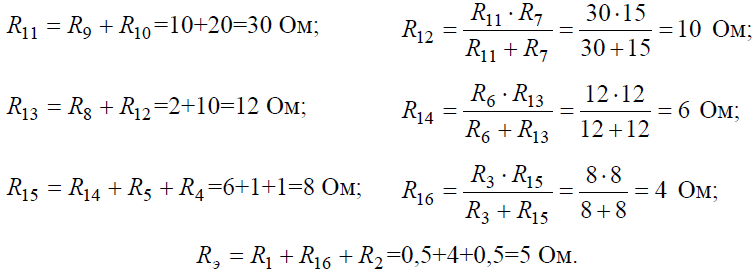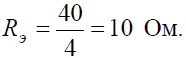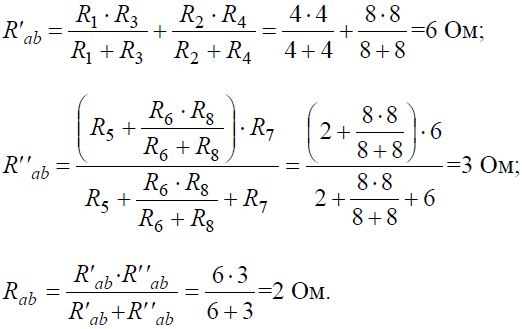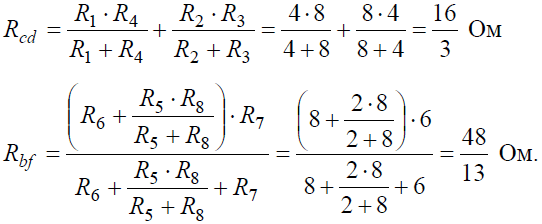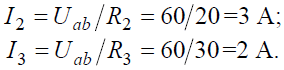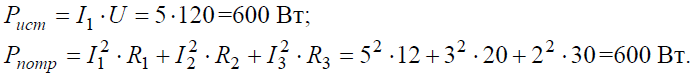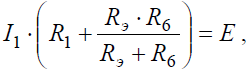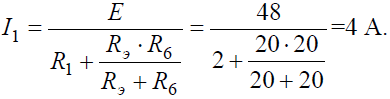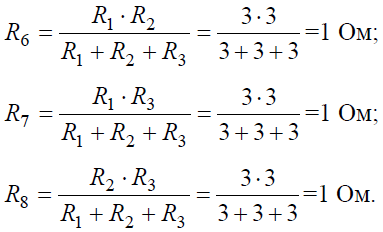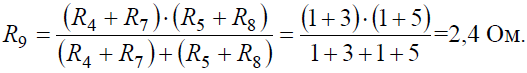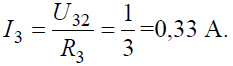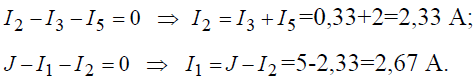Введение
Решение задач — неотъемлемая часть обучения
физике, поскольку в процессе решения задач
происходит формирование и обогащение физических
понятий, развивается физическое мышление
учащихся и совершенствуется их навыки
применения знаний на практике.
В ходе решения задач могут быть поставлены и
успешно реализованы следующие дидактические
цели:
- Выдвижение проблемы и создание проблемной
ситуации; - Обобщение новых сведений;
- Формирование практических умений и навыков;
- Проверка глубины и прочности знаний;
- Закрепление, обобщение и повторение материала;
- Реализация принципа политехнизма;
- Развитие творческих способностей учащихся.
Наряду с этим при решении задач у школьников
воспитываются трудолюбие, пытливость ума,
смекалка, самостоятельность в суждениях, интерес
к учению, воля и характер, упорство в достижении
поставленной цели. Для реализации перечисленных
целей особенно удобно использовать
нетрадиционные задачи.
§1. Задачи по расчету электрических
цепей постоянного тока
По школьной программе на рассмотрение данной
темы очень мало отводится времени, поэтому
учащиеся более или менее успешно овладевают
методами решения задач данного типа. Но часто
такие типы задач встречаются олимпиадных
заданиях, но базируются они на школьном курсе.
К таким, нестандартным задачам по расчету
электрических цепей постоянного тока можно
отнести задачи, схемы которых:
1) содержат большое число элементов –
резисторов или конденсаторов;
2) симметричны;
3) состоят из сложных смешанных соединений
элементов.
В общем случае всякую цепь можно рассчитать,
используя законы Кирхгофа. Однако эти законы не
входят в школьную программу. К тому же, правильно
решить систему из большого числа уравнений со
многими неизвестными под силу не многим учащимся
и этот путь не является лучшим способом тратить
время. Поэтому нужно уметь пользоваться
методами, позволяющими быстро найти
сопротивления и емкости контуров.
§2. Метод эквивалентных схем
Метод эквивалентных схем заключается в том, что
исходную схему надо представить в виде
последовательных участков, на каждом из которых
соединение элементов схемы либо
последовательно, либо параллельно. Для такого
представления схему необходимо упростить. Под
упрощением схемы будем понимать соединение или
разъединение каких-либо узлов схемы, удаление
или добавление резисторов, конденсаторов,
добиваясь того, чтобы новая схема из
последовательно и параллельно соединенных
элементов была эквивалентна исходной.
Эквивалентная схема – это такая схема, что при
подаче одинаковых напряжений на исходную и
преобразованную схемы, ток в обеих цепях будет
одинаков на соответствующих участках. В этом
случае все расчеты производятся с
преобразованной схемой.
Чтобы начертить эквивалентную схему для цепи
со сложным смешанным соединением резисторов
можно воспользоваться несколькими приемами. Мы
ограничимся рассмотрением в подробностях лишь
одного из них – способа эквипотенциальных узлов.
Этот способ заключается в том, что в
симметричных схемах отыскиваются точки с
равными потенциалами. Эти узлы соединяются между
собой, причем, если между этими точками был
включен какой-то участок схемы, то его
отбрасывают, так как из-за равенства потенциалов
на концах ток по нему не течет и этот участок
никак не влияет на общее сопротивление схемы.
Таким образом, замена нескольких узлов равных
потенциалов приводит к более простой
эквивалентной схеме. Но иногда бывает
целесообразнее обратная замена одного узла
несколькими узлами с равными потенциалами, что
не нарушает электрических условий в остальной
части.
Рассмотрим примеры решения задач эти методом.
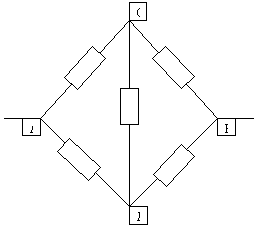
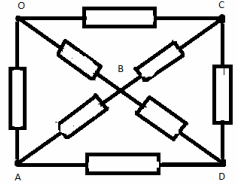
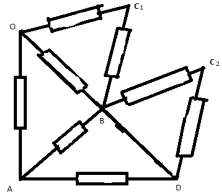
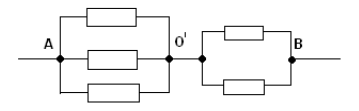
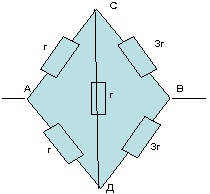
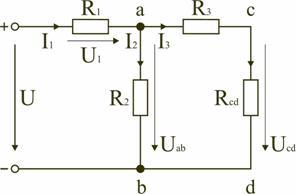
З а д а ч а №1
Рассчитать сопротивление между точками А и В
данного участка цепи. Все резисторы одинаковы и
их сопротивления равны r.
Решение:
В силу симметричности ветвей цепи точки С И Д
являются эквипотенциальными. Поэтому резистор
между ними мы можем исключить. Эквипотенциальные
точки С и Д соединяем в один узел. Получаем очень
простую эквивалентную схему:
Сопротивление которой равно:
RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.
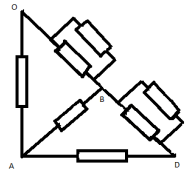
З а д а ч а № 2
Решение:
В точках F и F` потенциалы равны, значит
сопротивление между ними можно отбросить.
Эквивалентная схема выглядит так:
Сопротивления участков DNB;F`C`D`; D`, N`, B`; FCD равны
между собой и равны R1:
1/R1=1/2r+1/r=3/2r
R1=2/3*r
С учетом этого получается новая эквивалентная
схема:
Ее сопротивление и сопротивление исходной цепи
RАВ равно:
1/RАВ=1/r+R1+R1+1/r+R1+R1=6/7r
RАВ=(7/6)*r.
З а д а ч а № 3.
Решение:
Точки С и Д имеют равные потенциалы.
Исключением сопротивление между ними. Получаем
эквивалентную схему:
Искомое сопротивление RАВ равно:
1/RАВ=1/2r+1/2r+1/r=2/r
RАВ=r/2.
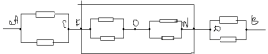
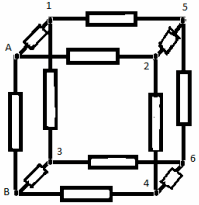
З а д а ч а № 4.
Решение:
Как видно из схемы узлы 1,2,3 имеют равные
потенциалы. Соединим их в узел 1. Узлы 4,5,6 имеют
тоже равные потенциалы- соединим их в узел 2.
Получим такую эквивалентную схему:
Сопротивление на участке А-1, R 1-равно
сопротивлению на участке 2-В,R3 и равно:
R1=R3=r/3
Сопротивление на участке 1-2 равно: R2=r/6.
Теперь получается эквивалентная схема:
Общее сопротивление RАВ равно:
RАВ= R1+ R2+ R3=(5/6)*r.
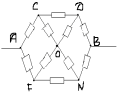
З а д а ч а № 5.
Решение:
Точки C и F-эквивалентные. Соединим их в один
узел. Тогда эквивалентная схема будет иметь
следующий вид:
Сопротивление на участке АС:
Rас=r/2
Сопротивление на участке FN:
RFN =
Сопротивление на участке DB:
RDB =r/2
Получается эквивалентная схема:
Искомое общее сопротивление равно:
RAB= r.
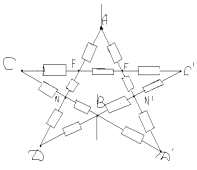
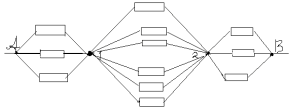
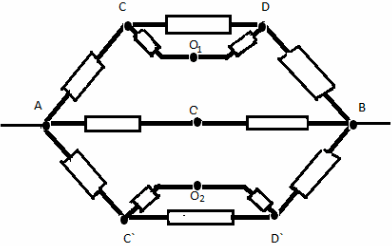
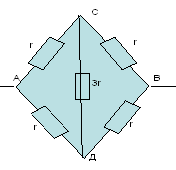
Задача №6
Решение:
Заменим общий узел О тремя узлами с равными
потенциалами О, О1 , О2. Получим
эквивалентную систему:
Сопротивление на участке ABCD:
R1=(3/2)*r
Сопротивление на участке A`B`C`D`:
R2= (8/3)*r
Сопротивление на участке ACВ
R3 = 2r.
Получаем эквивалентную схему:
Искомое общее сопротивление цепи RAB
равно:
RAB= (8/10)*r.
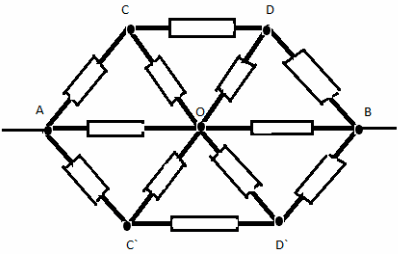
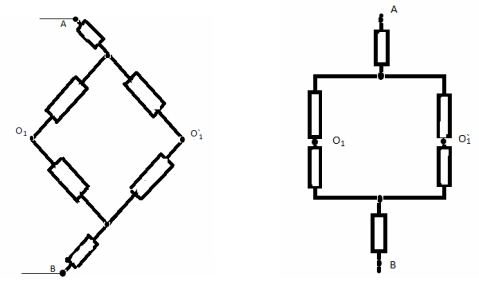
Задача №7.
Решение:
“Разделим” узел О на два эквипотенциальных
угла О1 и О2. Теперь схему можно
представить, как параллельные соединение двух
одинаковых цепей. Поэтому достаточно подробно
рассмотреть одну из них:
Сопротивление этой схемы R1 равно:
R1 = 3r
Тогда сопротивление всей цепи будет равно:
RAB = (3/2)*r
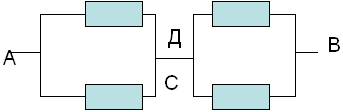
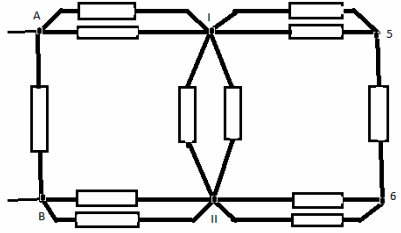
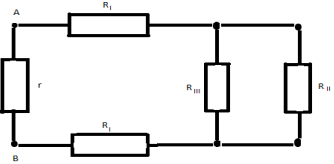
З а д а ч а №8
Решение:
Узлы 1 и 2 – эквипотенциальные, поэтому соединим
их в один узел I. Узлы 3 и 4 также эквипотенциальные
– соединимих в другой узел II. Эквивалентная
схема имеет вид:
Сопротивление на участке A- I равно
сопротивлению на участке B- II и равно:
RI =
Сопротивление участка I-5-6- II равно:
RII = 2r
Cопротивление участка I- II равно:
RIII =
Получаем окончательную эквивалентную схему:
Искомое общее сопротивление цепи RAB=(7/12)*r.
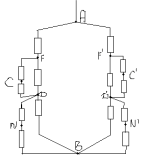
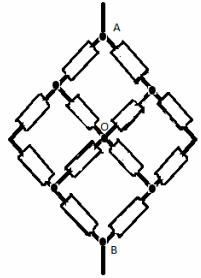
З а д а ч а №9
В ветви ОС заменим сопротивление на два
параллельно соединенных сопротивления по 2r.
Теперь узел С можно разделить на 2
эквипотенциальных узла С1 и С2.
Эквивалентная схема в этом случае выглядит так:
Сопротивление на участках ОСIB и DCIIB
одинаковы и равны, как легко подсчитать 2r. Опять
чертим соответствующую эквивалентную схему:
Сопротивление на участке AOB равно
сопротивлению на участке ADB и равно (7/4)*r. Таким
образом получаем окончательную эквивалентную
схему из трех параллельно соединенных
сопротивлений:
Ее общее сопротивление равно RAB= (7/15)*r
З а д а ч а № 10
Точки СОD имеют равные потенциалы – соединим их
в один узел ОI .Эквивалентная схема
изображена на рисунке :
Сопротивление на участке А ОI равно . На участке
ОIВ сопротивление равно .Получаем совсем
простую эквивалентную схему:
ЕЕ сопротивление равно искомому общему
сопротивлению
RAB=(5/6)*r
Задачи № 11 и № 12 решаются несколько иным
способом, чем предыдущие. В задаче №11 для ее
решения используется особое свойство
бесконечных цепей, а в задаче № 12 применяется
способ упрощения цепи.
Задача № 11
Решение
Выделим в этой цепи бесконечно повторяющееся
звено, оно состоит в данном случае из трех первых
сопротивлений. Если мы отбросим это звено, то
полное сопротивление бесконечной цепи R не
измениться от этого , так как получится точно
такая же бесконечная цепь. Так же ничего не
измениться, если мы выделенное звено подключим
обратно к бесконечному сопротивлению R, но при
этом следует обратить внимание , что часть звена
и бесконечная цепь сопротивлением R соединены
параллельно. Таким образом получаем
эквивалентную схему :
Получается уравнения
RAB=2ч +
RAB = R
Решая систему этих уравнений, получаем:
R=ч (1+ ).
§3. Обучение решению задач по расчету
электрических цепей способом эквипотенциальных
узлов
Задача – это проблема, для разрешения которой
ученику потребуются логические рассуждения и
выводы. Строящиеся на основе законов и методов
физики. Таким образом, с помощью задач происходит
активизация целенаправленного мышления
учащихся.
В то же время. Теоретические знания можно
считать усвоенными только тогда, когда они
удачно применяются на практике. Задачи по физике
описывают часто встречающиеся в жизни и на
производстве проблемы, которые могут быть решены
с помощью законов физики и, если ученик успешно
решает задачи, то можно сказать, что он хорошо
знает физику.
Для того, чтобы ученики успешно решали задачи,
недостаточно иметь набор методов и способов
решения задач, необходимо еще специально учить
школьников применению этих способов.
Рассмотрим план решения задач по расчету
электрических цепей постоянного тока методом
эквипотенциальных узлов.
- Чтение условия.
- Краткая запись условия.
- Перевод в единицы СИ.
- Анализ схемы:
- установить, является ли схема симметричной;
- установить точки равного потенциала;
- выбрать, что целесообразнее сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов; - начертить эквивалентную схему;
- найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом участке по законам
последовательного и параллельного соединения; - начертить эквивалентную схему, заменяя участки
соответствующими им расчетными сопротивлениями; - пункты 5 и 6 повторять до тех пор, пока не
останется одно сопротивление, величина которого
и будет решением задачи. - Анализ реальности ответа.
Подробнее об анализе схемы
а) установить, является ли схема симметричной.
Определение. Схема симметрична, если одна ее
половина является зеркальным отражением другой.
Причем симметрия должна быть не только
геометрической, но должны быть симметричны и
численные значения сопротивлений или
конденсаторов.
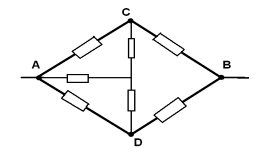
Примеры:
1)
Схема симметричная, так как ветви АСВ и АДВ
симметричны геометрически и отношение
сопротивления на одном участке АС:АД=1:1 такое же,
как и на другом участке СД:ДВ=1:1.
2)
Схема симметричная, так как отношение
сопротивлений на участке АС:АД=1:1 такое же, как и
на другом участке СВ:ДВ=3:3=1:1
3)
Схема не симметрична, так как отношения
сопротивлений численно
не симметричны -1:2 и 1:1.
б) установить точки равных потенциалов.
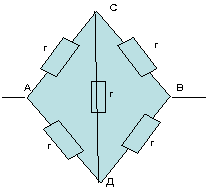
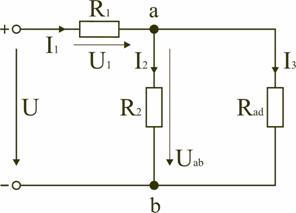
Пример:
Из соображений симметрии делаем вывод, что в
симметричных точках потенциалы равны. В данном
случае симметричными точками являются точки С и
Д. Таким образом, точки С и Д – эквипотенциальные
точки.
в) выбрать, что целесообразно сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов.
Мы видим в этом примере, что между точками
равных потенциалов С и Д включено сопротивление,
по которому ток не будет течь. Следовательно, мы
можем отбросить это сопротивление, а точки С и Д
соединить в один узел.
г) начертить эквивалентную схему.
Чертим эквивалентную схему. При этом получаем
схему с соединенными в одну точку точками С и Д.
д) найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом таком участке по
законам последовательного и параллельного
соединения.
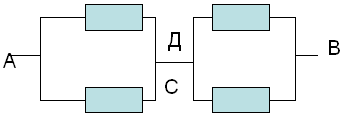
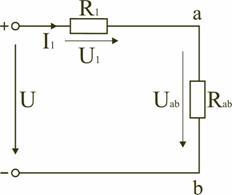
Из полученной эквивалентной схемы видно, что на
участке АС мы имеем два параллельно соединенных
резистора. Их общее сопротивление находится по
закону параллельного соединения:
1/ Rобщ=1/R1+1/R2+1/R3+…
Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.
На участке СВ картина аналогичная:
1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.
е)начертить эквивалентную схему, заменяя
участки соответствующими им расчетными
сопротивлениями.
Чертим эквивалентную схему подставляя в нее
рассчитанные сопротивления участков RAC и RCB:
ж)пункты д) и е) повторять до тех пор, пока
останется одно сопротивление, величина которого
и будет решением задачи.
Повторяем пункт д): на участке АВ имеем два
последовательно соединенных сопротивления. Их
общее сопротивление находим по закону
последовательного соединения:
Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.
Повторяем пункт е): чертим эквивалентную
схему:
Мы получили схему с одним сопротивлением,
величина которого равна сопротивлению исходной
схемы. Таким образом, мы получили ответ RAB = r.
Далее, для проверки усвоения данного материала
можно учащимся предложить задания для
самостоятельной работы, взятые из
дидактического материала. (см. приложение)
Литература
- Балаш. В.А. задачи по физике и методы их решения. —
М: Просвещение,1983. - Лукашик В.И. Физическая олимпиада.- М:
Просвещение, 2007 - Усова А.В., Бобров А.А. Формирование учебных
умений и навыков учащихся на уроках физики.- М:
Просвещение,1988 - Хацет А. Методы расчета эквивалентных схем
//Квант. - Чертов А. Г. Задачник по физике. – М.: Высшая
школа,1983 - Зиятдинов Ш.Г., Соловьянюк С.Г. (методические
рекомендации) г. Бирск,1994г - Марон А.Е., Марон Е.А. Физика. Дидактические
материалы. Москва, “Дрофа”, 2004г
Сопротивления
в электрических цепях могут быть
соединены последовательно, параллельно,
по смешанной схеме и по схемам «звезда»,
«треугольник». Расчет сложной схемы
упрощается, если сопротивления в этой
схеме заменяются одним эквивалентным
сопротивлением Rэкв,
и вся схема представляется в виде схемы
на рис. 1.3, где R=Rэкв,
а расчет токов и напряжений производится
с помощью законов Ома и Кирхгофа.
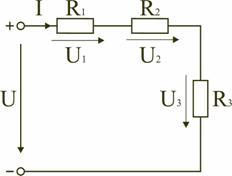
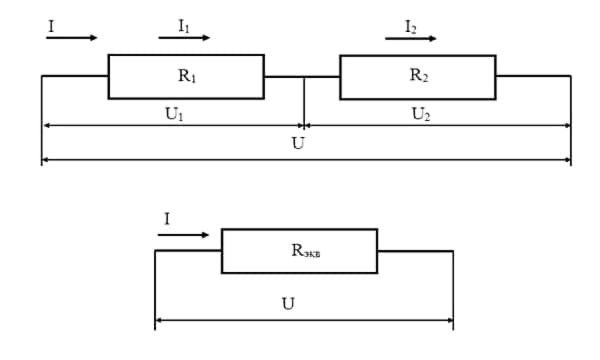
Электрическая
цепь с последовательным соединением
элементов
|
|
|
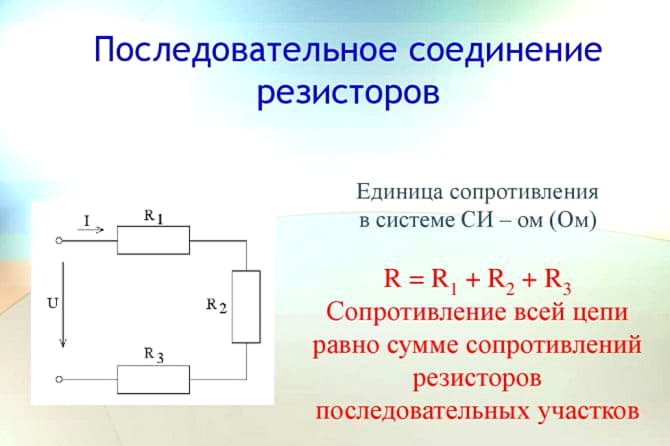
Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).
На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:
U
= U1
+ U2
+ U3 или
IRэкв
= IR1
+ IR2
+ IR3,
откуда
следует
(1.5)
Rэкв
= R1
+ R2
+ R3.
Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
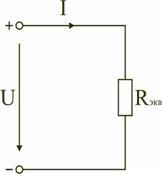
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением Rэкв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома
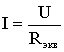
и
по вышеприведенным формулам рассчитывают
падение напряжений U1,
U2,
U3
на соответствующих участках электрической
цепи (рис. 1.4).
Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.
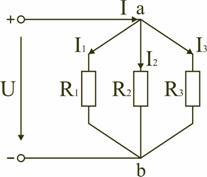
Электрическая
цепь с параллельным соединением элементов
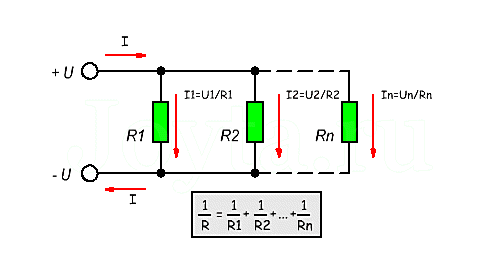
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).
Рис.
1.6
В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа (1.3) можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:
I
= I1
+ I2
+ I3,
т.е.
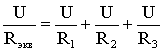
откуда
следует, что
(1.6)
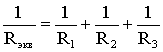
В
том случае, когда параллельно включены
два сопротивления R1
и R2,
они заменяются одним эквивалентным
сопротивлением
(1.7)
.
Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:
gэкв
= g1
+ g2
+ g3.
По
мере роста числа параллельно включенных
потребителей проводимость цепи gэкв
возрастает, и наоборот, общее сопротивление
Rэкв
уменьшается.
Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)
U
= IRэкв
= I1R1
= I2R2 =
I3R3.
Отсюда
следует, что
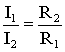
т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.
По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.
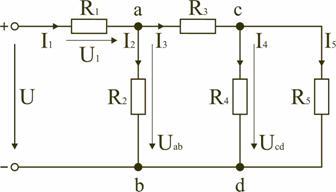
Электрическая
цепь со смешанным соединением элементов
Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.
Рис.
1.7
Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R1=R2=R3=R4=R5=R.
Сопротивления R4
и R5
включены параллельно, тогда сопротивление
участка цепи cd равно:
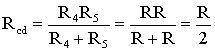
В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):
Рис.
1.8
На
схеме (рис. 1.8) сопротивление R3
и Rcd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:
.
Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):
Рис.
1.9
На
схеме (рис. 1.9) сопротивление R2
и Rad
соединены параллельно, тогда сопротивление
участка цепи аb равно
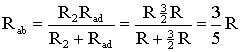
Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R1
и Rab
включены последовательно.
Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:
.
|
|
|
В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
Rэкв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.
Соединение
элементов электрической цепи по схемам
«звезда» и «треугольник»
В
электротехнических и электронных
устройствах элементы цепи соединяются
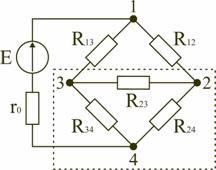
по мостовой схеме (рис. 1.12). Сопротивления
R12,
R13,
R24,
R34
включены в плечи моста, в диагональ 1–4
включен источник питания с ЭДС Е, другая
диагональ 3–4 называется измерительной
диагональю моста.
|
|
|
В
мостовой схеме сопротивления R13,
R12,
R23
и R24,
R34,
R23
соединены по схеме «треугольник».
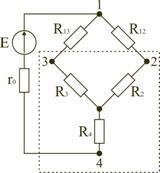
Эквивалентное сопротивление этой схемы
можно определить только после замены
одного из треугольников, например
треугольника R24
R34
R23
звездой R2
R3
R4
(рис. 1.13). Такая замена будет
эквивалентной, если она не вызовет
изменения токов всех остальных элементов
цепи. Для этого величины сопротивлений
звезды должны рассчитываться по следующим
соотношениям:
(1.8)

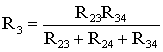
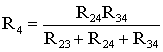
Для
замены схемы «звезда» эквивалентным
треугольником необходимо рассчитать
сопротивления треугольника:
(1.9)
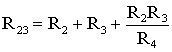
;
.
После
проведенных преобразований (рис. 1.13)
можно определить величину эквивалентного
сопротивления мостовой схемы (рис. 1.12)
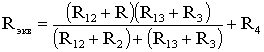
Главная
→
Примеры решения задач ТОЭ
→
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
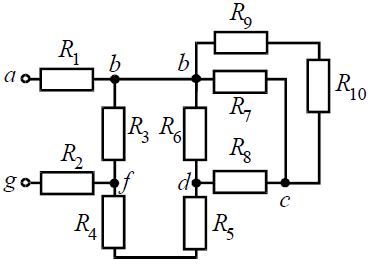
Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
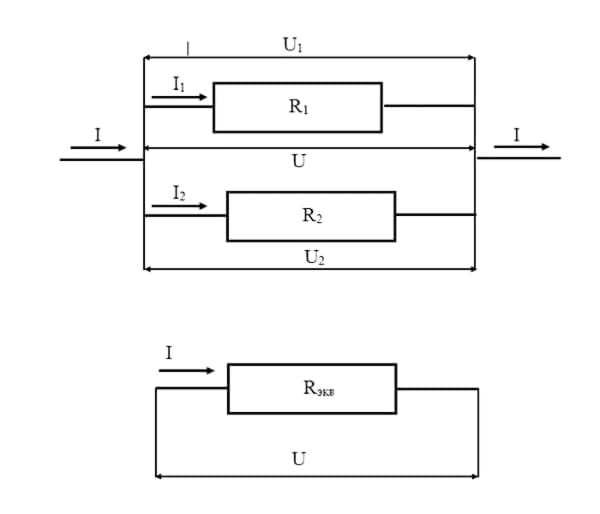
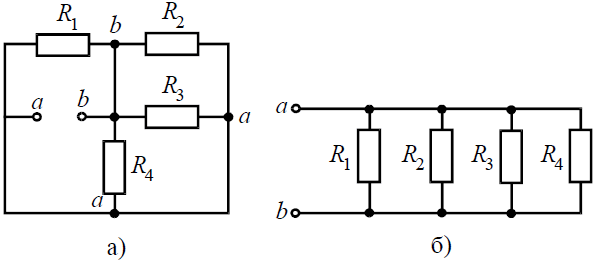
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
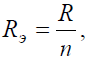
n — количество параллельно соединенных сопротивлений.
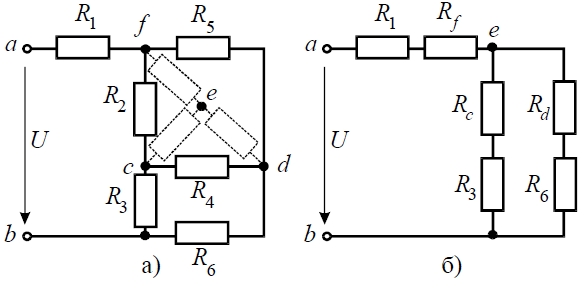
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).
Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
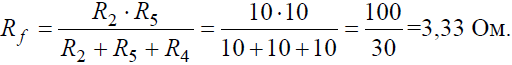
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
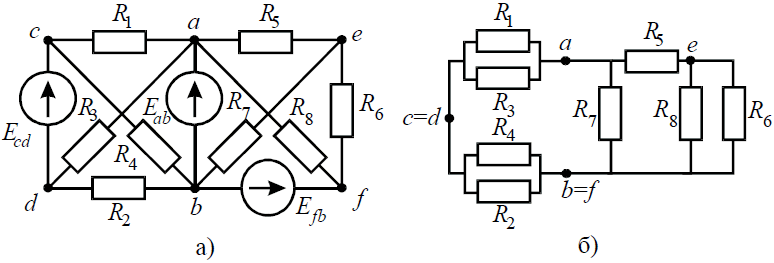
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
Рис. 4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
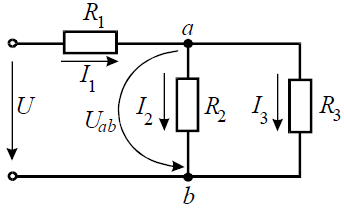
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.
Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
американские сигареты парламент.
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
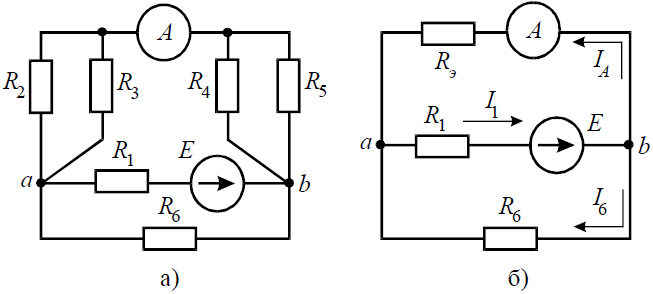
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б).
Величина эквивалентного сопротивления:
проститутки академическая. Смотри здесь строительство и ремонт деревянного дома.
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
Тогда амперметр покажет ток:
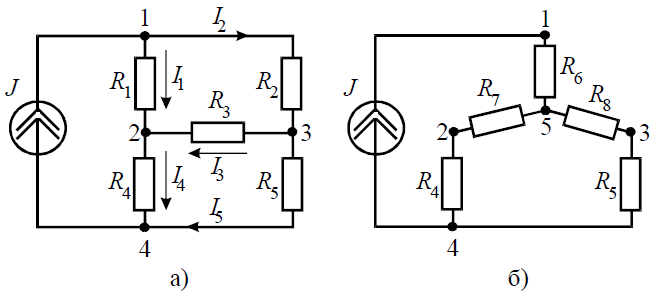
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I4 и I5:
Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований

№7 Эквивалентное преобразование треугольника и звезды сопротивлений.
Пусть требуется рассчитать цепь, показанную на рис. 7.1, а.
Рис. 7.1 — Преобразования электрической цепи
Расчет можно осуществить одним из описанных выше методов. Но так как в цепи имеется только один источник питания, наиболее простым было бы использование закона Ома. Однако попытка определения общего сопротивления цепи оказывается безрезультатной, так как здесь мы не находим ни последовательно, ни параллельно соединенных сопротивлений. Решить задачу помогает преобразование треугольника сопротивлений в эквивалентную звезду.
Треугольник и звезда сопротивлений имеют вид, показанный на рис. 7.2.
Рис. 7.2 — Треугольник и звезда сопротивлений
Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. В этом случае говорят, что схемы эквивалентны.
Можно показать, что условием эквивалентности являются следующие уравнения:
а) при преобразовании треугольника в звезду:
б) при преобразовании звузды в треугольник:
Например, сопротивление звезды R1, присоединенное к узлу 1, получается перемножением сопротивлений R12 и R31 треугольника, присоединенных к этому же узлу, и делением полученного произведения на сумму всех сопротивлений треугольника.
При обратном преобразовании сопротивление треугольника R12, лежащее между узлами 1 и 2, равно сумме сопротивлений звезды R1 и R2, присоединенных к этим узлам, плюс их произведение, деленное на сопротивление третьего луча звезды R3.
Пример 1.3. Рассчитать токи в цепи, изображенной на рис. 1.12, а, при следующих числовых значениях ее параметров: Е = 660 В, R1 = 20 Ом, R2 = 30 Ом, R3 = 5 Ом, R4 = 20 Ом, R5 = 50 Ом.
а) Решение преобразованием треугольника в звезду.
Теперь общее сопротивление цепи легко находится:
Ток, протекающий по источнику (одинаковый в заданной и преобразованной схемах), равен:
Токи в паралельных ветвях:
Возвращаемся к исходной схеме (рис. 7.1, а):
Ток в пятой ветви находим из первого закона Кирхгофа: I5 = I1–I3 = 26–28 = –2 A. Знак минус говорит о том, что действительное направление тока I5 противоположно указанному на схеме.
б) Решение преобразованием звезды в треугольник.
Преобразуем звезду, образуемую в схеме на рис. 7.1, а сопротивлениями R1, R5 и R3, в эквивалентный треугольник (рис. 7.1, в).
Определяем сопротивления треугольника:
Теперь рассчитываем преобразованную цепь. Сначала находим эквивалентные сопротивления участков ac и cd:
Затем определяем общее сопротивление и токи:
Возвращаемся к исходной схеме:
Рекомендуем подставить в приведенные формулы числовые значения параметров цепи и сравнить результаты вычислений с полученными в примере 1.3а.
Преобразование треугольник/звезда: что за сценой?
Преобразования треугольник/звезда позволяют нам заменить часть схемы другой схемой, которая, хотя и эквивалентна в поведении, но может значительно упростить анализ общей схемы. Здесь мы узнаем, откуда берутся эти преобразования.
Зачем?
Когда мы начали изучать электронику, резисторы были соединены либо последовательно, либо параллельно, и мы научились заменять такие комбинации их эквивалентными сопротивлениями, часто с целью уменьшения всей сети сопротивлений до единственного эквивалентного сопротивления, видимого из источника питания. После этого появились схемы (рисунок 1), которые содержали резисторы, которые не были ни последовательными, ни параллельными, но их всё же можно было убрать, тщательно определяя и сокращая фрагменты схемы в правильном порядке. Обратите внимание, что R1 не параллелен и не последователен ни с R2 , ни с R3 , но путем объединения R2 последовательно с R4 , и объединяя R3 последовательно с R5 , мы можем затем объединить эти два эквивалентных сопротивления параллельно и, наконец, объединив результат последовательно с R1 , получить полное сопротивление, видимое источнику питания, которое, используя закон Ома, поможет получить общий ток источника питания.
Но теперь мы подошли к схемам (рисунок 2), где нет никаких пар резисторов, которые включены последовательно или параллельно, – похоже, мы зашли в тупик. Одним из способов анализа этой схемы является использование закона напряжений Кирхгофа (второй закон) и закона токов Кирхгофа (первый закон) для получения алгебраических уравнений, которые мы можем решить для напряжений и токов. Хотя этот подход будет работать всегда (для этой и большинства других типов схем), он может быть довольно громоздким. Мы могли бы смириться с этим как с ценой возможности анализа этих более сложных схем, но иногда мы можем избежать оплаты этого счета, изменяя или «преобразовывая» фрагменты схемы, чтобы превратить ее в нечто, что мы можем уменьшить, используя только правила последовательного/параллельного объединения.

Для простоты мы будем рассматривать только цепи постоянного тока с резисторами, но эти принципы применимы к любой линейной системе переменного или постоянного тока. Кроме того, чтобы сфокусировать обсуждение на преобразованиях, мы найдем только общий ток, поставляемый источником напряжения, что означает, что мы стремимся свести всю сеть резисторов в единое эквивалентное сопротивление.
Давайте рассмотрим эти две схемы немного подробнее (рисунок 3). Мы видим, что единственная разница между ними заключается в том, что находится внутри пунктирных окружностей. В каждом случае цепь в окружности имеет три контакта, которые пересекают окружность для взаимодействия с остальной частью схемы. В левой цепи (рисунок 3(a)) резисторы подключены к контактам в конфигурации «треугольник» (в англоязычной литературе, конфигурация «delta», «дельта», названная в честь заглавной греческой буквы Δ). А в правой цепи резисторы подключены в конфигурации «звезда» (в англоязычной литературе, конфигурация «wye», «уай», названная в честь заглавной английской буквы Y, хотя в схеме она перевернута).
Теперь представьте, что резисторы внутри пунктирной окружности в левой цепи помещены в черный ящик, этот ящик удален из схемы и заменен другим черным ящиком, который заставляет схему вести себя точно так же. Далее представьте, что, когда вы открываете, этот новый ящик он содержит три резистора, расположенных как в правой цепи. Кто бы ни придумал второй черный ящик, он очень тщательно выбрал значения резисторов так, чтобы эти два блока были неразличимы для остальной части схемы: мы знаем, как анализировать правую схему, и теперь мы знаем, что когда мы это делаем, результаты можно применить к левой схеме, потому что они эквивалентны. Вот зачем выполнять преобразования «треугольник→звезда» и «звезда→треугольник».
Основные соотношения
Чтобы определить уравнения, связывающие резисторы в цепи, соединенной треугольником, с резисторами в цепи, соединенной звездой, нам ничего не нужно, кроме наших надежных формул для последовательных/параллельных соединений (и немного алгебры). Идея заключается в выравнивании эквивалентных сопротивлений между соответствующими парами контактов при отключенном оставшемся контакте (рисунок 4)

Выполнив это для эквивалентного сопротивления между контактами B-C, мы получим:
[R_B + R_C = frac left( R_ + R_ right) > + R_ + R_>]
Если мы повторим этот процесс для каждой другой пары контактов по очереди, мы получим еще два аналогичных уравнения, и любое из них даст нам необходимую нам информацию (при условии, что мы распознаем задействованную симметрию).
Частный случай: симметричные схемы
Если сопротивления в каждом плече цепи, соединенной треугольником или звездой, равны, такая цепь считается «симметричной». Это означает, что
[R_Y = R_A = R_B = R_C]
Комбинация этого условия с соотношением из предыдущего раздела сразу приводит к уравнению преобразования для случая симметрии.
Это гораздо более значительный результат, чем может показаться на первый взгляд, и причина довольно проста – когда инженеры проектируют схемы с соединениями треугольник или звезда, они часто стараются сделать эти схемы симметричными. Хотя, конечно, это не всегда возможно, и поэтому мы должны иметь возможность разобраться с общим случаем, когда схема не симметрична.
Общий случай преобразования треугольник→звезда
Для преобразования треугольник/звезда нам дана известная схема, соединенная треугольником, и мы хотим найти значения для эквивалентной схемы, соединенной звездой, – поэтому мы пытаемся найти < RA , RB , RC > для заданных < RAB , RBC , RAC >.
Мы начнем с того, что запишем наши основные соотношения из первоначального вида в несколько более компактной форме, определив новую величину, RΔS , которая равна сумме сопротивлений всех резисторов в цепи, соединенной треугольником.
Затем мы делаем перестановку нашего соотношения для получения вида линейного алгебраического уравнения с неизвестными < RA , RB , RC >.
Поскольку у нас есть три неизвестных, нам нужно еще два уравнения. Они получаются из эквивалентных сопротивлений, видимых при рассмотрении двух других пар контактов. Выполнив это (или используя симметрию) мы получаем
Сложив эти два уравнения вместе и вычтя наше первое уравнение, мы получим
Мы можем решить систему уравнению для двух других неизвестных сопротивлений (или использовать симметрию), чтобы получить
Эти отношения могут быть обобщены очень компактно. Сопротивление, подключенное к каждому узлу в эквивалентной цепи, соединенной звездой, равно произведению сопротивлений, подключенных к соответствующему узлу в цепи, соединенной треугольником, деленному на сумму сопротивлений всех резисторов в треугольнике. Обычно это выражается формулой, такой как
- RN – резистор, подключенный к контакту N в схеме «звезда»;
- RN1 и RN2 – резисторы, подключенные к контакту N в схеме «треугольник»
Общий случай преобразования звезда→треугольник
Для преобразования звезда→треугольник нам дана известная схема, соединенная звездой, и мы хотим найти значения для эквивалентной схемы, соединенной треугольником. Следовательно, мы пытаемся найти < RAB , RBC , RAC > для заданных < RA , RB , RC >.
Это не так просто, как в случае преобразования треугольник→звезда потому, что неизвестные сопротивления перемножаются вместе, делая результирующие уравнения нелинейными. К счастью, мы можем обойти это неудобство, рассмотрев отношения сопротивлений резисторов в каждой цепи. Например, взяв отношение RA к RB , мы получаем
Другими словами, отношение сопротивлений резисторов, подключенных к любым двум контактам в схеме звезда, равно отношению сопротивлений резисторов, соединяющих те же самые два контакта с третьим контактом в схеме треугольник. Следовательно, два других соотношения будут следующими
Вооружившись этим, мы могли бы вернуться к нашим основным соотношениям и продолжить работу с ними, но в качестве отправной точки проще использовать одно из отношений из общего случая преобразования треугольник→звезда.
[R_ = R_A left( over R_> + over R_ > + 1 right)]
Два других выражения получаются аналогично (или согласно симметрии):
Эти выражения могут быть обобщены очень компактно. Сопротивление, подключенное между каждой парой узлов в эквивалентной схеме, соединенной треугольником, равно сумме сопротивлений двух резисторов, подключенных к соответствующим узлам в схеме, соединенной звездой, плюс произведение сопротивлений этих двух резисторов, деленное на сопротивление третьего резистора.
Общий способ выразить это состоит в том, чтобы поместить правую часть под общим знаменателем, а затем отметить, что числитель в каждом выражении является суммой произведений каждой пары сопротивлений в цепи, соединенной звездой, а знаменатель – это сопротивление, подключенное к третьему контакту.
[R_P = R_A R_B + R_B R_C + R_A R_C]
Пример
Давайте поработаем с задачей, показанной на рисунке 5. Прежде чем мы начнем, давайте определим ожидаемый ответ, чтобы у нас была хорошая проверка того, является ли наш окончательный ответ правильным. Для этого рассмотрим роль мостового резистора 150 Ом. Этот резистор служит для уменьшения общего сопротивления, обеспечивая путь между левой и правой сторонами цепи. Следовательно, самое высокое эффективное сопротивление будет иметь место, если этот резистор будет удален полностью, и в этом случае полное сопротивление будет равно параллельной комбинации левой и правой сторон, что приведет к
С другой стороны, наименьшее общее сопротивление было бы получено путем уменьшения мостового резистора до прямого короткого замыкания, и в этом случае общее сопротивление было бы равно параллельной комбинации двух верхних резисторов, включенной последовательно с параллельной комбинацией двух нижних резисторов, что приведет к
Теперь мы ЗНАЕМ, что наш ответ ДОЛЖЕН быть между этими двумя предельными значениями. Во многих случаях простой анализ границ, такой как этот, приводит к ответу, который «достаточно хорошо» подходит для данной цели, но давайте предположим, что это не так. Используя приведенные выше уравнения преобразования треугольник→звезда, мы сначала определяем сумму сопротивлений резисторов треугольника.
А затем находим значение R1 , перемножив сопротивления двух резисторов, которые подключены к верхнему контакту, и разделив это произведение на сумму всех трех сопротивлений.
Повторим это же для R2 .
Мы могли бы повторить это еще раз для R3 , но давайте, вместо этого, определим R3 , используя свойства отношений.
Теперь, когда у нас есть все сопротивления для эквивалентной схемы звезда, мы можем очень легко определить общее сопротивление.
Поскольку это значение находится между нашими минимальной и максимальной границами, мы полностью уверены, что это правильный ответ, или, даже если мы допустили ошибку, наш ответ довольно близок к правильному. Поэтому суммарный ток равен
Заключение
Теперь мы увидели, что преобразования треугольник/звезда полезны, и, что более важно, увидели, как их можно легко выполнить, используя не более чем концепцию эквивалентных сопротивлений с использованием последовательных/параллельных комбинаций резисторов. Это может хорошо вам помочь, поскольку дает вам возможность вывести эти формулы на лету, если когда-нибудь возникнет в них необходимость, и у вас не будет подходящего справочного материала. Но что еще более важно, это должно служить для более прочного закрепления фундаментальных понятий в наборе инструментов, который хранится у вас в голове, позволяя вам использовать в своей работе еще более эффективные навыки анализа цепей.
В конце мы должны принять к сведению распространенное заблуждение, заключающееся в том, что преобразования треугольник↔звезда являются ЕДИНСТВЕННЫМ способом анализа цепей, которые нельзя уменьшить другими способами. В действительности, хотя эти преобразования могут сделать нашу жизнь проще, они не обязательны, поскольку ЛЮБОЙ контур, который можно проанализировать с их помощью, также можно проанализировать с помощью правил Кирхгофа, либо напрямую, либо с помощью одного из более формализованных методов их применения, включая метод контурных токов или метод узловых напряжений, а также с методиками, такими как эквивалентная схема Тевенина.
Физический портал для школьников и абитуриентов
Вы здесь
Подготовка к олимпиаде. Методы расчета резисторных схем постоянного тока. 3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»
Методы расчета резисторных схем постоянного тока
3. Преобразование и расчет цепей с помощью перехода «звезда» — «треугольник»
Рассматриваемый метод основан на том, что сложную схему, имеющую три вывода (узла), можно заменить другой, с тем же числом выводов (узлов). Замену следует произвести так, чтобы сопротивление участка между двумя любыми выводами новой схемы было таким же, как у прежней. В результате получится цепь, сопротивление которой эквивалентно сопротивлению данной по условию. Общее сопротивление обеих цепей будет одинаковым. Однако, поскольку в результате такого преобразования изменяются токи внутри цепи, такую замену можно проводить только в тех случаях, когда не надо находить распределение токов.
Подобные преобразования широко известны для случая двух выводов. Так, например, два резистора сопротивлениями R1 и R2, включенные последовательно, можно заменить одним резистором сопротивлением R1 + R2. Если резисторы включены параллельно, то их можно заменить одним резистором сопротивлением
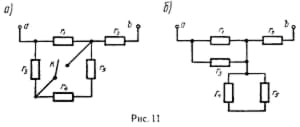
И в этих случаях распределение токов в цепи (или в части цепи) претерпевает изменения. Рассмотрим более сложное преобразование схем, имеющих три вывода (трехполюсников). Иначе это называется преобразованием «звезды» (рис. а) в «треугольник» (рис. б), и наоборот.
Сопротивления резисторов в схеме «звезда» обозначаются с индексом точки, с которой соединен этот резистор, например, резистор r1 соединен с точкой 1. В «треугольнике» индексы резисторов соответствуют точкам, между которыми они включены, например, резистор R13 подключен к точкам 1 и 3. Как отмечено выше, чтобы заменить одну из этих схем другой, нужно получить такие соотношения между их сопротивлениями, чтобы эквивалентные сопротивления между любыми точками были одинаковы для обеих схем (при условии сохранения числа этих точек). Так, в «звезде» сопротивление между точками 1 и 2 равно r1 + r2, в «треугольнике»
следовательно, для того чтобы сопротивления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы выполнялось следующее равенство:
Аналогично для точек 2 и 3 и для точек 1 и 3:
Сложим все эти уравнения и, поделив обе части на 2, получим:
Вычитая из этого уравнения поочередно предыдущие, получим:
Эти выражения легко запомнить:
знаменатель в каждой формуле есть сумма сопротивлений всех резисторов «треугольника», а в числителе дважды повторяется индекс, стоящий слева:
$r_1 rightarrow R_<12>R_<13>, r_2 rightarrow R_<12>R_<23>, r_3 rightarrow R_<13>R_<23>$.
Аналогично получают и формулы обратного преобразования:
Последние выражения также легко запомнить и проверить:
числитель у всех уравнений один и тот же, а в знаменателе стоит сопротивление резистора с индексом, которого не достает в левой части выражения.
Этот метод представляет собой наиболее универсальный подход к решению практически всех типов задач на разветвленные цепи.
Задача 27. Определите сопротивление цепи АВ (рис.), если R1 = R5 = 1 Ом, R2 = R6 = 2 Ом, R3 = R7 = 3 Ом, R4 = R8 = 4 Ом.
Решение. Преобразуем «треугольники» R1R2R8 и R4R5R6 в эквивалентные «звезды». Схема примет иной вид (рис.).
Сопротивления $r_1, r_2, …, r_6$ найдем по формулам:
Теперь нет никаких препятствий для расчета схемы, которая состоит из последовательно и параллельно соединенных резисторов (рис.). После простых расчетов получим
http://radioprog.ru/post/659
http://fizportal.ru/olympiads-method-1-12
Содержание материала
- Последовательное соединение элементов
- Последовательное соединение элементов
- Определение эквивалентного сопротивления
- Параллельное соединение резисторов. Калькулятор для расчета
- Основные преимущества
- Физические формулы и примеры вычислений
- Практическое применение
- Простое соединение
- Комбинированный контур
- Емкость в цепи переменного тока
- Виды устройств и их особенности
- Основные популярные типы
- Как рассчитать сложные схемы соединения резисторов
- Параллельное соединение
Последовательное соединение элементов
В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.
При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.
Последовательное подключение приборов
Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:
I = U/R.
Из вышестоящего выражения получаем значение R:
R = U/I (1).
Поскольку при последовательном соединении:
- I = I1 = I2 =…= IN (2),
- U = U1 + U2 +…+ UN (3),
формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:
- Rэкв = (U1 + U2 + …+ UN)/I,
- Rэкв = R1 + R2 + … + RN (4).
Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:
Rобщ = N·R (5).
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Основные преимущества
Светодиодные лампы Т8 значительно превосходят альтернативные образцы практически по всем показателям. К достоинствам приборов следует отнести:
- эффективность, высокие значения светового потока;
- экономичность;
- длительный срок службы;
- освещение имеет направленный характер, что позволяет организовать более эффективный и комфортный режим подсветки;
- подключение происходит мгновенно, чего не наблюдается у люминесцентных ламп;
- ровный, без мерцания режим работы;
- есть возможность работы при нестабильности напряжения в сети;
- не создают электромагнитных помех;
- нет вредного излучения в ультрафиолетовом диапазоне;
- попадание частиц жира или иных взвесей, находящихся в воздухе, не создает опасность перегрева и взрыва лампы, характерных для альтернативных конструкций;
- утилизация светодиодных устройств не требует специализированных мероприятий и может быть произведена обычным способом;
- подключать такие светильники можно напрямую к сети 220 В, без промежуточных устройств.
Помимо этих преимуществ, необходимо отметить широкие возможности выбора цветовой температуры ламп. Этот параметр позволяет создать в помещении определенную обстановку, позволяющую повысить концентрацию и увеличивающую работоспособность сотрудников. Такой результат достигается подключением ламп с холодным белым светом.
Если необходимо обеспечить более расслабленную, комфортную обстановку, выбирают экземпляры с теплым светом. Кроме этого, светодиоды хорошо переносят низкие температуры, что позволяет использовать их в неотапливаемых переходах, коридорах и прочих помещениях со сложными условиями эксплуатации.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
Практическое применение
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Комбинированный контур
Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:
Rp = (R3*R4)/(R3+R4).
Rp = (10*3)/ (10+3) = 2,3 Ом.
Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:
Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.
Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:
I = U/R = 5/2,3 = 2,2 A.
P = I*U = 2,2*5= 11 Вт.
Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.
Емкость в цепи переменного тока
При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.
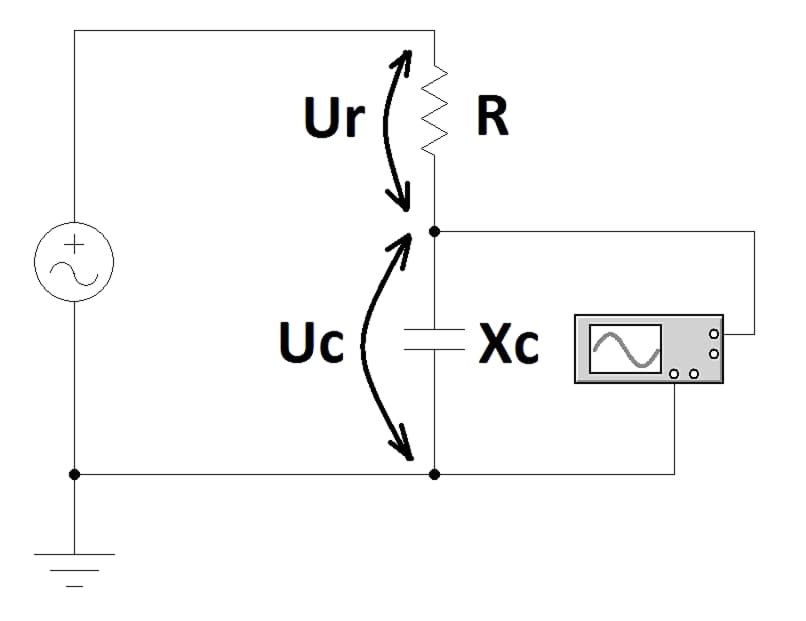
Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.
Для данной схемы вычисления имеют следующий вид.
Формула косвенного измерения
Здесь:
- Ur – разность потенциалов на резисторе, В;
- Uc – напряжение на обкладках, В;
- R – сопротивление резистора, ом;
- Xc – сопротивление ёмкости, ом;
- I – ток, протекающий в цепи, А.
Важно! Электрический кабель также обладает ёмкостью. Поэтому после снятия напряжения на нём остаётся некоторый заряд
Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше.
Виды устройств и их особенности
Разновидностей штепсельных розеток и блоков довольно много. У каждого типа свои конструктивные особенности и предназначение.
- Скрытые приборы монтируют прямо в стену — в специальные подрозетники.
- Открытые устройства выпускают для тех квартир, где электропроводка не спрятана в стену.
- Выдвижные розеточные блоки монтируют в стол или другую мебель. Их удобство в том, что после эксплуатации приборы легко спрятать от посторонних глаз и шаловливых детских рук.
Приборы отличаются методом зажима контактов. Он бывает винтовым и пружинным. В первом случае проводник фиксируют винтом, во втором — с помощью пружины. Надежность последних больше, однако в продаже их найти не так просто. На стенах устройства закрепляют тремя способами — лапками с зубчатыми краями, саморезами или специальной пластиной — суппортом, который облегчает как установку, так и демонтаж розетки.
Помимо обычных, недорогих устройств существуют модели, оснащенные заземляющими контактами. Это лепестки располагаются в верхней и нижней части, к ним крепят провод заземления. Для обеспечения безопасности выпускают розетки, оборудованные шторкам либо защитными крышками.
Основные популярные типы
К ним относятся:
- вид «С», он имеет 2 контакта — фазу и ноль, обычно покупается, если предназначен для техники малой либо средней мощности;
- тип «F», помимо традиционной пары оснащается еще одним контактом — заземляющим, эти розетки становятся более популярными, так как для квартир в новостройках заземляющий контур стал нормой;
- Вид «Е», отличающийся от предыдущего только формой контакта заземления, это штырь, такой же, как и элементы вилки розетки.
Последний тип встречается реже остальных, так как он менее удобен в эксплуатации: разворот штепселя на 180° при такой розетке невозможен.
Защищенность корпуса — следующее различие моделей. Степень безопасности обозначают индексом IP и двухзначным числом, следующим за этими буквами. Первая цифра обозначает класс защиты от пыли, твердых тел, вторая — от влаги.
- Для обычных жилых комнат достаточно моделей класса IP22 либо IP33.
- IP43 рекомендуют покупать для детских, так как эти розетки оснащены крышками/шторками, блокирующими гнезда, когда техника не используется.
- IP44 — тот минимум, что необходим для ванных комнат, кухонь, бань. Угрозой в них может быть не только сильная влажность, но и брызги воды. Подойдут они для монтажа в подвалах без отопления.
Установка розетки на открытом балконе — достаточное основание для покупки изделия с большей степенью защиты, это как минимум IP55.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
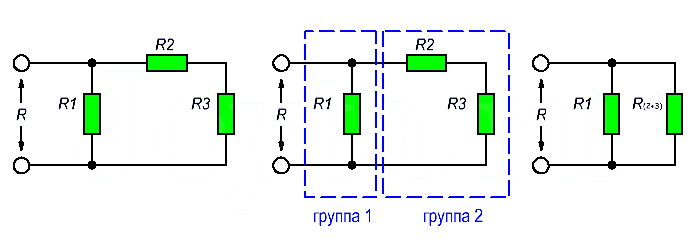
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Параллельное соединение
Реактивное сопротивление
При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.
Параллельное соединение
Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.
В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.
Если имеются N резистивных устройств, подключенных таким образом, то:
I = I1 + I2 + … + IN (6),
U = U1 = U2 = … = UN (7).
Из выражений (1), (6) и (7) имеем:
- Rобщ = U/(I1 + I2 + …+ IN),
- 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).
Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:
Rобщ = R · R / N·R = R / N (9).
Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.