Как составить функцию по графику ломаной - Исправление недочетов и поиск решений вместе с Examum.ru

Графики и формулы кусочно-линейных функций

Ситуация, когда движение или другое явление можно описать одной линейной функцией, определенной на интервале $-infty lt t lt +infty$, в действительности невозможна. Хотя бы потому, что возраст Вселенной велик, но не бесконечен.

На практике в течение некоторого времени тело может двигаться, потом – покоиться, потом – опять прийти в движение, но уже с другой скоростью и в другом направлении и т.п. Как задать подобную зависимость?

Допустим, турист идет из начальной точки по прямой тропинке в течение 2 ч со скоростью 5 км/ч, затем останавливается отдохнуть на 1ч и возвращается обратно по той же тропинке со скоростью 4 км/ч. Нам нужно найти формулу для расстояния s(t) от начальной точки на протяжении всего похода.

Изобразим зависимость s(t) графически:

Первый отрезок AB легко записать: $ s_1 (t) = 5t,0 le t lt 2$

С отрезком BC тоже всё ясно: $s_2 (t) = 10,2 le t lt 3$

Осталось найти формулу для отрезка CD. Для него известен угловой коэффициент, равный скорости k = -4; знак «минус» оттого, что турист возвращается обратно. Формула имеет вид $s_3 (t) = -4t+b$. Также, нам известны координаты C(3;10).

Подставляем: $10 = -4 cdot 3+b Rightarrow b =22$. Осталось рассчитать момент возвращения:

$$0 = -4t_{back}+22 Rightarrow t_{back} = 22:4 = 5,5$$ (ч)

Значит, формула движения на отрезке $CD:s_3 (t) = -4t+22,3 le t le 5,5.$

Получаем:

$$s(t) = {left{ begin{array}{c} 5t,0 le t lt 2 \ 10,2 le t lt 3 \ -4t+22,3 le t le 5,5 end{array} right.} $$

Важным свойством заданной функции является выполнение условий согласования:

$$ s_1 (2) = s_2 (2) = 10,s_2 (3) = s_3 (3) = 10$$

Наша функция «сшита» на концах промежуточных интервалов.

В общем случае:

Функция вида

$$x f(x) = {left{ begin{array}{c} k_1 x+b_1, x_1 le x lt x_2 \ k_2 x+b_2,x_2 le x lt x_3 \…\ k_n x+b_n,x_n le x lt x_{n+1} end{array} right.}$$

называется кусочно-линейной.

При этом для функции на краях интервалов выполняются условия согласования:

$$f_i (x_{i+1} ) = f_{i+1} (x_{i+1} ),i = overline {1,n-1} $$

Графиком кусочно-линейной функции является ломаная линия

Знак модуля в линейных функциях

По правилу раскрытия скобок модуля (см. §4 данного справочника)

$$ |x| = left[ begin{array}{cc} x, xge0 \ -x, x lt 0end{array} right.$$

Внимание!

Если в формуле для линейной функции содержится знак модуля, то после его раскрытия получается кусочно-линейная функция.

Например:

$$ y = 2|x|+5 = {left{ begin{array}{c} -2x+5, xge0 \ 2x+5, x lt 0end{array} right.} $$

Мы заменили квадратную скобку со значением «или» на фигурную скобку со значением «и», поскольку именно смысл объединения — «и того, и другого» — вкладывается в определение кусочно-линейной функции .

Примеры

Пример 1. Представьте функцию с модулем в виде кусочно-линейной и постройте её график:

а) $ y = |x| = {left{ begin{array}{c} -x, x lt0 \ x, x ge 0 end{array} right.}$

б) $ y = 2|x|-1 = {left{ begin{array}{c} -2x-1, x lt0 \ 2x-1, x ge 0 end{array} right.}$

в) $ y = |x+1| = {left{ begin{array}{c} -x-1, x lt0 \ x+1, x ge 0 end{array} right.}$

г) $ y = |x-2| = {left{ begin{array}{c} -x+2, x lt0 \ x-2, x ge 0 end{array} right.}$

Пример 2*. Представьте функцию с модулем в виде кусочно-линейной и постройте её график:

$$ y = |2|x|-1| = {left{ begin{array}{c} |-2x-1|, xlt0 \ |2x-1|,x ge 0 end{array} right.} = {left{ begin{array}{c} 2x+1, {left{ begin{array}{c} -2x-1 lt 0 \ x lt 0 end{array} right.} \ -2x-1, {left{ begin{array}{c} -2x-1 ge 0 \ x lt 0end{array} right.} \ -2x+1, {left{ begin{array}{c}2x-1 lt 0 \ x ge 0end{array} right.} \ 2x-1, {left{ begin{array}{c}2x-1 ge 0 \ x ge 0end{array} right.} end{array} right.}= $$

$$ = {left{ begin{array}{c} 2x+1, {left{ begin{array}{c} -2x lt 1 \ x lt 0 end{array} right.} \ -2x-1, {left{ begin{array}{c} -2x ge 1 \ x lt 0end{array} right.} \ -2x+1, {left{ begin{array}{c}2x lt 1 \ x ge 0end{array} right.} \ 2x-1, {left{ begin{array}{c}2x ge 1 \ x ge 0end{array} right.} end{array} right.}= {left{ begin{array}{c} 2x+1, {left{ begin{array}{c} x gt — frac{1}{2} \ x lt 0 end{array} right.} \ -2x-1, {left{ begin{array}{c} x le — frac{1}{2} \ x lt 0end{array} right.} \ -2x+1, {left{ begin{array}{c}x lt frac{1}{2} \ x ge 0end{array} right.} \ 2x-1, {left{ begin{array}{c}x ge frac{1}{2} \ x ge 0end{array} right.} end{array} right.}= {left{ begin{array}{c} -2x-1, x le — frac{1}{2} \ 2x+1, — frac{1}{2} lt x lt 0 \ -2x+1, 0 le x lt frac{1}{2} \ 2x-1, x ge frac{1}{2} end{array} right.} $$

Как видно из этого примера, аналитически выводить формулу для двух модулей очень нелегко.

Гораздо легче сразу построить график, если следовать следующим простым правилам преобразования.

Шаг 1. Строим y = 2x-1

Шаг 2. Строим y = 2|x|-1 по правилу: |x| отражает часть графика для положительных $x ge 0$ влево, зеркально относительно оси Y

Шаг 3. Строим y = |(2|x|-1)| по правилу: общий модуль отражает участок графика с отрицательными $y lt 0$ вверх, зеркально относительно оси X

Или на одном графике:

Источник

Функция f, определенная при всех х, называется кусочно-линейной, если она линейна на каждом интервале

и к тому же выполнены условия согласования, то есть в точках смены формул функция не терпит разрыв.

Непрерывная кусочно-линейная функция называется линейным сплайном . Её график есть ломаная с двумя бесконечными крайними звеньями – левым (отвечающим значениям x n ) и правым ( отвечающим значениям x x n )

Кусочно-элементарная функция может быть определена более чем двумя формулами

у

У =

1

0

х

1

-1

График – ломаная с двумя бесконечными крайними звеньями – левым (х1).

У=|x| — |x – 1|

Точки смены формул: х=0 и х=1.

У(0)=-1, у(1)=1.

График кусочно-линейной функции удобно строить, указывая на координатной плоскости вершины ломаной.

Кроме построения n вершин следует построить также две точки : одну левее вершины A 1 ( x 1; y ( x 1)), другую – правее вершины An ( xn ; y ( xn )).

Заметим, что разрывную кусочно-линейную функцию нельзя представить в виде линейной комбинации модулей двучленов .

Построить график функции у = х+ |x -2| — |X|.

Непрерывная кусочно-линейная функция называется линейным сплайном

1.Точки смены формул: Х-2=0, Х=2 ; Х=0

у

2

2.Составим таблицу:

0

3

2

-1

х

1

0

2

1

у

0

х

2

У( 0 )= 0+|0-2|-|0|=0+2-0= 2 ;

у( 2 )=2+|2-2|-|2|=2+0-2= 0 ;

у (-1 )= -1+|-1-2| — |-1|= -1+3-1= 1 ;

у( 3 )=3+|3-2| — |3|=3+1-3= 1 .

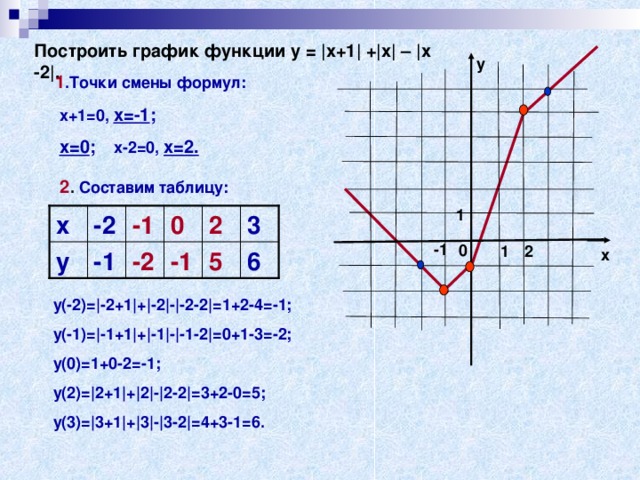
Построить график функции у = |х+1| +|х| – |х -2|.

у

1 .Точки смены формул:

х+1=0, х=-1 ;

х=0 ; х-2=0, х=2.

2 . Составим таблицу:

1

3

x

0

2

-2

-1

-1

0

2

1

x

у

-1

-2

-1

5

6

y(-2)=|-2+1|+|-2|-|-2-2|=1+2-4=-1;

y(-1)=|-1+1|+|-1|-|-1-2|=0+1-3=-2;

y(0)=1+0-2=-1;

y(2)=|2+1|+|2|-|2-2|=3+2-0=5;

y(3)=|3+1|+|3|-|3-2|=4+3-1=6.

|x – 1| = |x + 3|

Решите уравнение:

Решение. Рассмотрим функцию y = |x -1| — |x +3|

Построим график функции /методом линейного сплайна/

Точки смены формул:

х -1 = 0, х = 1; х + 3 =0, х = — 3.

y

2. Составим таблицу:

— 4

х

-3

2

1

1

— 4

4

4

у

— 4

0

x

1

y(- 4) =|- 4–1| — |- 4+3| =|- 5| — | -1| = 5-1=4;

y( -3 )=|- 3-1| — |-3+3|=|-4| = 4;

y( 1 )=|1-1| — |1+3| = — 4 ;

y(-1) = 0.

y(2)=|2-1| — |2+3|=1 – 5 = — 4.

Ответ: -1.

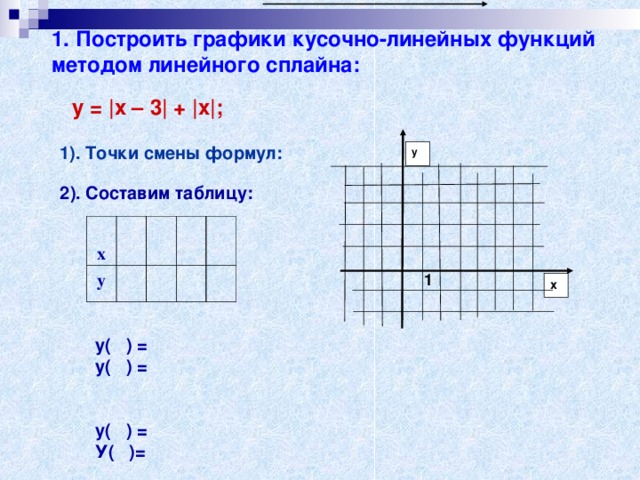
1. Построить графики кусочно-линейных функций методом линейного сплайна:

у = |x – 3| + |x|;

1). Точки смены формул:

у

2). Составим таблицу:

х

у

1

х

у( ) =

у( ) =

у( ) =

У( )=

2. Построить графики функций, используя УМК «Живая математика »

А) у = |2x – 4| + |x +1|

1) Точки смены формул:

2) y( ) =

y( ) =

y( ) =

у( ) =

Б) Постройте графики функций, установите закономерность :

a) у = |х – 4| б) y = |x| +1

y = |x + 3| y = |x| — 3

y = |x – 3| y = |x| — 5

y = |x + 4| y = |x| + 4

х

у

Используйте инструменты «Точка», «Отрезок», «Стрелка» на панели инструментов.

1. Меню «Графики».

2. Вкладка «Построить график».

.3. В окне «Калькулятор» задать формулу.

Постройте график функции:

1) У = 2х + 4

х

у

3) У =

х

у

2

4

1. Козина М.Е. Математика. 8-9 классы: сборник элективных курсов. – Волгоград: Учитель, 2006.

2. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 7 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2011

3. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 8 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение , 2011

4. ВикипедиЯ свободная энциклопедия

http://ru.wikipedia.org/wiki/Spline

Источник

15
Сен 2022

Категория: 10 Графики функций

2022-09-15
2022-09-15

Задача 1. На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите корень уравнения