8
Функция
принадлежности μA(x)
∈
[0,
1] ставит в соответствие каждому
числу
x
∈
X число
из интервала [0,1], характеризующее степень
принадлежности решения к подмножеству
А.
Т.е.
это некоторая не вероятностная
субъективная мера нечеткости, определяемая
в результате опроса экспертов о степени
соответствия элемента x понятию,
формализуемому нечетким множеством A.
В отличие от вероятностной меры, которая
является оценкой стохастической
неопределенности, имеющей дело с
неоднозначностью наступления некоторого
события в различные моменты времени,
нечеткая мера является численной оценкой
лингвистической неопределенности,
связанной с неоднозначностью и
расплывчатостью категорий человеческого
мышления. При построении функции
принадлежности μA(x)
с каждым нечетким множеством A ассоциируется
некоторое свойство, признак или атрибут,
который характеризует некоторую
совокупность объектов X. Чем в большей
степени конкретный объект x ∈
X
обладает
этим свойством, тем более близко к 1
соответствующее значение μA(x).
Если элемент x ∈
X определенно обладает этим свойством,
то μA(x)=1,
если же x ∈
X определенно не обладает этим свойством,
то μA(x)=0.
Основные
виды функций принадлежности
На
практике удобно использовать те функции
принадлежности, которые допускают
аналитическое представление в виде
некоторой простой математической
функции.
1.
Кусочно-линейные,
использующиеся
для задания неопределенностей типа:
«приблизительно равно», «среднее
значение», «расположен в интервале»,
«подобен объекту», «похож на предмет»
и т.п.
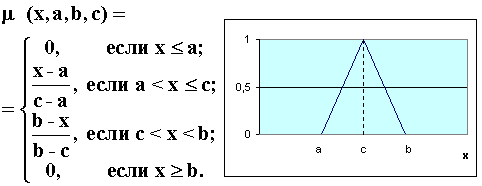
Треугольная
trimf
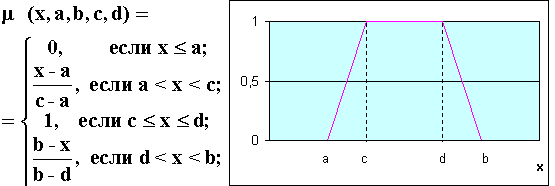
Трапецеидальная trapmf
2.
S-образные,
использующиеся
для задания неопределенностей типа:
«большое количество», «большое значение»,
«значительная величина», «высокий
уровень» и т.п.
Квадратичный
S-сплайн
smf
3.
Z-образные,
использующиеся
для задания неопределенностей типа
«малое количество», «небольшое значении
е», «незначительная величина», «низкий
уровень» и т.п.
Квадратичный
Z-сплайн
zmf
4.
П-образные,
использующиеся
для задания неопределенностей типа:
«приблизительно в пределах от и до»,
«примерно равно», «около» и т.п.
К
данному типу функций принадлежности
можно отнести целый класс кривых, которые
по своей форме напоминают колокол,
сглаженную трапецию или букву «П».
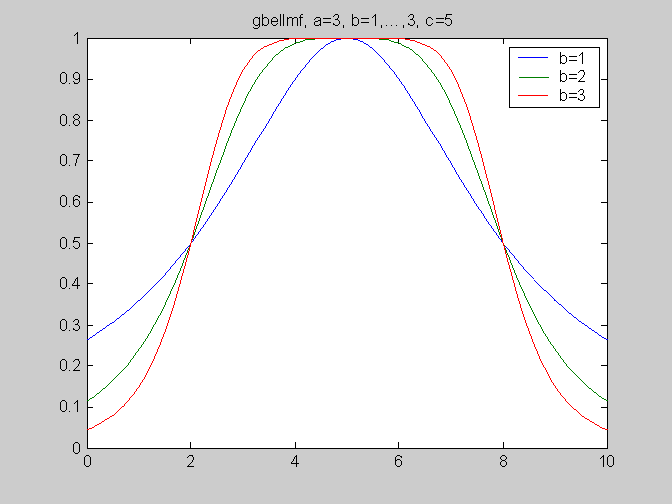
Колоколообразная
gbellmf
a —
коэффициент концентрации функции
принадлежности;
b – коэффициент
крутизны функции принадлежности;
c – координата
максимума функции принадлежности.
Гауссовская
gaussmf
a – координата
максимума функции принадлежности;
b – коэффициент
концентрации функции принадлежности.
Методы
построения функций принадлежности
Прямые
и косвенные
В
зависимости от числа привлеченных к
опросу экспертов как прямые, так и
косвенные методы делятся на одиночные
и групповые.
Прямые
В
прямых методах эксперт либо группа
экспертов просто задают для каждого
x
∈
X
значение функции принадлежности μA(x).
Как
правило, прямые методы построения
функций принадлежности используются
для таких свойств, которые могут быть
измерены в некоторой количественной
шкале. Например, такие физические
величины, как скорость, время, расстояние,
давление, температура и другие имеют
соответствующие единицы и эталоны для
своего измерения.
При
прямом построении функций принадлежности
следует учитывать, что теория нечетких
множеств не требует абсолютно точного
задания функций принадлежности. Зачастую
бывает достаточно зафиксировать лишь
наиболее характерные значения и вид
функции принадлежности.
Так,
например, если необходимо построить
нечеткое множество, которое представляет
свойство «скорость движения автомобиля
примерно 50 км/ч», на начальном этапе
может оказаться достаточным представить
соответствующее нечеткое множество
треугольной функцией принадлежности
с параметрами а = 40 км/ч, b = 60 км/ч и с = 50
км/ч. В последующем функция принадлежности
может быть уточнена опытным путем на
основе анализа результатов решения
конкретных задач.
Процесс
построения или задания нечеткого
множества на основе некоторого известного
заранее количественного значения
измеримого признака получил даже
специальное название — фаззификация
или приведение к нечеткости. Речь идет
о том, что хотя иногда нам бывает известно
некоторое значение измеримой величины,
мы признаем тот факт, что это значение
известно неточно, возможно с погрешностью
или случайной ошибкой. При этом, чем
меньше мы уверены в точности измерения
признака, тем большим будет интервал
носителя соответствующего нечеткого
множества. Следует помнить, что в
большинстве практических случаев
абсолютная точность измерения является
лишь удобной абстракцией для построения
математических моделей. Именно по этой
причине фаззификация позволяет более
адекватно представить объективно
присутствующую неточность результатов
физических измерений.
Метод
относительных частот (прямой групповой)
Пусть
имеется m
экспертов, n1 из
которых на вопрос о принадлежности
элемента x
∈
X нечеткому
множеству A отвечают положительно.
Другая часть экспертов n2 = m –
n1 отвечает
на этот вопрос отрицательно. Тогда
принимается μA(x)
= n1
/
(n1 + n2) = n1
/
m.
Пример. Рассмотрим
нечеткое множество A, соответствующее
понятию «скорость изменения температуры
положительная средняя». Объект x –
скорость изменения температуры. Экспертам
предъявляются различные значения
скорости изменения температуры x, и
каждому из них задается вопрос: считает
ли эксперт, что данная скорость изменения
температуры x положительная средняя.
Результаты опроса сведены в табл.
В
качестве непрерывного представления
данной нечеткой переменной можно
использовать гауссовскую ФП gaussmf с
максимумом функции принадлежности а=5
и коэффициентом концентрации функции
принадлежности b=1.7:
μ(x)
= exp [ – (x–5)2
/ 2*1.72]
Косвенные
Используются
при решении задач, для которых свойства
физических величин не могут быть
измерены. Наибольшее распространение
среди косвенных методов получил метод
парных сравнений.
Метод
парных сравнений
Интенсивность
принадлежности определяют, исходя из
попарных сравнений рассматриваемых
элементов.
Для
каждой пары элементов универсального
множества эксперт оценивает преимущество
одного элемента над другим по отношению
к свойству нечеткого множества. Парные
сравнения удобно представлять следующей
матрицей:
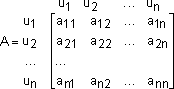
где
— уровень преимущество элемента над
(
),
определяемый по девятибальной шкале
Саати:
1
— если отсутствует преимущество элемента над
элементом ;
3
— если имеется слабое преимущество над
;
5
— если имеется существенное
преимущество над
;
7
— если имеется явное преимущество над
;
9
— если имеется абсолютное
преимущество над
;
2,
4, 6, 8 — промежуточные сравнительные
оценки.
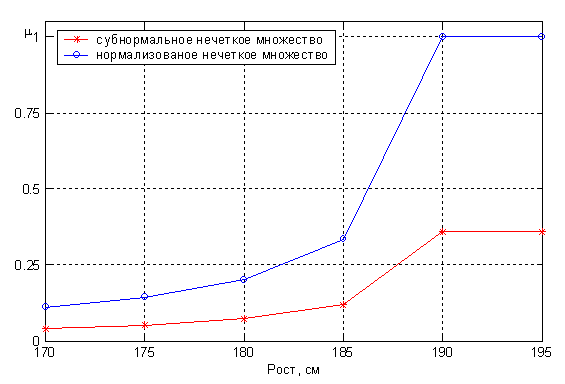
Пример. Построить
функцию принадлежности нечеткого
множества «высокий мужчина» на
универсальном множестве {170, 175, 180, 185,
190, 195}, если известны такие экспертные
парные сравнения:
-
абсолютное
преимущество 195 над 170; -
явное
преимущество 195 над 175; -
существенное
преимущество 195 над 180; -
слабое
преимущество 195 над 185; -
отсутствует
преимущество 195 над 190.
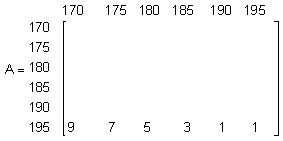
Приведенным
экспертным высказываниям соответствует
такая матрица парных сравнений:
При
согласованных мнениях эксперта матрица
парных сравнений обладает следующими
свойствами:
-
она
диагональная‚ т. е. aii=1
‚ i=1..n ; -
она
обратно симметрична‚ т. е. элементы‚
симметричные относительно главной
диагонали‚ связаны зависимостью
aij=1/aji ,
i,j=1..n ; -
она
транзитивна‚ т. е. aikakj=aij ,
i,j,k=1..n .
Наличие
этих свойств позволяет определить все
элементы матрицы парных сравнений:
После
определения всех элементов матрицы
парных сравнений, степени принадлежности
нечеткого множества вычисляются по
формуле:
|
|
Для
нормализации нечеткого множества
разделим все степени принадлежности
на максимальное значение, т.е. на 0.3588.
|
ui |
170 |
175 |
180 |
185 |
190 |
195 |
|
μ |
0.0399 |
0.0513 |
0.0718 |
0.1196 |
0.3588 |
0.3588 |
|
μ |
0.1111 |
0.1429 |
0.2000 |
0.3333 |
1.0000 |
1.0000 |
Соседние файлы в папке 41_fuzzy
- #
- #
- #
Введенное определение нечеткого множества (2.1) не накладывает ограничений на выбор функции принадлежности. Однако, на практике целесообразно использовать аналитическое представление функции принадлежности
μ
A
x
нечеткого множества A с элементами
x, нечетко обладающими определяющим множество свойством R. Типизация функций принадлежности в контексте решаемой технической задачи существенно упрощает соответствующие аналитические и численные расчеты при применении методов теории нечетких множеств. Выделяют следующие типовые функции принадлежности [32], [33].
Треугольные функции принадлежности, использующиеся для задания неопределенностей типа: «приблизительно равно», «среднее значение», «расположен в интервале», «подобен объекту», «похож на предмет» и т.п.:
- треугольная и трапецеидальная функции
- квадратичный и гармонический Z-сплайны
- Z-сигмоидальная и Z-линейная функции
- квадратичный и гармонический S-сплайны
- S-сигмоидальная и S-линейная функции
- колоколообразная и гауссова функции
trimf
x,a,b,c
=
0
,
x
≤
a
;
x
—
a
b
—
a
,
a
≤
x
≤
b
;
c
—
x
c
—
b
,
b
≤
x
≤
c
;
0
,
c
≤
x
;
trapmf
x,a,b,c,d
=
0
,
x
≤
a
;
x
—
a
b
—
a
,
a
≤
x
≤
b
;
1
,
b
≤
x
≤
c
;
d
—
x
d
—
c
,
c
≤
x
≤
d
;
0
,
d
≤
x
;
Z-образные функции принадлежности, использующиеся для задания неопределенностей типа: «малое количество», «небольшое значение», «незначительная величина», «низкий уровень» и т.п.:
zm
f
1
x,a,b
=
1
,
x
≤
a
;
1
—
2
x
—
a
b
—
a
2
,
a
<
x
≤
a
+
b
2
;
2
b
—
x
b
—
a
2
,
a
+
b
2
<
x
<
b
;
0
,
b
≤
x
;
zm
f
2
x,a,b
=
1
,
x
<
a
;
1
2
+
1
2
cos
x
—
a
b
—
a
;
a
≤
x
≤
b
;
0
,
x
>
b
;
sigmf
x,a,b
=
1
1 +
exp
—
a
x
—
b
,
a < 0;
zlinemf
x,c,d
=
1
,
—
∞
<
x
≤
c
;
d
—
x
b
—
c
,
c
<
x
≤
d
;
0
,
x
>
d
;
S-образные функции принадлежности, использующиеся для задания неопределенностей типа: «большое количество», «большое значение», «значительная величина», «высокий уровень» и т.п.:
sm
f
1
x,a,b
=
0
,
x
≤
a
;
2
x
—
a
b
—
a
2
,
a
<
x
≤
a
+
b
2
;
1
—
2
b
—
x
b
—
a
2
,
a
+
b
2
<
x
<
b
;
1
,
b
≤
x
;
sm
f
2
x,a,b
=
0
,
x
<
a;
1
2
+
1
2
cos
x
—
b
b
—
a
;
a
≤
x
≤
b
;
1
,
x > b;
sigmf
x,a,b
=
1
1 +
exp
—
a
x
—
b
,
a
>
0
;
slinemf
x,a,b
=
0
,
x
≤
a
;
x
—
a
b
—
a
,
a
<
x
≤
b
;
1
,
x
>
b
;
П-образные функции принадлежности, использующиеся для задания неопределенностей типа: «приблизительно в пределах от и до», «примерно равно», «около» и т.п.:
gbellmf
x,a,b,c
=
1
1
+
x
—
c
a
2b
;
gaussmf
x,σ,c
=
exp
—
x
—
c
2
2σ
2
Существует множество других функций принадлежности нечетких множеств, заданных как композиции вышеупомянутых базовых функций (двойная гауссова, двойная сигмоидальная и т.п.), либо как комбинации по участкам возрастания и убывания (сигмоидально-гауссова, сплайн-треугольная и т.п.).
Функция принадлежности
μ
A
x
– это некоторая не вероятностная субъективная мера нечеткости, определяемая в результате опроса экспертов о степени соответствия элемента x понятию, формализуемому нечетким множеством A . В отличие от вероятностной меры, которая является оценкой стохастической неопределенности, имеющей дело с неоднозначностью наступления некоторого события в различные моменты времени, нечеткая мера является численной оценкой лингвистической неопределенности, связанной с неоднозначностью и расплывчатостью категорий человеческого мышления. При построении функции принадлежности
μ
A
x
с каждым нечетким множеством A ассоциируется некоторое свойство, признак или атрибут R , который характеризует некоторую совокупность объектов X . Чем в большей степени конкретный объект
x ∈ X
обладает этим свойством R , тем более близко к соответствующее значение
μ
A
x
. Если элемент
x ∈ X
определенно обладает этим свойством R , то
μ
A
x
=
1
, если же
x ∈ X
определенно не обладает этим свойством R , то
μ
A
x
=
0
. Существуют прямые и косвенные методы построения функций принадлежности [18]—[20].
Прямые методы (наиболее известны методы относительных частот, параметрический, интервальный) целесообразно использовать для измеримых свойств, признаков и атрибутов, таких как скорость, время, температура, давление и т.п. При использовании прямых методов зачастую не требуется абсолютно точного поточечного задания
μ
A
x
. Как правило, бывает достаточно зафиксировать вид функции принадлежности и характерные точки, по которым дискретное представление функции принадлежности аппроксимируется непрерывным аналогом – наиболее подходящей типовой функцией принадлежности.
Косвенные методы (наиболее известен метод парных сравнений) используются в тех случаях, когда отсутствуют измеримые свойства объектов в рассматриваемой предметной области. В силу специфики рассматриваемых задач при построении нечетких систем автоматического управления, как правило, применяются прямые методы. В свою очередь, в зависимости от числа привлеченных к опросу экспертов как прямые, так и косвенные методы делятся на одиночные и групповые. Наиболее грубую оценку характеристических точек функции принадлежности можно получить путем опроса одного эксперта, который просто задает для каждого значения
x ∈ X
соответствующее значение
μ
A
x
.
Пример. Рассмотрим нечеткое множество A , соответствующее понятию «расход теплоносителя небольшой». Объект x – расход теплоносителя, X
0;
x
max
– множество физически возможных значений скорости изменения температуры. Эксперту предъявляются различные значения расхода теплоносителя x и задается вопрос: с какой степенью уверенности 0 ≤
μ
A
x
≤ 1 эксперт считает, что данный расход теплоносителя x небольшой. При
μ
A
x
=
0
– эксперт абсолютно уверен, что расход теплоносителя x небольшой. При
μ
A
x
=
1
– эксперт абсолютно уверен, что расход теплоносителя x нельзя классифицировать как небольшой.
Метод относительных частот. Пусть имеется m экспертов,
n
1
из которых на вопрос о принадлежности элемента
x ∈ X
нечеткому множеству A отвечают положительно. Другая часть экспертов
n
2
=
m
—
n
1
отвечает на этот вопрос отрицательно. Тогда принимается
μ
A
x
=
n
1
n
1
+
n
2
=
n
1
m
.
Пример. Рассмотрим нечеткое множество A , соответствующее понятию «скорость изменения температуры положительная средняя». Объект x – скорость изменения температуры, X
— x
max
;
x
max
– множество физически возможных значений скорости изменения температуры. Экспертам предъявляются различные значения скорости изменения температуры x и каждому из них задается вопрос: считает ли эксперт, что данная скорость изменения температуры x положительная средняя. Результаты опроса сведены в табл.2.1.
Табл.2.1
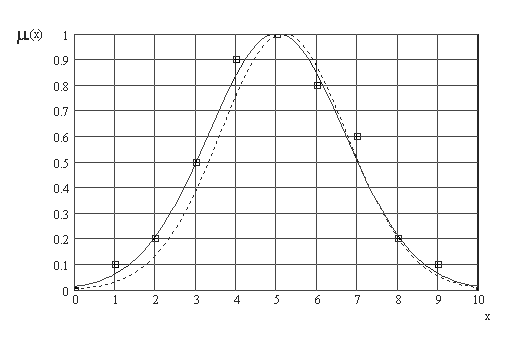
Для непрерывного представления нечеткой переменной используем какую нибудь из П-образных функций принадлежности, например, Гауссову. Из множества гауссовых функций
gaussmf
x,σ,c
=
exp
—
x — c
2
2 σ
2
через характерные точки функции принадлежности: точку перехода
μ
A
3= 0,5
и максимум
μ
A
5= 1
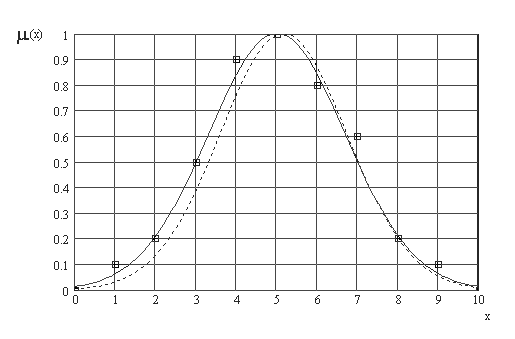
; проходит функция с параметрами σ = 1,7 , c = 5 . В качестве альтернативного метода перехода от дискретного ряда точек к непрерывному заданию функции принадлежности можно предложить поиск параметров Гауссовой функции принадлежности, максимально близко аппроксимирующей дискретный ряд по критерию СКО (рис.2.4).
Рис.2.4. Аппроксимация дискретного ряда () непрерывной Гауссовой функцией принадлежности ( – по характерным точкам, – – по СКО)
6.3. Методы построения функций принадлежности
Важным и трудным вопросом теории нечетких множеств является вопрос о методах построения функции принадлежности 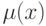
Фактически нечеткое множество — это множество упорядоченных пар вида <?(x/x>, где x принимает некоторое информативное значение, а ?(x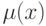

Один из методов построения функций принадлежности – методы экспертных оценок. Если имеются дискретные значения по ряду параметров, для представления можно использовать таблицы или матрицы.
Рассмотрим примеры построения нечетких множеств средствами программы MathCad.
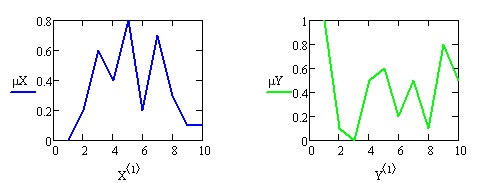
Пример 6.1. Построим нечеткие множества следующего вида: элементы множества ряд чисел 
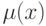
![[0,1]](https://intuit.ru/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png)
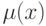
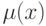


Рис.
6.2.
Нечеткие множества X и Y в виде матриц
Если параметры меняются непрерывно, функция принадлежности задается математической функцией. Существует ряд типовых форм кривых для задания функций принадлежности. Наибольшее распространение получили: треугольная, трапециевидная я и гауссова функции принадлежности.
Треугольная функция принадлежности
Определяется тройкой чисел 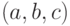
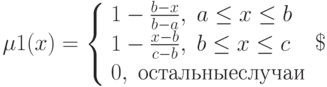
При 
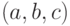
Трапециевидная функция принадлежности
Для задания необходима четверка чисел 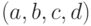
При 
Пример 6.2
Построим в MathCad нечеткие множества 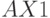
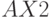

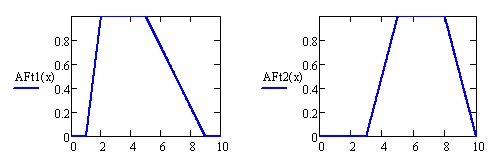
![xsubset [0,10]](https://intuit.ru/sites/default/files/tex_cache/704ea1c9762c8771b17fd99707805e37.png)
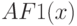



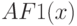
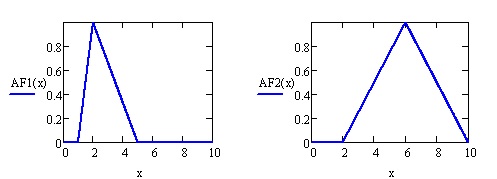
Пример 6.3
Построим в MathCad нечеткие множества 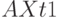
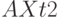

![xsubset [0,10]](https://intuit.ru/sites/default/files/tex_cache/704ea1c9762c8771b17fd99707805e37.png)
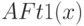


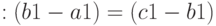
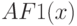
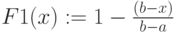

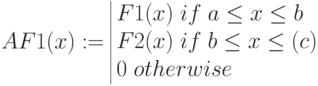
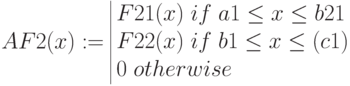
Рис.
6.3.
Треугольные функции принадлежности
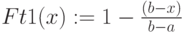
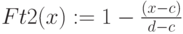
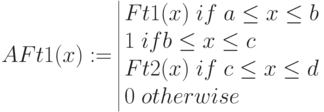
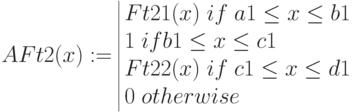
Рис.
6.4.
Трапециевидные функции принадлежности
6.4 Множества Α–уровня
Множеством 
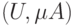


Множества 
Рассмотрим следующий пример. Пусть 
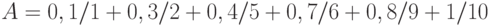
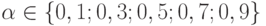


Построим множества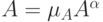
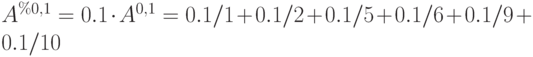
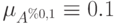
Аналогично
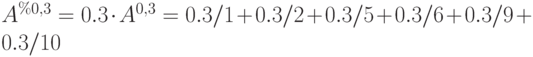
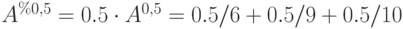

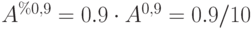
Составим нечеткое множество 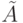
- объединим множества
:
- Из значений функции принадлежности, соединенных знаками логических сумм, выберем наибольшее (супремум) и будем считать его значением функции принадлежности нечеткого множества
на соответствующем элементе несущего множества:
.
В данном случае 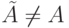
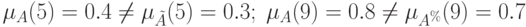



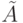
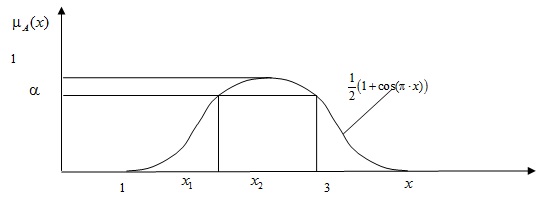
Рассмотрим нечеткое множество 
![xin [1,3]](https://intuit.ru/sites/default/files/tex_cache/2606370a91996b2a62c5a49afa43bdb3.png)
График показан на рис. 6.4. Множеством 
![[x_1, x_2]](https://intuit.ru/sites/default/files/tex_cache/5c5098079470feacb4129bd5592df89e.png)
Решением такого уравнения будут два числа: 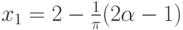
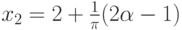
Следовательно, ![A^{%}=alphacdot [left(2-frac{1}{pi}arccos(2alpha-1)right)left(2+frac{1}{pi}arccos(2alpha-1)right)]](https://intuit.ru/sites/default/files/tex_cache/40d23f30a611549dc16f2c0d12f3bad8.png)
Разложение множества 
Ниже приведен график множества 
![A^{alpha}=[x_1,x_2]](https://intuit.ru/sites/default/files/tex_cache/d7db90a431e56309601be8b2bdd965f7.png)

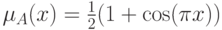
Рис.
6.5.
Множество альфа-уровня для нечеткого множества А с заданной функцией принадлежности
Разбив отрезок ![[0,1]](https://intuit.ru/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png)
Разобьем отрезок ![[0,1]](https://intuit.ru/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png)
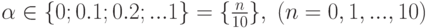

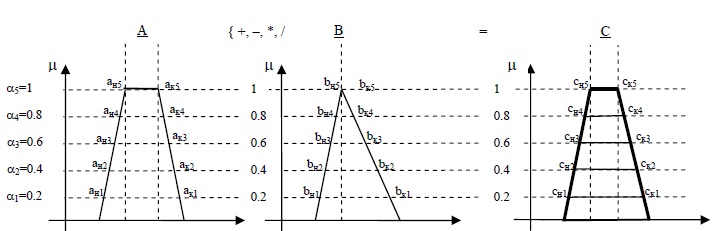
Операции над α-уровнями
Пусть 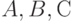
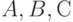

на уровне ![?_1 - [a_{н1}, a_{к1}], [b_{н1}, b_{к1}], [с_{н1}, с_{к1}]](https://intuit.ru/sites/default/files/tex_cache/863f2c5c3f3e0b71e48e03132145e08b.png)
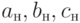
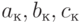
на уровне ![?_n – [a_{нn}, a_{кn}], [b_{нn}, b_{кn}], [с_{нn}, с_{кn}]](https://intuit.ru/sites/default/files/tex_cache/e11f074ea01123f7f60334db2d7223fa.png)
Рис.
6.6.
Множество альфа-ровней для нечетких множеств A,B,C
Арифметические операции над нечеткими множествами сводятся к операциям над интервалами соответствующего 
В основании всякой теории из любой области естествознания лежит очень важное, основополагающее для ее построения понятие элементарного объекта. Например, для механики – это материальная точка, для электродинамики – вектор напряженности поля. Для теории нечетких множеств основополагающим понятием является понятие нечеткого множества, которое характеризуется и определяется функцией принадлежности. Посредством нечетких множеств можно строго описывать присущие природе расплывчатые, не точно заданные объекты, без формализации которых нет надежды существенно продвинуться вперед в моделировании интеллектуальных процессов. Однако основной проблемой, затрудняющей интенсивное применение теории нечетких множеств при решении практических задач, является то, что функция принадлежности должна быть задана вне самой теории и, следовательно, ее адекватность не может быть проверена средствами теории. В каждом известном методе построения функции принадлежности формулируются свои требования и обоснования к выбору именно такого ее построения.
Л. Заде предложил оценивать степень принадлежности числами из отрезка . Фиксирование конкретных значений при этом носит субъективный характер. С одной стороны, для экспертных методов важным является характер измерений (первичные или производные) и тип шкалы, в которой получают информацию от эксперта и которая определяет допустимый вид операций, применяемых при экспертной оценке. С другой стороны, каждому объекту присущи два типа его свойств: те, которые можно непосредственно измерить, и те, которые являются качественными и требуют попарного сравнения объектов, обладающих оцениваемым свойством, чтобы определить их место по отношению к рассматриваемому понятию.
Существует ряд методов построения функции принадлежности нечеткого множества по экспертным оценкам, которые можно разделить на две группы: прямые и косвенные методы.
Прямые методы определяются тем, что эксперт или группа экспертов непосредственно задают правила определения значений функции принадлежности, характеризующей данное понятие. При этом, чем в большей степени элемент обладает рассматриваемым свойством, тем более близким к единице должно быть значение функции принадлежности. И наоборот, чем в меньшей степени элемент
обладает рассматриваемым свойством, тем ближе к нулю должно быть это значение. Если элемент
Определенно не обладает рассматриваемым свойством, то соответствующее значение функции принадлежности равно нулю. Если же элемент
Определенно Обладает рассматриваемым свойством, то это значение равно единице. Кроме того, значения функции принадлежности согласуются с экспертными предпочтениями на множестве объектов
следующим образом:
– для любых ,
тогда и только тогда, когда
предпочтительнее
, т. е. в большей степени обладает свойством
;
– для любых ,
тогда и только тогда, когда
и
в равной мере обладают свойством
.
Примеры прямых методов: непосредственное задание функции принадлежности таблицей, формулой, перечислением. Заде обосновывает назначение прямого метода следующим образом: «По своей природе оценка является приближением. Во многих случаях достаточна весьма приблизительная характеризация набора данных, поскольку в большинстве основных задач, решаемых человеком, не требуется высокая точность. Человеческий мозг использует допустимость такой неточности, кодируя информацию, достаточную для решения задачи, элементами нечетких множеств, которые приближенно описывают исходные данные. Поток информации, поступающий в мозг через органы зрения, слуха, осязания и др., суживается, таким образом, в тонкую струйку информации, необходимой для решения поставленной задачи с допустимой степенью точности».
Процесс построения или задания нечеткого множества на основе количественных значений измеряемого признака получил специальное название – Фаззификация, или приведение к нечеткости. Речь идет о том, что даже если исследователю бывает известно некоторое значение измеряемой величины, следует иметь в виду, что это значение известно неточно, возможно с погрешностью или случайной ошибкой. При этом, чем меньшей является уверенность в точности измерения признака, тем большим будет интервал носителя соответствующего нечеткого множества. Именно по этой причине фаззификация позволяет более адекватно представить объективно присутствующую неточность результатов физических измерений.
В Косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворять заранее сформулированным условиям. Экспертная информация формирует только исходные данные для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру обработки. Примерами дополнительных условий могут служить следующие: функция принадлежности должна отражать близость к заранее выделенному эталону; объекты множества являются точками в некотором параметрическом пространстве; результатом процедуры обработки должна быть функция принадлежности, удовлетворяющая условиям интервальной шкалы; при попарном сравнении объектов, если один объект по какой-то характеристике оценивается в
раз сильнее, чем другой, то второй объект обязательно оценивается в
раз сильнее, чем первый, и т. д.
Как правило, прямые методы используются для описания понятий, которые характеризуются измеримыми свойствами, такими, как высота, рост, вес, объем. В этом случае, в предположении, что в процессе измерений не делается случайных ошибок, удобно и естественно непосредственное задание значений степени принадлежности.
Однако реально ошибки всегда имеются. Кроме того, могут быть искажения, например, субъективная тенденция сдвигать количественные оценки объектов в направлении концов оценочной шкалы. Следовательно, прямые измерения, основанные на непосредственном определении функции принадлежности, могут использоваться только в том случае, когда такие ошибки незначительны или маловероятны.
Косвенные методы основаны на более пессимистических представлениях о людях как об «измерительных приборах». Рассмотрим, например, понятие «КРАСОТА», которое, в отличие от понятий «ДЛИНА» или «ВЫСОТА», является сложным и трудно формализуемым. Практически не существует универсальных элементарных измеримых свойств, через которые определяются подобные понятия. В таких случаях используются только ранговые измерения при попарном сравнении объектов. Косвенные методы более трудоемки, чем прямые, но их преимущество – в стойкости по отношению к искажениям в измерениях. Для косвенных методов обычно используется условие «безоговорочного экстремума»: при определении степени принадлежности множество исследуемых объектов должно содержать по крайней мере два объекта, численные представления которых на интервале принимают значения 0 и 1 соответственно.
Среди косвенных методов наибольшее применение получил так называемый метод попарных сравнений. Этот метод используется для конечных нечетких множеств и основан на естественном предположении, что непосредственное оценивание значений функции принадлежности в точках
,
затруднительно, однако попарное их сравнение в разных точках носителя проблем не вызывает. Пусть по результатам экспертного оценивания построена матрица
, каждый элемент которой оценивает величину отношения соответствующих неизвестных значений функции принадлежности, то есть

. (1.28)
Поставим задачу отыскания неизвестного набора значений,
.
Из соотношения (1.28) имеем

,
, (1.29)
И, кроме того,

. (1.30)
Из (1.29)–(1.30) следует, что матрица , составленная по правилу (1.28), является обратносимметричной и обладает транзитивностью. Такую матрицу будем называть согласованной.
Далее, из (1.28) получим 
,
Откуда, суммируя слева и справа по , имеем

То есть

. (1.31)
Совокупность соотношений (1.31) представляет собой систему линейных алгебраических уравнений относительно неизвестных значений функции принадлежности в точках ,
. Эта система в матричной форме имеет вид
, (1.32)
Где .
Отсюда следует, что для обратносимметричной согласованной матрицы имеется собственное число, равное
, и соответствующий этому числу положительный собственный вектор
, компонентами которого является искомый набор значений функции принадлежности. Таким образом, полученное соотношение устанавливает связь между матрицей попарных сравнений значений функции принадлежности и самими этими значениями. Понятно, что если задана матрица
, то неизвестный вектор
может быть получен путем расчета с использованием (1.32) собственного вектора этой матрицы, соответствующего собственному числу, равному
. Этот результат лежит в основе предложенного Т. Саати [22] метода анализа иерархий. Вместе с тем, как легко показать [21], искомый вектор
может быть получен и гораздо более простым способом. В целях упрощения записи введем следующие обозначения:
,
,
.
Тогда в соответствии с (1.28) матрица имеет вид

Вычислим суммы элементов для каждой из строк матрицы . Для произвольной
-й строки имеем

. (1.33)
Из соотношения (1.33) следует, что каждый компонент собственного вектора с точностью до константы может быть рассчитан непосредственно по элементам матрицы
. Константу
определим исходя из естественного требования к нормировке вектора
, в соответствии с которым введем условие

Просуммируем левую и правую части соотношения (1.33) по . При этом с учетом (1.34) получим

Тогда

. (1.35)
Таким образом, соотношение (1.35) позволяет рассчитать значения функции принадлежности, соответствующие каждому из элементов носителя. При этом понятно, что нечеткое множество, описываемое полученной функцией принадлежности, не является нормальным. Приведение множества к нормальному осуществляется стандартным образом по формуле

Отметим, что соотношение (1.35) позволит точно оценить значения компонентов функции принадлежности только в случае, если матрица является обратносимметричной и согласованной. Однако на практике эта матрица, содержащая результаты попарных сравнений значений функции принадлежности, формируемых экспертами, является обратносимметричной, но не удовлетворяет (1.30). В связи с этим вектор, определяемый в соответствии с (1.35), оценивает компоненты этой функции с погрешностью тем большей, чем сильнее реальная матрица
отличает-
Ся от требуемой.
Легко проверить, что получаемый в соответствии с (1.35) вектор является собственным вектором матрицы
, соответствующим собственному числу, равному
. Действительно, вычислим:
Что и требовалось.
Рассмотрим процедуру [21] коррекции реальной матрицы, приближающую эту матрицу к согласованной.
Используя реальную матрицу , введем матрицу
,
То есть

Убедимся в том, что диагональные элементы этой матрицы равны единице. Действительно,

.
Теперь, продолжая процедуру, вычислим

(1.37)
Получаемая при этом матрица будет более согласованной, нежели исходная. Продолжим операцию корректировки. При этом фактическая вычислительная процедура на каждой итерации коррекции может быть упрощена за счет объединения соотношений (1.36), (1.37).
При этом

Пусть проделано итераций коррекции, в результате которых получена матрица
. Тогда на очередной
-й итерации выполняются следующие вычисления:

,
(1.38)
Соотношения (1.38) позволяют рассчитать элементы матрицы непосредственно через элементы матрицы
. Сходимость предложенной процедуры проверена экспериментально.
Полученная в результате коррекции согласованная матрица попарных сравнений используется далее для расчета в соответствии с (1.35) искомых значений функции принадлежности.
Пример 1.8. Зададим нечеткое множество ,
Пусть по результатам экспертного оценивания получена матрица

Матрица представляет собой матрицу попарных сравнений значений функции принадлежности.
Эта матрица обратносимметрична, но не транзитивна. Например,. Действительно,
.
В связи с этим непосредственное использование матрицы для оценивания значений функции принадлежности невозможно.
Проведем процедуру коррекции.
Первая итерация
В соответствии с (1.38) вычислим:

Эта матрица существенно более согласована, нежели исходная. В самом деле, для той же тройки элементов имеем
.
Выполним еще одну итерацию коррекции, в результате которой получим

Эта матрица практически согласована. В частности, .
Процедура коррекции завершена. Теперь, используя полученную матрицу, в соответствии с (1.35) рассчитаем значения функции принадлежности в точках . При этом
Далее, после нормализации окончательно имеем описание нечеткого множества
Контрольные вопросы
1. Что такое нечеткое множество и каковы основные способы его задания?
2. Каковы основные характеристики нечетких множеств?
3. Проведите сравнительный анализ основных форм задания функций принадлежности.
4. В каких случаях для построения функций принадлежности используются прямые и косвенные методы?
5. В чем положительные особенности прямых и косвенных методов?
| < Предыдущая | Следующая > |
|---|

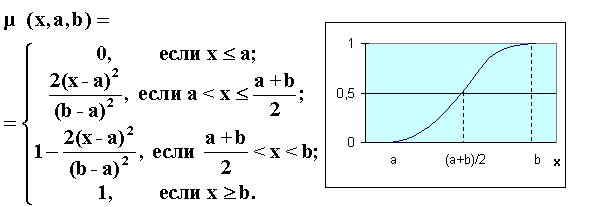


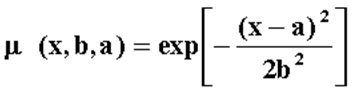


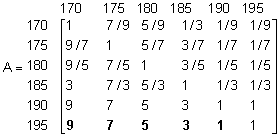



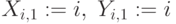
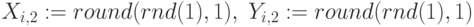
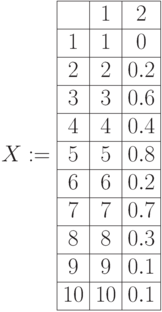
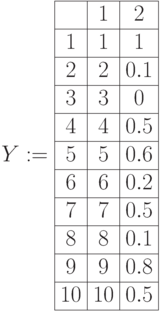
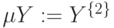
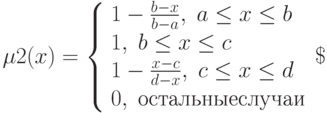



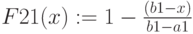
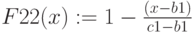
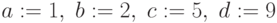
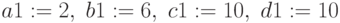


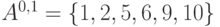

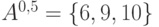
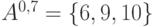

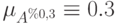
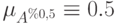
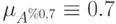
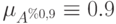
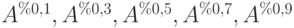 :
: 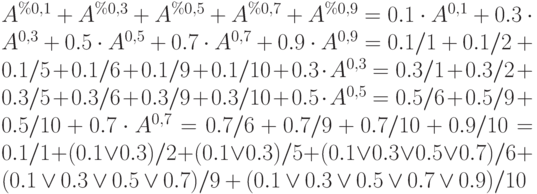
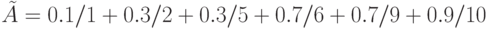 .
. ![mu_A(x)=frac{1}{2}(1+cos(pi x))=alpha,; xin [1,3]](https://intuit.ru/sites/default/files/tex_cache/eda89ac6993f9336a3657d0d6470d449.png)
![A=int_{0}^{1}alpha [left(2-frac{1}{pi}arccos(2alpha-1)right),left(2+frac{1}{pi}arccos(2alpha-1)right)]](https://intuit.ru/sites/default/files/tex_cache/fa560ab6144b9894728009df516b626a.png)
![Aapprox sum_{n=0}^{10}frac{n}{10}[left(2-frac{1}{pi}arccosleft(frac{n-5}{5}right)right),left(2+frac{1}{pi}arccosleft(frac{n-5}{5}rightright)]](https://intuit.ru/sites/default/files/tex_cache/b4c11cf45d338b3271d845db360765d5.png)