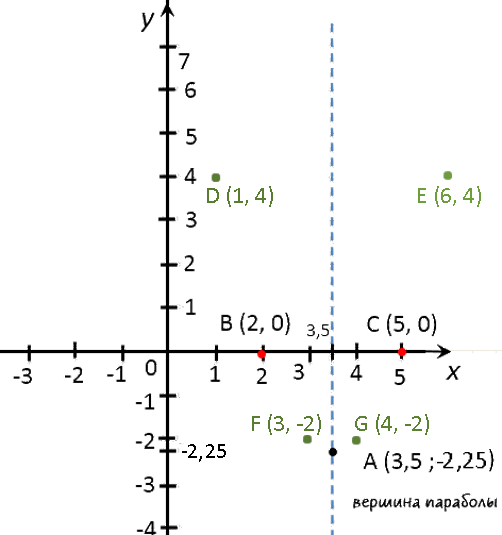Как составить график квадратного уравнения - Исправление недочетов и поиск решений вместе с Examum.ru

Download Article

When graphed, quadratic equations of the form ax² + bx + c or a(x — h)² + k give a smooth U-shaped or a reverse U-shaped curve called a parabola.^[1]Graphing a quadratic equation is a matter of finding its vertex, direction, and, often, its x and y intercepts. In the cases of relatively simple quadratic equations, it may also be enough to plug in a range of x values and plot a curve based on the resulting points. See Step 1 below to get started.

Steps

1
Determine which form of quadratic equation you have. The quadratic equation can be written in three different forms: the standard form, vertex form, and the quadratic form. You can use either form to graph a quadratic equation; the process for graphing each is slightly different. If you’re doing a homework problem, you’ll usually receive the problem in one of these two forms — in other words, you won’t be able to choose, so it’s best to understand both. The two forms of quadratic equation are:^[2]
- Standard form.^[3] In this form, the quadratic equation is written as: f(x) = ax² + bx + c where a, b, and c are real numbers and a is not equal to zero.
  - For example, two standard form quadratic equations are f(x) = x² + 2x + 1 and f(x) = 9x² + 10x -8.
- Vertex form.^[4] In this form, the quadratic equation is written as: f(x) = a(x — h)² + k where a, h, and k are real numbers and a does not equal zero. Vertex form is so named because h and k directly give you the vertex (central point) of your parabola at the point (h,k).
  - Two vertex form equations are f(x) = 9(x — 4)² + 18 and -3(x — 5)² + 1
- To graph either of these types of equations, we need to first find the vertex of the parabola, which is the central point (h,k) at the «tip» of the curve. The coordinates of the vertex in standard form are given by: h = -b/2a and k = f(h), while in vertex form, h and k are specified in the equation.
2
Define your variables. To be able to solve a quadratic problem, the variables a, b, and c (or a, h, and k) usually need to be defined. An average algebra problem will give you a quadratic equation with the variables filled in, usually in standard form, but sometimes in vertex form.^[5]
- For example, for the standard form equation f(x) = 2x² +16x + 39, we have a = 2, b = 16, and c = 39.
- For the vertex form equation f(x) = 4(x — 5)² + 12, we have a = 4, h = 5, and k = 12.^[6]
Advertisement
3
Calculate h. In vertex form equations, your value for h is already given, but in standard form equations, it must be calculated. Remember that, for standard form equations, h = -b/2a.^[7]
- In our standard form example (f(x) = 2x² +16x + 39), h = -b/2a = -16/2(2). Solving, we find that h = -4.
- In our vertex form example (f(x) = 4(x — 5)² + 12), we know h = 5 without doing any math.
4
Calculate k. As with h, k is already known in vertex form equations. For standard form equations, remember that k = f(h). In other words, you can find k by replacing every instance of x in your equation with the value you just found for h.^[8]
- We have determined in our standard form example that h = -4. To find k, we solve our equation with our value for h replacing x:
  - k = 2(-4)² + 16(-4) + 39.
  - k = 2(16) — 64 + 39.
  - k = 32 — 64 + 39 = 7
- In our vertex form example, again, we know the value of k (which is 12) without having to do any math.
5
Plot your vertex. The vertex of your parabola will be the point (h, k) — h specifies the x coordinate, while k specifies the y coordinate. The vertex is the central point in your parabola — either the very bottom of a «U» or the very top of an upside-down «U.» Knowing the vertex is an essential part of graphing an accurate parabola — often, in schoolwork, specifying the vertex will be a required part of a question.^[9]
- In our standard form example, our vertex will be at (-4,7). So, our parabola will peak 4 spaces to the left of 0 and 7 spaces above (0,0). We should plot this point on our graph, being sure to label coordinates.
- In our vertex form example, our vertex is at (5,12). We should plot a point 5 spaces to the right and 12 spaces above (0,0).
6
Draw the parabola’s axis (optional). A parabola’s axis of symmetry is the line running through its middle which divides it perfectly in half. Across this axis, the left side of the parabola will mirror the right side. For quadratics of the form ax² + bx + c or a(x — h)² + k, the axis is a line parallel to the y-axis (in other words, perfectly vertical) and passing through the vertex.
- In the case of our standard form example, the axis is a line parallel to the y-axis and passing through the point (-4, 7). Though it’s not part of the parabola itself, lightly marking this line on your graph can eventually help you see how the parabola curves symmetrically.
7
Find the direction of opening. After having figured out the vertex and axis of the parabola, we next need to know whether the parabola opens upwards or downwards. Luckily, this is easy. If «a» is positive, the parabola will open upwards, while if «a» is negative, the parabola will open downwards (i.e., it will be turned upside-down.)^[10]
- For our standard form example (f(x) = 2x² +16x + 39), we know we have a parabola opening upwards because, in our equation, a = 2 (positive).
- For our vertex form example (f(x) = 4(x — 5)² + 12), we know we have also have a parabola opening upwards because a = 4 (positive).
8
If necessary, find and plot x intercepts.^[11] Often, on schoolwork, you’ll be asked to find a parabola’s x-intercepts (which are either one or two points where the parabola meets the x axis). Even if you’re not to find them, these two points can be invaluable for drawing an accurate parabola. However, not all parabolas have x-intercepts. If your parabola has a vertex opens upward and has a vertex above the x axis or if it opens downward and has a vertex below the x axis, it won’t have any x intercepts. Otherwise, solve for your x intercepts with one of the following methods:
- Simply set f(x) = 0 and solve the equation. This method may work for simple quadratic equations, especially in vertex form, but will prove exceedingly difficult for more complicated ones. See below for an example
  - f(x) = 4(x — 12)² — 4
  - 0 = 4(x — 12)² — 4
  - 4 = 4(x — 12)²
  - 1 = (x — 12)²
  - SqRt(1) = (x — 12)
  - +/- 1 = x -12. x = 11 and 13 are the parabola’s x-intercepts.
- Factor your equation. Some equations in the ax² + bx + c form can be easily factored into the form (dx + e)(fx +g), where dx × fx = ax², (dx × g + fx × e) = bx, and e × g = c. In this case, your x intercepts are the values for x which make either term in parentheses = 0. For example:
  - x² + 2x + 1
  - = (x + 1)(x + 1)
  - In this case, your only x intercept is -1 because setting x equal to -1 will make either of the factored terms in parentheses equal 0.
- Use the quadratic formula.^[12] If you can’t easily solve for your x intercepts or factor your equation, use a special equation called the quadratic formula designed for this very purpose. If it isn’t already, get your equation into the form ax² + bx + c, then plug a, b, and c into the formula x = (-b +/- SqRt(b² — 4ac))/2a.^[13] Note that this often gives you two answers for x, which is OK — this just means your parabola has two x intercepts. See below for an example:
  - -5x² + 1x + 10 gets plugged into the quadratic formula as follows:
  - x = (-1 +/- SqRt(1² — 4(-5)(10)))/2(-5)
  - x = (-1 +/- SqRt(1 + 200))/-10
  - x = (-1 +/- SqRt(201))/-10
  - x = (-1 +/- 14.18)/-10
  - x = (13.18/-10) and (-15.18/-10). The parabola’s x intercepts are at approximately x = -1.318 and 1.518
  - Our previous standard form example, 2x² + 16x + 39 gets plugged into the quadratic formula as follows:
  - x = (-16 +/- SqRt(16² — 4(2)(39)))/2(2)
  - x = (-16 +/- SqRt(256 — 312))/4
  - x = (-16 +/- SqRt(-56)/-10
  - Because finding the square root of a negative number is impossible, we know that no x intercepts exist for this particular parabola.
9
If necessary, find and plot the y intercept.^[14] Though it’s often not necessary to find an equation’s y intercept (the point at which the parabola passes through the y axis), you may eventually be required to, especially if you’re in school. This process is fairly easy — just set x = 0, then solve your equation for f(x) or y, which gives you the y value at which your parabola passes through the y axis. Unlike x intercepts, standard parabolas can only have one y intercept. Note — for standard form equations, the y intercept is at y = c.
- For example, we know our quadratic equation 2x² + 16x + 39 has a y intercept at y = 39, but it can also be found as follows:
  - f(x) = 2x² + 16x + 39
  - f(x) = 2(0)² + 16(0) + 39
  - f(x) = 39. The parabola’s y intercept is at y = 39. As noted above, the y intercept is at y = c.
- Our vertex form equation 4(x — 5)² + 12 has a y intercept that can be found as follows:
  - f(x) = 4(x — 5)² + 12
  - f(x) = 4(0 — 5)² + 12
  - f(x) = 4(-5)² + 12
  - f(x) = 4(25) + 12
  - f(x) = 112. The parabola’s y intercept is at y = 112.
10
If necessary, plot additional points, then graph. You should now have a vertex, direction, x intercept(s), and, possibly, a y intercept for your equation. At this point, you can either attempt to draw your parabola using the points you have as a guideline, or you can find more points to «fill out» your parabola so that the curve you draw is more accurate. The easiest way to do this is simply to plug in a few x values on either side of your vertex, then plot these points using the y values you obtain. Often, teachers will require you to obtain a certain number of points before you draw your parabola.^[15]
- Let’s revisit the equation x² + 2x + 1. We already know its only x intercept is at x = -1. Because it only touches the x intercept at one point, we can infer that its vertex is its x intercept, which means its vertex is (-1,0). We effectively only have one point for this parabola — not nearly enough to draw a good parabola. Let’s find a few more to ensure we draw an accurate graph.
  - Let’s find the y values for the following x values: 0, 1, -2, and -3.
  - For 0: f(x) = (0)² + 2(0) + 1 = 1. Our point is (0,1).
  - For 1: f(x) = (1)² + 2(1) + 1 = 4. Our point is (1,4).
  - For -2: f(x) = (-2)² + 2(-2) + 1 = 1. Our point is (-2,1).
  - For -3: f(x) = (-3)² + 2(-3) + 1 = 4. Our point is (-3,4).
  - Plot these points to the graph and draw your U-shaped curve. Note that the parabola is perfectly symmetrical — when your points on one side of the parabola lie on whole numbers, you can usually save yourself some work by simply reflecting a given point across the parabola’s axis of symmetry to find the corresponding point on the other side of the parabola.

Add New Question

Question

How can you tell if a parabola will have a maximum or a minimum?

Jake Adams

Academic Tutor & Test Prep Specialist

Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.

Academic Tutor & Test Prep Specialist

Expert Answer
Question

On my homework, I got x^2-x-2 and I graphed it, so how do I find the axis of symmetry?

Did you find the vertex when graphing it? If so, the axis of symmetry is the vertical line running through the vertex. To check your answer, it should have the equation x = 1/2.
Question

How do I solve a system of equations algebraically?

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Note that in f(x) = ax² + bx + c, if b or c equal zero, those numbers disappear. For example, 12x² + 0x + 6 becomes 12x² + 6 because 0x is 0.
Round numbers or use fractions as your algebra teacher tells you to. This will help you graph your quadratic equations properly.

References

About This Article

Article SummaryX

To graph a quadratic equation, start by solving for h in vertex form, or taking -b divided by 2 times a in standard form. Then, define or calculate the value of k and plot the point (h, k), which is the vertex of your parabola. In the equation, determine whether a is positive, which means the parabola will open upwards, or negative, which means it will open downwards. To find the x-intercepts, set the function of x equal to 0 which can help you graph the parabola. For tips on finding the y-intercept and other points on the line, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 500,123 times.

Reader Success Stories

«This helped a lot. Thanks! I needed this to further understand and expand my knowledge on quadratic equations and…» more

Did this article help you?

Источник

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции y=x^2 имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции y=x^2 , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент a=1 , то график квадратичной функции имеет ровно такую же форму, как график функции y=x^2 при любых значениях остальных коэффициентов.

График функции y=-x^2 имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции y=-x^2 симметричен графику функции y=x^2 относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если D<0 ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если a>0 ,то график функции выглядит как-то так:

2. Если D=0 ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если a>0 ,то график функции выглядит примерно так:

3. Если D>0 ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

$x_1={-b+sqrt{D}}/{2a}$ , $x_2={-b-sqrt{D}}/{2a}$

Если a>0 ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

$x_0=-{b/{2a}}$

$y_0=-{D/{4a}}=y(x_0)$

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как a=2>0 ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

$x_1={-3+7}/4=1$ , $x_1={-3-7}/4=-2,5$

3. Координаты вершины параболы:

$x_0=-{b/{2a}}=-3/4 =-0,75$

$y_0=-{D/{4a}}=-49/8=-6,125$

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

$x_0=-{b/{2a}}=-3/4 =-0,75$

$y_0=-{D/{4a}}=-49/8=-6,125$

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2. Уравнение квадратичной функции имеет вид — в этом уравнении x_0;y_0 — координаты вершины параболы

или в уравнении квадратичной функции a=1 , и второй коэффициент — четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

сначала построить график функции ,
затем одинаты всех точек графика умножить на 2,
затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции a=1 , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

2. Координаты вершины параболы: $x_0={x_1+x_2}/2={2-1}/2=1/2$

$y_0=y(-1)=({1/2}-2)({1/2}+1)=-9/4=-2,25$

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,

— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

Скачать таблицу квадратичная функция

И.В. Фельдман, репетитор по математике.

Источник

Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.

Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.

Что называют квадратичной функцией

Запомните!

Квадратичная функция — это функция вида

y = ax² + bx + c,

где a,
b и с — заданные числа.

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».

Квадратичная функция	Коэффициенты
y = 2x² − 7x + 9	a = 2 b = −7 с = 9
y = 3x² − 1	a = 3 b = 0 с = −1
y = −3x² + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

Запомните!

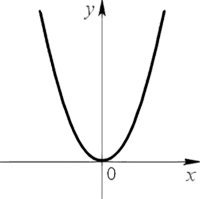
График квадратичной функции называют параболой.

Парабола выглядит следующим образом.

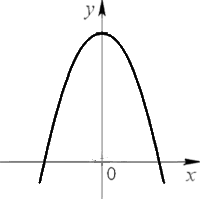
Также парабола может быть перевернутой.

Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции «y = x² −7x + 10».

Направление ветвей параболы

Запомните!

Если «a > 0», то ветви направлены вверх.

Если «a < 0», то ветви направлены вниз.

В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
Координаты вершины параболы

Запомните!

Чтобы найти «x₀»
(координата вершины по оси «Ox»)
нужно использовать формулу:

Найдем «x₀» для нашей функции «y = x² −7x + 10».

Теперь нам нужно найти «y₀»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x₀» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».

y₀(3,5) =
(3,5)² − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =

−12,25 + 10 = −2,25

Выпишем полученные координаты вершины параболы.

(·) A (3,5; −2,25) — вершина параболы.

Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy».

Нули функции

Для начала давайте разберемся, что называют нулями функции.

Запомните!

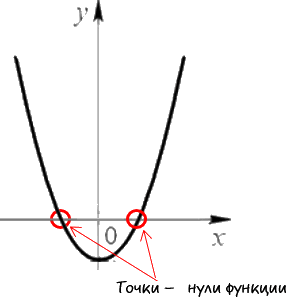
Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).

Наглядно нули функции на графике выглядят так:

Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.

Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.

Запомните!

Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».

Подставим в заданную функцию «y = x² −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .

0 = x² −7x + 10
x² −7x + 10 = 0

x_1;2 =

7 ±
√49 − 4 · 1 · 10

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 5	x₂ = 2

Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.

(·) B (5; 0)
(·) C (2; 0)

Отметим полученные точки («нули функции») на системе координат.

Дополнительные точки для построения графика

Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.

x	1	3	4	6
y

Для каждого выбранного значения «x»
рассчитаем «y».

y(1) = 1² − 7 · 1 + 10 = 1 − 7 + 10 =
4
y(3) = 3² − 7 · 3 + 10 = 9 − 21 + 10 =
−2
y(4) = 4² − 7 · 4 + 10 = 16 − 28 + 10 =
−2
y(6) = 6² − 7 · 6 + 10 = 36 − 42 + 10 =
4

Запишем полученные результаты в таблицу.

x	1	3	4	6
y	4	−2	−2	4

Отметим полученные точки графика на системе координат (зеленые точки).

Теперь мы готовы построить график.
На забудьте после построения подписать график функции.

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.

Пусть требуется построить график функции
«y = −3x² − 6x − 4».

Направление ветвей параболы

«a = −3» — ветви параболы направлены вниз.

Координаты вершины параболы

x₀ =
x₀ = =

= −1

y₀(−1) = (−3) · (−1)² − 6 · (−1) − 4 =
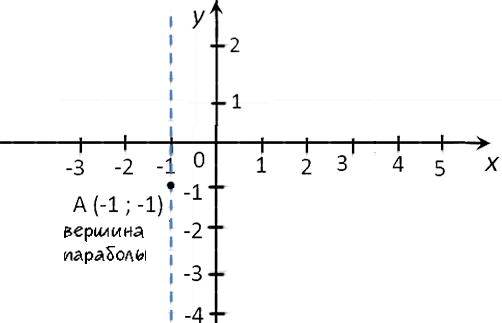
−3 · 1 + 6 − 4 = −1

(·) A (−1; −1)

— вершина параболы.
Нули функции
Точки пересечения с осью «Ox» (y = 0).

0 = −3x² − 6x − 4

−3x² − 6x − 4 = 0 |·(−1)

3x² + 6x + 4 = 0

x_1;2 =

−6 ±
√6² − 4 · 3 · 4

2 · 1

x_1;2 =

x_1;2 =

Ответ: нет действительных корней.

Так как корней нет, значит, график функции не пересекает ось
«Ox».

Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x² − 6x − 4».

y(−3) = −3 · (−3)² − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13

y(−2) = −3 · (−2)² − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4

y(0) = −3 · 0² − 6 · 0 − 4
= −4

y(1) = −3 · 1² − 6 · 1 − 4
= −3 −6 − 4 = −13

x	−3	−2	0	1
y	−13	−4	−4	−13

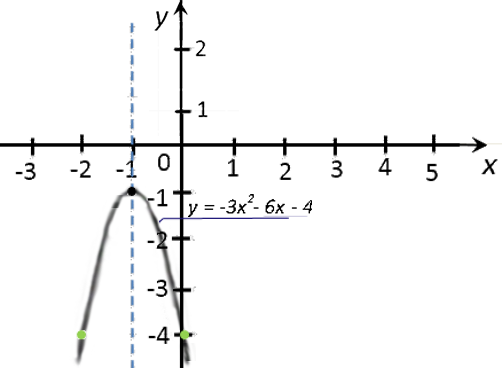
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Загрузить PDF

График квадратного уравнения вида ax² + bx + c или a(x — h)² + k представляет собой параболу (U-образную кривую). Для построения графика такого уравнения необходимо найти вершину параболы, ее направление и точки пересечения с осями Х и Y. Если вам дано относительно простое квадратное уравнение, то вы можете подставить в него разные значения «х», найти соответствующие значения «у» и построить график.

Шаги

1
Квадратное уравнение может быть записано в стандартном виде и в нестандартном виде. Вы можете использовать любой вид уравнения для построения графика квадратного уравнения (способ построения немного отличается). Как правило, в задачах квадратные уравнения приводятся в стандартном виде, но эта статья расскажет вам об обоих видах записи квадратного уравнения.
- Стандартный вид: f(x) = ax² + bx + c, где a, b, c — действительные числа и а ≠ 0.
  - Например, два уравнения стандартного вида: f(x) = x² + 2x + 1 и f(x) = 9x² + 10x -8.
- Нестандартный вид: f(x) = a(x — h)² + k, где a, h, k — действительные числа и а ≠ 0.
  - Например, два уравнения нестандартного вида: f(x) = 9(x — 4)² + 18 и -3(x — 5)² + 1.
- Для построения графика квадратного уравнения любого вида сначала нужно найти вершину параболы, которая имеет координаты (h, k). Координаты вершины параболы в уравнениях стандартного вида вычисляются по формулам: h = -b/2a и k = f(h); координаты вершины параболы в уравнениях нестандартного вида можно получить непосредственно из уравнений.
2
Для построения графика необходимо найти численные значения коэффициентов a, b, c (или a, h, k). В большинстве задач квадратные уравнения даются с численными значениями коэффициентов.
- Например, в стандартном уравнении f(x) = 2x² +16x + 39 a = 2, b = 16, c = 39.
- Например, в нестандартном уравнении f(x) = 4(x — 5)² + 12, a = 4, h = 5, k = 12.
3
Вычислите h в стандартном уравнении (в нестандартном оно уже дано) по формуле: h = -b/2a.
- В нашем примере стандартного уравнения f(x) = 2x² +16x + 39 h = -b/2a = -16/2(2) = -4.
- В нашем примере нестандартного уравнения f(x) = 4(x — 5)² + 12 h = 5.
4
Вычислите k в стандартном уравнении (в нестандартном оно уже дано). Помните, что k = f(h), то есть вы можете найти k, подставив в исходное уравнение найденное значение h вместо «х».
- Вы нашли, что h = -4 (для стандартного уравнения). Для вычисления k подставьте это значение вместо «х»:
  - k = 2(-4)² + 16(-4) + 39.
  - k = 2(16) — 64 + 39.
  - k = 32 — 64 + 39 = 7
- В нестандартном уравнении k = 12.
5
Нанесите вершину с координатами (h, k) на координатной плоскости. h откладывается по оси X, а k – по оси Y. Вершина параболы является либо самой нижней точкой (если парабола направлена вверх), либо самой верхней точкой (если парабола направлена вниз).
- В нашем примере стандартного уравнения вершина имеет координаты (-4, 7). Нанесите эту точку на координатной плоскости.
- В нашем примере нестандартного уравнения вершина имеет координаты (5, 12). Нанесите эту точку на координатной плоскости.
6
Проведите ось симметрии параболы (не обязательно). Ось симметрии проходит через вершину параболы параллельно оси Y (то есть строго вертикально). Ось симметрии делит параболу пополам (то есть парабола зеркально симметрична относительно этой оси).
- В нашем примере стандартного уравнения ось симметрии является прямой, параллельной оси Y и проходящей через точку (-4, 7). Хотя эта прямая и не является частью самой параболы, она дает представление о симметричности параболы.
7
Определите направление параболы — вверх или вниз. Это очень легко сделать. Если коэффициент «а» положительный, то парабола направлена вверх, а если коэффициент «а» отрицательный, то парабола направлена вниз.
- В нашем примере стандартного уравнения f(x) = 2x² +16x + 39 парабола направлена вверх, так как а = 2 (положительный коэффициент).
- В нашем примере нестандартного уравнения f(x) = 4(x — 5)² + 12 парабола также направлена вверх, так как а = 4 (положительный коэффициент).
8
Если нужно, найдите и нанесите точки пересечения с осью Х. Эти точки очень помогут вам при построении параболы. Их может быть две, одна или ни одной (если парабола направлена вверх, а ее вершина лежит выше оси Х, или если парабола направлена вниз, а ее вершина лежит ниже оси Х). Для вычисления координат точек пересечения с осью Х выполните следующие действия:
- Приравняйте уравнение к нулю: f(х) = 0 и решите его. Этот метод работает с простыми квадратными уравнениями (особенно нестандартного вида), но может оказаться чрезвычайно трудным в случае сложных уравнений. В нашем примере:
  - f(x) = 4(x — 12)² — 4
  - 0 = 4(x — 12)² — 4
  - 4 = 4(x — 12)²
  - 1 = (x — 12)²
  - √1 = (x — 12)
  - +/-1 = x -12. Точки пересечения параболы с осью Х имеют координаты (11,0) и (13,0).
- Разложите квадратное уравнение стандартного вида на множители: ax² + bx + c = (dx + e)(fx +g), где dx × fx = ax², (dx × g + fx × e) = bx, e × g = c. Затем приравняйте каждый двучлен к 0 и найдите значения «х». Например:
  - x² + 2x + 1
  - = (x + 1)(x + 1)
  - В этом случае существует единственная точка пересечения параболы с осью Х с координатами (-1,0), потому что при х + 1= 0 х = -1.
- Если вы не можете разложить уравнение на множители, решите его при помощи формулы для вычисления корней квадратного уравнения: x = (-b +/- √(b² — 4ac))/2a.
  - Например: -5x² + 1x + 10.
  - x = (-1 +/- √(1² — 4(-5)(10)))/2(-5)
  - x = (-1 +/- √ (1 + 200))/-10
  - x = (-1 +/- √ (201))/-10
  - x = (-1 +/- 14,18)/-10
  - x = (13,18/-10) и (-15,18/-10). Точки пересечения параболы с осью Х имеют координаты (-1,318,0) и (1,518,0).
  - В нашем примере уравнения стандартного вида 2x² + 16x + 39:
  - x = (-16 +/- √(16² — 4(2)(39)))/2(2)
  - x = (-16 +/- √(256 — 312))/4
  - x = (-16 +/- √(-56)/-10
  - Так как извлечь квадратный корень из отрицательного числа нельзя, то в этом случае парабола не пересекает ось Х.
9
Если нужно, найдите и нанесите точки пересечения с осью Y. Это очень легко – подставьте х = 0 в исходное уравнение и найдите значение «у». Точка пересечения с осью Y всегда одна. Примечание: в уравнениях стандартного вида точка пересечения имеет координаты (0,с).
- Например, парабола квадратного уравнения 2x² + 16x + 39 пересекается с осью Y в точке с координатами (0, 39), так как с = 39. Но это можно и вычислить:
  - f(x) = 2x² + 16x + 39
  - f(x) = 2(0)² + 16(0) + 39
  - f(x) = 39, то есть парабола данного квадратного уравнения пересекается с осью Y в точке с координатами (0, 39).
- В нашем примере уравнения нестандартного вида 4(x — 5)² + 12 точка пересечения с осью Y вычисляется следующим образом:
  - f(x) = 4(x — 5)² + 12
  - f(x) = 4(0 — 5)² + 12
  - f(x) = 4(-5)² + 12
  - f(x) = 4(25) + 12
  - f(x) = 112, то есть парабола данного квадратного уравнения пересекается с осью Y в точке с координатами (0, 112).
10
Вы нашли (и нанесли) вершину параболы, ее направление и точки пересечения с осями Х и Y. Вы можете построить параболы по этим точкам или найти и нанести дополнительные точки и только потом строить параболу. Для этого подставьте несколько значений «х» (по обе стороны от вершины) в исходное уравнение, чтобы вычислить соответствующие значения «у».
- Вернемся к уравнению x² + 2x + 1. Вы уже знаете, то точкой пересечения графика этого уравнения с осью Х является точка с координатами (-1,0). Если парабола имеет только одну точку пересечения с осью Х, то это вершина параболы, лежащая на оси Х. В этом случае одной точки недостаточно для построения правильной параболы. Поэтому найдите несколько дополнительных точек.
  - Допустим х = 0, х = 1, х = -2, х = -3.
  - х = 0: f(x) = (0)² + 2(0) + 1 = 1. Координаты точки: (0,1).
  - х = 1: f(x) = (1)² + 2(1) + 1 = 4. Координаты точки: (1,4).
  - х = -2: f(x) = (-2)² + 2(-2) + 1 = 1. Координаты точки: (-2,1).
  - х = -3: f(x) = (-3)² + 2(-3) + 1 = 4. Координаты точки: (-3,4).
  - Нанесите эти точки на координатной плоскости и постройте параболу (соедините точки U-образной кривой). Обратите внимание, что парабола абсолютно симметрична – любую точку на одной ветке параболы можно зеркально отразить (относительно оси симметрии) на другой ветке параболы. Этим вы сэкономите время, так как вам не нужно вычислять координаты точек на обеих ветвях параболы.
Реклама

Советы

Округляйте дробные числа (если это требование преподавателя) – так вы построите правильную параболу.
Если в f(x) = ax² + bx + c коэффициенты b или c равны нулю, то членов с этими коэффициентами в уравнении нет. Например, 12x² + 0x + 6 превращается в 12x² + 6, потому что 0x равен 0.

Об этой статье

Эту страницу просматривали 53 281 раз.

Была ли эта статья полезной?

Источник

Home » 8 класс » Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?

Урок: как построить параболу или квадратичную функцию?

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Парабола — это график функции описанный формулой ax²+bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:

1 ) Формула параболы y=ax²+bx+c,
если а>0 то ветви параболы направленны вверх,
а<0 то ветви параболы направлены вниз.
Свободный член c эта точке пересекается параболы с осью OY;

2 ) Вершина параболы, ее находят по формуле x=(-b)/2a, найденный x подставляем в уравнение параболы и находим y;

3) Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax²+bx+c=0;

Виды уравнений:

a) Полное квадратное уравнение имеет вид ax²+bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax²+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax²+bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax²+c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

Как решать квадратные уравнения посмотреть тут.

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x²+4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)²+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x²+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b²-4ac=16-12=4
x=(-b±√(D))/2a
x₁=(-4+2)/2=-1
x₂=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x²+4x+3 значения
y=(-4)²+4*(-4)+3=16-16+3=3
y=(-3)²+4*(-3)+3=9-12+3=0
y=(-1)²+4*(-1)+3=1-4+3=0
y=(0)²+4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x²+4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1<0.
a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)²+4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x²+4x=0
Неполное квадратное уравнение вида ax²+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x²+4x значения
y=0²+4*0=0
y=-(1)²+4*1=-1+4=3
y=-(3)²+4*3=-9+13=3
y=-(4)²+4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x²-4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0)²-4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x²-4=0
Неполное квадратное уравнение вида ax² +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x²=4
x₁=2
x₂=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x²-4 значения
y=(-2)²-4=4-4=0
y=(-1)²-4=1-4=-3
y=1²-4=1-4=-3
y=2²-4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.

Источник