Математическая модель игры Доббль
Время на прочтение
12 мин
Количество просмотров 43K
Уровни сложности чтения
-
Я слишком молод, чтобы думать
- Введение и правила игры
- Как они это делают?
- Матрица инцидентности для игры Доббль
- Каких двух карточек не хватает в комплекте игры?
- Почему в игре на 2 карточки меньше максимально возможного количества?
- Благодарности
-
Сделай мне умно
- Введение и правила игры
- Как они это делают?
- При чём тут карточки?
- Проективные плоскости малых порядков
- Матрица инцидентности для игры Доббль
- Каких двух карточек не хватает в комплекте игры?
- Почему в игре на 2 карточки меньше максимально возможного количества?
- Благодарности
-
Кошмар
- Введение и правила игры
- Как они это делают?
- Конечная геометрия для грудничков
- При чём тут карточки?
- Проективные плоскости малых порядков
- Как построить проективную плоскость?
- Матрица инцидентности для игры Доббль
- Каких двух карточек не хватает в комплекте игры?
- Почему в игре на 2 карточки меньше максимально возможного количества?
- Благодарности
Введение и правила игры
Несколько лет назад я купил игру Доббль (Dobble, оригинальное название “Spot It!”). Это очень простая, быстрая и весёлая игра, которую я считаю одной из лучших настольных игр вообще.
В комплекте игры 55 карточек с 8 разными символами на каждой. Вот как выглядят эти карточки:
Рис. 1. Пример карточек игры.
На каждых двух карточках совпадает один и только один символ. На приведённом рисунке это символ карандаша:
Рис. 2. Совпадающие символы на карточках.
Игрок, первый увидевший совпадение, делает с одной из карточек действие, зависящее от тура игры. Например, забирает её себе или подкидывает сопернику.
Часто это приводит к тому, что одна из карточек, для которой игроки ищут совпадения, меняется. Из-за этого приходится искать новое совпадение, которое может быть совсем другим символом:
Рис. 3, 4. Первая карточка заменяется на новую. Теперь между ними новое совпадение — символ клоуна.
Как они это делают?
На первый взгляд, кажется невероятным, что на двух карточках ровно одно совпадение, ни больше, ни меньше. Сразу возникают вопросы — сколько всего символов в игре? Их не может быть слишком мало (тогда на карточках будет больше одного совпадения) или слишком много (тогда на карточках может вообще не оказаться совпадений).
Кроме того, очевидно, что символы расположены на карточках в особом порядке, который гарантирует единственное совпадение для любых двух карточек.
Элементарные навыки гугл-фу приводят нас на сайт stackoverflow, где описано, почему так происходит: http://stackoverflow.com/questions/6240113/what-are-the-mathematical-computational-principles-behind-this-game
В игре используются принципы конечной геометрии. Хотя в этом словосочетании есть слово “геометрия”, это понятие относится больше к комбинаторике, чем к геометрии. Она оперирует конечным количеством точек, которые могут располагаться, в частности, в виде проективной плоскости.
Карточки и символы в игре являются элементами проективной плоскости 7 порядка. Это значит, что на каждой карточке n+1 символ, а общее количество уникальных символов в игре — n^2+n+1, т.е. 57 символов.
Существуют плоскости как более низких, так и более высоких порядков. Например, существует плоскость 5 порядка. Для неё на карточке изображены 6 символов, а общее количество уникальных символов в игре — 5^2+5+1 = 31. Проективная плоскость такой конфигурации используется в более простом варианте игры Доббль под названием “Доббль 1,2,3”.
Связь между точками и линиями для проективной плоскости задаётся при помощи матрицы инцидентности. Её вид представлен в разделе “Матрица инцидентности для игры Доббль”.
Конечная геометрия для грудничков
Много позже написания оригинальной статьи я посетил лекцию Алексея Савватеева, где он рассказал о проективной геометрии намного короче и понятнее. Но так как переписывать из-за этого половину статьи у меня нет ни сил, ни желания, то я просто рекомендую его книгу «Математика для гуманитариев», если моя попытка дикаря объяснить устройство автомобиля на пальцах будет непонятной или скучной.
Сначала зайдём на википедию и почитаем несколько статей. Первая статья описывает понятие конечной геометрии:
Конечная геометрия — это любая геометрическая система, имеющая конечное количество точек. [1]
Пока всё просто. Если ручкой на бумаге нарисовать несколько точек, то они уже будут составлять некую конечную геометрию.
Дальше многих ждёт сюрприз:
Например, евклидова геометрия не является конечной, так как евклидова прямая содержит неограниченное число точек, а точнее говоря, содержит ровно столько точек, сколько существует вещественных чисел. [1]
Для нас это значит, что тот листок бумаги, на котором нарисованы наши точки, не является плоскостью с точки зрения конечной геометрии. Это просто носитель точек.
Существуют два вида геометрии на плоскости: аффинная и проективная. В аффинной геометрии используется обычное понятие параллельности прямых. [1]
Вспомним, какими аксиомами описывается афинная геометрия:
Аффинная геометрия на плоскости — это непустое множество X (элементы которого называются «точками»), с непустым набором L подмножеств X (элементы которого называются «прямая»), таких, что:
- Для двух различных точек существует только одна прямая, которая содержит обе точки.
- Для прямой ℓ и точки p, не принадлежащей ℓ, существует одна и только одна прямая ℓ′, содержащая p, такая, что ℓ ∩ ℓ′ = ∅ .
- Существует множество из четырёх точек, никакие три из которых не лежат на одной прямой. [1]
Эти аксиомы дают нам возможность понять, как выглядит простейшая афинная плоскость в конечной геометрии:
Простейшая аффинная плоскость содержит лишь 4 точки, и называется аффинной плоскостью второго порядка. Каждая пара точек определяет уникальную прямую, поэтому указанная плоскость содержит 6 прямых. [1]
Не очень понятно? Всё верно. Если присмотреться к определению афинной геометрии, то можно заметить, что она оперирует с понятиями теории множеств (элемент, множество, подмножество).
Это значит, что прямые могут выглядеть совсем не как привычные прямые Евклидовой геометрии.
На самом деле так и есть. Если взглянуть на рисунок афинной плоскости второго порядка, то мы увидим такую картину:
Рис. 5. Афинная плоскость второго порядка. (Источник ru.wikipedia.org)
Точки здесь выглядят как обычные чёрные точки, а вот прямые — это разноцветные отрезки. Прямые одинакового цвета считаются параллельными.
Как легко заметить, прямые тут не бесконечной длины. По секрету скажу, что понятия длины тут вообще нет, а прямые могут иметь любую форму, как мы вскоре увидим.
Наверняка %username% до сих пор сомневается, что изображение этой плоскости удовлетворяет аксиомам афинной геометрии. Давайте проверим:
- Берём 2 любых точки, например, левую верхнюю и левую нижнюю.
Обе эти точки содержит только одна левая красная прямая.
Правая красная прямая не содержит ни одной из этих точек, а остальные прямые содержат только одну из них. - Берём левую красную прямую и правую верхнюю точку. Очевидно, что только одна прямая (правая красная) параллельна левой красной прямой, так как проходит через правую верхнюю точку, но не проходит ни через одну из двух левых точек.
- На рисунке хорошо видно, что какие бы 3 точки мы ни взяли, одна из них лежит на прямой, отличной от прямой, на которой лежат обе другие точки.
Две прямых, составляющие диагонали квадрата, не пересекаются, так как не имеют общих точек.
Если вы хорошо поняли содержание предыдущей картинки, то вот картинка посложней:
Рис. 6. Афинная плоскость третьего порядка. (Источник ru.wikipedia.org)
Здесь мы видим 9 точек и 12 прямых. Да-да, %username%, эти эллипсы — на самом деле прямые в терминах конечной геометрии.
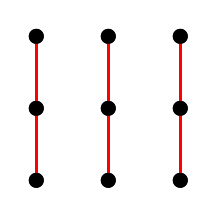
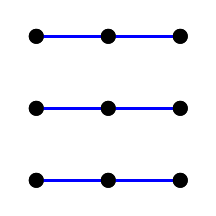
Фигуры одинакового цвета — это параллельные прямые. Их трудно заметить, поэтому разделим картинку на несколько:
| Плоскость №1 | Плоскость №2 | Плоскость №3 | Плоскость №4 |
|---|---|---|---|
 |
 |
 |
 |
Рис. 7. Параллельные прямые афинной плоскости третьего порядка.
Здесь проверка выполнения аксиом займёт чуть больше времени:
- Берём 2 любых точки, например, центральную верхнюю и правую нижнюю. Через них проходит только одна из фиолетовых прямых.
- Берём левую красную прямую и правую нижнюю точку. Аналогично плоскости второго порядка, только одна правая красная прямая проходит через эту точку, но не проходит ни через одну из трёх левых точек.
- Здесь чуть сложнее, чем в случае с плоскостью 2 порядка. Формулировка аксиомы гласит, что нужно найти хотя бы одно (непустое) множество из четырёх точек, в котором никакие три не лежат не одной прямой.
Очевидно, что 12 множеств с тремя точками, через которых проходят линии на рисунке, не удовлетворяют этому условию. Но ему удовлетворяет, например, множество из четырёх угловых точек.
В более общем случае, конечная аффинная плоскость порядка n имеет n^2 точек и n^2 + n прямых; каждая прямая содержит n точек, и каждая точка принадлежит n + 1 прямой. [1]
С афинной геометрией закончили, переходим ко второму типу геометрии на плоскости — проективной.
В проективной геометрии наоборот, любые две прямые пересекаются в единственно возможной точке, и потому параллельных прямых не существует. [1]
Предыдущее предложение описывает вторую аксиому проективной геометрии. Первая и третья — такие же, как в афинной.
Поскольку третья аксиома требует существования как минимум четырёх точек, плоскость должна содержать как минимум 7 точек, чтобы удовлетворить условиям первых двух аксиом. В этой простейшей из проективных плоскостей имеется также 7 прямых; каждая точка принадлежит трём прямым, и каждая прямая содержит три точки. Такую проективную плоскость часто называют «плоскостью Фано». [1]
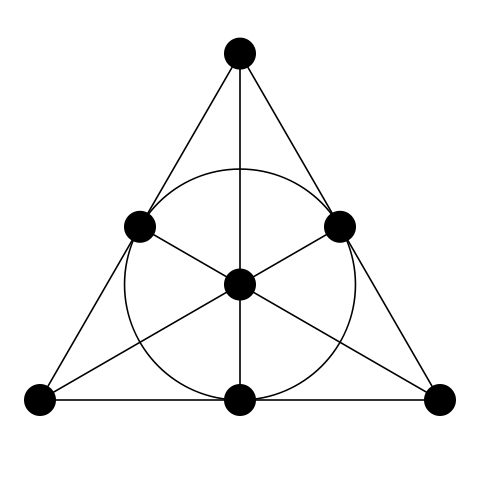
Рис. 8. Плоскость Фано. (Источник en.wikipedia.org)
На этом рисунке сложно сразу разобрать все 7 прямых, так что вот пони-вариант той же плоскости:
Рис. 9. Плоскость Фано с раскрашенными прямыми. (Источник mathpuzzle.com. Используется с разрешения Ed Pegg Jr.)
Итак, плоскость Фано — это проективная плоскость 2 порядка с 7 точками и 7 линиями.
При чём тут карточки?
Что будет, если мы переформулируем 2 аксиомы конечной геометрии, заменив “прямую” на “символ” и “точку” на “карточку”?
Получится вот что:
- Для двух различных карточек существует только один символ, который изображён на обеих карточках.
- Для двух различных символов существует только одна карточка, которая содержит оба этих символа.
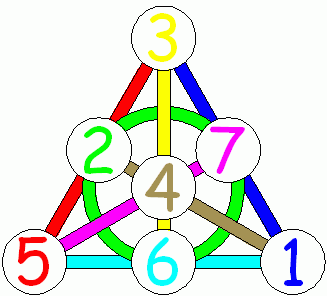
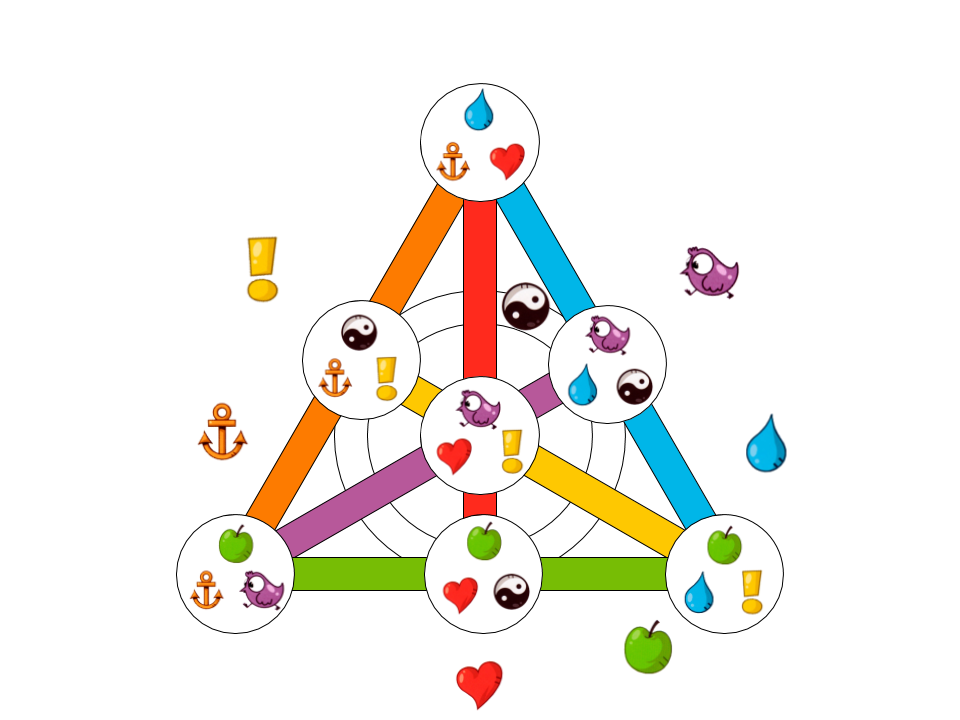
Теперь на основе этих знаний посмотрим, как выглядел бы Доббль в простейшем случае. В нём было бы 7 карточек и 7 символов, на каждой карточке было бы по 3 символа (т.к. в одной точке пересекаются 3 прямые):
Рис. 10. Пример минимально возможного набора карточек для Доббля.
Тут используются следующие 7 символов:






Какие бы 2 карточки мы ни взяли, они будут иметь общий символ, изображённый рядом с прямой, на которой лежат обе карточки.
Например, у карточки в левом нижнем углу и карточки в середине правой грани общий символ 

Проективные плоскости малых порядков
На сайте Wolfram можно найти визуальную демонстрацию проективных плоскостей малых порядков: http://demonstrations.wolfram.com/ProjectivePlanesOfLowOrder/
Она оформлена в виде документа в формате CDF (Computable Document Format), для которого нужно установить CDF Player.
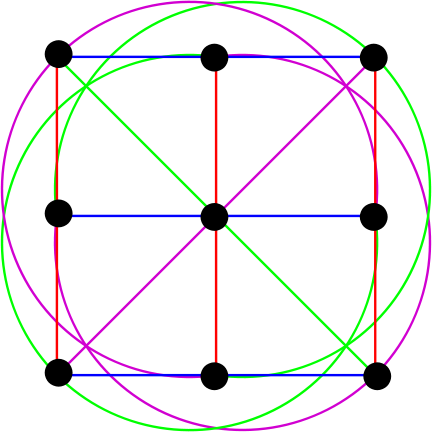
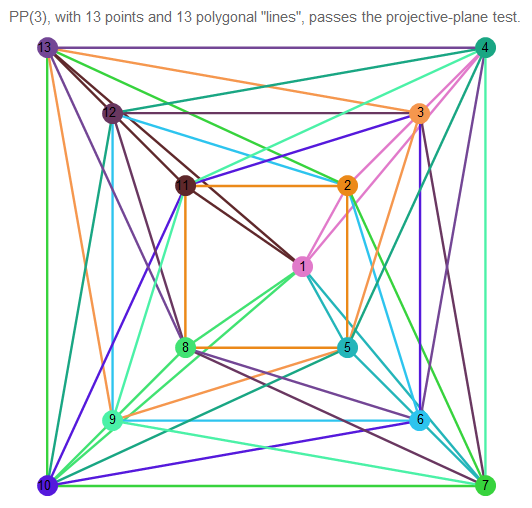
Вот пример проективной плоскости 3 порядка:
Рис. 11. Изображение проективной плоскости 3 порядка.
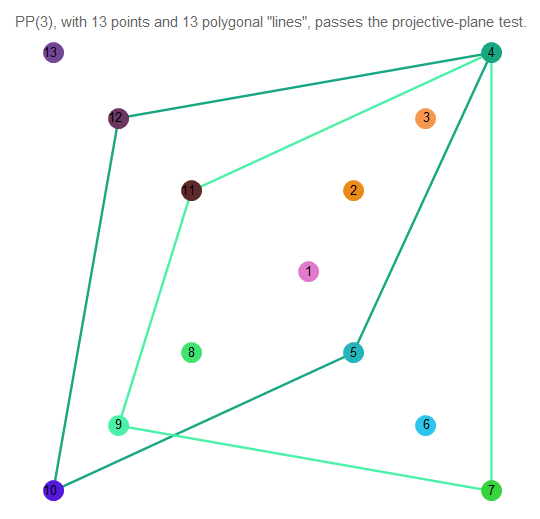
Трудно понять, что происходит, поэтому возьмём 2 произвольные прямые:
Рис. 12. Пересечение двух линий проективной плоскости 3 порядка.
Как мы видим, они пересекаются ровно в одной точке. Сами линии содержат по 4 точки.
Чтобы убедиться, что через каждую точку проходит 4 прямые, придётся переключать отображаемые пары прямых в интерактивном документе и сосредоточить внимание на какой-то точке.
Проективные плоскости более высоких порядков изображены на рисунках ниже.
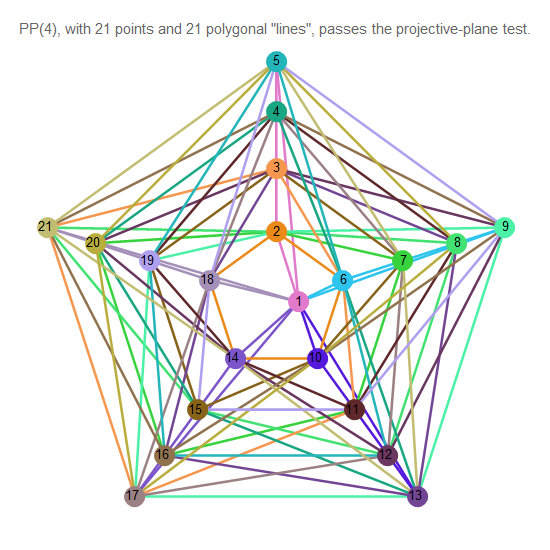
Рис. 13. Проективная плоскость порядка 4
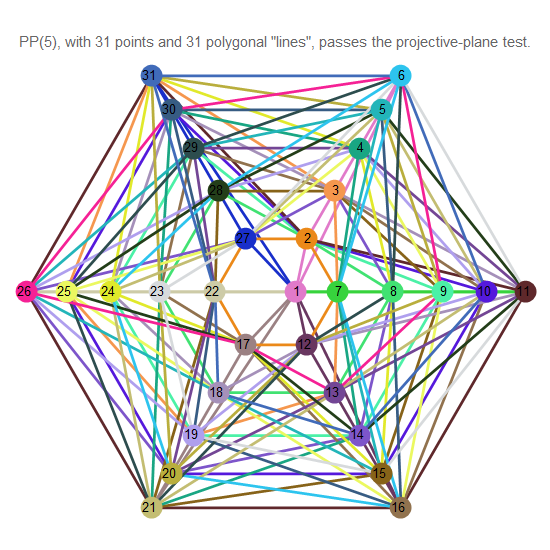
Рис. 14. Проективная плоскость порядка 5
Рис. 15. Проективная плоскость порядка 7
В приведённой последовательности отсутствует изображение для проективной плоскости 6 порядка. Это не ошибка.
Хотя Wolfram генерирует графическое представление такой структуры, она не удовлетворяет аксиомам проективной геометрии, и не является проективной плоскостью.
Предполагается, но до сих пор не доказано, что порядок конечной плоскости всегда является степенью простого числа. [1]
Как построить проективную плоскость?
Графическое представление проективной плоскости выглядит интересно и наглядно, но как найти такую комбинацию точек, чтобы она обладала вышеописанными свойствами?
Проще всего — посетив сайты, где размещены предрасчитанные данные для проективных плоскостей разных порядков.
Например, для проективной плоскости 7 порядка можно посетить такую страницу: https://web.archive.org/web/20170619110638/https://www.uwyo.edu/moorhouse/pub/planes/pg27.txt
Там представлена матрица из чисел. Строки — это карточки (точки) в понятиях Доббля. Числа в строках — это порядковые номера символов (линий), начиная с нуля, которые нарисованы на каждой карточке (проходят через данную точку).
Также можно воспользоваться услугами математических пакетов, таких, как Matlab, чтобы построить матрицу инцидентности проективной плоскости. [2] [3]
Матрицы инцидентности
Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность). [2]
Одним из простейших примеров матрицы инцидентности может служить матрица размером 2х1 для неориентированного графа из двух вершин, соединённых одним ребром:
Рис. 16. Неориентированный граф из двух вершин, соединённых одним ребром, и его матрица инцидентности.
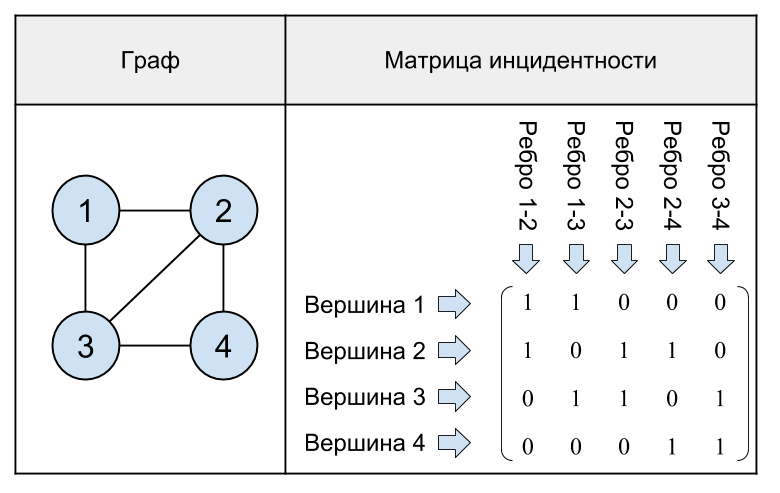
Более сложный пример графа и его матрицы инцидентности:
Рис. 17. Неориентированный граф с 4-мя вершинами и его матрица инцидентности.
Как видно из последнего примера, в матрице инцидентности графа в каждом столбце ровно две единицы, т.к. одно ребро соединяет две вершины.
Проективная плоскость является гиперграфом, так как одна прямая (ребро) соединяет несколько точек (вершин). Поэтому в матрице инцидентности проективной плоскости единицы в каждом столбце встречаются n+1 раз, где n — порядок проективной плоскости.
Для плоскости Фано, изображённой на рис. 9, матрица инцидентности будет иметь следующий вид:
Рис. 18. Матрица инцидентности плоскости Фано.
Для упрощения восприятия нули не показаны, а единицы заменены на символ Х.
В таком представлении проективной плоскости хорошо заметен принцип двойственности точек и прямых — прямая проходит ровно через 3 точки, и, в то же время, точка принадлежит ровно трём прямым.
Построение проективной плоскости перебором
Текущих знаний о свойствах матрицы инцидентности достаточно, чтобы построить её для проективной плоскости любого порядка n. Для этого можно использовать следующий псевдокод:
Для всех столбцов
Для всех строк
Если в столбце стоит n+1 единиц, то перейти к следующему столбцу
Если в строке стоит n+1 единиц, то перейти к следующей строке
Для каждого предыдущего столбца Х
Если в столбце Х на текущей строке стоит единица
и
Если уже есть совпадения в строках для столбца Х и текущего столбца,
то перейти к следующей строке
Поставить единицу
Перейти на следующую строку
Перейти на следующий столбецСледуя этому алгоритму, мы получим симметричную матрицу для плоскости Фано:
Рис. 19. Матрица инцидентности плоскости Фано, построенная по алгоритму псевдокода.
Эта матрица не совпадает с предыдущей. На самом деле, это неважно.
Перестановка любых двух строк матрицы инцидентности равносильна перенумерации вершин графа.
Перестановка любых двух столбцов матрицы инцидентности равносильна перенумерации рёбер графа (если их заранее пронумеровать).
Матрица инцидентности для игры Доббль
Для игры Доббль в матрице инцидентности строки отвечают за карточки, а столбцы — за символы на них.
Таким образом, перестановка любых двух столбцов матрицы инцидентности равносильна изменению очерёдности следования символов на карточке. Однако, символы на карточке неупорядочены, поэтому данная операция не влияет на внешний вид карточек.
Перестановка двух строк означает, что на всех карточках два соответствующих символа заменяют друг друга.
Последняя операция меняет внешний вид карточек, а значит, что тот набор символов, который мы видим в игре — лишь одна из возможных комбинаций.
Количество наборов символов для отдельно взятой карточки есть сочетание без повторений из 57 элементов по 8 элементам. Оно вычисляется по формуле
Матрица инцидентности для игры Доббль показана в таблице ниже. Она транспонирована, т.е. строки — это символы, а столбцы — это карточки (картинка кликабельна). Хабр не даёт вставить картинку нужного размера и качества, поэтому фулсайз вариант отдельной ссылкой: https://github.com/Skybladev2/DobbleMathModel/blob/master/images/Dobble%20incidence%20matrix.png
Рис. 20. Матрица инцидентности игры Доббль.
Каких двух карточек не хватает в комплекте игры?
Всего в таблице с матрицей инцидентности игры 57 строк и 55 столбцов. Это значит, что в игре могло быть ещё 2 карточки.
Значит, символы, которые должны быть на этих карточках, встречаются в игре реже, чем остальные. Количество символов в игре показано в последнем столбце таблицы.
Количество символов с недостающих карточек таково:
,
,
,
,
,
,
,
,
,
,
,
,
и
(всего 14 символов) встречаются по 7 раз.встречается 6 раз.
Как выглядят недостающие карточки? Для ответа на этот вопрос возьмём любой из представленных выше символов в матрице инцидентности (кроме снеговика), и поместим его на недостающую карточку (например, предпоследний столбец).
Затем найдём все карточки (столбцы), на которых изображён этот символ. Это значит, на всех этих карточках символы совпадают, и других совпадений быть не может.
Так как на этих карточках уже есть совпадение с выбранным символом, вычеркнем из предпоследнего столбца все символы, которые встречаются на остальных карточках.
Недостающие символы, которые не были вычеркнуты, и составляют символы одной из оставшихся карточек. Так как их получилось ровно 8, то вид второй недостающей карточки определяется однозначно.
Вот эти 2 карточки:

Рис. 21. Возможный вид недостающих карточек №56 и №57.
Осталось ответить на последний вопрос — не влияет ли отсутствие этих карточек на свойство совпадения единственного символа между двумя карточками (т.е. вдруг между какими-то карточками нет совпадений)?
Ответ на него очевиден, если ещё взглянуть на матрицу инцидентности игры — нет, не влияет. Между любыми двумя карточками (столбцами) по-прежнему единственное совпадение.
Почему в игре на 2 карточки меньше максимально возможного количества?
Изначально правила для пяти мини игр были не в буклете, а на пяти отдельных карточках. При этом максимум можно было напечатать лишь 60 карточек. Поэтому авторы игры решили убрать 2 карточки, чтобы в итоге получилось 55 карточек с символами + 5 карточек с правилами. (Отдельное спасибо Guillaume Gille-Naves за разъяснение).
Благодарности
Выражаю огромную благодарность сети магазинов настольных игр “Игровед” за помощь в написании статьи.
Благодарю Ed Pegg Jr за предоставленное изображение плоскости Фано.
Отдельно хочу отметить одного анонимуса и Master-а за помощь в проверке статьи.
Благодарю магазин «Настольный град» за помощь в подготовке к публикации статьи.
От всего сердца благодарю авторов игры Igor Polouchine, Denis Blanchot, Guillaume Gille-Naves, а также компанию Asmodee за предоставленное право на использование изображений из игры.
У нас зимняя пора всегда насыщена всевозможными настольными играми. Дед Мороз помог в этом году :)))) — чуть пополнил наш парк настольных игр. О них чуть позже напишу.
А сейчас хочу рассказать об игре DOBBLE
В свое время очень мне понравилась эта игра. Мы увидели ее у знакомых, а потом нашли и купили в подарок. Хочу сказать очень интересная и увлекательная игра для взрослых и детей на тренировку зрительной памяти, внимания, реакции и смекалки!!!!
Суть игры очень проста. В комплект входят 55 карточек. На каждой карточке по 8 различных изображений, которые отличаются формой, цветом и размерами. Изображения могут быть совершенно разными! Важно, что любые две карточки содержат по одному одинаковому изображению, которые могут отличатся только размером и расположение на карточке.
Предлагаю сделать подобную игру! Времени для изготовления потребуется пару часиков.
Если конечно не отвлекаться на новые игры, которые мой ребенок за этих пару часиков придумал и реализовал (правда до половины) три штуки :)))
Нам понадобится:
— Плотный картон формата А4 для карточек.
— Наклейки с маленькими изображениями. Всего понадобится 57 изображений по 8 копий каждого. Желательно подбирать наклейки большего и меньшего размера. У меня были самые маленькие наклейки 1,2 на 1,2 см и самые большие 2,5 на 2,5 см.
— ножницы, карандаш.
Процесс изготовления:
1. На каждом листе картона чертим 6 одинаковых кругов — основа наших карточек, у меня получились круги диаметром 9,5 см. Вырезаем круглые карточки, нам понадобится 57 карточек (не 55)
В покупном варианте игры 55 карточек…
2. Нумеруем наши наклейки от 0 до 56.
Если на одном листе повторяются однотипные наклейки можно их пронумеровать чередуя номера с соседним листом наклеек. У меня были однотипные наклейки: овощи, рыбки и смайлики, во время нумерации я старалась чтобы подряд не было например 5 рыбок. В таком случае при наклеивании может получится карточка на которой будет 5 однотипных изображений.
И самый главный момент — порядок наклеивания наклеек на карточки!! Тут методом подбора не получится. Ведь сама изюминка игры в том, что любые две карточки содержат только по одному одинаковому изображению.
Есть уже готовое математическое (скорее даже геометрическое) решение данного момента, которое я тут выложить не могу, но с удовольствием подскажу всем желающим (пишите на почту)
3. Нумеруем все карточки с изнанки карандашиком. Нумерация нужна что бы не запутаться и что бы в случае ошибки исправить определенную карточку (ошибка может проявится во время игры).
Теперь наклеиваем картинки на карточки по схеме:
1 карточка — картинки номер 0,1,2,3,4,5,6,49
2 карточка — ….
3 карточка — …
В итоге получаем 55 карточек
ВСЕ ГОТОВО!!!
С помощь таких карточек можно играть как минимум в 5 различных вариантов игр. Правила лучше всего поискать в интернете.
Будут вопросы — обращайтесь!!! Моя почта указана на правой панели блога. Все заявки по алгоритму пишите только на почту.
С этой игрой участвую в проекте ИГРА НА УРА
УДАЧИ и ИНТЕРЕСНЫХ ВАМ ИГР!!!
Для создания игры вам понадобятся картинки на каждую букву алфавита. Букв алфавита 26, а картинок к ним 35.
Создание Dobble требует определённого количества картинок для карточек. В нашем случае при раскладе 6 картинок на карточку понадобится 31 картинка. К большому сожалению, не войдут слова на буквы Y и Z (yellow, baby, fly, zebra).
Картинки нужно пронумеровать и желательно составить список, что изображено под каким номером, например,
1-apple
2-acorn
3-bus
4-cinema
5-cat и так далее.
Затем нужно сгенерировать последовательность расположения для 31-й картинки. Можно сделать это с помощью dobble online generator. На сайте нажмите RUN, запустится скрипт, в который нужно вписать желаемое количество картинок для одной карточки. Программа выдаст набор цифр. Скопируйте. Это и будет ваше руководство.
31 dobble instruction
All 31 cards content with 6 symbols on each: [1, 2, 3, 4, 5, 26] [6, 7, 8, 9, 10, 26] [11, 12, 13, 14, 15, 26] [16, 17, 18, 19, 20, 26] [21, 22, 23, 24, 25, 26] [1, 7, 13, 19, 25, 28] [2, 8, 14, 20, 21, 28] [3, 9, 15, 16, 22, 28] [4, 10, 11, 17, 23, 28] [5, 6, 12, 18, 24, 28] [1, 12, 23, 9, 20, 29] [2, 13, 24, 10, 16, 29] [3, 14, 25, 6, 17, 29] [4, 15, 21, 7, 18, 29] [5, 11, 22, 8, 19, 29] [1, 17, 8, 24, 15, 30] [2, 18, 9, 25, 11, 30] [3, 19, 10, 21, 12, 30] [4, 20, 6, 22, 13, 30] [5, 16, 7, 23, 14, 30] [1, 22, 18, 14, 10, 31] [2, 23, 19, 15, 6, 31] [3, 24, 20, 11, 7, 31] [4, 25, 16, 12, 8, 31] [5, 21, 17, 13, 9, 31] [1, 6, 11, 16, 21, 27] [2, 7, 12, 17, 22, 27] [3, 8, 13, 18, 23, 27] [4, 9, 14, 19, 24, 27] [5, 10, 15, 20, 25, 27] [26, 27, 28, 29, 30, 31]
[свернуть]
13 саквы.4 pictures dobble instruction
All 13 cards content with 4 symbols on each: [1, 2, 3, 10] [4, 5, 6, 10] [7, 8, 9, 10] [1, 5, 9, 12] [2, 6, 7, 12] [3, 4, 8, 12] [1, 8, 6, 13] [2, 9, 4, 13] [3, 7, 5, 13] [1, 4, 7, 11] [2, 5, 8, 11] [3, 6, 9, 11] [10, 11, 12, 13]
[свернуть]
31 cards/6 pictures dobble generator
: [1, 2, 3, 4, 5, 26] [6, 7, 8, 9, 10, 26] [11, 12, 13, 14, 15, 26] [16, 17, 18, 19, 20, 26] [21, 22, 23, 24, 25, 26] [1, 7, 13, 19, 25, 28] [2, 8, 14, 20, 21, 28] [3, 9, 15, 16, 22, 28] [4, 10, 11, 17, 23, 28] [5, 6, 12, 18, 24, 28] [1, 12, 23, 9, 20, 29] [2, 13, 24, 10, 16, 29] [3, 14, 25, 6, 17, 29] [4, 15, 21, 7, 18, 29] [5, 11, 22, 8, 19, 29] [1, 17, 8, 24, 15, 30] [2, 18, 9, 25, 11, 30] [3, 19, 10, 21, 12, 30] [4, 20, 6, 22, 13, 30] [5, 16, 7, 23, 14, 30] [1, 22, 18, 14, 10, 31] [2, 23, 19, 15, 6, 31] [3, 24, 20, 11, 7, 31] [4, 25, 16, 12, 8, 31] [5, 21, 17, 13, 9, 31] [1, 6, 11, 16, 21, 27] [2, 7, 12, 17, 22, 27] [3, 8, 13, 18, 23, 27] [4, 9, 14, 19, 24, 27] [5, 10, 15, 20, 25, 27] [26, 27, 28, 29, 30, 31]
[свернуть]
Остаётся создать сами карточки. Самый простой способ — использовать Power Point. Нарисуйте круг подходящего размера (классическая карточка примерно 8см в диаметре), скопируйте, сделайте 6 кругов на лист. Формат слайда лучше взять 4:3. Начинайте размещать картинки в заданном порядке. Для 31-го круга получится 6 листов (6X5+1).
Возможно, моя первая попытка создания игры далека от идеала, но делюсь тем, что получилось. Последняя карточка лишняя, но мне хотелось, чтобы три последние картинки не пропали. Слово yellow я намеренно пропустила, так как мои карточки будут не цветными.
Инструкции для Dobble с 5-7-8 картинками на карточке смотрите ниже.
Classic Dobble 57 instruction — 8
All 57 cards content with 8 symbols on each: [1, 2, 3, 4, 5, 6, 7, 50] [8, 9, 10, 11, 12, 13, 14, 50] [15, 16, 17, 18, 19, 20, 21, 50] [22, 23, 24, 25, 26, 27, 28, 50] [29, 30, 31, 32, 33, 34, 35, 50] [36, 37, 38, 39, 40, 41, 42, 50] [43, 44, 45, 46, 47, 48, 49, 50] [1, 9, 17, 25, 33, 41, 49, 52] [2, 10, 18, 26, 34, 42, 43, 52] [3, 11, 19, 27, 35, 36, 44, 52] [4, 12, 20, 28, 29, 37, 45, 52] [5, 13, 21, 22, 30, 38, 46, 52] [6, 14, 15, 23, 31, 39, 47, 52] [7, 8, 16, 24, 32, 40, 48, 52] [1, 16, 31, 46, 12, 27, 42, 53] [2, 17, 32, 47, 13, 28, 36, 53] [3, 18, 33, 48, 14, 22, 37, 53] [4, 19, 34, 49, 8, 23, 38, 53] [5, 20, 35, 43, 9, 24, 39, 53] [6, 21, 29, 44, 10, 25, 40, 53] [7, 15, 30, 45, 11, 26, 41, 53] [1, 23, 45, 18, 40, 13, 35, 54] [2, 24, 46, 19, 41, 14, 29, 54] [3, 25, 47, 20, 42, 8, 30, 54] [4, 26, 48, 21, 36, 9, 31, 54] [5, 27, 49, 15, 37, 10, 32, 54] [6, 28, 43, 16, 38, 11, 33, 54] [7, 22, 44, 17, 39, 12, 34, 54] [1, 30, 10, 39, 19, 48, 28, 55] [2, 31, 11, 40, 20, 49, 22, 55] [3, 32, 12, 41, 21, 43, 23, 55] [4, 33, 13, 42, 15, 44, 24, 55] [5, 34, 14, 36, 16, 45, 25, 55] [6, 35, 8, 37, 17, 46, 26, 55] [7, 29, 9, 38, 18, 47, 27, 55] [1, 37, 24, 11, 47, 34, 21, 56] [2, 38, 25, 12, 48, 35, 15, 56] [3, 39, 26, 13, 49, 29, 16, 56] [4, 40, 27, 14, 43, 30, 17, 56] [5, 41, 28, 8, 44, 31, 18, 56] [6, 42, 22, 9, 45, 32, 19, 56] [7, 36, 23, 10, 46, 33, 20, 56] [1, 44, 38, 32, 26, 20, 14, 57] [2, 45, 39, 33, 27, 21, 8, 57] [3, 46, 40, 34, 28, 15, 9, 57] [4, 47, 41, 35, 22, 16, 10, 57] [5, 48, 42, 29, 23, 17, 11, 57] [6, 49, 36, 30, 24, 18, 12, 57] [7, 43, 37, 31, 25, 19, 13, 57] [1, 8, 15, 22, 29, 36, 43, 51] [2, 9, 16, 23, 30, 37, 44, 51] [3, 10, 17, 24, 31, 38, 45, 51] [4, 11, 18, 25, 32, 39, 46, 51] [5, 12, 19, 26, 33, 40, 47, 51] [6, 13, 20, 27, 34, 41, 48, 51] [7, 14, 21, 28, 35, 42, 49, 51] [50, 51, 52, 53, 54, 55, 56, 57]
[свернуть]
Правила игры (взято с smitkit.weebly.com)

Игра “доббль” – очень увлекательная настольная игра, развивающая внимание, наблюдательность и быстроту реакции. В классическом исполнении представляет собой круглые карточки, на которых изображены разнообразные предметы, животные, символы. Особенность карточек в том, что на любой отдельно взятой паре карточек обязательно присутствует один совпадающий рисунок. В эту игру можно играть в нескольких вариантах.
Вариант 1 – Башня
Каждый участник получает по одной карточке и в закрытую кладет перед собой. Оставшаяся колода помещается в центр лицевой стороной вверх. Игроки одновременно открывают свои карточки и стараются как можно быстрее найти совпадение между своей карточкой и той, что в центре. Тот, кто справится первым, забирает центральную карточку себе, открывая таким образом новую. После этого действия повторяются. Выигрывает тот, кто соберет больше карточек.
Вариант 2 – Подарочек
Вся механика такая же, как и в предыдущем варианте за одним исключением: игроки ищут совпадения между центральной и карточкой другого участника. Отыскав повторяющийся элемент быстрее всех, ребенок “подкидывает подарочек” сопернику, складывая в его колоду центральный образец. Победителем становится тот, у кого в конце игры накопится меньше карточек.
Вариант 3 – Колодец
Все карты раздаются игрокам, только последняя кладется в центр лицом вверх. Цель каждого из
соревнующихся – самым первым избавиться от своих карт, формируя башню посередине путем нахождения совпадений между своей и центральной карточками.
Вариант 4 – Горячая картошка
Игра идет раундами. Каждый раз участникам раздается по одной карте. Одновременно они открывают свои карточки и на скорость ищут совпадения между ними. Кто находит их первым, кладет свою карту поверх карты соперника. Тот, кому по итогам раунда все скинули карточки, оставляет их себе. Начинается новый тур. Побеждает игрок, накопивший меньше всех штрафных карточек.
Вариант 5 – Собери их все
На стол выкладываются карточки по количеству игроков лицевой стороной вниз, в центре формируется колода. По команде все карточки одновременно открываются. Задача участников собрать больше всех карточек, находя и называя совпадения между центральной и любой другой из них.
Создатель проекта «Педагоги в квадрате», педагог-психолог высшей квалификационной категории, методист. Стаж работы педагогом-психологом — 13 лет.
Знакомство с игрой
Доббль — игра, в которой взрослые и дети могут играть на равных. Собирайте карточки, ищите дубли, реагируйте быстрее всех, и вы станете чемпионом. В наборе собрано 55 карточек. В любой паре карт есть только два одинаковых изображения. И сделать это нужно быстро, опередив соперников.
Производители Доббль (Дабл) рекомендуют играть начиная с 6 лет, но и самые маленькие любители карт будут увлеченно искать похожие картинки и обыгрывать взрослых. Dobble превратит любую скучную вечеринку в бодрое соревнование на скорость и сообразительность. Просто найдите повторяющиеся карточки игры (дубли)и заберите карточку себе быстрее противников.
В яркой жестяной коробке содержится 55 цветных карт игры Доббль и инструкция с правилами к ней.

Так выглядит жестяная коробка, в которой находятся карты
Плюсов больше чем минусов
Доббль известна как одна из наиболее увлекательных настолок. Стоит собрать одну пару и в Вас проснется азарт. С каждым пополнением арсенала тяга собрать всю колоду будет возрастать. Правила игры в Доббль не занимают много времени на объяснения. Любой детский праздник пройдёт весело, стоит положить на стол эти затейливые карты.
Добл не надоедает, ведь в одном развлечении есть целых 5 мини-игр. Каждая из них призвана развивать и тренировать такие навыки, как скорость мышление, визуальная память и реакция. В борьбе за победу нельзя медлить ни секунды, иначе соперник сможет забрать карту себе. А войдя в раж, игрокам потребуется недюжинная сосредоточенность, чтобы не схватить карту, не назвав парную картинку, рискуя потерять её.
Это шустрое и весёлое занятие рассчитанное на все возраста. Выкрикивать пары и забирать выигранную карту будут и взрослые, увлекшиеся соперничеством в картах. Игра Double сделает досуг интересным даже тогда, когда собралась кампания «от мала до велика».
Дети смогут не напрягаясь обыграть родителей, стоит им хотя бы на секунду задуматься. Если такой набор лежит дома, у вас не возникнет вопроса: «Чем заняться, когда скучно?».

Пример возможного хода игры
Пять преимуществ Доббля
У игры много плюсов, игнорировать которые невозможно. Планируя досуг, стоит понимать насколько это занятие будет интересно для Вашей компании. Дубль заинтересует любого человека, в возрасте от 6 лет, а значит все будут удовлетворены выбором.
Настольные игры серии Доббль рассчитаны на все возраста, поэтому подходят для веселых семейных вечеров.
Красивое оформление игры, делает из неё хороший подарок по случаю Дня Рождения.
Дабл не требует специальных навыков, а значит у всех участников возможности победить ровны. Нередко дети обыгрывают взрослых.
Набор относится к разряду развивающих развлечений. Играть в него весело и полезно.
Правила игры Доббль несложны и не требуют большого количества времени для изучения, оставляя все свободное время на ход игры.

В жестяной коробке также находятся правила игры
Кому понравится
Assmode настольная игра Доббль собрала уже немало хороших отзывов и вошла в список популярных игр, по версии сайта Игровед.
Логика игры составлена так, что участвовать в ней без проблем смогут все. Взрослый и ребёнок будут одинаково увлечены поиском карточки, на которой повторяется картинка.
Компактные размеры делают из неё удобное дорожное развлечение. Поэтому многие люди, которым предстоит длительная поездка в поезде, приобретают её, чтобы скрасить долгие часы в вагоне.
Понравятся красочные повторяющиеся карточки и тем, кто любит походы. Когда на улице уже темно, костер уже потушен, а спать всё еще не хочется, самое время поиграть в игру Дубль в палатке при свете фонариков.
Даже в квартире, если вдруг отключили свет, ждать возвращения электричества будет веселее, проявляя смекалку в карточном сражении. Развлечение рассчитано на большое количество участников и одновременно участвовать в ней могут до 12 человек.
Одним из преимуществ игры можно считать её скорость, ведь один кон занимает всего несколько минут. За ней можно провести целый вечер или занять обеденный перерыв на работе, отдыхая от дневной суеты. Максимальная длительность «боя» — 15 минут.

Карточки для игры
Правила
Появилась свободная минутка и самое время поиграть в Доббль. Правила игры расписаны на 5 мини-игр. В каждой вариации игроки должны собрать наибольшее количество карт или, наоборот, остаться с пустыми руками.
В каждой паре карт, из 8 рисунков, есть всего 2 одинаковых, которые игроки должны найти быстрее соперников. Подсматривать в ассортимент соперников не имеет смысла, ведь играя в Доббль, карточки достают из коробки и играют прямо на глазах.
Башня
В первой мини-игре, которая называется «Разбери башню», всем участникам сдается по одной карточке, а оставшаяся колода кладется на стол, рубашкой вверх. Ведущий переворачивает верхнюю карту и участники, соревнуясь на скорость, ищут повторяющееся изображение.
Тот, кто первый нашел дублирующийся элемент, забирает карточку себе. Разбирайте башню и возводите свою. Цель: собрать больше всех карточек.

Правила игры
Колодец
Бывают и игры, в которых задача участников избавиться от карт. В таком случае, делается все ровно наоборот. Ведущий сдает игрокам все карточки поровну, а последнюю кладет в центр, картинками вверх.
Дальше игроки одновременно переворачивают верхнюю карту со своей колоды и быстро ищет одинаковое изображение с центральной колодой. Тот, кто первый назвал дубль, убирает картинки из своего колоды и кладет её наверх в центр.
Теперь повторы ищут по ней. Цикл повторяется, пока один из участников не останется с пустыми руками. Первый, избавившийся от карт, игрок становится победителем. Такой вариант игры называется «Колодец».
Горячая картошка
Мини-игра похожа на одноименную детскую забаву, в которой игроки должны как можно быстрее отдать обжигающую «картофелину» в виде мячика другим. Каждому игроку раздается по карточке, которую они переворачивают так, чтобы было видно всем.
Сравнив свои картинки и элементы у своих противников, Вы должны быстро найти сходство и назвать его, указав на владельца карты-дубля. Тогда карта перемещается в руки нового владельца и сравнение уже идёт по ней. При нахождении дубля, все карты игрока отправляются к противнику. Проигрывает тот, кто соберёт все карты у себя.
Собери их все
В центр кладется одно перевернутое изображение, а вокруг выкладывается столько же карт, сколько игроков. По команде «Старт», картинки переворачиваются и игроки на скорость ищут дубли. При выкрикивании повтора, и участник забирает карту из перевернутых.
Дальше сравнение проводится по забранной из колоды карте. Так повторяется, пока все карты не будут на руках. Обратите внимание: центральную карту забирать нельзя. Выигрывает тот, кто собрал больше всего карт.

Пример игры с тремя игроками
Отправленный подарочек
В пятой версии настольной игры Дубль игроки должны дарить друг другу «Подарочек». каждому игроку сдается по одной карте, рисунком вниз. Оставшуюся колоду в открытую раскладывают на столе. Дальше, все игроки одновременно переворачивают свои карты. Оставляйте их на столе, чтобы соперники видели содержимое.
Участники должны выискивать дубли в картах противника и изображений из центра, преподнося ему в подарок дополнительную карту. Побеждает игрок, получивший меньшее количество карт, так что будьте быстрым и внимательным, чтобы на вас картинок просто не осталось.
Другие версии игры
Assmode Доббль, настолько увлекает, что иногда возникает желание поиграть прямо сейчас. Это расстраивает, когда купить игру в этот же момент нет возможности, например, если вы находитесь на отдыхе. А так хочется поиграть в настольную игру Доббль на пляже!
Отчаиваться не стоит, ведь можно сделать игру Доббль своими руками. Достаточно просто найти плотную бумагу и вырезать 55 круглых карточек. На каждой заготовке рисуются 8 разных картинок, из расчета, чтобы на каждой паре совпадал всего один рисунок.
Если у Вас есть доступ к принтеру, можно распечатать карты на плотной бумаге для фото. Сами картинки можно найти в интернете. С таким набором можно играть, главное знать правила игры Дубль.
Помимо стандартной версии игры, в продажу выпущен Spot It настольная игра Цифры и формы. Такая вариации не менее увлекательна и подходит для игры с самыми младшими. С помощью Дубля дети смогут проще выучить названия числительных и геометрических фигур.

Содержимое коробки
Видео обзор
Чтобы понять, насколько Доббль подходит для Вашего досуга, предлагаем посмотреть Видео-обзор, в которым игра рассмотрена со всех сторон.
Вам понравится
Если вы прониклись настольной игрой Доббль от Assmode и хотите поиграть в другие весёлые и быстрые игры на внимательность, предлагаем вам список настольных развлечений.
Среди них вы найдете развивающие карточные настольные игры, а так же сможете выбрать достойное занятие для отдыха с друзьями и семьей. Все перечисленные наборы разработаны для разных возрастов и подходят для игры в дороге.
- Карточная игра Экспромт развивает ораторские навыки и учит быстро реагировать на сложившиеся обстоятельства. Вытягивайте картинки и составляйте импровизированный рассказ на основе увиденного. Каждый человек мыслит по своему, а потому игра становится менее интересной даже в 100й раз. Составляйте предложения, придумывайте истории, открывайте в себе творческое начало. Поведайте своей компании, как на самом деле взаимосвязаны самолёт и плюшевый медведь. В составе игры используются простые картинки, поэтому играть в неё смогут и взрослые, и дети.
- Почему во время вечеринки один из участников сделал что-то странное? Может он играет в игру Блеф-пати. Цель игры: выполнить выпавшее действие так, чтобы никто не догадался, что именно вам выпало. Невзначай выпейте чужой напиток, будто перепутали его со своим и спросите где находится иностранное государство, сославшись на плохую память. Но главное не только остаться не пойманным, но и отловить других на выполнении заданий. Задания привнесут интригу на вечеринке и окунет в детективную жизнь, где у всех есть свои тайны.
- Диксит окунет вас в мир фантазии. Проанализировав увиденный необычный рисунок, вам нужно понять, о чем подумал ведущий. Конечно, читать мысли не придется, ведь Вам скажут фразу, которая подтолкнет вас к правильному ответу. Почувствуйте себя в роли психолога и научитесь «видеть людей насквозь».
- Зевс — настолка для тех, кто всегда мечтал побывать на вершине Олимпа. Карточная игра удобна в путешествиях и всегда проходит шумно и весело. Чтобы угнаться за богом Грома и Молний, выкидывайте правильные карты и поднимайтесь как можно выше, пока встанете на вершину наравне с другими Богами.
- Призвание Музы — вдохновлять. Красивые карты с необычными сюжетами, о которых нужно рассказывать используя свое окружение. Две соперничающие команды вручают друг другу 6 карт с историями и одну с описанием вдохновения. Угадаете ли вы, о чем думала муза? Показывать необходимо не предмет на карте, а ассоциацию, которая у всех может быть разной. Придется потрудиться, чтобы понять, что же означала салфетка и как она относится к балерине.
- Все в детстве придумывали себе кодовые имена, играя в войнушку. Теперь игра стала серьёзнее и с помощью игральных карт вы не только должны понять кто под каким псевдонимом скрывается, но и кому можно доверять. Целых две секретных службы ведут вражду. Как понять Свой ли Кетчуп и стоит ли доверять Року? Найдите всех друзей и не попадитесь врагу, ведь это будет означать поражение! Кодовые имена за короткий срок вошли во многие хитпарады настольных игр и считаются одним из лучших развлечений для компаний.
Скажите пару слов в комментариях и в соцсетях (группы Вконтакте, Одноклассники)











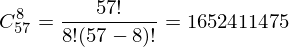

 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  и
и 
 встречается 6 раз.
встречается 6 раз.
