Заданы выборочные совокупности, извлечённые из соответствующих генеральных совокупностей. Требуется:
1) составить интервальное распределение выборки с шагом h, взяв за начало первого интервала х0;
2) вычислить статистические оценки ; ; ;
3) построить полигон частот, гистограмму.
Были испытаны 25 ламп на продолжительность горения и получены следующие результаты (в часах):
773 792 815 827 843 854 861 869 877 886 889 892 885 901 903
905 911 918 919 923 929 937 941 955 981
h = 40; х0 = 760
1) Для полученной выборочной совокупности объёмом , построим интервальное распределение.
Определяем границы интервалов и группируем данные по соответствующим интервалам. Границы интервалов , получаем – следующим образом:
.
Верхняя граница последнего интервала: .
Таблица 1.
№ интервала Интервал Частота
1 760 – 800 2
2 800 – 840 2
3 840 – 880 5
4 880 – 920 10
5 920 – 960 5
6 960 – 1000 1
∑ – 25
2) вычислим статистические оценки ; ; ;
Выборочное среднее – оценка математического ожидания: .
Выборочная дисперсия – оценка дисперсии (смещенная): .
Выборочное среднее квадратическое отклонение .
– середина го интервала
Интервальное статистическое распределение
Если признак может
принимать любые значения из некоторого
промежутка, т.е. является непрерывной
случайной величиной, то необходимо
промежуток между наименьшим и наибольшим
значениями признака в выборке разбить
на несколько интервалов одинаковой
(или разной) длины. При
этом количество интервалов k
не должно
быть меньше 6 – 10 и больше 20 – 25 (выбор
числа интервалов зависит от объема
выборки n).
При подборе
количества интервалов можно пользоваться
приближенной формулой, которую предложил
американский статистик Sturgess
(Стерджесс):
– целая часть
числа х.
Затем определяем
длину частичного интервала группировки:
,
где R
=
–
размах выборки.
Находим границы
каждого из непересекающихся частичных
интервалов
:
a1
= xmin
–
;
b1
= a1
+ h;
a2
= b1;
b2
= a2
+ h
и т.д.
Далее
каждому интервалу требуется поставить
в соответствие число выборочных значений
признака, попавших в этот интервал. В
результате получим интервальное
статистическое распределение:
Таблица
3.3
|
Интервалы |
[a1; |
[a2; |
[a3; |
… |
[ak; |
|
Частоты |
m1 |
m2 |
m3 |
… |
mk |
Используя
интервальное статистическое распределение,
можно вычислить относительную частоту,
накопленную частоту, эмпирическую
функцию распределения, так же как и для
дискретного статистического распределения.
Если
в интервальном распределении каждый
интервал
заменить числом, лежащим в его середине
(ai
+
bi)/2,
то получим дискретное статистическое
распределение. Такая замена вполне
естественна, так как, например, при
измерении размера детали с точностью
до одного миллиметра, всем размерам из
промежутка [49,5 мм; 50,5 мм) будет
соответствовать одно число, равное 50.
Для графического
изображения интервального распределения
используется гистограмма.
Для ее построения в прямоугольной
системе координат по оси абсцисс
откладываем границы интервалов
группировки и на этих интервалах как
на основаниях строим прямоугольники,
высоты которых откладываются на оси
ординат. Различают:
а) гистограмму
абсолютных частот,
когда высота прямоугольника равна
;
б) гистограмму
относительных частот,
когда высота прямоугольника равна
.
Гистограмма
является выборочным
аналогом графика плотности вероятности.
Площадь на интервале (aj;
am)
можно интерпретировать как приближенное
значение вероятности попадания случайной
величины Х
в этот интервал, т.е.
.
Основное свойство
гистограммы:
ее площадь для абсолютных частот равна
n,
а для относительных частот равна
единице.
Отношение
относительной частоты к длине частичного
интервала h
называют плотностью
распределения частоты
на интервале
(рис. 3.5).
Рис. 3.5. Гистограмма
относительных частот
При построении
графика эмпирической функции распределения
для интервального ряда необходимо
учитывать, что функция определена только
на концах интервалов.
Таким образом,
статистическое распределение выборки
можно рассматривать как статистический
аналог для распределения генеральной
совокупности. Из-за случайных колебаний
эти два распределения, как правило, не
будут совпадать, но можно ожидать, что
при большом объеме выборки ее распределение
будет служить приближением для генеральной
совокупности, т.е.
,
если
.
Пример
2.
Получены данные о выработке продукции
30-ю рабочими в отчетном месяце в процентах
к предыдущему месяцу
|
n |
Х |
|||||||||
|
1-10 |
125 |
91 |
82 |
93 |
101 |
111 |
109 |
103 |
121 |
90 |
|
11-20 |
79 |
105 |
115 |
95 |
84 |
130 |
104 |
117 |
127 |
107 |
|
21-30 |
85 |
76 |
98 |
104 |
126 |
113 |
98 |
84 |
113 |
123 |
Необходимо:
-
составить
интервальное статистическое распределение; -
построить
гистограмму относительных частот.
Решение
1. Определим величину
частичных интервалов:
Построим 6
непересекающихся интервалов:
[70,5; 81,5), [81,5; 92,5),
[92,5; 103,5),
[103,5; 114,5), [114,5;
125,5), [125,5; 136,5).
Первый интервал
[70,5; 81,5) содержит два значения (76 и 79),
поэтому m1
= 2. Второй
интервал [81,5; 92,5) содержит шесть значений
(82, 84, 84, 85, 90, 91), поэтому m2
= 6 и т.д.
Полученные данные внесем в таблицу
интервального статистического
распределения:
Таблица 3.4
|
Интервалы |
[70,5- 81,5) |
[81,5- 92,5) |
[92,5- 103,5) |
[103,5- 114,5) |
[114,5- 125,5) |
[125,5- 136,5) |
|
Частоты |
2 |
6 |
6 |
8 |
5 |
3 |
2. Для построения
гистограммы вычислим значения
относительных частот wi
и значения плотности распределения
частоты на интервале
:
Таблица 3.5
|
Интервалы |
[70,5- 81,5) |
[81,5- 92,5) |
[92,5- 103,5) |
[103,5- 114,5) |
[114,5- 125,5) |
[125,5- 136,5) |
|
mi |
2 |
6 |
6 |
8 |
5 |
3 |
|
wi |
0,07 |
0,20 |
0,20 |
0,27 |
0,17 |
0,10 |
|
|
0,006 |
0,018 |
0,018 |
0,024 |
0,015 |
0,009 |
Изобразим
данные последней строки табл. 3.5 на
графике
(рис. 3.6).
Обведем гистограмму
плавной линией f*(x)
так, чтобы приблизительно были равны
площади, ограниченные гистограммой и
кривой f*(x),
которую называют эмпирической
плотностью распределения относительных
частот. В
генеральной совокупности ей соответствует
плотность вероятности f(x).
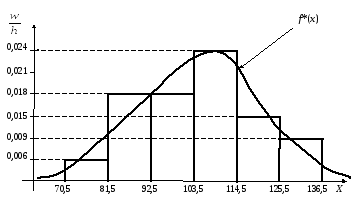
3.6. Гистограмма относительных частот
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k — число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) — это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) — середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения:
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) — соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) — нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) — середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) — результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | — |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
 |
 |
Теория вероятностей |
 |
 |
Решение задачи |
 |
 |
18 февраля 2021 |
 |
 |
Выполнен, номер заказа №16401 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
245 руб. |
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!
Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):
Приведены выборочные совокупности из соответствующих генеральных совокупностей. Требуется: 1) по не сгруппированным данным найти выборочную среднюю; 2) найти доверительный интервал для оценки неизвестного математического ожидания признака X генеральной совокупности (генеральной средней), если признак X распределён по нормальному закону; известно –надёжность и – среднее квадратическое отклонение; 3) составить интервальное распределение выборки с шагом h, взяв за начало первого интервала х0; 4) построить гистограмму частот; 5) дать экономическую интерпретацию полученных результатов. Проведено выборочное обследование объёма промышленного производства на предприятии за 16 месяцев и получены следующие результаты: 750; 950; 1000; 1050; 1050; 1150; 1150; 1150; 1200; 1200; 1250; 1250; 1350; 1400; 1400; 1550. = 0,98; = 200; h = 200; x0 = 700.
Решение
1) по не сгруппированным данным найдем выборочную среднюю; 2) найдем доверительный интервал для оценки неизвестного математического ожидания признака X генеральной совокупности (генеральной средней), если признак X распределён по нормальному закону; известно –надёжность и – среднее квадратическое отклонение; Доверительный интервал для математического ожидания a нормально распределенной случайной величины равен: где t – такое значение аргумента функции Лапласа, при котором . По таблице функции Лапласа находим t из равенства: Получаем и искомый доверительный интервал имеет вид: 3) составим интервальное распределение выборки с шагом h, взяв за начало первого интервала х0; Шаг Интервалы Частоты 4) построим гистограмму частот; 5) дадим экономическую интерпретацию полученных результатов. Средний объём промышленного производства на предприятии за 16 месяцев равен . С надежностью % можно ожидать, что средний объём промышленного производства (генеральная совокупность) будут находиться в пределах от . Вид гистограммы частот подтвердил, что данный признак Х можно считать подчиняющимся закону нормального распределения. Это даёт основание при вычислении интервальных оценок параметров использовать формулы нормального распределения.
Похожие готовые решения по теории вероятности:
- Из генеральной совокупности извлечена выборка объемом n. Оценить с надежностью 0,95 математическое ожидание
- Измерения времени, необходимого для изготовления определенной детали, дали следующие результаты (в минутах): 10,1 11
- Дана выборка значений случайной величины: 2 2 2 2 2,2 2,2 2,2 2,5 2,5 2,5 2,5 2,9 2,9 3 3 3 3 3 Найти выборочные среднее
- Требуется по заданной выборке, состоящей из 𝑛 элементов некоторого признака 𝑋, найти 1. Вариационный и статистический
- Даны измерения твердости 16 образцов легированной стали (в условных единицах). В предположении, что выборка
- В результате испытания случайная величина X приняла значения: X1, X2, X3 … , X16. X1 = 4, X2 = 9, X3 = 5, X4 = 4, X5 = 2, X6 = 2, X7
- В результате испытания случайная величина X приняла значения: X1, X2, X3 … , X16. X1 = 4, X2 = 9, X3 = 5, X4 = 4, X5 = 2, X6
- В результате испытания случайная величина X приняла значения: X1, X2, X3 … , X16. X1 = 2, X2 = 4, X3 = 3, X4 = 5, X5 = 9, X6
- Размер детали задан полем допуска 10 – 12 мм. Оказалось, что средний размер детали равен 11,4 мм, а среднее квадратическое отклонение
- Вычислите вероятности попадания случайной величины 𝑋 = 𝑁(1; 4) в промежутки
- Фирма производит определенный тип электронных приборов. Специальное тестирование показало, что средний срок службы большой партии
- Значения веса пойманной рыбы подчиняется нормальному закону распределения с математическим ожиданием 375 г, средним квадратическим











