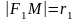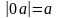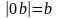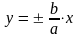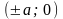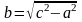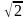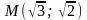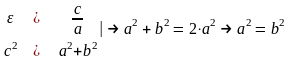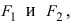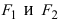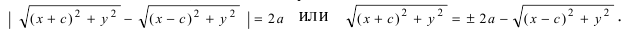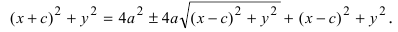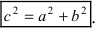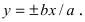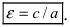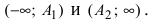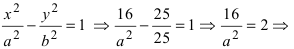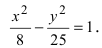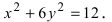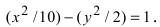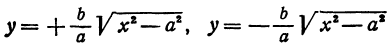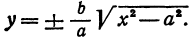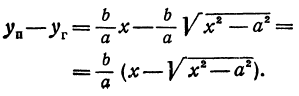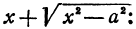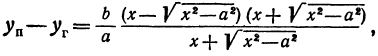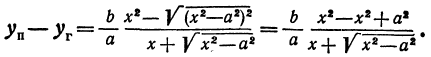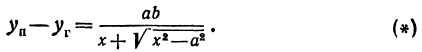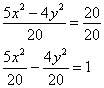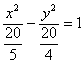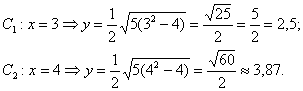Каноническое уравнение гиперболы по двум точкам
| Две точки с координатами |
|
Первая координата |
|
Вторая координата |
| Каноническое уравнение гиперболы |
| Большая полуось гиперболы |
| Малая/мнимая полуось гиперболы |
| Эксцентриситет гиперболы |
| Фокальный параметр |
| Фокальное расстояние |
| Перицентрическое расстояние |
Уравнение гиперболы в каноническом виде имеет вот такой вид.
Так же как и при расчете уравнения эллипса по двум точкам, мы можем по двум точкам однозначно построить гиперболу, выраженную через вышеуказанную формулу.
Используя универсальный калькулятор расчет кривой второго порядка на плоскости по точкам, мы легко определим значения 
Кроме этого, зная эти параметры можно рассчитать следующее:
Большая полуось 
Фокальное расстояние 
Мнимая полуось 
Связь между тремя параметрами выражена в одной формуле
Эксцентриситет — коэффициент, численно равный, отношению фокусного расстояния к большой полуоси гиперболы
Фокальный параметр —расстояние от фокуса до гиперболы вдоль прямой, параллельной оси ординат
Прицельный параметр — расстояние от фокуса до асимптоты. Численно равен малой полуоси гиперболы.
Перицентрическое расстояние —расстояние от фокуса до ближайшей вершины гиперболы
Примеры задач
Cоставить каноническое уравнение гиперболы по двум точкам
Вводим данные в поля ввода. Можем писать как выражение, учитвая что квадратный корень обозначается sqrt, а можем сначала получить численные значения и подставить уже окончательные результаты.
В результате получим
| Каноническое уравнение гиперболы |
 |
| Большая полуось гиперболы |
|
4.47213595499958 |
| Малая/мнимая полуось гиперболы |
|
3.4641016147913444 |
| Эксцентриситет гиперболы |
|
1.1661903789073205 |
| Фокальный параметр |
|
1.79999999928 |
| Фокальное расстояние |
|
5.830951894536603 |
| Перицентрическое расстояние |
|
0.8309518945366023 |
Есть небольшая погрешность в вычислениях, вместо 2.9999999999 должно быть 3. Но думаю, что клиенты отнесутся с снисхождением, к одной десяти миллионной погрешности.
Удачных расчетов!
Гиперболой
называется геометрическое место точек,
для которых разность
расстояний от двух фиксированных точек
(называемых фокусами) есть величина
постоянная. Причем указанная разность
берется по абсолютному значению и
необходимо, что бы она была меньше
расстояния между фокусами и не равна
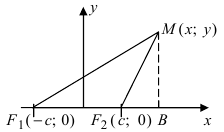
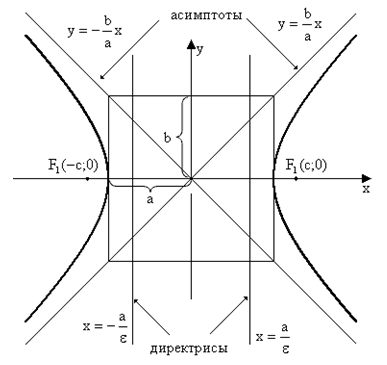
нулю. (См. Рис.23)

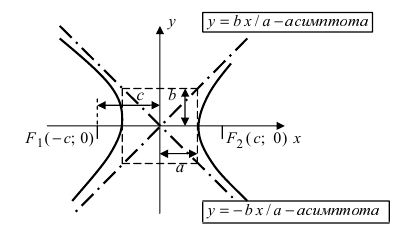
Рис.23
На
рисунке:
—
— левый фокальный радиус;
—
—
правый фокальный радиус;
—
(- с; 0) – координаты левого фокуса (точки
F1);
—
(с; 0) — координаты правого фокуса (точки
F2);
—
— действительная
полуось
гиперболы;
—
— мнимая
полуось гиперболы;
—
точка (а; 0) – правая вершина гиперболы;
—
точка (- а; 0) – левая вершина гиперболы;
—
прямые
— асимптоты гиперболы.
Названия
полуосей не случайны: точки
гиперболе принадлежат, а точки
—
гиперболе не принадлежат (потому и ось
– мнимая), но мнимая полуось, хотя и не
является частью гиперболы, вполне
определяет ее форму, поскольку именно
между асимптотами гиперболы и располагаются
ветви ее.
Каноническое уравнение гиперболы
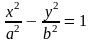
(смотри
замечание о каноничности уравнения).
Связь между полуосями и координатами фокусов гиперболы
При
этом важным является выражение,
связывающее действительную, мнимую
полуось и координату фокуса (сравните
с формой аналогичной связи для параметров
эллипса)
.
Эксцентриситет
гиперболы

Пример 19 (о нахождении уравнения гиперболы)
Эксцентриситет
гиперболы равен
.
Найти каноническое уравнение гиперболы,
если точка
гиперболе принадлежит.
Решение
Прежде
всего, что ищем конкретно? – Ищем значения
a
и b
в каноническом уравнении гиперболы.
Неизвестных величин две, следовательно,
и уравнений для их нахождения должно
быть два.
Первое
уравнение получим из того факта, что
нам известен эксцентриситет гиперболы
и известна связь
между полуосями и координатами фокуса
гиперболы:
.
Это
первое равенство, а второе получим,
используя тот факт, что точка М гиперболе
принадлежит, т.е., ее координаты обращают
каноническое уравнение гиперболы в
тождество:
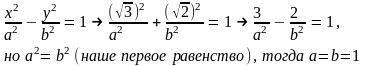
и,
окончательно, получаем
Ответ
Искомая
гипербола описывается каноническим
уравнением
x2
— y2
= 1.
Пример 20 (прямая и гипербола)
Через
точку М(0; — 1) и правую вершину гиперболы
3∙x2
— 4∙y2
= 12
проведена
прямая. Найти вторую точку пересечения
прямой с гиперболой.
Решение
Задачу
будем решать в два шага:
—
найдем уравнение прямой;
—
найдем координату точки пересечения
прямой и гиперболы.
Шаг
1
Для
нахождения уравнения прямой, проходящей
через точку М(0; — 1) и правую вершину
гиперболы необходимо знать координаты
правой вершины гиперболы. Найдем вторую
точку из уравнения гиперболы, приведя
данное уравнение к каноническому
виду,
зная при этом, что в каноническом
уравнении важно все: равно выражение
именно
единице, а в самом выражении – значения
действительной и мнимой полуоси – это
знаменатели дробей, в которых числители
x2
и y2.

Откуда
в уравнении гиперболы a
= 2, b
=
,
или координаты правой вершины М2(2;
0). А вот теперь ищем уравнение
прямой, проходящей через две данные
точки
М и М2

Шаг
2
Ищем
координаты точек пересечения найденной
прямой и данной гиперболы. Эти координаты
удовлетворяют обоим уравнениям, т.е.
являются решением системы уравнений
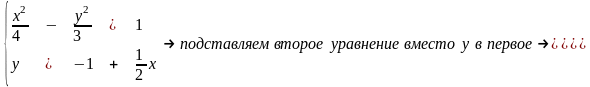
Решаем
полученное уравнение и находим, что x1
= — 4, x2
= 2.
Подставляем
найденные x1
и x2
во второе уравнение системы и находим
координаты точек пересечения прямой с
гиперболой N1(-
4; -3) и N2(2;
0).
Не
трудно убедиться (проверьте самостоятельно)
что точка М гиперболе не принадлежит,
а значит, точек пересечения будет две.
Ответ
Точки
пересечения прямой и гиперболы — N1(-
4; -3) и N2(2;
0).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Гипербола:
Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек
Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы
Рис. 31. Вывод уравнения гиперболы.
Расстояние между фокусами (фокусное расстояние) равно 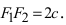
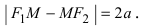
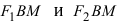
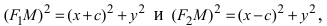
Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим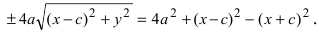
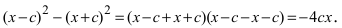
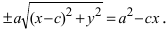
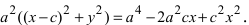
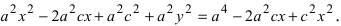
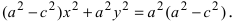
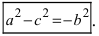
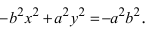
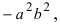
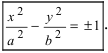
Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки 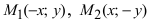
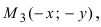
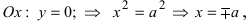
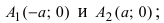
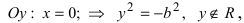
Рис. 32. Асимптоты и параметры гиперболы
Определение: Найденные точки 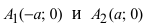
Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым 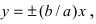
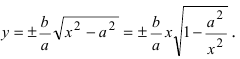
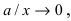
Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.
В данном конкретном случае параметр а называется действительной, а параметр b — мнимой полуосями гиперболы.
Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы
Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству 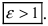
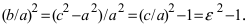
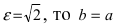
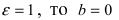
Пример:
Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5).
Решение:
Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины:
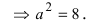
Пример:
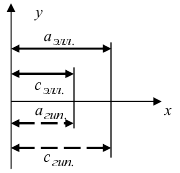
Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах эллипса
Решение:
Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: 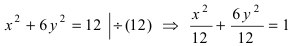
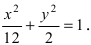
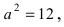
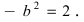
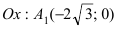
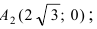
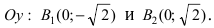
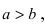
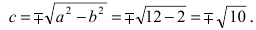
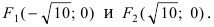
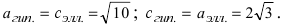
Рис. 33. Параметры эллипса и гиперболы
Вычислим длину мнимой полуоси 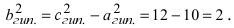
Гипербола в высшей математике
Рассмотрим уравнение
Решая его относительно 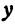
или одну двузначную функцию
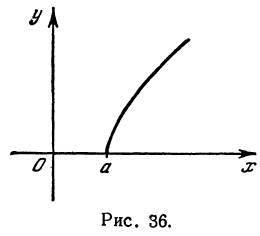
Функция 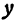

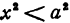
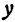
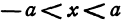
При 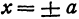
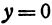
При 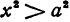
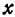
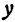
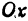
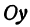
Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой.
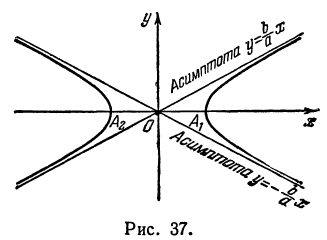
Гипербола в силу симметрии имеет вид, указанный на рис. 37.
Точки пересечения гиперболы с осью 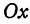
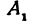
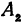
Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью.
Рассмотрим прямую, заданную уравнением 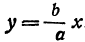
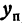
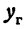
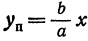
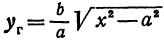
Умножим и разделим правую часть на
или
Окончательно
Будем придавать 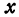
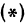

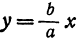
Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением 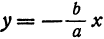
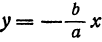
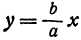
Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы.
Таким образом, гипербола имеет две асимптоты, определяемые уравнениями 
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Эллипс
3.4.1. Каноническое уравнение и построение гиперболы
Общая структура изложения материала будет напоминать предыдущий параграф. Начнём с общего понятия гиперболы и задачи на её построение.
Каноническое уравнение гиперболы имеет вид , где
– положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие
, то
есть, значение «а» может быть и меньше, чем «бэ».
Надо сказать, довольно неожиданно… – уравнение «школьной» гиперболы и
близко не напоминает каноническую запись. Но эта загадка нас ещё подождёт, а пока раскинем на экране своего воображения график функции …. Какие мысли?
У гиперболы две симметричные ветви.
У гиперболы две асимптоты.
Неплохой прогресс! Данными свойствами обладает любая гипербола, и сейчас вы с неподдельным восхищением заглянем в декольте этой линии:
Задача 99
Построить гиперболу, заданную уравнением
Решение: на первом шаге приведём данное уравнение к каноническому виду . Пожалуйста, запомните типовой порядок действий. Справа необходимо получить «единицу», поэтому
обе части исходного уравнения делим на 20:
Здесь можно сократить обе дроби, но технически грамотнее сделать каждую из них трёхэтажной (см. Приложение Школьные
материалы):
и только после этого провести сокращение:
Выделяем квадраты в знаменателях:
Готово.
Почему преобразования лучше проводить именно так? Ведь дроби левой части можно сразу сократить и получить
.
Дело в том, что в рассматриваемом примере немного повезло: число 20 делится и на 4 и на 5. В общем случае получится что-нибудь вроде 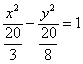
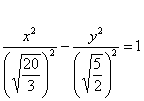
Воспользуемся плодом наших трудов – каноническим уравнением :
Как построить гиперболу?
Существует два подхода к построению гиперболы – геометрический и алгебраический. С практической точки зрения вычерчивание с помощью циркуля я бы
даже сказал утопично, поэтому гораздо выгоднее вновь привлечь на помощь нехитрые расчёты.
Целесообразно придерживаться следующего алгоритма (читайте и смотрите на чертёж ниже):
1) Сначала находим асимптоты. Если гипербола задана каноническим уравнением , то её асимптотами являются прямые
. В нашем случае:
. Данный пункт
обязателен! Это принципиальная особенность чертежа, и будет грубой ошибкой, если ветви гиперболы «вылезут» за свои асимптоты.
2) Теперь находим две вершины гиперболы, которые расположены на оси абсцисс в точках . Выводится элементарно: если
, то каноническое уравнение
превращается в
, откуда и следует,
что . Наша гипербола имеет вершины
3) Ищем дополнительные точки. Обычно хватает двух-трёх. В каноническом положении гипербола симметрична относительно начала
координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Методика точно такая же, как и при построении эллипса. Из канонического уравнения на черновике выражаем:
и уравнение распадается на две функции:
– определяет верхние дуги гиперболы (то, что нам надо);
– определяет нижние дуги гиперболы.
Напрашивается нахождение точек с абсциссами :
4) Изобразим асимптоты , вершины
, дополнительные
и
симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы:
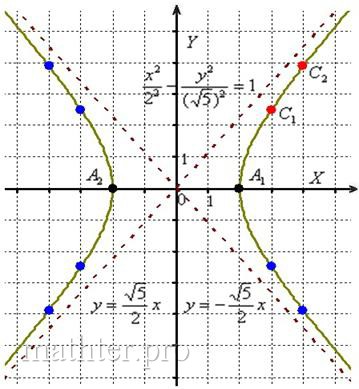
, но это вполне преодолимая проблема.
Отрезок называют действительной осью гиперболы;
Число называют действительной полуосью гиперболы;
число – мнимой полуосью.
В нашем случае: ,
, и, очевидно, если гиперболу повернуть вокруг центра симметрии и / или переместить, то эти значения не
изменятся.


| Оглавление |
Автор: Aлeксaндр Eмeлин
Гипербола: определение, свойства, построение
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и
есть величина постоянная
, меньшая расстояния
между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.
Фокальное свойство гиперболы
Точки и
называются фокусами гиперболы, расстояние
между ними — фокусным расстоянием, середина
отрезка
— центром гиперболы, число
— длиной действительной оси гиперболы (соответственно,
— действительной полуосью гиперболы). Отрезки
и
, соединяющие произвольную точку
гиперболы с ее фокусами, называются фокальными радиусами точки
. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение , где
, называется эксцентриситетом гиперболы. Из определения
следует, что
.
Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:
(3.50)
Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов и
. Для произвольной точки
, принадлежащей гиперболе, имеем:
Записывая это уравнение в координатной форме, получаем:
Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:
где , т.е. выбранная система координат является канонической.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.
Директориальное свойство гиперболы
Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее (рис.3.41,а). При
, когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.
Гиперболу с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
(фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директориальное свойство гиперболы). Здесь
и
— один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
В самом деле, например, для фокуса и директрисы
(рис.3.41,а) условие
можно записать в координатной форме:
Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса
и директрисы
:
Уравнение гиперболы в полярной системе координат
Уравнение правой ветви гиперболы в полярной системе координат (рис.3.41,б) имеет вид
, где
— фокальный параметр гиперболы.
В самом деле, выберем в качестве полюса полярной системы координат правый фокус гиперболы, а в качестве полярной оси — луч с началом в точке
, принадлежащий прямой
, но не содержащий точки
(рис.3.41,б). Тогда для произвольной точки
, принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем
. Выражаем расстояние между точками
и
(см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение гиперболы имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замены
:
что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для гиперболы,
для эллипса).
Геометрический смысл коэффициентов в уравнении гиперболы
Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение , находим абсциссы точек пересечения:
. Следовательно, вершины имеют координаты
. Длина отрезка, соединяющего вершины, равна
. Этот отрезок называется действительной осью гиперболы, а число
— действительной полуосью гиперболы. Подставляя
, получаем
. Длина отрезка оси ординат, соединяющего точки
, равна
. Этот отрезок называется мнимой осью гиперболы, а число
— мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.
Замечания 3.10.
1. Прямые ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).
2. Прямые , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).
Для равносторонней гиперболы, описываемой уравнением (т.е. при
), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат
(рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид
(гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).
В самом деле, повернем каноническую систему координат на угол (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами
Подставляя эти выражения в уравнение равносторонней гиперболы и приводя подобные члены, получаем
3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.
Действительно, если точка принадлежит гиперболе
. то и точки
и
, симметричные точке
относительно координатных осей, также принадлежат той же гиперболе.
Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.
4. Из уравнения гиперболы в полярных координатах (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси (
при
).
5. Эксцентриситет характеризует форму гиперболы. Чем больше
, тем шире ветви гиперболы, а чем ближе
к единице, тем ветви гиперболы уже (рис.3.43,а).
Действительно, величина угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника:
. Учитывая, что
и
, получаем
Чем больше , тем больше угол
. Для равносторонней гиперболы
имеем
и
. Для
угол
тупой, а для
угол
острый (рис.3.43,а).
6. Две гиперболы, определяемые в одной и той же системе координат уравнениями и
называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы
приводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет гиперболу с центром в точке
, оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение
определяет сопряженную гиперболу с центром в точке
.
Параметрическое уравнение гиперболы
Параметрическое уравнение гиперболы в канонической системе координат имеет вид
где — гиперболический косинус, a
гиперболический синус.
Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству .
Пример 3.21. Изобразить гиперболу в канонической системе координат
. Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — действительная полуось,
— мнимая полуось гиперболы. Строим основной прямоугольник со сторонами
с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя
в уравнение гиперболы, получаем
Следовательно, точки с координатами и
принадлежат гиперболе. Вычисляем фокусное расстояние
эксцентриситет ; фокальныи параметр
. Составляем уравнения асимптот
, то есть
, и уравнения директрис:
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.




)
;M_2(-2sqrt{5}:3))