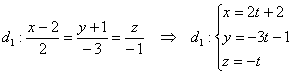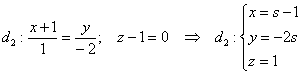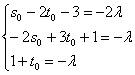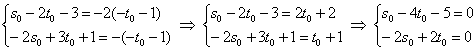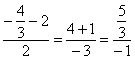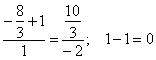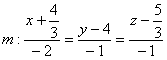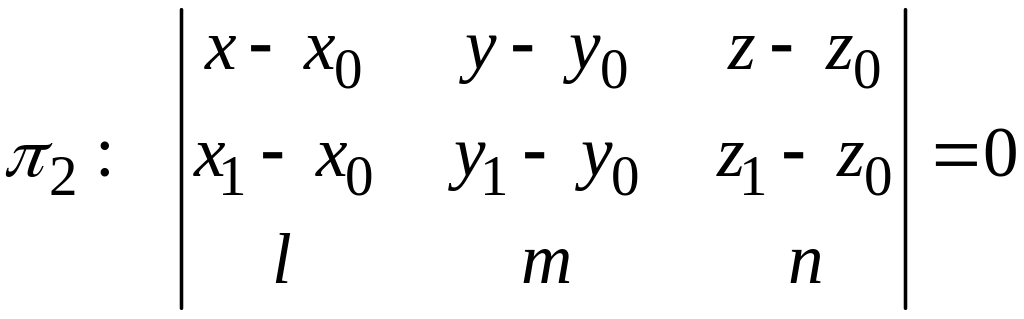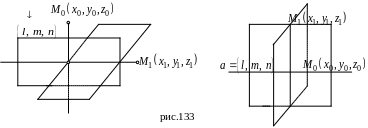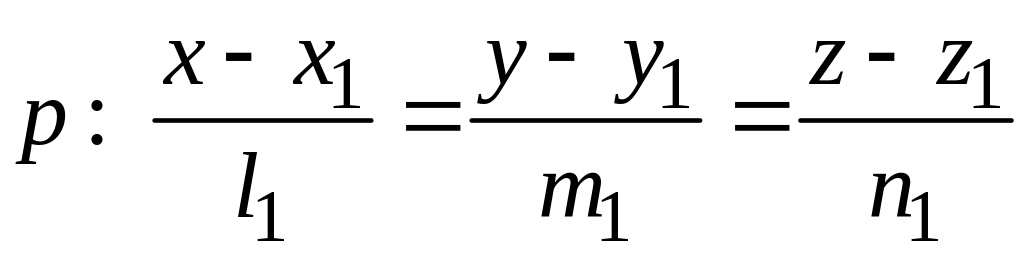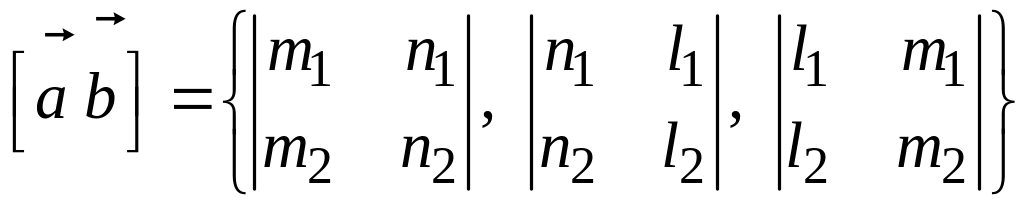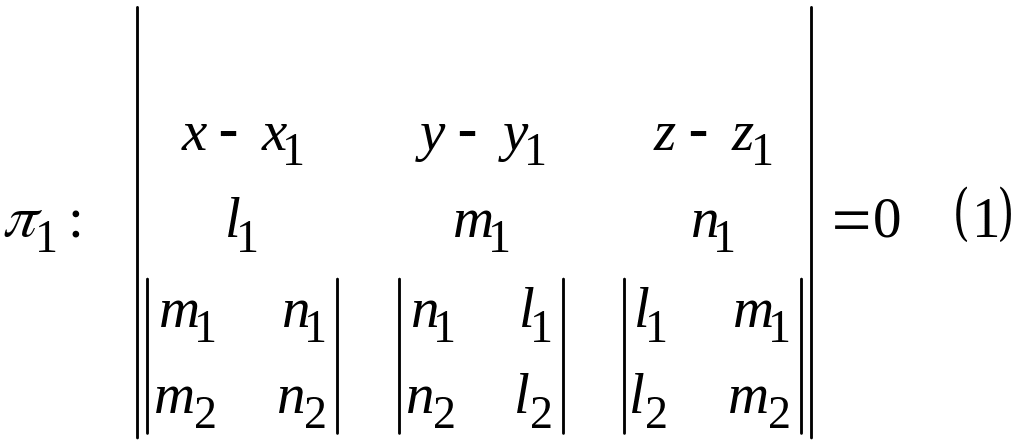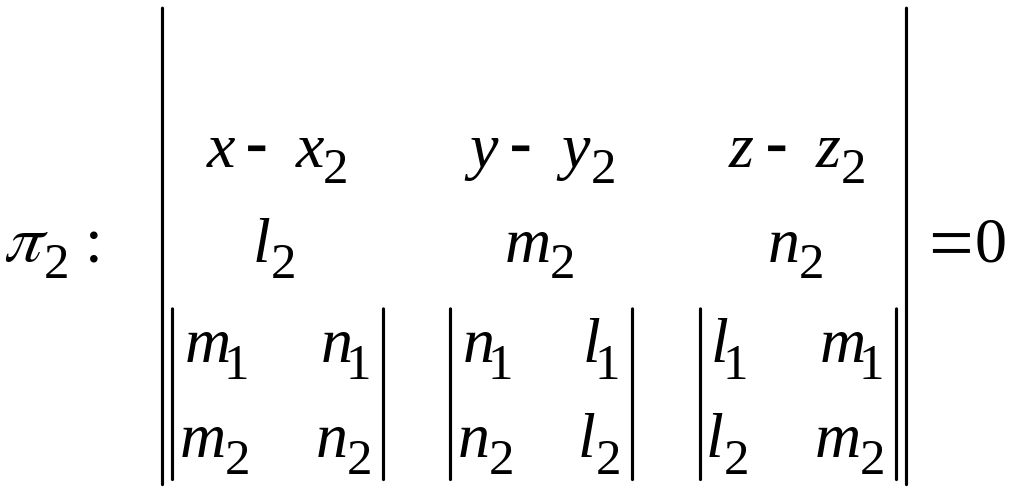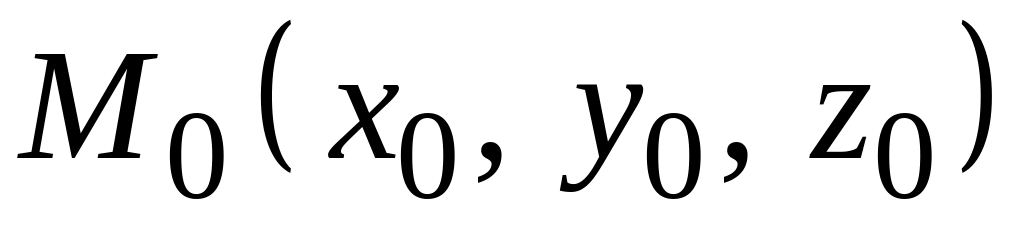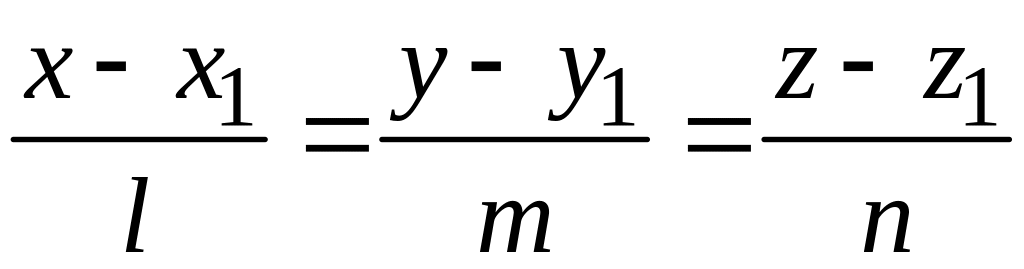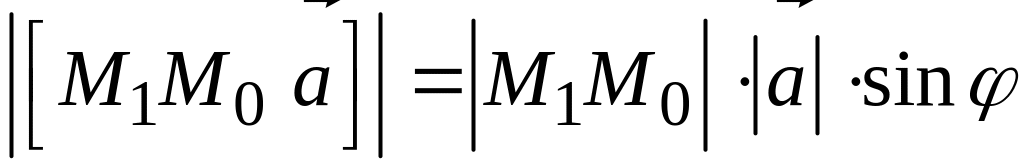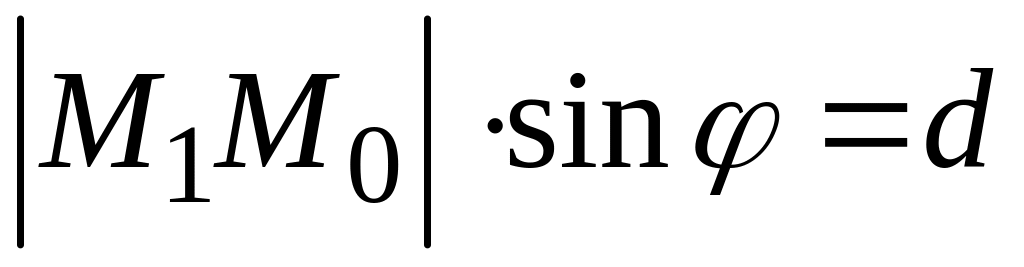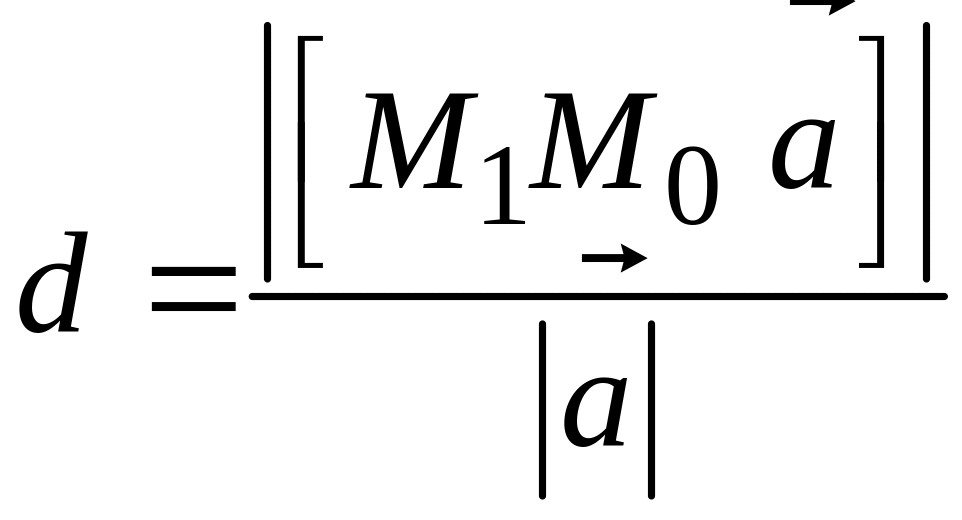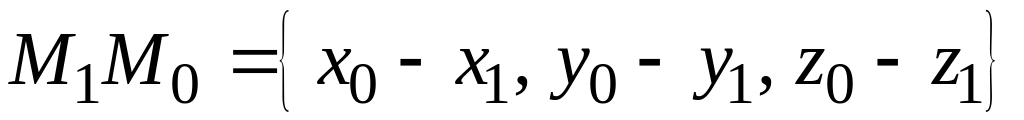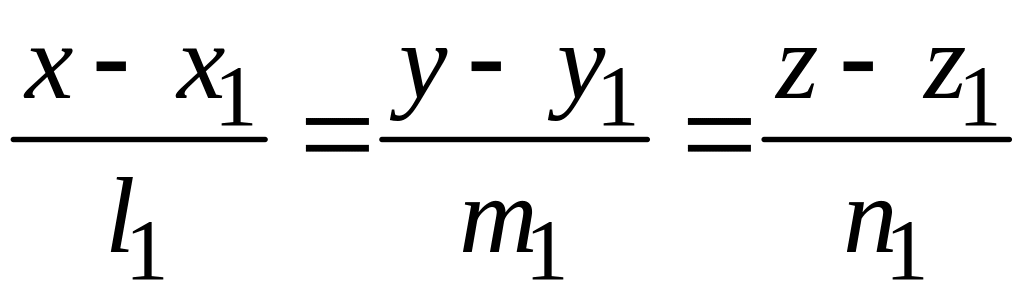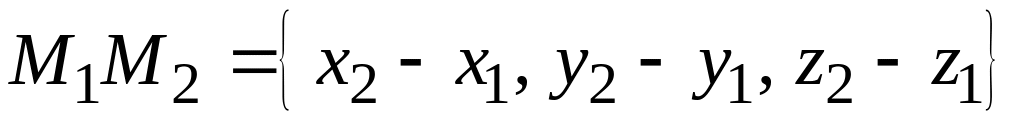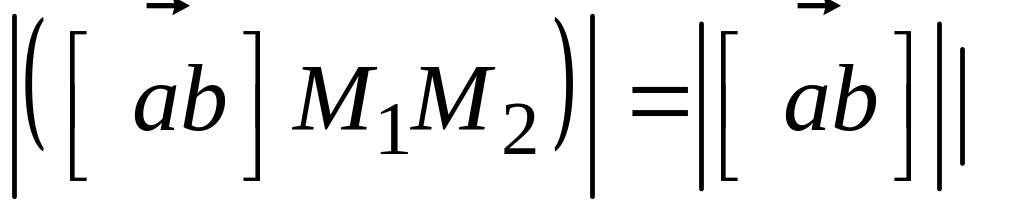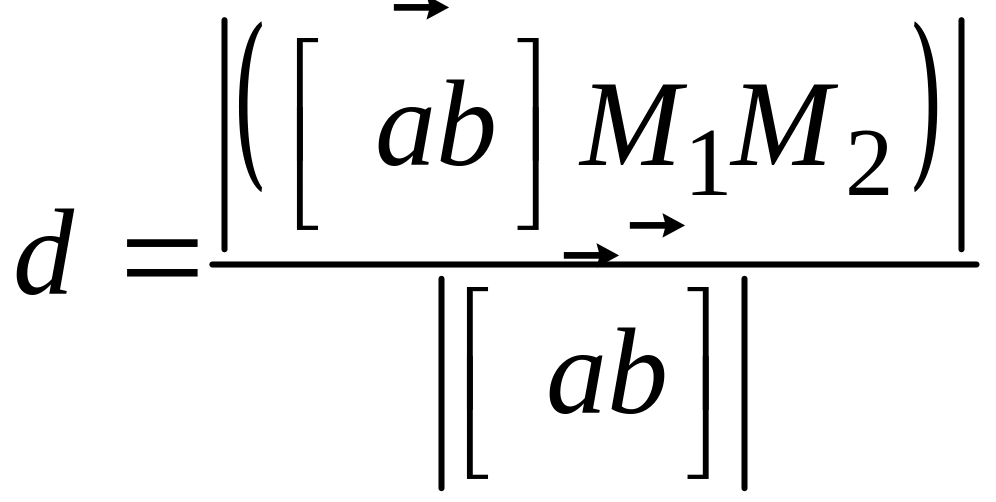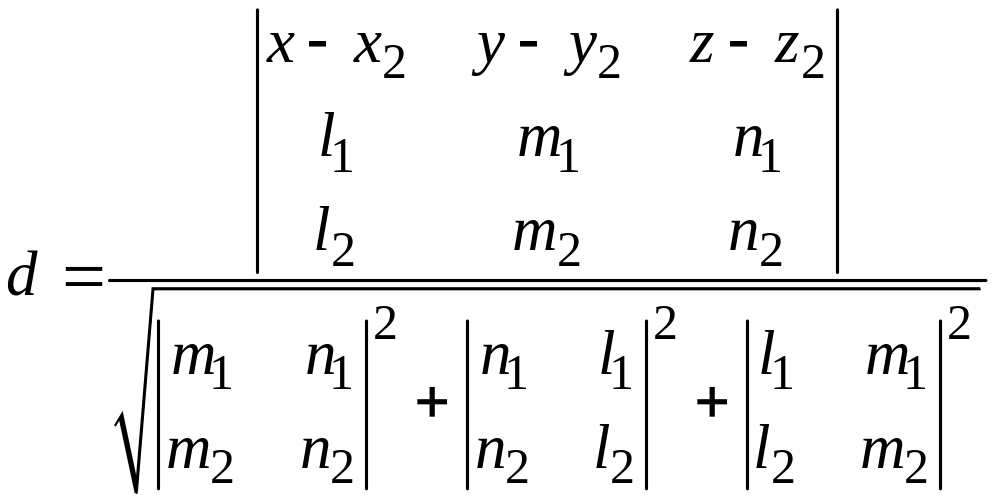Как составить каноническое уравнение перпендикуляра к прямой

Уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой

В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

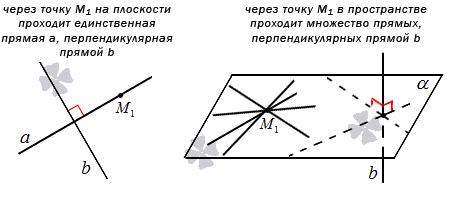
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.

Если плоскость α проходит через заданную точку М 1 перпендикулярно к заданной прямой b , то прямые, лежащие в этой плоскости, в том числе и проходящая через М 1 являются перпендикулярными заданной прямой b .

Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.

Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Если на плоскости с системой координат О х у z имеем прямую b , то ей соответствует уравнение прямой на плоскости, задается точка с координатами M 1 ( x 1 , y 1 ) , а необходимо составить уравнение прямой a , которая проходит через точку М 1 , причем перпендикулярно прямой b .

По условию имеем координаты точки М 1 . Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a , или координаты нормального вектора прямой a , или угловой коэффициент прямой a .

Необходимо получить данные из заданного уравнения прямой b . По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a . Отсюда получим, что угловые коэффициенты обозначаются как k b и k a . Они связаны при помощи соотношения k b · k a = — 1 .

Получили, что направляющий вектор прямой b имеет вид b → = ( b x , b y ) , отсюда нормальный вектор — n a → = ( A 2 , B 2 ) , где значения A 2 = b x , B 2 = b y . Тогда запишем общее уравнение прямой, проходящее через точку с координатами M 1 ( x 1 , y 1 ) , имеющее нормальный вектор n a → = ( A 2 , B 2 ) , имеющее вид A 2 · ( x — x 1 ) + B 2 · ( y — y 1 ) = 0 .

Нормальный вектор прямой b определен и имеет вид n b → = ( A 1 , B 1 ) , тогда направляющий вектор прямой a является вектором a → = ( a x , a y ) , где значения a x = A 1 , a y = B 1 . Значит осталось составить каноническое или параметрическое уравнение прямой a , проходящее через точку с координатами M 1 ( x 1 , y 1 ) с направляющим вектором a → = ( a x , a y ) , имеющее вид x — x 1 a x = y — y 1 a y или x = x 1 + a x · λ y = y 1 + a y · λ соответственно.

После нахождения углового коэффициента k b прямой b можно высчитать угловой коэффициент прямой a . Он будет равен — 1 k b . Отсюда следует, что можно записать уравнение прямой a , проходящей через M 1 ( x 1 , y 1 ) с угловым коэффициентом — 1 k b в виде y — y 1 = — 1 k b · ( x — x 1 ) .

Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.

Решение примеров

Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.

Записать уравнение прямой а, которая проходит через точку с координатами M 1 ( 7 , — 9 ) и перпендикулярна прямой b , которое задано каноническим уравнением прямой x — 2 3 = y + 4 1 .

Из условия имеем, что b → = ( 3 , 1 ) является направляющим вектором прямой x — 2 3 = y + 4 1 . Координаты вектора b → = 3 , 1 являются координатами нормального вектора прямой a , так как прямые a и b взаимно перпендикулярны. Значит, получаем n a → = ( 3 , 1 ) . Теперь необходимо записать уравнение прямой, проходящее через точку M 1 ( 7 , — 9 ) , имеющее нормальный вектор с координатами n a → = ( 3 , 1 ) .

Получим уравнение вида: 3 · ( x — 7 ) + 1 · ( y — ( — 9 ) ) = 0 ⇔ 3 x + y — 12 = 0

Полученное уравнение является искомым.

Ответ: 3 x + y — 12 = 0 .

Составить уравнение прямой, которая проходит через начало координат системы координат О х у z , перпендикулярно прямой 2 x — y + 1 = 0 .

Имеем, что n b → = ( 2 , — 1 ) является нормальным вектором заданной прямой. Отсюда a → = ( 2 , — 1 ) — координаты искомого направляющего вектора прямой.

Зафиксируем уравнение прямой, проходящую через начало координат с направляющим вектором a → = ( 2 , — 1 ) . Получим, что x — 0 2 = y + 0 — 1 ⇔ x 2 = y — 1 . Полученное выражение является уравнение прямой, проходящей через начало координат перпендикулярно прямой 2 x — y + 1 = 0 .

Ответ: x 2 = y — 1 .

Записать уравнение прямой, проходящей через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 .

Из уравнения y = — 5 2 x + 6 угловой коэффициент имеет значение — 5 2 . Угловой коэффициент прямой, которая перпендикулярна ей имеет значение — 1 — 5 2 = 2 5 . Отсюда делаем вывод, что прямая, проходящая через точку с координатами M 1 ( 5 , — 3 ) перпендикулярно прямой y = — 5 2 x + 6 , равна y — ( — 3 ) = 2 5 · x — 5 ⇔ y = 2 5 x — 5 .

Уравнение перпендикулярной прямой

Альтернативная формула
Прямая, проходящая через точку M₁(x₁; y₁) и перпендикулярная прямой Ax+By+C=0 , представляется уравнением

назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения перпендикулярной прямой (см. также как составить уравнение параллельной прямой).

Пример №1 . Составить уравнение прямой, проходящей через точку (2; -1) и перпендикулярной 4x-9y=3 .
Решение. Данную прямую можно представить уравнением y = 4 /₉x – 1 /₃ (a = 4 /₉). Уравнение искомой прямой есть y+1 = -9/4(x-2) , т.е. 9x+4y-14=0 .

Пример №2 . Решая пример 1 (A=4, B=-9) по формуле (2), найдем 4(y+1)+9(x-2)=0 , т.е. 9x+4y-14=0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-3, -2) перпендикулярно прямой 2y+1=0 .
Решение. Здесь A=0, B=2. Формула (2) дает -2(x+3)=0, т.е. x+3=0 . Формула (1) неприменима, так как a=0 .

Уравнение перпендикулярной прямой

Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?

Пусть y=k₁x+b₁ — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид

Если эта прямая проходит через точку M(x_o; y_o), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение x_o и y_o, мы найдем b.

1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.

Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то

Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид

Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:

Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)

2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).

Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.

Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.

3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).

Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.

Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.



5.5.3. Как найти прямую, содержащую общий перпендикуляр?

в) Эта задачка посложнее будет. «Чайникам» рекомендую пропустить данный пункт, не хочу охлаждать вашу искреннюю симпатию к

аналитической геометрии =) Кстати, и более подготовленным читателям, возможно, лучше тоже повременить – дело в том, что по сложности эту задачу

надо бы поставить последней в параграфе, но по логике изложения она должна располагаться здесь. …Впрочем, танцуйте читайте все!

Итак, требуется найти уравнения прямой , которая содержит общий

перпендикуляр скрещивающихся прямых.

Общий перпендикуляр скрещивающихся прямых – это отрезок, соединяющий данные прямые и перпендикулярный данным прямым:

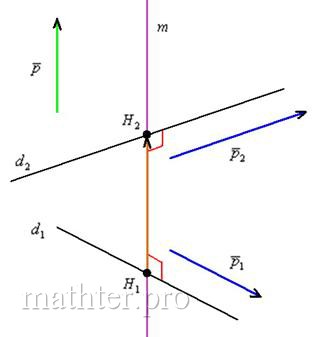
Вот наш красавец:  – общий перпендикуляр прямых . Он

единственный. Другого такого нет. Нам же требуется составить уравнения прямой ,

которая содержит данный отрезок.

Что известно о прямой «эм»? Известен её направляющий вектор , найденный

в предыдущем пункте. Но, к сожалению, мы не знаем ни одной точки, принадлежащей прямой «эм», не знаем и концов перпендикуляра – точек . Где эта перпендикулярная прямая пересекает две исходные прямые? В Африке, в

Антарктиде? Из первоначального обзора и анализа условия вообще не видно, как решать задачу….

Но есть хитрый ход, связанный с использованием параметрических уравнений прямой.

Решение оформим по пунктам:

1) Перепишем уравнения первой прямой в параметрической форме:

Рассмотрим точку . Координат мы не знаем. НО. Если точка

принадлежит данной прямой, то её координатам  соответствует вполне

конкретное значение параметра, обозначим его через . Тогда координаты

точки запишутся в виде:
, или:

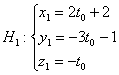
Жизнь налаживается, одна неизвестная – это всё-таки не три неизвестных.

2) Аналогичные действия проведём со второй прямой. Перепишем её уравнения в параметрическом

виде:

Если точка  принадлежит данной прямой, то при вполне конкретном

значении  её координаты должны удовлетворять

параметрическим уравнениям:
, или:

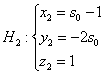
3) Запишем вектор . Ну и что, что нам не известны координаты точек – это же не

мешает из координат конца вектора  вычесть соответствующие координаты начала :

4) Вектор , как и ранее найденный вектор , является направляющим вектором прямой . Таким образом, они коллинеарны, и один вектор можно линейно

выразить через другой с некоторым коэффициентом пропорциональности «лямбда»:
или покоординатно:

Получилась самая, что ни на есть обычная система линейных уравнений с тремя неизвестными , которая стандартно разрешима, например, методом Крамера. Но так извращаться мы, конечно, не будем. Выразим из

3-го уравнения  и подставим эту «лямбду» в первые два уравнения:

Из 2-го уравнения выразим  и подставим в 1-е уравнение:
, а «лямбда» нам не потребуется.

То, что значения параметров получились одинаковыми – чистая случайность.

5) Небо полностью проясняется, подставим найденные значения  в наши

точки:
       

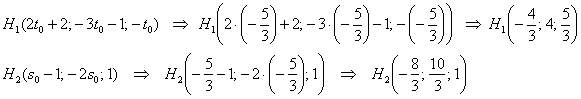
Сам вектор  нам не нужен, так как уже найден его коллега .

И после длинного пути всегда интересно выполнить проверку. Подставим координаты точки  в уравнения :

 –  получены верные равенства.

Подставим координаты  в уравнения :

 – получены верные равенства.

Вывод: найденные точки действительно принадлежат соответствующим прямым.

6) Заключительный аккорд: составим уравнения прямой  по точке  (можно взять ) и направляющему вектору :

В принципе, можно подобрать «хорошую» точку с целыми координатами, но это уже косметика.

5.5.4. Как найти расстояние между скрещивающимися прямыми?

5.5.2. Скрещивающиеся прямые

| Оглавление |



Автор: Aлeксaндр Eмeлин

Уравнение
перпендикуляра, опущенного из точки

на
прямую, заданную каноническими уравнениями

относительно
декартовой прямоугольной системы
координат, можно записать в виде
пересечения двух плоскостей:

,

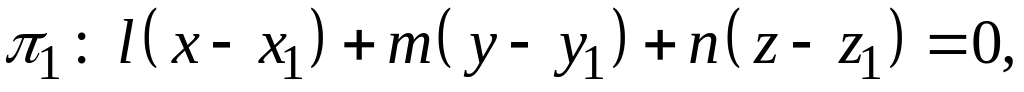
т
ак
как первое из этих уравнений выражает
плоскость, проходящую через точку

перпендикулярно данной прямой, а второе
– плоскость, проходящую через данную
точку

и данную прямую. Эти две плоскости
пересекаются по прямой, проходящей
через точку

и пересекающей данную прямую под углом

(рис. 133).

§ 92. Уравнение общего перпендикуляра к двум неколлинеарным прямым

Пусть
две прямые p
и
q
заданы своими каноническими уравнениями:

,

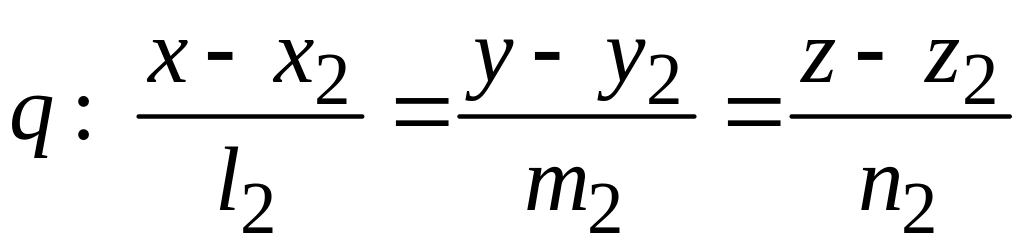
относительно
декартовой прямоугольной системы
координат. Предположим, что направляющие
векторы этих прямых

и

неколлинеарны,
т.е. что данные прямые или скрещиваются,
или пересекаются. Пусть l
– прямая, которая пересекает обе прямые
под углом

.

Тогда
за направляющий вектор прямой l
можно взять векторное произведение

направляющих векторов данных прямых:

.

Общий перпендикуляр l
к двум данным прямым можно определить
как прямую, по которой пересекается
плоскость

,
проходящая через прямую р
компланарно вектору

,
с плоскостью

,
проходящей через прямую q
компланарно

,
(рис.134). Уравнение плоскости

,
имеет вид:

Так как
эта плоскость проходит через точку

прямой р,
и коллинеарна векторам

и

.

Аналогично составляется уравнение
плоскости

:

.
(2)

Общий
перпендикуляр l
к данным прямым выражается уравнениями
(1) и (2).

§ 93. Расстояние от точки до прямой в пространстве

Пусть
в пространстве заданы точка

и прямая l
каноническими уравнениями

.

относительно
декартовой прямоугольной системы
координат.

Расстояние
d
от точки

до прямой l
можно определить как высоту параллелограмма,
сторонами которого служит вектор

и направляющий вектор

прямой l
отложенный от точки

этой прямой. Поэтому для определения
расстояния d
рассмотрим модуль векторного произведения:

.

Но

,
следовательно (рис. 135),

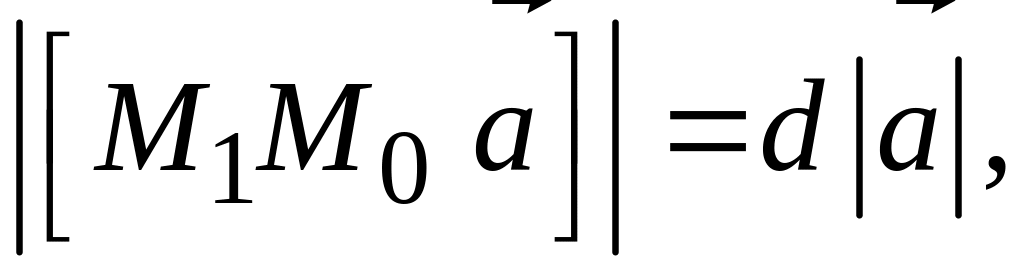
откуда

.

Так как

,

то

Потому

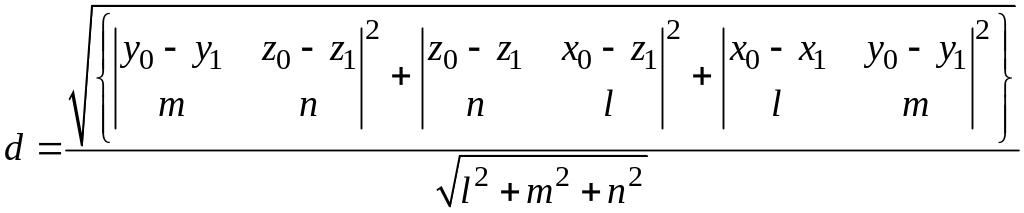
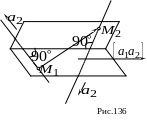
§ 94. Кротчайшее расстояние между двумя прямыми

Если две прямые скрещиваются, т.е. не
лежат в одной плоскости, то кротчайшее
расстояние между ними (как доказывается
в элементарной геометрии) есть длина
отрезка общего перпендикуляра к этим
двум прямым, концы которого лежат на
этих прямых. Отсюда следует, что кротчайшее
расстояние между двумя скрещивающимися
прямыми равно величине ортогональной
проекции любого отрезка

концы которого лежат на этих прямых
(рис. 136) на любую прямую, перпендикулярную
к данным; это очевидно при проектировании
точек

и

на общий перпендикуляр к данным прямым;
величина проекции не изменится, если
спроектировать отрезок на любую прямую,
параллельную этому перпендикуляру.
Пусть две скрещивающиеся прямые заданы
каноническими уравнениями

,

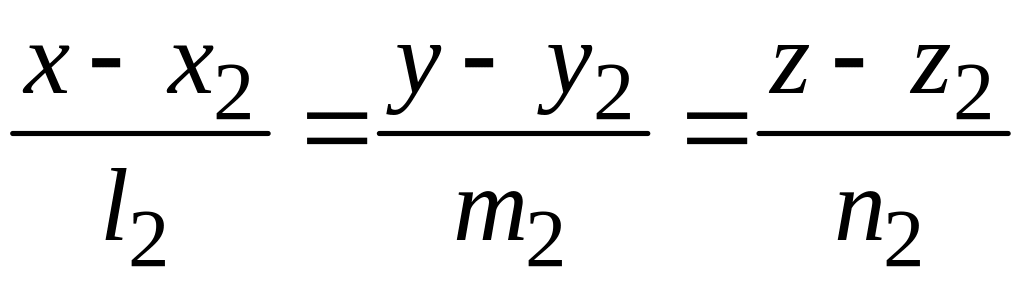
относительно
декартовой прямоугольной системы
координат. Кратчайшее расстояние между
ними равно абсолютной величине проекции
вектора

,

начало

конец которого

лежат соответственно на первой и второй
прямых, на прямую, параллельную вектору

,

перпендикулярному
направляющим векторам:

;

данных прямых.

Так как

пр.

,

то
кротчайшее расстояние d
между двумя скрещивающимися вычисляется
по формуле

,

или в координатах

.

Отметим, что эта формула верна и для
двух пересекающихся прямых: числитель
обратится в нуль, а знаменатель отличен
от нуля, и мы получим d
= 0 в соответствии с определением
кротчайшего расстояния между двумя
пересекающимися прямыми.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как составить уравнение прямой перпендикулярной данной прямой и проходящей через данную точку?

Пусть y=k₁x+b₁ — данная прямая. С учётом условия перпендикулярности прямых уравнение прямой, перпендикулярной данной, имеет вид

   

Если эта прямая проходит через точку M(x_o; y_o), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение x_o и y_o, мы найдем b.

Примеры.

1) Написать уравнение прямой, проходящей через точку A(-10;3), перпендикулярной прямой y=5x-11.

Решение:

Так как прямые перпендикулярны, если их угловые коэффициенты обратны по абсолютной величине и противоположны по знаку, то

   

Значит уравнение прямой, перпендикулярной прямой y=5x-11, имеет вид

   

Так как прямая проходит через точку A(-10;3), то координаты A удовлетворяют уравнению прямой:

   

откуда b=1.

Итак, уравнение прямой, перпендикулярной прямой y=5x-11 и проходящей через точку A(-10;3)

   

Ответ: y= -0,2x+1.

2) Написать уравнение прямой, перпендикулярной прямой x= -2, проходящей через точку M(-5;9).

Решение:

Прямая x= -2 перпендикулярна оси абсцисс. Значит, прямая, уравнение которой мы ищем, параллельна оси абсцисс, то есть ищем уравнение прямой в виде y=b.

Так как искомая прямая проходит через точку M(-5;9), то координаты M удовлетворяют уравнению прямой: y=9.

Ответ: y=9.

3) Написать уравнение прямой, перпендикулярной прямой y=4, проходящей через точку F(7;-5).

Решение:

Прямая y=4 перпендикулярна оси ординат. Следовательно, прямая, уравнение которой мы ищем, параллельна оси ординат, а значит, её уравнение имеет вид x=a.

Так как эта прямая проходит через точку F(7;-5), то координаты F удовлетворяют уравнению прямой: x=7.

Ответ: x=7.

Как написать уравнение перпендикуляра, опущенного из точки на прямую

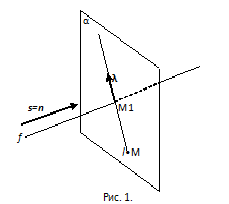
Вопрос относится к аналитической геометрии. При этом возможны две ситуации. Первая из них простейшая, относящаяся к прямым на плоскости. Вторая задача, относится к прямым и плоскостям в пространстве. Читателю следует иметь представление о простейших методах векторной алгебры.

Инструкция

Первый случай. Дана прямая у=kx+b на плоскости. Требуется найти уравнение перпендикулярной ей прямой, проходящей через точку M(m, n). Уравнение этой прямой ищите в виде y=cx+d. Используйте геометрический смысл коэффициента k. Это тангенс угла наклона α прямой к оси абсцисс k=tgα. Тогда с=tg(α+π/2)=-ctgα=-1/tgα=-1/k. На данный момент найдено уравнение перпендикулярной прямой в виде y=-(1/k)x+d, в котором осталось уточнить d. Для этого используйте координаты заданной точки М(m, n). Запишите уравнение n=-(1/k)m+d, из которого d=n-(1/k)m. Теперь можно дать ответ y=-(1/k)x+n-(1/k)m. Существуют и другие виды уравнений плоской прямой. Поэтому есть и другие способы решений. Правда, все они легко преобразуются друг в друга.

Пространственный случай. Пусть известная прямая f задана каноническими уравнениями (если это не так, приведите их к каноническому виду). f: (x-x0)/m=(y-y0)/n=(z-z0)/p, где М0(x0, y0, z0) – произвольная точка этой прямой, а s={m,n,p} – ее направляющий вектор. Заданная точка М(a,b,c). Сначала найдите плоскость α, перпендикулярную прямой f, содержащую М. Для этого используйте одну из форм общего уравнения прямой A(x-a)+B(y-b)+C(z-c)=0. Ее направляющий вектор n={A,B,C} совпадает с вектором s (см. рис. 1). Поэтому n={m,n,p} и уравнение α: m(x-a)+n(y-b)+p(z-c)=0.

Теперь найдите точку М1(x1,y1,z1) пересечения плоскости α и прямой f путем решения системы уравнений (x-x0)/m=(y-y0)/n=(z-z0)/p и m(x-a)+n(y-b)+p(z-c)=0. В процессе решения возникнет одинаковая для всех искомых координат величина u= [m(x0-a)+n(y0-b)+p(z0-c)]/(m^2+n^2+p^2). Тогда решение x1=x0-mu, y1=y0-nu, z1=z0-pu.

На этом шаге поиска перпендикулярной прямой ℓ, найдите ее направляющий вектор g=M1M={x1-a,y1-b,z1-c}={х0-mu-a,y0-nu-b,z0-pu-c}. Положите координаты этого вектора m1=х0-mu-a, n1=y0-nu-b, p1=z0-pu-c и запишите ответ ℓ: (x-a)/(х0-mu-a)=(y-b)/(y0-nu-b)=(z-c)/(z0-pu-c).

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?