Написать канонические и параметрические уравнения прямой, образованной пересечением плоскостей
Решение
1) Найдем координаты фиксированной точки. Из исходной системы уравнений
исключим z.
Положим z=0, тогда:
откуда находим: x=1, y= -2.
Таким образом, нашли координаты фиксированной точки M0(1,-2,0).
2) Направляющий вектор определяется как векторное произведение нормалей двух плоскостей, образующих прямую:
3) Запишем канонические уравнения:
4) Обозначив,
получаем параметрические уравнения:
x=t+1, y=4t-2, z=4
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
5.4.4. Прямая, заданная пересечением двух плоскостей
Если плоскости пересекаются, то система линейных уравнений

То есть прямая задана уравнениями двух плоскостей. Типовая и
распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:
Задача 151
Записать канонические уравнения прямой
Решение: чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух
плоскостей….
1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? Методом подбора. В системе уравнений обнулим
какую-нибудь координату, например, . Тогда получается система двух линейных
уравнений с двумя неизвестными: . Почленно складываем уравнения и находим
решение системы:
Таким образом, точка принадлежит данной прямой. Но принадлежит ли?
Выполним проверку – подставим её координаты в исходную систему уравнений:
Получены верные равенства, значит, действительно .
В процессе подбора обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в
системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует
проводить мысленно или на черновике.
2) Как найти направляющий вектор прямой? Существует готовая формула: если прямая задана пересечением двух
плоскостей 

В нашей задаче:
Однако всех формул не упомнишь и поэтому очень важно понимать, откуда они взялись. Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей: и
, поэтому вектор «пэ» можно найти как векторное произведение векторов нормали:
.

«снимаем» их векторы нормали:
и находим направляющий вектор прямой:
Проверим результат с помощью скалярного произведения:
, ч.т.п.
И, наконец, завершающий этап:
3) Составим канонические уравнения прямой по точке и
направляющему вектору :
Ответ:
Аналогичная задача для самостоятельного решения:
Задача 152
Записать канонические уравнения прямой
Будьте внимательны! Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения
и подставьте в моё уравнение (или наоборот).
Полное решение и ответ в конце книги.
И сейчас самое время перейти к простейшим задачам с пространственной прямой:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Прямую
линию в пространстве можно определить
как линию пересечения двух непараллельных
плоскостей.
. (7.1)
Часто
удобнее канонический вид уравнения
прямой.
Определение
7.1. Любой ненулевой вектор
,
параллельный данной прямой будем
называть направляющим вектором прямой.
Задача
7.1. Составить уравнение прямой
,
проходящей через точку
параллельно вектору
.
Решение.
Рассмотрим
вектор
,
начало которого совпадает с точкой
,
а конец − в произвольной точке
.
Чтобы
точка
лежала на прямой
,
вектор
должен быть параллелен вектору
.
Условие параллельности векторов состоит
в пропорциональности сходственных
координат, из чего следует
(7.2)
Это
уравнение называется каноническим
уравнением прямой
в пространстве.
Приравняв
выражение (7.2) параметру
,
получим параметрические
уравнения прямой.
(7.3)
Эти
уравнения имеют наглядное физическое
истолкование. Если принять что,
−время,
а
вектор скорости, то уравнения (7.3) − это
три проекции уравнения движения точки
на координатные оси.
Уравнение
прямой, проходящей через две заданные
точки
и
получим из уравнения (7.2), приняв, что
направляющий вектор
(7.4)
и
подставив выражение (7.4) в (7.2):
(7.5)
Чтобы
привести к каноническому
виду уравнение
прямой, заданной как линия пересечения
двух плоскостей, нужно найти направляющий
вектор прямой и точку, лежащую на прямой.
Длина вектора − произвольная, точка,
лежащая на прямой − любая.
Пусть
прямая есть линия пересечения плоскостей
(7.6)
. (7.6)
Направляющий
вектор прямой
ортогонален каждому из нармальных
векторов плоскостей
и
.
Поэтому
определим вектор
,
как векторное произведение нормальных
векторов
(7.7)
Компоненты
вектора
будут иметь вид
(7.8)
Для
определения координат точки, лежащей
на прямой, добавим в систему уравнений
(7.6) уравнение третьей плоскости. Удобно
добавить одну из координатных плоскостей
или
.
Чтобы
получающаяся система уравнений второго
порядка имела единственное решение, её
главный определитель не должен обращаться
в нуль. Это накладывает ограничения на
выбор координатной плоскости.
Пусть
.
Пусть в полученной системе уравнений
. (7.9)
главный
определитель
.
Тогда
координаты искомой точки определяются
по формулам Крамера
. (7.10)
Искомое
каноническое уравнение запишем в
следующем виде
(7.11)
-
Уравнение прямой, проходящей через 2 заданные точки в пространстве. Параметрическое уравнение прямой. Нахождение точки пересечения прямой и плоскости.
Чтобы
точка M
лежала на прямой L,
вектор M1M
должен быть параллелен вектору q.
Условие параллельности векторов состоит
в пропорциональности сходственных
координат, из чего следует
(1)
Уравнение
прямой, проходящей через две заданные
точки
M1(x1,y1,z1)
и M2(x2,y2,z2)
получим из уравнения (1), приняв, что
направляющий вектор
(2)
и
подставив выражение (2) в (1):
(3)
Приравняв
выражение (1) параметру t,
получим параметрические
уравнения прямой.
(4)
Эти
уравнения имеют наглядное физическое
истолкование. Если принять что, t
−время, а
вектор скорости, то уравнения (4) − это
три проекции уравнения движения точки
на координатные оси.
Найти
точку пересечения прямой:
(1)
и
плоскости:
(2)
Решение.
Приравняем
выражение (1) к параметру t
и выразим через него x,
y
и z
(3)
(4)
Подставим
x,
y
и z
из (4) в уравнение плоскости.
(5)
Координаты
точки пересечения прямой и плоскости
получим, подставив значение t0,
найденное из (5) в уравнения (4).
(6)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение прямой как результат пересечения плоскостей
| Коэффициенты первой плоскости | |
| Коэффициенты второй плоскости | |
| Уравнение первой плоскости |
| Уравнение второй плоскости |
| Уравнение прямой как пересечение двух плоскостей |
Определяем уравнение прямой в пространстве если нам известны общие уравнения двух плоскостей.
Обновление от 13 октября 2019 года: Используется алгоритм описанный в статье ФРС. Фундаментальное решение системы уравнений
Если первая плоскость задана уравнением вида
а другая плоскость уравнением вида
и они перескаются, то уравнение полученной прямой можно найти по двум точкам, принадлежащих одновременно этим плоскостям.
Прямая в пространстве, проходящая через две точки )
)
(cfrac{x-x_0}{x_1-x_0}=cfrac{y-y_0}{y_1-y_0}=cfrac{z-z_0}{z_1-z_0})
B принципе этого достаточно что бы решить уравнение. Положим что z=0 ( можно брать любое число, но с нулем оно как то удобнее) тогда уравнения плоскости приобретают вид
Получили систему линейных уравнений которая легко решается.
Определили таким образом точку
Теперь пусть z=1 и решаем систему
и получаем вторую точку
Эти две точки принадлежат обеим плоскостям и значит уравнение прямой имеет вид
(cfrac{x-x_0}{x_1-x_0}=cfrac{y-y_0}{y_1-y_0}=cfrac{z}{1})
Есть еще второй способ, использующий вектора. Рассмотрим и его.
Если известна точка в пространстве )
то уравнение прямой имеет вид
(cfrac{x-x_0}{m}=cfrac{y-y_0}{n}=cfrac{z-z_0}{p})
Узнав координаты точки )
Для этого вычислим векторное произведение
(begin{pmatrix}i&j&k\A_1&B_1&C_1\A_2&B_2&C_2end{pmatrix}=im+jn+kp)
и подставив вычисленные значения в уравнение
(cfrac{x-x_0}{m}=cfrac{y-y_0}{n}=cfrac{z-z_0}{p})
мы узнаем уравнение прямой в пространстве, как пресечение двух плоскостей.
Созданный онлайн калькулятор позволяет автоматически находить уравнение прямой по двум заданным общим уравнениям плоскостей.
Условие параллельности плоскостей
Две плоскости заданные уравнениями вида
лишь тогда параллельны, когда верным становится соотношение
(cfrac{A_1}{A_2}=cfrac{B_1}{B_2}=cfrac{C_1}{C_2})
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Существует несколько различных типов уравнений, описывающих кривую первого порядка, называемую прямой. Каждый из них оптимален для какой-то своей цели. Давайте познакомимся с ними поближе.
Каноническое уравнение прямой в пространстве
Определение 1
Канонический вид уравнения прямой в пространстве выглядит как следующее равенство:
$frac{x – x_0}{α} = frac{y – y_0}{β} = frac{z – z_0}{γ}$,
где буквы $(x_0, y_0, z_0)$ используются для обозначения координат любой точки, возлежащей на данной прямой, а $(α, β, γ)$ — координаты направляющего эту прямую вектора, как несложно догадаться, они не могут быть нулевыми.
Не во всех случаях удобно и практично пользоваться каноническим уравнением, поэтому частенько возникает надобность использовать какое-то другое, например, можно прибегнуть к параметрическому.
Для каких прямых не представляется возможным или нельзя написать каноническое уравнение?
Глядя на это уравнение, видно, что его возможно использовать только в том случае, если координаты направляющих векторов исследуемых прямых не равны нулю, для таких прямых стоит воспользоваться параметрическими уравнениями.
Определение 2
Параметрический вид уравнений прямой в пространстве такой:
$begin{cases} x = x_1 + α cdot λ \ y = y_1 + β cdot λ \ z = z_1 + γ cdot λ \ end{cases}$,
где $x_1, y_1, z_1$ — координаты некоторой точки, находящейся на описываемой прямой, $α, β, γ$ — координаты параллельного или лежащего на данной прямой вектора, $λ$ — произвольное число-коэффициент, иногда для его обозначения используют слово “параметр”.
Параметрическое уравнение как раз удобно применять если одна из координат направляющего вектора равна нулю.
Чтобы произвести переход от параметрического вида уравнения к каноническому виду уравнения прямой в пространстве, осуществите вывод канонического уравнения прямой из параметрического.
«Каноническое уравнение прямой в пространстве» 👇
Для этого следует в к каждом уравнении перенести $λ$ в левую часть, а затем приравнять уравнения. Никакой магии, а только самая что ни на есть пресловутая арифметика:
$begin{cases} λ = frac{x — x_1}{ α} \ λ = frac{y — y_1}{β} \ λ = frac{z — z_1}{γ} \ end{cases}$
$frac{x – x_0}{α} = frac{y – y_0}{β} = frac{z – z_0}{γ}$
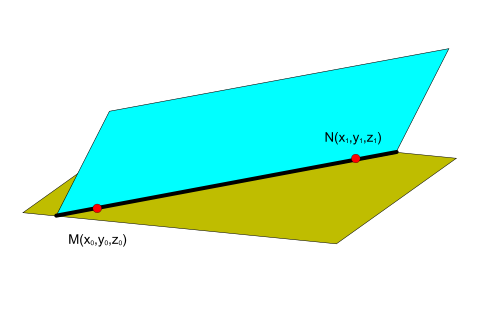
Уравнение прямой, образуемой пересечением двух плоскостей
Рисунок 1. Связь канонического и общего уравнения прямой
Для того чтобы составить каноническое уравнение прямой в пространстве, заданной пересечением плоскостей, необходимо познакомиться поближе с 2 исследуемыми плоскостями.
Любую плоскость, находящуюся в пространстве, можно описать с помощью равенства:
$Ax + By + Cz + D = 0$,
где $A, B, C$ и $D$ — постоянные, причём $A, B, C$ не могут быть одновременно все нулевыми.
Соответственно, не нужно быть гением, чтобы понять, что если две плоскости пересечены между собой, то на их общей части будет возлежать некая прямая. Чтобы её найти, нужно получить общее решение следующей системы уравнений:
$begin{cases} A_1x + B_1y + C_1z + D_1 = 0 \ A_2x + B_2y + C_2z + D_2 = 0 \ end{cases}$
С помощью же частного решения этой системы уравнений можно узнать, принадлежит ли какая-либо точка трёхмерной системы координат описанным уравнениями плоскостям и, конечно же, нашей прямой. Для этого нужно просто подставить её икс, игрек и зет в систему.
Приведённая система уравнений является своеобразной “формулой”, служащей для нахождения общего уравнения прямой в пространстве.
Иногда в каких-либо практических задачах требуется получить из уравнения прямой в пространстве в общем виде параметрические или канонические уравнения, тогда в первую очередь вам стоит узнать координаты её направляющего вектора и какую-либо точку, находящуюся на изучаемой прямой.
Ну что ж, давайте решать нашу задачу. На первом этапе вычислим $x, y, z$ для направляющего вектора.
Найдём нормальные вектора для плоскостей. Если кто забыл, нормальный вектор — это такой вектор, который является перпендикулярным (ортогональным) к данной плоскости или прямой.
Для этого из нашего очаровательного примера системы уравнений необходимо взять коэффициенты из уравнений. В итоге для 1-ой плоскости вектор-нормаль будет выглядеть как $(A_1; B_1; C_1)$, а для второй как $(A_2; B_2; C_2)$.
Теперь необходимо перемножить оба вектора и получить их произведение, здесь $(i, j, k)$ — координаты единичного вектора.
$overline{a} = [overline{n} cdot overline{n}] = left| begin{array}{ccc} overline{i} & overline{j} & overline{k} \ A_1 & B_1 & C_1 \ A_2 & B_2 & C_2 \ end{array} right| = overline{i} cdot left| begin{array}{cc}\B_1 & C_1 \ B_2 & C_2\ end{array} right| — overline{j} cdot left| begin{array}{cc}\ A_1 & C_1 \ A_2 & C_2 \ end{array} right| + overline{k} cdot left| begin{array}{cc} \ A_1 & B_1 \ A_2 & B_2 \ end{array} right| $
$|overline{n} cdot overline{n}| = overline{i} cdot (B_1 cdot C_2 – C_1 cdot B_2) — overline{j} cdot (A_1 cdot C_2 – A_2 cdot C_1) + overline{k} cdot (A_1 cdot B_2 – A_2 cdot B_1)$
Следующим этапом выполняем поиск координат точки, возлежащей на искомой прямой.
Для выполнения этого наиболее «сложного» пункта необходимо выбрать одну наиболее нравящуюся вам координату $x, y$ или $z$ и вместо неё подставить в систему уравнений, описывающую плоскости, нулевое значение.
Пример 1
Составьте каноническое уравнение прямой, получаемой из системы уравнений, описывающей пару пересечённых плоскостей:
$begin{cases} 2x – y + 3z + 4 = 0 \ x + 5y – 3z – 7 = 0 \ end{cases}$
Найдём направляющий вектор, для этого сначала запишем вектора нормалей плоскостей:
$overline{n_1}(2;-1;3), overline{n_2}(1;-5;-3)$
Ну а сейчас пора вычислить сам направляющий вектор:
$overline{a} = left| begin{array}{ccc} overline{i} & overline{j} & overline{k} \ 2 & -1 & 3 \ 1 & 5 & -3 \ end{array} right| = overline{i} cdot left| begin{array}{cc}\ -1 & 3 \ 5 & -3\ end{array} right| — overline{j} cdot left| begin{array}{cc}\ 2 & 3 \ 1 & -3 \ end{array} right| + overline{k} cdot left| begin{array}{cc} \ 2 & -1 \ 1 & 5 \ end{array} right| $
$overline{a} = (3 – 15) cdot overline{i} — (-6-3) cdot overline{j} + (10 +1) cdot overline{k} = -12 overline{i} + 9 overline{j} + 11 overline{k}$
Найдём точку, находящуюся на нашей прямой, тут всё просто, приравняем $y$ к нулю и внедрим в нашу систему уравнений:
$begin{cases} 2x + 3z + 4 = 0 \ x – 3z – 7 = 0 \ end{cases}$
Решение вышеприведённой системы уравнений будет: $x = 1, z = -2$, то есть координаты точки, возлежащей на нашей прямой, будут $(1; 0; -2)$.
Подставим все полученные нами цифры и получим следующее уравнение:
$frac{x-1}{-12} = frac{y}{9} = frac{z+2}{11}$
Составление канонического уравнения прямой по координатам двух точек
На практике это очень распространённая и любимая во многих вузах и других учебных заведениях задача — нужно найти уравнение прямой в пространстве, проходящей через 2 точки. Примем заранее, что эти две точки не обладают одинаковыми $x, y, z$.
Для того чтобы написать уравнение прямой в пространстве, проходящей через 2 точки, воспользуйтесь координатами ваших точек и внедрите их в следующее уравнение:
$frac{x – x_1}{x2 – x_1} = frac{y – y_1}{y_2 – y_1} = frac{z – z_1}{z_2 – z_1}$
Это уравнение можно вывести из параметрического уравнения прямой.
Допустим, у нас есть две точки с координатами $(x_1; y_1; z_1)$, и для второй $(x_2; y_2; z_2)$.
Найти направляющий вектор для изучаемой прямой при наличии пары точек несложно, вектор с координатами $(x_2 – y_1; y_2 – y_2;z_2 – z_2)$ и будет желаемой частью результата.
Придумаем точку, находящуюся на нашей прямой, пусть она будет обладать координатами $(x_1;y_1;z_1)$.
Помещаем обнаруженные нами координаты вектора и точки в каноничное уравнение прямой в пространстве и получим уравнение прямой, проходящей через 2 точки.
Если же необходимо выразить именно параметрические уравнения из координат двух точек, через которые проведена некая одна прямая, то тут тоже всё довольно просто и без неожиданностей:
$begin{cases} x = x_1 + (x_2 — x_1) cdot λ \ y = y_1 + (y_2 — y_1)cdot λ \ z = z_1 + (z_2 — z_1) cdot λ \ end{cases}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

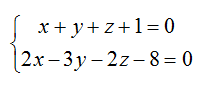
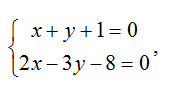
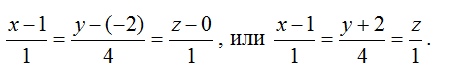
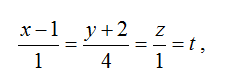












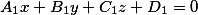
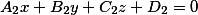
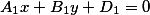
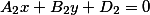
)
=0)
=0)
)
)
