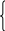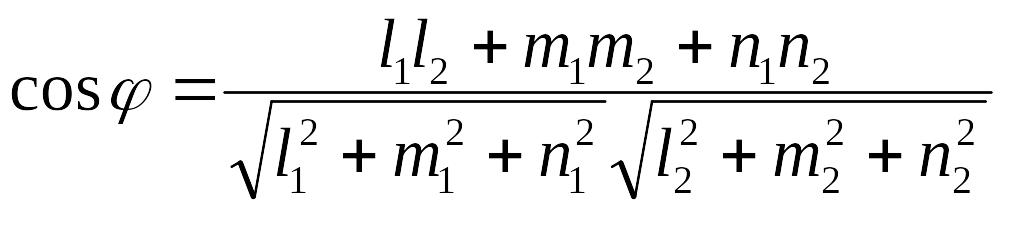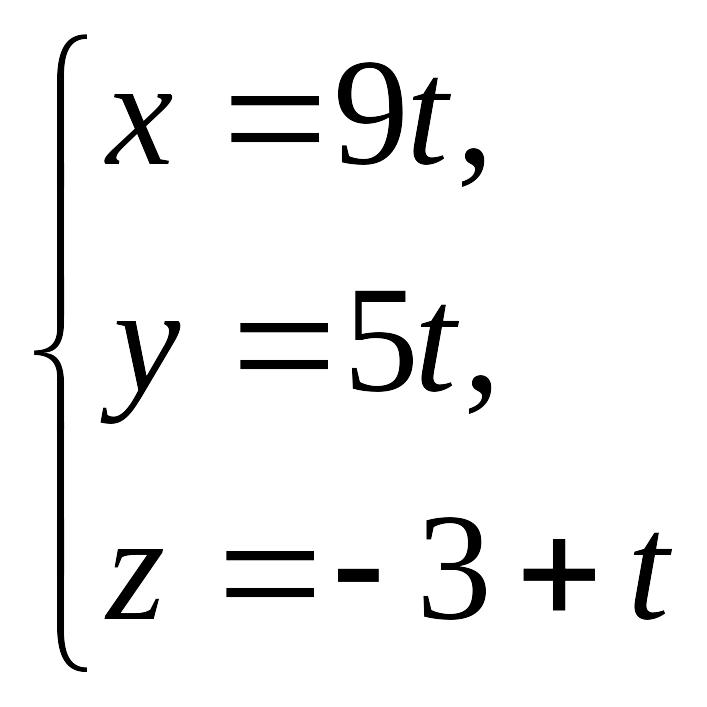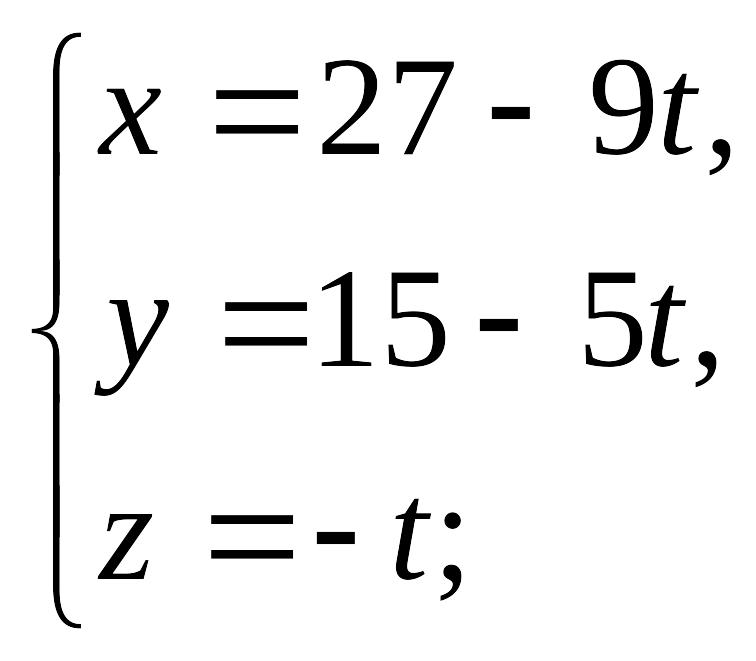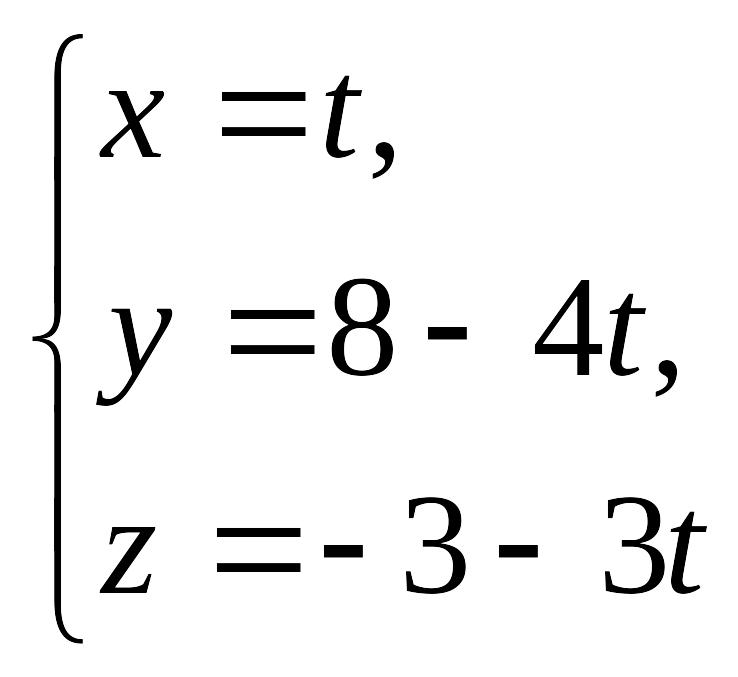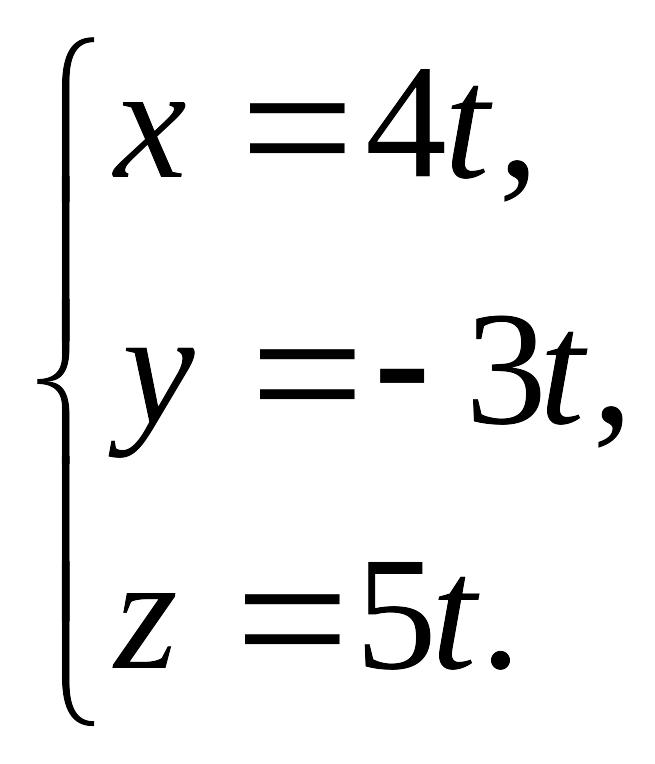Как составить каноническое уравнение прямой по двум точкам

Уравнение
прямой, проходящей через две различные
точки М₁(х₁,
y₁,
z₁)
и М₂(х₂,
y₂,
z₂)
имеет вид

_{EMBED
Equation.3}


,
(12.3)

где
направляющий вектор EMBED Equation.3

=
EMBED Equation.3

.

Пример
12.2. Составить
канонические уравнения прямой, проходящей
через две заданные точки EMBED Equation.3

(1,-2,1)
и EMBED Equation.3

(3,1,-1)

Решение.
Применяя
формулу (3.3), имеем

_{EMBED
Equation.3}

.
Тогда канонические уравнения прямой
имеют вид EMBED Equation.3

.

12.3. Параметрические уравнения прямой.

Параметрические
уравнения прямой получается из
канонических уравнений (12.2).Примем за
параметр EMBED Equation.3

каждое из соотношений (12.2), -¥<
t
<+¥
; таким образом получим

EMBED Equation.3

,

следовательно
x–
х₁
=lt;
y
– y1=
mt;
z
— z₁=
nt,

x
=x₁
+lt,

y
= y₁
+mt,
(12.4)

z
= z₁
+ nt

—
параметрические
уравнения прямой.

Пример
12.3. Составить
параметрические уравнения прямой
EMBED Equation.3

Решение.
Найдем
координаты точки, лежащей на прямой.
Положим EMBED Equation.3

.Тогда
система уравнений примет вид

EMBED
Equation.3

Решая
эту систему, получим EMBED Equation.3

.

Следовательно,
на прямой фиксирована точка EMBED Equation.3

.

Найдем координаты
направляющего вектора прямой

EMBED
Equation.3

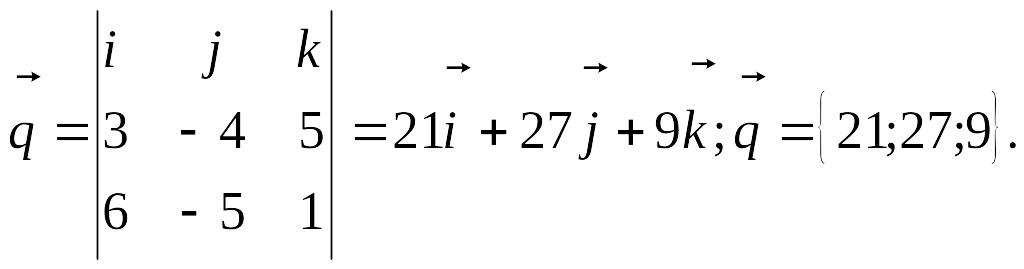
Тогда параметрические
уравнения прямой примут вид

EMBED
Equation.3

12.4.Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых.

Определение
угла между прямыми сводится к определению
угла между их направляющими векторами
EMBED Equation.3

;
_{EMBED Equation.3}

.

Из определения
скалярного произведения имеем:

_{EMBED Equation.3}

(12.5)

Условие
параллельности прямых эквивалентно
условию коллинеарности их направляющих
векторов EMBED Equation.3

и EMBED Equation.3

:

_{EMBED Equation.3}

(12.6)

Условие
перпендикулярности: ( EMBED Equation.3

,
EMBED Equation.3

)
= 0:

l₁l₂
+ m₁m₂
+n₁n₂
= 0
(12.7)

Пример
12.4 . Найти
угол между прямой, проходящей через две
точки EMBED Equation.3

и прямой

EMBED Equation.3

.

Решение.
Координаты направляющего вектора первой
прямой EMBED Equation.3

.
Для второй прямой направляющим является
вектор EMBED Equation.3

.
Угол между направляющими векторами
вычислим, используя формулу (12.5),

EMBED
Equation.3

EMBED Equation.3

.

Вопросы для самопроверки

1. Как
   записывается общее уравнение прямой
   в пространстве?

2. Как
   записываются параметрические уравнения
   прямой в пространстве?

3. Как
   записываются уравнения прямой, проходящей
   через две точки в пространстве?

4. Как
   вычисляются углы между двумя прямыми
   в пространстве?

5. Каковы
   условия параллельности и перпендикулярности
   двух прямых в пространстве?

Задачи для самостоятельного решения

1.Исследовать
взаимное расположение следующих пар
прямых в пространстве

1)
EMBED Equation.3

и EMBED Equation.3

2)
EMBED Equation.3

и EMBED Equation.3

3)
EMBED Equation.3

и EMBED Equation.3

4)
EMBED Equation.3

и EMBED Equation.3

Ответ.
1) совпадают; 2) параллельны; 3) скрещиваются;
4) пересекаются.

2.
Составить параметрические уравнения
прямой: EMBED Equation.3

Ответ.
EMBED Equation.3

3.
Написать параметрические уравнения
прямой, проведенной через начало
координат перпендикулярно плоскости
EMBED Equation.3

Ответ.
EMBED Equation.3

4.
Составить канонические уравнения
прямой, проходящей через точку М₁(2;
0 -3) параллельно: 1) вектору EMBED Equation.DSMT4

2) прямой EMBED Equation.DSMT4

3)
оси Ох; 4)
оси Оу; 5)
оси Оz.

Ответ.1)
EMBED Equation.DSMT4

2)
EMBED Equation.DSMT4

3)
EMBED Equation.DSMT4

4) EMBED Equation.DSMT4

5) EMBED Equation.DSMT4

5.
Через точки EMBED Equation.DSMT4

и EMBED Equation.DSMT4

проведена
прямая. Определить точки пересечения
этой прямой с координатными плоскостями.

Ответ.
EMBED Equation.DSMT4

,
EMBED Equation.DSMT4

,
EMBED Equation.DSMT4

.

6.
Даны вершины треугольника А(
3; 6; -7), В (-5;
2; 3) и
С
(4; -7; -2). Составить параметрические
уравнения его медианы, проведенной из
вершины С.

Ответ.
EMBED Equation.DSMT4

7.
Даны вершины треугольника А(
2; -1; -3), В (5;
2; -7) и
С
(-7; 11; 6). Составить канонические уравнения
биссектрисы его внешнего угла при
вершине А.

Ответ.
EMBED Equation.DSMT4

8.
Даны вершины треугольника А(
1; -2; -4), В (3;
1; -3) и
С
(5; 1; -7). Составить параметрические
уравнения его высоты, опущенной из
вершины В
на противоположную сторону.

Ответ.
EMBED
Equation.DSMT4

9.
Составить канонические уравнения
следующих прямых:

1)
EMBED Equation.DSMT4

2) EMBED Equation.DSMT4

Ответ.
1) EMBED
Equation.DSMT4

2)
EMBED Equation.DSMT4

10.
Доказать параллельность прямых:

1)
EMBED Equation.DSMT4

и EMBED Equation.DSMT4

2)
EMBED Equation.DSMT4

и

EMBED
Equation.DSMT4

11.
Доказать перпендикулярность прямых:

1)
EMBED Equation.DSMT4

и EMBED Equation.DSMT4

2)
EMBED Equation.DSMT4

и

EMBED Equation.DSMT4

12.
Найти тупой угол между прямыми

EMBED
Equation.DSMT4

и EMBED Equation.DSMT4

.

Ответ.135°

13.
Даны прямые

EMBED Equation.DSMT4

и EMBED Equation.DSMT4

;

при
каком значении m
они
пересекаются?

Ответ.
m
= 3.

14.
Составить уравнение прямой, которая
проходит через точку М(
-4; -5; 3) и пересекает две прямые

EMBED Equation.DSMT4

,
EMBED Equation.DSMT4

.

Ответ.
EMBED
Equation.DSMT4

Занятие
13.Смешанные задачи, относящиеся к
уравнению плоскости и уравнениям прямой

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

  30.04.20226.23 Mб1Учебное пособие 400223.doc

Суть уравнения прямой, проходящей через две заданные точки

Можно представить, что на плоскости с координатами Oxy расположена пара точек: (M_{0}(x_{0},y_{0})), (M_{1}(x_{1},y_{1}))

Необходимо сделать вывод формулы для прямой, которая пересекает эти заданные точки.

Точка (М (х, у)) соответствует прямой (M_{0} M_{1}) только в том случае, когда ее радиус-вектор (vec{OM}) соответствует следующему условию:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(vec{OM}=left(1-t right)times vec{OM_{0}}+ttimes vec{OM_{1}})

Где t является некоторым действительным числом (параметром). Координатная форма уравнения имеет следующий вид:

Данное равенство в алгебре называют аффинным уравнением прямой с пересечением двух точек в пространстве: (M_{0}(x_{0},y_{0})) и (M_{1}(x_{1},y_{1})).

Определив параметр t с помощью первого и второго уравнений системы, можно получить доказательство следующего соотношения:

(frac{x-x_{0}}{x_{1}-x_{0}}=t=frac{y-y_{0}}{y_{1}-y_{0}})

Если исключить коэффициент t, то можно вывести уравнение прямой, проходящей через две точки: (M_{0}(x_{0},y_{0})) и (M_{1}(x_{1},y_{1})).

Формула будет иметь следующий вид:

(frac{x-x_{0}}{x_{1}-x_{0}}=frac{y-y_{0}}{y_{1}-y_{0}})

Данное равенство вытекает из канонического уравнения, если выбрать направляющим вектором:

(vec{p}=avec{i}+bvec{j})

Вектор (vec{M_{0}M_{1}}) будет равен:

(vec{M_{0}M_{1}}=left(x_{1}-x_{0} right)vec{i}+left(y_{1}-y_{0} right)vec{j})

То есть, замещая следующие параметры:

(a=x_{1}-x_{0})

(b=y_{1}-y_{0})

Уравнение прямой в отрезках

Пусть координатные оси включают две точки: (X_{1}left(x_{1},0 right)) и (Y_{1}left(0, y_{1} right))

Следует отметить следующее условие:

(x_{1}neq 0)

(y_{1}neq 0)

Необходимо записать уравнение прямой, которая проходит через заданные точки, подставив в формулу:

(x_{0}=x_{1})

(y_{0}=0)

(x_{1}=0)

(y_{1}=y_{1})

В результате уравнение принимает следующий вид:

(frac{x-x_{1}}{0-x_{1}}=frac{y-0}{y_{1}-0}Leftrightarrow -frac{x}{x_{1}}+1=frac{y}{y_{1}}Leftrightarrow 1=frac{x}{x_{1}}+frac{y}{y_{1}})

Если поменять местами правую и левую части уравнения, то равенство примет такой вид:

(frac{x}{x_{1}}+frac{y}{y_{1}}=1)

(x_{1}neq 0)

(y_{1}neq 0)

Данную формулу называют уравнением прямой в отрезках. С помощью прямой, которая пересекает точки: (X_{1}left(x_{1},0 right)) и (Y_{1}left(0, y_{1} right))

координатные оси делят на отрезки х₁ на оси абсцисс и у₁ на оси ординат. Длины отрезков будут рассчитаны следующим образом:

(OX_{1}=left|x_{1} right|)

(OY_{1}=left|y_{1} right|)

Как записать формулу, канонический вид

Какой-либо вектор, отличный от нуля, проходит по данной прямой или параллельно ей, называют направляющим вектором этой прямой. Для обозначения направляющего вектора произвольной прямой используют букву (bar{a})

Координаты данного вектора обозначают с помощью букв l, m, n. Таким образом, можно прийти к следующему уравнению:

(bar{a}=left{l; m; n right})

При известном значении одной точки (M_{0}left(x_{0};y_{0};z_{0} right)) и направляющего вектора (bar{a}=left{l; m; n right}) прямой, то для нее будут записаны следующие уравнения:

(frac{x-x_{0}}{l}=frac{y-y_{0}}{m}=frac{z-z_{0}}{n})

Уравнение в таком виде называют каноническим.

Параметрическое уравнение прямой, проходящей через две точки

Канонические уравнения для прямой, которая пересекает следующие точки:

(M_{1}left(x_{1};y_{1};z_{1} right))

(M_{2}left(x_{2};y_{2};z_{2} right))

будет записано в следующем виде:

(frac{x-x_{1}}{x_{2}-x_{1}}=frac{y-y_{1}}{y_{2}-y_{1}}=frac{z-z_{1}}{z_{2}-z_{1}})

Равные отношения можно обозначить буквой t в канонических уравнениях. В итоге они приобретают такой вид:

(frac{x-x_{0}}{l}=frac{y-y_{0}}{m}=frac{z-z_{0}}{n}=t)

Исход из этого, получается равенство:

(x=x_{0}+lt)

(y=y_{0}+mt)

(z=z_{0}+nt)

Данные равенства являются параметрическими уравнениями прямой, которая пересекает точку (M_{0}left(x_{0};y_{0}; z right)) в направлении вектора (bar{a}=left{l; m; n right})

В данном случае t является произвольно изменяющимся параметром, x, y, z представляют собой функции от t. Если изменяется t, то значения x, y, z также меняются. Таким образом, точка M (x; y; z) перемещается вдоль прямой. Если параметр t использовать в качестве переменного времени, а уравнения представить в виде формул, описывающих движение точки М, то с помощью данных уравнений можно определить прямолинейное и равномерное движение точки М. При t равным 0 точка М будет совпадать с точкой M₀.

Скорость V точки М обладает постоянным значением и рассчитывается по формуле:

(V=sqrt{l^{2}+m^{2}+n^{2}})

Примеры задач с решением

Задача 1

Необходимо построить прямую, которая проходит через следующие точки: А (2, 1, 1), В (3, 1, -2).

Решение

Уравнение прямой, которая проходит через точки:

(Aleft(x_{1},y_{1},z_{1} right))

(Bleft(x_{2},y_{2},z_{2} right))

будет иметь следующий вид:

(frac{x-x_{1}}{x_{2}-x_{1}}=frac{y-y_{1}}{y_{2}-y_{1}}=frac{z-z_{1}}{z_{2}-z_{1}})

После того, как координаты точек А и В будут применены к первому уравнению, оно будет записано в такой форме:

(frac{x-2}{3-2}=frac{y-1}{1-1}=frac{z-1}{-2-1})

После некоторых преобразований получается:

(frac{x-2}{1}=frac{y-1}{0}=frac{z-1}{-3})

В данном случае наличие ноля в знаменателе не обозначает деление на ноль. Параметрическое уравнение прямой будет записано таким образом:

(t=frac{x-2}{1})

(t=frac{ y-1}{0})

(t=frac{z-1}{-3})

Если выразить переменные x, y, z с помощью параметра t, в итоге получится:

(x = t + 2)

(y = 1)

(z = -3 * t + 1)

Ответ: каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2), будет записано в следующем виде:

(frac{x-2}{1}=frac{y-1}{0}=frac{z-1}{-3})

Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2), будет записано в следующем виде:

(x = t + 2)

(y = 1)

(z = -3 * t + 1)

Задача 2

Требуется построить прямую, которая проходит через точки А (1, 1/5, 1) и В (-2, 1/2, -2).

Решение

Уравнение для прямой, которая пересекает заданные точки:

(Aleft(x_{1},y_{1},z_{1} right))

(Bleft(x_{2},y_{2},z_{2} right))

будет записано таким образом:

(frac{x-x_{1}}{x_{2}-x_{1}}=frac{y-y_{1}}{y_{2}-y_{1}}=frac{z-z_{1}}{z_{2}-z_{1}})

После подстановки координат точек А и В в исходную формулу, она приобретет такой вид:

(frac{x-1}{-2-1}=frac{y-frac{1}{5}}{frac{1}{2}-frac{1}{5}}=frac{z-1}{-2-1})

или

(frac{x-1}{-3}=frac{y-frac{1}{5}}{frac{3}{10}}=frac{z-1}{-3})

Далее можно записать параметрическое уравнение прямой:

(t=frac{x-1}{-3})

(t=frac{y-frac{1}{5}}{frac{3}{10}})

(t=frac{z-1}{-3})

Выразив переменные x, y, z с помощью параметра t, можно получить следующее уравнение:

(x=-3times t+1)

(y=frac{3}{10}t+frac{1}{5})

(z=-3times t+1)

Ответ: каноническое уравнение прямой, пересекающей заданные точки A(1, 1/5, 1) и B(−2, 1/2, −2) записано в следующем виде:

(frac{x-1}{-3}=frac{y-frac{1}{5}}{frac{3}{10}}=frac{z-1}{-3})

параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

(x=-3times t+1)

(y=frac{3}{10}t+frac{1}{5})

(z=-3times t+1)

Существует несколько различных типов уравнений, описывающих кривую первого порядка, называемую прямой. Каждый из них оптимален для какой-то своей цели. Давайте познакомимся с ними поближе.

Каноническое уравнение прямой в пространстве

Не во всех случаях удобно и практично пользоваться каноническим уравнением, поэтому частенько возникает надобность использовать какое-то другое, например, можно прибегнуть к параметрическому.

Для каких прямых не представляется возможным или нельзя написать каноническое уравнение?

Глядя на это уравнение, видно, что его возможно использовать только в том случае, если координаты направляющих векторов исследуемых прямых не равны нулю, для таких прямых стоит воспользоваться параметрическими уравнениями.

Параметрическое уравнение как раз удобно применять если одна из координат направляющего вектора равна нулю.

Чтобы произвести переход от параметрического вида уравнения к каноническому виду уравнения прямой в пространстве, осуществите вывод канонического уравнения прямой из параметрического.

«Каноническое уравнение прямой в пространстве» 👇

Для этого следует в к каждом уравнении перенести $λ$ в левую часть, а затем приравнять уравнения. Никакой магии, а только самая что ни на есть пресловутая арифметика:

$begin{cases} λ = frac{x — x_1}{ α} \ λ = frac{y — y_1}{β} \ λ = frac{z — z_1}{γ} \ end{cases}$

$frac{x – x_0}{α} = frac{y – y_0}{β} = frac{z – z_0}{γ}$

Уравнение прямой, образуемой пересечением двух плоскостей

Для того чтобы составить каноническое уравнение прямой в пространстве, заданной пересечением плоскостей, необходимо познакомиться поближе с 2 исследуемыми плоскостями.

Любую плоскость, находящуюся в пространстве, можно описать с помощью равенства:

$Ax + By + Cz + D = 0$,

где $A, B, C$ и $D$ — постоянные, причём $A, B, C$ не могут быть одновременно все нулевыми.

Соответственно, не нужно быть гением, чтобы понять, что если две плоскости пересечены между собой, то на их общей части будет возлежать некая прямая. Чтобы её найти, нужно получить общее решение следующей системы уравнений:

$begin{cases} A_1x + B_1y + C_1z + D_1 = 0 \ A_2x + B_2y + C_2z + D_2 = 0 \ end{cases}$

С помощью же частного решения этой системы уравнений можно узнать, принадлежит ли какая-либо точка трёхмерной системы координат описанным уравнениями плоскостям и, конечно же, нашей прямой. Для этого нужно просто подставить её икс, игрек и зет в систему.

Приведённая система уравнений является своеобразной “формулой”, служащей для нахождения общего уравнения прямой в пространстве.

Иногда в каких-либо практических задачах требуется получить из уравнения прямой в пространстве в общем виде параметрические или канонические уравнения, тогда в первую очередь вам стоит узнать координаты её направляющего вектора и какую-либо точку, находящуюся на изучаемой прямой.

Ну что ж, давайте решать нашу задачу. На первом этапе вычислим $x, y, z$ для направляющего вектора.

Найдём нормальные вектора для плоскостей. Если кто забыл, нормальный вектор — это такой вектор, который является перпендикулярным (ортогональным) к данной плоскости или прямой.

Для этого из нашего очаровательного примера системы уравнений необходимо взять коэффициенты из уравнений. В итоге для 1-ой плоскости вектор-нормаль будет выглядеть как $(A_1; B_1; C_1)$, а для второй как $(A_2; B_2; C_2)$.

Теперь необходимо перемножить оба вектора и получить их произведение, здесь $(i, j, k)$ — координаты единичного вектора.

$overline{a} = [overline{n} cdot overline{n}] = left| begin{array}{ccc} overline{i} & overline{j} & overline{k} \ A_1 & B_1 & C_1 \ A_2 & B_2 & C_2 \ end{array} right| = overline{i} cdot left| begin{array}{cc}\B_1 & C_1 \ B_2 & C_2\ end{array} right| — overline{j} cdot left| begin{array}{cc}\ A_1 & C_1 \ A_2 & C_2 \ end{array} right| + overline{k} cdot left| begin{array}{cc} \ A_1 & B_1 \ A_2 & B_2 \ end{array} right| $

$|overline{n} cdot overline{n}| = overline{i} cdot (B_1 cdot C_2 – C_1 cdot B_2) — overline{j} cdot (A_1 cdot C_2 – A_2 cdot C_1) + overline{k} cdot (A_1 cdot B_2 – A_2 cdot B_1)$

Следующим этапом выполняем поиск координат точки, возлежащей на искомой прямой.

Для выполнения этого наиболее «сложного» пункта необходимо выбрать одну наиболее нравящуюся вам координату $x, y$ или $z$ и вместо неё подставить в систему уравнений, описывающую плоскости, нулевое значение.

Составление канонического уравнения прямой по координатам двух точек

На практике это очень распространённая и любимая во многих вузах и других учебных заведениях задача — нужно найти уравнение прямой в пространстве, проходящей через 2 точки. Примем заранее, что эти две точки не обладают одинаковыми $x, y, z$.

Для того чтобы написать уравнение прямой в пространстве, проходящей через 2 точки, воспользуйтесь координатами ваших точек и внедрите их в следующее уравнение:

$frac{x – x_1}{x2 – x_1} = frac{y – y_1}{y_2 – y_1} = frac{z – z_1}{z_2 – z_1}$

Это уравнение можно вывести из параметрического уравнения прямой.

Допустим, у нас есть две точки с координатами $(x_1; y_1; z_1)$, и для второй $(x_2; y_2; z_2)$.

Найти направляющий вектор для изучаемой прямой при наличии пары точек несложно, вектор с координатами $(x_2 – y_1; y_2 – y_2;z_2 – z_2)$ и будет желаемой частью результата.

Придумаем точку, находящуюся на нашей прямой, пусть она будет обладать координатами $(x_1;y_1;z_1)$.

Помещаем обнаруженные нами координаты вектора и точки в каноничное уравнение прямой в пространстве и получим уравнение прямой, проходящей через 2 точки.

Если же необходимо выразить именно параметрические уравнения из координат двух точек, через которые проведена некая одна прямая, то тут тоже всё довольно просто и без неожиданностей:

$begin{cases} x = x_1 + (x_2 — x_1) cdot λ \ y = y_1 + (y_2 — y_1)cdot λ \ z = z_1 + (z_2 — z_1) cdot λ \ end{cases}$

Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.

Здесь будет калькулятор

Уравнение прямой с угловым коэффициентом

Уравнение прямой с угловым коэффициентом

y=kx+by=kx+b,

где kk — угловой коэффициент, а bb — свободный коэффициент.

Уравнения данного вида составляются следующим образом по формуле:

y−y0=k(x−x0)y-y_0=k(x-x_0),

где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.

Задача 1

Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.

Решение

Подставляем значения в формулу:

y−y0=k(x−x0)y-y_0=k(x-x_0)

y−2=1⋅(x−1)y-2=1cdot(x-1)

Приводим подобные слагаемые:

y=x+1y=x+1

Ответ

y=x+1y=x+1

Общее уравнение прямой

Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:

y−x−1=0y-x-1=0

Уравнение прямой по двум точкам

Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:

Уравнение прямой по двум точкам

x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},

где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.

Задача 2

Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).

Решение

x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1

x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}

x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}

x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}

x−4=−y−12x-4=frac{-y-1}{2}

y+1=2⋅(4−x)y+1=2cdot(4-x)

y=8−2x−1y=8-2x-1

y=−2x+7y=-2x+7

Ответ

y=−2x+7y=-2x+7

Уравнение прямой при помощи точки и вектора нормали

Уравнение прямой по точке и нормали

(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,

где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.

Задача 3

Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).

Решение

x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5

(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,

(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,

x−7+40−5y=0x-7+40-5y=0

x−5y=−40+7x-5y=-40+7

x−5y=−33x-5y=-33

5y=x+335y=x+33

y=x5+335y=frac{x}{5}+frac{33}{5}

Проверка

Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.

8=75+3358=frac{7}{5}+frac{33}{5}

8=88=8 — верно, ответ правильный.

Ответ

y=x5+335y=frac{x}{5}+frac{33}{5}

Прямая в пространстве

Уравнение прямой, заданной в пространстве имеет такой вид:

Уравнение прямой в пространстве

x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},

где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.

Задача 4

Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).

Решение

x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7

x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}

x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}

Проверка

Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:

1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.

Такой вид уравнения прямой называется каноническим.

Ответ

x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}

Тест по теме “Составление уравнения прямой”