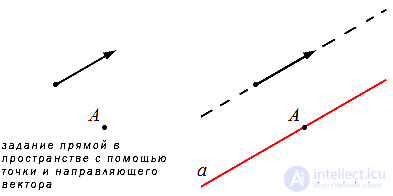
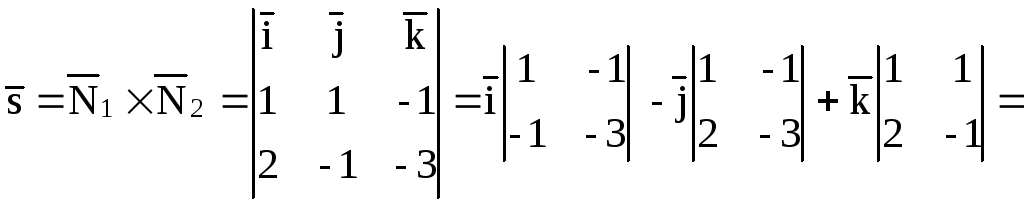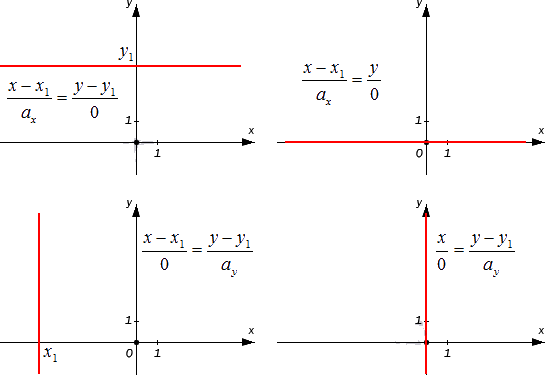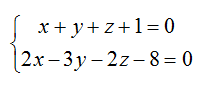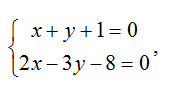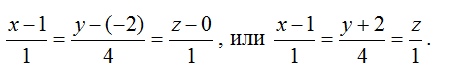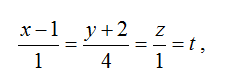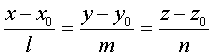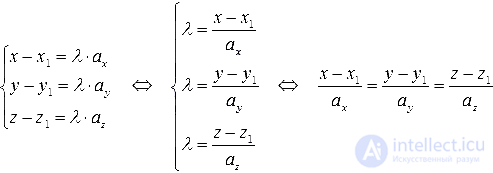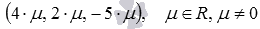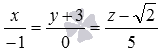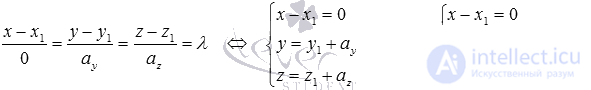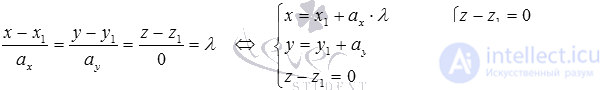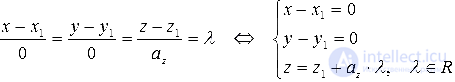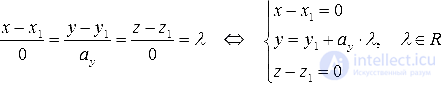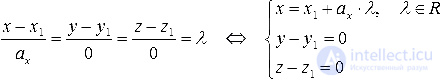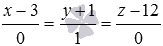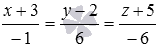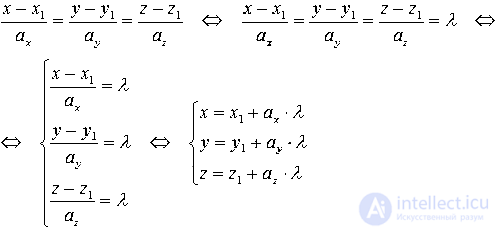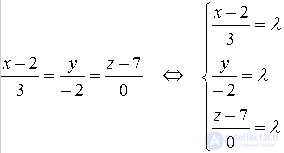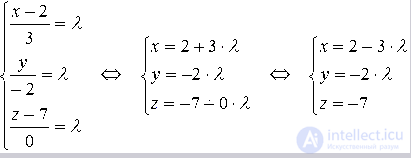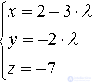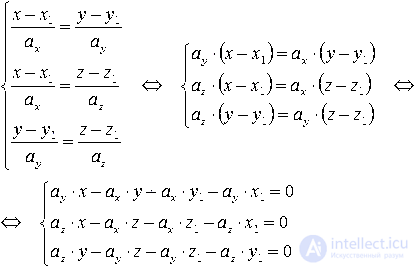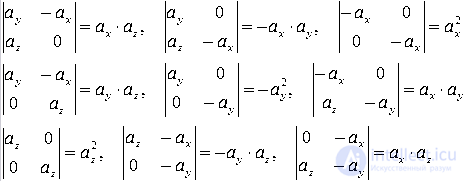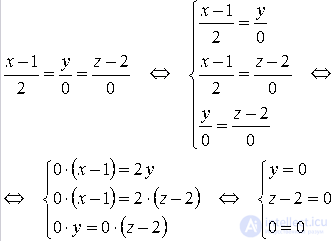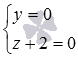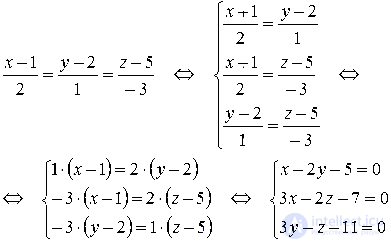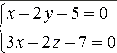Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.
Понятие канонического уравнения прямой
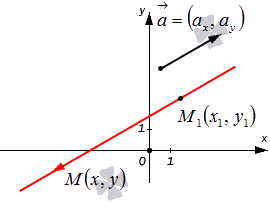
Допустим, что у нас есть декартова (прямоугольная) система координат, в которой задана прямая. Нам известны координаты произвольно взятой точки этой прямой M1(x1, y1), а также ее направляющего вектора a→=(ax, ay). Попробуем составить уравнение, которое описывало бы эту прямую.
Возьмем плавающую точку M(x, y). Тогда вектор M1M→ можно считать направляющим для исходной прямой. Его координаты будут равны x-x1, y-y1 (если нужно, повторите материал о том, как правильно вычислять координаты вектора с помощью координат отдельных его точек).
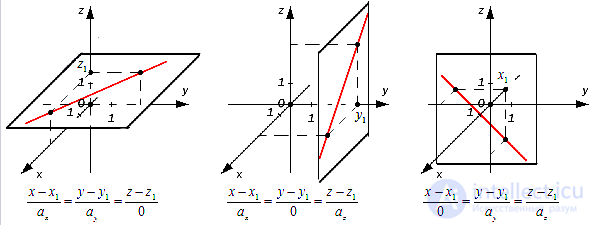
Множество произвольно взятых точек M(x, y) будут определять нужную нам прямую с направляющим вектором a→=(ax, ay) только в одном случае – если векторы M1M→ и a→=(ax, ay) будут коллинеарны по отношению друг к другу. Посмотрите на картинку:
Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:
M1M→=λ·a→, λ∈R
Если преобразовать полученное равенство в координатную форму, то мы получим:
x-x1=λ·axy-y1=λ·ay
При условии, что ax≠0 и ay≠0, получим:
x-x1=λ·axy-y1=λ·ay⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay
Итог наших преобразований и будет каноническим уравнением прямой на плоскости. Запись вида x-x1ax=y-y1ay также называют уравнением прямой в каноническом виде.
Таким образом, с помощью уравнения x-x1ax=y-y1ay можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор a→=(ax, ay) и проходит через точку M1(x1, y1).
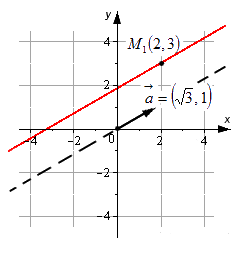
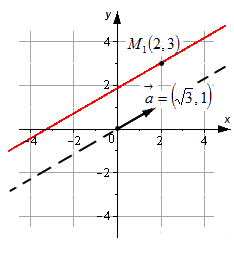
Примером уравнения подобного типа является, например, x-23=y-31. Прямая, которая задана с его помощью, проходит через M1(2, 3) и имеет направляющий вектор a→=3, 1. Ее можно увидеть на рисунке:
Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:
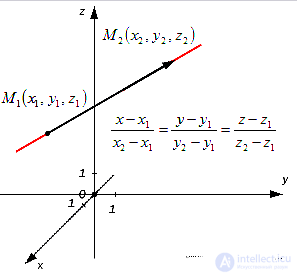
1. Если прямая, имеющая направляющий вектор a→=(ax, ay), проходит через две точки – M1(x1, y1) и M2(x2, y2), то уравнение для нее может быть записано как в виде x-x1ax=y-y1ay, так и x-x2ax=y-y2ay.
2. Если заданная прямая имеет направляющий вектор с координатами a→=(ax, ay), то множество всех ее векторов можно обозначить как μ·a→=(μ·ax, μ·ay), μ∈R, μ≠0. Таким образом, любое уравнение прямой в каноническом виде x-x1μ·ax=y-y1μ·ay будет соответствовать этой прямой.
Разберем важный пример задачи на нахождение канонического уравнения.
В прямоугольной системе координат на плоскости задана прямая, которая проходит через точку M1(2, -4) и имеет направляющий вектор с координатами a→=(1, -3). Запишите каноническое уравнение, описывающее данную прямую.
Решение
Для начала вспомним общий вид нужного нам канонического уравнения – x-x1ax=y-y1ay. Подставим в него имеющиеся значения x1=2, y1=-4, ax=1, ay=-3 и подсчитаем:
x-x1ax=y-y1ay⇔x-21=y-(-4)-3⇔x-21=y+4-3
Получившееся в итоге равенство и будет нужным ответом.
Ответ: x-21=y+4-3
Канонические уравнения прямой на плоскости с ax или ay, равными нулю
Если значение хотя бы одной переменной a является нулевым, то уравнение плоскости используют в первоначальном виде. Сразу две переменные нулевыми не могут быть по определению, поскольку нулевой вектор не бывает направляющим. В таком случае мы можем считать запись x-x1ax=y-y1ay условной и понимать ее как равенство ay(x-x1)=ax(y-y1).
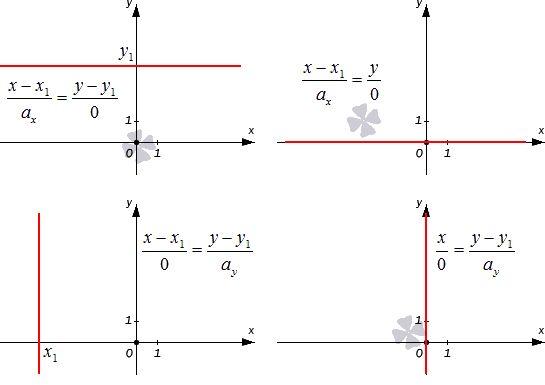
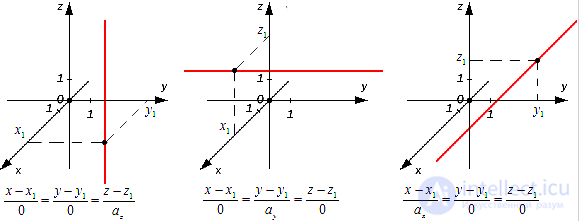
Разберем случаи канонических уравнений на плоскости с одним нулевым a более подробно. Допустим, что x-x10=y-y1ay при ax=0, а исходная прямая будет проходить через M1(x1, y1). В таком случае она является параллельной оси ординат (если x1=0, то она будет с ней совпадать). Докажем это утверждение.
Для этой прямой вектор a→=(0, ay) будет считаться направляющим. Этот вектор является коллинеарным по отношению к координатному вектору j→=(0,1).
Если же нулевым является значение второго параметра, то есть ay=0, то мы получаем равенство вида x-x1ax=y-y10. Это уравнение описывает прямую, проходящую через M1(x1, y1), которая расположена параллельно оси абсцисс. Это утверждение верно, поскольку a→=(ax, 0) является для этой прямой направляющим вектором, а он в свою очередь является коллинеарным по отношению к координатному вектору i→=(1, 0).
Проиллюстрируем два частных случая канонического уравнения, описанные выше:
На плоскости задана прямая, параллельная оси Oy. Известно, что она проходит через точку M123, -17. Запишите каноническое уравнение для нее.
Решение
Если прямая по отношению оси ординат является параллельной, то мы можем взять координатный вектор j→=(0, 1) в качестве направляющего для нее. В таком случае искомое уравнение выглядит следующим образом:
x-230=y—171⇔x-230=y+171
Ответ: x-230=y+171
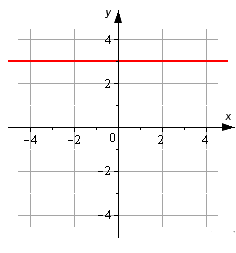
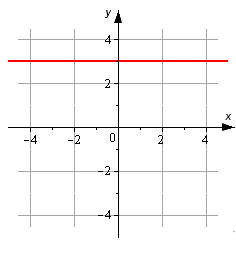
На рисунке изображена прямая. Запишите ее каноническое уравнение.
Решение
Мы видим, что исходная прямая проходит параллельно оси Ox через точку M1(0, 3). Мы берем координатный вектор i→=(1, 0) в качестве направляющего. Теперь у нас есть все данные, чтобы записать нужное уравнение.
x-01=y-30⇔x1=y-30
Ответ: x1=y-30
Преобразование канонического уравнения прямой в другие виды уравнений
Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.
Стандартной форме записи канонического уравнения x-x1ax=y-y1ay можно поставить в соответствие систему параметрических уравнений на плоскости x=x1+ax·λy=y1+ay·λ. Чтобы преобразовать один вид уравнения в другой, нам надо приравнять правую и левую часть исходного равенства к параметру λ. После этого надо выполнить разрешение получившихся равенств относительно переменных x и y:
x-x1ax=y-y1ay⇔x-x1ax=y-y1ay=λ⇔⇔x-x1ax=λy-y1ay=λ⇔x=x1+ax·λy=y1+ay·λ
Покажем на примере, как именно выполняется это действие с конкретными числами.
У нас есть прямая, заданная на плоскости с помощью канонического уравнения x+23=y-111. Запишите параметрические уравнения исходной прямой.
Решение
Сначала поставим знак равенства между отдельными частями уравнения и переменной λ и получим x+23=λy-111=λ.
Далее можно перейти к формулированию необходимых параметрических уравнений:
x+23=λy-111=λ⇔x+2=3·λy-1=11·λ⇔x=-2+3·λy=1+11·λ
Ответ: x=-2+3·λy=1+11·λ
Из канонического уравнения можно получить не только параметрические, но и общие уравнения прямой. Вспомним понятие пропорции: запись ab=cd можно представить в виде a·d=b·c с сохранением смысла. Значит, что x-x1ax=y-y1ay⇔ay(x-x1)=ax(y-y1)⇔ayx-axy-ayx1+axy1=0.
Это и есть общее уравнение прямой. Это станет более очевидно, если мы добавим в него значения параметров ay=A, -ax=B, -ayx1+axy1=C.
Прямая на плоскости описана с помощью канонического уравнения x-12=y+40. Вычислите общее уравнение этой прямой.
Решение
Делаем указанные выше действия по порядку.
x-12=y+40⇔0·(x-1)=2·(y+4)⇔y+4=0
Ответ: y+4=0 .
Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.
На плоскости задана прямая с помощью уравнения x+33=y-22. Запишите уравнение этой же прямой в отрезках.
Решение
Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.
x+33=y-22⇔2·(x+3)=3·(y-2)⇔2x-3y+6+23=0
Далее переходим к формулировке уравнения прямой в отрезках.
2x-3y+6+23=0⇔2x-3y=-6+23⇔⇔2-(6+23)x-3-(6+23)y=1⇔x-6+232+y6+233=1⇔x-3+3+y33+2=1
Ответ: x-3+3+y33+2=1
Достаточно легко решить и задачу, обратную этой, т.е. привести уравнение прямой на плоскости обратно к каноническому. Допустим, у нас есть общее уравнение прямой в стандартной формулировке – Ax+By+C=0. При условии A≠0 мы можем перенести By вправо с противоположным знаком. Получим Ax+C=-By. Теперь выносим A за скобки и преобразуем равенство так:
Ax+CA=-By
Получившееся уравнение мы записываем в виде пропорции: x+CA-B=yA.
У нас получилось нужное нам каноническое уравнение прямой на плоскости.
А как сделать преобразование, если B≠0? Переносим все слагаемые, кроме Ax, вправо с противоположными знаками. Получаем, что Ax=-By-C. Выносим -B за скобки:
Ax=-By+CB
Формируем пропорцию: x-B=y+CBA
Есть общее уравнение прямой x+3y-1=0. Перепишите его в каноническом виде.
Решение
Оставим с левой стороны только одну переменную x. Получим:
x=-3y+1
Теперь вынесем -3 за скобки: x=-3y-13. Преобразуем равенство в пропорцию и получим необходимый ответ:
x-3=y-131
Ответ: x-3=y-131
Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.
Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x=x1+ax·λy=y1+ay·λ и приравнять обе части равенств. Схема решения выглядит так:
x=x1+ax·λy=y1+ay·λ⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay
Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.
Прямая на плоскости описана с помощью системы параметрических уравнений x=3+0·λy=-2-4·λ. Запишите каноническое уравнение для этой прямой.
Решение
Для начала преобразуем исходные уравнения в систему x=3+0·λy=-2-4·λ. Следующим шагом будет выражение параметра в каждом уравнении:
x=3+0·λy=-2-4·λ⇔λ=x-30λ=y+2-4
Ставим знак равенства между получившимися частями и получаем нужное нам каноническое уравнение: x-30=y+2-4
Ответ: x-30=y+2-4
Как решать задачи на составление канонических уравнений
В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.
На плоскости задана прямая, каноническое уравнение которой имеет вид x-12=y+12-3. Выясните, лежат ли на ней точки M13, -312 и M2(5, -4).
Решение
Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.
3-12=-312+12-2⇔1=1
Результат говорит нам, что точка M13, -312 принадлежит исходной прямой.
Точно так же поступим и с координатами второй точки:
5-12=-4+12-3⇔2=76
Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.
Ответ: первая точка лежит на заданной прямой, а вторая нет.
Есть две точки M1(2, 4) и M2(-1, 3). Будет ли прямая, которая задана в той же плоскости с помощью уравнения x-20=y-32, проходить через них?
Решение
Вспомним, что запись x-20=y-32 можно понимать как 2·(x-2)=0·(y-3)⇔x-2=0. Подставим координаты заданных точек в это равенство и проверим.
Начнем с первой точки M1(2, 4) : 2-2=0⇔0=0
Равенство верное, значит, эта точка расположена на заданной прямой.
Подставляем данные второй точки: -1-2=0⇔-3=0.
Равенство неверное, значит, точка M2(-1, 3) не лежит на исходной прямой.
Ответ: через точку M1(2, 4) прямая проходит, а через M2(-1, 3) нет.
Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.
Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.
Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.
Прямая на плоскости проходит через точку M1(0, -3) и через точку M2(2, -2). Сформулируйте для этой прямой канонической уравнение.
Решение
Eсли у нас есть координаты двух точек, то мы можем вычислить по ним координаты вектора M1M2→=2, 1. По отношению к прямой, чье уравнение мы составляем, он будет направляющим вектором. После этого мы можем записать следующее:
x-02=y-(-3)1⇔x2=y+31
Также можно использовать координаты второй точки. Тогда мы получим: x-22=y-(-2)1⇔x-22=y+21
Ответ: x2=y+31
Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.
Известно, что точка M1(1, 3) принадлежит некоторой прямой, которая параллельна второй прямой, заданной с помощью уравнения x2=y-5. Запишите каноническое уравнение первой прямой.
Решение
Для первой прямой можно определить направляющий вектор a→=2, -5. Его можно рассматривать и в качестве направляющего для второй прямой, что следует из самого определения направляющих векторов. Это позволяет нам получить всю информацию, нужную для записи искомого уравнения: x-12=y-3-5
Ответ: x-12=y-3-5
Через точку M1(-1, 6) проходит прямая, которая является перпендикулярной другой прямой, определенной на плоскости с помощью уравнения 2x-4y-7=0. Запишите каноническое уравнение первой прямой.
Решение
Из данного уравнения мы можем взять координаты нормального вектора второй прямой – 2, 4. Мы знаем, что этот вектор является направляющим по отношению к первой. Тогда мы можем записать искомое уравнение:
x-(-1)2=y-64⇔x+11=y-62
Ответ: x+11=y-62
3.1. Канонические
уравнения прямой.
Пусть в системе
координат Oxyz
дана прямая, которая проходит через
точку

вектор, параллельный данной прямой.
Векторназываетсянаправляющим
вектором прямой.
Возьмем на прямой точку и рассмотрим вектор
Векторы
коллинеарны, следовательно, их
соответствующие координаты пропорциональны:
(3.3.1)
Эти уравнения
называются каноническими
уравнениями прямой.
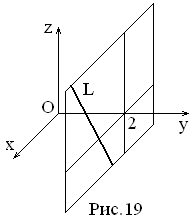
уравнения прямой, проходящей через
точку M(1,
2, –1) параллельно вектору
Решение:
Вектор
является направляющим вектором искомой
прямой. Применяя формулы (3.1.1), получим:
Это канонические
уравнения прямой.
Замечание:
Обращение в нуль одного из знаменателей
означает обращение в нуль соответствующего
числителя, то есть y
– 2 = 0; y
= 2. Данная прямая лежит в плоскости y
= 2, параллельной плоскости Oxz.
3.2.
Параметрические
уравнения прямой.
Пусть прямая
задана каноническими уравнениями
Обозначим тогда
Величина t
называется параметром и может принимать
любые значения:
.
Выразим x,
y
и z
через t
:
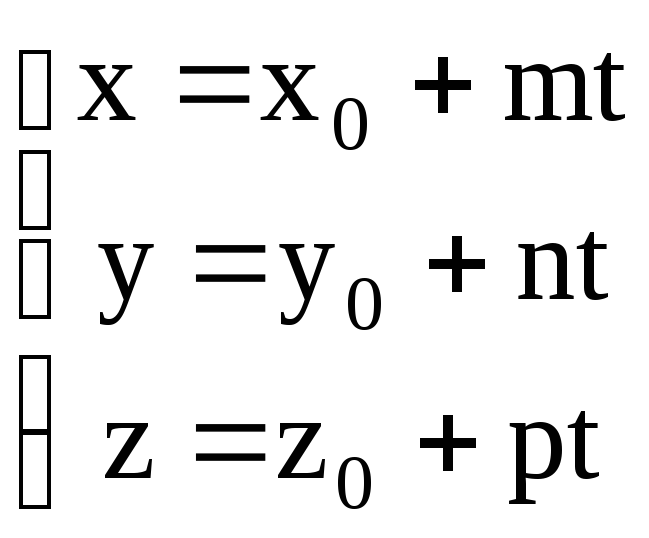
Полученные уравнения
называются параметрическими
уравнениями прямой.
Пример 1:
Составить
параметрические уравнения прямой,
проходящей через точку M
(1, 2, –1) параллельно вектору
Решение:
Канонические уравнения этой прямой
получены в примере пункта 3.1:
Для нахождения
параметрических уравнений прямой
применим вывод формул (3.2.1):
Итак,

прямой.
Ответ:
Пример 2.
Составить
параметрические уравнения прямой,
проходящей через точку M
(–1, 0, 1) параллельно вектору
гдеA
(2, 1, –1), B
(–1, 3, 2).
Решение:
Вектор является направляющим
вектором искомой прямой.
Найдем вектор .
= (–3; 2; 3). По формулам
(3.2.1) запишем уравнения прямой:

параметрические уравнения прямой.
3.3. Уравнения
прямой, проходящей через две заданные
точки.
Через две заданные
точки в пространстве проходит единственная
прямая (см. рис.20). Пусть даны точки
Вектор
можно принять за направляющий вектор
данной прямой. Тогда уравнения прямой
наход
по формулам (3.1.1):).
(3.3.1)
Пример 1.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
Решение:
Применяем
формулу (3.3.1)
Получили канонические
уравнения прямой. Для получения
параметрических уравнений применим
вывод формул (3.2.1). Получим

уравнения прямой.
Пример 2.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
Решение:
По формулам
(3.3.1) получим:
Это канонические
уравнения.
Переходим к
параметрическим уравнениям:

уравнения.
Полученная прямая
параллельна оси oz
(см. рис.21).
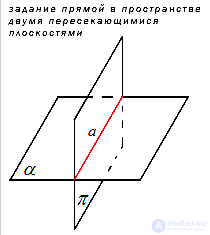
3.4. Прямая как
линия пересечения двух плоскостей.
Пусть в
пространстве даны две плоскости
и
Если эти плоскости
не совпадают и не параллельны, то они
пересекаются по прямой:
Эта система двух
линейных уравнений задает прямую как
линию пересечения двух плоскостей. От
уравнений (3.4.1) можно перейти к каноническим
уравнениям (3.1.1) или параметрическим
уравнениям (3.2.1). Для этого необходимо
найти точку
лежащую на прямой, и направляющий вектор
Координаты точки
получим из системы (3.4.1), придав одной
из координат произвольное значение
(например,z
= 0). За направляющий вектор
можно взять векторное произведение
векторовто есть
Пример 1.
Составить
канонические уравнения прямой
Решение: Пусть
z
= 0. Решим систему
Сложив эти уравнения,
получим: 3x
+ 6 = 0
x
= –2. Подставим найденное значение x
= –2 в первое уравнение системы и получим:
–2 + y
+ 1 = 0
y
= 1.
Итак, точка
лежит на искомой прямой.
Для нахождения
направляющего вектора прямой запишем
нормальные векторы плоскостей:
и найдем их векторное произведение:
Уравнения прямой
находим по формулам (3.1.1):
Ответ: .
Другой способ:
Канонические и параметрические
уравнения прямой (3.4.1) легко получить,
найдя две различные точки на прямой из
системы (3.4.1), а затем применив формулы
(3.3.1) и вывод формул (3.2.1).
Пример 2.
Составить канонические и параметрические
уравнения прямой
Решение:
Пусть y
= 0. Тогда система примет вид:
Сложив уравнения,
получим: 2x
+ 4 = 0; x
= –2. Подставим x
= –2 во второе уравнение системы и
получим: –2 –z
+1 = 0
z
= –1. Итак, нашли точку
Для нахождения
второй точки положим x
= 0. Будем иметь:
То есть
Далее применяем
формулы (3.3.1):
Получили канонические
уравнения прямой.
Составим
параметрические уравнения прямой:
Ответ:
; 
3.5. Взаимное
расположение двух прямых в пространстве.
Пусть прямые
заданы уравнениями:
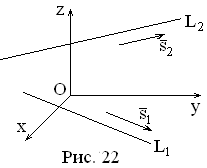
;
:
.
Под углом между
этими прямыми понимают угол между их
направляющими векторами
(см. рис.22). Этот угол
находим по формуле из векторной алгебры:
или
(3.5.1)
Если прямые перпендикулярны
(),то
Следовательно,
(3.5.2)
Это условие
перпендикулярности двух прямых в
пространстве.
Если прямые
параллельны (),то их направляющие
векторы коллинеарны (),
то есть
(3.5.3)
Это условие
параллельности двух прямых в пространстве.
Пример 1. Найти
угол между прямыми:
а).
и
б). и
Решение:
а). Запишем направляющий вектор прямой
Найдем направляющий вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему
Затем найдем их векторное произведение:
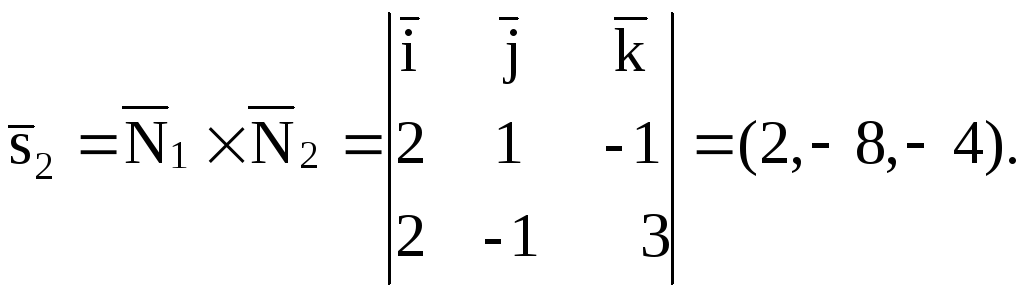
пункта 3.4).
По формуле (3.5.1)
получим:
Следовательно,
б). Запишем
направляющие векторы данных прямых:
Векторы
коллинеарны, так как их соответствующие
координаты пропорциональны:
Значит прямые
параллельны (
),
то есть
Ответ: а).
б).
Пример 2. Доказать
перпендикулярность прямых:
и
Решение:
Запишем направляющий вектор первой
прямой
Найдем направляющий
вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему:
Вычислим их векторное произведение:

Применим условие
перпендикулярности прямых (3.5.2):
Условие выполнено;
следовательно, прямые перпендикулярны
().
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #
Понятие канонического уравнения прямой
Чтобы разобраться, что такое каноническое уравнение, нужно рассмотреть следующий пример. Дана прямоугольная система координат, в которой задана некая произвольная прямая. Известны координаты произвольной точки на отрезке [M_{1}left(x_{1}, y_{1}right)] и координаты направляющего вектора [bar{a}=left(a_{x^{prime}} a_{y}right)]. Используя все имеющиеся данные составим и запишем уравнение, которое будет описывать данную заданную прямую.
Рассмотрим точку [mathrm{M}(x, y)]. Вектор [overline{M_{1} M}] можно отнести к направляющим исходной линии в координатной плоскости. Координатами вектора будут точки [left(x-x_{1}, y-y_{1}right)]. Чтобы правильно определить векторные координаты, необходимо вспомнить основное правило решения векторов.
Произвольные точки [M(x, y)] будут являться основой для необходимой прямой с направляющим вектором [bar{a}=left(a_{x}, a_{y}right)], только тогда, когда вектора [overline{M_{1} M}] и [bar{a}=left(a_{x}, a_{y}right)] будут являться коллинеарными по отношению друг к другу.
Исходя из этого можно составить формулу коллинеарности двух векторов.
Формула
[overline{M_{1} M}=lambda cdot overline{mathrm{a}}, lambda in R]
Где:
После преобразования данного равенства в координатную форму, можно получить следующее уравнение:
[begin{aligned} &x-x_{1}=lambda cdot a_{x} \ &y-y_{1}=lambda cdot a_{y} end{aligned}]
Однако, обязательно выполнение главных условий: [a_{x} neq 0] и [a_{y} neq 0].
При выполнении вышеперечисленных условий, получаем следующие равенства:
[begin{aligned} &x-x_{1}=lambda cdot a_{x} Rightarrow lambda=frac{x-x_{1}}{a_{x}} \ &y-y_{1}=lambda cdot a_{y} Rightarrow lambda=frac{x-x_{1}}{a_{x}} \ &Leftrightarrow frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}} end{aligned}]
Все выполненные преобразования привели к тому, что мы получили окончательную формулу канонического уравнения на плоскости [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}].
Иначе такое равенство, еще называют уравнением прямой канонического вида.
Используя данную запись [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}], можно в прямоугольной системе координат задать прямую, которой будет характерен направляющий вектор [bar{a}=left(a_{x}, a_{y}right)]. Также данная линия будет проходить через заданную точку [M_{1}left(x_{1}, y_{1}right)].
Например: задано уравнение [frac{x-2}{sqrt{3}}=frac{y-3}{1}]. Задается линия, которая будет проходить через точки [M_{1}(2,3)]. Ее направляющий вектор имеет координатные точки: [bar{a}=(sqrt{3}, 1)].
Когда любая прямая в системе координат проходит через две любые точки [M_{1}left(x_{1}, y_{1}right)] и [M_{2}left(x_{2}, y_{2}right)] и имеет направляющий вектор [bar{a}=left(a_{x}, a_{y}right)], множество всех векторов можно записать как [mu cdot overline{mathrm{a}}=left(mu cdot mathrm{a}{x^{prime}} mu cdot a{y}right), mu in R, mu neq 0].
Таким образом, каждое уравнение прямой канонического вида [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}], будет соответствовать заданной прямой на плоскости.
Пример 1
В системе координат задана прямая, которая проходит через точки [M_{1}(2,4)], и имеет направляющий вектор [bar{a}=(1,-3)].
Решение задачи:
Составим и запишем общий вид канонического уравнения [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}].
Далее подставим в него заданные значения [x_{1}=2, y_{1}=-4, a_{x}=1, a_{y}=-3].
Проведем необходимый расчет и получим следующую запись:
[frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}} Leftrightarrow frac{x-2}{1}=frac{y-(-4)}{-2} Leftrightarrow frac{x-2}{1}=frac{y+4}{-3}].
Ответ: [frac{x-2}{1}=frac{y+4}{-3}]
Каноническое уравнение на плоскости с точками ax и ay равными нулевому значению
При условии, что одно из значений переменной является нулю, будет использоваться первоначальный вид уравнения. Две переменные нулевыми быть не могут, так как это невозможно по определению. Направляющий вектор не может быть нулевым.
В такой ситуации выражение [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}] считается условным, и его нужно понимать как равенство [a_{y}left(x-x_{1}right)=a_{x}left(y-y_{1}right)].
Если [frac{x-x_{1}}{0}=frac{y-y_{1}}{a_{y}}] при [a_{x}=0], а заданная прямая проходит через точки [M_{1}left(x_{1}, y_{1}right)]. В данном случае она является параллельной относительно оси ординат. Если [x_{1}=0], то прямая будет совпадать с осью координат.
Утверждение необходимо доказать. Для заданной прямой вектор [bar{a}=left(a_{x}, a_{y}right)] является направляющим. Также данный вектор будет являться коллинеарным по отношению к координатному вектору [bar{j}=(0.1)].
Если второй параметр является нулевым значением, то [a_{y}=0] и мы получим равенство [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{0}]. Данное уравнение характеризует прямую, которая проходит через точку [M_{1}left(x_{1}, y_{1}right)] и располагается параллельно оси абсцисс. Это утверждение будет правдивым, так как [bar{a}=left(a_{x^{prime}} 0right)], и является для прямой направляющим вектором. А вектор, в свою очередь, коллинеарен по отношению к вектору координат [bar{j}=(0.1)].
Примеры 2 — 3
На координатной плоскости задана прямая, которая расположена параллельно оси Oy. Она проходит через точку
[M_{1}left(sqrt[3]{2},-frac{1}{7}right)].
Необходимо составить каноническое уравнение для заданной прямой, используя исходные данные.
Решение:
Так как прямая по отношению к координатной оси является параллельной, можно использовать координатный вектор
[bar{j}=(0.1)]. Данный вектор будет служить, как направляющий.
Искомое уравнение будет выглядеть в следующем виде:
[frac{x-sqrt[3]{2}}{0}=frac{y-left(-frac{1}{7}right)}{1} Leftrightarrow
frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}].
Ответ: [frac{x-sqrt[3]{2}}{0}=frac{y+frac{1}{7}}{1}].
Согласно графику, нужно составить каноническое уравнение прямой.
Решение:
Исходя из графика можно сказать, что линия параллельна оси Ox и проходит через точку [M_{1}(0,3)].
Используем координатный вектор как направляющий.
Записываем каноническое уравнение: [frac{x-0}{1}=frac{y-3}{0} Leftrightarrow
frac{x}{1}=frac{y-3}{0}].
Ответ: [frac{x}{1}=frac{y-3}{0}].
Преобразование канонического уравнения прямой в уравнение другого вида
Стандартную форму канонического уравнения [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}] можно поставить в систему параметрических уравнений для плоскости.
Для преобразования одного вида уравнения в другой необходимо одну часть уравнения приравнять к другой.
[begin{aligned} &frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}} Leftrightarrow frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}=lambda Leftrightarrow frac{x-x_{1}}{a_{y}}=lambda Rightarrow \ &frac{y-y_{1}}{a_{y}}=lambda Leftrightarrow x=x_{1}+a_{x} cdot lambda Rightarrow y=y_{1}+a_{y} cdot lambda end{aligned}]
Примеры 4 — 5
Задана прямая на плоскости в виде канонического уравнения [frac{x+2}{3}=frac{y-1}{11}].
Необходимо записать параметрическое уравнение для прямой.
Принцип решения задачи:
Нужно поставить знак равенства между отдельными частями уравнения и переменной [lambda]. Получается
следующий вид уравнения: [frac{x+2}{3}=lambda] и [frac{y-1}{11}=lambda].
Далее можно записать необходимы уравнения параметрического вида:
[frac{x+2}{3}=lambda] и [frac{y-1}{11}=lambda.].
[Leftrightarrow x+2=3 cdot lambda] и
[y-1=11 cdot lambda Leftrightarrow x=-2+3 cdot lambda] и [y=1+11 cdot lambda]
Ответ: [x=-2+3 cdot lambda] и [y=1+11 cdot lambda].
Задана на плоскости прямая при помощи канонического уравнения [frac{x-1}{2}=frac{y+4}{0}].
Необходимо составить общей вид канонического уравнения для данной прямой.
Решение:
Аналогичным образом решаем задачу, как в предыдущем примере:
[frac{x-1}{2}=lambda] и [frac{y+4}{0}=lambda].
[Leftrightarrow x-1=2 cdot lambda] и [y+4=0
cdot lambda Leftrightarrow x=-2+1 cdot lambda] и [y=-4+0 cdot lambda]
[Leftrightarrow 0
cdot(x-1)=2 cdot(y+4) Leftrightarrow y+4=0]
Ответ: [y+4=0].
Нет времени решать самому?
Наши эксперты помогут!
Принцип решения задач на составление канонических уравнений
Первым делом канонические уравнения применяется для тех задач, где необходимо вычислить принадлежность точки к заданному отрезку на плоскости.
Рассмотрим несколько вариантов задач, и подробно опишем их решение.
Примеры 6 — 8
Задана линия, каноническое уравнение которой выглядит следующим образом:
[frac{x-1}{2}=frac{y+frac{1}{2}}{-3}].
Нужно определить принадлежат ли две точки [M_{1}left(3,-3 frac{1}{2}right)] и [M_{2}(5,-4)]
прямой.
Решение:
Для того чтобы проверить принадлежность прямой, нужно подставить заданные координаты точек в каноническое
уравнение.
Выполнив данное действие получим верное равенство: [frac{3-1}{2}=frac{-3 frac{1}{2}+frac{1}{2}}{-2}
Leftrightarrow 1=1].
Согласно результату, можно сказать что точка [M_{1}left(3,-3 frac{1}{2}right)] принадлежит заданному
отрезку.
Аналогичным образом нужно поступить и с другой точкой.
[frac{5-1}{2}=frac{-4 frac{1}{2}+frac{1}{2}}{-3} Leftrightarrow 2=frac{7}{6}]
Полученное в ходе решения равенство не является верным, следовательно, точка [M_{2}(5,-4)] не будет ей
принадлежать.
Ответ: прямой принадлежат координаты точки [M_{1}left(3,-3 frac{1}{2}right)], координаты точки
[M_{2}(5,-4)] нет.
Заданы координаты двух точек [M_{1}(2,4)] и [M_{2}(-1,3)]. Нужно определить, будет ли заданная прямая на
плоскости с помощью уравнения [frac{x-2}{0}=frac{y-3}{2}], проходить через заданные координаты.
Решение:
Уравнение [frac{x-2}{0}=frac{y-3}{2}] можно преобразовать, и записать как [2 cdot(x-2)=0 cdot(y-3)
Leftrightarrow x-2=0].
Заданные координаты точек подставим преобразованное уравнение, и произведем проверку.
Для точки [M_{1}(2,4) 2-2=0 Leftrightarrow 0=0].
Так как равенство верное, можно сделать вывод, что точка принадлежит прямой.
Аналогичным образом проводится проверка второй точки: [M_{2}(-1,3)]
[-1-2=0 Leftrightarrow-3=0].
Равенство неверное, поэтому точка [M_{2}(-1,3)] не принадлежит прямой.
Ответ: через точку [M_{1}(2,4)] прямая будет проходить, так как равенство верное, через точку
[M_{2}(-1,3)] нет.
Задачи, в которых заданы точки с координатами, будут являться наиболее простыми по отношению нахождения
канонического уравнения прямой.
Наиболее сложнее решаются задачи, когда предварительно необходимо определить координаты точек, через которые
проходит прямая.
Наиболее распространенной является тип задач, где нужно доказать прохождение прямой, через заданные точки.
Задана прямая, которая проходит через точки [M_{1}(0,-3)] и [M_{2}(2,-2)] в прямоугольной системе координат. Согласно условию задачи, необходимо составить каноническое уравнение.
Решение:
Вычислим координаты вектора [overline{M_{1} M_{2}}=(2.1)], по уже известной методике решения, используя заданные точки. По отношению к прямой данный вектор будет направляющим.
[frac{x-0}{2}=frac{y-(-3)}{1} Leftrightarrow frac{x}{2}=frac{y+3}{1}]
Ответ: [frac{x-0}{2}=frac{y-(-3)}{1} Leftrightarrow frac{x}{2}=frac{y+3}{1}].
Написать канонические и параметрические уравнения прямой, образованной пересечением плоскостей
Решение
1) Найдем координаты фиксированной точки. Из исходной системы уравнений
исключим z.
Положим z=0, тогда:
откуда находим: x=1, y= -2.
Таким образом, нашли координаты фиксированной точки M0(1,-2,0).
2) Направляющий вектор определяется как векторное произведение нормалей двух плоскостей, образующих прямую:
3) Запишем канонические уравнения:
4) Обозначив,
получаем параметрические уравнения:
x=t+1, y=4t-2, z=4
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Привет, мой друг, тебе интересно узнать все про прямая в пространстве, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
прямая в пространстве, скрещивающие прямые, параллельные прямые, каноническое уравнение прямой , настоятельно рекомендую прочитать все из категории Линейная алгебра и аналитическая геометрия.
Прямая, проходящая через точку 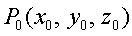
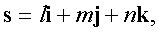
либо параметрическим уравнением прямой
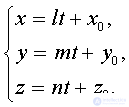
Вектор s называется вектором прямой.
Прямая линия в пространстве
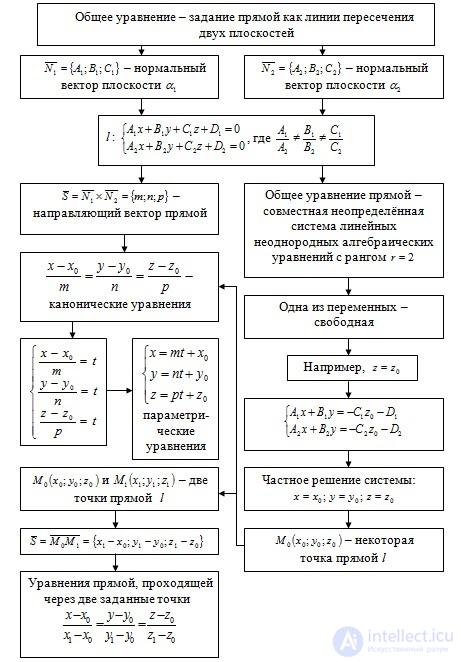
Общее уравнение прямой как линии пересечения двух плоскостей
каноническое уравнение прямой
Общее уравнение прямой совместная неопределеннная система линейных неоднородных алгебраических уравнений с рангом r = 2
Уравнение прямой проходящей через две заданные точки
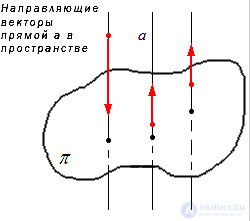
В разделе прямая на плоскости мы дали представление о точке и прямой на плоскости. Прямую линию в пространстве следует представлять абсолютно аналогично: мысленно отмечаем две точки в пространстве и проводим с помощью линейки линию от одной точки до другой и за пределы точек в бесконечность.
Все обозначения точек, прямых и отрезков в пространстве аналогичны случаю на плоскости.
Вообще, прямая линия целиком принадлежит некоторой плоскости в пространстве. Это утверждение вытекает из аксиом:
- через две точки проходит единственная прямая;
- если две точки прямой лежат в некоторой плоскости, то все точки прямой лежат в этой плоскости.
Существует еще одна аксиома, которая позволяет рассматривать прямую в пространстве как пересечение двух плоскостей: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Взаимное расположение прямых в пространстве.
Перейдем к вариантам взаимного расположения двух прямых в пространстве.
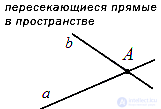
Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки).
Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку. В этом случае эти две прямые лежат в некоторой плоскости трехмерного пространства. Если две прямые в пространстве пересекаются, то мы приходим к понятию угла между пересекающимися прямыми.
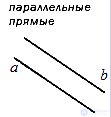
В-третьих, две прямые в пространстве могут быть параллельными. В этом случае они лежат в одной плоскости и не имеют общих точек. Рекомендуем к изучению статью
параллельные прямые , параллельность прямых.
После того как мы дали определение параллельных прямых в пространстве, следует сказать о направляющих векторах прямой линии в силу их важности. Любой ненулевой вектор, лежащий на этой прямой или на прямой, которая параллельна данной, будем называть направляющим вектором прямой. Направляющий вектор прямой очень часто используется при решении задач, связанных с прямой линией в пространстве.
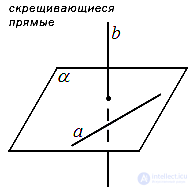
Наконец, две прямые в трехмерном пространстве могут быть скрещивающимися. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости. Такое взаимное расположение двух прямых в пространстве приводит нас к понятию угла между скрещивающимися прямыми.
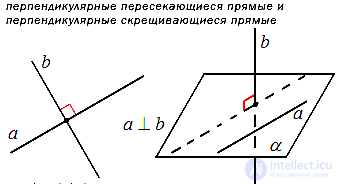
Особое практическое значение имеет случай, когда угол между пересекающимися или скрещивающимися прямыми в трехмерном пространстве равен девяноста градусам. Такие прямые называют перпендикулярными (смотрите статью перпендикулярные прямые, перпендикулярность прямых).
Способы задания прямой в пространстве.
Существует несколько способов, позволяющих однозначно определить прямую линию в пространстве. Перечислим основные из них.
Мы знаем из аксиомы, что через две точки проходит прямая, причем только одна. Таким образом, если мы отметим две точки в пространстве, то это позволит однозначно определить прямую линию, проходящую через них.
Если в трехмерном пространстве введена прямоугольная система координат и задана прямая с помощью указания координат двух ее точек, то мы имеем возможность составить уравнение прямой, проходящей через две заданные точки.
Второй способ задания прямой в пространстве основан на теореме: через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и причем только одна.
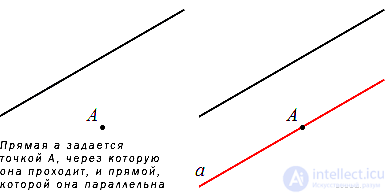
Таким образом, если задать прямую (или отрезок этой прямой) и не лежащую на ней точку, то мы однозначно определим прямую, параллельную заданной и проходящей через данную точку.
Рекомендуем также ознакомиться со статьей уравнение прямой, проходящей через заданную точку параллельно заданной прямой.
Можно указать точку, через которую проходит прямая и ее направляющий вектор. Это также позволит однозначно определить прямую.
Если прямая задана таким способом относительно зафиксированной прямоугольной системы координат, то мы можем сразу записать ее канонические уравнения прямой в пространстве и параметрические уравнения прямой в пространстве.
Следующий способ задания прямой в пространстве основан на аксиоме стереометрии: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Таким образом, задав две пересекающиеся плоскости, мы однозначно определим прямую в пространстве.
Смотрите также статью уравнения прямой в пространстве — уравнения двух пересекающихся плоскостей.
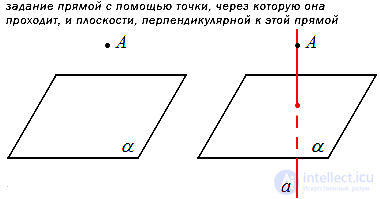
Еще один способ задания прямой в пространстве следует из теоремы (ее доказательство Вы можете найти в книгах, указанных в конце этой статьи): если задана плоскость и не лежащая в ней точка, то существует единственная прямая, проходящая через эту точку и перпендикулярная к заданной плоскости.
Таким образом, чтобы определить прямую, можно задать плоскость, которой искомая прямая перпендикулярна, и точку, через которую эта прямая проходит.
Если прямая задана таким способом относительно введенной прямоугольной системы координат, то будет полезно владеть материалом статьи уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости.
Канонические уравнения прямой в пространстве — примеры задач с решением
Продолжим изучать уравнения прямой в пространстве. В этой статье рассмотрим канонические уравнения прямой в пространстве. Этот вид уравнений прямой удобен при решении многих задач, поэтому канонические уравнения прямой в пространстве заслуживают детального и всестороннего изучения.
Сначала мы выведем канонические уравнения прямой в трехмерном пространстве и приведем примеры. Далее научимся определять координаты направляющего вектора прямой по известным каноническим уравнениям прямой, а также составлять канонические уравнения прямой при известном направляющем векторе и заданной точке прямой. После этого остановимся на частных случаях канонических уравнений прямой в пространстве и получим уравнения прямой проходящей через две заданные точки пространства. В заключении рассмотрим связь канонических уравнений прямой с другими видами уравнений этой прямой в пространстве и подробно разберем решения характерных задач.
Канонические уравнения прямой в пространстве – описание и примеры.
Получим канонические уравнения прямой a в трехмерном пространстве. Аналогичные действия мы проводили, когда рассматривали каноническое уравнение прямой на плоскости.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz. Зададим в ней прямую. Выберем следующий способ задания прямой линии в пространстве: укажем точку, через которую проходит прямая a, и направляющий вектор прямой a. Будем считать, что точка 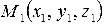
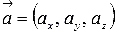
Очевидно, что множество точек 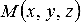


Запишем необходимое и достаточное условие коллинеарности векторов 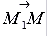
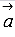

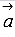
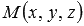
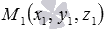
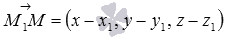
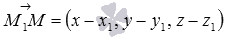
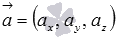
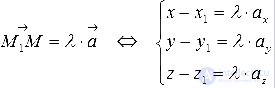
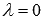
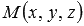
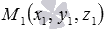
Если 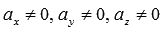
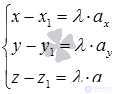
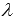
Полученные уравнения вида 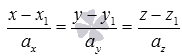
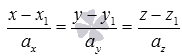
Запись вида 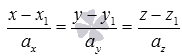
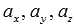
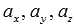
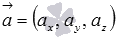
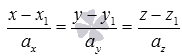
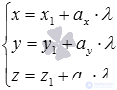
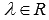
Обратите внимание на следующие важные факты:
Приведем пару примеров канонических уравнений прямой в пространстве:
Составление канонических уравнений прямой в пространстве.
Итак, канонические уравнения прямой в фиксированной прямоугольной системе координат Oxyz в трехмерном пространстве вида 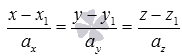
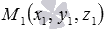
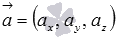
Покажем решения таких задач.
Пример.
Прямая в прямоугольной системе координат Oxyz в трехмерном пространстве задана каноническими уравнениями прямой вида 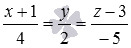
Решение.
Числа, стоящие в знаменателях канонических уравнений прямой, являются соответствующими координатами направляющего вектора этой прямой, то есть, 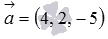

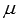
Ответ:
Пример.
Напишите канонические уравнения прямой, которая в прямоугольной системе координат Oxyz в пространстве проходит через точку 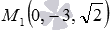
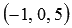
Решение.
Из условия имеем 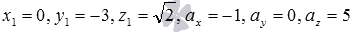
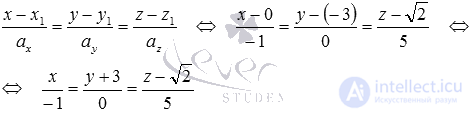
Ответ:
Мы рассмотрели простейшую задачу на составление канонических уравнений прямой в заданной прямоугольной системе координат в трехмерном пространстве, когда известны координаты направляющего вектора прямой и координаты некоторой точки прямой. Однако намного чаще встречаются задачи, в которых сначала требуется найти координаты направляющего вектора прямой, а уже потом записывать канонические уравнения прямой. В качестве примера можно привести задачи на нахождение уравнений прямой, проходящей через заданную точку пространства параллельно заданной прямой и задачи на нахождение уравнений прямой, проходящей через заданную точку пространства перпендикулярно к заданной плоскости.
Частные случаи канонических уравнений прямой в пространстве.
Мы уже отмечали, что одно или два из чисел 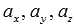
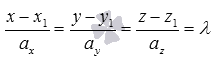
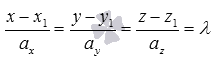
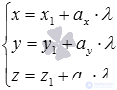
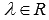
Давайте рассмотрим подробнее все эти частные случаи канонических уравнений прямой в пространстве.
Пусть 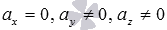
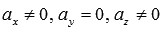
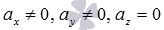
или
или
В этих случаях в прямоугольной системе координат Oxyz в пространстве прямые лежат в плоскостях 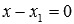
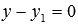
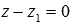
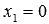

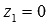
При 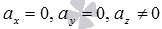

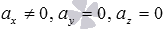
или
или
соответственно.
В этих случаях прямые параллельны координатным осям Oz, Oy или Ox соответственно (или совпадают с этими осями при 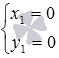
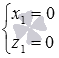
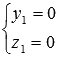
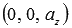
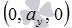
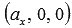
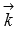
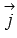
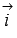
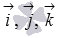
Осталось для закрепления материала этого пункта рассмотреть решения примеров.
Пример.
Напишите канонические уравнения координатных прямых Ox, Oy и Oz.
Решение.
Направляющими векторами координатных прямых Ox, Oy и Oz являются координатные векторы 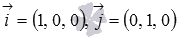
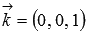

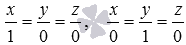
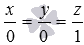
Ответ:
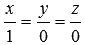
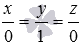
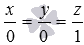
Пример.
Составьте канонические уравнения прямой, которая в прямоугольной системе координат Oxyz в пространстве проходит через точку 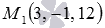
Решение.
Так как прямая, канонические уравнения которой нам требуется составить, параллельна координатной оси Oy, то ее направляющим вектором является вектор 

Ответ:
Канонические уравнения прямой проходящей через две заданные точки пространства.
Поставим себе задачу: написать канонические уравнения прямой, проходящей в прямоугольной системе координат Oxyz в трехмерном пространстве через две несовпадающие точки 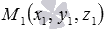
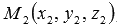
В качестве направляющего вектора заданной прямой можно принять вектор 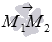
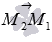
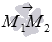
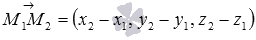
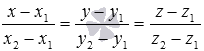

Пример.
Напишите канонические уравнения прямой, проходящей через две точки трехмерного пространства 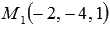
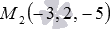
Решение.
Ответ:
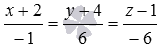
Переход от канонических уравнений прямой в пространстве к другим видам уравнений прямой.
Для решения некоторых задач канонические уравнения прямой в пространстве 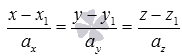
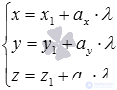
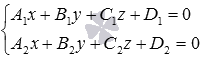
От уравнений прямой в каноническом виде легко перейти к параметрическим уравнениям этой прямой. Для этого требуется каждую из дробей в канонических уравнениях прямой в пространстве принять равной параметру 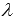
При этом параметр 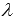
Пример.
Прямая в трехмерном пространстве в заданной прямоугольной системе координат Oxyz определена каноническими уравнениями прямой вида 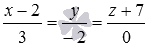
Решение.
Примем каждую из дробей равной λ:
. Разрешив первое уравнение системы относительно переменной x, второе – относительно y, третье – относительно z, получим требуемые параметрические уравнения прямой:
Ответ:
Теперь покажем, как из канонических уравнений прямой 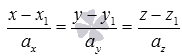
Двойное равенство 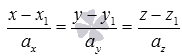
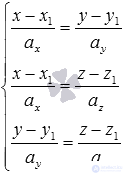
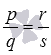
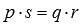
Итак, мы получили
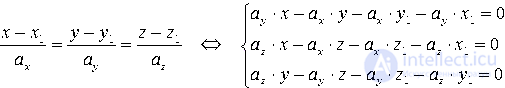
Так как числа ax, ay и az одновременно не равны нулю, то ранг основной матрицы полученной системы равен двум, так как
а хотя бы один из определителей второго порядка
отличен от нуля.
Следовательно, из системы можно исключить уравнение, которое не участвует в образовании базисного минора. Таким образом, канонические уравнения прямой в пространстве будут эквивалентны системе из двух линейных уравнений с тремя неизвестными, которые и являются уравнениями пересекающихся плоскостей, причем линией пересечения этих плоскостей будет прямая, определяемая каноническими уравнениями прямой вида 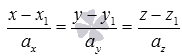
Для ясности приведем подробное решение примера, на практике все проще.
Пример.
Напишите уравнения двух пересекающихся плоскостей, которые определяют прямую, заданную в прямоугольной системе координат Oxyz в пространстве каноническими уравнениями прямой 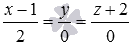
Решение.
Попарно приравняем дроби, составляющие канонические уравнения прямой в пространстве:
Последнее уравнение полученной системы можно исключить, так как оно верно для любых значений переменных x, y и z. Тогда 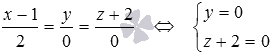
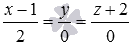
Ответ:
Пример.
Прямая в прямоугольной системе координат в пространстве задана каноническими уравнениями вида 
Решение.
Приравняем попарно дроби, образующие канонические уравнения прямой:
Определитель основной матрицы полученной системы линейных уравнений равен нулю 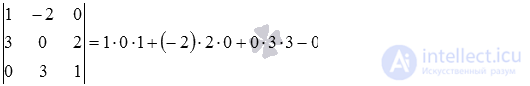
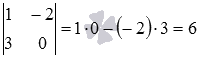
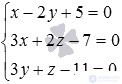

Ответ:
Вау!! 😲 Ты еще не читал? Это зря!
- задачи линейная алгебра , задачи аналитическая геометрия ,
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про прямая в пространстве Надеюсь, что теперь ты понял что такое прямая в пространстве, скрещивающие прямые, параллельные прямые, каноническое уравнение прямой
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Линейная алгебра и аналитическая геометрия