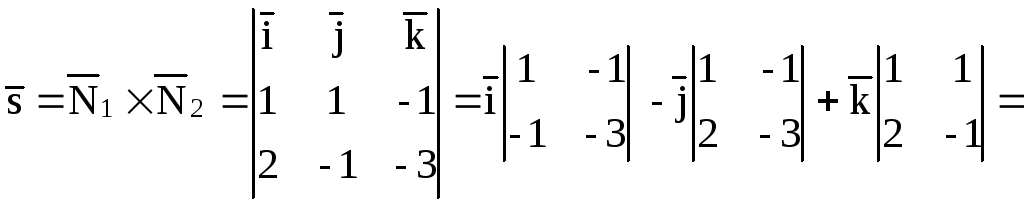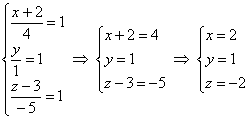Как составить каноническое уравнение прямой проходящей через точку параллельно вектору

3.1. Канонические
уравнения прямой.

Пусть в системе
координат Oxyz
дана прямая, которая проходит через
точку

(см. рис.18).Обозначим через
вектор, параллельный данной прямой.
Векторназываетсянаправляющим
вектором прямой.
Возьмем на прямой точку и рассмотрим вектор
Векторыколлинеарны, следовательно, их
соответствующие координаты пропорциональны:

(3.3.1)

Эти уравнения
называются каноническими
уравнениями прямой.

Пример: Написать
уравнения прямой, проходящей через
точку M(1,
2, –1) параллельно вектору

Решение:
Вектор
является направляющим вектором искомой
прямой. Применяя формулы (3.1.1), получим:

Это канонические
уравнения прямой.

Замечание:
Обращение в нуль одного из знаменателей
означает обращение в нуль соответствующего
числителя, то есть y
– 2 = 0; y
= 2. Данная прямая лежит в плоскости y
= 2, параллельной плоскости Oxz.

3.2.
Параметрические
уравнения прямой.

Пусть прямая
задана каноническими уравнениями

Обозначим тогдаВеличина t
называется параметром и может принимать
любые значения:
.

Выразим x,
y
и z
через t
:

(3.2.1)

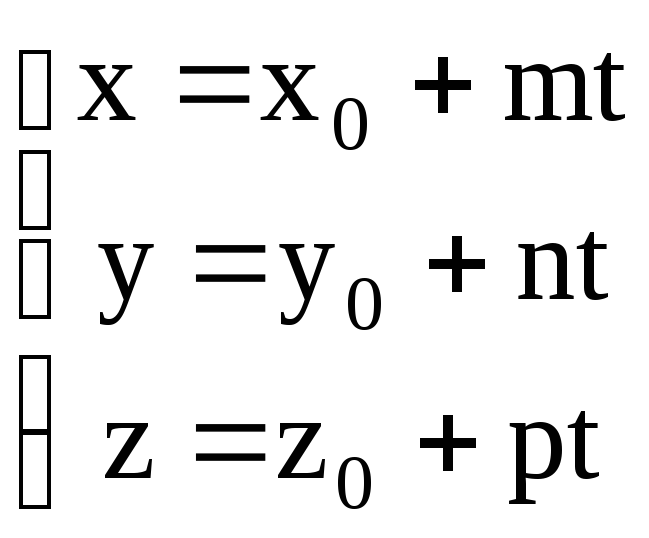
Полученные уравнения
называются параметрическими
уравнениями прямой.

Пример 1:
Составить
параметрические уравнения прямой,
проходящей через точку M
(1, 2, –1) параллельно вектору

Решение:
Канонические уравнения этой прямой
получены в примере пункта 3.1:

Для нахождения
параметрических уравнений прямой
применим вывод формул (3.2.1):

Итак,
— параметрические уравнения данной
прямой.

Ответ:

Пример 2.
Составить
параметрические уравнения прямой,
проходящей через точку M
(–1, 0, 1) параллельно вектору
гдеA
(2, 1, –1), B
(–1, 3, 2).

Решение:
Вектор является направляющим
вектором искомой прямой.

Найдем вектор .

= (–3; 2; 3). По формулам
(3.2.1) запишем уравнения прямой:

— это искомые
параметрические уравнения прямой.

3.3. Уравнения
прямой, проходящей через две заданные
точки.

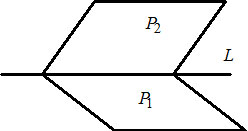
Через две заданные
точки в пространстве проходит единственная
прямая (см. рис.20). Пусть даны точки
Векторможно принять за направляющий вектор
данной прямой. Тогда уравнения прямой
находим
по формулам (3.1.1):).

(3.3.1)

Пример 1.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки

Решение:

Применяем
формулу (3.3.1)

Получили канонические
уравнения прямой. Для получения
параметрических уравнений применим
вывод формул (3.2.1). Получим

— это параметрические
уравнения прямой.

Пример 2.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки

Решение:

По формулам
(3.3.1) получим:

Это канонические
уравнения.

Переходим к
параметрическим уравнениям:

— параметрические
уравнения.

Полученная прямая
параллельна оси oz
(см. рис.21).

3.4. Прямая как
линия пересечения двух плоскостей.

Пусть в
пространстве даны две плоскости

и

Если эти плоскости
не совпадают и не параллельны, то они
пересекаются по прямой:

Эта система двух
линейных уравнений задает прямую как
линию пересечения двух плоскостей. От
уравнений (3.4.1) можно перейти к каноническим
уравнениям (3.1.1) или параметрическим
уравнениям (3.2.1). Для этого необходимо
найти точку
лежащую на прямой, и направляющий векторКоординаты точкиполучим из системы (3.4.1), придав одной
из координат произвольное значение
(например,z
= 0). За направляющий вектор
можно взять векторное произведение
векторовто есть

Пример 1.
Составить
канонические уравнения прямой

Решение: Пусть
z
= 0. Решим систему

Сложив эти уравнения,
получим: 3x
+ 6 = 0
x
= –2. Подставим найденное значение x
= –2 в первое уравнение системы и получим:
–2 + y
+ 1 = 0
y
= 1.

Итак, точка
лежит на искомой прямой.

Для нахождения
направляющего вектора прямой запишем
нормальные векторы плоскостей:
и найдем их векторное произведение:

Уравнения прямой
находим по формулам (3.1.1):

Ответ: .

Другой способ:
Канонические и параметрические
уравнения прямой (3.4.1) легко получить,
найдя две различные точки на прямой из
системы (3.4.1), а затем применив формулы
(3.3.1) и вывод формул (3.2.1).

Пример 2.
Составить канонические и параметрические
уравнения прямой

Решение:
Пусть y
= 0. Тогда система примет вид:

Сложив уравнения,
получим: 2x
+ 4 = 0; x
= –2. Подставим x
= –2 во второе уравнение системы и
получим: –2 –z
+1 = 0
z
= –1. Итак, нашли точку

Для нахождения
второй точки положим x
= 0. Будем иметь:

То есть

Далее применяем
формулы (3.3.1):

Получили канонические
уравнения прямой.

Составим
параметрические уравнения прямой:

Ответ:

; .

3.5. Взаимное
расположение двух прямых в пространстве.

Пусть прямые
заданы уравнениями:

:

;: .

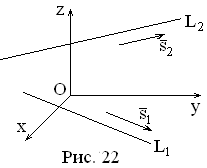
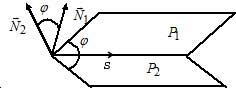
Под углом между
этими прямыми понимают угол между их
направляющими векторами
(см. рис.22). Этот уголнаходим по формуле из векторной алгебры:

или

(3.5.1)

Если прямые перпендикулярны
(),то
Следовательно,

(3.5.2)

Это условие
перпендикулярности двух прямых в
пространстве.

Если прямые
параллельны (),то их направляющие
векторы коллинеарны (),
то есть

(3.5.3)

Это условие
параллельности двух прямых в пространстве.

Пример 1. Найти
угол между прямыми:

а).
и

б). и

Решение:
а). Запишем направляющий вектор прямой
Найдем направляющий векторвторой прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему

Затем найдем их векторное произведение:

(см. пример 1
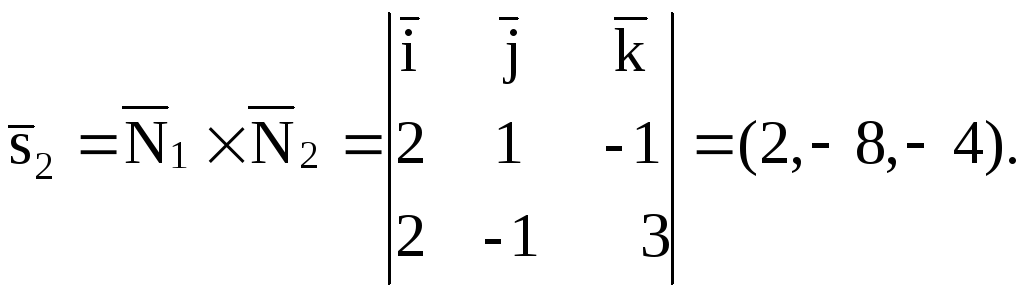
пункта 3.4).

По формуле (3.5.1)
получим:

Следовательно,

б). Запишем
направляющие векторы данных прямых:
Векторыколлинеарны, так как их соответствующие
координаты пропорциональны:

Значит прямые
параллельны (),
то есть

Ответ: а).
б).

Пример 2. Доказать
перпендикулярность прямых:

и

Решение:
Запишем направляющий вектор первой
прямой

Найдем направляющий
вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему:

Вычислим их векторное произведение:

(См. пример 1пункта 3.4).

Применим условие
перпендикулярности прямых (3.5.2):

Условие выполнено;
следовательно, прямые перпендикулярны
().

Соседние файлы в предмете Математика

• #
• #
• #
• #
• #
• #
• #
• #
• #

  03.03.20154.96 Кб8Содержание OneNote.onetoc2

• #

б) Прямая, параллельная заданной прямой, должна быть параллельна ее направляющему вектору. Направляющий вектор прямой $frac<5>=frac<2>=frac<-1>$ имеет координаты $overline S(5, 2, -1).$ Далее, находим уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(5, 2, -1)$ как и в пункте а):

в) ось OX имеет направляющий вектор $i=(1, 0, 0).$ Таким образом, ищем уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $i(1, 0, 0):$

д) Прямая, заданная как пересечение двух плоскостей перпендикулярна нормалям обеих плоскостей , поэтому Направляющий вектор прямой

$left<begin3x-y+2z-7=0,\ x+3y-2z-3=0; endright.$ можно найти как векторное произведение нормалей заданных плоскостей.

Для плоскости $P_1:$ $3x-y+2z-7=0$ нормальный вектор имеет координаты $N_1(3, -1, 2);$

для плосости $P_2:$ $x+3y-2z-3,$ нормальный вектор имеет координаты $N_2(1, 3, -2).$

Находим векторное произведение:

Таким образом, направляющий вектор прямой $left<begin3x-y+2z-7=0,\ x+3y-2z-3=0; endright.$ имеет координаты $overline S (-4, 8, 10).$

Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(-4, 8, 10):$

е) Найдем направляющий вектор прямой $x=-2+t, y=2t, z=1-frac<1><2>t.$ Для этого запишем уравнение этой прямой в каноническом виде:

Отсюда находим направляющий вектор $overline Sleft(1, 2, -frac<1><2>right).$ Умножим координаты направляющего вектора на 2 (чтобы избавиться от дроби): $overline S_1(2, 4, -1).$

Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(2, 4, -1):$

2.199(a). Написать уравнение прямой, проходящей через две заданные точки $M_1 (1, -2, 1)$ и $M_2(3, 1, -1).$

Решение.

Воспользуемся формулой (3) уравнения прямой в пространстве:

$frac=frac=frac -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$

Подставляем заданные точки:

2.204. Найти расстояние между параллельными прямыми

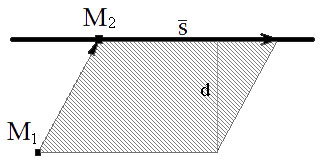
Решение.

Расстояние между параллельными прямыми $L_1$ и $L_2$ равно расстоянию от произвольной точки прямой $L_1$ до прямой $L_2.$ Следовательно, его можно найти по формуле $$d(L_1, L_2)=d(M_1, L_2)=frac<|[overline, overline S]|><|overline S|>,$$ где $M_1-$ произвольная точка прямой $L_1,$ $M_2 — $произвольная точка прямой $L_2,$ $overline S -$ направляющий вектор прямой $L_2.$

Из канонических уравнений прямых берем точки $M_1=(2, -1, 0)in L_1,$ $M_2=(7, 1, 3)in L_2,$ $overline S=(3, 4, 2). $

Отсюда находим $overline=(7-2, 1-(-1),3-0)=(5, 2, 3);$

Ответ: 3.

2.205 (а). Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $L:$ $left<begin2x-2y+z+3=0,\ 3x-2y+2z+17=0 endright.$

Решение.

Для того, чтобы найти расстояние от точки $A$ до прямой $L,$ нам необходимо выбрать произвольную точку $M,$ принадлежащую прямой $L$ и найти направляющий вектор этой прямой.

Выбираем точку $M.$ Пусть координата $z=0.$ Подставим это значение в данную систему:

Таким образом, $M=(-14, -frac<25><2>, 0)$

Направляющий вектор найдем, как векторное произведение нормалей заданных плоскостей:

Для плоскости $P_1:$ $2x-2y+z+3=0$ нормальный вектор имеет координаты $N_1(2, -2, 1);$

для плосости $P_2:$ $3x+2y+2z+17=0,$ нормальный вектор имеет координаты $N_2(3, -2, 2).$

Находим векторное произведение:

Таким образом, направляющий вектор прямой $left<begin2x-2y+z+3=0,\ 3x-2y+2z+17=0 endright.$

имеет координаты $overline S (-2, -1, 2).$

Теперь можно воспользоваться формулой $$d(A, L)=frac<|[overline, overline S]|><|overline S|>.$$

$overline=left(2-(-14),3-left(-frac<25><2>right),-1-0right)=left(16, 15frac<1><2>, -1right)$

Ответ: $d(A, L)=15.$

2.212. Написать каноническое уравнение прямой, которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $P: 3x-2y-3z-7=0$ и пересекает прямую $L: frac<3>=frac<-2>=frac<2>.$

Решение.

Запишем уравнение плоскости $P_1,$ которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $3x-2y-3z-7=0:$

$P: 3x-2y-3z-7=0Rightarrow overline N=(3; -2; -3).$ Искомая плоскость проходит через точку $M_0(3, -2, -4)$ перпендикулярно вектору $overline N(3, -2, -3).$

$P_1: 3x-9-2y-4-3z-12=0 Rightarrow$

Далее найдем точку пересечения плоскости $P_1$ и прямой $L.$ Для этого запишем уравнение прямой $L$ в параметрической форме:

Далее, подставим значения $x, y$ и $z,$ выраженные через $t$ в уравнение плоскости $P_1,$ и из полученного уравнения выразм $t:$

Подставляя найденное занчение $t$ в уравнение прямой $L,$ найдем координаты точки пересечения:

Таким образом, прямая $L$ и плоскость $P_1$ пересекаются в точке $M_1(8, -8, 5).$

Теперь запишем уравнение прямой, проходящей через точки $M_0(3, -2. -4)$ и $M_1(8, -8, 5)$— это и будет искомая прямая. Воспользуемся формулой ( 3) $frac=frac=frac :$

2.199.

б) Написать уравнение прямой, проходящей через две заданные точки $M_1 (3, -1, 0)$ и $M_2(1, 0, -3).$

б) Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $ L:$ $left<beginx=3t+5,\ y=2t,\z=-2t-25. endright.$

2.206. Доказать, что прямые $L_1: left<begin2x+2y-z-10=0,\ x-y-z-22=0, endright.$ и $L_2: frac<3>=frac<-1>=frac<4>.$ параллельны и найти расстояние $rho(L_1, L_2)$

2.207. Составить уравнения прямой, проходящей через точки пересечения плоскости $x-3y+2z+1=0$ с прямыми $frac<5>=frac<-2>=frac<-1>$ и $frac<4>=frac<-6>=frac<2>.$

2.211. Написать уравнение прямой, проходящей через точку $M_0(7, 1, 0)$ параллельно плоскости $2x+3y-z-15=0$ и пересекающей прямую $frac<1>=frac<4>=frac<2>.$

Канонические уравнения прямой в пространстве: теория, примеры, решение задач

Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.

В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через 2 заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.

Что такое каноническое уравнение прямой в пространстве

О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.

Допустим, у нас есть прямоугольная система координат O x y z , в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой a , а точку M , то можно записать, что M 1 ( x 1 , y 1 , z 1 ) лежит на прямой a и направляющим вектором этой прямой будет a → = ( a x , a y , a z ) . Чтобы множество точек M ( x , y , z ) определяло прямую a , векторы M 1 M → и a → должны быть коллинеарными,

Если мы знаем координаты векторов M 1 M → и a → , то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты a → . Для того чтобы получить координаты M 1 M → , нам необходимо вычислить разность между M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) . Запишем:

M 1 M → = x — x 1 , y — y 1 , z — z 1

После этого нужное нам условие мы можем сформулировать так: M 1 M → = x — x 1 , y — y 1 , z — z 1 и a → = ( a x , a y , a z ) : M 1 M → = λ · a → ⇔ x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z

Здесь значением переменной λ может быть любое действительное число или ноль. Если λ = 0 , то M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) совпадут, что не противоречит нашим рассуждениям.

При значениях a x ≠ 0 , a y ≠ 0 , a z ≠ 0 мы можем разрешить относительно параметра λ все уравнения системы x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z

Между правыми частями после этого можно будет поставить знак равенства:

x — x 1 = λ · a x y — y 1 = λ · a y z — z 1 = λ · a z ⇔ λ = x — x 1 a x λ = y — y 1 a y λ = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z

В итоге у нас получились уравнения x — x 1 a x = y — y 1 a y = z — z 1 a z , с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.

Такая запись используется даже при нулевых значениях одного или двух параметров a x , a y , a z , поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны 0 , поскольку направляющий вектор a → = ( a x , a y , a z ) нулевым не бывает.

Если один-два параметра a равны 0 , то уравнение x — x 1 a x = y — y 1 a y = z — z 1 a z носит условный характер. Его следует считать равным следующей записи:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , λ ∈ R .

Частные случаи канонических уравнений мы разберем в третьем пункте статьи.

Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.

1) если исходная прямая будет проходить через две точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , то канонические уравнения примут следующий вид:

x — x 1 a x = y — y 1 a y = z — z 1 a z или x — x 2 a x = y — y 2 a y = z — z 2 a z .

2) поскольку a → = ( a x , a y , a z ) является направляющим вектором исходной прямой, то таковыми будут являться и все векторы μ · a → = μ · a x , μ · a y , μ · a z , μ ∈ R , μ ≠ 0 . Тогда прямая может быть определена с помощью уравнения x — x 1 a x = y — y 1 a y = z — z 1 a z или x — x 1 μ · a x = y — y 1 μ · a y = z — z 1 μ · a z .

Вот несколько примеров таких уравнений с заданными значениями:

x — 3 2 = y + 1 — 1 2 = z ln 7

Тут x 1 = 3 , y 1 = — 1 , z 1 = 0 , a x = 2 , a y = — 1 2 , a z = ln 7 .

x — 4 0 = y + 2 1 = z + 1 0

Тут M 1 ( 4 , — 2 , — 1 ) , a → = ( 0 , 1 , 0 ) .

Как составить каноническое уравнение прямой в пространстве

Мы выяснили, что канонические уравнения вида x — x 1 a x = y — y 1 a y = z — z 1 a z будут соответствовать прямой, проходящей через точку M 1 ( x 1 , y 1 , z 1 ) , а вектор a → = ( a x , a y , a z ) будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.

Разберем пару конкретных задач.

У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x + 1 4 = y 2 = z — 3 — 5 . Запишите координаты всех направляющих векторов для нее.

Решение

Чтобы получить координаты направляющего вектора, нам надо просто взять значения знаменателей из уравнения. Мы получим, что одним из направляющих векторов будет a → = ( 4 , 2 , — 5 ) , а множество всех подобных векторов можно сформулировать как μ · a → = 4 · μ , 2 · μ , — 5 · μ . Здесь параметр μ – любое действительное число (за исключением нуля).

Ответ: 4 · μ , 2 · μ , — 5 · μ , μ ∈ R , μ ≠ 0

Запишите канонические уравнения, если прямая в пространстве проходит через M 1 ( 0 , — 3 , 2 ) и имеет направляющий вектор с координатами — 1 , 0 , 5 .

Решение

У нас есть данные, что x 1 = 0 , y 1 = — 3 , z 1 = 2 , a x = — 1 , a y = 0 , a z = 5 . Этого вполне достаточно, чтобы сразу перейти к записи канонических уравнений.

x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — 0 — 1 = y — ( — 3 ) 0 = z — 2 5 ⇔ ⇔ x — 1 = y + 3 0 = z — 2 5

Ответ: x — 1 = y + 3 0 = z — 2 5

Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.

Канонические уравнения с одним или двумя a, равными нулю

Ранее мы уже говорили, что одно-два значения параметров a x , a y , a z в уравнениях могут иметь нулевые значения. При этом запись x — x 1 a x = y — y 1 a y = z — z 1 a z = λ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при λ ∈ R ):

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Рассмотрим эти случаи подробнее. Допустим, что a x = 0 , a y ≠ 0 , a z ≠ 0 , a x ≠ 0 , a y = 0 , a z ≠ 0 , либо a x ≠ 0 , a y ≠ 0 , a z = 0 . В таком случае нужные уравнения мы можем записать так:

В первом случае:
x — x 1 0 = y — y 1 a y = z — z 1 a z = λ ⇔ x — x 1 = 0 y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x — x 1 = 0 y — y 1 a y = z — z 1 a z = λ

Во втором случае:
x — x 1 a x = y — y 1 0 = z — z 1 a z = λ ⇔ x = x 1 + a x · λ y — y 1 = 0 z = z 1 + a z · λ ⇔ y — y 1 = 0 x — x 1 a x = z — z 1 a z = λ

В третьем случае:
x — x 1 a x = y — y 1 a y = z — z 1 0 = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z — z 1 = 0 ⇔ z — z 1 = 0 x — x 1 a x = y — y 1 a y = λ

Получается, что при таком значении параметров нужные прямые находятся в плоскостях x — x 1 = 0 , y — y 1 = 0 или z — z 1 = 0 , которые располагаются параллельно координатным плоскостям (если x 1 = 0 , y 1 = 0 либо z 1 = 0 ). Примеры таких прямых показаны на иллюстрации.

Следовательно, мы сможем записать канонические уравнения немного иначе.

1. В первом случае: x — x 1 0 = y — y 1 0 = z — z 1 a z = λ ⇔ x — x 1 = 0 y — y 1 = 0 z = z 1 + a z · λ , λ ∈ R
2. Во втором: x — x 1 0 = y — y 1 a y = z — z 1 0 = λ ⇔ x — x 1 = 0 y = y 1 + a y · λ , λ ∈ R z — z 1 = 0
3. В третьем: x — x 1 a x = y — y 1 0 = z — z 1 0 = λ ⇔ x = x 1 + a x · λ , λ ∈ R y = y 1 = 0 z — z 1 = 0

Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: x 1 = 0 y 1 = 0 , x 1 = 0 z 1 = 0 , y 1 = 0 z 1 = 0 . Их направляющие векторы имеют координаты 0 , 0 , a z , 0 , a y , 0 , a x , 0 , 0 . Если обозначить направляющие векторы координатных прямых как i → , j → , k → , то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:

Покажем на примерах, как применяются эти правила.

Найдите канонические уравнения, с помощью которых можно определить в пространстве координатные прямые O z , O x , O y .

Решение

Координатные векторы i → = ( 1 , 0 , 0 ) , j → = 0 , 1 , 0 , k → = ( 0 , 0 , 1 ) будут для исходных прямых направляющими. Также мы знаем, что наши прямые будут обязательно проходить через точку O ( 0 , 0 , 0 ) , поскольку она является началом координат. Теперь у нас есть все данные, чтобы записать нужные канонические уравнения.

Для прямой O x : x 1 = y 0 = z 0

Для прямой O y : x 0 = y 1 = z 0

Для прямой O z : x 0 = y 0 = z 1

Ответ: x 1 = y 0 = z 0 , x 0 = y 1 = z 0 , x 0 = y 0 = z 1 .

В пространстве задана прямая, которая проходит через точку M 1 ( 3 , — 1 , 12 ) . Также известно, что она расположена параллельно оси ординат. Запишите канонические уравнения этой прямой.

Решение

Учитывая условие параллельности, мы можем сказать, что вектор j → = 0 , 1 , 0 будет для нужной прямой направляющим. Следовательно, искомые уравнения будут иметь вид:

x — 3 0 = y — ( — 1 ) 1 = z — 12 0 ⇔ x — 3 0 = y + 1 1 = z — 12 0

Ответ: x — 3 0 = y + 1 1 = z — 12 0

Как записать каноническое уравнение прямой, которая проходит через две заданные точки

Допустим, что у нас есть две несовпадающие точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?

Для начала примем вектор M 1 M 2 → (или M 2 M 1 → ) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:

M 1 M 2 → = x 2 — x 1 , y 2 — y 1 , z 2 — z 1

Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:

x — x 1 x 2 — x 1 = y — y 1 y 2 — y 1 = z — z 1 z 2 — z 1 x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1

Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:

Приведем пример решения задачи.

в пространстве есть две точки с координатами M 1 ( — 2 , 4 , 1 ) и M 2 ( — 3 , 2 , — 5 ) , через которые проходит прямая. Запишите канонические уравнения для нее.

Решение

Согласно условиям, x 1 = — 2 , y 1 = — 4 , z 1 = 1 , x 2 = — 3 , y 2 = 2 , z 2 = — 5 . Нам требуется подставить эти значения в каноническое уравнение:

x — ( — 2 ) — 3 — ( — 2 ) = y — ( — 4 ) 2 — ( — 4 ) = z — 1 — 5 — 1 ⇔ x + 2 — 1 = y + 4 6 = z — 1 — 6

Если мы возьмем уравнения вида x — x 2 x 2 — x 1 = y — y 2 y 2 — y 1 = z — z 2 z 2 — z 1 , то у нас получится: x — ( — 3 ) — 3 — ( — 2 ) = y — 2 2 — ( — 4 ) = z — ( — 5 ) — 5 — 1 ⇔ x + 3 — 1 = y — 2 6 = z + 5 — 6

Ответ: x + 3 — 1 = y — 2 6 = z + 5 — 6 либо x + 3 — 1 = y — 2 6 = z + 5 — 6 .

Преобразование канонических уравнений прямой в пространстве в другие виды уравнений

Иногда пользоваться каноническими уравнениями вида x — x 1 a x = y — y 1 a y = z — z 1 a z не очень удобно. Для решения некоторых задач лучше использовать запись x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.

Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру λ и разрешим эти уравнения относительно других переменных. В итоге получим:

x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ ⇔ x — x 1 a x = λ y — y 1 a y = λ z — z 1 a z = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Значение параметра λ может быть любым действительным числом, ведь и x , y , z могут принимать любые действительные значения.

В прямоугольной системе координат в трехмерном пространстве задана прямая, которая определена уравнением x — 2 3 = y — 2 = z + 7 0 . Запишите каноническое уравнение в параметрическом виде.

Решение

Сначала приравниваем каждую часть дроби к λ .

x — 2 3 = y — 2 = z + 7 0 ⇔ x — 2 3 = λ y — 2 = λ z + 7 0 = λ

Теперь разрешаем первую часть относительно x , вторую – относительно y , третью – относительно z . У нас получится:

x — 2 3 = λ y — 2 = λ z + 7 0 = λ ⇔ x = 2 + 3 · λ y = — 2 · λ z = — 7 + 0 · λ ⇔ x = 2 + 3 · λ y = — 2 · λ z = — 7

Ответ: x = 2 + 3 · λ y = — 2 · λ z = — 7

Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).

Равенство x — x 1 a x = y — y 1 a y = z — z 1 a z нужно для начала представить в виде системы уравнений:

x — x 1 a x = y — y 1 a y x — x 1 a x = z — z 1 a x y — y 1 a y = z — z 1 a z

Поскольку p q = r s мы понимаем как p · s = q · r , то можно записать:

x — x 1 a x = y — y 1 a y x — x 1 a x = z — z 1 a z y — y 1 a y = z — z 1 a z ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) a z · ( x — x 1 ) = a x · ( z — z 1 ) a z · ( y — y 1 ) = a y · ( z — z 1 ) ⇔ ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0 a z · x — a x · z + a x · z 1 — a z · x 1 = 0 a z · y — a y · z + a y · z 1 — a z · y 1 = 0

В итоге у нас вышло, что:

x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0 a z · x — a x · z + a x · z 1 — a z · x 1 = 0 a z · y — a y · z + a y · z 1 — a z · y 1 = 0

Выше мы отмечали, что все три параметра a не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен 2 , поскольку a y — a x 0 a z 0 — a x 0 a z — a y = 0 и один из определителей второго порядка не равен 0 :

a y — a x a z 0 = a x · a z , a y 0 a z — a x = a x · a y , — a x 0 0 — a x = a x 2 a y — a x 0 a z = a y · a z , a y 0 0 — a y = — a y 2 , — a x 0 a z — a y = a x · a y a z 0 0 a z = a z 2 , a z — a x 0 — a y = — a y · a z , 0 — a x a z — a y = a x · a z

Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать 3 неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.

Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.

Прямая задана каноническим уравнением x — 1 2 = y 0 = z + 2 0 . Напишите для нее уравнение пересекающихся плоскостей.

Решение

Начнем с попарного приравнивания дробей.

x — 1 2 = y 0 = z + 2 0 ⇔ x — 1 2 = y 0 x — 1 2 = z + 2 0 y 0 = z + 2 0 ⇔ ⇔ 0 · ( x — 1 ) = 2 y 0 · ( x — 1 ) = 2 · ( z + 2 ) 0 · y = 0 · ( z + 2 ) ⇔ y = 0 z + 2 = 0 0 = 0

Теперь исключаем из расчетов последнее уравнение, потому что оно будет верным при любых x , y и z . В таком случае x — 1 2 = y 0 = z + 2 0 ⇔ y = 0 z + 2 = 0 .

Это и есть уравнения двух пересекающихся плоскостей, которые при пересечении образуют прямую, заданную с помощью уравнения x — 1 2 = y 0 = z + 2 0

Ответ: y = 0 z + 2 = 0

Прямая задана уравнениями x + 1 2 = y — 2 1 = z — 5 — 3 , найдите уравнение двух плоскостей, пересекающихся по данной прямой.

Решение

Приравниваем дроби попарно.

x + 1 2 = y — 2 1 = z — 5 — 3 ⇔ x + 1 2 = y — 2 1 x + 1 2 = z — 5 — 3 y — 2 1 = z — 5 — 3 ⇔ ⇔ 1 · ( x + 1 ) = 2 · ( y — 2 ) — 3 · ( x + 1 ) = 2 · ( z — 5 ) — 3 · ( y — 2 ) = 1 · ( z — 5 ) ⇔ x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + 7 — 11 = 0

Получаем, что определитель основной матрицы полученной системы будет равен 0 :

1 — 2 0 3 0 2 0 3 1 = 1 · 0 · 1 + ( — 2 ) · 2 · 0 + 0 · 3 · 3 — 0 · 0 · 0 — 1 · 2 · 3 — ( — 2 ) · 3 · 1 = 0

Минор второго порядка нулевым при этом не будет: 1 — 2 3 0 = 1 · 0 — ( — 2 ) · 3 = 6 . Тогда мы можем принять его в качестве базисного минора.

В итоге мы можем вычислить ранг основной матрицы системы x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + z — 11 = 0 . Это будет 2. Третье уравнение исключаем из расчета и получаем:

x — 2 y + 5 = 0 3 x + 2 z — 7 = 0 3 y + z — 11 = 0 ⇔ x — 2 y + 5 = 0 3 x + 2 z — 7 = 0

Ответ: x — 2 y + 5 = 0 3 x + 2 z — 7 = 0

Прямая в пространстве, всевозможные уравнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения прямой в пространстве:

1) $left{begin{array}{lcl}A_1x+B_1y+C_1z+D_1=0quad (P_1)\ A_2x+B_2y+C_2z+D_2=0quad (P_2)end{array}right. — $ общее уравнение прямой $L$ в пространстве, как линии пересечения двух плоскостей $P_1$ и $P_2.$

 

2) $frac{x-x_0}{m}=frac{y-y_0}{n}=frac{z-z_0}{p} -$  каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline{S}=(m, n, p).$ Вектор $overline S$ является направляющим вектором прямой $L.$

 

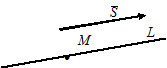
3) $frac{x-x_1}{x_2-x_1}=frac{y-y_1}{y_2-y_1}=frac{z-z_1}{z_2-z_1} -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$ 

4) Приравнивая каждую из частей канонического уравнения 2 к прараметру $t,$ получаем параметрическое уравнение прямой:

$$left{begin{array}{lcl}x=x_0+mt\ y=y_0+nt\z=z_0+ptend{array}right.  $$

Расположение двух прямых в пространстве.

Пусть $L_1:$ $frac{x-x_1}{m_1}=frac{y-y_1}{n_1}=frac{z-z_1}{p_1}$ $overline{S}_1=(m_1, n_1, p_1);$

            $L_2:$ $frac{x-x_2}{m_2}=frac{y-y_2}{n_2}=frac{z-z_2}{p_2},$ $overline{S}_2=(m_2, n_2, p_2).$

Условие параллельности двух прямых: Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline{S}_1paralleloverline{S}_2Leftrightarrow$ $frac{m_1}{m_2}=frac{n_1}{n_2}=frac{p_1}{p_2}.$

Условие перпендикулярности двух прямых: $L_1perp L_2Leftrightarrow$ $overline{S}_1perpoverline{S}_2Leftrightarrow$  ${m_1}cdot{m_2}+{n_1}cdot{n_2}+p_1cdot p_2=0.$

Угол между прямыми:

 $coswidehat{(L_1, L_2)}=$ $frac{overline{S}_1cdotoverline{S}_2}{|overline S_1|cdot|overline S_2|}=frac{{m_1}cdot{m_2}+{n_1}cdot{n_2}+p_1cdot p_2}{sqrt{m_1^2+n_1^2+p_1^2}cdotsqrt{m_2^2+n_2^2+p_2^2}}.$

  

 Расстояние от точки до прямой равно длине перпендикуляра, опущенного из точки на данную прямую.

Пусть прямая $L$ задана уравнением $frac{x-x_0}{m}=frac{y-y_0}{n}=frac{z-z_0}{p},$ следовательно $overline S=(m, n, p).$  Пусть также $M_2=(x_2, y_2, z_2) -$ произвольная точка, принадлежащая прямой $L.$ Тогда расстояние от точки $M_1=(x_1, y_1, z_1)$ до прямой $L$ можно найти по формуле: $$d(M_1, L)=frac{|[overline{M_1M_2}, overline S]|}{|overline S|}.$$

Примеры.

2.198. Написать каноническое уравнение прямой, проходящей через точку $M_0(2, 0, -3)$ параллельно:

а) вектору $q(2, -3, 5);$

б) прямой $frac{x-1}{5}=frac{y+2}{2}=frac{z+1}{-1};$

в) оси $OX;$

д) прямой $left{begin{array}{lcl}3x-y+2z-7=0,\ x+3y-2z-3=0; end{array}right.  $

е) прямой $x=-2+t, y=2t, z=1-frac{1}{2}t.$

Решение.

а) Воспользуемся формулой (2) уравнения прямой в пространстве: 

$frac{x-x_0}{m}=frac{y-y_0}{n}=frac{z-z_0}{p} -$  каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline{S}=(m, n, p).$

По условию  $M_0(2, 0, -3)$ и $overline{S}=q(2,-3,5).$

Таким образом, $frac{x-2}{2}=frac{y-0}{-3}=frac{z-(-3)}{5}Rightarrowfrac{x-2}{2}=frac{y}{-3}=frac{z+3}{5}.$

Ответ: $frac{x-2}{2}=frac{y}{-3}=frac{z+3}{5}.$

б) Прямая, параллельная заданной прямой, должна быть параллельна ее направляющему вектору. Направляющий вектор прямой  $frac{x-1}{5}=frac{y+2}{2}=frac{z+1}{-1}$ имеет координаты $overline S(5, 2, -1).$ Далее, находим уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(5, 2, -1)$ как и в пункте а):

$frac{x-2}{5}=frac{y-0}{2}=frac{z-(-3)}{-1}Rightarrowfrac{x-2}{5}=frac{y}{2}=frac{z+3}{-1}.$

Ответ: $frac{x-2}{5}=frac{y}{2}=frac{z+3}{-1}.$

в) ось OX имеет направляющий вектор $i=(1, 0, 0).$ Таким образом, ищем уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $i(1, 0, 0):$

$frac{x-2}{1}=frac{y-0}{0}=frac{z-(-3)}{0}Rightarrowfrac{x-2}{1}=frac{y}{0}=frac{z+3}{0}.$

Ответ: $frac{x-2}{1}=frac{y}{0}=frac{z+3}{0}.$

д) Прямая, заданная как пересечение двух плоскостей перпендикулярна нормалям обеих плоскостей, поэтому Направляющий вектор прямой 

$left{begin{array}{lcl}3x-y+2z-7=0,\ x+3y-2z-3=0; end{array}right.$ можно найти как векторное произведение нормалей заданных плоскостей.

Для плоскости $P_1:$ $3x-y+2z-7=0$ нормальный вектор имеет координаты $N_1(3, -1, 2);$

для плосости $P_2:$ $x+3y-2z-3,$ нормальный вектор имеет координаты $N_2(1, 3, -2).$

Находим векторное произведение:

$[N_1, N_2]=begin{vmatrix}i&j&k\3&-1&2\1&3&-2end{vmatrix}=i(2-6)-j(-6-2)+k(9+1)=-4i+8j+10k.$



5.4.1. Канонические уравнения прямой

Для лёгкого понимания темы целесообразно освоить или вспомнить уравнение «плоской» прямой, поскольку будет очень много похожих вещей. Но будут и отличия, на одно из которых вы уже наверняка обратили внимание. Я выделил прописной буквой окончание слова «уравнениЯ», подчеркивая, что оно находится ВО МНОЖЕСТВЕННОМ ЧИСЛЕ. И это не случайно: особенность пространственной прямой состоит в том, что она задаётся не одним уравнением, а некоторым множеством уравнений.

Теперь о совпадениях: пространственную прямую точно так же обозначают строчными латинскими буквами , как вариант, с подстрочными индексами: . Либо двумя точками, принадлежащими данной прямой: .

И точно так же – её можно задать несколькими способами. Начнём с канонов, точки и направляющего вектора:

Если известна некоторая точка пространства , принадлежащая прямой, и направляющий вектор  данной прямой, то  канонические уравнения этой прямой выражаются формулами:

Приведённая запись предполагает, что координаты направляющего вектора  не равны нулю. Что делать, если одна или две координаты нулевые, мы рассмотрим чуть позже.

Задача 143

Составить канонические уравнения прямой по точке  и направляющему вектору

Решение: по соответствующим формулам:

Ответ:

Что следует отметить в этом очень простом примере? Во-первых, полученные уравнения НЕ НАДО сокращать на единицу:

Сократить, точнее, можно, но это режет глаз и создаёт неудобства в ходе решения задач.

А во-вторых, проверка, которая очень легко (и быстро!) выполняется устно:

Сначала смотрим на знаменатели уравнений и сверяемся – правильно ли там записаны координаты направляющего вектора ? Нет, не подумайте, у нас не урок в детском садике «Тормозок», эта мера позволит исключить ошибку по невнимательности. Никто не застрахован от «наваждения», или вдруг вы условие неправильно переписали?

Далее подставляем координаты точки  в найденные уравнения:

 – получены верные равенства, значит, координаты точки  удовлетворяют нашим уравнениям, и сама точка действительно принадлежит данной прямой.

Довольно часто требуется найти какую-нибудь другую точку , принадлежащую данной прямой. Как это сделать? Берём полученные уравнения  и мысленно «отщипываем», например, левый кусочек: . Теперь этот кусочек приравниваем к любому числу (помним, что ноль уже был), например, к единице: .

Так как , то и два других «куска» тоже должны быть равны единице. По сути, нужно решить систему:

Проверим, удовлетворяет ли точка  уравнениям :
 – получены верные равенства, значит, точка  действительно принадлежит данной прямой.

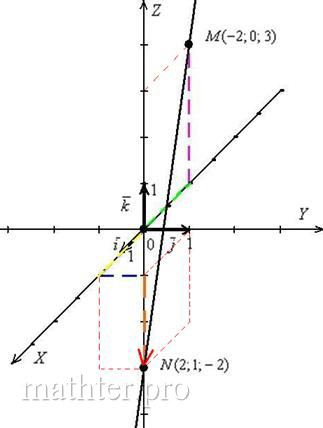
Выполним чертёж в прямоугольной системе координат:

Заодно вспомним, как правильно откладывать точки в пространстве. Строим точку :

– от начала координат в отрицательном направлении оси  откладываем отрезок первой координаты  (зелёный пунктир);

– вторая координата  нулевая, поэтому «не уходим» с оси  ни влево, ни вправо;

– в соответствие с третьей координатой  отмеряем три единицы вверх (фиолетовый пунктир). Строим точку :

– отмеряем две единицы «на себя» (желтый пунктир), одну единицу вправо (синий пунктир) и две единицы вниз (коричневый пунктир). Коричневый пунктир и сама точка  наложились на координатную ось, заметьте, что они находятся в нижнем полупространстве и расположены  ПЕРЕД осью .

Сама прямая  проходит над осью  и, если меня не подводит глазомер, над осью . Не подводит, убедился аналитически. Если бы прямая  проходила ЗА осью , то следовало бы стереть частичку линии  сверху и снизу точки скрещивания.

У прямой бесконечно много направляющих векторов, например:
 (красная стрелка). Получился в точности исходный вектор , но это чистая случайность (такую уж я выбрал точку ). Любой коллинеарный вектор, например,   тоже будет направляющим вектором данной прямой (вспоминаем, как их получить)

Разберёмся с частными случаями, когда одна или две координаты направляющего вектора нулевые. Попутно продолжим тренировать пространственное воображение. Изобразите в тетради декартову систему координат . Напоминаю удобный масштаб:  2 клетки = 1 ед. – по осям  и диагональ одной клетки = 1 ед. – по оси .

Теперь я буду рассказывать о прямых, а вы их мысленно представляйте! Рассмотрим все шесть случаев:

1) Для точки  и направляющего вектора  канонические уравнения прямой распадаются на три отдельных уравнения:

или короче:

Что это за прямая?

Поскольку направляющий вектор  коллинеарен орту , то такая прямая будет параллельна оси , в частности, уравнения  задают саму ось абсцисс. В чём смысл уравнений ? «Игрек» и «зет» ВСЕГДА (при любом «икс») равны нулю. А это ось . Кроме того, есть и другая интерпретация – ведь перед нами уравнения двух плоскостей! Уравнение  задаёт координатную плоскость , а уравнение  – плоскость . Смотрим на чертёж и ищем их пересечение!

Задача 144

Составить уравнения прямой по точке  и вектору .

Решение и ответ в одну строчку:

Какому условию удовлетворяет каждая точка этой прямой? «Иксовая» координата может быть любой:  (на практике данное уравнение, как правило, не записывают). А вот «игрековая» и «зетовая» координата постоянны, равны конкретным числам: .

Самостоятельно осмысливаем два «родственных» случая:

2) Канонические уравнения прямой, проходящей через точку  параллельно вектору , выражаются формулами .

Такие прямые будут параллельны координатной оси , в частности, уравнения   ( любое) задают координатную саму ось ординат.

3) Канонические уравнения прямой, проходящей через точку  параллельно вектору , выражаются формулами . Данные прямые параллельны координатной оси , а уравнения   ( любое) задают саму ось аппликат.

Обкатываем вторую тройку:

4) Для точки  и направляющего вектора  канонические уравнения прямой распадаются на пропорцию  и уравнение плоскости .

Задача 145

Составить уравнения прямой по точке  и вектору .

Решение и ответ в одну строчку:

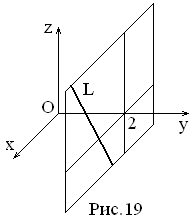
Разберём суть полученной записи. Уравнение  задаёт плоскость, причём данная плоскость будет параллельна «родной» координатной плоскости . Из пропорции  легко выразить уравнение «плоской» прямой, единственное, эта прямая будет находиться не на плоскости , а на высоте .

Если высота нулевая: , то уравнения принимают вид , и вот это уже в точности наша «плоская» прямая, лежащая в плоскости .

Таким образом, рассмотренный случай задаёт прямую, параллельную координатной плоскости . Действительно, задумайтесь, ведь направляющий вектор  параллелен данной плоскости, ибо «зетовая» координата равна нулю.

Аналогично – читаем, вдумываемся и представляем:

5) Прямая, заданная точкой  и направляющим вектором , параллельна координатной плоскости , и её канонические уравнения выражаются формулами: . В частности, уравнения  определяют прямую, лежащую в плоскости .

6) Прямая, заданная точкой  и направляющим вектором , параллельна координ атной плоскости , и её канонические уравнения выражаются формулами: . В частности, уравнения  определяют прямую, лежащую в плоскости .

Настала пора закусить – составляем уравнения и вникаем в их смысл:

Задача 146

Записать канонические уравнения прямой, если известна точка и направляющий вектор  данной прямой:

а) ;

б) .

в) Прямая проходит через точку  параллельно оси .

Это задание для самостоятельного решения, ответы в конце книги.

5.4.2. Как составить уравнения прямой по двум точкам?

5.3.7. Взаимное расположение трёх плоскостей

| Оглавление |



Автор: Aлeксaндр Eмeлин