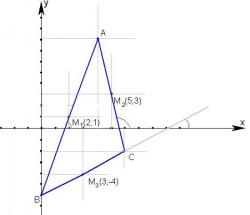
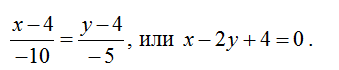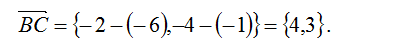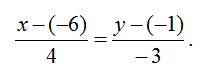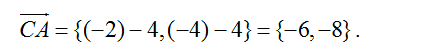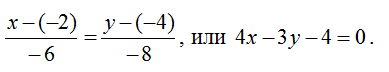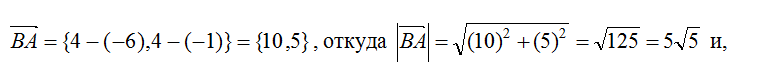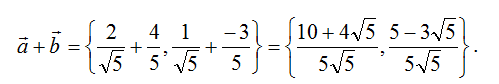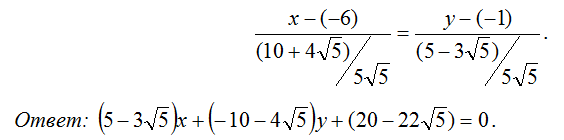Как составить каноническое уравнение треугольника по точкам - Исправление недочетов и поиск решений вместе с Examum.ru

По известным координатам вершин треугольника А(4;4), В(-6;-1), С(-2;-4) записать для его сторон уравнения в общем виде и уравнение в общем виде биссектрисы угла АВС.

Решение

Так как нам известны координаты вершин, то проще всего получить уравнение стороны в канонической форме – формула, от которого легко перейти к уравнению в общей форме. Для канонического уравнения нам нужны координаты точки, принадлежащей стороне и координаты направляющего вектора (параллельного рассматриваемому).

1. Найдем уравнение стороны АВ. В качестве точки прямой можно взять точку А с заданными координатами, а в качестве направляющего вектора – вектор АВ. Найдем координаты вектора АВ:

2. Тогда каноническое уравнение стороны АВ запишется:

3. Аналогично можно получить уравнения остальных сторон треугольника: для стороны ВС: координаты вектора

4. Откуда каноническое уравнение:

Следовательно, общее уравнение: 3x+4y+22=0.

5. Для стороны CА: координаты направляющего вектора

6. Каноническое уравнение:

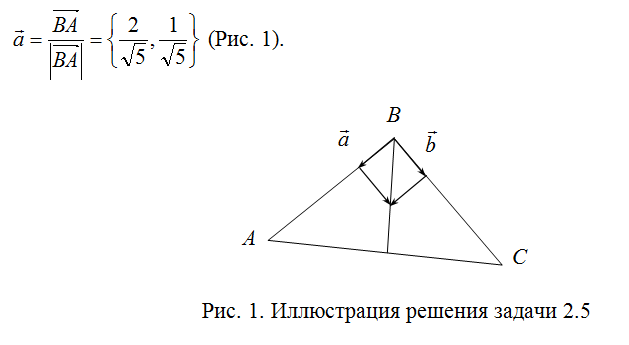
7. Выведем общее уравнение для биссектрисы. Известно, что биссектриса делит угол пополам. Если на сторонах АВ и ВС треугольника отложить орты (соответственно a и b) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов a и b).

8. Для нахождения орта a необходимо знать координаты вектора BA:

соответственно a определится как:

9. Аналогично определим орт b:

Теперь определим их сумму:

10. Тогда каноническое уравнение биссектрисы:

Источник

Как составить уравнение сторон треугольника по координатам его вершин?

Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.

Пример.

Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)

Составить уравнения сторон треугольника.

Решение:

1) Составим уравнение прямой AB, проходящей через 2 точки A и B.

Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:

$[left{ begin{array}{l} 1 = k cdot ( - 5) + b; \ - 4 = k cdot 7 + b; \ end{array} right. Rightarrow k = - frac{5}{{12}};b = - frac{{13}}{{12}}.]$

Таким образом, уравнение стороны AB

$[y = - frac{5}{{12}}x - frac{{13}}{{12}}.]$

2) Прямая BC проходит через точки B(7;-4) и C(3;7):

$[left{ begin{array}{l} - 4 = k cdot 7 + b; \ 7 = k cdot 3 + b; \ end{array} right. Rightarrow k = - frac{{11}}{4};b = frac{{61}}{4}.]$

Отсюда уравнение стороны BC —

$[y = - frac{{11}}{4}x + frac{{61}}{4}.]$

3) Прямая AC проходит через точки A(-5;1) и C(3;7):

$[left{ begin{array}{l} 1 = k cdot ( - 5) + b; \ 7 = k cdot 3 + b; \ end{array} right. Rightarrow k = frac{3}{4};b = frac{{19}}{4}.]$

Уравнение стороны AC —

$[y = frac{3}{4}x + frac{{19}}{4}.]$

Источник

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Есть множество способов определить треугольник. В аналитической геометрии один из этих способов — задать координаты трех его вершин. Эти три точки определяют треугольник однозначно, но для полноты картины нужно еще составить уравнения сторон, соединяющих вершины.

Вам заданы координаты трех точек. Обозначим их как (x1, y1), (x2, y2), (x3, y3). Предполагается, что эти точки являются вершинами некоторого треугольника. Задача состоит в том, чтобы составить уравнения его сторон — точнее уравнения тех прямых, на которых лежат эти стороны. Эти уравнения должны иметь вид:
y = k1*x + b1;
y = k2*x + b2;
y = k3*x + b3.Таким образом, вам предстоит найти угловые коэффициенты k1, k2, k3 и смещения b1, b2, b3.

Убедитесь, что все точки различны между собой. Если какие-то две совпадают, то треугольник вырождается в отрезок.

Найдите уравнение прямой, проходящей через точки (x1, y1), (x2, y2). Если x1 = x2, то искомая прямая вертикальна и ее уравнение x = x1. Если y1 = y2, то прямая горизонтальна и ее уравнение y = y1. В общем случае эти координаты не будут равны друг другу.

Подставляя координаты (x1, y1), (x2, y2) в общее уравнение прямой, вы получите систему из двух линейных уравнений:k1*x1 + b1 = y1;
k1*x2 + b1 = y2.Вычтите одно уравнение из другого и решите полученное уравнение относительно k1:k1*(x2 — x1) = y2 — y1, следовательно, k1 = (y2 — y1)/(x2 — x1).

Подставляя найденное выражение в любое из исходных уравнений, найдите выражение для b1:((y2 — y1)/(x2 — x1))*x1 + b1 = y1;
b1 = y1 — ((y2 — y1)/(x2 — x1))*x1.Поскольку уже известно, что x2 ≠ x1, можно упростить выражение, умножив y1 на (x2 — x1)/(x2 — x1). Тогда для b1 вы получите следующее выражение:b1 = (x1*y2 — x2*y1)/(x2 — x1).

Проверьте, не лежит ли третья из заданных точек на найденной прямой. Для этого подставьте значения (x3, y3) в выведенное уравнение и посмотрите, соблюдается ли равенство. Если оно соблюдается, следовательно, все три точки лежат на одной прямой, и треугольник вырождается в отрезок.

Тем же способом, что описан выше, выведите уравнения для прямых, проходящих через точки (x2, y2), (x3, y3) и (x1, y1), (x3, y3).

Окончательный вид уравнений для сторон треугольника, заданного координатами вершин, выглядит так:(1) y = ((y2 — y1)*x + (x1*y2 — x2*y1))/(x2 — x1);
(2) y = ((y3 — y2)*x + (x2*y3 — x3*y2))/(x3 — x2);
(3) y = ((y3 — y1)*x + (x1*y3 — x3*y1))/(x3 — x1).

Источник

vk.com/club152685050

Если это условие выполняется, то прямые лежат в одной плоскости, то есть они или параллельны, если координаты направляющих векторов пропорциональны, или пересекаются, если координаты направляющих векторов не пропорциональны.

В противном случае, если сформулированное условие не выполня-

ется, то прямые скрещиваются.
Если даны две плоскости A1x B1 y C1z D1 0 и	A2 x B2 y C2 z D2 0 ,

то уравнение всякой плоскости, проходящей через линию пересече-

ния	заданных	плоскостей,	имеет	вид:
A1x B1 y C1z D1 A2 x B2 y C2 z D2 0, где	— переменный	параметр.

Это уравнение называется уравнением пучка плоскостей.

Пример 1.

Даны точки L( 6, 0), N(0, 8). Через середину отрезка LN провести прямую, отсекающую на оси ОХ отрезок втрое больший, чем на оси

OY.

Решение.

Найдем координаты точки М, являющейся серединой отрезка LN:

хм = ( 6 + 0)/ 2 = 3 , yм = (0 + 8)/ 2 = 4, тогда М( 3, 4). Уравнение

прямой будем искать в виде x / a + y / b = 1. По условию a = 3b, следовательно, уравнение примет вид x / 3b + y / b = 1. Для определения b используем условие прохождения искомой прямой через точку

М( 3, 4). Так как точка М лежит на искомой прямой, то ее координа-

ты удовлетворяют уравнению прямой, то есть ( 3)/(3b) + 4/ b = 1, откуда b = 3. Подставляя это значение в равенство a = 3b, получим a = 9. Таким образом, уравнение искомой прямой: x/ 9 + y/ 3 = 1 или

x + 3y 9 = 0.

Ответ. Уравнение прямой: x + 3y 9 = 0.

Пример 2.

Составить уравнения прямых, параллельных прямой x 3y = 0 и отсекающих от двух пересекающихся прямых 3x 2y 1 = 0,

4x 5y + 1 = 0 треугольник, площадь которого равна 3,5 кв. единиц.

Решение.

vk.com/club152685050

Уравнения искомых прямых имеют вид x 3y + с = 0. Коэффициент с определим, использовав площадь треугольника. Найдем координаты вершин треугольника, имеющего площадь 3,5; для чего решим следующие системы уравнений:

3x 2y 1 0,	3x 2y 1 0,	4x 5y 1 0,
		x 3y c 0;	x 3y c 0.
4x 5y 1 0;

Решая выписанные системы уравнений, получим координаты вершин соответственно:

А(1, 1), B 2c 3 / 7, 3c 1 / 7 , С 5c 3 / 7, 4c 1 / 7 .

Воспользуемся формулой для нахождения площади треугольника по известным координатам его вершин:

S 1/ 2 x1 y2 y3 x2 y3 y1 x3 y1 y2 .

Подставив в эту формулу найденные координаты вершин треугольника, получим выражение площади S = (c 2)2/ 14, по условию S = 3,5, поэтому (c 2)2 = 49, откуда получим два значения: с1 = 9, с2 = 5. Таким образом, уравнения искомых прямых будут иметь вид: x 3y + 9 = 0 и x 3y 5 = 0.

Ответ: x 3y + 9 = 0, x 3y 5 = 0.

Пример 3.

Даны вершины треугольника А(2, 2), В(3, 5) и С(5, 1). Составить уравнение перпендикуляра, опущенного из вершины С на биссектрису внутреннего угла при вершине В.

Решение.

Чтобы составить уравнение перпендикуляра СD, опущенного на биссектрису угла B, необходимо знать угловой коэффициент этой биссектрисы, или (что то же самое) ее направляющий вектор. Направляющий вектор биссектрисы равен сумме (единичных) направляющих векторов сторон угла. Направляющий вектор стороны BA: (-1,3), стороны BC: (2,6). Соответствующие единичные вектора: (-1,3)/ 10 , (1,3)/ 10 , значит, направляющий вектор биссетрисы равен (0,6)/ 10 или (т.к. направляющий вектор определяется с точностью до множителя) (0,1). Тогда направляющий вектор перпендику — ляра к биссектрисе будет (1,0), т.е. эта прямая параллельна оси OX, откуда следует ее уравнение y=1.

Ответ. Уравнение перпендикуляра: y 1 = 0.

vk.com/club152685050

Пример 4.

Даны вершины треугольника А(12, 4), В(0, 5) и С( 12, 11). Найти: 1) длины сторон, 2) уравнения сторон, 3) уравнение высо-

ты, проведенной из вершины В, 4) длину этой высоты, 5) уравнение медианы, проведенной из точки А, 6) длину этой медианы, 7) уравнение биссектрисы угла С, центр тяжести треугольника, 9) площадь треугольника, 10) угол С.

Указания.

1). Длины сторон треугольника определяем по формуле расстоя-

ния между двумя точками d 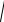x2 x1 2 y2 y1 2 . Ответ: АВ = 15, АС = 25, ВС = 20.

2). Каждая сторона треугольника проходит через две точки, поэтому для составления уравнений сторон нужно воспользоваться

формулой (y y1) / (y2 y1) = (x x1) / (x2 x1).

Ответ: АВ: 3x + 4y 20 = 0,	AC: 7x 24y 180 = 0,
BC: 4x 3y + 15 = 0.

3). Чтобы составить уравнение высоты, проведенной из точки В на сторону AC, необходимо знать угловой коэффициент этой высоты. Прежде всего следует определить угловой коэффициент АС и из

условия перпендикулярности k1 · k2 = 1 можно будет определить угловой коэффициент прямой BD, перпендикулярной к АС. Уравнение

высоты составить, пользуясь формулой y y0 = k(x x0). Ответ: 3x + 4y 20 = 0.

4). Для определения длины высоты BD воспользуемся формулой

расстояния от точки В до прямой АС: d Ax0 By0 C / A2 B2 . Ответ: BD = 12.

5). Чтобы составить уравнение медианы, нужно сначала найти координаты точки М, являющейся серединой отрезка ВС, для этого

применим формулу хм = (хв + хс)/ 2, yм = (yв + yс)/ 2, М( 6, 3). Далее можно написать уравнение медианы АМ, используя форму-

лу нахождения уравнения прямой, проходящей через две точки. Ответ: АМ: x + 18y + 60 = 0.

6). Длину медианы определим по формуле расстояния между двумя точками А и М.

vk.com/club152685050

Ответ: AM 5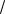13

7). Для составления уравнения биссектрисы угла С, необходимо использовать свойство биссектрисы угла. А именно, направляющий вектор биссектрисы равен сумме (единичных) направляющих векторов сторон. Направляющий вектор стороны CA: (24,7), стороны CB: (12,16). Соответствующие единичные вектора: (24,7)/25, (3,4)/5. Складывая их, получаем направляющий вектор биссектрисы: (39,27)/ 25. Тогда уравнение биссектрисы угла C имеет вид:

	x 12		y 11	или 9x 13 y 35 .
39
		27
Ответ:	СK:	9x 13y 35 = 0.

8). Центр тяжести треугольника находится в точке пересечения медиан и определяется по формулам:

x0 = (x1 + x2 + x3) / 3, y0 = (y1 + y2 + y3) / 3. Ответ: О(0, 10 / 3).

9). Площадь треугольника находится по формуле:

S 1 / 2	AB, AC	, АВ = { 12, 9, 0},	АC = { 24, 7, 0}.

Ответ:	SABC = 150 кв. единиц.

10) Чтобы определить угол С, необходимо знать угловые коэффициенты сторон ВС и АС, которые образуют этот угол. Воспользовавшись уравнениями сторон ВС и АС, полученными в п. 2 определяем:

kBC = 4/3, kAC = 7/24, тогда tgC = (kBC kAC) / (1 + kBC · kAC) = 1/4, тогда угол С = arctg (1/4).

Второй способ:

	(CA, CB)		, где СА = {24, 7}, CB = {12, 16}.


C arccos		CA		CB

Ответ: Угол С = arctg (1/4).

Пример 5.

Написать каноническое и параметрическое уравнения прямой, заданной пересечением плоскостей:

3x 4 y 5z 10 0,
	z 17 0.
6x 5y

Решение.

Найдем координаты направляющего вектора данной прямой: a = [n1, n2], где n1, n2 — векторы нормали к данным плоскостям,

vk.com/club152685050

n1 = {3, 4, 5},	n2	= {6, 5, 1}.
		По правилу нахождения векторного произведения:
a		i	j	k					4	5	3	5	3	4	21, 27, 9 1 / 3 7, 9, 3 .


	3	4	5				,	,
					5	1	6	1	6	5
		6	5	1

Итак, в качестве направляющего вектора можно взять а = {7, 9, 3}. Выберем теперь какую-нибудь точку на данной прямой. Для этого нужно придать конкретное значение одной из координат, тогда значение двух других определяется системой уравнений.

Положим, например z = 0, тогда исходные уравнения примут вид: 3x 4y 10 = 0, 6x 5y 17 = 0. Решая эту систему, получим x0 = 2,

y0 = 1. Следовательно, на прямой выбрана точка М0(2, 1, 0). Зная направляющий вектор а и точку М0, можно составить каноническое

уравнение прямой: (x 2)/ 7 = (y + 1)/ 9 = z / 3. Тогда параметрическое уравнение прямой примет вид: x = 2 + 7t, y = 1 + 9t, z = 3t.

Ответ. Каноническое уравнение: (x 2)/ 7 = (y + 1)/ 9 = z / 3. Параметрическое уравнение: x = 2 + 7t, y = 1 + 9t, z = 3t.

Пример 6.

Написать уравнение проекции прямой (x 2) / 6 = (y + 1) / ( 5) = = (z 5) / 4 на плоскость x 3y + 2z 7 = 0.

Решение.

Проекция прямой на плоскость представляет собой линию пересечения этой плоскости и плоскости, проходящей через данную прямую перпендикулярно данной плоскости. Составим уравнение плос-

кости, проходящей через прямую (x 2) / 6 = (y + 1) / ( 5) = (z 5) / 4 перпендикулярно плоскости x 3y + 2z 7 = 0. Пусть M(x, y, z) — произвольная точка искомой плоскости, М0(2, 1, 5) — принадлежащая ей точка прямой, тогда векторы М0М = {x 2, y + 1, z 5}, а ={6, 5, 4},

n = {1, 3, 2} лежат в одной плоскости, поэтому их смешанное произ — ведение равно нулю, то есть М0М · а · n = 0 или в координатах:

x 2	y 1	z 5	0.

6	5	4
1	3	2

vk.com/club152685050

Раскладывая определитель по первой строке, получим уравнение плоскости: (x 2) · 2 (y + 1) · 8 + (z 5) ( 13) = 0, которое после упроще-

ний примет вид: 2x 8y 13z + 53 = 0.

Таким образом, искомая проекция определяется уравнениями:

x 3y + 2z 7 = 0, 2x 8y 13z + 53 = 0.

Ответ. Уравнение проекции, заданное пересечением плоскостей: x 3y + 2z 7 = 0, 2x 8y 13z + 53 = 0.

Пример 7.

Составить уравнение прямой, проходящей через точку М0(2, 3, 5), перпендикулярно двум данным прямым:

(x 1) / ( 1) = (y 3) / 2 = (z + 5) / 2 , (x 2) / 6 = (y + 1) / 3 = (z + 7) / ( 2).

Решение.

Уравнение прямой ищем в виде (x 2) / m = (y + 3) / n = (z 5) / p. Коэффициенты m, n, p, определяемые с точностью до постоянного множителя, в силу условия перпендикулярности прямых должны удовлетворять системе двух уравнений:

( 1)m 2n 2 p 0,6m 3n 2 p 0.

Складывая и вычитая почленно эти уравнения получим

5m + 5n = 0, 3m 2n = 0, откуда m = n, m = (2 / 3) p. Полагая, например, р = 3, получим m = 2, n = 2. Следовательно, уравнение прямой принимает вид: (x 2) / 2 = (y + 3) / ( 2) = (z 5) / 3.

Ответ. Уравнение прямой (x 2) / 2 = (y + 3) / ( 2) = (z 5) / 3.

Пример 8.

Найти точку пересечения плоскости 3x 4y + 5z + 16 = 0 и прямой

x = 6 + 2t,

y = 7 t, z = 8 3t.

Решение.

Решим совместно систему уравнений прямой и плоскости. Подставим выражения для x, y, z в уравнение плоскости:

3( 6 + 2t) 4(7 t) + 5(8 3t) + 16 = 0.

После упрощения получим: 5t + 10 = 0, откуда t = 2. Из уравне-

ния прямой при t = 2 находим координаты точки пересечения x = 2, y = 5, z = 2.

Ответ. Искомой точкой пересечения является точка S( 2, 5, 2).

Соседние файлы в предмете Аналитическая геометрия

Источник