Как составить каноническую форму

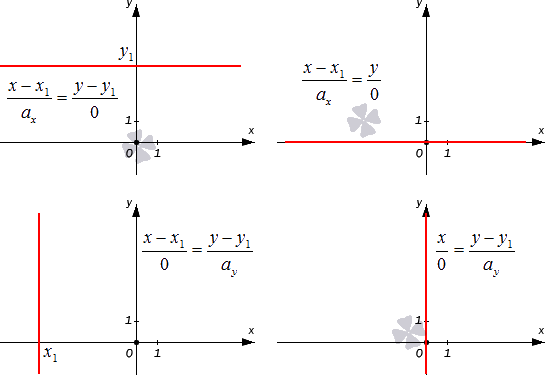
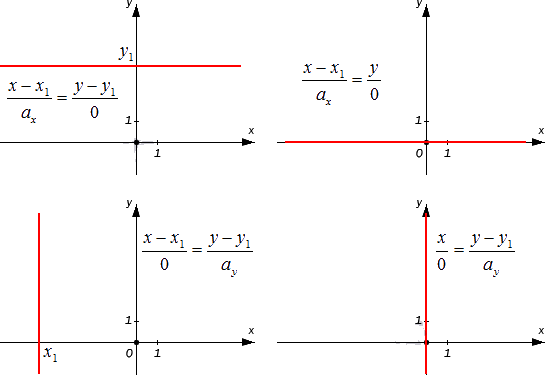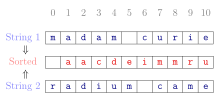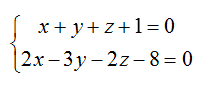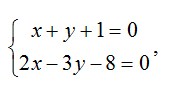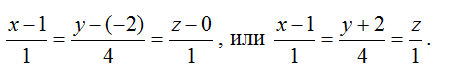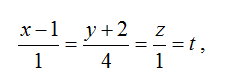задачи
линейного программирования

2.1. Определение и формы записи

В
случае, когда все ограничения являются
уравнениями и все переменные удовлетворяют
условию неотрицательности, задачу
линейного программирования называют
канонической.Она может быть
представлена в координатной, векторной
или матричной форме записи.

а)
каноническая задача ЛП в координатной
форме имеет вид:

;
(2.1.1)

,

.

Данную
задачу можно записать, используя знак
суммирования:

,

,

,

,
.

б)
каноническая задача ЛП в векторной
форме имеет вид:
,

,
(2.1.2)

,

где
;;

,

;;.

в) каноническая
задача ЛП в матричной форме имеет вид:

,

,

,

где
,,.

2.2. Приведение общей задачи линейного

программирования к канонической форме

При
составлении математических моделей
экономических задач ограничения в
основном формируются в системы неравенств.
Поэтому необходимо уметь переходить
от них к системам уравнений. Например,
рассмотрим линейное неравенство

(2.2.1)

и
прибавим к его левой части некоторую
величину
такую, чтобы неравенство превратилось
в равенство.

,
(2.2.2)

где

.

Неотрицательная
переменная
называется дополнительной переменной.
Следующая теорема даёт основание для
возможности такого преобразования.

Теорема
2.2.1.Каждому решениюнеравенства ( 2.2.1) соответствует
единственное решениеуравнения (2.2.2) и неравенства,
и, наоборот, каждому решению уравнения
(2.2.2)ссоответствует решениенеравенства ( 2.2.1).

Доказательство.Пустьрешение
неравенства ( 2.2.1). Тогда.
Возьмём число.
Ясно, что.
Подставив в уравнение (2.2.2), получим

.

Первая
часть теоремы доказана.

Пусть теперь
векторудовлетворяет уравнению (2.2.2) с,
т.е..
Отбрасывая в левой части последнего
равенства неотрицательную величину,
получаем,
и т.д.

Таким
образом, доказанная теорема фактически
устанавливает возможность приведения
всякой задачи ЛП к каноническому виду.
Для этого достаточно в каждое ограничение,
имеющее вид неравенства, ввести свою
дополнительную неотрицательную
переменную. Причём, в неравенства вида
( 1.2.1) эти переменные войдут со знаком
« + », а в неравенствах вида (1.2.2 ) – со
знаком « – ». Дополнительные переменные
вводятся в целевую функцию с нулевыми
коэффициентами и поэтому на её значение
не влияют.

Замечание.
В дальнейшем мы будем излагать
симплекс-метод для канонической задачи
ЛП при исследовании целевой функции на
минимум. В тех задачах, где требуется
найти максимум
,
достаточно рассмотреть функцию,
найти её минимальное значение, а затем,
меняя знак на противоположный, определить
искомое максимальное значение.

3. Графический метод решения задач

линейного
программирования

3.1. Общие понятия, примеры

В
тех случаях, когда в задаче ЛП лишь две
переменные, можно использовать для
решения графический метод. Пусть
требуется найти максимальное ( минимальное
) значение функции
при ограничениях

(3.1.1)

Данный метод
основывается на возможности графического
изображения области допустимых решений
задачи, т.е. удовлетворяющих системе
(3.1.1), и нахождения среди них оптимального
решения. Область допустимых решений
задачи строится как пересечение (общая
часть) областей решений каждого из
заданных ограничений (3.1.1). Каждое из
них определяет полуплоскость с границей
,.
Для того, чтобы определить, какая из
двух полуплоскостей является областью
решений, достаточно координаты какой-либо
точки, не лежащей на прямой, подставить
в неравенство: если оно удовлетворяется,
то областью решений является полуплоскость,
содержащая данную точку, если же
неравенство не удовлетворяется, то
областью решений является полуплоскость,
не содержащая данную точку.

Пересечение
этих полуплоскостей образует некоторую
область, называемую многоугольником
решений, который является выпуклым
множеством. (Допустим, что система
ограничений совместна, а многоугольник
её решений ограничен.) Для нахождения
среди допустимых решений оптимального
используются линии уровня и опорные
прямые.

Линией
уровняназывается прямая, на которой
целевая функцияпринимает постоянное значение. Уравнение
линии уровня имеет вид

,
где
.
Все линии уровня параллельны между
собой . Их нормаль.

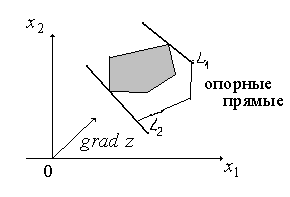
Опорной
прямойназывается линия уровня,
которая имеет хотя бы одну общую точку
с областью допустимых решений, по
отношению к которой эта область находится
в одной из полуплоскостей (рис. 1).

Рис.
1

Значения
возрастают в направлении вектора.
Поэтому необходимо передвигать линию
уровняв направлении этого вектора параллельно
самой себе до опорной прямойL₁
в задаче на максимум и в противоположном
направлении – в задаче на минимум (до
опорной прямойL₂).

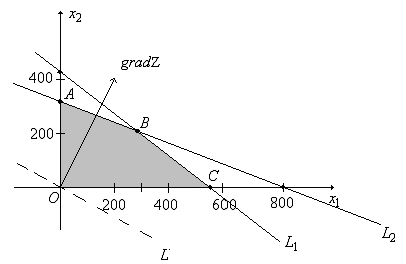
Приведём
решение примера 1.1. Напомним, что нужно
найти максимум функции
при ограничениях

Решение.
Строим область допустимых решений.
Нумеруем ограничения задачи. В
прямоугольной декартовой системе
координат (рис. 2) строим прямую
,
соответствующую ограничению (1). Находим,
какая из полуплоскостей, на которые эта
прямая делит всю координатную плоскость,
является областью решений неравенства
(1).

Для
этого достаточно координаты какой —
либо точки, не лежащей на прямой,
подставить в неравенство. Так как прямая
не проходит через начало координат,
подставляемв первое ограничение.
Получим строгое неравенство.
Следовательно, точкалежит в полуплоскости решений. Аналогично
строим прямуюи область решений ограничения (2). Находим
общую часть полуплоскостей решений,
учитывая ограничения (3). Полученную
область допустимых решений выделим на
рис.2 тёмным цветом.

Рис.2

Строим
линию уровня
и вектор,
который указывает направление возрастания
функциии
перпендикулярен прямой

.
Линию уровня
перемещаем параллельно самой себе в
направлениидо опорной прямой. Получим, что максимума
целевая функция достигнет в точкеточке
пересечения прямыхи.
Решая систему из уравнений этих прямых,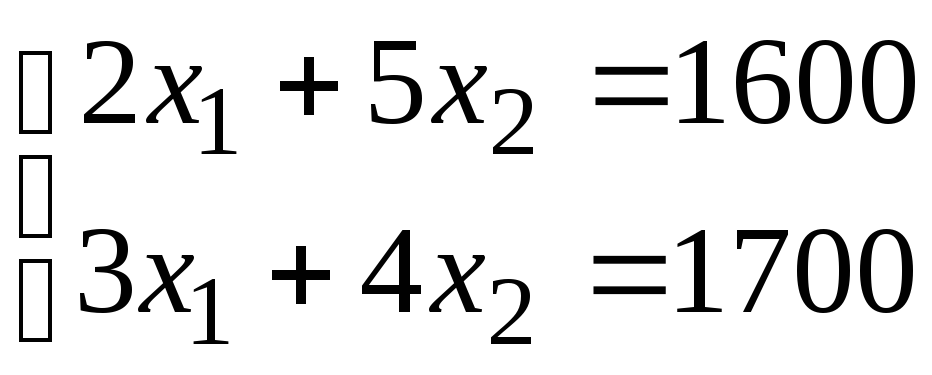
получим координаты точки.
Следовательно,,
а,оптимальное
решение.

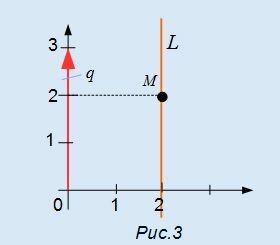
Пример
3.1. Найти минимум функции
при системе ограничений

Решение.
Строим область допустимых решений
(см. рис.3), вектор
и одну из линий уровня.
Перемещаем линию уровня в направлении,
противоположном,
так как решается задача на отыскание
минимума функции. Опорная прямая проходит
в этом случае через точку А (рис.3),
координаты которой найдём из решения
системы

Рис.3

Итак,
.
Вычисляем.

Замечание.
В действительности от вида области
допустимых решений и целевой функции
задача ЛП может иметь единственное
решение, бесконечное множество решений
или не иметь ни одного решения.

Пример
3.2. Найти минимум функции
при ограничениях

Решение.
Строим область допустимых решений,
нормаль линий уровня
и одну из линий уровня,
имеющую общие точки с этой областью.
Перемещаем линию уровняв направлении, противоположном направлению
нормали,
так как решается задача на отыскание
минимума функции. Нормаль линий уровняи нормаль граничной прямой,
в направлении которой перемещаются
линии уровня, параллельны, так как их
координаты пропорциональны.
Следовательно, опорная прямая совпадает
с граничной прямойобласти допустимых решений и проходит
через две угловые точки этой областии(рис.4).

Рис.4

Задача имеет
бесконечное множество оптимальных
решений, являющихся точками отрезка
.
Эти точки,находим, решая соответствующие системы
уравнений:

;

;

,

;
,
;

;

.

Вычисляем
.

Ответ:

при,.

Пример
3.3. Решить задачу линейного программирования

,

Решение.
Строим область допустимых решений,
нормаль
и одну из линий уровня. В данной задаче
необходимо найти максимум целевой
функции, поэтому линию уровняперемещаем в направлении нормали. Ввиду
того, что в этом направлении область
допустимых решений не ограничена, линия
уровня уходит в бесконечность (рис.5).

Рис.
5

Задача
не имеет решения вследствие неограниченности
целевой функции.

Ответ:
.

Соседние файлы в папке математика_2

• #
• #

Приведение кривой второго порядка к каноническому виду

Пример . Дано уравнение кривой 3x 2 +10xy+3y 2 -2x-14y-13=0 в системе координат (0,i,j), где i =(1,0) и j =(0,1).
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.

Решение. Приводим квадратичную форму B=3x 2 +10xy+3y 2 к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:

Характеристическое уравнение:
; λ₁=-2, λ₂=8. Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать 8x₁ 2 -2y₁ 2 , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B. .
Собственный вектор, отвечающий числу λ=-2 при x₁=1: x ₁=(1,-1).
В качестве единичного собственного вектора принимаем вектор , где – длина вектора x ₁.
Координаты второго собственного вектора, соответствующего второму собственному числу λ=8, находим из системы
.
x ₂=(1,1); .
Итак, имеем новый ортонормированный базис ( i ₁, j ₁).
По формулам (5) пункта 4.3.3. переходим к новому базису:
или

Задание. Привести к каноническому виду уравнение линии 17x 2 + 12xy + 8y 2 — 20 = 0.
Решение.Пример 2

Задание. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм и определить её вид. Уравнение кривой второго порядка путем выделения полного квадрата привести к каноническому виду. Решение

Задание. Привести уравнение к каноническому виду: 16x 2 — 9y 2 -64x — 8y +199 = 0.
Решение.Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить гиперболу на чертеже, указав фокусы, асимптоты и директрисы.
Решение:Скачать решение

Задание. Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет, уравнения директрис. Изобразить эллипс на чертеже, указав оси симметрии, фокусы и директрисы.
Решение:Скачать решение

Каноническое уравнение прямой на плоскости: теория, примеры, решение задач

Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.

Понятие канонического уравнения прямой

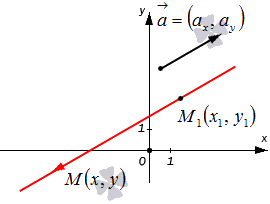
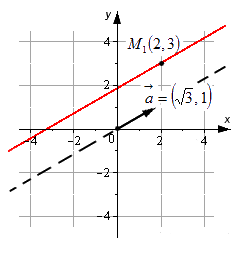
Допустим, что у нас есть декартова (прямоугольная) система координат, в которой задана прямая. Нам известны координаты произвольно взятой точки этой прямой M 1 ( x 1 , y 1 ) , а также ее направляющего вектора a → = ( a x , a y ) . Попробуем составить уравнение, которое описывало бы эту прямую.

Возьмем плавающую точку M ( x , y ) . Тогда вектор M 1 M → можно считать направляющим для исходной прямой. Его координаты будут равны x — x 1 , y — y 1 (если нужно, повторите материал о том, как правильно вычислять координаты вектора с помощью координат отдельных его точек).

Множество произвольно взятых точек M ( x , y ) будут определять нужную нам прямую с направляющим вектором a → = ( a x , a y ) только в одном случае – если векторы M 1 M → и a → = ( a x , a y ) будут коллинеарны по отношению друг к другу. Посмотрите на картинку:

Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:

M 1 M → = λ · a → , λ ∈ R

Если преобразовать полученное равенство в координатную форму, то мы получим:

x — x 1 = λ · a x y — y 1 = λ · a y

При условии, что a x ≠ 0 и a y ≠ 0 , получим:

x — x 1 = λ · a x y — y 1 = λ · a y ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

Итог наших преобразований и будет каноническим уравнением прямой на плоскости. Запись вида x — x 1 a x = y — y 1 a y также называют уравнением прямой в каноническом виде.

Таким образом, с помощью уравнения x — x 1 a x = y — y 1 a y можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор a → = ( a x , a y ) и проходит через точку M 1 ( x 1 , y 1 ) .

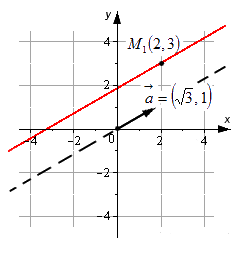
Примером уравнения подобного типа является, например, x — 2 3 = y — 3 1 . Прямая, которая задана с его помощью, проходит через M 1 ( 2 , 3 ) и имеет направляющий вектор a → = 3 , 1 . Ее можно увидеть на рисунке:

Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:

1. Если прямая, имеющая направляющий вектор a → = ( a x , a y ) , проходит через две точки – M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) , то уравнение для нее может быть записано как в виде x — x 1 a x = y — y 1 a y , так и x — x 2 a x = y — y 2 a y .

2. Если заданная прямая имеет направляющий вектор с координатами a → = ( a x , a y ) , то множество всех ее векторов можно обозначить как μ · a → = ( μ · a x , μ · a y ) , μ ∈ R , μ ≠ 0 . Таким образом, любое уравнение прямой в каноническом виде x — x 1 μ · a x = y — y 1 μ · a y будет соответствовать этой прямой.

Разберем важный пример задачи на нахождение канонического уравнения.

В прямоугольной системе координат на плоскости задана прямая, которая проходит через точку M 1 ( 2 , — 4 ) и имеет направляющий вектор с координатами a → = ( 1 , — 3 ) . Запишите каноническое уравнение, описывающее данную прямую.

Решение

Для начала вспомним общий вид нужного нам канонического уравнения – x — x 1 a x = y — y 1 a y . Подставим в него имеющиеся значения x 1 = 2 , y 1 = — 4 , a x = 1 , a y = — 3 и подсчитаем:

x — x 1 a x = y — y 1 a y ⇔ x — 2 1 = y — ( — 4 ) — 3 ⇔ x — 2 1 = y + 4 — 3

Получившееся в итоге равенство и будет нужным ответом.

Ответ: x — 2 1 = y + 4 — 3

Канонические уравнения прямой на плоскости с a x или a y , равными нулю

Если значение хотя бы одной переменной a является нулевым, то уравнение плоскости используют в первоначальном виде. Сразу две переменные нулевыми не могут быть по определению, поскольку нулевой вектор не бывает направляющим. В таком случае мы можем считать запись x — x 1 a x = y — y 1 a y условной и понимать ее как равенство a y ( x — x 1 ) = a x ( y — y 1 ) .

Разберем случаи канонических уравнений на плоскости с одним нулевым a более подробно. Допустим, что x — x 1 0 = y — y 1 a y при a x = 0 , а исходная прямая будет проходить через M 1 ( x 1 , y 1 ) . В таком случае она является параллельной оси ординат (если x 1 = 0 , то она будет с ней совпадать). Докажем это утверждение.

Для этой прямой вектор a → = ( 0 , a y ) будет считаться направляющим. Этот вектор является коллинеарным по отношению к координатному вектору j → = ( 0 , 1 ) .

Если же нулевым является значение второго параметра, то есть a y = 0 , то мы получаем равенство вида x — x 1 a x = y — y 1 0 . Это уравнение описывает прямую, проходящую через M 1 ( x 1 , y 1 ) , которая расположена параллельно оси абсцисс. Это утверждение верно, поскольку a → = ( a x , 0 ) является для этой прямой направляющим вектором, а он в свою очередь является коллинеарным по отношению к координатному вектору i → = ( 1 , 0 ) .

Проиллюстрируем два частных случая канонического уравнения, описанные выше:

На плоскости задана прямая, параллельная оси O y . Известно, что она проходит через точку M 1 2 3 , — 1 7 . Запишите каноническое уравнение для нее.

Решение

Если прямая по отношению оси ординат является параллельной, то мы можем взять координатный вектор j → = ( 0 , 1 ) в качестве направляющего для нее. В таком случае искомое уравнение выглядит следующим образом:

x — 2 3 0 = y — — 1 7 1 ⇔ x — 2 3 0 = y + 1 7 1

Ответ: x — 2 3 0 = y + 1 7 1

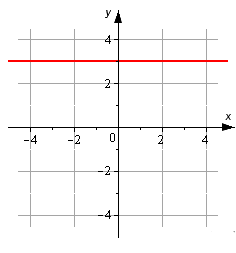
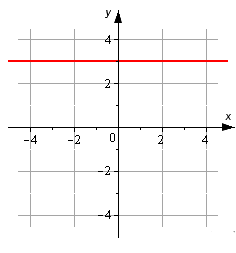
На рисунке изображена прямая. Запишите ее каноническое уравнение.

Решение

Мы видим, что исходная прямая проходит параллельно оси O x через точку M 1 ( 0 , 3 ) . Мы берем координатный вектор i → = ( 1 , 0 ) в качестве направляющего. Теперь у нас есть все данные, чтобы записать нужное уравнение.

x — 0 1 = y — 3 0 ⇔ x 1 = y — 3 0

Ответ: x 1 = y — 3 0

Преобразование канонического уравнения прямой в другие виды уравнений

Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.

Стандартной форме записи канонического уравнения x — x 1 a x = y — y 1 a y можно поставить в соответствие систему параметрических уравнений на плоскости x = x 1 + a x · λ y = y 1 + a y · λ . Чтобы преобразовать один вид уравнения в другой, нам надо приравнять правую и левую часть исходного равенства к параметру λ . После этого надо выполнить разрешение получившихся равенств относительно переменных x и y :

x — x 1 a x = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y = λ ⇔ ⇔ x — x 1 a x = λ y — y 1 a y = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ

Покажем на примере, как именно выполняется это действие с конкретными числами.

У нас есть прямая, заданная на плоскости с помощью канонического уравнения x + 2 3 = y — 1 11 . Запишите параметрические уравнения исходной прямой.

Решение

Сначала поставим знак равенства между отдельными частями уравнения и переменной λ и получим x + 2 3 = λ y — 1 11 = λ .

Далее можно перейти к формулированию необходимых параметрических уравнений:

x + 2 3 = λ y — 1 11 = λ ⇔ x + 2 = 3 · λ y — 1 = 11 · λ ⇔ x = — 2 + 3 · λ y = 1 + 11 · λ

Ответ: x = — 2 + 3 · λ y = 1 + 11 · λ

Из канонического уравнения можно получить не только параметрические, но и общие уравнения прямой. Вспомним понятие пропорции: запись a b = c d можно представить в виде a · d = b · c с сохранением смысла. Значит, что x — x 1 a x = y — y 1 a y ⇔ a y ( x — x 1 ) = a x ( y — y 1 ) ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 .

Это и есть общее уравнение прямой. Это станет более очевидно, если мы добавим в него значения параметров a y = A , — a x = B , — a y x 1 + a x y 1 = C .

Прямая на плоскости описана с помощью канонического уравнения x — 1 2 = y + 4 0 . Вычислите общее уравнение этой прямой.

Решение

Делаем указанные выше действия по порядку.

x — 1 2 = y + 4 0 ⇔ 0 · ( x — 1 ) = 2 · ( y + 4 ) ⇔ y + 4 = 0

Ответ: y + 4 = 0 .

Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.

На плоскости задана прямая с помощью уравнения x + 3 3 = y — 2 2 . Запишите уравнение этой же прямой в отрезках.

Решение

Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.

x + 3 3 = y — 2 2 ⇔ 2 · ( x + 3 ) = 3 · ( y — 2 ) ⇔ 2 x — 3 y + 6 + 2 3 = 0

Далее переходим к формулировке уравнения прямой в отрезках.

2 x — 3 y + 6 + 2 3 = 0 ⇔ 2 x — 3 y = — 6 + 2 3 ⇔ ⇔ 2 — ( 6 + 2 3 ) x — 3 — ( 6 + 2 3 ) y = 1 ⇔ x — 6 + 2 3 2 + y 6 + 2 3 3 = 1 ⇔ x — 3 + 3 + y 3 3 + 2 = 1

Ответ: x — 3 + 3 + y 3 3 + 2 = 1

Достаточно легко решить и задачу, обратную этой, т.е. привести уравнение прямой на плоскости обратно к каноническому. Допустим, у нас есть общее уравнение прямой в стандартной формулировке – A x + B y + C = 0 . При условии A ≠ 0 мы можем перенести B y вправо с противоположным знаком. Получим A x + C = — B y . Теперь выносим A за скобки и преобразуем равенство так:

Получившееся уравнение мы записываем в виде пропорции: x + C A — B = y A .

У нас получилось нужное нам каноническое уравнение прямой на плоскости.

А как сделать преобразование, если B ≠ 0 ? Переносим все слагаемые, кроме A x , вправо с противоположными знаками. Получаем, что A x = — B y — C . Выносим — B за скобки:

Формируем пропорцию: x — B = y + C B A

Есть общее уравнение прямой x + 3 y — 1 = 0 . Перепишите его в каноническом виде.

Решение

Оставим с левой стороны только одну переменную x . Получим:

Теперь вынесем — 3 за скобки: x = — 3 y — 1 3 . Преобразуем равенство в пропорцию и получим необходимый ответ:

Ответ: x — 3 = y — 1 3 1

Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.

Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x = x 1 + a x · λ y = y 1 + a y · λ и приравнять обе части равенств. Схема решения выглядит так:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y ⇔ x — x 1 a x = y — y 1 a y

Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.

Прямая на плоскости описана с помощью системы параметрических уравнений x = 3 + 0 · λ y = — 2 — 4 · λ . Запишите каноническое уравнение для этой прямой.

Решение

Для начала преобразуем исходные уравнения в систему x = 3 + 0 · λ y = — 2 — 4 · λ . Следующим шагом будет выражение параметра в каждом уравнении:

x = 3 + 0 · λ y = — 2 — 4 · λ ⇔ λ = x — 3 0 λ = y + 2 — 4

Ставим знак равенства между получившимися частями и получаем нужное нам каноническое уравнение: x — 3 0 = y + 2 — 4

Ответ: x — 3 0 = y + 2 — 4

Как решать задачи на составление канонических уравнений

В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.

На плоскости задана прямая, каноническое уравнение которой имеет вид x — 1 2 = y + 1 2 — 3 . Выясните, лежат ли на ней точки M 1 3 , — 3 1 2 и M 2 ( 5 , — 4 ) .

Решение

Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.

3 — 1 2 = — 3 1 2 + 1 2 — 2 ⇔ 1 = 1

Результат говорит нам, что точка M 1 3 , — 3 1 2 принадлежит исходной прямой.

Точно так же поступим и с координатами второй точки:

5 — 1 2 = — 4 + 1 2 — 3 ⇔ 2 = 7 6

Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.

Ответ: первая точка лежит на заданной прямой, а вторая нет.

Есть две точки M 1 ( 2 , 4 ) и M 2 ( — 1 , 3 ) . Будет ли прямая, которая задана в той же плоскости с помощью уравнения x — 2 0 = y — 3 2 , проходить через них?

Решение

Вспомним, что запись x — 2 0 = y — 3 2 можно понимать как 2 · ( x — 2 ) = 0 · ( y — 3 ) ⇔ x — 2 = 0 . Подставим координаты заданных точек в это равенство и проверим.

Начнем с первой точки M 1 ( 2 , 4 ) : 2 — 2 = 0 ⇔ 0 = 0

Равенство верное, значит, эта точка расположена на заданной прямой.

Подставляем данные второй точки: — 1 — 2 = 0 ⇔ — 3 = 0 .

Равенство неверное, значит, точка M 2 ( — 1 , 3 ) не лежит на исходной прямой.

Ответ: через точку M 1 ( 2 , 4 ) прямая проходит, а через M 2 ( — 1 , 3 ) нет.

Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.

Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.

Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.

Прямая на плоскости проходит через точку M 1 ( 0 , — 3 ) и через точку M 2 ( 2 , — 2 ) . Сформулируйте для этой прямой канонической уравнение.

Решение

Eсли у нас есть координаты двух точек, то мы можем вычислить по ним координаты вектора M 1 M 2 → = 2 , 1 . По отношению к прямой, чье уравнение мы составляем, он будет направляющим вектором. После этого мы можем записать следующее:

x — 0 2 = y — ( — 3 ) 1 ⇔ x 2 = y + 3 1

Также можно использовать координаты второй точки. Тогда мы получим: x — 2 2 = y — ( — 2 ) 1 ⇔ x — 2 2 = y + 2 1

Ответ: x 2 = y + 3 1

Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.

Известно, что точка M 1 ( 1 , 3 ) принадлежит некоторой прямой, которая параллельна второй прямой, заданной с помощью уравнения x 2 = y — 5 . Запишите каноническое уравнение первой прямой.

Решение

Для первой прямой можно определить направляющий вектор a → = 2 , — 5 . Его можно рассматривать и в качестве направляющего для второй прямой, что следует из самого определения направляющих векторов. Это позволяет нам получить всю информацию, нужную для записи искомого уравнения: x — 1 2 = y — 3 — 5

Ответ: x — 1 2 = y — 3 — 5

Через точку M 1 ( — 1 , 6 ) проходит прямая, которая является перпендикулярной другой прямой, определенной на плоскости с помощью уравнения 2 x — 4 y — 7 = 0 . Запишите каноническое уравнение первой прямой.

Решение

Из данного уравнения мы можем взять координаты нормального вектора второй прямой – 2 , 4 . Мы знаем, что этот вектор является направляющим по отношению к первой. Тогда мы можем записать искомое уравнение:

x — ( — 1 ) 2 = y — 6 4 ⇔ x + 1 1 = y — 6 2

Каноническое уравнение прямой на плоскости

В данной статье мы рассмотрим каноническое уравнение прямой на плоскости. Определим понятие направляющего вектора прямой. Рассмотрим примеры построения канонического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим метод преобразования уравнения в каноническом виде в параметрический и общий виды.

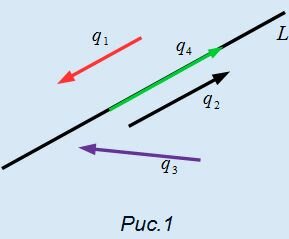
Определение 1. Любой ненулевой вектор, параллельный данной прямой называется направляющим вектором этой прямой.

На рисунке Рис.1 представлена прямая L и векторы q₁, q₂, q₃, q₄. Из определения следует, что векторы q₁, q₂, q₄ являются направляющими векторами прямой L, а q₃ − нет.

Каноническое уравнение прямой L на плоскости представляется следующей формулой:

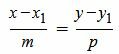(1)

где x₁, y₁ координаты некоторой точки M₁ на прямой L. Вектор q=<m, p> является направляющим вектором прямой L.

Надо отметить, что при записи уравнения прямой в каноническом виде, допускается, чтобы один из чисел m и p была равна нулю (одновременно m и p не могут быть равным нулю, т.к. направляющий вектор прямой не должен быть нулевым вектором). Равенство нулю одного из знаменателей означает равенство нулю соответствующего числителя. В этом можно убедится, записав уравнение (1) в следующем виде:

.

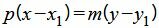(2)

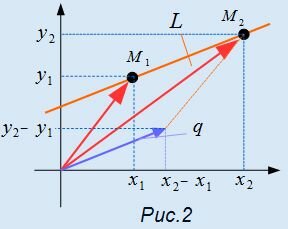
Выше мы отметили, что прямая L проходит через точку M₁(x₁, y₁). В этом можно убедится, подставив x=x₁, y=y₁ в уравнение (1).

.

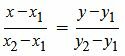(3)

Чтобы убедится, что точки M₁(x₁, y₁) и M₂(x₂, y₂) находятся на прямой L, поочередно подставим в уравнение (3) координаты точек M₁ и M₂. Получим тождества, следовательно эти точки принадлежат прямой L.

Сравним уравнения (1) и (3). Тогда можно записать q=<m, p>=<x₂−x₁, y₂−y₁>. На рисунке Рис.2 представлен вектор q, которая является разностью векторов, соответствующих точкам M₂ и M₁. Этот вектор является направляющим вектором прямой L. Следовательно, для определения направляющего вектора прямой, достаточно взять две точки на данной прямой и найти разность между соответсвующими координатами этих точек.

Таким образом, прямая на плоскости определяется точкой и направляющим вектором или двумя точками.

Онлайн калькулятор, для построения прямой через две точки находится тут.

Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q=<−3, 5>. Построить каноническое уравнение прямой.

Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):

.

.

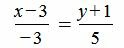
Пример 2. Прямая проходит через точку M=(2, 2) и имеет направляющий вектор q=<0, 3>. Построить каноническое уравнение прямой.

Решение. Для построения канонического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):

.

.

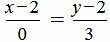
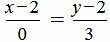
На рисунке Рис.3 изображена прямая L, точка M=(2, 2) и направляющий вектор q=<0, 3>. Прямая проходит через точку M и параллельна направляющему вектору q.

Пример 3. Прямая проходит через точки M₁=(−7, 2) и M₂=(−4, 4). Построить каноническое уравнение прямой. Воспользуемся формулой (3). Подставим координаты точек в уравнение (3):

.

Упростим полученное уравнение:

.

.

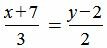
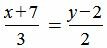
Приведение канонического уравнения прямой на плоскости к параметрическому виду

Для приведения канонического уравнения прямой на плоскости к параметрическому виду, обозначим каждую часть уравнения (1) переменным t:

.

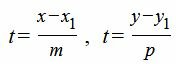
Выразим переменные x и y через t:

,

(4)

где t называется параметром, а уравнение (4) называется параметрическим уравнением прямой.

Для построения уравнения прямой, представленной параметрическом виде (4), достаточно задать параметру t любые значения и вычислить из уравнений (4) соответствующие координаты x и y некоторых точек. Затем провести через эти точки прямую.

Обратное преобразование смотрите здесь.

Пример 4. Каноническое уравнение прямой задана следующим уравнением:

.

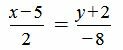(5)

Найти параметрическое уравнение прямой.

Решение. Обозначим через t левую и правую части уравнения (5):

.

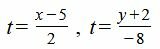
Выразим переменные x и y через t:

.

.

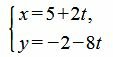
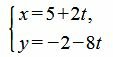
Приведение канонического уравнения прямой на плоскости к общему виду

Пусть прямая на плоскости задана каноническим уравнением прямой (1). Преобразовав (1) получим:

,

.

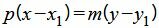
(6)

Сделаем следующие обозначения:

Тогда уравнение (6) можно записать в следующем виде:

где n=<A,B> − называется нормальным вектором прямой.

Нетрудно заметить, что нормальный и направляющий векторы прямой перепендикулярны, т.е. скалярное произведение этих векторов равно нулю:

(n,q)=(<A,B>,<m,p>) =(<p,−m>,<m,p>)=pm−mp=0.

Обратное преобразование смотрите здесь.

Пример 5. Каноническое уравнение прямой задана следующим уравнением:

.

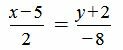(7)

Записать общее уравнение прямой.

Решение. Сделаем преобразования уравнения (7):

Понятие канонического уравнения прямой

Чтобы разобраться, что такое каноническое уравнение, нужно рассмотреть следующий пример. Дана прямоугольная система координат, в которой задана некая произвольная прямая. Известны координаты произвольной точки на отрезке [M_{1}left(x_{1}, y_{1}right)] и координаты направляющего вектора [bar{a}=left(a_{x^{prime}} a_{y}right)]. Используя все имеющиеся данные составим и запишем уравнение, которое будет описывать данную заданную прямую.

Рассмотрим точку [mathrm{M}(x, y)]. Вектор [overline{M_{1} M}] можно отнести к направляющим  исходной линии в координатной плоскости. Координатами вектора будут точки [left(x-x_{1}, y-y_{1}right)]. Чтобы правильно определить векторные координаты, необходимо вспомнить основное правило решения векторов.

Произвольные точки [M(x, y)] будут являться основой для необходимой прямой с направляющим вектором [bar{a}=left(a_{x}, a_{y}right)], только тогда, когда вектора [overline{M_{1} M}] и [bar{a}=left(a_{x}, a_{y}right)] будут являться коллинеарными по отношению друг к другу.

Исходя из этого можно составить формулу коллинеарности двух векторов.

 Где:

После преобразования данного равенства в координатную форму, можно получить следующее уравнение:

[begin{aligned}
&x-x_{1}=lambda cdot a_{x} \
&y-y_{1}=lambda cdot a_{y}
end{aligned}]

Однако, обязательно выполнение главных условий: [a_{x} neq 0] и [a_{y} neq 0].

При выполнении вышеперечисленных условий, получаем следующие равенства:

[begin{aligned}
&x-x_{1}=lambda cdot a_{x} Rightarrow lambda=frac{x-x_{1}}{a_{x}} \
&y-y_{1}=lambda cdot a_{y} Rightarrow lambda=frac{x-x_{1}}{a_{x}} \
&Leftrightarrow frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}
end{aligned}]

Все выполненные преобразования привели к тому, что мы получили окончательную формулу канонического уравнения на плоскости [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}].

Иначе такое равенство, еще называют уравнением прямой канонического вида.

Используя данную запись [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}], можно в прямоугольной системе координат задать прямую, которой будет характерен направляющий вектор [bar{a}=left(a_{x}, a_{y}right)]. Также данная линия будет проходить через заданную точку [M_{1}left(x_{1}, y_{1}right)].

Например: задано уравнение [frac{x-2}{sqrt{3}}=frac{y-3}{1}]. Задается линия, которая будет проходить через точки [M_{1}(2,3)]. Ее направляющий вектор имеет координатные точки: [bar{a}=(sqrt{3}, 1)].

Когда любая прямая в системе координат проходит через две любые точки [M_{1}left(x_{1}, y_{1}right)] и [M_{2}left(x_{2}, y_{2}right)] и имеет направляющий вектор [bar{a}=left(a_{x}, a_{y}right)], множество всех векторов можно записать как [mu cdot overline{mathrm{a}}=left(mu cdot mathrm{a}{x^{prime}} mu cdot a{y}right), mu in R, mu neq 0].

Таким образом, каждое уравнение прямой канонического вида [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}], будет соответствовать заданной прямой на плоскости.

Каноническое уравнение на плоскости с точками a_x и a_y равными нулевому значению

При условии, что одно из значений переменной является нулю, будет использоваться первоначальный вид уравнения. Две переменные нулевыми быть не могут, так как это невозможно по определению. Направляющий вектор не может быть нулевым.    

В такой ситуации выражение [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}] считается условным, и его нужно понимать как равенство [a_{y}left(x-x_{1}right)=a_{x}left(y-y_{1}right)].

Если [frac{x-x_{1}}{0}=frac{y-y_{1}}{a_{y}}] при [a_{x}=0], а заданная прямая проходит через точки [M_{1}left(x_{1}, y_{1}right)]. В данном случае она является параллельной относительно оси ординат.  Если [x_{1}=0], то прямая будет совпадать с осью координат.

Утверждение необходимо доказать. Для заданной прямой вектор [bar{a}=left(a_{x}, a_{y}right)] является направляющим. Также данный вектор будет являться коллинеарным по отношению к координатному вектору [bar{j}=(0.1)].

Если второй параметр является нулевым значением, то [a_{y}=0] и мы получим равенство [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{0}]. Данное уравнение характеризует прямую, которая проходит через точку [M_{1}left(x_{1}, y_{1}right)] и располагается параллельно оси абсцисс. Это утверждение будет правдивым, так как [bar{a}=left(a_{x^{prime}} 0right)], и является для прямой направляющим вектором. А вектор, в свою очередь, коллинеарен по отношению к вектору координат [bar{j}=(0.1)].

Преобразование канонического уравнения прямой в уравнение другого вида

Стандартную форму канонического уравнения [frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}] можно поставить в систему параметрических уравнений для плоскости.

Для преобразования одного вида уравнения в другой необходимо одну часть уравнения приравнять к другой.

[begin{aligned}
&frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}} Leftrightarrow frac{x-x_{1}}{a_{x}}=frac{y-y_{1}}{a_{y}}=lambda Leftrightarrow frac{x-x_{1}}{a_{y}}=lambda Rightarrow \
&frac{y-y_{1}}{a_{y}}=lambda Leftrightarrow x=x_{1}+a_{x} cdot lambda Rightarrow y=y_{1}+a_{y} cdot lambda
end{aligned}]

Принцип решения задач на составление канонических уравнений

Первым делом канонические уравнения применяется для тех задач, где необходимо вычислить принадлежность точки к заданному отрезку на плоскости.

Рассмотрим несколько вариантов задач, и подробно опишем их решение.

From Wikipedia, the free encyclopedia

In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. Often, it is one which provides the simplest representation of an object and allows it to be identified in a unique way. The distinction between «canonical» and «normal» forms varies from subfield to subfield. In most fields, a canonical form specifies a unique representation for every object, while a normal form simply specifies its form, without the requirement of uniqueness.^[1]

The canonical form of a positive integer in decimal representation is a finite sequence of digits that does not begin with zero. More generally, for a class of objects on which an equivalence relation is defined, a canonical form consists in the choice of a specific object in each class. For example:

• Jordan normal form is a canonical form for matrix similarity.
• The row echelon form is a canonical form, when one considers as equivalent a matrix and its left product by an invertible matrix.

In computer science, and more specifically in computer algebra, when representing mathematical objects in a computer, there are usually many different ways to represent the same object. In this context, a canonical form is a representation such that every object has a unique representation (with canonicalization being the process through which a representation is put into its canonical form).^[2] Thus, the equality of two objects can easily be tested by testing the equality of their canonical forms.

Despite this advantage, canonical forms frequently depend on arbitrary choices (like ordering the variables), which introduce difficulties for testing the equality of two objects resulting on independent computations. Therefore, in computer algebra, normal form is a weaker notion: A normal form is a representation such that zero is uniquely represented. This allows testing for equality by putting the difference of two objects in normal form.

Canonical form can also mean a differential form that is defined in a natural (canonical) way.

Definition[edit]

Given a set S of objects with an equivalence relation R on S, a canonical form is given by designating some objects of S to be «in canonical form», such that every object under consideration is equivalent to exactly one object in canonical form. In other words, the canonical forms in S represent the equivalence classes, once and only once. To test whether two objects are equivalent, it then suffices to test equality on their canonical forms.
A canonical form thus provides a classification theorem and more, in that it not only classifies every class, but also gives a distinguished (canonical) representative for each object in the class.

Formally, a canonicalization with respect to an equivalence relation R on a set S is a mapping c:S→S such that for all s, s₁, s₂ ∈ S:

1. c(s) = c(c(s))   (idempotence),
2. s₁ R s₂ if and only if c(s₁) = c(s₂)   (decisiveness), and
3. s R c(s)   (representativeness).

Property 3 is redundant; it follows by applying 2 to 1.

In practical terms, it is often advantageous to be able to recognize the canonical forms. There is also a practical, algorithmic question to consider: how to pass from a given object s in S to its canonical form s*? Canonical forms are generally used to make operating with equivalence classes more effective. For example, in modular arithmetic, the canonical form for a residue class is usually taken as the least non-negative integer in it. Operations on classes are carried out by combining these representatives, and then reducing the result to its least non-negative residue.
The uniqueness requirement is sometimes relaxed, allowing the forms to be unique up to some finer equivalence relation, such as allowing for reordering of terms (if there is no natural ordering on terms).

A canonical form may simply be a convention, or a deep theorem. For example, polynomials are conventionally written with the terms in descending powers: it is more usual to write x² + x + 30 than x + 30 + x², although the two forms define the same polynomial. By contrast, the existence of Jordan canonical form for a matrix is a deep theorem.

History[edit]

According to OED and LSJ, the term canonical stems from the Ancient Greek word kanonikós (κανονικός, «regular, according to rule») from kanṓn (κᾰνών, «rod, rule»). The sense of norm, standard, or archetype has been used in many disciplines. Mathematical usage is attested in a 1738 letter from Logan.^[3] The German term kanonische Form is attested in a 1846 paper by Eisenstein,^[4] later the same year Richelot uses the term Normalform in a paper,^[5] and in 1851 Sylvester writes:^[6]

«I now proceed to […] the mode of reducing Algebraical Functions to their simplest and most symmetrical, or as my admirable friend M. Hermite well proposes to call them, their Canonical forms.»

In the same period, usage is attested by Hesse («Normalform»),^[7] Hermite («forme canonique»),^[8] Borchardt («forme canonique»),^[9] and Cayley («canonical form»).^[10]

In 1865, the Dictionary of Science, Literature and Art defines canonical form as:

«In Mathematics, denotes a form, usually the simplest or most symmetrical, to which, without loss of generality, all functions of the same class can be reduced.»

Examples[edit]

Note: in this section, «up to» some equivalence relation E means that the canonical form is not unique in general, but that if one object has two different canonical forms, they are E-equivalent.

Large number notation[edit]

Standard form is used by many mathematicians and scientists to write extremely large numbers in a more concise and understandable way, the most prominent of which being the scientific notation.^[11]

Number theory[edit]

• Canonical representation of a positive integer
• Canonical form of a continued fraction

Linear algebra[edit]

Objects	A is equivalent to B if:	Normal form	Notes
Normal matrices over the complex numbers	for some unitary matrix U	Diagonal matrices (up to reordering)	This is the Spectral theorem
Matrices over the complex numbers	for some unitary matrices U and V	Diagonal matrices with real positive entries (in descending order)	Singular value decomposition
Matrices over an algebraically closed field	for some invertible matrix P	Jordan normal form (up to reordering of blocks)
Matrices over an algebraically closed field	for some invertible matrix P	Weyr canonical form (up to reordering of blocks)
Matrices over a field	for some invertible matrix P	Frobenius normal form
Matrices over a principal ideal domain	for some invertible matrices P and Q	Smith normal form	The equivalence is the same as allowing invertible elementary row and column transformations
Matrices over the integers	for some unimodular matrix U	Hermite normal form
Matrices over the integers modulo n		Howell normal form
Finite-dimensional vector spaces over a field K	A and B are isomorphic as vector spaces	, n a non-negative integer

Algebra[edit]

Objects	A is equivalent to B if:	Normal form
Finitely generated R-modules with R a principal ideal domain	A and B are isomorphic as R-modules	Primary decomposition (up to reordering) or invariant factor decomposition

Geometry[edit]

In analytic geometry:

• The equation of a line: Ax + By = C, with A² + B² = 1 and C ≥ 0
• The equation of a circle:

By contrast, there are alternative forms for writing equations. For example, the equation of a line may be written as a linear equation in point-slope and slope-intercept form.

Convex polyhedra can be put into canonical form such that:

• All faces are flat,
• All edges are tangent to the unit sphere, and
• The centroid of the polyhedron is at the origin.^[12]

Integrable systems[edit]

Every differentiable manifold has a cotangent bundle. That bundle can always be endowed with a certain differential form, called the canonical one-form. This form gives the cotangent bundle the structure of a symplectic manifold, and allows vector fields on the manifold to be integrated by means of the Euler-Lagrange equations, or by means of Hamiltonian mechanics. Such systems of integrable differential equations are called integrable systems.

Dynamical systems[edit]

The study of dynamical systems overlaps with that of integrable systems; there one has the idea of a normal form (dynamical systems).

Three dimensional geometry[edit]

In the study of manifolds in three dimensions, one has the first fundamental form, the second fundamental form and the third fundamental form.

Functional analysis[edit]

Objects	A is equivalent to B if:	Normal form
Hilbert spaces	If A and B are both Hilbert spaces of infinite dimension, then A and B are isometrically isomorphic.	sequence spaces (up to exchanging the index set I with another index set of the same cardinality)
Commutative C*-algebras with unit	A and B are isomorphic as C*-algebras	The algebra of continuous functions on a compact Hausdorff space, up to homeomorphism of the base space.

Classical logic[edit]

• Negation normal form
• Conjunctive normal form
• Disjunctive normal form
• Algebraic normal form
• Prenex normal form
• Skolem normal form
• Blake canonical form, also known as the complete sum of prime implicants, the complete sum, or the disjunctive prime form

Set theory[edit]

• Cantor normal form of an ordinal number

Game theory[edit]

• Normal form game

Proof theory[edit]

• Normal form (natural deduction)

Rewriting systems[edit]

The symbolic manipulation of a formula from one form to another is called a «rewriting» of that formula. One can study the abstract properties of rewriting generic formulas, by studying the collection of rules by which formulas can be validly manipulated. These are the «rewriting rules»—an integral part of an abstract rewriting system. A common question is whether it is possible to bring some generic expression to a single, common form, the normal form. If different sequences of rewrites still result in the same form, then that form can be termed a normal form, with the rewrite being called a confluent. It is not always possible to obtain a normal form.

Lambda calculus[edit]

• A lambda term is in beta normal form if no beta reduction is possible; lambda calculus is a particular case of an abstract rewriting system. In the untyped lambda calculus, for example, the term doesn’t have a normal form. In the typed lambda calculus, every well-formed term can be rewritten to its normal form.

Graph theory[edit]

In graph theory, a branch of mathematics, graph canonization is the problem of finding a canonical form of a given graph G. A canonical form is a labeled graph Canon(G) that is isomorphic to G, such that every graph that is isomorphic to G has the same canonical form as G. Thus, from a solution to the graph canonization problem, one could also solve the problem of graph isomorphism: to test whether two graphs G and H are isomorphic, compute their canonical forms Canon(G) and Canon(H), and test whether these two canonical forms are identical.

Computing[edit]

In computing, the reduction of data to any kind of canonical form is commonly called data normalization.

For instance, database normalization is the process of organizing the fields and tables of a relational database to minimize redundancy and dependency.^[13]

In the field of software security, a common vulnerability is unchecked malicious input (see Code injection). The mitigation for this problem is proper input validation. Before input validation is performed, the input is usually normalized by eliminating encoding (e.g., HTML encoding) and reducing the input data to a single common character set.

Other forms of data, typically associated with signal processing (including audio and imaging) or machine learning, can be normalized in order to provide a limited range of values.

In content management, the concept of a single source of truth (SSOT) is applicable, just as it is in database normalization generally and in software development. Competent content management systems provide logical ways of obtaining it, such as transclusion.

See also[edit]

• Canonicalization
• Canonical basis
• Canonical class
• Normalization (disambiguation)
• Standardization

Notes[edit]

References[edit]

• Shilov, Georgi E. (1977), Silverman, Richard A. (ed.), Linear Algebra, Dover, ISBN 0-486-63518-X.
• Hansen, Vagn Lundsgaard (2006), Functional Analysis: Entering Hilbert Space, World Scientific Publishing, ISBN 981-256-563-9.