Как составить картографические проекции

1.
Графический метод (в настоящее время
не применяется)

Проекция Бирунни
определяется радиус окружности, строится
взаимоперпендикулярные прямые экватора
и полюса, берется одинаковое расстояние
по
меридианам и по главным меридианам и
соединяются.

Проекция Мюфлинга
использовалась в СССР и России до 28 года
в качестве основы топокарт, проекция
составлялась отдельно на листе карты
способом
засечек.

2. Оптический
метод или оптикомеханический.

Необходимо
иметь исходные проекции, которые с
помощью оптики и подвижного экрана
можно преобразовывать в другую проекцию
(меняется масштаб и форма изображения)

1. Аналитический
   метод

   Делится
   на два способа:

1.Основан
на решении прямой задачи мат. картографии
(часто применяется)

1.1 Классический
(применяется в большинстве случаев)

Задается вид сетки
и в соответствии с этим записываются
уравнения, если задаем цилиндрическую
прямоугольную то х=f(φ)-ширина
у=f(λ).
Из
условной сетки находим наши функции
затем задается желаемый вид искажения
→интегрируем уравнение и решаем m=n,
результат х,у и строим сетку
проекции.

1.2 Перспективный
применяется на любой фигуре (цилиндр,
конус, плоскость). Перспективные-конические
— редко применяются, чаще перспективные
— азимутальные и цилиндрические.

1.3 Способ
комбинации уравнения исходных проекций

А)
к одной проекции

Б)
к разным проекциям — проекция Сансона
равновеликая синусоидальная и
цилиндрическая проекция из класса
псевдоиилиндрических.

1.4 Получение
проекций при разложении проекции в ряд
и использование гармонических полиномов.

Разработаны
Вахренеевой проекции равноугольные
или близкие к ним «+» простота получения,
небольшая величина искажения; «-«
невозможность изобразить приполярные
районы. Имеет преимущество перед
цилиндрическими и коническими проекциями.

1.5 Получение
проекций при введении дополнительных
постоянных или функций. У
псевдо-цилиндрических и псевдо-конических
дополнительные
функции могут быть ведены сразу в наши
функции или быть самостоятельными
функциями.

1.6 Способ
преобразования исходных проекций.
Определяется количество старых точек
по которым вычисляются новые

2.
Обратная задача – когда задаем параметры
искажений, по которым находим функции
прекции и вычисляем прямоуголные
координаты Х, У.

— вычисление по
кривизне меридианов и параллелей

— аппроксимация
эскиза изображения проекции

Особенности прямой
задачи мат. картографии: составление и
решение функций простое, решение не
сложное, но не известно распределение
искажений.

Особенности
обратной задачи мат.картографии:
составление функции проекции сложное.
Берутся функции частных производных
2-го, 3-го и выше порядка, вычисления
сложные и длительные, но получаем
проекцию с нужными параметрами
(искажениями).

4. Факторы влияющие на выбор проекции.

Картографическкая
проекция- это математически определенное
отображение поверхности эллипсоида
или шара на плоскости.
В основу этого отображения положена
система географических или геодезических
координат, графическим выражением
которых являются меридианы и параллели.

Обоснование
выбора проекции зависит от многих
факторов, которые можно разделить на
три группы:

1) Факторы,
характеризующие объект картографирования

—
географическое положение территории

—
размеры
и формы картографируемой территории

—
формы
границ

—
степени показа смежных территорий.

2) Факторы,
характеризующую саму карту, способы и
условия ее использования

• назначение
  карты

• масштаб

• специализация
  карты, содержание, требование к точности
  решаемых задач. 3)Факторы, характеризующие
  саму проекцию

• характер
  распределения искажений

• условие
  обеспечения минимума искажений

• допустимые
  максимальные искажения

• кривизна
  изображения (ортодромии и локсодромии
  — линии, пересекающие все меридианы и
  параллели под одним углом)

• кривизна
  линии сетки

• стереографичность
  проекции

• условие
  ортогональности и симметричности сетки

• наличие
  полюсов, разрывов и перекрытий

3)
Получение искажений (в каких точках
или линиях минимальное искажение).
Основывается на втором факторе.

Исходя
из условий первой группы факторов,
сначала набираются совокупности
проекций, из которых целесообразно
производить
выбор, а затем выбирается конкретная
проекция. Исходя из фактора формы границ
для многих территорий выбирают:
цилиндрические проекции (если
картогорафируемая территория расположена
вблизи экватора и симметрична относительно
его); конические проекции для областей,
расположенных в средних широтах и не
симметричных экватору; азимутальные
проекции для полярных и прочих компактных
территорий; поперечные и косые
цилиндрические проекции для
изображения территорий, вытянутых вдоль
меридианов и вертикалей; поперечные и
косые азимутальные для показа территории,
очертания которых близки к окружности.

Вторая
группа факторов определяет относительную
значимость факторов третьей группы.
После выделения всех зна­чимых факторов
1 и 2 группы, выполняется ранжирование
факторов 3 группы, определяется
относительная значимость каждого
из них и выбирается конкретная проекция.

В
настояшее время существуют 2 крупные
системы карт: карты для решения
научно-технических задач (высокая
точ­ность картометрических работ) и
карты для широкого круга пользования
(для приблизительных измерений и
зрительной оценки
территории).

Для
избежания трансформации картографического
изображения из одной проекции в другую
используют те проекции, которые
имеются на первоисточнике, либо для
изображения картографической сетки
используют каталоги координат уз­ловых
точек, приведенных в альбомах картпроекций.

Классификации
картографических проекций по характеру
искажений

Неизбежным
же свойством изображений являются
искажения. Характер искажений определяется
в зависимости от того, что искажается
– длина, угол или площадь. Если величина
искажений в большей или меньшей степени
зависит от размеров и формы изображаемой
территории, то характер искажений
всецело зависит от самой проекции. Вот
почему при выборе проекции решающую
роль играет характер искажений.

По
характеру
искажения проекции
делятся на:

1)
Равноугольные
(конформные) – углы
и азимуты передаются без искажений,
т.к. масштабы длин в точках не зависят
от направления. Как следствие, в этих
проекциях сохраняется подобие в
бесконечно малых частях. Картографическая
сетка в этих проекциях ортогональна.
На картах в равноугольных проекциях
можно измерять углы и азимуты, на них
удобно производить измерение длин по
всем направлениям.
Угол на местности
всегда равен углу на карте, линия прямая
на местности, прямая на карте. Главным
примером данной проекции является
поперечно-цилиндрическая проекция
Меркатора.

2)
Равновеликие
(эквивалентные) –
масштаб площадей остается постоянным
и равным единице, а следовательно площади
передаются без искажений. На картах в
равновеликих проекциях можно делать
сопоставление площадей.

3)
Равнопромежуточные
(эквидистантные) –
масштаб по одному из главных направлений
сохраняется и равен единице (а=1 или b=1)

4)
Произвольные
– присутствуют
все виды искажений.

Свойства
равноугольности, равновеликости,
равнопромежуточности одновременно на
одной и той же проекции несовместимы.
Проекции, на которой всюду отсутствовали
бы искажения длин, т.е. было бы сохранено
постоянство масштаба, не существует.
На карте могут отсутствовать либо
искажения углов, либо площадей, но
одновременно отсутствовать искажения
углов и площадей не могут. Поэтому
характерным свойством картографической
проекции является обязательное наличие
на карте того или иного искажения.

Картпроекции
топографических карт в России и зарубежом.

Топографические
карты составляют в таких картографических
проекциях,
которые позволяют получать полное
геометрическое подобие очертаний
местности и практически сохранять по
любым направлениям постоянство масштаба.
Обусловлено это тем, что искажения за
счет проектирования остаются в данном
случае за пределами возможной точности
измерений по картам. В России для
топографических карт принята равноугольная
поперечноцилиндрическая проекция
Гаусса-Крюгера, вычисленная по
элементам эллипсоида
Красовского (исключение
– карта масштаба 1:1000000, которая во всем
мире строится в видоизмененной
поликонической проекции, используемой
как многогранная). Применительно к
созданию обзорно-топографических и
собственно топографических карт
поверхность Земли проектируют по
шестиградусным зонам, топографических
планов — по трехградусным, в каждой из
которых строят самостоятоятедьную
систему прямоугольных координат, имеющую
в качестве осей средний меридиан зоны
и экватор. Соответственно на топографических
картах, в отличие от других географических
карт, дается не только градусная сетка
долгот и широт, но и километровая
квадратная сетка.

Выбор
картографической проекции для
топографических карт зависит от размеров
картографируемой территории и ее
географического положения. Большинство
стран мира для составления топографических
карт используют равноугольные проекции,
сохраняющие равенство углов между
направлениями на карте и на местности
и подобие бесконечно малых фигур. В норм
конич проекции меридианы представ-т
собой прямые, расход-ся из точки полюса,
а параллели — дуги концентрич-х окружностей.
Воображ конус касается земного шара
или сечет его в районе средних широт,
поэтому в такой проекции удобнее
картографир-ть террит России, Канады,
США, вытянутые с запада на восток в
средних широтах

ТОПОГРАФИЯ

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Ликбез по картографическим проекциям с картинками

Визуализация данных самого разного рода, имеющих некое географическое распределение, в последнее время получает все большее и большее распространение. Тут, на Хабре, статьи с картами встречаются чуть ли не каждую неделю. Карты в статьях очень разные, но роднит их одно: как правило, в них используются всего две картографические проекции, при том — не самые удачные из существующих. Мне бы хотелось дать несколько наглядных примеров проекций, которые выглядят более эстетично и лучше приспособлены для разных видов визуализации. В этой статье будут рассмотрены общемировые проекции и проекции большей части Земли, так как визуализация чего-либо на карте мира, пожалуй, является наиболее распространенной из подобных задач.

Легкое введение

Поскольку статья ориентирована на вопросы визуализации данных, я не буду касаться глубоко теории проекций (датумов, конформности, равноугольности и тому подобного), кроме общих принципов их построения. Также, я буду говорить тут о «проекциях», формально подразумевая «систему координат», coordinate reference system, потому что для карт таких масштабов не имеет смысла отдельно рассматривать проекцию и датум. Математики здесь тоже практически не будет, кроме простой геометрии. Желающие ознакомиться с математическими принципами, могут это сделать по статьям на Wolfram MathWorld. Так что изучающим программирование в области геоинформационных систем или их опытным пользователям, эта статья, возможно, будет не очень полезна.

Перед началом, объясню пару вещей. Все примеры будут даваться с использованием набора данных государственных границ с вот этого сайта и набора данных Blue Marble Next Generation с сайта NASA. Последний включает в себя синтезированные безоблачные снимки земной поверхности за каждый из двенадцати месяцев 2004-го года, что позволит внести некоторое разнообразие в иллюстрации.

Я очень люблю открытый софт, но использовать GDAL в данном случае мне показалось неэффективно — некоторых не очень ходовых, но полезных проекций в его реализации на данный момент либо нет, либо я плохо смотрел исходники, а потому иллюстрации я готовил в коммерческой программе GlobalMapper, которой пользуюсь уже много лет, и которая славится поддержкой внушительного списка систем координат.

Названия проекций и некоторые термины я буду давать и англоязычные, потому что если кому-то захочется поискать материалы по этой теме, русскоязычных источников в сети найдется несколько меньше (объем статей в Википедии на русском меньше в несколько раз). Для большинства проекций я постараюсь дать не только названия, но и коды EPSG и/или WKID, а также название проекции в библиотеке PROJ.4, широко используемой в открытом софте (например, в пакете R) для поддержки систем координат.

Некоторые проекции, возможно, окажутся кому-то знакомыми по картинке с xkcd, но все из них тут рассмотрены не будут.

Проблема

Начнем с того, что же это за самые распространенные проекции, и что с ними не так.

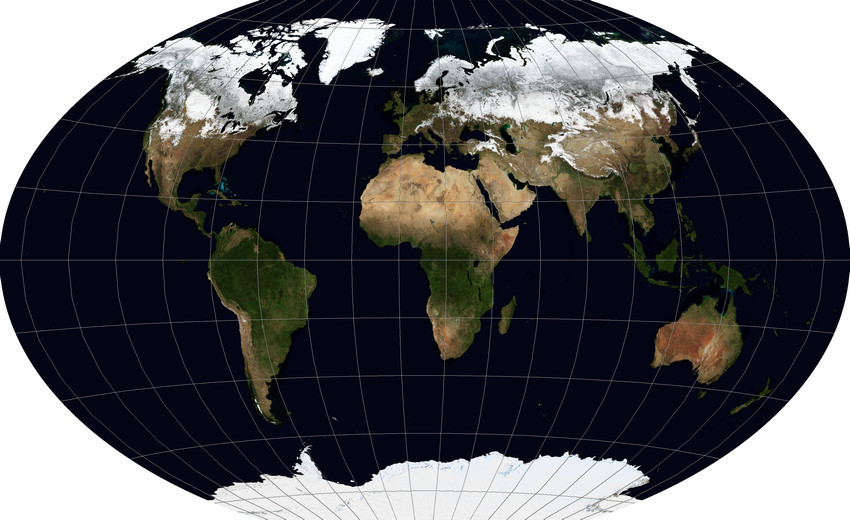
Первая проекция — так называемая

«Географическая»

, она же – Geographic projection, Latitude/Longitude, Plate carrée EPSG:4326 WKID:54001 PROJ.4:longlat. Строго говоря, она даже не совсем является проекцией, потому что получается путем интерпретации полярных угловых координат, как линейных прямоугольных, без всяких вычислений. Эту проекцию используют, потому что она способна отобразить всю поверхность Земли целиком и потому, что она самая простая математически, а данные очень часто распространяются не спроецированными, то есть именно в географических координатах (градусах широты и долготы).

Что же получается? Получается прямоугольник, где точки полюсов обращены в линии (верхнюю и нижнюю границы). Чем дальше от экватора, тем сильнее любой объект на карте оказывается сплюснут по вертикали и растянут по горизонтали. Как я уже сказал, это худо-бедно годится для отображения глобальных наборов данных, но полярные территории (Канада, Норвегия, Швеция, север России, Финляндия, Гренландия, Антарктида, Исландия) оказываются искажены. Проекции, которые позволяют избежать этого, существуют, и о них пойдет речь дальше. Единственная причина использовать эту проекцию — ее предельная простота программной реализации — нужно просто отобразить систему координат от -180º до 180º по X и от -90º до 90º по Y на плоскость, считая угловые единицы линейными.

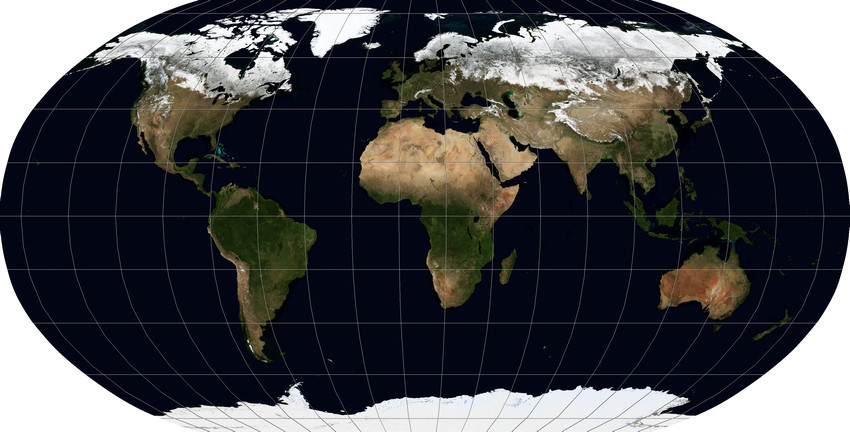
Другая весьма популярная проекция —

«проекция Меркатора»

, Mercator projection PROJ.4:merc. Она также используется для визуализации данных, покрывающих весь мир, но ее популярность продиктована не только простотой — ее варианты являются стандартом де-факто для глобальных картографических сервисов, таких как Google Maps, Bing Maps, Here. С ней глубоко связаны картографические библиотеки OpenLayers, Leaflet, API упомянутых выше сервисов. В варианте Google и OpenStreetMap она носит название Web Mercator и имеет код EPSG/WKID:3857, иногда на нее также ссылаются, как на EPSG:900913. Принцип ее построения не сильно сложнее Географической – это проекция на цилиндр, чья ось совпадает с географической осью Земли, проецирование происходит линиями, выходящими из центра планеты, от чего ошибка растяжения приполярных областей по горизонтали оказывается скомпенсирована пропорциональным растяжением по вертикали. Проблема с этим только в том, что карта получится слишком большой по вертикали, если попытаться отобразить и север Гренландии. Потому обычно отбрасывают 16° полярных областей (в равной пропорции или больше — с юга).

На чей-то взгляд выглядит чуть лучше, чем Географическая, но одну проблему мы уже упомянули, а вторая — чем ближе объект к полюсам, тем он кажется больше, хотя его форма уже не так искажена. Потому, если предмет визуализации — плотность маркеров на единицу территории или расстояния, такой способ отображения будет вводить в заблуждение. При грамотном выборе способа визуализации, конечно, это можно скомпенсировать, а для каких-то случаев это вообще не проблема: например, если величина какого-то показателя в целой стране соотнесена с цветом этой страны на карте, эффект растяжения площадей не сказывается. Эта проекция сохраняет только форму объектов, потому очертания континентов и стран выглядят довольно узнаваемо. И, как я уже сказал, она — ваш первый и самый простой вариант при создании интерактивных веб-карт.

Варианты решения

Что же делать с глобальными данными, если нам по какой-то причине понадобилась проекция, лучше сохраняющая такие свойства объектов, как форма, площадь, расстояния и углы? Законы геометрии не дают нам сохранить все эти свойства сразу, развернув круглую поверхность Земли на плоскость. Однако, для визуализации данных более всего важна эстетика и восприятие, а не сохранение свойств, как для навигационных или измерительных задач. Потому становится возможным подобрать такую проекцию, искажения в которой были бы равномерно распределены по свойствам. И таких проекций существует довольно много. Существуют три самых известных, обладающих сходными свойствами:

«Тройная проекция Винкеля»

Winkel Tripel WKID:54042 PROJ.4:wintri,

«проекция Робинсона»

Robinson projection WKID:54030 PROJ.4:robin,

«проекция Каврайского»

(Kavrayskiy projection). Первая и последняя имеют визуально минимальные искажения, а неспециалисту, не видя градусной сетки, вообще весьма сложно различить их, потому я приведу иллюстрацию для Winkel Tripel, как той, которая лично мне нравится больше всего.

Вот так описание этой проекции выглядит в формате ESRI WKT:
PROJCS["Robinson",
GEOGCS["GCS_WGS_1984",
DATUM["D_WGS84",
SPHEROID["WGS84",6378137,298.257223563]
],
PRIMEM["Greenwich",0],
UNIT["Degree",0.017453292519943295]
],
PROJECTION["Robinson"],
PARAMETER["central_meridian",0],
PARAMETER["false_easting",0],
PARAMETER["false_northing",0],
UNIT["Meter",1]
]

Как легко видеть, хотя искажение контуров и некоторое увеличение площади стран к полюсам здесь также наблюдаются, но это нельзя даже сравнивать с растяжением Географической проекции и пропорциональным увеличением проекции Меркатора.

Тут стоит сделать небольшое отступление и обратить внимание на то, что вид этой проекции по умолчанию страдает одним недостатком, который касается и других общемировых проекций. Дело в том, что если за центральный меридиан — линию, соединяющую северный и южный полюс через центр карты (longitude of origin) — принять нулевой меридиан, то карта будет разрезана по 180-му. Но при этом треть Чукотки окажется на левом краю карты, а две трети — на правом. Чтобы сделать карту красивее, разрез должен проходить где-то в районе 169-го западного меридиана восточнее острова Ратманова, для чего за центральный должен быть принят 11-й. Вот иллюстрация того, что получается:

А вот измененное для этого случая описание в ESRI WKT:
PROJCS["Robinson",
GEOGCS["GCS_WGS_1984",
DATUM["D_WGS84",
SPHEROID["WGS84",6378137,298.257223563]
],
PRIMEM["Greenwich",0],
UNIT["Degree",0.017453292519943295]
],
PROJECTION["Robinson"],
PARAMETER["central_meridian",11],
PARAMETER["false_easting",0],
PARAMETER["false_northing",0],
UNIT["Meter",1]
]

В формате определения системы координат для PROJ.4 долгота центра проекции задается параметром +lon_0=.

11-й меридиан — «магическое» число: практически все мировые проекции, имеющие равномерный масштаб вдоль экватора, могут быть разрезаны по Берингову проливу, если за центральный принять именно его, а не нулевой.

Замечу, что задумываясь о выборе проекции, стоит принимать во внимание все существующие реальные требования к визуализации. Например, если данные касаются климата, то может иметь смысл либо нанести на карту линии широты, либо использовать проекцию, где они горизонтальны, а не загибаются к краям карты (то есть, отказаться от Тройной Винкеля в пользу, например, Робинсона). В данном случае, это позволит легче и точнее оценить относительную близость разных мест к полюсам и экватору. Еще один весомый плюс проекции Робинсона — то, что она поддерживается множеством софта, в том числе открытого, тогда как про некоторые другие этого сказать нельзя.

Иногда, когда требуется максимально сохранить какое-то свойство, например — соотношение площадей объектов (стран) — эстетическая сторона страдает. Но поскольку это все же может для чего-то понадобиться, я приведу один пример такой проекции —

«проекцию Моллвейде»

, Mollweide projection WKID:54009 PROJ.4:moll.

Как видно, она довольно сильно напоминает проекцию Робинсона, но с той разницей, что полюса все же стянуты в точки, от чего форма приполярных областей выглядит сильно искаженной. Но пропорции площадей стран, как и требовалось, сохраняются куда лучше.

Самым молодым конкурентом этих проекций является проекция

Natural Earth

PROJ.4:natearth — она представляет из себя гибрид проекций Каврайского и Робинсона, а ее параметры были подобраны группой американских, швейцарских и словенских специалистов в 2007 году, тогда как возраст большинства картографических проекций — не менее полувека.

Для перепроецирования данных в нее существует некоторое количество инструментов, которые были написаны специально для этого, но ее поддержка еще далека от повсеместной.

Немного экзотики и специальных случаев

Конечно, все многообразие проекций на этом не заканчивается. Их изобретено немало. Некоторые просто выглядят странно (скажем, проекция Бонне изображает Землю в виде фигуры, напоминающей разрезанное яблоко или стилизованное сердце), некоторые — предназначены для особых ситуаций. Например, готов поспорить, что очень многие видели на картинках карту мира, которая похожа на корку мандарина, которую сняли и расплющили. Это, наверняка, была

«Разрывная гомолосинусоидальная проекция Гуда»

Interrupted Goode Homolosine projection WKID:54052.

Вид ее вполне достоин названия. Ее назначение — отображать размер объектов (и в некоторой степени — форму) близко к естественным пропорциям. Ее главная проблема, кроме названия и странного вида, состоит в том, что путем подбора центрального меридиана невозможно добиться того, чтобы ни один крупный кусок суши не был разрезан. Обязательно пострадает что-то из списка: Гренландия, Исландия, Чукотка, Аляска. Лично на мой взгляд, проще привести отдельно изображения стран, чем использовать такую карту, если вы не хотите стилизовать свою работу под середину XX века.

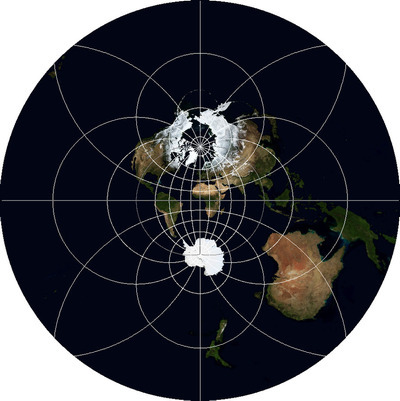
Существуют проекции, которые по своей природе никак не отнести к общемировым, но мне бы хотелось рассмотреть их здесь, потому что они способны показать земной шар, то есть как-бы вид планеты из космоса. Одна из них —

«Проекция вертикальной ближней перспективы»

Vertical Near-Side Perspective projection WKID:54049. Ее особое свойство — показывать земную поверхность в такой перспективе, как она выглядит с определенной высоты. Высота над эллипсоидом (идеализированной фигурой, моделирующей Землю) задается для этой проекции в явном виде.

На иллюстрации эта проекция имеет широту и долготу центра, равные широте и долготе Москвы, а высоту — 5000000 метров. Чем больше это расстояние, тем сильнее изображение Земли становится похоже на ее изображение в проекции, которую мы рассмотрим последней.

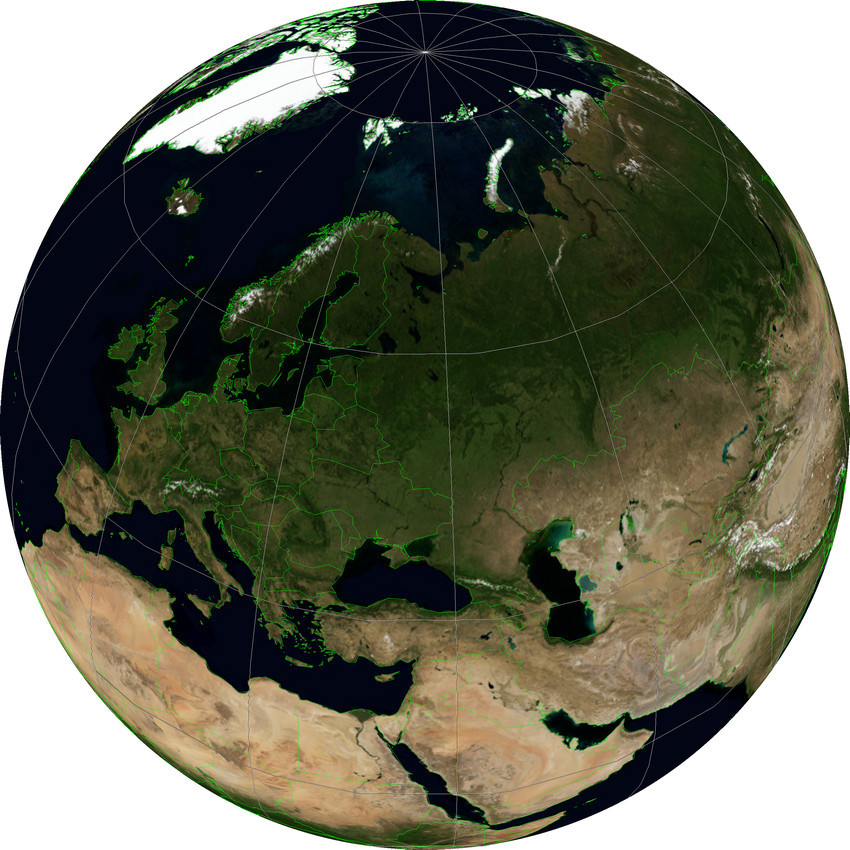
Проекция, которая показывает вид на Землю в параллельной перспективе, то есть как-бы с бесконечного расстояния, называется

«Ортографическая проекция»

Orthographic projection WKID:43041 PROJ.4:ortho. В каком-то смысле, она знакома всем, кто когда-либо пользовался Google Earth. Я говорю, что в каком-то смысле, потому что «направление взгляда» в этой проекции всегда перпендикулярно поверхности Земли, тогда как в Google Earth его можно наклонять как угодно.

Для нее, как и для предыдущей проекции, можно задать центральные широту и долготу, чтобы ориентировать Землю желаемым образом. Например, можно показать полушарие с центром в какой-то точке, о которой идет речь — скажем, иллюстрируя транспортные потоки континентального масштаба, исходящие от одного предприятия. Сделав две карты с противоположными значениями координат, можно получить карту всего мира (правда, на краях искажения будут очень велики). Генерация последовательности карт с плавным изменением центральной точки даст кадры для анимации вращающейся планеты без всякой трехмерной графики.

Если статья окажется интересной, постараюсь написать продолжение о проекциях, используемых для отображения отдельных стран или регионов, ориентированную, как и эта статья, на базовые свойства этих проекций для задачи визуализации данных, инфографики и тому подобного.

Проекции в картографии

Работа древних землемеров не выходила за пределы геодезических измерений и расчетов для расстановки вех вдоль маршрута будущей дороги или обозначения границ земельных участков. Но посте­пенно накапливалось множество данных – расстояния между городами, препятствия на пути, расположение водных объектов, лесных массивов, особенности ландшафта, границы государств и материков. Карты захватывали все большие территории, становились более детальными, но при этом возрастала и их погрешность.

Поскольку Земля представляет собой геоид (фигуру, близкую к эллипсоиду), для изображения поверхности геоида Земли на карте необходимо развернуть, спроецировать эту поверхность на плоскость тем или иным способом. Методы отображения геоида на плоской карте называются картографическими проекциями. Существует несколько видов проекций, и каждая из них вносит в плоское изображение свои искажения длин, углов, площадей или формы фигур.

Как сделать точную карту?

Полностью избежать искажений при построении карты невозможно. Однако можно избавиться от какого-либо одного типа искажений. Так называемые равновеликие проекции сохраняют площади, но при этом искажают углы и формы. Равновеликими проекциями удобно пользоваться в экономических, почвенных и других мелкомасштабных тематических картах – для того, чтобы с их помощью рассчитывать, например, площади территорий, подвергшихся загрязнению, или управлять лесными хозяйствами. Примером такой проекции служит равновеликая коническая проекция Альберса, разработанная в 1805 г. немецким картографом Хейнрихом Альберсом.

Равноугольные проекции — это проекции без искажений углов. Такие проекции удобны для решения навигационных задач. Угол на местности всегда равен углу на такой карте, а прямая линия на местности изображается прямой линией на карте. Это позволяет мореплавателям и путешественникам прокладывать маршрут и точно следовать ему с помощью показаний компаса. Однако линейный масштаб карты при такой проекции зависит от положения точки на ней.

Самой древней равноугольной проекцией считается стереографическая проекция, которая была придумана Аполлонием Пергским около 200 г. до нашей эры. Эта проекция и по сей день используется для карт звезд­ного неба, в фотографии – для отображения сфериче­ских панорам, в кристаллографии – для изображения точечных групп симметрии кристаллов. Но использование этой проекции в мореплавании было бы затруднительным в силу слишком больших линейных искажений.

Проекция Меркатора

В 1569 г. фламандский географ Герхард Меркатор (латинизированное имя Герарда Кремера) разработал и впервые применил в своем атласе (полное название «Атлас, или Космографические рассуждения о сотворении мира и вид сотворенного») равноугольную цилиндрическую проекцию, названную впоследствии его именем и ставшую одной из основных и самых распространенных картографических проекций.

Для построения цилиндрической проекции Меркатора земной геоид помещают внутри цилиндра так, чтобы геоид касался цилиндра по экватору. Проекцию получают, проводя лучи из центра геоида до пересечения с поверхностью цилиндра. Если после этого цилиндр разрезать вдоль оси и развернуть, то получится плоская карта поверхности Земли. Образно это можно представить следующим образом: глобус оборачивается листом бумаги по экватору, в центр глобуса помещается лампа и на листе бумаги отображаются спроецированные лампой изображения материков, островов, рек и т. п. Если бы на бумагу был нанесен способный засвечиваться слой, то, развернув лист, мы получили бы готовую карту.

Полюса в такой проекции расположены на бесконечном расстоянии от экватора, и, следовательно, не могут быть изображены на карте. На практике карта имеет верхний и нижний пределы широт – примерно до 80° СШ и ЮШ.

Параллели и меридианы картографической сетки изображаются на карте параллельными прямыми линиями, при этом они всегда перпендикулярны. Расстояния между меридианами одинаковы, а вот расстояние между параллелями равно расстоянию между меридианами вблизи экватора, но быстро увеличивается при приближении к полюсам.

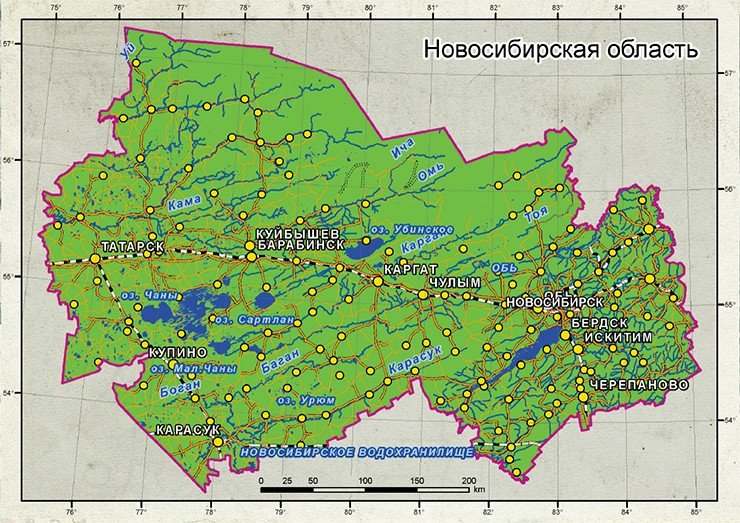
Масштаб в этой проекции не является постоянным, он увеличивается от экватора к полюсам как обратный косинус широты, но масштабы по вертикали и по горизонтали всегда равны.

Равенство вертикального и горизонтального масштабов обеспечивает равноугольность проекции – угол между двумя линиями на местности равен углу между изображением этих линий на карте. Благодаря этому хорошо отображается форма небольших объектов. Но искажения площади увеличиваются по направлению к полярным регионам. Например, несмотря на то, что Гренландия составляет всего одну восьмую размера Южной Америки, в проекции Меркатора она представляется больше. Большие искажения площадей делают проекцию Меркатора непригодной для общегеографических карт мира.

Линия, проведенная между двумя точками на карте в этой проекции, пересекает меридианы под одним и тем же углом. Эта линия называется румбом или локсо­дромией. Надо отметить, что эта линия не описывает кратчайшее расстояние между точками, но в проекции Меркатора всегда изображается прямой линией. Этот факт делает проекцию идеальной для нужд навигации. Если мореплаватель желает отправиться, например, из Испании в Вест-Индию, все, что ему нужно сделать, это провести линию между двумя точками, и штурман будет знать, какого направления по компасу постоянно придерживаться, чтобы приплыть к месту назначения.

С точностью до сантиметра

Для применения проекции Меркатора (как, впрочем, и любой другой) необходимо определить систему координат на земной поверхности и корректно выбрать так называемый референц-эллипсоид – эллипсоид вращения, приближенно описывающий форму поверхности Земли (геоида). Для местных карт в России в качестве такого референц-эллипсоида с 1946 г. используется эллипсоид Красовского. В большинстве европейских стран вместо него используется эллипсоид Бесселя. Самым популярным в наши дни эллипсоидом, предназначенным для составления общемировых карт, является мировая геодезическая система 1984 г. WGS-84. Она определяет трехмерную систему координат для позиционирования на земной поверхности относительно центра масс Земли, погрешность составляет менее 2 см. Классическая равноугольная цилиндрическая проекция Меркатора применяется к соответствующему эллипсоиду. Так, например, сервис Яндекс.Карты использует эллиптическую WGS-84 проекцию Меркатора.

В последнее время в связи со стремительным развитием картографических веб-сервисов большое распространение получил другой вариант проекции Меркатора – на базе сферы, а не эллипсоида. Этот выбор обусловлен более простыми расчетами, которые могут быть быстро выполнены клиентами этих сервисов прямо в браузере. Часто эту проекцию называют «сфериче­ским Меркатором». Такой вариант проекции Меркатора используется сервисами Google Maps, а также 2ГИС.

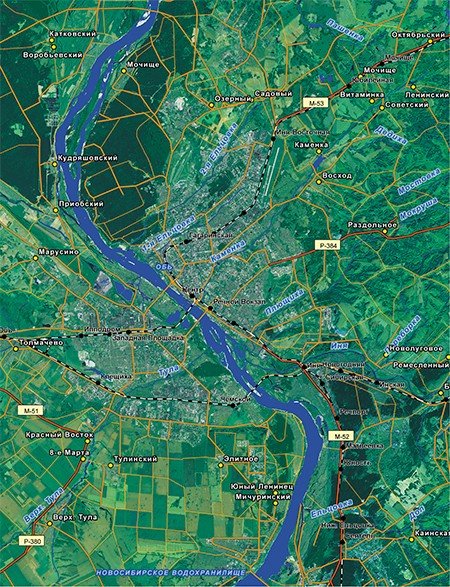
Еще одним известным вариантом проекции Меркатора является равно­угольная проекция Гаусса-Крюгера. Она была введена выдающимся немецким ученым Карлом Фридрихом Гауссом в 1820—1830 гг. для картографирования Германии – так называемой ганноверской триангуляции. В 1912 и 1919 гг. ее развил немецкий геодезист Л. Крюгер.

По сути, она является поперечной цилиндрической проекцией. Поверхность земного эллипсоида делится на трех- или шестиградусные зоны, ограниченные меридианами от полюса до полюса. Цилиндр касается среднего меридиана зоны, и она проецируется на этот цилиндр. Всего можно выделить 60 шестиградусных или 120 трехградусных зон.

В России для топографических карт масштаба 1 : 1000000 применяют шестиградусные зоны. Для топографических планов масштаба 1 : 5000 и 1:2000 применяются трехградусные зоны, осевые меридианы которых совпадают с осевыми и граничными меридианами шестиградусных зон. При съемках городов и территорий под строительство крупных инженерных сооружений могут быть использованы частные зоны с осевым меридианом посередине объекта.

Многомерная карта

Современные информационные технологии позволяют не просто нанести контуры объекта на карту, но и менять его вид в зависимости от масштаба, связать с его географическим положением множество других атрибутов, таких как адрес, информация о расположенных в данном здании организациях, количество этажей и т. п., делая электронную карту многомерной, разномасштабной, интегрируя в ней одновременно несколько справочных баз данных. Для обработки этого массива информации и представления его в удобном для пользователя виде необходимы достаточно сложные программные продукты, так называемые геоинформационные системы, разработку и поддержку которых могут осуществить лишь достаточно крупные, обладающие необходимым опытом IT-компании. Но, несмотря на то, что современные электронные карты мало похожи на своих бумажных предшественников, все равно в их основе лежат картография и тот или иной способ отображения земной поверхности на плоскость.

Для иллюстрации методов современной картографии можно рассмотреть опыт работы компании «Дата Ист» (Новосибирск), занимающейся разработкой программного обеспечения в области геоинформационных технологий.

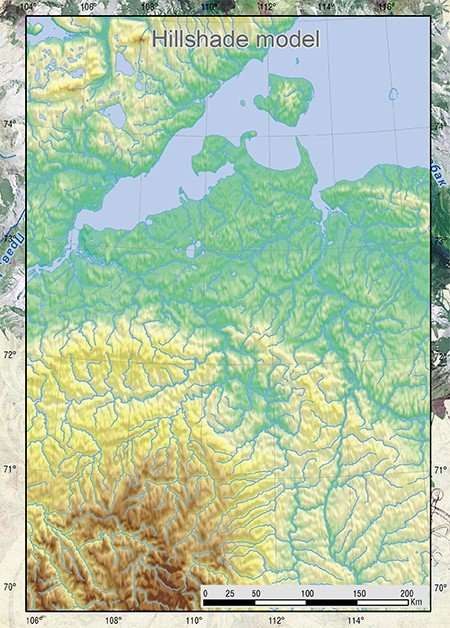
Проекция, которая выбирается для построения электронной карты, зависит от назначения карты. Для карт общего пользования и для навигационных карт, как правило, применяется проекция Меркатора с системой координат WGS-84. Например, эта система координат использовалась в проекте «Мобильный Новосибирск», созданном по заказу мэрии города Новосибирска для городского муниципального портала.

Для крупномасштабных карт с целью минимизации линейных искажений используются как зональные равноугольные проекции (Гаусса-Крюгера), так и неравноугольные проекции (например, коническая равно­промежуточная проекция – Equidistant conic).

Сегодня карты создаются с широким привлечением аэрофотосъемки и спутниковых фотографий. Для качественной работы над картами в компании «Дата Ист» создан архив космических снимков, охватывающих территории Новосибирской, Кемеровской, Томской, Омской областей, Алтайского края, Республик Алтай и Хакасия, других регионов России. С помощью этого архива, кроме крупномасштабных карт территории, можно изготавливать схемы отдельных объектов и участ­ков под заказ. При этом в зависимости от территории и необходимого масштаба применяется та или иная проекция.

Со времен Меркатора картография изменилась радикально. Информационная революция затронула эту область человеческой деятельности, наверное, больше всех. Вместо томов бумажных карт теперь каждому путешественнику, туристу, водителю доступны компактные электронные навигаторы, содержащие в себе массу полезной информации о географических объектах.

Но суть карт осталась той же – показать нам в удобном и ясном виде, с указанием точных географических координат, расположение объектов окружающего нас мира.

Литература

ГОСТ Р 50828-95. Геоинформационное картографирование. Пространственные данные, цифровые и электронные карты. Общие требования. М., 1995.

Капралов Е. Г. и др. Основы геоинформатики: в 2 кн. / Учеб. пособие для студ. вузов / Под ред. Тикунова В. С. М.: Академия, 2004. 352, 480 c.

Жалковский Е. А. и др. Цифровая картография и геоинформатика / Краткий терминологический словарь. М.: Картгеоцентр-Геодезиздат, 1999. 46 с.

Баранов Ю. Б. и др. Геоинформатика. Толковый словарь основных терминов. М.: ГИС-Ассоциация, 1999.

ДеМерс Н. Н. Географические информационные системы. Основы.: Пер. с англ. М.: Дата+, 1999.

Карты любезно предоставлены ООО «Дата Ист» (г. Новосибирск)