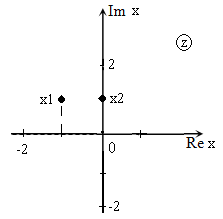Как составить квадратное уравнение по его корням комплексных чисел - Исправление недочетов и поиск решений вместе с Examum.ru

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Определение 1

Двучленным называется уравнение вида $x^{n} =A$.

Рассмотрим три случая:

В случае если $A$ — это положительное действительное число, то корни уравнения находятся по формуле

[x_{k} =sqrt[{n}]{A} cdot left(cos frac{2kpi }{n} +icdot sin frac{2kpi }{n} right),, , , k=0,..,n-1.]

В случае если $A$ — это отрицательное действительное число, то корни уравнения находятся по формуле

[x_{k} =sqrt[{n}]{|A|} cdot left(cos frac{pi +2kpi }{n} +icdot sin frac{pi +2kpi }{n} right),, , , k=0,..,n-1.]

В случае если $A$ — это комплексное число, то корни уравнения находятся по формуле

[x_{k} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1.]

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Пример 1

Решить уравнение: $x^{3} =8$.

Решение:

Так как $A>0$, то $x_{k} =sqrt[{3}]{8} cdot left(cos frac{2kpi }{3} +icdot sin frac{2kpi }{3} right),, , , k=0,..,2$.

При $k=0$ получаем $x_{0} =sqrt[{3}]{8} cdot left(cos 0+icdot sin 0right)=sqrt[{3}]{8} =2$.

При $k=1$ получаем

[x_{1} =sqrt[{3}]{8} cdot left(cos frac{2pi }{3} +icdot sin frac{2pi }{3} right)=sqrt[{3}]{8} cdot (-frac{1}{2} +frac{sqrt{3} }{2} cdot i)=2cdot (-frac{1}{2} +frac{sqrt{3} }{2} cdot i)=-1+sqrt{3} cdot i.]

При $k=2$ получаем

[x_{2} =sqrt[{3}]{8} cdot left(cos frac{4pi }{3} +icdot sin frac{4pi }{3} right)=sqrt[{3}]{8} cdot (-frac{1}{2} -frac{sqrt{3} }{2} cdot i)=2cdot (-frac{1}{2} -frac{sqrt{3} }{2} cdot i)=-1-sqrt{3} cdot i.]

Пример 2

Решить уравнение: $x^{3} =1+i$.

«Квадратное уравнение с комплексными корнями» 👇

Решение:

Так как $A$ — комплексное число, то

[x_{k} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1,, , , k=0,..,2.]

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

[r=sqrt{1^{2} +1^{2} } =sqrt{1+1} =sqrt{2} ]

Вычислим аргумент исходного комплексного числа:

[varphi =arg z=arctgfrac{1}{1} =arctg1=frac{pi }{4} ]

Подставим полученные значения и получим:

[A=sqrt{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} )]

Уравнение перепишем в виде:

[x^{3} =sqrt{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} )]

При $k=0$ получаем $x_{0} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4}{3} +icdot sin frac{pi /4}{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)=sqrt[{6}]{2} cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)$.

При $k=1$ получаем

[begin{array}{l} {x_{1} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4+2pi }{3} +icdot sin frac{pi /4+2pi }{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right)=} \ {=sqrt[{6}]{2} cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right)} end{array}]

При $k=2$ получаем

[begin{array}{l} {x_{2} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4+4pi }{3} +icdot sin frac{pi /4+4pi }{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right)=} \ {=sqrt[{6}]{2} cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right)} end{array}]

Определение 2

Квадратным называется уравнение вида $ax^{2} +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^{2} -4ac$, при этом

[x_{1,2} =frac{-bpm sqrt{D} }{2a} .]

Примечание 1

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

Пример 3

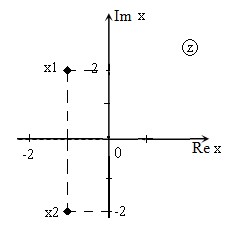
Решить уравнение $x^{2} +2x+5=0$ и изобразить корни на плоскости.

Решение:

Вычислим дискриминант:

[D=2^{2} -4cdot 1cdot 5=4-20=-16.]

Так как $D

[x_{1,2} =frac{-2pm sqrt{-16} }{2} =frac{-2pm icdot sqrt{16} }{2} =frac{-2pm icdot 4}{2} =-1pm 2i.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

Рис. 1

Примечание 2

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Определение 3

Комплексное число вида $overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Примечание 3

Известно, что если $x_{1,2} $ являются корнями квадратного уравнения $ax^{2} +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_{1} )(x-x_{2} )=0$. В общем случае $x_{1,2} $ являются комплексными корнями.

Пример 4

Зная корни уравнения $x_{1,2} =1pm 2i$, записать исходное уравнение.

Решение:

Запишем уравнение следующим образом:

[(x-(1-2i))cdot (x-(1+2i))=0.]

Выполним умножение комплексных чисел

[x^{2} -(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0][x^{2} -x+2icdot x-x-2icdot x+1-4i^{2} =0] [x^{2} -2x+1+4=0] [x^{2} -2x+5=0]

Следовательно, $x^{2} -2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Пример 5

Решить уравнение: $z^{2} +(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.

Решение:

Вычислим дискриминант:

[D=(1-2i)^{2} +4cdot 1cdot (1+i)=1-4i+4i^{2} +4+4i=1-4+4=1.]

Так как $D>0$, уравнение имеет два корня:

[x_{1} =frac{-(1-2i))-sqrt{1} }{2} =frac{-1+2i-1}{2} =frac{-2+2i}{2} =-1+i.] [x_{2} =frac{-(1-2i))+sqrt{1} }{2} =frac{-1+2i+1}{2} =frac{2i}{2} =i.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

Рис. 2

Примечание 4

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ <3>=8$.

Так как $A>0$, то $x_ =sqrt[<3>] <8>cdot left(cos frac<2kpi > <3>+icdot sin frac<2kpi > <3>right),, , , k=0. 2$.

При $k=0$ получаем $x_ <0>=sqrt[<3>] <8>cdot left(cos 0+icdot sin 0right)=sqrt[<3>] <8>=2$.

При $k=1$ получаем

[x_ <1>=sqrt[<3>] <8>cdot left(cos frac<2pi > <3>+icdot sin frac<2pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=-1+sqrt <3>cdot i.]

При $k=2$ получаем

[x_ <2>=sqrt[<3>] <8>cdot left(cos frac<4pi > <3>+icdot sin frac<4pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=-1-sqrt <3>cdot i.]

Решить уравнение: $x^ <3>=1+i$.

Готовые работы на аналогичную тему

Так как $A$ — комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

[varphi =arg z=arctgfrac<1> <1>=arctg1=frac<pi > <4>]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ <0>=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi /4> <3>+icdot sin frac<pi /4> <3>right)=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)=sqrt[<6>] <2>cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)$.

При $k=1$ получаем

При $k=2$ получаем

Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом

Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.

[D=2^ <2>-4cdot 1cdot 5=4-20=-16.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.

Зная корни уравнения $x_ <1,2>=1pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

[x^ <2>-(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ <2>-x+2icdot x-x-2icdot x+1-4i^ <2>=0] [x^ <2>-2x+1+4=0] [x^ <2>-2x+5=0]

Следовательно, $x^ <2>-2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ <2>+(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13.11.2021

Квадратное уравнение с комплексными коэффициентами

Аргументы квадратного уравнения

Точность вычисления (знаков после запятой)

Вы ввели следующее выражение

Результат решения заданного уравнения

Расчет квадратных уравнений, содержащие комплексные коэффициенты

Как известно, квадратное уравнение: имеет корни, которые вычисляются по простой форумуле .

Онлайн решений очень много, наш же бот, вычисляет квадратное уравнение, если его коэффициенты являются комплексными числами.

В русскоязычном секторе Интернета, такого сервиса нет, и наш бот будет тут первым.

Хотелось бы заметить, что коэффициентами квадратного уравнения могут быть не только комплексные числовые значения, но и произвольное комплексное выражение. Это несомненно расширяет возможности представленного сервиса, и дает определенные преимущества.

Ну и естественно, для тех кто хорошо учился в школе, и понимающих, что комплексные числа это лишь расширенное представление наших «обычных» действительных чисел, следует вывод, что данный сервис правильно считает и в том случае, если числа в коэффициентах имеют действительные значения.

Для того, что бы по известным корням можно было построить произвольное уравнение, в том числе и квадратное с комплексными коэфициентами можно воспользоватся ресурсом Создание полинома (многочлена) одной переменной онлайн

Синтаксис

Для всех кто пользуется XMPP клиентами: ur2_i

Коэффициенты уравнения могут быть как действительными так и мнимыми значениями.

Более того, каждый коэффициент может быть выражен не только числом, но и каким либо выражением

Элементы уравнения вводятся по принципу слева направо, от элемента с более высокой степенью переменной х, к более низкой.

Каждый элемент уравнения должен быть разделен пробелами.

Примеры

Пишем в поле ввода коэффициенты

Не забудьте, что как минимум одним пробелом разделяются эти значения

ответ будет следующий

Давайте проверим, а правильно ли нам посчитал бот эти корни. Для этого воспользуемся Аргумент и значения функции комплексной переменной и посчитаем чему же будет равно значение функции, при полученных корнях

При выборе первого корня ответ будет такой:

Вы ввели следующее выражение

Результат решения заданного уравнения

Вы ввели следующую функицю

Табличное представление значений функции

Переменная x	Значение функции f(x)
-0.007843258+0.125005019i	0+0.000009959i

Несмотря на небольшую погрешность, результат говорит нам о том что расчеты проведены верно

Здесь мы видим, что коэффициенты представлены в виде комплексных выражений, но для бота это не помеха.

Квадратное уравнение с комплексными корнями и коэффициентами

Пусть задано квадратное уравнение $ax^2+bx+c=0$, где коэффициенты $a$, $b$ и $c$ — в общем случае являются комплексными. Его решение находим с помощью дискриминанта

В общем случае и дискриминант, и корни уравнения являются комплексными числами.

Задание. Составить квадратное уравнение, которое имеет корни $z_<1>=1-i$ и $z_<2>=4-5i$. Решить его.

Решение. Известно, что если $z_1$, $z_2$ — корни квадратного уравнения $z^2+bz+c=0$, то указанное уравнение можно записать в виде $(z-z_1)(z-z_2)=0$. А тогда, учитывая этот факт, имеем, что искомое уравнение можно записать следующим образом:

Раскрываем скобки и выполняем операции над комплексными числами:

$z^<2>+(-5+6 i) z-(1+9 i)=0$ — искомое квадратное уравнение.

Решим полученное уравнение. Найдем дискриминант:

$$D=(-5+6 i)^<2>-4 cdot 1 cdot(-(1+9 i))=-11-60 i+4+36 i=$$ $$=-7-24 i$$

Так как при извлечении корня из комплексного числа в результате получится комплексное число, то корень из дискриминанта будем искать в виде $sqrt=a+b i$. То есть

$$sqrt<-7-24 i>=a+b i Rightarrow-7-24 i=(a+b i)^ <2>Rightarrow$$ $$Rightarrow-7-24 i=a^<2>+2 a b i-b^<2>$$

Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно, получим систему для нахождения неизвестных значений $a$ и $b$:

решив которую, имеем, что $a_1=3$, $b_1=-4$ или $a_2=-3$, $b_2=4$. Рассматривая любую из полученных пар, например, первую, получаем, что $sqrt=3-4 i$, а тогда

Ответ. $z^<2>+(-5+6 i) z-(1+9 i)=0$

источники:

http://abakbot.ru/online-16/151-mnimoe-kvadratnoe-uravnenie

http://www.webmath.ru/poleznoe/formules_16_14.php

Источник

Пусть задано квадратное уравнение $ax^2+bx+c=0$, где коэффициенты
$a$,
$b$ и
$c$ — в общем случае являются комплексными.
Его решение находим с помощью дискриминанта

$$D=b^{2}-4 a c$$

тогда

$$x_{1,2}=frac{-b pm sqrt{D}}{2 a}$$

В общем случае и дискриминант, и корни уравнения являются
комплексными числами.

Пример

Задание. Составить квадратное уравнение, которое имеет корни
$z_{1}=1-i$ и
$z_{2}=4-5i$. Решить его.

Решение. Известно, что если
$z_1$, $z_2$ — корни квадратного уравнения
$z^2+bz+c=0$, то указанное уравнение можно записать в виде
$(z-z_1)(z-z_2)=0$. А тогда, учитывая этот факт, имеем, что
искомое уравнение можно записать следующим образом:

$$(z-(1-i))(z-(4-5 i))=0$$

Раскрываем скобки и выполняем операции над комплексными числами:

$$z^{2}-(4-5 i) z-(1-i) z+(1-i)(4-5 i)=0$$
$$z^{2}+z(-4+5 i-1+i)+4-5 i-4 i+5 i^{2}=0$$

$z^{2}+(-5+6 i) z-(1+9 i)=0$ — искомое квадратное уравнение.

Решим полученное уравнение. Найдем дискриминант:

$$D=(-5+6 i)^{2}-4 cdot 1 cdot(-(1+9 i))=-11-60 i+4+36 i=$$
$$=-7-24 i$$

Так как при извлечении корня из комплексного числа в
результате получится комплексное число, то корень из
дискриминанта будем искать в виде $sqrt{D}=a+b i$. То есть

$$sqrt{-7-24 i}=a+b i Rightarrow-7-24 i=(a+b i)^{2} Rightarrow$$
$$Rightarrow-7-24 i=a^{2}+2 a b i-b^{2}$$

Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно,
получим систему для нахождения неизвестных значений $a$ и
$b$:

$$left{begin{array}{l}a^{2}-b^{2}=-7 \ 2 a b=-24end{array}right.$$

решив которую, имеем, что $a_1=3$,
$b_1=-4$ или $a_2=-3$, $b_2=4$. Рассматривая любую из
полученных пар, например, первую, получаем, что
$sqrt{D}=3-4 i$, а тогда

$$z_{1}=frac{-(-5+6 i)+(3-4 i)}{2 cdot 1}=4-5 i$$
$$z_{2}=frac{-(-5+6 i)-(3-4 i)}{2 cdot 1}=1-i$$

Ответ. $z^{2}+(-5+6 i) z-(1+9 i)=0$

Читать дальше: элементарные функции комплексного аргумента.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Скачать материал

Сейчас обучается 50 человек из 27 регионов

Сейчас обучается 83 человека из 35 регионов

Сейчас обучается 136 человек из 43 регионов

Описание презентации по отдельным слайдам:

1 слайд

Решение квадратных уравнений с помощью комплексных чисел
2 слайд

«Комплексное число –
это тонкое и поразительное средство божественного духа,
почти амфибия между бытием и небытием».
Г. Лейбниц
3 слайд

Термин “мнимые числа” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века — Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа i(мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа” так же был введен Гауссом в 1831 году. Слово «комплекс» (от латинского complexus) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. образующих единое целое.
4 слайд

Н. Н. Богомолов и В. С. Владимиров — к проблемам квантовой теории поля.
Большой вклад в развитие теории функций комплексного переменного внесли русские и советские ученые:
Н. И. Мусхелишвили занимался ее применениями к теории упругости;
М. В. Келдыш и
М. А. Лаврентьев — к аэро- и гидродинамике;
5 слайд

Обозначение:
– алгебраическая форма записи комплексного числа
6 слайд

Множество комплексных чисел обозначается С,
N
Z
Q
I
R
C
7 слайд

Число a называется действительной частью комплексного числа z. Обозначается a=Re z.
Число b называется мнимой частью комплексного числа z. Обозначается b=Im z.
8 слайд

Мнимая ось
Действительная ось
+1
+i
0
1
1
a
b
M(a; b)
z=a+jb
9 слайд

Примеры:
1) Изобразите комплексные числа
10 слайд

2) Запишите комплексные числа, изображенные на координатной плоскости, в алгебраической форме.
+1
+i
0
1
1
-2
4
3
2
-3
-4
-5
11 слайд

3) На какой из координатных плоскостей изображено число
+i
+1
0
1.
2.
3.
4.
+i
+i
+i
+1
+1
+1
0
0
0
12 слайд

Степени мнимой единицы
По определению:
Таким образом, можно вывести формулу для вычисления
13 слайд

Если показатель степени m при j делится на 4 без остатка, то
Если при делении показателя степени m при j на 4 получается остаток 1, то
Если при делении показателя степени m при j на 4 получается остаток 2, то
Если при делении показателя m при j на 4 получается остаток 3, то
14 слайд

Примеры:
Вычислите:
Если показатель степени m при j делится на 4 без остатка, то
Если при делении показателя степени m при j на 4 получается остаток 1, то
Если при делении показателя степени m при j на 4 получается остаток 2, то
Если при делении показателя m при j на 4 получается остаток 3, то
16 слайд

Решение квадратных уравнений с помощью комплексных чисел
Исследование алгебраических уравнений является одним из важнейших вопросов математики. Например, действительных корней не имеет квадратное уравнение с отрицательным дискриминантом. Простейшим таким уравнением является уравнение
x²+1=0
Для того чтобы это уравнение имело решение, необходимо расширить множество действительных чисел путем присоединения к нему корня уравнения
x²=-1
Обозначим этот корень через i,тогда по определению i²+1=0
i²=-, а следовательно i=√-1
17 слайд

На множестве С можно находить корни любых квадратных уравнений!
Как извлечь квадратный корень из отрицательных действительных чисел?
Решение квадратных уравнений с действительными коэффициентами и D<0.
Решение квадратных уравнений с комплексными коэффициентами.
18 слайд

Как извлечь квадратный корень из отрицательных действительных чисел?

Определение: квадратным корнем(корнем второй степени) из комплексного числа z называют комплексное число, квадрат которого равен z.
Формула извлечения квадратного корня из отрицательных действительных чисел

Пример: z=√-4
Решение:
Проверка: (-2i)²=(-2)²*i²=4*(-1)=-4
(2i)²=2²*i²=4*(-1)=-4
19 слайд

Решите:
√-1=
√-3=
√-9=
√-5=
20 слайд

Решение квадратных уравнений с действительными коэффициентами и D<0.
21 слайд

Решите:
x2 – x + 10 = 0

x2 – 4x + 13 = 0

x2 – 2x + 15 = 0
22 слайд

Как извлечь квадратный корень из любого комплексного числа?
Теорема: Если b≠0, то
Что равносильно системе условий:
24 слайд

Решение квадратных уравнений с комплексными коэффициентами.
Так как множества и совпадают между собой , то для решения квадратных уравнений с комплексными коэффициентами можно сохранить привычную формулу корней квадратного уравнения:

Пример :
i
25 слайд

Решите:
х2 + (1 – 2i) х – 2i = 0
26 слайд

Итоги урока
Мне больше всего удалось…
Для меня было открытием то, что …
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
27 слайд

Домашнее задание
Решить уравнения:
z^2-2z+5=0
z^2+3z+6=0
z^2-4z+25=0
3z^2-3z+3=0
28 слайд

Спасибо за внимание!!!!

Краткое описание документа:

Урок на тему: «Решение квадратных уравнений с помощью комплексных чисел».

Цели:

Образовательные: расширить понятие числа, ввести понятие комплексного числа, действия над комплексными числами, заданными в алгебраической форме.

Воспитательные: прививать интерес к математике, ознакомить учащихся с историей развития комплексных чисел, воспитывать

Развивающие: развивать творческое мышление, пространственное мышление, научить применять теоретические знания при решении практических задач, формировать активность и самостоятельность при работе в группах.

Используемые технологии и методы: 1) проблемный диалог; 2) информационно- коммуникационные технологии.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 265 026 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

11.08.2018
251
0

11.08.2018
398
0

11.08.2018
884
3

10.08.2018
1219
37

10.08.2018
761
29

Вам будут интересны эти курсы:

Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Источник