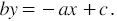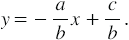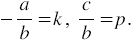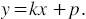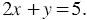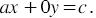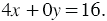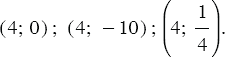- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Системы линейных уравнений с двумя переменными
- Линейное уравнение с двумя переменными и его график
Определение
Случай 1:
Допустим нам задано линейное уравнение 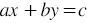
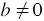
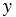
Так как по условию 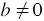
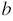
Обозначим коэффициенты следующим образом:
Тогда запишем
Но эта формула задает линейную функцию, графиком которой является невертикальная прямая, поэтому графиком уравнения 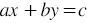
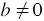
Пример 1. Построим график уравнения
Решение: Данное уравнение является линейным уравнением с двумя переменными, у которого 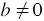
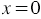

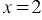
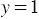
Случай 2:
Пусть задано линейное уравнение 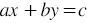
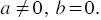
Пример 2. Построим график уравнения
Решение: Найдем несколько решений данного уравнения:
Очевидно, что любая пара чисел, которая имеет вид 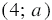
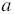
То есть графиком уравнения вида 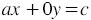
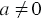
Случай 3:
Пусть задано линейное уравнение 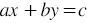
Если с=0, то уравнение принимает вид:
0x+0y=0.
В этом случае любая пара чисел будет являться решением данного уравнения, а значит, графиком уравнения будет являться вся координатная плоскость.
Советуем посмотреть:
Уравнения с двумя переменными
Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными
Решение систем линейных уравнений методом подстановки
Решение систем линейных уравнений методом сложения
Решение задач с помощью систем линейных уравнений
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 957,
Мерзляк, Полонский, Якир, Учебник
Номер 997,
Мерзляк, Полонский, Якир, Учебник
Номер 1012,
Мерзляк, Полонский, Якир, Учебник
Номер 1020,
Мерзляк, Полонский, Якир, Учебник
Номер 1053,
Мерзляк, Полонский, Якир, Учебник
Номер 1087,
Мерзляк, Полонский, Якир, Учебник
Номер 1094,
Мерзляк, Полонский, Якир, Учебник
Номер 1110,
Мерзляк, Полонский, Якир, Учебник
Номер 1123,
Мерзляк, Полонский, Якир, Учебник
Номер 1129,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 91,
Мерзляк, Полонский, Якир, Учебник
Номер 134,
Мерзляк, Полонский, Якир, Учебник
Номер 173,
Мерзляк, Полонский, Якир, Учебник
Номер 205,
Мерзляк, Полонский, Якир, Учебник
Номер 302,
Мерзляк, Полонский, Якир, Учебник
Номер 310,
Мерзляк, Полонский, Якир, Учебник
Номер 371,
Мерзляк, Полонский, Якир, Учебник
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
Линейная функция — определение и вычисление с примерами решения
Содержание:
Рассмотрим уравнение с двумя неизвестными
где 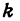
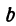
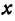
удовлетворяют следующие пары:
Для того чтобы найти пару чисел, удовлетворяющих уравнению , нужно придать произвольное числовое значение и подставить в уравнение , тогда получит определенное числовое значение. Например, если . Очевидно, что пара чисел и удовлетворяет уравнению. Так же и в случае уравнения (1) можно придать произвольное числовое значение и получить для соответствующее числовое значение.
Так как в данном уравнении может принимать любое числовое значение, то его называют переменной величиной. Поскольку выбор этого числового значения ничем не ограничен, то называют независимой переменной величиной или аргументом.
Для получаются также различные значения, но уже в зависимости от выбранного значения ; поэтому называют зависимым переменным или функцией.
Функцию , определяемую уравнением (1), называют линейной функцией.
Пример:
Вычислить значения линейной функции, определяемой уравнением , при следующих значениях независимого переменного: .
Решение:
Если ; если ; если .
Покажем, что если принять пару чисел и , удовлетворяющих уравнению (1), за абсциссу и ординату точки, то геометрическим местом этих точек будет прямая линия (рис. 14).
В самом деле, рассмотрим точку и точки и , координаты которых удовлетворяют уравнению (1), т. е. . Обозначим проекции точек , и на ось через , и , тогда , Проведем из точки прямую, параллельную оси . При этом получим
Предположим, что точки и , не лежат на родной прямой. Соединяя точку с точками , и , получим два прямоугольных треугольника и , из которых имеем:
Но так как и удовлетворяют уравнению (1), то
Выражения и являются отношениями противоположных катетов к прилежащим для углов и . Следовательно, и — а поэтому и так как углы острые. Это значит, что точки и лежат на одной прямой. Но мы предположили, что эти точки не лежат на одной прямой. Таким образом, мы пришли к противоречию, а это и доказывает, что точки и лежат на одной прямой. Обозначим угол через . Этот угол образован прямой с положительным направлением оси .
Так как и — произвольные точки, координаты которых удовлетворяют уравнению (1), то можно сделать следующее заключение: любая точка, координаты которой удовлетворяют уравнению (1), лежит на прямой, отсекающей на оси отрезок и образующей с положительным направлением оси угол такой, что .
Число называется начальной ординатой, число — угловым коэффициентом прямой.
Предыдущие рассуждения позволяют сделать вывод: линейная функция определяет на плоскости прямую, у которой начальная ордината равна , а угловой коэффициент .
Например, линейная функция определяет на координатной плоскости прямую, отсекающую на оси отрезок —4 и наклоненную к оси под углом в 60°, так как .
Если имеем определенную прямую, отсекающую на оси отрезок и наклоненную к оси под углом тангенс которого равен , то, взяв произвольную абсциссу, найдем на указанной прямой только одну точку, имеющую эту абсциссу, т. е. по заданному найдется только одна точка, а следовательно, и одно значение .
Очевидно, имеет место и такое предложение: Всякой прямой, отсекающей на оси отрезок и наклоненной к оси под углом, тангенс которого равен числу , соответствует линейная функция .
Координаты любой, точки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение называют уравнением прямой.
Таким образом, всякая линейная функция является уравнением некоторой прямой.
Отметим частные случаи.
1. Пусть , т. е. линейная функция определяется уравнением
Прямая, определяемая этим уравнением, проходит через начало координат. Здесь пропорционален , т. е. если увеличить (уменьшить) в несколько раз, то и увеличится (уменьшится) во столько же раз.
2. Пусть , т. е. , откуда . Линейная функция определяется уравнением
Этому уравнению соответствует прямая, параллельная оси и отстоящая от нее на расстояние .
На основании всего сказанного в этом параграфе легко решаются следующие задачи.
Пример:
Даны точки и . Нужно узнать, лежат ли эти точки на прямой, уравнение которой имеет вид
Решение:
Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки в уравнение, получим . Это тождество, следовательно, точка лежит на прямой. Подставляя координаты точки , получаем . Отсюда видно, что точка не лежит на прямой.
Пример:
Построить прямую, уравнение которой
Решение:
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим произвольное значение, например , и найдем из уравнения значение . Значит, точка лежит на прямой. Это первая точка. Теперь дадим какое-нибудь другое значение, например , и вычислим у из уравнения . Получим. Точка лежит на прямой. Это вторая точка. Строим точки и (рис. 15) и проводим через них прямую, это и есть искомая прямая.
Основное свойство линейной функции
Рассмотрим линейную функцию . Найдем значение этой функции при :
Здесь первое и второе значения различны, они отличаются друг от друга на величину Величину разности , на которую изменяется при переходе от к , назовем приращением независимого переменного . Эту величину часто будем обозначать через , так что . Найдем, насколько изменилось значение при изменении , на . Для этого вычтем из значение :
т. е. приращение линейной функции пропорционально приращению независимого переменного.
Это и есть основное свойство линейной функции.
Заметим, что , может быть больше, а может быть и меньше, чем . Поэтому может быть как положительным, так и отрицательным числом, иначе говоря, приращение независимого переменного может быть любого знака. То же самое относится и к приращению функции, т. е. к величине.
Пример:
Найдем приращение функции , если приращение независимого переменного .
Решение:
По основному свойству . Приращение этой же функции , если , будет равно . В этом случае приращения независимого переменного и функции отрицательны, т. е. в этом случае и независимое переменное и функция не увеличиваются, а уменьшаются.
Пример:
Найдем приращение функции при изменении на . Решение:
Задачи на прямую
Пример:
Найти угол между двумя прямыми, заданными уравнениями
Решение:
При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).
Угол является внешним по отношению к треугольнику , поэтому он равен сумме двух внутренних углов треугольника, с ним не смежных, т. е. откуда Но углы и , непосредственно неизвестны, а известны их тангенсы. Поэтому напишем
Пример:
Найти угол между прямыми, заданными уравнениями . Здесь ;
Решение:
Применяя формулу (1), получим:
Если же будем считать, что то
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.
Если заданы две параллельные прямые, то углы и , равны, как соответственные, следовательно, тангенсы их тоже равны
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.
Если прямые перпендикулярны, то угол между ними равен 90°, т. е. . Но тангенс прямого угла не существует, поэтому формула (1) не должна давать ответа, а это может быть только в том случае, когда знаменатель равен нулю (на нуль делить нельзя):
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример:
Найдем угол между прямыми, заданными уравнениями Здесь угловые коэффициенты (первый равен 3, а второй ) обратны по величине и противоположны по знаку.
Решение:
Следовательно, рассматриваемые прямые перпендикулярны.
Пример:
Даны две точки: , где , (т. е. эти точки не лежат на одной прямой, параллельной оси ). Написать уравнение прямой, проходящей через точки и .
Решение:
Искомая прямая не параллельна оси , поэтому ее уравнение можно написать в виде . Значит, для решения задачи надо определить числа и . Так как прямая проходит через точки , и , то координаты этих точек должны удовлетворять уравнению , т. е.
В уравнениях и все числа, кроме и , известны, поэтому эти уравнения можно рассматривать как систему уравнений относительно и .
Решая систему, находим:
Подставляя найденные выражения в уравнение , получим
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси . Полученному уравнению можно придать форму, удобную для запоминания, а именно:
Пример:
Написать уравнение прямой, проходящей через данную точку и образующей с осью угол .
Решение:
Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла . Обозначим . Значит, уравнение прямой можно написать в виде , где пока число неизвестно.
Так как прямая должна проходить через точку , то координаты точки удовлетворяют этому уравнению, т. е.
Находим отсюда неизвестное , получим . Подставляя найденное в уравнение , будем иметь
Это и есть уравнение прямой, проходящей через точку в заданном направлении.
Если в уравнении (4) менять направление, не меняя точку , то получим уравнение всех прямых, проходящих через заданную точку. Уравнение , в котором переменное, а и не меняются, называется уравнением пучка прямых, проходящих через точку .
Пример:
Напишем уравнение прямой, проходящей через точку и образующей с осью угол 45°.
Решение:
Так как , то угловой коэффициент равен 1; . Уравнение прямой запишется в виде
Общее уравнение прямой. Неявная линейная функция
Рассмотрим уравнение первой степени с двумя неизвестными
Решим его относительно :
т. е. мы получили линейную функцию, где ,
Уравнения (1) и (2) равносильны, поэтому пара чисел и , удовлетворяющих уравнению (2), будет удовлетворять и уравнению (1). Так как уравнению (2) соответствует некоторая прямая, то эта же прямая будет соответствовать и уравнению (1).
Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой. Рассмотрим особо случай, когда , так как на нуль делить нельзя. Уравнение (1) примет вид или , откуда . Поэтому, каков бы ни был всегда равен . Это имеет место для прямой, параллельной оси ; в самом деле, на ней можно найти точку с любой ординатой, но все точки этой прямой имеют одну и ту же абсциссу. Таким образом, любому уравнению первой степени соответствует некоторая прямая. Придавая в уравнении (1) коэффициентам А, В и С различные значения, можно получить любое уравнение первой степени. Поэтому уравнение (1) называют общим уравнением прямой.
Из уравнения (1) (если ) можно определить , т. е. получить линейную функцию; поэтому говорят, что уравнение (1) определяет неявно линейную функцию или что уравнение (1) есть неявная линейная функция.
Система двух уравнений первой степени
Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке). Рассмотрим систему двух уравнений
Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения и , которые удовлетворяют и первому и второму уравнениям. Но так как и определяют точку, то следовательно, решить систему—это значит найти точку, лежащую и на первой и на второй прямых, т. е. найти точку пересечения прямых.
Пример:
Найдем точку пересечения двух прямых:
Решение:
Решая эту систему, получим: т. е. прямые пересекаются в точке (1, 2) (рис. 17).
Пример:
Найдем точку пересечения двух прямых:
Решение:
Решая эту систему, получим: Последнее равенство нелепо, значит, прямые не пересекаются, т. е. они параллельны.
Пример:
Найдем точку пересечения данных прямых
Решение:
Решая эту систему, получим:
Полученное равенство всегда справедливо, т. е. справедливо при любом значении . Это значит, что две прямые пересекаются в каждой своей точке, что может быть только тогда, когда они сливаются.
Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.
Примеры применения линейной функции
Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.
Пример:
Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения , где — начальное расстояние, —скорость, — время; это, как мы уже знаем, есть линейная функция.
Пример:
Закон Ома записывается в виде , где — напряжение, — сопротивление и —ток. Если не изменяется, то является линейной функцией тока .
Пример:
Если стоимость провоза единицы товара по железной дороге равна руб. за километр, то стоимость провоза единиц товара на км равна
Если же стоимость товара на месте равна руб., то после перевозки за него надо заплатить
Здесь — линейная функция .
Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.
Пример:
Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А к В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В —200 т. Перевозка одной тонны нефти на один километр обходится в руб.
Решение:
Обозначим расстояние от А до предполагаемого пункта С через . Тогда расстояние от города В до С равно 300 — . Стоимость перевозки одной тонны нефти из С в А равна руб., а перевозки 400 т—400 руб. Аналогично перевозка нефти из С в В будет стоить руб. Стоимость всех перевозок, которую обозначим через , будет выражаться так:
Это линейная функция. Если примем за абсциссу, а за ординату точки, то полученная линейная функция опредеяет уравнение некоторой прямой. Угловой коэффициент ее равен , т. е. положителен, следовательно, эта прямая образует с осью острый угол и поэтому с увеличением независимого переменного поднимается вверх. По смыслу задачи величина заключена между 0 и 300, т. е. . При величина у принимает значение 60000а, а при — значение 120000а. Ясно, что 60 000а есть наименьшее из возможных значений, 120 000а— наибольшее.
Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе А; если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к А, тем выгодней.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Квадратичная функция
- Тригонометрические функции
- Производные тригонометрических функции
- Производная сложной функции
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Координаты на плоскости
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://skysmart.ru/articles/mathematic/grafik-linejnoj-funkcii
http://www.evkova.org/linejnaya-funktsiya
ГДЗ и решебники
вип уровня
- ГДЗ
- 7 класс
- Алгебра
- Мерзляк
- Упражнение 994
Условие
Составьте линейное уравнение с двумя переменными, график которого пересекает оси координат в точках:
1) A(−4;0) и B(0;2);
2) C(0;−3) и D(5;0).
Решение 1
Решение 2
Популярные решебники
§ 1. Линейные уравнения с двумя переменными
В первом задании мы рассмотрели линейные уравнения с одной переменной. Например, уравнения `2x+5=0`, `3x+(8x-1)+9=0` являются линейными уравнениями с переменной `x`. Уравнение, содержащее переменные `x` и `y`, называется уравнением с двумя переменными. Например, уравнения `2x-3=5`, `x^2+xy-y^2=7` являются уравнениями с двумя переменными.
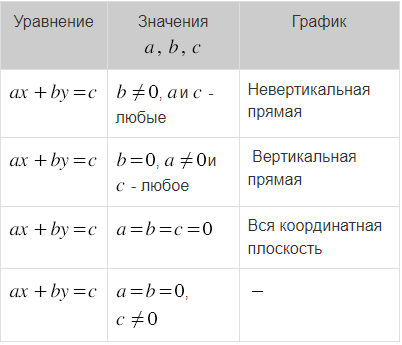
Уравнение вида `ax+by=c` называется линейным уравнением с двумя переменными, где `x` и `y` переменные, `a`, `b`, `c` — некоторые числа.
Например, уравнения `2x+y=3`, `x-y=0` являются линейными уравнениями с двумя переменными.
Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Например, `x=3`, `y=4` является решением уравнения `2x+3y=18`, будем эту пару чисел записывать так `(3;4)`. Очевидно, что пара чисел `(4;3)` не является решением уравнения, т. к. `2*4+3*3=17!=18`. При нахождении решений с двумя переменными на первом месте в паре чисел пишем значение для переменной `x`, а на втором месте – значение переменной `y`.
Если каждое решение одного уравнения является решением второго уравнения и обратно, то данные уравнения называются равносильными. Например, решения уравнений `2x+y=3` и `4x+2y=6` совпадают, следовательно, эти уравнения равносильные.
1) если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
2) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
Укажите три различных решения для уравнения `3x+y-2=0`.
Если `x=0`, то `y=2`; если `y=0`, то `x=2/3`; если `x=1`, то `y=-1`.
Таким образом, пары чисел `(0;2)`, `(2/3;0)`, `(1;-1)` являются решениями данного уравнения. Заметим, что данное уравнение имеет бесконечно много решений. Для заданного значения `x` значение `y=2-3x`, т. е. любая пара чисел `(x;2-3x)`, где `x` — любое число, является решением уравнения.
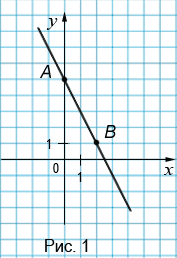
Рассмотрим координатную плоскость `Oxy` и отметим на ней все точки `(x,y)`, для которых пара чисел `x` и `y` является решениями уравнения. Например, рассмотрим уравнение `y=2`. Этому уравнению удовлетворяют все пары чисел `(x;2)`.Точки, для которых `x` — любое число, а `y=2`, лежат на прямой `y=2`. Эта прямая параллельна оси `x` и проходит через точку `(0;2)` (см. рис. 1).
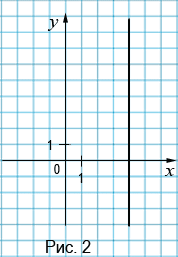
Рассмотрим уравнение `x=3`. Каждая пара чисел, являющаяся решением данного уравнения, изображается точкой с координатами `x` и `y` на координатной плоскости `Oxy`. Решениями данного уравнения являются пары чисел `(3;y)`. Точки с координатами `x=3` и `y` лежат на прямой `x=3`, эта прямая параллельна оси `Oy` и проходит через точку `(3;0)` (см. рис. 2).
Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями данного уравнения.
На рис. 1 графиком уравнения является прямая `y=2`, на рис. 2 графиком уравнения является прямая `x=3`.
Рассмотрим теперь уравнение `2x+3y-1=0`. Выразим переменную `y` через `x`, получаем `y=1/3-2/3x`, это уравнение задаёт линейную функцию, и нам известно, что её графиком является прямая. Чтобы построить эту прямую, достаточно рассмотреть две точки, координаты которых удовлетворяют уравнению, а затем через эти две точки провести прямую. При `x=0` `y=1/3` и при `x=1/2` `y=0`. График данного уравнения приведён на рис. 3.
Рассмотрим уравнение `(x-4)(x+y-4)=0`. Произведение двух скобок равно нулю, каждая скобка может равняться нулю. Наше уравнение распадётся на два уравнения: `x=4` и `x+y-4=0`. Графиком первого уравнения является прямая, параллельная оси `Oy` и проходящая через точку `(4;0)`. Графиком второго уравнения является график линейной функции `y=4-x`, эта прямая проходит через точки `(4;0)` и `(0;4)`. График данного уравнения приведён на рис. 4.
Постройте график уравнения `|x|+|y|=1`.
Этот пример можно решать двумя способами. Пусть `x>=0` и `y>=0`, точки с такими координатами лежат в первой четверти. Получаем уравнение `x+y=1`, так как `|x|=x` и `|y|=y`. Графиком данного уравнения является прямая, проходящая через точки `A(1;0)` и `B(0;1)`. Графику исходного уравнения принадлежат точки полученной прямой, лежащие в первой четверти, т. е. графику принадлежат точки отрезка `AB`, где `A(1;0)` и `B(0;1)`.
Пусть теперь `x<=0` и `y>=0` тогда получаем уравнение `-x+y=1`, рассматриваем точки полученной прямой, лежащие во второй четверти. Это будет отрезок `BC`, где `C(-1;0)`. При `x<=0`, `y<=0` получим отрезок `CD` где `D(0;-1)`, и при `>=0`, `y<=0` получим отрезок `DA`. Таким образом, график данного уравнения состоит из точек квадрата `ABCD` (рис. 5).
Этот пример можно решать другим способом. Пусть `y>=0`, тогда наше уравнение эквивалентно уравнению `y=1-|x|`. В первом задании мы строили график функции `y=|x|` (см. рис. 6). График функции `y=-|x|` получается зеркальным отражением относительно оси `Ox` графика функции `y=|x|` (см. рис. 7). График функции `y=1-|x|` получается из графика функции `y=-|x|` сдвигом вдоль оси `Oy` на единицу вверх (см. рис. 8). У полученного графика рассматриваем только точки, для которых `y>=0`. Получим ломаную `ABC` с рис. 5.
Далее рассматриваем `y<=0`, получим, что графиком уравнения при `y<=0` является ломаная `CDA` с рис. 5. В итоге получим квадрат `ABCD` с рис. 5.
Найдите все решения уравнения `xy=6`, для которых `x` и `y` являются натуральными числами.
Очевидно, что натуральные числа `x` и `y` являются делителями числа `6`. Поэтому `x` и `y` могут принимать значения `1;` `2;` `3;` `6`. Следовательно, искомыми решениями являются числа `(1;6)`, `(2;3)`, `(3;2)`, `(6;1)`.
Найти все решения уравнения `x^2+4x=y^2+2y+8`, для которых значения `x` и `y` являются целыми числами.
Обычно такие примеры формулируют так: найти все решения данного уравнения в целых числах.
Преобразуем данное уравнение: `x^2+4x+4-4=y^2+2y+1+7`,
`(x+2)^2=(y+1)^2+11`,
`(x+2)^2-(y+1)^2=11`,
`(x+2-y-1)*(x+2+y+1)=11`.
Если `x` и `y` целые числа, то выражения, стоящие в скобках, являются целыми числами. А это могут быть числа `+-1` и `+-11`. Решаем `4` системы уравнений:
$$ left{begin{array}{l}x+2-y-1=1,\ x+2+y+1=11;end{array}right.$$
$$ left{begin{array}{l}x+2-y-1=11,\ x+2+y+1=1;end{array}right.$$
$$ left{begin{array}{l}x+2-y-1=-1,\ x+2+y+1=-11;end{array}right.$$
$$ left{begin{array}{l}x+2-y-1=-11,\ x+2+y+1=-1.end{array}right.$$
Решая эти системы, получаем `4` решения: `(4;4)`, `(4;-6)`, `(-8;-6)`, `(-8;4)`.
Инфоурок
›
Алгебра
›Презентации›График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными
Скачать материал

Скачать материал


- Сейчас обучается 248 человек из 63 регионов


- Сейчас обучается 22 человека из 17 регионов




Описание презентации по отдельным слайдам:
-
1 слайд
График линейного
уравнения
с двумя переменными -
2 слайд
Какое уравнение называется линейным уравнением с двумя переменными?
-
3 слайд
Устные упражнения
Назовите уравнения, которые являются линейными уравнениями с двумя переменными и для них назовите коэффициенты a, b, c
а) 3х – у = 14
б) 5у + х² = 16
в) 7ху – 5у = 12
г) 5х + 2у = 0
д) 5m²-10n+16=0
е) a+b+c=0
ж)
з) -
4 слайд
Что называется решением уравнения с двумя переменными?
-
5 слайд
Проверьте, являются ли решением уравнения
2х + 5у = 12
пары чисел?
(-1; -2), (2; 1), (4; -4), (11; -2).Найдите еще какие-нибудь решения этого уравнения.
Сколько решений имеет уравнение с двумя переменными?
Как изображается решение линейного уравнения с двумя переменными на координатной плоскости?
Как расположены эти решения на координатной плоскости? -
6 слайд
Тема урока
« График линейного уравнения с двумя переменными»
-
7 слайд
Каждая пара чисел, являющаяся решением уравнения с переменными х и у, изображается в координатной плоскости точкой, координатами которой служит пара чисел. Все эти точки образуют график уравнения.
-
8 слайд
Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения.
-
9 слайд
Выясним, что представляет собой график уравнения 3х+2у-6=0
Подберите пять решений этого уравнения и результаты запишите в таблицу -
10 слайд
Отметьте точки с полученными координатами (х;у) на координатной плоскости
-
11 слайд
Выясните, как расположены эти точки на координатной плоскости?
Проведите через эти точки прямую и обозначьте её буквой m.Как можно назвать эту прямую?
Прямая m – это __________ уравнения.Закончите предложение:
Любая точка, координаты которой удовлетворяют уравнению ax + by + c = 0, принадлежит
___________________________________________ -
12 слайд
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
-
13 слайд
Алгоритм построения графика линейного уравнения с двумя переменными
Подобрать две точки, координаты которых являются решениями данного уравнения;
Составить таблицу значений для этих точек;Построить эти точки на координатной плоскости;
Провести прямую через эти точки. -
14 слайд
Постройте график линейного уравнения
2х + 3у- 12=0 -
15 слайд
Постройте график линейного уравнения
3х — 4у- 12=0 -
16 слайд
Самостоятельная работа
1 вариант
1. Какие из пар чисел (1;1), (6;5), (9;11) являются решением уравнения
5х – 4у — 1 =0?
2. Постройте график уравнения 2х + у = 4.
2 вариант
1. Какие из пар чисел (1;1), (1;2), (3;7) являются решением уравнения
7х – 3у — 1 =0?
2. Постройте график уравнения 4х + у – 4 = 0. -
17 слайд
Самостоятельная работа
1 вариант№1
(1;1), (9;11)2 вариант
№1
1. (1;2) -
-
-
-
21 слайд
Оцените свои знания, полученные на уроке
У меня все отлично
У меня все хорошо
Возникли трудности -
22 слайд
Домашняя работа.
П.7, №7.18(в,г), 7.21, 7.31, 7.36
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 265 994 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы
Презентация по математике на тему «Тригонометрия»
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.
- Тема: § 6. Синус и косинус. Тангенс и котангенс
- 20.11.2021
- 339
- 4

Рабочая программа по алгебре для 10 класса
- Учебник: «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Муравин Г.К., Муравина О.В.
- Тема: Глава 1. Функции и графики
- 20.11.2021
- 123
- 0


- 19.11.2021
- 1597
- 29




Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Основы туризма и гостеприимства»
-
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Этика делового общения»
-
Курс профессиональной переподготовки «Организация менеджмента в туризме»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Управление сервисами информационных технологий»
-
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
-
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
-
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
-
Курс профессиональной переподготовки «Организация и управление процессом по предоставлению услуг по кредитному брокериджу»
-
Настоящий материал опубликован пользователем Левкина Татьяна Николаевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 4 года и 11 месяцев
- Подписчики: 0
- Всего просмотров: 6673
-
Всего материалов:
7