Информатика. 10 класса. Босова Л.Л. Оглавление
§ 20. Преобразование логических выражений
Способ определения истинности логического выражения путём построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т. к. за счёт существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики.
20.1. Основные законы алгебры логики.
Приведём основные законы алгебры логики.
1. Переместительные (коммутативные) законы:
А & В = В & А;
A v В = В v А.
2. Сочетательные (ассоциативные) законы:
(А&В)&С = А&(В&С);
(A v В) v С = A v (В v С).
3. Распределительные (дистрибутивные) законы:
А & (В v С) = (А & В) v (А & С);
A v (В & С) = (A v В) & (A v С).
4. Законы идемпотентности (отсутствия степеней и коэффициентов):
А & А = А;
A v А = А.
5. Закон противоречия:
А &
= 0.
6. Закон исключённого третьего:
A v
= 1.
7. Закон двойного отрицания:
= А.
8. Законы работы с константами:
A v 1 = 1; A v O = A;
А & 1 = А; А & 0 = 0.
9. Законы де Моргана:
10. Законы поглощения:
А & (A v В) = А;
A v (А & В) = А.
Справедливость законов можно доказать построением таблиц истинности.
Пример 1. Упростим логическое выражение
Последовательно применим дистрибутивный закон и закон исключённого третьего:
Пример 2. Упростим логическое выражение

Аналогичные законы выполняются для операций объединения, пересечения и дополнения множеств. Например:

Пробуйте самостоятельно доказать один из этих законов с помощью кругов Эйлера.
Пример 3. На числовой прямой даны отрезки В = [2; 12] и С = [7; 18]. Каким должен быть отрезок А, чтобы предикат
становился истинным высказыванием при любых значениях х.
Преобразуем исходное выражение, избавившись от импликации:

причём это минимально возможное множество А.
Множество В — это отрезок [2; 12].
Множество
Изобразим это графически:

Пересечением этих множеств будет служить промежуток [2; 7[. В качестве ответа мы можем взять этот промежуток, а также любой другой, его включающий.
Чему равна минимальная длина отрезка А? Укажите ещё несколько вариантов множества А.
Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение
тождественно истинно (т. е. принимает значение 1 при любом неотрицательном целом значении десятичной переменной х)? Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел.
Прежде всего, вспомним, что представляет собой поразрядная конъюнкция двух целых десятичных чисел, например 27 и 22.

Обратите внимание на то, что если в некотором бите хотя бы одного сомножителя есть 0, то 0 есть и в этом бите результата, а 1 в результате получается только тогда, когда в соответствующих битах каждого сомножителя есть 1.
Введём обозначения:

Перепишем исходное выражение в наших обозначениях:

Рассмотрим предикат М(х) = (х & 28 ? 0). В числе 28 = 111002 4-й, 3-й и 2-й биты содержат единицы, а 1-й и 0-й — нули. Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 4, 3 или 2 содержит единицу. Если и 4-й, и 3-й, и 2-й биты числа х нулевые, то высказывание х & 28 ? 0 будет ложным.
Рассмотрим предикат N(x) = (х & 45 ? 0). В числе 45 = 1011012 5-й, 3-й, 2-й и 0-й биты содержат единицы, 4-й и 1-й — нули.
Следовательно, множеством истинности этого предиката являются такие числа х, у которых хотя бы один из битов с номерами 5, 3, 2 или 0 содержит единицу. Если и 5-й, и 3-й, и 2-й, и 0-й биты числа х нулевые, то высказывание х & 45 ? 0 будет ложным.
Рассмотрим предикат К(х) = (х & 17 = 0). В числе 17 = 100012 3-й, 2-й и 1-й биты содержат нули, 4-й и 0-й — единицы. Побитовая конъюнкция 17 и х будет равна нулю, если в числе х 4-й и 0-й биты будут содержать нули. Множество истинности этого предиката — все х с нулями в 4-м и 0-м битах.
По условию задачи надо, чтобы
Запишем это выражение для рассмотренных множеств истинности:

Объединением множеств М и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством К будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т. е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.
Искомое число а должно быть таким, чтобы при любом неотрицательном целом значении переменной х: х & а ? 0, и кроме того, оно должно быть минимальным из возможных. Этим условиям удовлетворяет число 1011002. Действительно, единицы в нём стоят в тех и только в тех битах, которые нужны для выполнения условия х & а ? 0.
Итак, требуемое число 1011002 или 4410.
Приведите пример такого десятичного числа а, что для него х & а ? 0 при любом неотрицательном целом значении десятичной переменной х, но само число а не является минимально возможным.
Пример 5. Выясним, сколько решений имеет следующая система из двух уравнений:

Рассмотрим первое уравнение: (х1 ? х2) & (х2 ? х3) & (х3 ? x4) = 1.
Конъюнкция истинна тогда и только тогда, когда истинны все образующие её высказывания. Следовательно, каждая из трёх входящих в конъюнкцию импликаций должна быть равна 1.
Начнем строить дерево решений, представив на нём значения переменных х1 и х2 при которых х1 ? х2 = 1.
Продолжим строить дерево решений. Значения переменной х3 будем выбирать такими, чтобы при имеющихся х2 импликация х2 ? х3 оставалась истинной.
То же самое проделаем для переменной х4.

На дереве видно, что рассматриваемое нами уравнение имеет 5 решений — 5 разных наборов значений логических переменных x1, х2, х3, х4, при которых выполняется равенство:

Следовательно, как и первое уравнение, это уравнение имеет 5 решений. Представим их в табличной форме:

Решение исходной системы логических уравнений — это множество различных наборов значений логических переменных х1, х2, х3, х4, у1, у2, у3, у4 таких, что при подстановке каждого из них в систему оба уравнения превращаются в истинные равенства.
Начнём строить такие наборы или двоичные цепочки. Их началом может служить любой из пяти наборов — решений первого уравнения, а концом — любой из пяти наборов — решений второго уравнения. Например, на основе одного из решений первого уравнения можно построить следующие пять решений системы:

Всего мы можем построить 5 • 5 = 25 решений системы.
Вспомните, как называется теорема комбинаторики, которую мы применили для подсчёта количества решений системы.
20.2. Логические функции
Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.
Совокупность значений п аргументов удобно интерпретировать как строку нулей и единиц длины n. Существует ровно 2n различных двоичных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, общее количество различных булевых функций от n аргументов равно
Для n = 2 существует 16 различных логических функций.
Рассмотрим их подробнее.


С увеличением числа аргументов количество логических функций резко возрастает. Так, для трёх переменных существует 256 различных логических функций! Но изучать их все нет никакой необходимости. Дело в том, что путём преобразований функция любого количества переменных может быть выражена через функции только двух переменных. Более того, можно использовать не все, а лишь некоторые логические функции двух переменных. Например:
1) F2 и F11 (конъюнкция и отрицание второго аргумента);
2) F8 и F13 (дизъюнкция и отрицание первого аргумента);
3) F9 (стрелка Пирса, отрицание дизъюнкции);
4) F15 (штрих Шеффера, отрицание конъюнкции).
Два последних примера говорят о том, что при желании всю алгебру логики можно свести к одной функции! Но чаще всего логические функции записываются в виде логического выражения через отрицание, конъюнкцию и дизъюнкцию.
20.3. Составление логического выражения по таблице истинности и его упрощение
Ранее мы выяснили, что для любого логического выражения можно составить таблицу истинности. Справедливо и обратное: для всякой таблицы истинности можно составить соответствующее ей логическое выражение.
Алгоритм составления логического выражения по таблице истинности достаточно прост. Для этого надо:
1) отметить в таблице истинности наборы переменных, при которых значение логического выражения равно единице;
2) для каждого отмеченного набора записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — её отрицание;
3) все полученные конъюнкции связать операциями дизъюнкции.
Пример 6. Имеется следующая таблица истинности:

После выполнения двух первых шагов алгоритма получим:

После выполнения третьего шага получаем логическое выражение:
Попробуем упростить полученное логическое выражение. Прежде всего, вынесем за скобки В — общий сомножитель, имеющийся у всех трёх слагаемых, затем — сомножитель
, а далее используем законы алгебры логики.

САМОЕ ГЛАВНОЕ
Способ определения истинности логического выражения путём построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т. к. за счёт существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики. Аналогичные законы имеют место и в алгебре множеств.
Логическая функция может быть задана с помощью таблицы истинности или аналитически, т. е. с помощью логического выражения.
Для всякой таблицы истинности можно составить соответствующее ей логическое выражение.
Вопросы и задания
1. Какие из рассмотренных законов алгебры логики аналогичны законам алгебры чисел, а какие нет?
2. Докажите второй закон де Моргана с помощью таблиц истинности.
3. Путём преобразования докажите равносильность следующих высказываний:
4. Упростите логические формулы:
*5. Найдите X,
6. На числовой прямой даны два отрезка: Р = [10; 25] и Q = [20; 55]. Укажите наибольшую возможную длину такого отрезка А, что выражение (х ? А) ? ((х ? Р) v (x ? Q)) истинно при любом значении переменной х.
7. Элементами множеств А, Р и Q являются натуральные числа, причём Р = {2, 4, 6, 8, 10, 12} и Q = {2, 6, 12, 18, 24}.
*8. На числовой прямой даны два отрезка: М = [10; 60] и N = [40; 80]. Укажите наименьшую возможную длину такого отрезка А, что выражение истинно при любом значении переменной х.
9. Для какого наименьшего неотрицательного целого десятичного числа А формула x & 25 ? 0 ? (x & 17 = 0 ? (x & А ? 0) тождественно истинна, т. е. принимает значение 1 при любом неотрицательном целом значении десятичной переменной х? (Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел.)
*10. Определите наибольшее натуральное десятичное число А, при котором выражение ((x & 46 = 0) v (х & 18 = 0)) ? ((х & 115 ? 0) v (х & А = 0)) тождественно истинно, т. е. принимает значение 1 при любом натуральном значении десятичной переменной х. (Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел.)
11. Сколько различных решений имеет система уравнений:
12. Сколько существует различных логических функций от четырёх переменных?
13. По заданной таблице истинности составьте логические выражения для функций F1, F2.
14. По известным таблицам истинности запишите аналитическое представление импликации, эквиваленции и строгой дизъюнкции.
15. Логические функции штрих Шеффера и стрелка Пирса названы так в честь математиков, исследовавших их свойства. Подготовьте краткую биографическую справку об одном из этих учёных.
16. По заданной таблице истинности составьте логические выражения для функций F1, F2.
17. Запишите логическое выражение для логической функции F(A, В, С), равной 1 на наборах 011, 101, 110, 111. Попытайтесь упростить полученное выражение.
§ 19. Таблицы истинности
§ 20. Преобразование логических выражений
§ 21. Элементы схемотехники. Логические схемы
Информатика, 10 класс. Урок № 12.
Тема — Преобразование логических выражений
Перечень вопросов, рассматриваемых в теме: основные законы алгебры логики, преобразование логических выражений, логические функции, построение логического выражения с данной таблицей истинности и его упрощение, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ).
Глоссарий по теме: основные законы алгебры логики, логические функции, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ)
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса
— М.: БИНОМ. Лаборатория знаний, 2017 (с.197—209)
Открытые электронные ресурсы по теме:
http://lbz.ru/metodist/authors/informatika/3/eor10.php
http://kpolyakov.spb.ru/school/ege.htm
Теоретический материал для самостоятельного изучения.
Способ определения истинности логического выражения путем построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т.к. за счет существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики.
Основные законы алгебры логики
Справедливость законов можно доказать построением таблиц истинности.
Пример 1. Упростим логическое выражение
Последовательно применим дистрибутивный закон и закон исключенного третьего:
В общем случае можно предложить следующую последовательность действий:
- Заменить операции строгая дизъюнкция, импликация, эквиваленция на их выражения через операции конъюнкция, дизъюнкция, инверсия;
- Раскрыть отрицания сложных выражений по законам де Моргана.
- Используя законы алгебры логики, упростить выражение.
Пример 2. Упростим логическое выражение 
Здесь последовательно использованы замена операции импликация, закон де Моргана, распределительный закон, закон противоречия и операция с константой, закон идемпотентности и поглощения.
Аналогичные законы выполняются для операции объединения, пересечения и дополнения множеств. Например:
Пример 3. На числовой прямой даны отрезки B = [2;12] и C = [7;18]. Каким должен быть отрезок A, чтобы предикат 
Преобразуем исходное выражение, избавившись от импликации:
A, B, C — множества. Для них можно записать 
Будем считать, что
Тогда 
Так как множество B — это отрезок [2;12], а множество 



Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение

Введем обозначения:
Перепишем исходное выражение в наших обозначениях и преобразуем его:

Рассмотрим предикат 

Рассмотрим предикат 

Рассмотрим предикат 
По условию задачи надо, чтобы 
Запишем это выражение для рассмотренных множеств истинности:
Так как 

Объединением множеств M и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством K будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т.е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.
Искомое число a должно быть таким, чтобы при любом неотрицательном целом значении переменной х: 
Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.
Совокупность значений n аргументов удобно интерпретировать как строку нулей и единиц длины n. Существует ровно различных двоичных строк длины n. Так как на каждой такой строке некая функция может принимать значение 0 или 1, общее количество различных булевых функций от n аргументов равно
.
Для n=2 существует 16 различных логических функций. Рассмотрим их подробнее.
|
A |
B |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14 |
F15 |
F16 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
F1(A,B) = 0 — константа «ложь»;
F2(A,B) = A&B — конъюнкция;
F3(A,B) = 
F4(A,B) = A — функция, равная первому аргументу;
F5(A,B) = 
F6(A,B) = B — функция, равная второму аргументу;
F7(A,B) = 
F8(A,B) = A˅B — дизъюнкция;
F9(A,B) = 
F10(A,B) = 
F11(A,B) = 
F12(A,B) = 
F13(A,B) = 
F14(A,B) = 
F15(A,B) = 
F16(A,B) = 1 — константа «истина».
С увеличением числа аргументов количество логических функций резко возрастает. Отметим, что путем преобразований функция любого количества переменных может быть выражена через функции только двух переменных. Более того, можно использовать не все, а лишь некоторые логические функции двух переменных. Например:
- F2 и F11 (конъюнкция и отрицание второго аргумента);
- F8 и F13 (дизъюнкция и отрицание первого аргумента);
- F9 (стрелка Пирса, отрицание дизъюнкции);
- F15 (штрих Шеффера, отрицание конъюнкции).
Последние два примера говорят о том, что при желании всю алгебру логики можно свести к одной функции.
Любую логическую формулу путем тождественных преобразований можно привести к формуле, содержащей только операции отрицания, конъюнкции и дизъюнкции:
Такой способ представления логической формулы называется нормальной формой.
При решении задач часто требуется по таблице истинности логической формулы записать ее аналитическое выражение. Для этого используются понятия совершенной дизъюнктивной нормальной формы (СДНФ) и совершенной конъюнктивной нормальной формы (СКНФ).
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, в которой каждая переменная встречается не более одного раза (либо сама, либо ее отрицание). Например, запись 
Аналогично, выражение 
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций. Например, выражение 
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций. Например, выражение 
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные (либо сами, либо их отрицания). Например, выражение 

Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные (либо сами, либо их отрицания). Например, выражение 
Для всякой таблицы истинности можно составить соответствующее ей логическое выражение. Для этого необходимо:
- Отметить в таблице истинности наборы переменных, при которых значение логического выражения равно единице;
- Для каждого отмеченного набора записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — её отрицание;
- Все полученные конъюнкции связать операциями дизъюнкции.
Пример 5. Имеется следующая таблица истинности:
После выполнения первых двух шагов алгоритма получим:
После выполнения третьего шага получаем логическое выражение:
Попробуем упростить полученное выражение. Прежде всего, вынесем за скобки 
Алгебра логики
Алгебра логики
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Основоположником алгебры логики является английский математик и логик Дж. Буль (1815–1864), положивший в основу своего логического учения аналогию между алгеброй и логикой. Любое высказывание он записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и др.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Например, «3 умножить на 3 равно 9», «Архангельск севернее Вологды» — истинные высказывания, а «Пять меньше трех», «Марс — звезда» — ложные.
Очевидно, что не всякое предложение может быть логическим высказыванием, т. к. не всегда есть смысл говорить о его ложности или истинности. Например, высказывание «Информатика — интересный предмет» неопределенно и требует дополнительных сведений, а высказывание «Для ученика 10-А класса Иванова А. А. информатика — интересный предмет» в зависимости от интересов Иванова А. А. может принимать значение «истина» или «ложь».
Кроме двузначной алгебры высказываний, в которой принимаются только два значения — «истинно» и «ложно», существует многозначная алгебра высказываний. В такой алгебре, кроме значений «истинно» и «ложно», употребляются такие истинностные значения, как «вероятно», «возможно», «невозможно» и т. д.
В алгебре логики различаются простые (элементарные) высказывания, обозначаемые латинскими буквами (A, B, C, D, …), и сложные (составные), составленные из нескольких простых с помощью логических связок, например таких, как «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний.
Обозначим как А высказывание «Алгебра логики успешно применяется в теории электрических схем», а через В — «Алгебра логики применяется при синтезе релейно-контактных схем».
Тогда составное высказывание «Алгебра логики успешно применяется в теории электрических цепей и при синтезе релейно-контактных схем» можно кратко записать как А и В; здесь «и» — логическая связка. Очевидно, что поскольку элементарные высказывания А и В истинны, то истинно и составное высказывание А и В.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
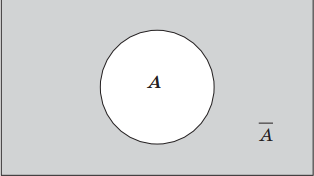
1. Логическое отрицание, инверсия (лат. inversion — переворачивание) — логическая операция, в результате которой из данного высказывания (например, А) получается новое высказывание (не А), которое называется отрицанием исходного высказывания, обозначается символически чертой сверху ($A↖{-}$) или такими условными обозначениями, как ¬, ‘not’, и читается: «не А», «А ложно», «неверно, что А», «отрицание А». Например, «Марс — планета Солнечной системы» (высказывание А); «Марс — не планета Солнечной системы» ($A↖{-}$); высказывание «10 — простое число» (высказывание В) ложно; высказывание «10 — не простое число» (высказывание B ) истинно.
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
или
Высказывание $A↖{-}$ ложно, когда А истинно, и истинно, когда А ложно.
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A↖{-}$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.
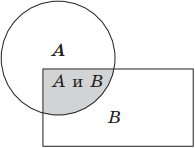
2. Конъюнкция (лат. conjunctio — соединение) — логическое умножение, операция, требующая как минимум двух логических величин (операндов) и соединяющая два или более высказываний при помощи связки «и» (например, «А и В»), которая символически обозначается с помощью знака ∧ (А ∧ В) и читается: «А и В». Для обозначения конъюнкции применяются также следующие знаки: А ∙ В; А & В, А and В, а иногда между высказываниями не ставится никакого знака: АВ. Пример логического умножения: «Этот треугольник равнобедренный и прямоугольный». Данное высказывание может быть истинным только в том случае, если выполняются оба условия, в противном случае высказывание ложно.
Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.
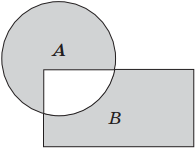
3. Дизъюнкция (лат. disjunction — разделение) — логическое сложение, операция, соединяющая два или более высказываний при помощи связки «или» (например, «А или В»), которая символически обозначается с помощью знака ∨ (А ∨ В) и читается: «А или В». Для обозначения дизъюнкции применяются также следующие знаки: А + В; А or В; А | B. Пример логического сложения: «Число x делится на 3 или на 5». Это высказывание будет истинным, если выполняются оба условия или хотя бы одно из условий.
Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.
4. Дизъюнкция строго-разделительная, сложение по модулю два — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле, которая символически обозначается с помощью знаков ∨ ∨ или ⊕ (А ∨ ∨ В, А ⊕ В) и читается: «либо А, либо В». Пример сложения по модулю два — высказывание «Этот треугольник тупоугольный или остроугольный». Высказывание истинно, если выполняется какое-то одно из условий.
Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
или
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
5. Импликация (лат. implisito — тесно связываю) — логическая операция, соединяющая два высказывания при помощи связки «если…, то» в сложное высказывание, которое символически обозначается с помощью знака → (А → В) и читается: «если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяется также знак ⊃ (A ⊃ B). Пример импликации: «Если полученный четырехугольник квадрат, то около него можно описать окружность». Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием. Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь. Например, «Если 3 * 3 = 9 (А), то Солнце — планета (В)», результат импликации А → В — ложь.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
6. Эквивалентность, двойная импликация, равнозначность (лат. aequalis — равный и valentis — имеющий силу) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В, которое читается: «А эквивалентно B». Для обозначения эквивалентности применяются также следующие знаки: ⇔, ∼. Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Примером эквивалентности является высказывание: «Треугольник будет прямоугольным тогда и только тогда, когда один из углов равен 90 градусам».
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖{-} ∧B) ∧ (A ∧ B↖{-})$ |
| Импликация | А → В | $A↖{-} ∨ B$ |
| Эквивалентность | А ∼ В | $(A↖{-} ∧ B↖{-}) ∨ (A ∧ B)$ |
Приоритет выполнения логических операций следующий: отрицание («не») имеет самый высокий приоритет, затем выполняется конъюнкция («и»), после конъюнкции — дизъюнкция («или»).
С помощью логических переменных и логических операций любое логическое высказывание можно формализовать, т. е. заменить логической формулой. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определять истинность или ложность составного высказывания. Например, высказывание «Если пять больше двух (А), то вторник всегда наступает после понедельника (В)» — импликация А → В, и результат операции в данном случае — «истина». В логических операциях смысл высказываний не учитывается, рассматривается только их истинность или ложность.
Рассмотрим, например, построение составного высказывания из высказываний А и В, которое было бы ложно тогда и только тогда, когда оба высказывания истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А высказывание может быть, например, таким: «Этот мяч полностью красный или полностью синий». Следовательно, если утверждение А «Этот мяч полностью красный» — истина, и утверждение В «Этот мяч полностью синий» — истина, то составное утверждение — ложь, т. к. одновременно и красным, и синим мяч быть не может.
Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ∨ (X < 3)) → (X < 4) :
1) X = 1; 2) X = 12; 3) X = 3.
Решение. Последовательность выполнения операций следующая: сначала выполняются операции сравнения в скобках, затем дизъюнкция, и последней выполняется операция импликации. Операция дизъюнкции ∨ ложна тогда и только тогда, когда оба операнда ложны. Таблица истинности для импликации имеет вид
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Отсюда получаем:
1) для X = 1:
((1 > 3) ∨ (1 < 3)) → (1 < 4) = ложь ∨ истина → истина = истина → истина = истина;
2) для X = 12:
((12 > 3) ∨ (12 < 3) → (12 < 4) = истина ∨ ложь → ложь = истина → ложь = ложь;
3) для X = 3:
((3 > 3) ∨ (3 < 3)) → (3<4) = ложь ∨ ложь → истина = ложь → истина = истина.
Пример 2. Указать множество целых значений X, для которых истинно выражение ¬((X > 2) → (X > 5)) .
Решение. Операция отрицания применена ко всему выражению ((X > 2) → (X > 5)) , следовательно, когда выражение ¬((X > 2) → (X > 5)) истинно, выражение ((X > 2) →(X > 5)) ложно. Поэтому необходимо определить, для каких значений X выражение ((X > 2) → (X > 5)) ложно. Операция импликации принимает значение «ложь» только в одном случае: когда из истины следует ложь. А это выполняется только для X = 3; X = 4; X = 5.
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Под логическим выражением следует понимать такую запись, которая может принимать логическое значение «истина» или «ложь». При таком определении среди логических выражений необходимо различать:
- выражения, которые используют операции сравнения («больше», «меньше», «равно», «не равно» и т. п.) и принимают логические значения (например, выражение а > b , где а = 5 и b = 7, равно значению «ложь»);
- непосредственные логические выражения, связанные с логическими величинами и логическими операциями (например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина).
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 ≤ a ∨ A ∨ sin(π/a — π/b) < 1 ∧ ¬B ∧ ¬(b^a + a^b > a + b ∨ A ∧ B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) ba + ab > a + b, после подстановки получим: 32 + 23 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (ba + ab > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
4) sin(π/a — π/b) < 1 = sin(π/2 — π/3) < 1 = истина.
После этих вычислений окончательно получим: истина ∨ А ∧ истина ∧ ¬В ∧ ¬истина.
Теперь должны быть выполнены операции отрицания, затем логического умножения и сложения:
5) ¬В = ¬ложь = истина; ¬истина = ложь;
6) A ∧ истина ∧ истина ∧ ложь = истина ∧ истина ∧ истина ∧ ложь = ложь;
7) истина ∨ ложь = истина.
Таким образом, результат логического выражения при заданных значениях— «истина».
Примечание. Учитывая, что исходное выражение есть, в конечном итоге, сумма двух слагаемых, и значение одного из них 1 ≤ a = 1 ≤ 2 = истина, без дальнейших вычислений можно сказать, что результат для всего выражения тоже «истина».
Тождественные преобразования логических выражений
В алгебре логики выполняются основные законы, позволяющие производить тождественные преобразования логических выражений.
| Закон | Для ∨ | Для ∧ |
| Переместительный | A ∨ B = B ∨ A | A ∧ B = B ∧ A |
| Сочетательный | A ∨ (B ∨ C) = (B ∨ A) ∨ C | A ∧ (B ∧ C) = (A ∧ B) ∧ C |
| Распределительный | A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) | A ∨ B ∧ C = (A ∨ B) ∧ (A ∨ C) |
| Правила де Моргана | ${A ∨ B}↖{-}$ = $A↖{-} ∧ B↖{-}$ | ${A ∧ B}↖{-}$ = $A↖{-} ∨ B↖{-}$ |
| Идемпотенции | A ∨ A = A | A ∧ A = A |
| Поглощения | A ∨ A ∧ B = A | A ∧ (A ∨ B) = A |
| Склеивания | (A ∧ B) ∨ (A↖{-} ∧ B) = B | (A ∨ B) ∧ (A↖{-} ∨ B) = B |
| Операция переменной с ее инверсией | $A ∨ A↖{-}$ = 1 | $A ∧ A↖{-}$ = 0 |
| Операция с константами | A ∨ 0 = A A ∨ 1 = 1 |
A ∧ 1 = A A ∧ 0 = 0 |
| Двойного отрицания | $A↖{=}$ = A |
Доказательства этих утверждений производят на основании построения таблиц истинности для соответствующих записей.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определенному виду путем использования основных законов алгебры логики. Под упрощением формулы, не содержащей операций импликации и эквивалентности, понимают равносильное преобразование, приводящее к формуле, которая содержит либо меньшее по сравнению с исходной число операций, либо меньшее число переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т. п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Рассмотрим на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1) X1 ∧ X2 ∨ X1 ∧ X2 ∪ ¬X1 ∧ X2 = X1 ∧ X2 ∨ ¬X1 ∧ X2 = (X1 ∨ ¬X1) ∧ X2 = 1 ∧ X2 = X2 .
Для преобразования здесь можно применить закон идемпотенции, распределительный закон; операцию переменной с инверсией и операцию с константой.
2) X1 ∨ X1 ∧ X2 = X1 ∨ (1 ∨ 1 ∧ X2) = X1 ∨ (1 ∨ X2) = X1 .
Здесь для упрощения применяется закон поглощения.
3) ¬(X1 ∧ X2) ∨ X2 = (¬X1 ∨ ¬X2) ∨ X2 = ¬X1 ∨ ¬X2 ∨ X2 = ¬X1 ∨ 1 = 1 .
При преобразовании применяются правило де Моргана, операция переменной с ее инверсией, операция с константой
Примеры решения задач
Пример 1. Найти логическое выражение, равносильное выражению A ∧ ¬(¬B ∨ C) .
Решение. Применяем правило де Моргана для В и С: ¬(¬B ∨ C) = B ∧ ¬C .
Получаем выражение, равносильное исходному: A ∧ ¬(¬B ∨ C) = A ∧ B ∧ ¬C .
Ответ: A ∧ B ∧ ¬C.
Пример 2. Указать значение логических переменных А, В, С, для которых значение логического выражения (A ∨ B) → (B ∨ ¬C ∨ B) ложно.
Решение. Операция импликации ложна только в случае, когд а из истинной посылки следует ложь. Следовательно, для заданного выражения посылка A ∨ B должна принимать значение «истина», а следствие, т. е. выражение B ∨ ¬C ∨ B , — «ложь».
1) A ∨ B — результат дизъюнкции — «истина», если хотя бы один из операндов — «истина»;
2) B ∨ ¬C ∨ B — выражение ложно, если все слагаемые имеют значение «ложь», т. е. В — «ложь»; ¬C — «ложь», а следовательно, переменная С имеет значение «истина»;
3) если рассмотреть посылку и учесть, что В — «ложь», то получим, что значение А — «истина».
Ответ: А — истина, В — ложь, С — истина.
Пример 3. Каково наибольшее целое число X, при котором истинно высказывание (35 < X · X) → (X < (X — 3)) ?
Решение. Запишем таблицу истинности для операции импликации:
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Выражение X < (X — 3) ложно при любых положительных значениях X. Следовательно, для того чтобы результатом импликации была «истина», необходимо и достаточно, чтобы выражение 35 < X · X также было ложно. Максимальное целое значение X, для которого 35 < X · X ложно, равно 5.
Ответ: X = 5.
Использование логических выражений для описания геометрических областей
Логические выражения могут быть использованы для описания геометрических областей. В этом случае задача формулируется так: записать для заданной геометрической области такое логическое выражение, которое принимает значение «истина» для значений x, y тогда и только тогда, когда любая точка с координатами (x; y) принадлежит геометрической области.
Рассмотрим описание геометрической области с помощью логического выражения на примерах.
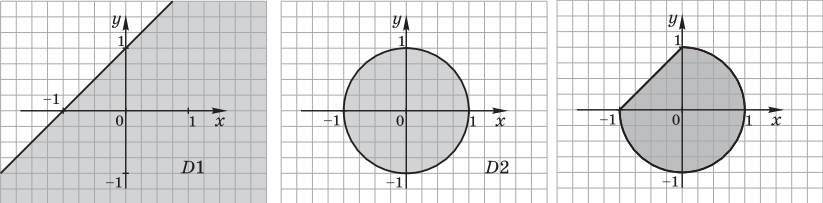
Пример 1. Задано изображение геометрической области. Записать логическое выражение, описывающее множество точек, принадлежащих ей.
1) 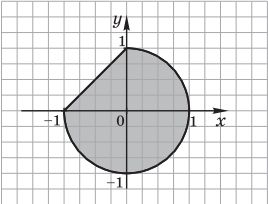
Решение. Заданную геометрическую область можно представить в виде набора следующих областей: первая область — D1 — полуплоскость ${x}/{-1} +{y}/{1} ≤ 1$, вторая — D2 — круг с центром в начале координат $x^2 + y^2 ≤ 1$. Их пересечение D1 $∩$ D2 представляет собой искомую область.
Результат: логическое выражение ${x}/{-1}+{y}/{1} ≤ 1 ∧ x^2 + y^2 ≤ 1$.
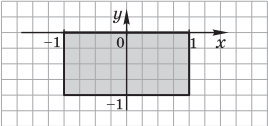
2)
Эту область можно записать так: |x| ≤ 1 ∧ y ≤ 0 ∧ y ≥ -1 .
Примечание. При построении логического выражения используются нестрогие неравенства, а это значит, что границы фигур также принадлежат заштрихованной области. Если использовать строгие неравенства, то границы учитываться не будут. Границы, не принадлежащие области, обычно изображаются пунктиром.
Можно решить обратную задачу, а именно: нарисовать область для заданного логического выражнения.
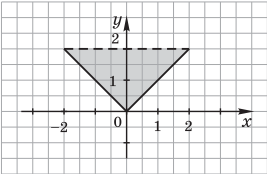
Пример 2. Нарисовать и заштриховать область, для точек которой выполняется логическое условие y ≥ x ∧ y + x ≥ 0 ∧ y < 2 .
Решение. Искомая область представляет собой пересечение трех полуплоскостей. Строим на плоскости (x, y) прямые y = x; y = –x; y = 2. Это границы области, причем последняя граница y = 2 не принадлежит области, поэтому ее наносим пунктирной линией. Для выполнения неравенства y ≥ x нужно, чтобы точки находились слева от прямой y = x, а неравенство y = –x выполняется для точек, которые находятся справа от прямой y = –x. Условие y < 2 выполняется для точек, лежащих ниже прямой y = 2. В результате получим область, которая изображена на рис.:
Использование логических функций для описания электрических схем
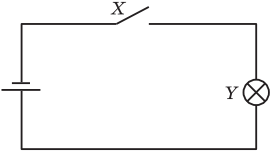
Логические функции очень удобны для описания работы электрических схем. Так, для схемы, представленной на рис., где значение переменной X — это состояние выключателя (если он включен, значение X — «истина», а если выключен — «ложь»), это значение Y — это состояние лампочки (если она горит — значение «истина», а если нет — «ложь»), логическая функция запишется так: Y = X . Функцию Y называют функцией проводимости.
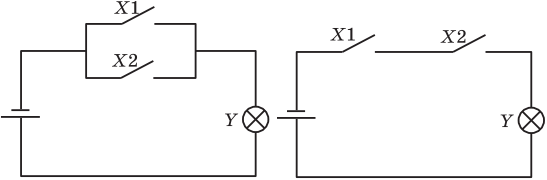
Для схемы, представленной на рис., логическая функция Y имеет вид: Y = X1 ∪ X2, т. к. достаточно одного включенного выключателя, чтобы горела лампочка. В схеме на рис., для того чтобы горела лампочка, должны быть включены оба выключателя, следовательно, функция проводимости имеет вид: Y = X1 ∧ X2 .
Для более сложной схемы функция проводимости будет иметь вид: Y = (X11 ∨ (X12 ∧ X13)) ∧ X2 ∧ (X31 ∨ X32).
Схема также может содержать контакты на замыкание. В этом случае размыкаемый контакт как выключатель обеспечивает загорание лампочки, когда кнопка отпущена, а не нажата. Для таких схем размыкающий выключатель описывается отрицанием.
Две схемы называются равносильными, если через одну из них ток проходит тогда, когда он проходит и через другую. Из двух равносильных схем более простой считается схема, функция проводимости которой содержит меньшее число элементов. Задача нахождения наиболее простых схем среди равносильных очень важна.
Использование аппарата алгебры логики при проектировании логических схем
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера. Любая информация при обработке на компьютере представляется в двоичной форме, т. е. кодируется некоторой последовательностью 0 и 1. Обработку двоичных сигналов, соответствующих 0 и 1, выполняют в компьютере логические элементы. Логические элементы, которые выполняют основные логические операции И, ИЛИ, НЕ, представлены на рис.
Условные обозначения логических элементов являются стандартными и используются при составлении логических схем компьютера. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу компьютера.
Технически компьютерный логический элемент реализуется в виде электрической схемы, которая представляет собой соединение различных деталей: диодов, транзисторов, резисторов, конденсаторов. На вход логического элемента, который называют также вентилем, поступают электрические сигналы высокого и низкого уровней напряжения, на выход выдается один выходной сигнал также либо высокого, либо низкого уровня. Эти уровни соответствуют одному из состояний двоичной системы: 1 — 0; ИСТИНА — ЛОЖЬ. Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических схем описывают с помощью таблиц истинности. Условное обозначение на схеме ИЛИ знак «1» — от устаревшего обозначения дизъюнкции как «>=1» (значение дизъюнкции равно 1, если сумма двух операндов больше или равна 1). Знак «&» на схеме И является сокращенной записью английского слова and.
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы ${X1}↖{-} ∧ X2 ∨ {X1 ∨ X2}↖{-} ∨ X1$.
| X1 | X2 | ${X1}↖{-}$ | ${X1}↖{-}$ X2 | X1 ∧ X2 | ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
- в таблице истинности функции выбирают наборы аргументов, для которых логические формы равны 1 («истина»);
- все выбранные логические наборы как логические произведения аргументов записывают, последовательно соединив их между собой операцией логической суммы (дизъюнкции);
- для аргументов, которые являются ложными, в построенной записи проставляют операцию отрицания.
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ∧ X2 ∨ X1 ∧ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Ответ: F(X1, X2) = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
- в таблице истинности выбирают наборы аргументов, для которых логические формы равны 0 («ложь»);
- все выбранные логические наборы как логические суммы аргументов записывают последовательно, соединив их между собой операцией логического произведения (конъюнкции);
- для аргументов, которые являются истинными, в построенной записи проставляют операцию отрицания.
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ∨ X2 ∧ X1 ∨ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Таким образом, получена запись логической функции в КНФ.
Ответ: X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2 = X1 ∧ ${X1}↖{-}$ ∨ X1 ∧ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ ${X2}↖{-}$ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ 0 = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 |
| 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 .
Ее можно упростить: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 = X2 ∧ (X1 ∨ ${X1}↖{-}$) = X2 ∧ 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
| X1 | X2 | X3 | F(X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | • | X1 ∧ X2 ∧ X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 ∧ X3 |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | • | X1 ∧ X2 ∧ ${X3}↖{-}$ |
| 1 | 0 | 0 | 1 | • | X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∧ X ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∪ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$.
Формула достаточно громоздка, и ее следует упростить:
X1 ∧ X2 ∧ X3 ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∨ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ = X2 ∧ X3 ∧ (X1 ∨ ${X1}↖{-}$) ∨ X1 ∧ ${X3}↖{-}$ ∧ (X2 ∨ ${X2}↖{-}$) = X2 ∧ X3 ∨ X1 ∧ ${X3}↖{-}$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
Решение. Очевидно, что результатом решения будет таблица, в которой искомая функция Y(X1, X2, X3) будет иметь значение «истина», если какие-либо две переменные имеют значение «истина».
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
Из условия 4 следует, что Борис не увлекается ни лыжами, ни теннисом, а из условий 3 и 5, что Петр не умеет играть в футбол, хоккей, теннис и бадминтон. Следовательно, любимые виды спорта Петра — лыжи и плавание. Занесем это в таблицу, а оставшиеся клетки столбцов «Лыжи» и «Плавание» заполним нулями.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
Из условий 1 и 2 следует, что Борис не футболист. Таким образом, в футбол играет Алексей. Продолжим заполнять таблицу. Внесем в пустые ячейки строки «Алексей» нули.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.
Преобразование логических выражений
Логическая формула имеет нормальную
форму, если в ней отсутствуют знаки
эквивалентности, импликации, двойного
отрицания, при этом знаки отрицания
находятся только при переменных.
Основные формулы преобразования
логических выражений:
-
А
А.
-
(
А
В)
А + В. -
(
А
+ В) А
В. -
А
В
А + В. -
А
В
А В + А
В. -
А
В
А В + А
В. -
А В
В А. -
А + В В
+ А. -
А + (В + C)
(A + В) + C. -
А (В
C)
(A
В) C. -
А (В + C)
A
В + A
C. -
А + (В C)
(A
+ В) (A
+ C). -
A + A
B
A. -
А + А А.
-
А А
А. -
А + 1 1.
-
А 1
А. -
А + 0 A.
-
А 0
0. -
А
+ А 1. -
А
А
0.
Задача. Упростить следующую логическую
формулу:
.
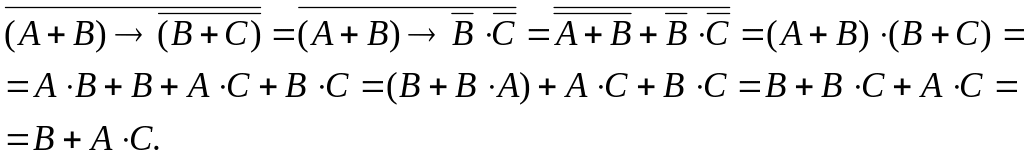
Составление логических схем
Удобным способом представления логических
выражений являются схемы: переключательные,
логические и др.
З
адача
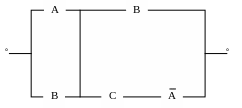
1. Составить переключательную схему,
соответствующую логическому выражению
АВ + СВ.
П
ереключательная
схема включает в себя элементы
параллельного и последовательного
соединений. Параллельное соединение
соответствует операции ИЛИ, а
последовательное – операции И.
Задача 2. Составить по данной схеме
логическое выражение и упростить его.
С
оставим
логическое выражение: (А + В)(В
+ СА).
У
простим
его: (А + В)(В
+ СА)
АВ + АСА
+ ВВ + ВСА
АВ
+ 0 + + 0 + ВСА
АВ
+ ВСА.
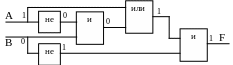
Задача 3. Составить логическое
выражение F по данной
схеме.
F
В данной логической схеме логические
операции И, ИЛИ, НЕ представлены
соответствующими обозначениями.
Логическое выражение будет следующим:
F
= АВ
(В + С).
Задача 4. Вычислить значение F,
если А=истина, В=ложь.
Подставим на схеме значения логических
переменных А и В, обозначив 1 –
истина, 0 – ложь, и вычислим значение F.
З
адача
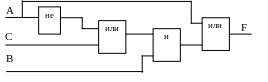
5. Составить логическую схему по
данному логическому выражению: F
= А + В(С
+ А).
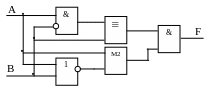
Задача 6. По данной комбинационной
схеме устройства составить логическое
выражение F.
В
данной схеме использованы следующие
обозначения: & – конъюнкция, 1 –
дизъюнкция, –
эквивалентность, М2 – сложение по модулю
2, – отрицание.
F
= (А
B
B)
(A
A+B).
Логические задачи
При решении логических задач вначале
обозначают простые высказывания как
логические переменные латинскими
буквами, затем составляют логические
выражения и упрощают их с помощью формул
преобразования логических выражений
(см. выше).
Задача 1. Кто из учеников А, В,
С и D играет, а кто
не играет в шахматы, если известно
следующее:
а) если А или В играет, то С
не играет;
б) если В не играет, то играют С
и D;
в) С играет.
Решение. Определим следующие простые
высказывания:
А – «Ученик А играет в шахматы»;
В – «Ученик В играет в шахматы»;
С – «Ученик С играет в шахматы»;
D – «Ученик D играет
в шахматы».
Запишем сложные высказывания, выражающие
известные факты:
а)
;
б)
;
с) С.
Запишем произведение указанных сложных
высказываний:
.
Упростим эту формулу:
Ответ. В шахматы играют ученики C
и D, а ученики A
и B – не играют.
Задача 2. Один из трех братьев поставил
на скатерть кляксу. На вопрос “Кто это
сделал?” получены такие ответы:
1. Алеша: “Витя не ставил кляксу. Это
сделал Боря.”
2. Боря: “Это Витя поставил кляксу. Алеша
не пачкал скатерть.”
3. Витя: “Боря не мог этого сделать. Я
сегодня не готовил уроки.”
Оказалось, что двое мальчиков в каждом
из двух своих заявлений сказали правду,
а один оба раза сказал неправду. Кто
поставил кляксу?
Введем обозначения:
А – «Алеша поставил кляксу»;
В – «Боря поставил кляксу»;
V – «Витя поставил
кляксу».
Запишем теперь суждения мальчиков
формулами:
1
.
V
B.
2
.
V
A.
По словам Вити, он не делал сегодня
уроки, но это не означает, что он не мог
поставить кляксу. Поэтому
3
.
B
(V+V),
т.е. В.
По условию задачи, две формулы истинны,
а одна ложна. Следовательно, получим
F
=(VB)(VA)B+(VB)(VA)B+(VB)(VA)B.
Преобразуем данное логическое выражение:
F
= VBVAB
+ VBVAB
+ VBVAB
= 0 + 0 + (V
+B)VAB
=
=
(V+B)VAB
= VVAB
+ BVAB
= VAB
+ VAB
= VAB.
Таким образом, кляксу поставил Витя.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В предложенной работе будет подробно рассмотрен вопрос преобразования логических выражений. Кроме этого, предлагаем вам пройти краткий курс по логике, где будут рассматриваться основные законы и понятия. Преобразование логических выражений – это довольно непростой процесс, если не ознакомиться со всеми нюансами самого предмета.
Курс информатики будет казаться простым и доставлять удовольствие, если внимательно прочитать данную статью и ознакомиться с правилами и законами преобразования, решения задач и составления схем. Предлагаем приступить прямо сейчас.
Наука логика
Основы логики – это довольно непростой предмет, по нему написано очень много томов. В данной статье будут рассмотрены азы и законы преобразования логических выражений, то есть информация будет максимально сжатой и концентрированной. Это необходимо для рассмотрения более осмысленно компьютерных технологий и построения схем.
Для начала что такое логика и зачем она нужна? Важно отметить, что это целая наука, которая рассматривает формы и способы рассуждения. Все, что мы видим, слышим или делаем, подчиняется законам. Бросили мяч с высоты — он обязательно летит вниз, так как подчиняется законам физики. Завариваем утром ароматный кофе, добавляем сахар, а сыпучие вещества моментально растворяются в воде, подчиняясь законам физики. Мы ведем беседу с друзьями, делимся своими планами: «Если я хорошо защищу работу, то получу красный диплом», «У меня не получится приехать на машине, так как она находится в ремонте». Не замечая, мы строим все наши разговоры, опираясь именно на логику и ее законы. Так зачем нужна наука логика? Конечно, зная ее законы, вы сможете безошибочно определять исход какого-либо события, так как не придется действовать наугад и рисковать.
Хоть мышление является довольно сложным процессом, тем не менее можно его разделить на некие составляющие, точнее, формы (с помощью чего происходит выражение мысли):
- понятия;
- высказывания;
- умозаключения;
- доказательства.
Далее предлагаем вам перейти к логическим функциям и преобразованию логических выражений. Информатика окажется для вас веселым и довольно простым предметом, если внимательно читать данную статью.
Логические функции
Сейчас мы предлагаем познакомиться с логическими функциями. Часто в билетах единого государственного экзамена в части В попадаются задачи на преобразование логических выражений в числовых отрезках. Их невозможно решить без знания функций логики.
Какова основная задача данной науки? Конечно, изучение логических выражений (как сложных, так и простых). Как получается сложное высказывание? Путем слияния простых, что происходит благодаря связкам, которые принято называть функциями.
Всего можно выделить пять связок:
- инверсия (то есть отрицание, при помощи данной функции можно получить высказывание, обратное данному: я сегодня иду в кино – я сегодня не иду в кино);
- дизъюнкция (эту функцию часто называют логическим сложением, для того чтобы стало понятно, приведем простой пример из жизни: «если у меня будет болеть голова или живот, то я не пойду в школу» — это выражение будет истинным, если учтено хоть одно из требований);
- конъюнкция (часто называют логическим умножением: «если я помою посуду и сделаю уроки, то пойду гулять с друзьями» — это выражение будет истинным, если будут учтены два условия);
- импликация (в логике эту функцию называют следованием, к сожалению, ее нельзя проиллюстрировать жизненной ситуацией; ложной функция будет в том случае, если что-то хотели сделать, но не получилось, в остальных случаях функция будет истинной);
- эквиваленция (или равенство, если два высказывания истинны или ложны, то в результате мы получаем истину).
Важно отметить, что в информатике любое простое выражение обозначается заглавной буквой латинского алфавита. Далее нужно обязательно запомнить таблицу истинности к каждой функции. Обратите внимание на то, что заучивать ее не обязательно, довольно будет только понимания функций.
Таблицы истинности
Конъюнкция
|
Первое выражение (А) |
Второе выражение (В) |
Результат (С) |
|
Л |
Л |
Л |
|
И |
Л |
Л |
|
Л |
И |
Л |
|
И |
И |
И |
Дизъюнкция
|
А |
В |
С |
|
Л |
Л |
Л |
|
И |
Л |
И |
|
Л |
И |
И |
|
И |
И |
И |
Инверсия
Импликация
|
А |
В |
С |
|
Л |
Л |
И |
|
И |
Л |
Л |
|
Л |
И |
И |
|
И |
И |
И |
Эквиваленция
|
А |
В |
С |
|
Л |
Л |
И |
|
И |
Л |
Л |
|
Л |
И |
Л |
|
И |
И |
И |
Кроме этого, важно отметить и тот факт, что ложь в логике обозначается цифрой 0, а истинное выражение — цифрой 1. Для своего удобства можно применять и знаки плюса и минуса. Обратите свое внимание на то, что ложные и истинные выражения в предложенных таблицах обозначены буквами «Л» и «И» соответственно.
Построение
Перед тем как переходить к преобразованию логических выражений, необходимо познакомиться с самим их построением. Любое составное или, как было сказано раньше, сложное выражение состоит из двух частей:
- переменные, которые обозначаются большими буквами латинского алфавита;
- знаки, которые обозначают функцию и соединяют простые выражения между собой.
Как составить выражение на языке алгебры логики? Для этого нужно сделать несколько вещей:
- разделить все высказывание на простые выражения;
- обозначить эти элементы буквами;
- выделить связи между простыми выражениями;
- записать получившееся выражение с помощью специальных символов алгебры логики.
Предлагаем рассмотреть простой пример: (Z*F=5 или Z*F=4) И (Z*F не равно 5 или Z*F не равно 4). Необходимо вместо переменных подставить 2. После этого мы получаем выражение (4=5 или 4=4) и (4 не равно 5 или 4 не равно 4). После проведенных операций мы должны выделить выражения и связи между ними, должно получиться следующим образом: (Z или F) и (не Z или не F). После этого нам необходимо преобразовать эту запись, подставив значения высказываний. В том случае, если выражение верное, то необходимо подставить 1, в противном случае – 0. Мы получаем: G=1 и 1. После необходимых вычислений мы получим результат: G=1, то есть сложное выражение является истинным.
Законы
Сейчас предлагаем вам рассмотреть законы логики и правила преобразования логических выражений. Важно упомянуть то, что любое логическое выражение может быть преобразовано в другое при помощи законов логики. Сейчас мы подробно рассмотрим все десять правил.
Первый в нашем списке – «закон двойного отрицания». То есть выражение «не (не А)» будет равняться выражению «А».
Коммуникативный закон есть и в математике, его запомнить довольно просто. А+В=В+А, А*В=В*А.
Сочетательный закон — (D+E)+F=(D+F)+E, тот же закон применим и к логическому умножению.
Распределительный закон – это элементарное открытие скобок. Пример: (А+В)*С=(А*С)+(В*С).
Закон де Моргана: не(А+В)=неА*неВ, не(А*В)=неА+неВ, АимпликацияВ=неА+В, не(АимпликацияВ)=А*неВ.
Идемпотентность: Х+Х=Х или С*С=С.
Исключение констант: Х+1=1, Х+0=Х; Х*1=Х, Х*0=0.
Следующим мы выделим закон противоречия, следуя ему, можно утверждать следующее равенство: В*неВ=0.
В логике есть и закон поглощения, который на практике выглядит следующим образом: С+(С*D)=С или С*(С+D)=С.
Так же важно для преобразования логических выражений запомнить закон исключения: (С*Е)+(неС*Е)=Е или (С+Е)*(неС+Е)=Е.
Если подробно рассмотреть и запомнить все представленные в данном разделе законы, то проблем с преобразованием никогда не возникнет. Не менее важен и порядок выполнения функций. Уделяйте этому пункту больше внимания, правильное распределение порядка функций – это залог правильного решения задачи.
Правила и законы преобразования и упрощения, порядок выполнения действий с примерами
Логические законы и правила преобразования логических выражений очень просты для запоминания. Если вы сомневаетесь в правдивости хоть одного из них, то проверьте самостоятельно. Для этого необходимо потратить 10 минут своего времени и составить таблицы истинности для получения ответа.
Сейчас предлагаем рассмотреть логические законы и правила преобразования логических выражений на конкретных примерах. Это необходимо для того, чтобы как следует закрепить полученные знания. Обратите особое внимание на очередность действий.
Нам дано: С+(неС*Е). Необходимо упростить выражение. Первым делом предлагаем раскрыть скобки. Тогда мы получаем выражение: (С+неС)*(С+Е). Отметим сразу, что логическое сложение двух противоположных высказываний дает нам истину. Что получаем в итоге: 1*(С+Е). Опять открываем скобки: (1*С)+(1+Е). Сейчас еще раз вспоминаем законы и получаем ответ: С+Е.
Как вы уже увидели, все достаточно просто. Для решения таких задач необходимо запомнить законы, которые были перечислены в прошлом разделе. Предлагаем переходить к решению логических задач, так как это задание уже немного сложнее предыдущего.
Решение задач
Мы познакомились с азами науки под названием «логика», преобразование логических выражений мы коротко рассмотрели, законы перечислили. Наиболее сложные задания с составлением логических выражений – это задачи. Важно отметить, что они могут решаться с помощью рассуждения, преобразования выражения или табличным методом. Предлагаем рассмотреть одну из них подробно.
Три мальчика (Кирилл, Антон и Костя) находились в одной комнате. Вдруг мама из кухни слышит звук разбитой чашки. Прибежала к сыновьям и спросила: «Кто это сделал?» Ответ был следующим: Кирилл сказал, что чашку разбил не Костя, а Антон; Антон сказал, что это сделал Костя, а не Кирилл; Костя утверждает, что виновником не является Антон. Нам известно, что кто-то один из мальчиков сказал маме неправду. Нужно выяснить, кто разбил чашку.
Если рассуждать логически, то ответы Кирилла и Антона противоречат друг другу, так же, как и Кирилла с Костей. Следовательно, они не могут быть оба правдивыми. Делаем следующее умозаключение — Антон и Костя сказали правду, а Кирилл является виновником разбитой чашки. Это был применен метод размышления. Сейчас просмотрим решение этой же задачи, только при помощи метода преобразования выражения. Для начала введем сокращения:
- КР – чашка разбита Кириллом;
- А – чашка разбита Антоном;
- К – виновник Костя.
Ответы мальчиков:
- Кирилл – неК, А;
- Антон – неКР, К;
- Костя – неА.
Предлагаем составить выражение, если Костя солгал, а Кирилл и Антон сказали правду: неК*А=1 и К*неКР=1 и А=1. Преобразовывая выражение, мы получаем противоречие: 0=1. Наше предположение неверно, стоит проверить другие предположения.
Если мы предполагаем, что Кирилл солгал, а Антон и Костя сказали маме правду, то получаем следующее выражение: К*неА=1 и К*неКР=1 и неА=1. Упростив выражение, мы получаем КР*неА*неК=1. Это говорит о том, что наше предположение было верным, действительно, Кирилл разбил чашку и солгал маме.
Табличный метод решения
Рассмотренные законы логики и преобразование логических выражений, безусловно, помогли нам справиться с задачей, которая представлена в предыдущем разделе. Сейчас предлагаем рассмотреть табличный метод решения на следующей задаче.
Дмитрий, Анатолий и Людмила являются поклонниками почтовой переписки, нам известно, что все живут в разных частях света и имеют разное хобби. Определите, кто живет в каком городе и чем увлекается. Известны следующие факты:
- Дмитрий никогда не бывал в Париже, а Людмила — в Риме;
- тот, кто живет в Париже, не любит кино;
- человек, который живет в Риме, занимается вокалом;
- Людмила испытывает отвращение к балету.
Для того чтобы решить задачу, нужно составить небольшую таблицу.
|
Франция |
Италия |
США |
Вокал |
Балет |
Кино |
|
|
Дмитрий |
||||||
|
Анатолий |
||||||
|
Людмила |
Далее от вас требуется максимум внимания. Все, что вы прочитали в условии, должно отразиться в этой таблице. По ходу заполнения станет ясно следующее:
- Дмитрий живет в Риме и занимается вокалом;
- Анатолий живет в Париже и часто посещает балет;
- Людмила – это большая поклонница киноискусства, которая проживает в США.
Обратите еще раз свое внимание на то, что истинное выражение отмечается цифрой 1, а ложное – 0. Заполняя таблицу данными символами, вы быстро найдете ответ на вопрос, который вас интересует.
Микросхематика
Примеры преобразования логических выражений, которые мы рассмотрели, являются довольно сложными на первый взгляд. В билетах единого государственного экзамена условие может вовсе даваться в виде микросхемы.
Важно знать, что все цифровые устройства основываются на логических элементах, то есть неких устройствах, которые выполняют одну логическую функцию.
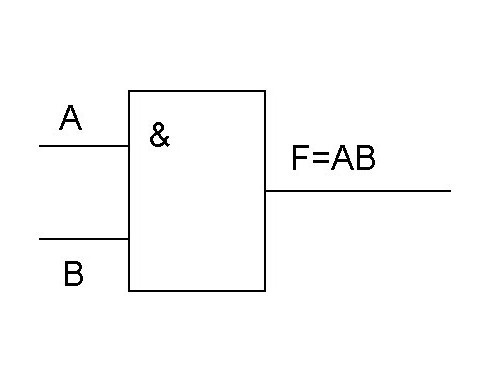
Мы уже говорили о такой функции, как конъюнкция (логическое умножение). Его принято обозначать символом &. Эта функция необходима для конъюнкции нескольких значений. На картинке вы видите схему логического умножения.
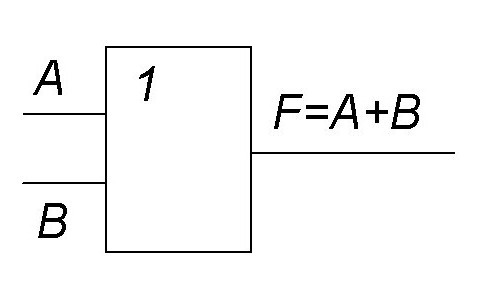
Функция дизъюнкция необходима для реализации дизъюнкции некоторых входных значений. При записи выражения эту функцию принято обозначать символом Ú. На картинке представлена схема.
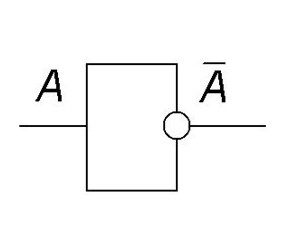
Функция инверсии служит преобразователем одного выражения в противоположное. На рисунке вы видите, как выглядит схема «не».
Пример упрощения формулы №1
Рассмотренные правила преобразования логических выражений необходимо закрепить на практике. Именно преследуя эту цель, мы предлагаем решить самостоятельно два примера средней сложности и сопоставить с результатами в данном разделе статьи.
Если вы еще не успели запомнить формулы преобразования логических выражений, то можете сделать себе небольшую «напоминалку». Вы увидите, что вскоре вы не будете в нее подсматривать.
Пример: (Х+Т)*(неХ+Т)*(М+неТ). Не стоит слепо списывать, попробуйте решить пример самостоятельно.
В ходе упрощения мы получаем следующие записи: Т*(М+неТ)=(Т*М)+(Т*неТ)=(Т*неМ)+0=(Т+0)*(М+0)=Т*М.
Как видите, из довольно длинного и громоздкого сложного выражения мы получили короткое Т*М. Если у вас не получилось решить самостоятельно данный пример, то обратитесь еще раз в пункт, где мы рассматривали преобразование логических выражений, задачи.
Пример упрощения формулы №2
В данном разделе предлагаем вам упростить выражение (Е+Н)*(Е+К). Разберем решение поэтапно. Первым делом нам необходимо раскрыть скобки, вспоминаем курс начальной математики. В результате мы получаем следующее выражение: Е*Е+Е*К+Н*Е+Н*К. Далее мы замечаем, что в полученном выражении есть часть Е*Е, вспоминаем закон идемпотентности и преобразовываем запись: Е+Е*К+Н*Е+Н*К. Следующим этапом преобразуем часть Е+Е*К, воспользовавшись вынесением за скобки переменной Е и свойством: А+1=1. Мы получаем выражение: Е+Н*Е+Н*К. Следуем аналогично последнему пункту и выносим за скобки Е. В результате мы получаем ответ: Е+Н*К.
Обратите свое внимание на то, что задания только кажутся сложными на первый взгляд. Чтобы «щелкать их, как семечки», необходимо просто выучить основные законы логики.