Как составить логическое выражение по задаче - Исправление недочетов и поиск решений вместе с Examum.ru

Примеры решения задач «Логические основы работы компьютера»

Теория по этой теме по этой теме Пройти тестирование по этой теме Контрольная по этой теме

№1.

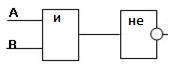
Дана логическая функция: F(А,В) = ¬ (А / В). Постройте соответствующую ей функциональную схему.

Решение:

Функциональная схема будет содержать 2 входа А и В. Рассмотрим логическое выражение и определим порядок действий в нем:

1) первым выполняется логическое умножение А / В, следовательно, сигналы с входов А и В подаются на конъюнктор;

2) далее выполняется логическое отрицание ¬(А / В), следовательно, сигнал, полученный на выходе из конъюнктора должен быть инвертирован, т.е. подан на инвертор.

Выход инвертора является выходом функциональной схемы.

Изобразим схему, следуя данным действиям:

№2.

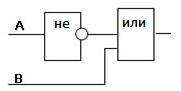
Определите логическую функцию, соответствующую заданной функциональной схеме:

Решение:

Функциональная схема содержит 2 входа А и В. Вход А инвертирован и его выход является входом дизъюнктора. Вход В подает сигнал на дизъюнктор. Выход дизъюнктора является выходом функциональной схемы.

Итак, последовательность действий:

1) ¬A — сигнал входа А инвертирован;

2) ¬A / B — на дизъюнктор подают инвертированный сигнал входа А и нормальный входа В.

Выход дизъюнктора является выходом функциональной схемы. Следовательно, логическая функция F –это функция двух переменных А и В и имеет вид:

F(A, B) = ¬A / B

Ответ: F(A, B) = ¬A / B

№3.

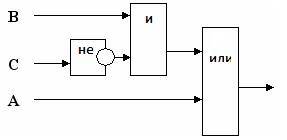
Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F=A/B/ ¬C, если А=1, В=1, С=1.

Решение:

Значение логического выражения — 1

№4.

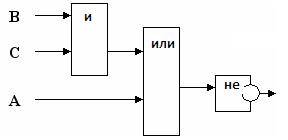
Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F= ¬(A/B/C),если А=0, В=1, С=1.

Решение:

Значение логического выражения — 1

Источник

Решение задач

Пример

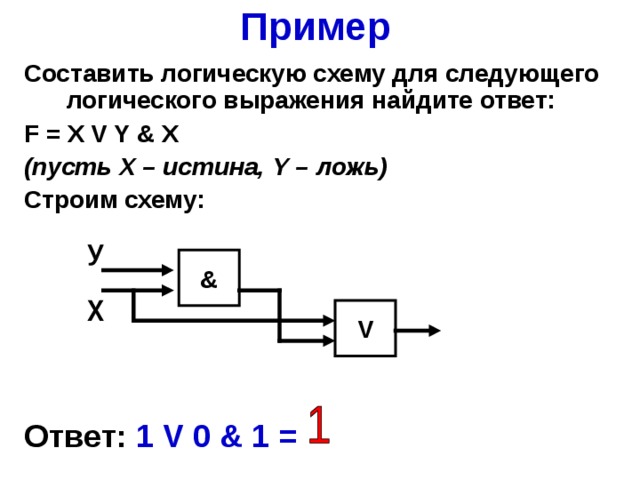
Составить логическую схему для следующего логического выражения найдите ответ:

F = X V Y & X

( пусть Х – истина, Y – ложь)

Строим схему:

Ответ: 1 V 0 & 1 =

Пример

Постройте логическую схему, соответствующую логическому выражению F = X & Y V ¬(Y V X) . Вычислить значения выражения для X=1 , Y=0 .

Постройте логическую схему по логическому выражению и найдите значение логического выражения

F = A V B& ¬ C , если А=1, В=1, С=1

F = ¬ ( A V B&C ), если А=0, В=1, С=1

F = ¬ A V B&C , если А=1, В=0, С=1

F = ( A V B ) & ( C V B ), если А=0, В=1, С= 0

Постройте логическую схему по логическому выражению и найдите значение логического выражения

F = ¬ ( A&B&C ) V (B&C V ¬A ) , если А= 1 , В=1, С= 0

F = ¬ ( A&B&C ), если А=0, В= 0 , С=1

F = B& ¬ A V ¬B &A , если А=0, В= 0

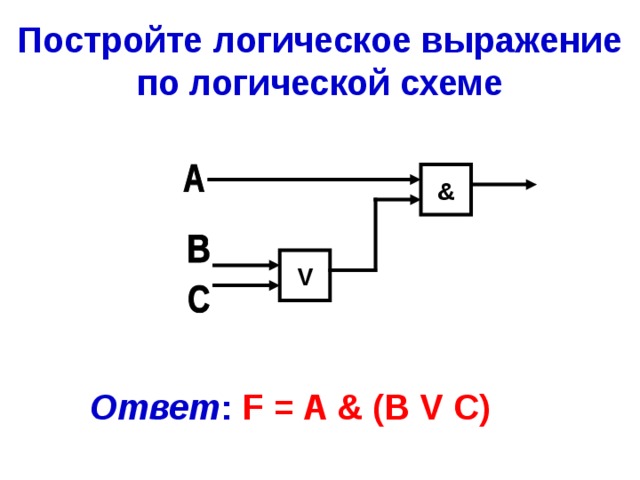
Постройте логическое выражение по логической схеме

Ответ : F = A & (B V C)

Постройте логическое выражение по логической схеме

Ответ : F = (A V( ¬A & B)) & ¬B

Постройте логическое выражение по логической схеме

Ответ : F = A&B&( ¬ B V ¬ C) V D

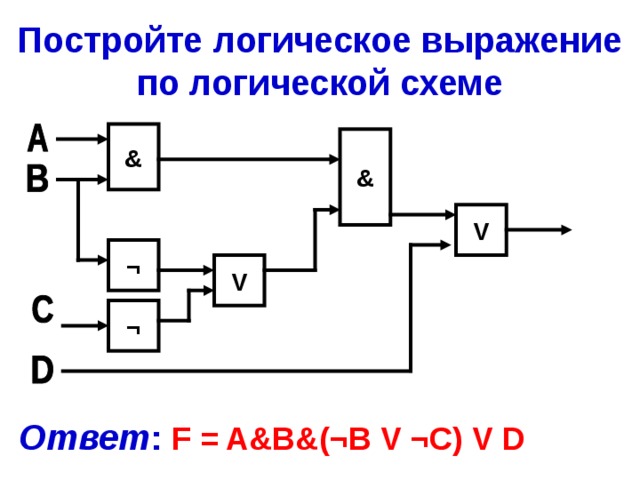
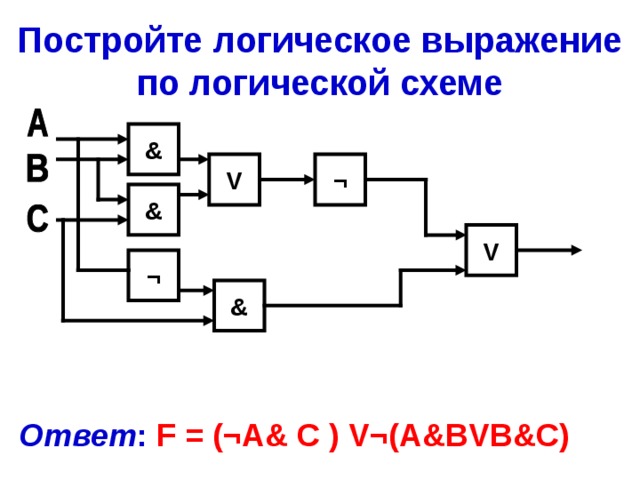
Постройте логическое выражение по логической схеме

Ответ : F = (¬A& C ) V ¬ (A&BVB&C)

Домашнее задание

Составьте логические схемы к логическим выражениям:

F = BV(C& ¬A)V(A&B)

F = ¬(A&B)VC&D

Источник

Время выполнения

4 часа

Цель работы

Изучить основы алгебры логики.

Задачи лабораторной работы

В результате прохождения занятия студент должен:

1. знать:

определения основных понятий (простое и сложное высказывания, логические операции, логические выражения, логическая функция);
порядок выполнения логических операций;
алгоритм построения таблиц истинности;
схемы базовых логических элементов;
законы логики и правила преобразования логических выражений;

2. уметь:

применять загоны логики для упрощения логических выражений;
строить таблицы истинности;
строить логические схемы сложных выражений.

Общие теоретические сведения

Основные понятия алгебры логики

Логической основой компьютера является алгебра логики, которая рассматривает логические операции над высказываниями.

Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Пример. «3 – простое число» является высказыванием, поскольку оно истинно.

Не всякое предложение является логическим высказыванием.

Пример. предложение «Давайте пойдем в кино» не является высказыванием. Вопросительные и побудительные предложения высказываниями не являются.

Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.

Пример. «x+2>5» — высказывательная форма, которая при x>3 является истинной, иначе ложной.

Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным. Слова и словосочетания «не», «и», «или», «если…, то», «тогда и только тогда» и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.

Высказывания, образованные из других высказываний с помощью логических связок, называются составными (сложными). Высказывания, которые не являются составными, называются элементарными (простыми).

Пример. высказывание «Число 6 делится на 2» — простое высказывание. Высказывание «Число 6 делится на 2, и число 6 делится на 3» — составное высказывание, образованное из двух простых с помощью логической связки «и».

Истинность или ложность составных высказываний зависит от истинности или ложности элементарных высказываний, из которых они состоят.

Чтобы обращаться к логическим высказываниям, им назначают имена.

Пример. Обозначим через А простое высказывание «число 6 делится на 2», а через В простое высказывание «число 6 делится на 3». Тогда составное высказывание «Число 6 делится на 2, и число 6 делится на 3» можно записать как «А и В». Здесь «и» – логическая связка, А, В – логические переменные, которые могут принимать только два значения – «истина» или «ложь», обозначаемые, соответственно, «1» и «0».

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение (табл. 1).

Таблица 1. Основные логические операции

Обозначение операции	Читается	Название операции	Альтернативные обозначения
¬	НЕ	Отрицание (инверсия)	Черта сверху
	И	Конъюнкция (логическое умножение)	∙ &
	ИЛИ	Дизъюнкция (логическое сложение)	+
→	Если … то	Импликация
↔	Тогда и только тогда	Эквиваленция	~
XOR	Либо …либо	Исключающее ИЛИ (сложение по модулю 2)

НЕ Операция, выражаемая словом «не», называется отрицанием и обозначается чертой над высказыванием (или знаком ¬). Высказывание ¬А истинно, когда A ложно, и ложно, когда A истинно.

Пример. Пусть А=«Сегодня пасмурно», тогда ¬А=«Сегодня не пасмурно».

И Операция, выражаемая связкой «и», называется конъюнкцией (лат. conjunctio – соединение) или логическим умножением и обозначается точкой « • » (может также обозначаться знаками или &). Высказывание А • В истинно тогда и только тогда, когда оба высказывания А и В истинны.

Пример. Высказывание «Число 6 делится на 2, и число 6 делится на 3» — истинно, а высказывание «Число 6 делится на 2, и число 6 больше 10» — ложно.

ИЛИ Операция, выражаемая связкой «или» (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio – разделение) или логическим сложением и обозначается знаком

(или плюсом). Высказывание АВ ложно тогда и только тогда, когда оба высказывания А и В ложны.

Пример: Высказывание «Число 6 делится на 2 или число 6 больше 10» — истинно, а высказывание «Число 6 делится на 5 или число 6 больше 10» — ложно.

ЕСЛИ … ТО Операция, выражаемая связками «если …, то», «из … следует», «… влечет …», называется импликацией (лат. implico – тесно связаны) и обозначается знаком → . Высказывание А→В ложно тогда и только тогда, когда А истинно, а В ложно.

Пример. Высказывание «если студент сдал все экзамены на «отлично», то он получит стипендию». Очевидно, эту импликацию следует признать ложной лишь в том случае, когда студент сдал на «отлично» все экзамены, но стипендии не получил. В остальных случаях, когда не все экзамены сданы на «отлично» и стипендия получена (например, в силу того, что студент проживает в малообеспеченной семье) либо когда экзамены вообще не сданы и о стипендии не может быть и речи, импликацию можно признать истинной.

РАВНОСИЛЬНО Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «… равносильно …», называется эквиваленцией или двойной импликацией и обозначается знаком ↔ или ~ . Высказывание А↔В истинно тогда и только тогда, когда значения А и В совпадают.

Пример: Высказывание «Число является четным тогда и только тогда, когда оно делится без остатка на 2» является истинным, а высказывание «Число является нечетным тогда и только тогда, когда оно делится без остатка на 2» — ложно.

ЛИБО … ЛИБО Операция, выражаемая связками «Либо … либо», называется исключающее ИЛИ или сложением по модулю 2 и обозначается XOR или . Высказывание АВ истинно тогда и только тогда, когда значения А и В не совпадают.

Пример. Высказывание «Число 6 либо нечетно либо делится без остатка на 2» является истинным, а высказывание «Либо число 6 четно либо число 6 делится на 3» – ложно, так как истинны оба высказывания входящие в него.

Замечание. Импликацию можно выразить через дизъюнкцию и отрицание:

Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:

Исключающее ИЛИ можно выразить через отрицание, дизъюнкцию и конъюнкцию:

Вывод. Операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.

Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания («не»), затем конъюнкция («и»), после конъюнкции – дизъюнкция («или») и исключающего или и в последнюю очередь – импликация и эквиваленция.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).

Логическая формула — это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).

Логическая функция — это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.

Пример. – логическая функция двух переменных A и B.

Значения логической функции для разных сочетаний значений входных переменных – или, как это иначе называют, наборов входных переменных – обычно задаются специальной таблицей. Такая таблица называется таблицей истинности.

Приведем таблицу истинности основных логических операций (табл. 2)

Таблица 2

A	B
1	1	0	1	1	1	1	0
1	0	0	0	1	0	0	1
0	1	1	0	1	1	0	1
0	0	1	0	0	1	1	0

Опираясь на данные таблицы истинности основных логических операций можно составлять таблицы истинности для более сложных формул.

Алгоритм построения таблиц истинности для сложных выражений:

1. Определить количество строк:

количество строк = 2ⁿ + строка для заголовка,
n — количество простых высказываний.

2. Определить количество столбцов:

количество столбцов = количество переменных + количество логических операций;
определить количество переменных (простых выражений);
определить количество логических операций и последовательность их выполнения.

Пример 1. Составить таблицу истинности для формулы И–НЕ, которую можно записать так:.

1. Определить количество строк:

На входе два простых высказывания: А и В, поэтому n=2 и количество строк =2²+1=5.

2. Определить количество столбцов:

Выражение состоит из двух простых выражений (A и B) и двух логических операций (1 инверсия, 1 конъюнкция), т.е. количество столбцов таблицы истинности = 4.

3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 3).

Таблица 3. Таблица истинности для логической операции

A	B
1	1	1	0
1	0	0	1
0	1	0	1
0	0	0	1

Подобным образом можно составить таблицу истинности для формулы ИЛИ–НЕ, которую можно записать так:

Таблица 4. Таблица истинности для логической операции

A	B
1	1	1	0
1	0	1	0
0	1	1	0
0	0	0	1

Примечание: И–НЕ называют также «штрих Шеффера» (обозначают | ) или «антиконъюнкция»; ИЛИ–НЕ называют также «стрелка Пирса» (обозначают ↓) или «антидизъюнкция».

Пример 2. Составить таблицу истинности логического выражения .

Решение:

1. Определить количество строк:

На входе два простых высказывания: А и В, поэтому n=2 и количество строк=2²+1= 5.

2. Определить количество столбцов:

Выражение состоит из двух простых выражений (A и B) и пяти логических операций (2 инверсии, 2 конъюнкции, 1 дизъюнкция), т.е. количество столбцов таблицы истинности = 7.

Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции.

3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 5).

Таблица 5. Таблица истинности для логической операции

A	B					C
1	1	0	0	0	0	0
1	0	0	1	0	1	1
0	1	1	0	1	0	1
0	0	1	1	0	0	0

Логические формулы можно также представлять с помощью языка логических схем.

Существует три базовых логических элемента, которые реализуют три основные логические операции:

логический элемент «И» – логическое умножение – конъюнктор;
логический элемент «ИЛИ» – логическое сложение – дизъюнктор;
логический элемент «НЕ» – инверсию – инвертор.

Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из “кирпичиков”.

Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.

Преобразование сигнала логическим элементом задается таблицей состояний, которая фактически является таблицей истинности, соответствующей логической функции, только представлена в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисления.

Алгоритм построения логических схем.

Определить число логических переменных.
Определить количество логических операций и их порядок.
Изобразить для каждой логической операции соответствующий ей логический элемент.
Соединить логические элементы в порядке выполнения логических операций.

Пример. По заданной логической функции построить логическую схему.

Решение.

Число логических переменных = 2 (A и B).
Количество операций = 5 (2 инверсии, 2 конъюнкции, 1 дизъюнкция). Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции.
Схема будет содержать 2 инвертора, 2 конъюнктора и 1 дизъюнктор.
Построение надо начинать с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые, в свою очередь, подаются один входной сигнал нормальный и один инвертированный (с инверторов).

Логические законы и правила преобразования логических выражений

Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.

В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений.

1. Закон двойного отрицания: ;

2. Переместительный (коммутативный) закон:

3. Сочетательный (ассоциативный) закон:

4. Распределительный (дистрибутивный) закон:

5. Законы де Моргана:

6. Закон идемпотентности:

7. Законы исключения констант:

8. Закон противоречия:;

9. Закон исключения третьего: ;

11. Правило исключения импликации: ;

12. Правило исключения эквиваленции: .

Справедливость этих законов можно доказать составив таблицу истинности выражений в правой и левой части и сравнив соответствующие значения.

Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.

Пример. Упростить логическое выражение .

Решение:

Согласно закону де Моргана:

Согласно сочетательному закону:

Согласно закону противоречия и закону идемпотентности:

Согласно закону исключения 0:

Окончательно получаем
/

Видеоурок по выполнению заданий лабораторной работы

Текст задания (с данными своего варианта).
Представление по каждому пункту задания подробного решения.

Технология выполнения работы

В данной работе необходимо составить таблицу истинности логического выражения, построить схему логической функции и упростить логическое выражение заданные каждому студенту в соответствии с его вариантом, записать ход рассуждений и полученные результаты.

Вопросы для защиты работы

Что такое высказывание (приведите пример)?
Что такое составное высказывание (приведите пример)?
Как называются и как обозначаются (в языке математики) следующие операции: ИЛИ, НЕ, И, ЕСЛИ … ТО, ТОГДА И ТОЛЬКО ТОГДА, ЛИБО …ЛИБО?
Укажите приоритеты выполнения логических операций.
Составьте таблицу истинности для следующих операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.
Изобразите функциональные элементы: конъюнктор, дизъюнктор, инвертор.
Какие логические выражения называются равносильными?
Записать основные законы алгебры логики.

Источник

Удобным способом
представления логических выражений
являются логические схемы. Вот как
изображаются на
таких схемах три основные логические
операции:

С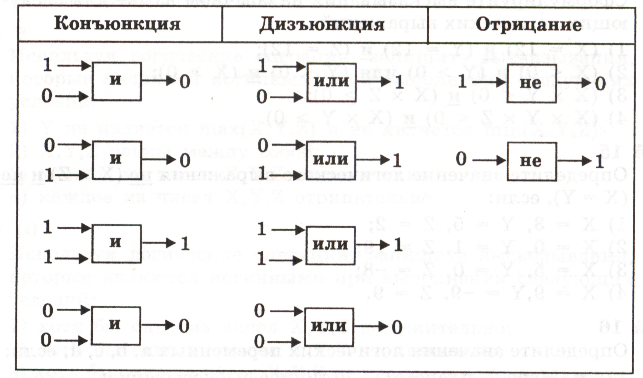хематическое
изображение логических операций

В этой таблице
использованы следующие
обозначения:
1 — истина; 0
— ложь. Цифры в начале входящих стрелок
— логические операнды; цифры а конце
выходящих стрелок — результаты операций.

Данная таблица —
та же таблица истинности, только
представленная в форме логических
схем. В такой форме удобно изображать
цепочки логических операций и производить
их вычисления.

Пример 5.
Для вычисления логического выражения:
1 или
0 и
1 нарисовать
схему, отражающую последовательность
выполнения логических операций. По
схеме вычислить значение логического
выражения.

Решение.

Здесь
наглядно отражено то, что первой
выполняется операция
и,
затем или.
Теперь в порядке слева – направо припишем
к выходящим стрелкам результаты операций:

В результате
получилась
1, т.е.
«ИСТИНА».

Пример 6.
Дано выражение:
не
(1 и
(0 или
1) и
1).

Вычислить значение
выражения с
помощью
логической схемы.

Решение.
Логическая схема с результатами
вычислений выглядит так:

2.1.4. Импликация и эквивалентность

Импликация
(условное
высказывание).
В русском языке
этой логической операции соответствуют
союзы если
…, то; когда …, тогда; коль скоро…, то
и т. п.

Выражение,
начинающееся после союзов
если, когда, коль скоро,
называется основанием условного
высказывания.

Выражение, стоящее
после слов
то, тогда,
называется следствием. В логических
формулах операция импликации обозначается
знаком «→». Импликация — двухместная
операция; записывается так: А→В.

Эквивалентность.
Языковой аналог —
союзы если
и только если; тогда и только тогда,
когда …
Эквивалентность обозначается
знаком «≡»
или «↔».

Пример 7.

А) Дано сложное
высказывание: «Если выглянет
солнце, то
станет тепло». Преобразовать к логической
формуле.

Решение.

Обозначим через
А
простое высказывание «выглянет солнце»,
а через В
— «станет тепло». Тогда логическая
форма сложного высказывания имеет вид
А→В.

Б) Дано сложное
высказывание: «Людоед голоден тогда и
только тогда, когда он давно
не
ел». Преобразовать к логической формуле.

Решение.

Обозначим через
А
простое высказывание «людоед голоден»,
а через В
— «он давно не ел». Тогда логическая
формула сложного
высказывания имеет вид А
≡ В.

Таблица истинности
операций импликации и эквивалентности

А	В	А→В	А ≡ В
0	0	1	1
0	1	1	0
1	0	0	0
1	1	1	1

Порядок
всех
пяти логических операций по убыванию
старшинства следующий: отрицание,
конъюнкция, дизъюнкция, импликация,
эквивалентность.

Пример 8.
Определить истинность формулы

F
= ((C

В) → В)
& (А & В)
→ В.

Для решения задачи
построим таблицу истинности этой
формулы, перебрав все варианты значений
логических переменных А, В, С. Введем
числовые обозначения для логических
величин: 1
— ИСТИНА,
0 — ЛОЖЬ.

A	B	C	C/B	(C/B)→B	A&B	((C/B)→B)&(A&B)	F
0	0	0	0	1	0	0	1
0	0	1	1	0	0	0	1
0	1	0	1	1	0	0	1
0	1	1	1	1	0	0	1
1	0	0	0	1	0	0	1
1	0	1	1	0	0	0	1
1	1	0	1	1	1	1	1
1	1	1	1	1	1	1	1

Ответ:
формула
является тождественно истинной.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

План урока:

Способы решению задач по логике

Табличный способ – этапы, особенности

Сравнение методов решения

Построение таблиц истинности для различных типов задач

Построение электрических схем, реализующих логические операции

Способы решения задач по логике

Многие задачи можно решить, используя инструменты алгебры логики. Чтобы получить результат, можно пойти 3 путями:

рассуждая над условием;
решая логические операции;
используя таблицы истинности.

Логический подход подразумевает перевод условия из естественного языка на язык символов, схем и формул. Для такой формализации высказываний нужно выполнить ряд шагов.

Этапы решения логических задач:

Разобраться с условием на естественном языке, выделив простые высказывания, и дать им символьные обозначения (латиница).
Записать условие в виде формулы. Решить ее поэтапно, упрощая, учитывая приоритеты (( ), ¬, &, V).
Просчитать формулы строчно или при помощи таблиц истинности, учитывая законы алгебры логики.
Проверить, соответствует ли полученный результат условию задачи.

Табличный способ – этапы, особенности

Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.

Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи.

Метод таблиц

Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.

Существует общий алгоритм построения таблиц:

Определить число логических значений/переменных (n) в примере.
Установить вид, число и тип операций. Важно заранее определить очередность действий, выразить это при помощи скобок.
Полученные данные позволяют рассчитать сколько нужно столбцов – это сумма числа переменных и операций.
Нарисовать таблицу, заполнить шапку, записав обозначение переменных и выбранные действия.
Определить, сколько существует наборов логических переменных (т.е. число строчек) по формуле m = 2ⁿ+ 1 (шапка).
Заполнить столбцы, вписав наборы значений логических переменных (0 или 1).
Записать результаты логических операций, указанных в шапке для каждой совокупности значений.
Сделать выводы на основании полученных результатов.

Если необходимо перебрать все значения простых выражений, то для задач:

с 2-мя переменными может быть только 4 набора логических переменных;

Если словесно описывать все эти комбинаций, на каждый из примеров понадобится десятки строк текста.

Обязательно учитывают приоритет операций:

Указанные в скобках.
Отрицание.
Логическая конъюнкция чисел.
Дизъюнкция.
Строгая дизъюнкция.
Импликация.
Эквивалентность.

Обозначение логических операций:

Сравнение методов решения

Метод рассуждений

Он заключается в пошаговом анализе условий с промежуточными выводами на каждом этапе. Выполняется анализ таблицы истинности каждого логического выражения.

Пример №1.

Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по таким специальностям: гитарист, плотник, егерь и стоматолог.

Известно, что:

дом плотника правее егеря;
стоматолог проживает левее егеря;
дом гитариста с самого краю;
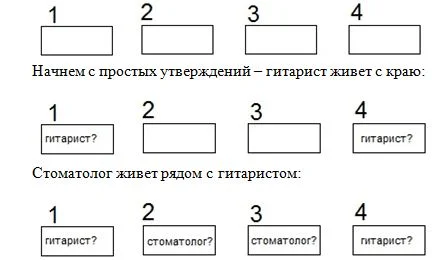
стоматолог живет рядом с гитаристом;
Владимир не гитарист, и его дом не соседствует с гитаристом;
дома Дмитрия и егеря соседние;
здание, в котором прописан Андрей, правее стоматолога;
между домами Андрея и Дмитрия один дом.

Чтобы рассуждать было проще, добавим изображение зданий, присвоим им номера:

Но стоматолог живет левее егеря, а правее егеря – плотник. Получается, что дом гитариста не может быть последним, а дом стоматолога не может быть предпоследними. То есть, егерь живет в предпоследнем доме:

Между домами Андрея и Дмитрия стоит один дом, значит, дом Андрея не может быть предпоследним, получается номер – 4, что автоматом исключает проживание там Дмитрия и Владимира.

Условие задачи заняло 2 предложения, а рассуждений получилось на 2 страницы.

Такой подход лучше не использовать, если условие сложное или много данных.

Табличный метод

Более удачным подходом к решению задач с большим количеством данных (несколько множеств), считается табличный, или графический (диаграммы).

Чтобы построить таблицу истинности логических выражений, следует:

Разбить задачу на простейшие утверждения, которые обозначить символами (большие буквы латинского алфавита).
Записать условие задачи, как составное выражение из символов логических операций.
Нарисовать таблицу истинности для полученных данных.
Выбрать такой вариант, при котором полученные значения подходят под условие.
Проверить соответствие выбранного варианта и условия задачи.

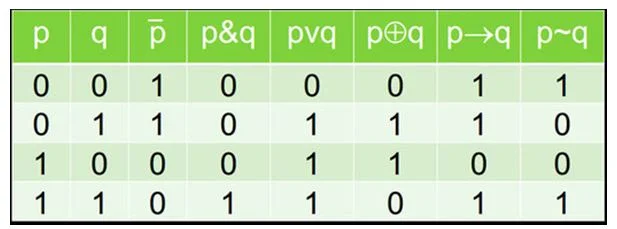
Чтобы преобразовывать условие задачи в логические выражения и операции, удобно пользоваться такой сводной таблицей истинности логических операций:

Рассмотрим тот же пример.

Определяем, что только гитарист может жить в первом доме, далее смотрим на заметки и условия и получаем таких жителей:

Метод компактнее, для некоторых задач нагляднее.

Построение таблиц истинности для различных типов задач

Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.

Пример 2.

Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.

Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:

А — «Первый студент летал в Англию»;

В — «Второй студент летал в Англию»;

С — «Третий студент летал в Англию».

Запишем выясненные данные при помощи логических операций:

Пример 3.

Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:

Если А получит максимальный бал, то максимальный бал получат Ви С.
А и С получат или не получат максимальный бал одновременно.
Необходимым условием получения высшего бала С класса является получение высшего бала В классом.

По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.

Выясним, какие же классы добились высшего бала.

Разбиваем условие задачи на элементарные высказывания:

А – «А добьется высшего бала»;

В – «В добьется высшего бала»;

С – «С добьется высшего бала».

Запишем логические операции, описанные в примере:

Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.

Пример 4.

Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:

последняя – гласная (Х1);
или первая буква согласная (Х2)
вторая – согласная (Х3).

¬(Х1→Х2)VХ3

Предложенные имена: Арина, Артур, Кэтрин, София.

Решим задачу, используя таблицу.

Сначала решим пошагово, выполняя операции по приоритету:

Указанному условию соответствует первое имя.

Пример 5.

Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.

Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.

Маша Марина: «Саша заняла второе место, а Света – первое».

Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».

Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».

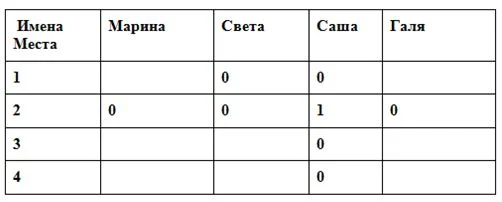
Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».

Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».

Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.

Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.

Построение электронных схем, реализующих логические операции

Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.

Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.

Электросхема с конъюнктором

Рассмотрим все варианты:

Все контакты включены, тогда источник света горит.
Первый контакт в положении «выключено» – свет не горит.
Второй контакт выключен – лампа не светит.
Все контакты отключены – свет не горит.

Заключение – эта электрическая цепь реализует операцию «И».

Дизъюнктор, схема электропитания

Рассмотрим этот вид электрической цепочки:

Все контакты включены – лампа горит.
Первый контакт включен, второй выключен – свет горит.
Обратная ситуация – выключен первый, включен второй – лампа светится.
Все контакты выключены – света нет.

Заключение – такой вид электросхем соответствует логической операции «ИЛИ».

Инвертор в электросхемах

В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.

Заключение: схема соответствует логической операции «НЕ».

Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.

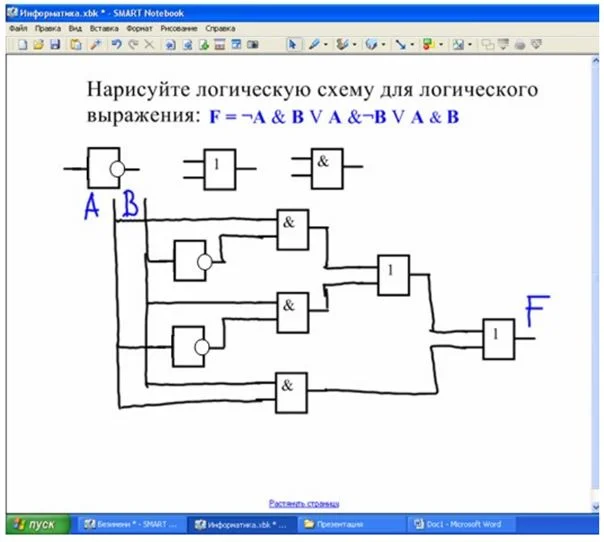
Обозначение логических элементов

Удобно создавать электросхемы в ПО SmartNotebook, которое используется с интерактивной доской.

Источник