ЛОГИЧЕСКИЕ
СВЯЗКИ — символы логических языков,
используемые для образования сложных
высказываний (формул) из элементарных.
Логическими связками называют также
соответствующие этим символам союзы
естественного языка. Обычно используются
такие логические связки, как конъюнкция
(союз “и”, символические обозначения:
&, л и точка в виде знака умножения,
которые часто опускают, записывая
конъюнкцию А и В как AB), дизъюнкция
(нестрогий союз “или”, обозначается
как “v”), импликация
(“если…, то”, обозначается с помощью
знака <о” и различного рода стрелок),
отрицание
(“неверно, что…”, обозначается: -ι,
ЛОГИЧЕСКИЕ СВЯЗКИ или чертой над
отрицаемым выражением). Из перечисленных
отрицание является одноместной (унарной)
связкой. Другие являются двухместными
(бинарными). В принципе логические связки
могут быть сколь угодно местными, но на
практике более, чем бинарные, используются
очень редко. В классической логике
(Логика,
Логика высказываний) любые многоместные
логические связки выразимы через
перечисленные. Некоторый практический
смысл
дает использование тернарной логической
связки, называемой условной дизъюнкцией,
связывающей три высказывания А, В и С и
означающей, что “А в случае В, и С в
случае нв-?” или формально: (В з А)&(-,
В э О (Сидоренко Е. А. Пропозициональное
исчисление
с условной дизъюнкцией.— В кн.: Методы
логического анализа. М.,1977).
Классическая
логика
рассматривает логические связки
экстенсионально (игнорируя содержательный
смысл связываемых ими высказываний)
как функции истинности, определяемые
истинностными значениями связываемых
ими высказываний. При двух имеющих место
в этой логике истинностных значе
ниях
1 (истинно) и 0 (ложно) высказывания А и В
могут иметь четыре возможных набора
упорядоченных истинностных зна^ чений:
, <1,0>, <0,1>, <0,0>. Пропозициональная
истинностная функция
ставит в соответствие каждому
перечисленному набору одно из значений
истинности — 1 или 0. Всгго таких функций
16. Конъюнкция приписывает выражению
А&.В значение
1 только в случае, когда как Л, так и В
истинны, т. е. оба имеют значение 1, в
остальных случаях значение А&.В равно
0. Дизъюнкция Α ν В, напротив, ложна только
в одном случае, когда ложны как А, так и
В. Импликация А э В является ложной
только при истинном (антецеденте) А и
ложном (консеквенте) В. В остальных
случаях А => В принимает значение 1. Из
четырех одноместных функций интерес
представляет только отрицание, меняющее
значение высказывания на противоположное:
когда А — истинно, —А — ложно, и наоборот.
Все другие унарные и бинарные классические
функции могут быть выражены через
представленные. Когда принятая в
соответствующей семантике система
логических связок позволяет дать
определение
всех остальных, ее называют функционально
полной. К полным системам в классической
логике относятся, в частности, конъюнкция
и отрицание; дизъюнкция и отрицание;
импликация и отрицание. Конъюнкция и
дизъюнкция определимы друг через друга
за счет эквивалентностей (А&В) =
-i(-i/4v-i.ß) и (A v В) a -,(-Α&-ιΒ), именуемых
законами де Моргана, а также: (A^B)s(-iA^ В),
(А&В) s -,(А э -ιΒ), (Α ν В) = ((А => В) •зА).
Любая эквивалентность
видаЛ = В имеет силу только тогда, когда
общезначима (всегда истинна) конъюнкция
(А =) В)&(В э А).
Функции
антидизъюнкция и антиконъюнкция,
определимые соответственно как -ι(Α ν
В) и —(А&.В), также представляют каждая
в отдельности функционально полную
систему связок. Это последнее обстоятельство
было известно уже Ч. Пирсу (неопубликованная
при его жизни работа 1880 г.) и было
переоткрыто X. Шеффером (H. M. Shefier). Используя
антидизъюнкцию как единственную
логическую связку, Шеффер в 1913 построил
полное исчисление
высказываний. Антидизъюнкцию обозначают
А В и называют штрихом Ше4)фера, читая
данное
выражение, как “не-Д и не-В”. Ж. Нико (J.
G. P. Nicod) употребил то же обозначение для
антиконъюнкции (“Неверно, что одновременно
А и В”) и с помощью только этой связки
в 1917 сформулировал полное исчисление
высказываний с одной (всего!) аксиомой
и одним правилом вывода. Т. о., штрихом
Шеффера называют по сути саму вертикальную
черту, которая у разных авторов может
обозначать как антидизъюнкцию, так и
антиконъюнкцию.
Экстенсиональность
логических связок придает им однозначность,
упрощает проблему построения логических
исчислений, дает возможность
решать для последних метатеоретические
проблемы непротиворечивости, разрешимости,
полноты (см. Металогика).
Однако в некоторых случаях
истинностно-функциональная трактовка
связок приводит к значительному
несоответствию с тем, как они понимаются
в естественном языке. Так, указанная
истинностная интерпретация
импликации вынуждает признавать верными
предложения вида “Если А, то В” даже в
том случае, когда между высказываниями
А и В (и, соответственно, событиями, о
которых в них идет речь)
нет никакой реальной связи. Достаточно,
чтобы А было ложным или В — истинным.
Поэтому из двух предложений: “Если А,
то В” и “Если В, то А”, по крайней мере
одно приходится признавать верным, что
плохо сообразуется с обычным употреблением
условной связки. Импликацию в данном
случае специально называют “материальной”,
отличая ее тем самым от условного союза,
предполагающего, что между антецедентом
и консеквентом истинного условного
высказывания имеется действительная
связь.
При этом материальная импликация может
прекрасно использоваться во многих
контекстах, напр., математических, когда
при этом не забывают о ее специфических
особенностях. В некоторых случаях,
однако, именно контекст
не позволяет трактовать условный союз
как материальную импликацию, предполагая
взаимосвязь
высказываний. Для анализа таких контекстов
приходится строить специальные
неклассические
логики, напр., релевантные (см.
Релевантная
логика), в язык
которых вместо материальной импликации
(или наряду с ней) вводятся другие
импликации, которые понимаются
интенсионально (содержательно) и верность
которых не может быть обоснована
истинностно-функционально. Интенсионально
могут трактоваться также другие
логические связки
27.
Таблица истинности сложных суждений.
28.
Отношение между сложными высказываниями.
29.
Закон тождества.
Закон
тождества или иными словами закон
определенности мышления. В ходе любого
обсуждения той или иной проблемы, будь
это судебное заседание или научная
дискуссия объект мысли, рассматриваемый
в данном конкретном случае должен
оставаться самим собой. За этим законом
объективно стоит определенность или
тождественность объектов бытия самим
себе. При всей изменчивости существующей
реальности любой объект мысли на данный
момент его рассмотрения остается равным
самому себе, т.к. в противном случае
невозможно определить что же является
предметом рассмотрения. Своеобразным
отражением закона постоянства и является
логический закон тождества, требующий
не подменять рассматриваемый или
исследуемый объект мысли чем-то иным.
30. Закон
непротиворечивости.
Закон логического
непротиворечия, согласно этому закону
необходимым требованием нормального
мышления является принцип: два
противоположных высказывания об одном
и том же объекте мысли в одном и том же
отношении одновременно истинным быть
не могут. Сознательное использование
этого закона в практике мышления
позволяет избегать противоречивых
высказываний и обеспечивает логическую
убедительность и обоснованность
приводимых аргументов в доказательстве.
31. Закон
исключительного третьего.
Закон исключенного
третьего является дополнением к закону
логического непротиворечия и утверждает,
что из двух противоречащих друг другу
высказываний, одно истинно, другое
ложно, а третьего не дано. При знании
истинности одного из противоречащих
суждений можно отбрасывать другое как,
несомненно, не истинное, не прибегая к
доказыванию этой неистинности.
32. Закон
достаточного основания.
Закон достаточного
основания был сформулирован уже в Новое
время в ХУII в. немецким философом
Лейбницем. Этот закон требует, чтобы
выдвигаемое утверждение, если оно не
самоочевидно, было достаточно обосновано.
По поводу этого закона в современной
логике нет однозначного мнения. Что
касается обоснованности теоретических
утверждений, то вряд ли здесь можно
обойтись данным законом. В юридической
деятельности этот закон сохраняет свое
значение в полном объеме. Любое юридическое
решение не может не быть достаточно
обоснованным.
33.Понятие умозаключения.
Виды умозаключения.
Умозаключение –
это форма мышления, посредством которой
из одного или нескольких суждений
выводится новое суждение. Например:
“Все космонавты – мужественные люди”.
Это означает: “Некоторые мужественные
люди – космонавты”. Любое умозаключение
состоит из посылок, заключения и вывода.
Посылками умозаключения называются
исходные суждения, из которых выводится
новое суждение. Заключением называется
новое суждение, полученное логическим
путем из посылок. Логический переход
от посылок к заключению называется
выводом. Например: “Судья не может
участвовать в рассмотрении дела, если
он является потерпевшим (1). Судья Н. –
потерпевший (2). Значит, он не может
участвовать в рассмотрении дела (3)”. В
этом умозаключении 1-е и 2-е суждения
являются посылками, 3-е суждение –
заключением. Поскольку всякое умозаключение
вообще, безотносительно к его формам,
представляет собой логическое следование
одних знаний из других, то в зависимости
от характера логического следования,
от направленности хода мысли в
умозаключении можно выделить три
коренных, фундаментальных типа, которые
и будут положены в основу всего
последующего анализа выводного знания.
Это дедукция, индукция и традукция.
Дедукция– это умозаключение от более
общего знания к менее общему. Типичный
пример дедукции, идущий от древности:
Все люди смертны. Сократ – человек.
Следовательно, Сократ смертен. Индукция
– умозаключение от менее общего знания
к более общему. Например: наблюдая за
движением каждой из планет Солнечной
системы, можно сделать общий вывод: “Все
планеты движутся с Запада на Восток”.
Традукция – умозаключение, в котором
посылки и заключение – одной и той же
степени общности (умозаключение по
аналогии). Пример: “На Земле, где есть
атмосфера, смена дня и ночи, времен года,
есть также и жизнь. На Марсе, подобно
Земле, есть атмосфера, смена дня и ночи,
смена времен года. Возможно, что на Марсе
тоже есть жизнь”
В зависимости от
строгости правил вывода различают два
вида умозаключений: демонстративные
(необходимые) и недемонстративные
(правдоподобные). Демонстративные
умозаключения характеризуются тем, что
заключение в них с необходимостью
следует из посылок, т. е. логическое
следование в такого рода выводах
представляет собой логический закон.
В недемонстративных умозаключениях
правила вывода обеспечивают лишь
вероятное следование заключения из
посылок.
Непосредственные
и посредственные умозаключения.
Дедуктивные
умозаключения подразделяются, прежде
всего, на непосредственные и опосредованные.
Дедуктивным называется умозаключение,
в котором переход от общего знания к
частному является логически необходимым.
Непосредственные умозаключения – это
такие, которые делаются из одной посылки.
Опосредованные – те, которые делаются
из нескольких (двух и более) посылок.
Непосредственные умозаключения можно
получать, прежде всего, из простых
суждений – как атрибутивных, так и
реляционных (суждений с отношением).
Правила дедуктивного вывода определяются
характером посылок, которые могут быть
простыми (категорическими) или сложными
суждениями.
Суждение, содержащее
новое знание, может быть получено
посредством преобразования некоторого
суждения. Поскольку исходное (преобразуемое)
суждение рассматривается как посылка,
а новое, полученное в результате
преобразования суждение – как заключение,
высказывания, построенные посредством
преобразования суждений, называются
непосредственными умозаключениями. К
ним относятся: 1) превращение, 2) обращение,
3) противопоставление предикату, 4)
умозаключения по логическому квадрату.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
In logic, a logical connective (also called a logical operator, sentential connective, or sentential operator) is a logical constant. They can be used to connect logical formulas. For instance in the syntax of propositional logic, the binary connective 



Common connectives include negation, disjunction, conjunction, and implication. In standard systems of classical logic, these connectives are interpreted as truth functions, though they receive a variety of alternative interpretations in nonclassical logics. Their classical interpretations are similar to the meanings of natural language expressions such as English «not», «or», «and», and «if», but not identical. Discrepancies between natural language connectives and those of classical logic have motivated nonclassical approaches to natural language meaning as well as approaches which pair a classical compositional semantics with a robust pragmatics.
A logical connective is similar to, but not equivalent to, a syntax commonly used in programming languages called a conditional operator.[1][better source needed]
Overview[edit]
In formal languages, truth functions are represented by unambiguous symbols. This allows logical statements to not be understood in an ambiguous way. These symbols are called logical connectives, logical operators, propositional operators, or, in classical logic, truth-functional connectives. For the rules which allow new well-formed formulas to be constructed by joining other well-formed formulas using truth-functional connectives, see well-formed formula.
Logical connectives can be used to link zero or more statements, so one can speak about n-ary logical connectives. The boolean constants True and False can be thought of as zero-ary operators. Negation is a 1-ary connective, and so on.
| Symbol, name | Truth table |
Venn diagram |
|||||
|---|---|---|---|---|---|---|---|
| Zeroary connectives (constants) | |||||||
| ⊤ | Truth/tautology | 1 | |||||
| ⊥ | Falsity/contradiction | 0 | |||||
| Unary connectives | |||||||
| P = | 0 | 1 | |||||
| Proposition P | 0 | 1 | |||||
| ¬ | Negation | 1 | 0 | ||||
| Binary connectives | |||||||
| P = | 0 | 1 | |||||
| Q = | 0 | 1 | 0 | 1 | |||
| Proposition P | 0 | 0 | 1 | 1 | |||
| Proposition Q | 0 | 1 | 0 | 1 | |||
| ∧ | Conjunction | 0 | 0 | 0 | 1 | ||
| ↑ | Alternative denial | 1 | 1 | 1 | 0 | ||
| ∨ | Disjunction | 0 | 1 | 1 | 1 | ||
| ↓ | Joint denial | 1 | 0 | 0 | 0 | ||
| → | Material conditional | 1 | 1 | 0 | 1 | ||
 |
Exclusive or | 0 | 1 | 1 | 0 | ||
| ↔ | Biconditional | 1 | 0 | 0 | 1 | ||
| ← | Converse implication | 1 | 0 | 1 | 1 | ||
| More information |
List of common logical connectives[edit]
Commonly used logical connectives include:[2]
- Negation (not): ¬ , N (prefix), ~[3]
- Conjunction (and): ∧ , K (prefix), & , ∙
- Disjunction (or): ∨, A (prefix)
- Material implication (if…then): → , C (prefix), ⇒ , ⊃
- Biconditional (if and only if): ↔ , E (prefix), ≡ , =
Alternative names for biconditional are iff, xnor, and bi-implication.
For example, the meaning of the statements it is raining (denoted by P) and I am indoors (denoted by Q) is transformed, when the two are combined with logical connectives:
It is also common to consider the always true formula and the always false formula to be connective:
- True formula (⊤, 1, V [prefix], or T)
- False formula (⊥, 0, O [prefix], or F)
History of notations[edit]
Some authors used letters for connectives at some time of the history: u. for conjunction (German’s «und» for «and») and o. for disjunction (German’s «oder» for «or») in earlier works by Hilbert (1904); Np for negation, Kpq for conjunction, Dpq for alternative denial, Apq for disjunction, Xpq for joint denial, Cpq for implication, Epq for biconditional in Łukasiewicz (1929);[15] cf. Polish notation.
Redundancy[edit]
Such a logical connective as converse implication «←» is actually the same as material conditional with swapped arguments; thus, the symbol for converse implication is redundant. In some logical calculi (notably, in classical logic), certain essentially different compound statements are logically equivalent. A less trivial example of a redundancy is the classical equivalence between ¬P ∨ Q and P → Q. Therefore, a classical-based logical system does not need the conditional operator «→» if «¬» (not) and «∨» (or) are already in use, or may use the «→» only as a syntactic sugar for a compound having one negation and one disjunction.
There are sixteen Boolean functions associating the input truth values P and Q with four-digit binary outputs.[16] These correspond to possible choices of binary logical connectives for classical logic. Different implementations of classical logic can choose different functionally complete subsets of connectives.
One approach is to choose a minimal set, and define other connectives by some logical form, as in the example with the material conditional above.
The following are the minimal functionally complete sets of operators in classical logic whose arities do not exceed 2:
- One element
- {↑}, {↓}.
- Two elements
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
- Three elements
,
,
,
,
,
.
Another approach is to use with equal rights connectives of a certain convenient and functionally complete, but not minimal set. This approach requires more propositional axioms, and each equivalence between logical forms must be either an axiom or provable as a theorem.
The situation, however, is more complicated in intuitionistic logic. Of its five connectives, {∧, ∨, →, ¬, ⊥}, only negation «¬» can be reduced to other connectives (see False (logic) § False, negation and contradiction for more). Neither conjunction, disjunction, nor material conditional has an equivalent form constructed from the other four logical connectives.
Natural language[edit]
The standard logical connectives of classical logic have rough equivalents in the grammars of natural languages. In English, as in many languages, such expressions are typically grammatical conjunctions. However, they can also take the form of complementizers, verb suffixes, and particles. The denotations of natural language connectives is a major topic of research in formal semantics, a field that studies the logical structure of natural languages.
The meanings of natural language connectives are not precisely identical to their nearest equivalents in classical logic. In particular, disjunction can receive an exclusive interpretation in many languages. Some researchers have taken this fact as evidence that natural language semantics is nonclassical. However, others maintain classical semantics by positing pragmatic accounts of exclusivity which create the illusion of nonclassicality. In such accounts, exclusivity is typically treated as a scalar implicature. Related puzzles involving disjunction include free choice inferences, Hurford’s Constraint, and the contribution of disjunction in alternative questions.
Other apparent discrepancies between natural language and classical logic include the paradoxes of material implication, donkey anaphora and the problem of counterfactual conditionals. These phenomena have been taken as motivation for identifying the denotations of natural language conditionals with logical operators including the strict conditional, the variably strict conditional, as well as various dynamic operators.
The following table shows the standard classically definable approximations for the English connectives.
| English word | Connective | Symbol | Logical gate |
|---|---|---|---|
| not | negation | «¬» | NOT |
| and | conjunction | «∧» | AND |
| or | disjunction | «∨» | OR |
| if…then | material implication | «→» | IMPLY |
| …if | converse implication | «←» | |
| if and only if | biconditional | «↔» | XNOR |
| not both | alternative denial | «↑» | NAND |
| neither…nor | joint denial | «↓» | NOR |
| but not | material nonimplication | «↛» | NIMPLY |
Properties[edit]
Some logical connectives possess properties that may be expressed in the theorems containing the connective. Some of those properties that a logical connective may have are:
- Associativity
- Within an expression containing two or more of the same associative connectives in a row, the order of the operations does not matter as long as the sequence of the operands is not changed.
- Commutativity
- The operands of the connective may be swapped, preserving logical equivalence to the original expression.
- Distributivity
- A connective denoted by · distributes over another connective denoted by +, if a · (b + c) = (a · b) + (a · c) for all operands a, b, c.
- Idempotence
- Whenever the operands of the operation are the same, the compound is logically equivalent to the operand.
- Absorption
- A pair of connectives ∧, ∨ satisfies the absorption law if
for all operands a, b.
- Monotonicity
- If f(a1, …, an) ≤ f(b1, …, bn) for all a1, …, an, b1, …, bn ∈ {0,1} such that a1 ≤ b1, a2 ≤ b2, …, an ≤ bn. E.g., ∨, ∧, ⊤, ⊥.
- Affinity
- Each variable always makes a difference in the truth-value of the operation or it never makes a difference. E.g., ¬, ↔,
, ⊤, ⊥.
- Duality
- To read the truth-value assignments for the operation from top to bottom on its truth table is the same as taking the complement of reading the table of the same or another connective from bottom to top. Without resorting to truth tables it may be formulated as g̃(¬a1, …, ¬an) = ¬g(a1, …, an). E.g., ¬.
- Truth-preserving
- The compound all those arguments are tautologies is a tautology itself. E.g., ∨, ∧, ⊤, →, ↔, ⊂ (see validity).
- Falsehood-preserving
- The compound all those argument are contradictions is a contradiction itself. E.g., ∨, ∧,
, ⊥, ⊄, ⊅ (see validity).
- Involutivity (for unary connectives)
- f(f(a)) = a. E.g. negation in classical logic.
For classical and intuitionistic logic, the «=» symbol means that corresponding implications «…→…» and «…←…» for logical compounds can be both proved as theorems, and the «≤» symbol means that «…→…» for logical compounds is a consequence of corresponding «…→…» connectives for propositional variables. Some many-valued logics may have incompatible definitions of equivalence and order (entailment).
Both conjunction and disjunction are associative, commutative and idempotent in classical logic, most varieties of many-valued logic and intuitionistic logic. The same is true about distributivity of conjunction over disjunction and disjunction over conjunction, as well as for the absorption law.
In classical logic and some varieties of many-valued logic, conjunction and disjunction are dual, and negation is self-dual, the latter is also self-dual in intuitionistic logic.
|
This section needs expansion. You can help by adding to it. (March 2012) |
Order of precedence[edit]
As a way of reducing the number of necessary parentheses, one may introduce precedence rules: ¬ has higher precedence than ∧, ∧ higher than ∨, and ∨ higher than →. So for example, 

Here is a table that shows a commonly used precedence of logical operators.[17]
| Operator | Precedence |
|---|---|
 |
1 |
 |
2 |
 |
3 |
 |
4 |
 |
5 |
However, not all compilers use the same order; for instance, an ordering in which disjunction is lower precedence than implication or bi-implication has also been used.[18] Sometimes precedence between conjunction and disjunction is unspecified requiring to provide it explicitly in given formula with parentheses. The order of precedence determines which connective is the «main connective» when interpreting a non-atomic formula.
Computer science[edit]
|
This section needs expansion. You can help by adding to it. (March 2012) |
A truth-functional approach to logical operators is implemented as logic gates in digital circuits. Practically all digital circuits (the major exception is DRAM) are built up from NAND, NOR, NOT, and transmission gates; see more details in Truth function in computer science. Logical operators over bit vectors (corresponding to finite Boolean algebras) are bitwise operations.
But not every usage of a logical connective in computer programming has a Boolean semantic. For example, lazy evaluation is sometimes implemented for P ∧ Q and P ∨ Q, so these connectives are not commutative if either or both of the expressions P, Q have side effects. Also, a conditional, which in some sense corresponds to the material conditional connective, is essentially non-Boolean because for if (P) then Q;, the consequent Q is not executed if the antecedent P is false (although a compound as a whole is successful ≈ «true» in such case). This is closer to intuitionist and constructivist views on the material conditional— rather than to classical logic’s views.
Table and Hasse diagram[edit]
The 16 logical connectives can be partially ordered to produce the following Hasse diagram.
The partial order is defined by declaring that 


See also[edit]
- Boolean domain
- Boolean function
- Boolean logic
- Boolean-valued function
- Four-valued logic
- List of Boolean algebra topics
- Logical constant
- Modal operator
- Propositional calculus
- Truth function
- Truth table
- Truth values
References[edit]
- ^ Cogwheel. «What is the difference between logical and conditional /operator/». Stack Overflow. Retrieved 9 April 2015.
- ^ «Connective | logic». Encyclopedia Britannica. Retrieved 2020-09-02.
- ^ Weisstein, Eric W. «Negation». mathworld.wolfram.com. Retrieved 2020-09-02.
- ^ a b Heyting (1929) Die formalen Regeln der intuitionistischen Logik.
- ^ Denis Roegel (2002),
A brief survey of 20th century logical notations (see chart on page 2). - ^ a b c d Russell (1908) Mathematical logic as based on the theory of types (American Journal of Mathematics 30, p222–262, also in From Frege to Gödel edited by van Heijenoort).
- ^ Peano (1889) Arithmetices principia, nova methodo exposita.
- ^ a b Schönfinkel (1924) Über die Bausteine der mathematischen Logik, translated as On the building blocks of mathematical logic in From Frege to Gödel edited by van Heijenoort.
- ^ Peirce (1867) On an improvement in Boole’s calculus of logic.
- ^ Hilbert (1917/1918) Prinzipien der Mathematik (Bernays’ course notes).
- ^ Vax (1982) Lexique logique, Presses Universitaires de France.
- ^ Tarski (1940) Introduction to logic and to the methodology of deductive sciences.
- ^ Gentzen (1934) Untersuchungen über das logische Schließen.
- ^ Chazal (1996) : Éléments de logique formelle.
- ^ See Roegel
- ^ Bocheński (1959), A Précis of Mathematical Logic, passim.
- ^ O’Donnell, John; Hall, Cordelia; Page, Rex (2007), Discrete Mathematics Using a Computer, Springer, p. 120, ISBN 9781846285981.
- ^ Jackson, Daniel (2012), Software Abstractions: Logic, Language, and Analysis, MIT Press, p. 263, ISBN 9780262017152.
Sources[edit]
- Bocheński, Józef Maria (1959), A Précis of Mathematical Logic, translated from the French and German editions by Otto Bird, D. Reidel, Dordrecht, South Holland.
- Enderton, Herbert (2001), A Mathematical Introduction to Logic (2nd ed.), Boston, MA: Academic Press, ISBN 978-0-12-238452-3
- Gamut, L.T.F (1991), «Chapter 2», Logic, Language and Meaning, vol. 1, University of Chicago Press, pp. 54–64, OCLC 21372380
- Rautenberg, W. (2010), A Concise Introduction to Mathematical Logic (3rd ed.), New York: Springer Science+Business Media, doi:10.1007/978-1-4419-1221-3, ISBN 978-1-4419-1220-6.
- Humberstone, Lloyd (2011). The Connectives. MIT Press. ISBN 978-0-262-01654-4.
External links[edit]
- «Propositional connective», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Lloyd Humberstone (2010), «Sentence Connectives in Formal Logic», Stanford Encyclopedia of Philosophy (An abstract algebraic logic approach to connectives.)
- John MacFarlane (2005), «Logical constants», Stanford Encyclopedia of Philosophy.
2.1. Высказывания
2.2. Логические связки (операции) над высказываниями
2.3. Пропозициональные формулы
2.4. Булевы функции. Таблицы истинности
2.5. Булевы функции одной переменной
2.6. Булевы функции двух переменных
2.7. Существенные и несущественные переменные
2.8. Равносильные формулы. Основные равносильности
2.9. Основные тавтологии
2.10. Основные равносильности
2.11. Понятие двойственной функции
2.12. Некоторые двойственные функции
2.13. Элементарные канонические формы
2.14. Нормальные формы формул
2.15. Приведение формул к нормальным формам
2.16. Минимизация д.н.ф.
2.17. Полные системы функций. Полином Жегалкина
2.18. Функционально замкнутые классы функций
2.19. Понятие алгоритма. Описание машины Тьюринга
2.1. Высказывания
Определение. Высказывание – повествовательное утверждение, которое либо истинно либо ложно (не то и другое одновременно).
Примеры высказываний: «Тише едешь – дальше будешь», «Париж – столица Франции». Но «Как бы чего не вышло» или «Миру – мир» не являются высказываниями.
Определение. Высказывание называется простым (элементарным), если оно рассматривается как одно неделимое целое.
Определение. Сложное высказывание – высказывание, составленное из простых с помощью логических связок.
2.2. Логические связки (операции) над высказываниями
Определение. Конъюнкцией («и») высказываний P и Q называется высказывание, истинное тогда и только тогда, когда оба истинны. Обозначается P&Q.
Таблица истинности:
|
P |
Q |
P&Q |
|
л |
л |
л |
|
л |
и |
л |
|
и |
л |
л |
|
и |
и |
и |
Определение. Дизъюнкцией («или») высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба ложны. Обозначается .
Таблица истинности:
|
P |
Q |
|
|
л |
л |
л |
|
л |
и |
и |
|
и |
л |
и |
|
и |
и |
и |
Определение. Отрицанием («не») высказывания P называется высказывание, ложное тогда и только тогда, когда P истинно. Обозначается или
.
Таблица истинности:
|
P |
|
|
л |
и |
|
и |
л |
Определение. Импликацией высказываний P и Q называется высказывание, ложное, когда P истинно, а Q ложно, и истинное во всех остальных случаях. Обозначается 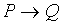
Таблица истинности:
|
P |
Q |
|
|
л |
л |
и |
|
л |
и |
и |
|
и |
л |
л |
|
и |
и |
и |
Определение. Эквивалентностью высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q совпадают, и ложное в противном случае. Обозначается или
.
Таблица истинности:
|
P |
Q |
|
|
л |
л |
и |
|
л |
и |
л |
|
и |
л |
л |
|
и |
и |
и |
Определение. Неравнозначностью (сложение по модулю 2) высказываний P и Q называется высказывание истинное, когда истинностные значения P и Q различны, и ложное в противном случае. Обозначается .
Таблица истинности:
|
P |
Q |
|
|
л |
л |
л |
|
л |
и |
и |
|
и |
л |
и |
|
и |
и |
л |
2.3. Пропозициональные формулы
Рассмотрим алфавит , где
,
,
.
Символы из называются переменными высказывания или пропозициональными переменными.
Символы из называются логическими связками.
Скобки из называются вспомогательными символами.
Определение. Пропозициональная формула определяется следующим образом:
1) пропозициональная переменная есть формула;
2) если P и Q – формулы, то Ø P, (P&Q), (PÚ Q) ,(P® Q) ,(PÅ Q) ,(P|Q), (P¯ Q) – формулы,
3) других формул нет.
При этом
а) внешние скобки у формул опускаются;
б) устанавливаются следующие приоритеты:
Ø – выполняется в первую очередь;
& – во вторую очередь;
Ú , ® , Å , |, ¯ – в третью очередь.
2.4. Булевы функции. Таблицы истинности
Определение. Булевой функцией 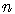
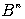
, где
.
Способы задания:
1) таблицами истинности; при этом 0 интерпретируется как «ложь», а 1 – как «истина»;
2) пропозициональными формулами.
Таблица истинностей некоторых логических связок:
|
x |
y |
x&y |
xÚ y |
Ø x |
x® y |
XÅ y |
x~y |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
2.5. Булевы функции одной переменной
|
|
|
Обозначение |
Наименование |
|
|
|
|
Константа 0 |
|
|
|
|
Тождественная |
|
|
|
|
Отрицание |
|
|
|
|
Константа 1 |
2.6. Булевы функции двух переменных
|
|
|
Обозначение |
Наименование |
|
|
0 0 0 0 |
|
Константа 0 |
|
|
0 0 0 1 |
|
Конъюнкция |
|
|
0 0 1 0 |
|
|
|
|
0 0 1 1 |
|
|
|
|
0 1 0 0 |
|
|
|
|
0 1 0 1 |
|
|
|
|
0 1 1 0 |
|
Сложение |
|
|
0 1 1 1 |
|
Дизъюнкция |
|
|
1 0 0 0 |
|
Стрелка Пирса |
|
|
1 0 0 1 |
|
Эквиваленция |
|
|
1 0 1 0 |
||
|
|
1 0 1 1 |
|
Импликация |
|
|
1 1 0 0 |
|
|
|
|
1 1 0 1 |
|
Импликация |
|
|
1 1 1 0 |
|
Штрих Шеффера |
|
|
1 1 1 1 |
1 |
Константа 1 |
2.7. Существенные и несущественные переменные
Определение. Переменная называется существенной для булевой функции
, если
.
Определение. Переменная называется несущественной для булевой функции
, если
.
2.8. Равносильные формулы. Основные равносильности
Определение. Формула называется тождественно истинной, или тавтологией, если эта формула принимает значение 1 при всех наборах значений переменных.
Определение. Формула называется тождественно ложной, или противоречием, если эта формула принимает значение 0 при всех наборах значений переменных.
2.9. Основные тавтологии
|
1. |
Закон исключенного третьего |
|
2. |
|
|
3. |
|
|
4. |
Цепное рассуждение |
|
5. |
|
|
6. |
Определение. Формулы P и Q называются равносильными (обозначается ), если при любых значениях переменных значение формулы P совпадает со значением Q.
2.10. Основные равносильности
|
1. |
Коммутативность |
|
3. 4. |
Ассоциативность |
|
5. 6. |
Дистрибутивность |
|
7. |
Идемпотентность |
|
9. |
Законы исключенного третьего и противоречия |
|
11. 12. |
Законы де Моргана |
|
13. 14. |
Законы поглощения |
|
15. |
Правило склеивания |
|
16. 18. |
|
|
20. |
Закон двойного отрицания |
|
21. 22. 23. 24. |
|
|
25. |
Коммутативность |
|
26. |
Ассоциативность |
|
27. |
Дистрибутивность |
|
28. 30. |
Замечание. Здесь P, Q и R —пропозициональные формулы.
2.11. Понятие двойственной функции
Определение. Функцией, двойственной к булевой функции , называется функция
.
Определение. Функция называется самодвойственной, если .
Теорема. (Принцип двойственности.) Пусть ,…,
и
— булевы функции и пусть
=
— сложная булева функция. Тогда
=
Следствие. Пусть P и Q —формулы. Если , тогда
.
Принцип двойственности позволяет получать из доказанных равносильностей целый ряд новых. Кроме того, СКНФ(f)=.
2.12. Некоторые двойственные функции
|
|
|
|
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
Замечание. |
2.13. Элементарные канонические формы
Определение. Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза.
Определение. Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более 1 раза.
2.14. Нормальные формы формул
Определение. Дизъюнктивной нормальной формой (Д.Н.Ф.) называется произвольная дизъюнкция элементарных конъюнкций.
Определение. Конъюнктивной нормальной формой (К.Н.Ф.) называется произвольная конъюнкция элементарных дизъюнкций.
Определение. К.Н.Ф. называется совершенной и обозначается С.К.Н.Ф., если каждая переменная входит в каждую элементарную дизъюнкцию ровно один раз с отрицанием или без.
Определение. Д.Н.Ф. называется совершенной и обозначается С.Д.Н.Ф, если каждая переменная входит в каждую элементарную конъюнкцию ровно один раз с отрицанием или без.
Пример: – Д.Н.Ф;
– С.Д.Н.Ф.
Теорема. Любая логическая функция кроме 0 имеет единственную С.Д.Н.Ф: .
Теорема. Любая логическая функция кроме 1 имеет единственную С.К.Н.Ф: .
Здесь 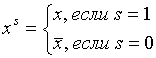
Пример. Пусть функция трех переменных задана таблицей истинности:
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Записать ее С.Д.Н.Ф. и С.К.Н.Ф.
С.Д.Н.Ф.(f)=
С.К.Н.Ф.(f)=
2.15. Приведение формул к нормальным формам
Любую логическую формулу (кроме 0) можно привести к С.Д.Н.Ф. следующим образом:
- Все не булевские операции заменить на булевские (&, Ú , Ø ) c помощью равносильностей:
;
;
;
;
.
- Все отрицания «спустить» до переменных с помощью законов де Моргана.
- Раскрыть скобки (дистрибутивность, ассоциативность).
- Удалить лишние конъюнкции, повторения переменных в конъюнкциях и константы.
Для приведения к С.Д.Н.Ф:
- Расщепить те конъюнкции, которые содержат не все переменные.
2.16. Минимизация д.н.ф.
Д.Н.Ф, содержащую минимальное число вхождений переменных, будем считать минимальной.
Приведем 2 наиболее простых метода минимизации Д.Н.Ф. функции:
- Группировка: элементарные конъюнкции
,
в ДНФ группируются в пары так, что после вынесения за скобку общего множителя K подформула
имела вид
или
. Далее заменяем
на эквивалентную ей конъюнкцию K.
Пример:
.
- Метод Блейка состоит в применении двух правил:
а) обобщенное склеивание – первое правило. С помощью формулы производим операцию обобщенного склеивания в Д.Н.Ф. пока это возможно. Для этого в Д.Н.Ф. отыскиваем подформулы вида
и добавляем к ним
. На этом этапе формула усложняется.
б) поглощение – второе правило. Оно основано на равенстве
.
Находим в Д.Н.Ф. конъюнкции с минимальным числом сомножителей и все конъюнкции, их содержащие, вычеркиваем.
Пример: .
Разумно в Д.Н.Ф. сначала применить метод группировки (как более простой), а затем метод Блейка.
2.17. Полные системы функций. Полином Жегалкина
Определение. Множество булевых функций называется полной системой, если любая булева функция может быть выражена через функции этого множества с помощью суперпозиции. Минимальная полная система называется базисом.
Примеры базисов:
— дизъюнктивный базис;
— конъюнктивный базис;
— базис Жегалкина;
— базис Пирса;
— базис Шеффера.
Определение Логическая функция, представленная над базисом называется многочленом Жегалкина. Он имеет вид:
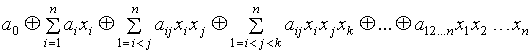
где константы .
2.18. Функционально замкнутые классы функций
Ведем следующие классы Поста:
=
– Класс функций, сохраняющих 0.
=
– Класс функций, сохраняющих 1.
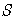
– Класс самодвойственных функций.
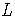
– Класс линейных функций.
=
– Класс монотонных функций.
Каждый класс Поста является функционально замкнутым, т.е. все функции, реализованные формулами над данным классом, также принадлежат данному классу.
Таблица принадлежности функциональным классам основных булевых функций:
|
|
|
|
|
|
|
|
|
— |
— |
|
|
— |
|
|
|
|
— |
— |
|
|
|
|
|
— |
— |
|
|
|
— |
|
— |
— |
— |
|
|
|
— |
— |
|
— |
|
|
— |
|
— |
|
— |
|
|
— |
— |
— |
— |
— |
Теорема. (Теорема Поста.) Для того, чтобы система булевых функций была полной, необходимо и достаточно, чтобы для каждого из классов
,
,
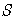
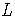
нашлась функция
из системы, не принадлежащая данному классу.
2.19. Понятие алгоритма. Описание машины Тьюринга
Для решения ряда однотипных задач иногда целесообразно использовать чисто механические вычислительные процессы. Описание таких процессов называют алгоритмами.
Интуитивно: алгоритм – это некоторое формальное предписание, действуя согласно которому, можно получить решение задачи. Примеры алгоритмов:
- Нахождение наибольшего общего делителя двух натуральных чисел.
- Извлечение корня квадратного из рационального числа с заданной точностью.
- Вычисление ранга матрицы, и так далее.
Перечисленные алгоритмы имеют ряд общих черт, которые естественно считать присущими любому алгоритму:
Дискретность. Решение задачи разбивается на этапы, каждый из которых прост и локален.
Детерминированность. После выполнения очередного этапа однозначно определено, что сделать на следующем этапе.
Направленность. Должно быть указано, что считать результатом применения алгоритма.
Массовость. Алгоритм служит для решения целого класса однотипных задач.
Конечность. Для решения задачи выполняется конечная последовательность шагов алгоритма.
Тезис Тьюринга Всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.
Определение. Машиной Тьюринга (м-т) называется тройка , где
—внешний алфавит, обычно
;
—внутренний алфавит, элементами которого являются состояния управляющего устройства,
—заключительное состояние,
—начальное состояние;
—программа, состоящая из команд вида:
, где
—один из символов:
(налево),
(направо),
(на месте),
,
.
Имеется бесконечная в обе стороны лента, разбитая на ячейки. В начальный момент в конечном числе ячеек записаны символы из , в остальных ячейках записан пустой символ, обозначаемый через
. Машина Тьюринга имеет головку, которая в любой момент времени обозревает некоторую ячейку, и управляющее устройство, которое может находиться в одном из состояний
.
Шаг работы м-т. Если м-т имеет состояние , в обозреваемой ячейке записан символ
, то выполняется команда
, м-т переходит в состояние
, в ячейке на место
, записывается
и головка сдвигается влево, вправо или остается на месте в зависимости от символа
.
В начальный момент м-т находится в состоянии , останавливается м-т, если перейдет в одно из заключительных состояний либо при отсутствии команды, которую можно выполнить.
Конфигурацией (машинным словом) называется слово , где
— слово на ленте левее головки,
— слово правее головки, включая символ под головкой.
Говорят, что м-т применима к слову
, если
, начав работу на слове
, машина остановится через конечное число шагов; если в результате получится слово
, то пишут
. Если
не остановится, то она не применима к слову
.
Определение. Под высказыванием принято понимать языковое предложение, о котором имеет смысл говорить, что оно истинно или ложно в данный момент времени.
Высказывания чаще всего обозначают маленькими латинскими буквами a, b, c, х1, х2, …
В логике высказываний интересуются не содержанием, а истинностью или ложностью высказываний. Истинностные значения – истина и ложь – будем обозначать И и Л соответственно. Множество {И, Л} называется множеством истинностных значений.
Определение. Высказывание называют простым (элементарным), если оно рассматривается как некое неделимое целое (аналогично элементу множества). Сложным (составным) называется высказывание, составленное из простых с помощью логических связок.
В естественном языке роль связок при составлении сложных предложений из простых играют следующие грамматические средства: союзы «и», «или», «не»; слова «если …, то», «либо … либо», «тогда и только тогда, когда» и др. В логике высказываний логические связки, используемые для составления сложных высказываний, обязаны быть определены точно. Рассмотрим логические связки (операции) над высказываниями, при которых истинностные значения составных высказываний определяются только истинностными значениями составляющих высказываний, а не их смыслом.
В дальнейшем значению «истина» будем ставить в соответствие 1, а «ложь» — 0. Каждой логической операции ставится в соответствие таблица истинности. Таблица истинности выражает значения истинности высказываний в зависимости от значений элементарных высказываний. В дальнейшем буден использовать таблицу истинности для установления истинностных значений сложных высказываний при данных значениях входящих в него элементарных высказываний.
Определение. Отрицанием высказывания является новое высказывание, истинное только тогда, когда исходное высказывание ложно (табл. 2.13).
Таблица 2.1 Таблица истинности для отрицания
|
номер набора |
a |
|
|
0 |
0 |
1 |
|
1 |
1 |
0 |
Отрицание обозначается через и читается как «не а», «неверно, что а».
Пример 15.
А – «Степан любит танцевать».
Тогда — «Не верно, что Степан любит танцевать».
Определение. Конъюнкцией двух высказываний является новое высказывание, которое истинно только тогда, когда оба исходных высказывания истинны (табл. 2.2).
Конъюнкция обозначается или a&b и читается как «a и b», «a, но b», «a, а b».
Таблица 2.2 Таблица истинности для конъюнкции
|
номер набора |
a |
b |
aÙb |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
2 |
1 |
0 |
0 |
|
3 |
1 |
1 |
1 |
Пример 16.
а – «Степан любит танцевать», b – «Степан любит петь».
Тогда — «Степан любит танцевать и петь».
Определение. Дизъюнкцией двух высказываний является новое высказывание, которое ложно только тогда, когда оба исходных высказывания ложны (табл. 2.3).
Дизъюнкция обозначается через и читается как «a или b».
Таблица 2.3 Таблица истинности для дизъюнкции
|
номер набора |
a |
b |
aÚb |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
1 |
|
3 |
1 |
1 |
1 |
Пример 17.
а – «Степан любит танцевать», b – «Степан любит петь».
Тогда — «Степан любит танцевать или петь».
Определение. Импликацией двух высказываний является новое высказывание, которое ложно только тогда, когда первое истинно, а второе – ложно (табл. 2.4).
Импликация обозначается a® b и читается как «если a, то b»; « из а следует b». При этом a называется посылкой или условием, b – следствием или заключением.
Таблица 2.4 Таблица истинности для импликации
|
номер набора |
a |
b |
a®b |
|
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
0 |
|
3 |
1 |
1 |
1 |
Пример 18.
а – «Степан любит танцевать», b – «Степан любит петь».
Тогда — «Если Степан любит танцевать, то он любит петь».
Определение.
Эквиваленцией (или эквивалентностью) двух высказываний является новое высказывание, которое считается истинным, когда оба высказывания либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях (табл. 2.5).
Таблица 2.5 Таблица истинности для эквивалентности
|
номер набора |
a |
b |
a»b |
|
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
2 |
1 |
0 |
0 |
|
3 |
1 |
1 |
1 |
Эквивалентность обозначается a» b и читается как «a эквивалентно b».
Пример 19.
а – «Степан любит танцевать», b – «Степан любит петь».
Тогда — «Для того, чтобы Степан любил танцевать, необходимо и достаточно, чтобы он любил петь».
Сведем все сказанное выше в единую таблицу и введем в рассмотрение еще три операции: сумма по модулю два, штрих Шеффера, стрелка Пирса (табл. 2.6).
Таблица 2.6 Краткие сведения о логических операциях
|
Обозначения логической операции |
Другие обозначения логической операции |
Набор истинностных значений, отвечающих данной логической операции |
Названия логической операции и связки |
Как читается выражение, приведенное в первом столбце |
|
|
10 |
отрицание |
неверно, что а; не а |
|
|
a |
a & b a×b ab min(a; b) |
0001 |
конъюнкция, логическое умножение, логическое «и» |
a и b |
|
a |
a+b max(a; b) |
0111 |
дизъюнкция, логическое сложение, логическое «или» |
а или b |
|
a® b |
a a |
1101 |
импликация, логическое следование |
если а, то b; а имплицирует b; а влечет b |
|
a » b |
a a « b a |
1001 |
эквиваленция, эквивалентность, равнозначность, тождественность |
а тогда и только тогда, когда b; а эквивалентно b |
|
a |
a+ b a D b |
0110 |
сумма по модулю два, разделительная дизъюнкция, разделительное «или» |
а плюс b; либо а, либо b |
|
а|b |
1110 |
штрих Шеффера, антиконъюнкция |
неверно, что а и b; а штрих Шеффера b |
|
|
a |
a o b |
1000 |
стрелка Пирса, антидизъюнкция, функция Вебба, функция Даггера |
ни а, ни b; а стрелка Пирса b |




























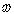
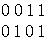
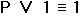
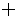
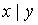
 a
a