Н. Макарова
ОБЩИЕ ФОРМУЛЫ
МАГИЧЕСКИХ КВАДРАТОВ
Часть I
В первой
части статьи рассматриваются общие формулы (схемы) магических квадратов
порядков 3 – 5. Такие формулы дают возможность строить как традиционные, так и
нетрадиционные магические квадраты.
Начну с
магических квадратов 3-го порядка. Общая формула магического квадрата данного
порядка приведена в [1]. Доказано, что из 9 чисел можно составить магический
квадрат 3-го порядка тогда и только тогда, когда эти числа можно разбить на три
арифметические прогрессии с одинаковой разностью b так, что первые члены этих
прогрессий тоже образуют арифметическую прогрессию с другой разностью c. То есть эти 9 чисел можно
записать следующими алгебраическими формулами:
a a
+ b a + 2b
a + c a
+ b + c a + 2b + c
a + 2c a
+ b + 2c a + 2b + 2c
Числа
образуют арифметические прогрессии и “вдоль”, и “поперёк” (и в строках, и в
столбцах показанной схемы). В квадрате эти числа расположатся, например, так
(рис. 1):
|
a + b |
a + 2b + 2c |
a + c |
|
a + 2c |
a + b + c |
a + 2b |
|
a + 2b + c |
a |
a + b + 2c |
Рис. 1
Очевидно,
что магическая константа квадрата, заданного такими формулами, определяется
следующей формулой: S = 3*(a + b + c). Выбирая любые натуральные значения переменных a, b и c, вы будете получать
нетрадиционные магические квадраты. Пусть, например: a = 5, b = 11, c = 7. Сразу можем вычислить
магическую константу квадрата: S = 3*(5 + 11 + 7) = 69. Вычислив элементы квадрата по формулам
рис. 1, получаем такой магический квадрат (рис. 1а):
|
16 |
41 |
12 |
|
19 |
23 |
27 |
|
34 |
5 |
30 |
Рис. 1а
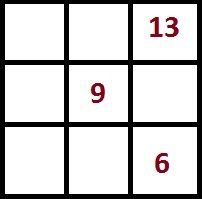
Рассмотрим магический квадрат
из простых чисел (рис. 2).
|
17 |
113 |
47 |
|
89 |
59 |
29 |
|
71 |
5 |
101 |
Рис. 2
Числа, составляющие этот
квадрат, складываются в такие арифметические прогрессии:
5, 17, 29
47, 59, 71
89, 101, 113
Здесь a = 5, b =
12, c = 42.
Рассмотрим
ещё один пример – магический квадрат из последовательных простых чисел (этот
квадрат взят в [1]), смотрите на рис. 3.
|
1480028141 |
1480028213 |
1480028159 |
|
1480028189 |
1480028171 |
1480028153 |
|
1480028183 |
1480028129 |
1480028201 |
Рис. 3
Здесь a = 1480028129, b = 12, c = 30.
Если c = 3b, то все 9 чисел являются
членами одной арифметической прогрессии с разностью b. Примером такого
магического квадрата является традиционный (классический) магический квадрат
(рис. 4):
Рис. 4
Понятно, что в этом
квадрате a = 1, b = 1, c = 3.
Приведу
пример нетрадиционного магического квадрата, составленного из членов арифметической
прогрессии длины 9 (рис. 5). Члены этой прогрессии простые числа.
|
409 |
1879 |
829 |
|
1459 |
1039 |
619 |
|
1249 |
199 |
1669 |
Рис. 5
В этом квадрате a = 199, b = 210, c = 630.
В
заключение покажу общую формулу магического квадрата 3-го порядка в том виде,
как она дана в [1], смотрите рис. 6.
|
a – c |
a – b + c |
a + b |
|
a + b + c |
a |
a – b – c |
|
a – b |
a + b – c |
a + c |
Рис. 6
Очевидно,
что при любых значениях переменных b и c магическая константа
квадрата, заданного такими формулами, будет равна 3a.
Если
расположить числа, составляющие квадрат с рис. 6, в виде трёх арифметических
прогрессий, это будет выглядеть так:
a – b – c a – c a + b – c
a – b a a
+ b
a – b + c a
+ c a + b + c
Предлагаю читателям
нерешённую задачу о магическом квадрате 3-го порядка. При решении задачи можно
воспользоваться приведённой общей формулой такого квадрата.
Задача:
построить наименьший
магический квадрат 3-го порядка из последовательных чисел Смита.
Об этой задаче смотрите
тему “Магические квадраты” на форуме dxdy.ru:
http://dxdy.ru/topic12959.html
Наименьший магический
квадрат 3-го порядка из произвольных чисел Смита построен, он есть в [1], а
также в моей статье “Нетрадиционные магические квадраты из чисел Смита” (http://www.natalimak1.narod.ru/netrsm.htm ). Продублирую этот
квадрат (рис. 7):
|
202 |
526 |
94 |
|
166 |
274 |
382 |
|
454 |
22 |
346 |
Рис. 7
В этом квадрате значения
переменных такие: a = 22, b = 180, c = 72 (соответственно формулам с
рис. 1).
Здесь надо
сделать важное замечание: когда мы будем строить магические квадраты из чисел
некоторого множества (например, из простых чисел или из чисел Смита),
необходимо, чтобы значение параметра a принадлежало этому
множеству, значения параметров b и c не обязаны принадлежать
этому множеству, а вот все элементы квадрата (вычисляемые по формулам с рис. 1
или же по формулам с рис. 6), должны принадлежать этому множеству.
Представленный
на рис. 7 магический квадрат из чисел Смита обладает интересным свойством: он
составлен из удвоенных простых чисел. На рис. 8 вы видите магический квадрат из
простых чисел, который получается, если разделить все элементы квадрата с рис.
7 на 2.
|
101 |
263 |
47 |
|
83 |
137 |
191 |
|
227 |
11 |
173 |
Рис. 8
Здесь a = 11, b = 90, c = 36 (тоже в соответствии с
формулами на рис. 1).
ОБЩИЕ ФОРМУЛЫ
МАГИЧЕСКИХ КВАДРАТОВ 4-го ПОРЯДКА
Переходим к магическим
квадратам 4-го порядка.
Прежде
всего, отмечу, что магический квадрат 4-го порядка, как и вообще магический
квадрат любого порядка, можно построить из чисел, образующих арифметическую
прогрессию. Для квадрата порядка 4 арифметическая прогрессия должна состоять из
16 членов. Как строить магические квадраты из чисел, образующих арифметическую
прогрессию, рассказано в моей статье о нетрадиционных магических квадратах из
простых чисел (http://www.natalimak1.narod.ru/netrpr1.htm ).
Здесь я
приведу пример магического квадрата, составленного из простых чисел, образующих
арифметическую прогрессию (рис. 9).
|
53297929 |
121195759 |
169694209 |
159994519 |
|
179393899 |
150294829 |
62997619 |
111496069 |
|
82396999 |
92096689 |
198793279 |
130895449 |
|
189093589 |
140595139 |
72697309 |
101796379 |
Рис. 9
Далее, так
же, как и магические квадраты порядка 3, магические квадраты порядка 4 могут
быть построены из таких 16 чисел, которые можно разбить на четыре
арифметические прогрессии длины 4 с одинаковой разностью b так, что первые члены этих
прогрессий тоже образуют арифметическую прогрессию с разностью c. Но для квадратов 4-го
порядка 16 чисел не обязательно должны удовлетворять этому условию, то есть это
условие для квадратов 4-го порядка является достаточным, но не является
необходимым (в отличие от квадратов 3-го порядка). В этом случае 16 чисел, из
которых составляется магический квадрат 4-го порядка, можно записать следующими
алгебраическими формулами:
a a
+ b a + 2b a + 3b
a + c a
+ b + c a + 2b + c a + 3b + c
a + 2c a
+ b + 2c a + 2b + 2c a + 3b + 2c
a + 3c a
+ b + 3c a + 2b + 3c a + 3b + 3c
В этой
схеме тоже числа образуют арифметические прогрессии “вдоль” и “поперёк”, в
строках и в столбцах. В магическом квадрате эти числа можно расположить,
например, так (рис. 10):
|
a |
a + 3b + c |
a + 3c |
a + 3b + 2c |
|
a + b + 3c |
a + 2b + 2c |
a + b |
a + 2b +c |
|
a + 3b |
a + c |
a + 3b + 3c |
a + 2c |
|
a + 2b + 3c |
a + b + 2c |
a + 2b |
a + b + c |
Рис. 10
Очевидно,
что магическая константа квадрата, заданного такими формулами, будет равна:
S = 4a + 6(b + c)
Возьмём
произвольные значения переменных: a = 7, b = 4, c = 3. Сразу можем вычислить
магическую константу будущего магического квадрата: S = 4*7 + 6*(4 + 3) = 70. Теперь вычислим все
элементы квадрата по формулам с рис. 10 и получим такой магический квадрат
(рис. 11):
|
7 |
22 |
16 |
25 |
|
20 |
21 |
11 |
18 |
|
19 |
10 |
28 |
13 |
|
24 |
17 |
15 |
14 |
Рис. 11
Отметим,
что магический квадрат, задаваемый формулой с рис. 10, является пандиагональным
и, значит, совершенным (для квадратов 4-го порядка все пандиагональные квадраты
являются совершенными). В этом легко убедиться, сложив элементы на любой
разломанной диагонали квадрата, изображённого на рис. 10. Сумма элементов для
всех разломанных диагоналей равна магической константе квадрата: 4a + 6(b + c). Таким образом, на рис. 10
представлена алгебраическая формула пандиагональных (совершенных) магических
квадратов 4-го порядка.
Если c = 4b, то все 16 чисел образуют
арифметическую прогрессию с разностью b. Этому случаю соответствует
магический квадрат, показанный на рис. 9.
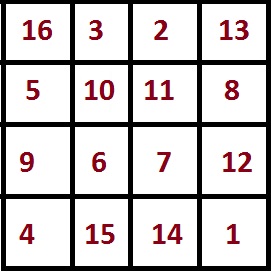
В случае a = 1, b = 1, c = 4 получаем традиционный
магический квадрат (рис. 12):
|
1 |
8 |
13 |
12 |
|
14 |
11 |
2 |
7 |
|
4 |
5 |
16 |
9 |
|
15 |
10 |
3 |
6 |
Рис. 12
Магические квадраты,
показанные на рис. 9, рис. 11 и рис. 12 являются совершенными.
А теперь
расположим элементы, представленные алгебраическими формулами, в магическим
квадрате следующим образом (рис. 13):
|
a |
a + b + 3c |
a + 2b + 3c |
a + 3b |
|
a + 3b + 2c |
a + 2b + c |
a + b + c |
a + 2c |
|
a + 3b + c |
a + 2b + 2c |
a + b + 2c |
a + c |
|
a + 3c |
a + b |
a + 2b |
a + 3b + 3c |
Рис. 13
Мы
получили формулу ассоциативного магического квадрата 4-го порядка. Положим: a = 1, b = 1, c = 4. Получим традиционный
ассоциативный магический квадрат (рис. 14):
|
1 |
14 |
15 |
4 |
|
12 |
7 |
6 |
9 |
|
8 |
11 |
10 |
5 |
|
13 |
2 |
3 |
16 |
Рис. 14
Теперь
возьмём произвольные значения переменных a, b и c, например, такие: a = 8, b = 33, c = 10. Сразу вычислим константу
будущего магического квадрата:
S = 4*8 + 6*(33 + 10) = 290.
Вычислив
элементы квадрата по формулам с рис. 13, получим следующий нетрадиционный
ассоциативный магический квадрат (рис. 15):
|
8 |
71 |
104 |
107 |
|
127 |
84 |
51 |
28 |
|
117 |
94 |
61 |
18 |
|
38 |
41 |
74 |
137 |
Рис. 15
И, наконец,
магический квадрат 4-го порядка можно построить из таких 16 чисел, которые
разбиваются на четыре арифметические прогрессии длины 4 с одинаковой разностью,
но при этом первые члены этих прогрессий никак не связаны между собой. В таком
случае эти 16 чисел можно записать следующими алгебраическими формулами:
a1 a1 + b a1 + 2b a1 + 3b
a2 a2 + b a2 + 2b a2 + 3b
a3 a3 + b a3 + 2b a3 + 3b
a4 a4 + b a4 + 2b a4 + 3b
В квадрате
эти числа можно расположить, например, так (рис. 16):
|
a1 |
a2 + b |
a3 + 2b |
a4 + 3b |
|
a4 + 2b |
a3 + 3b |
a2 |
a1 + b |
|
a2 + 3b |
a1 + 2b |
a4 + b |
a3 |
|
a3 + b |
a4 |
a1 + 3b |
a2 + 2b |
Рис. 16
Легко видеть, что магическая
константа квадрата с рис. 16 определяется по формуле:
(1) S = a1 + a2 + a3 + a4 + 6b
Магический
квадрат, задаваемый формулами с рис. 16, не является ни ассоциативным, ни
совершенным.
Для
примера приведу магический квадрат, составленный из чисел Смита, образующих
четыре арифметические прогрессии длины 4 с одинаковой разностью (рис. 17).
|
627 |
4619488 |
4633544 |
6633265 |
|
6633256 |
4633553 |
4619479 |
636 |
|
4619506 |
645 |
6633247 |
4633526 |
|
4633535 |
6633238 |
654 |
4619497 |
Рис. 17
Примечание: первая арифметическая
прогрессия найдена мной, остальные взяты с форума Портала Естественных наук,
тема “Числа Смита”.
http://e-science.ru/forum/index.php?showtopic=13749&st=0
Здесь a1 = 627, a2 = 4619479, a3 = 4633526, a4 = 6633238, b = 9. Проверим магическую
константу этого квадрата по формуле (1):
S = 627 + 4619479 +
4633526 + 6633238 + 6*9 = 15886924.
Всё верно, магическая
константа квадрата с рис. 17 действительно имеет такое значение.
На этом
закончим рассмотрение схем магических квадратов 4-го порядка, составляемых из
членов арифметических прогрессий, и перейдём к построению магических квадратов
из произвольных массивов чисел.
Самое
раннее упоминание об общих формулах магических квадратов я нашла в [2]. В книге
написано, что первая общая формула магического квадрата 4-го порядка была
опубликована в 1884 году в “Журнале элементарной математики” профессором В. П.
Ермаковым. Эту формулу можно представить в виде суммы двух магических квадратов
(рис. 18):
|
A |
C |
D |
B |
a + b |
-a — b |
|||
|
D |
B |
A |
C |
+ |
c — d |
-a — c |
a — c |
c + d |
|
B |
D |
C |
A |
-c + d |
-a + c |
a + c |
-c — d |
|
|
C |
A |
B |
D |
a — b |
-a + b |
Рис. 18
Цитата из [2]:
“Произвольно подбирая 8 чисел A, B, C, D, a, b, c, d и складывая оба квадрата “поклеточно”
(то есть складывая числа в совпавших клетках при наложении одного квадрата на
другой), мы получим искомый волшебный квадрат”.
Примечание: в пустых ячейках квадрата
на рис. 18 подразумеваются элементы равные 0.
Давайте
попробуем. Пусть A = 1, B = 2, C = 3, D = 4, a = 5, b = 6, c = 7, d = 8 (выбраны 8
последовательных чисел). Произведя указанные в формуле Ермакова операции,
получаем следующий магический квадрат (рис. 19):
|
1 |
14 |
-7 |
2 |
|
3 |
-10 |
-1 |
18 |
|
3 |
6 |
15 |
-14 |
|
3 |
0 |
3 |
4 |
Рис. 19
Не очень
красивый получился квадрат, во-первых, в нём есть отрицательные числа,
во-вторых, есть одинаковые числа. Но, тем не менее, этот квадрат магический. От
отрицательных чисел избавиться очень просто: увеличим все элементы квадрата,
например, на 15, в результате получится такой магический квадрат (рис. 20):
|
16 |
29 |
8 |
17 |
|
18 |
5 |
14 |
33 |
|
18 |
21 |
30 |
1 |
|
18 |
15 |
18 |
19 |
Рис. 20
А вот
получить по этой формуле (рис. 18) традиционный магический квадрат профессору
В. П. Ермакову не удалось.
Цитата из [2]: “По
поводу того, как подобрать эти 8 чисел, чтобы в клетках полученного квадрата
стояли все целые числа от 1 до 16 (то есть, чтобы квадрат оказался
традиционным), В. П. Ермаков пишет: “Мы не знаем простого решения этого вопроса
и предоставляем читателям найти таковое”.
Я
попробовала решить эту задачу, но с ходу не получилось. Предлагаю читателям
исследовать этот вопрос. Имеет ли вообще эта задача решение?
Более
совершенная формула магического квадрата 4-го порядка была предложена
Бергхольтом в 1910 году [4]. Эта формула приводится по [3]. Смотрите формулу на
рис. 21.
|
A — a |
C + a + c |
B + b — c |
D — b |
|
D + a — d |
B |
C |
A — a + d |
|
C — b + d |
A |
D |
B + b — d |
|
B + b |
D — a — c |
A — b + c |
C + a |
Рис. 21
При этом
приведены условия, при которых эта формула даёт ассоциативные магические
квадраты и совершенные магические квадраты.
Цитирую [3]: “На рис.
7.18 показана общая схема Бергхольта для построения любых магических квадратов
четвёртого порядка (совершенных при a = b
= d – c = ½(A – B
– C + D), симметрических при a + c
= d = b – c
и A + C = B
+ D)”.
Примечание: симметрическими здесь
называются ассоциативные квадраты.
Очевидно,
что магическая константа квадрата, заданного формулами с рис. 21, определяется
формулой
S = A + B + C + D. Такой же формулой
определяется магическая константа квадрата, заданного формулой Ермакова. Отметим,
что, исходя из формулы Бергхольта, формулу Ермакова можно записать в таком виде
(рис. 21а):
|
A |
C |
B |
D |
-a |
a + c |
b — c |
-b |
|
|
D |
B |
C |
A |
+ |
a — d |
-a + d |
||
|
C |
A |
D |
B |
-b + d |
b — d |
|||
|
B |
D |
A |
C |
b |
-a — c |
-b + c |
a |
Рис. 21а
Посмотрим,
какой магический квадрат получится по формуле Бергхольта при тех же значениях
переменных, которые мы использовали при построении квадрата по формуле
Ермакова. Этот квадрат изображён на рис. 22.
|
-4 |
15 |
1 |
-2 |
|
1 |
2 |
3 |
4 |
|
5 |
1 |
4 |
0 |
|
8 |
-8 |
2 |
8 |
Рис. 22
Квадрат
тоже содержит и отрицательные числа, и одинаковые числа, как и квадрат,
полученный по формуле Ермакова. Но квадраты получились разные, хотя и с
одинаковой магической константой.
Важно, что
в отличие от формулы Ермакова, в формуле Бергхольта легко подобрать числа так,
что полученный магический квадрат будет традиционным. Приведу один пример. На
рис. 23 изображён традиционный магический квадрат, полученный по формуле Бергхольта
при таких значениях переменных:
A = 1, B = 8, C = 10, D = 15, a = -1, b = -1, c = 2, d = 1.
|
2 |
11 |
5 |
16 |
|
13 |
8 |
10 |
3 |
|
12 |
1 |
15 |
6 |
|
7 |
14 |
4 |
9 |
Рис. 23
Таким
образом, формула Бергхольта является действительно общей формулой магических
квадратов 4-го порядка, по которой можно построить и традиционные, и
нетрадиционные магические квадраты, а при определённых условиях также ассоциативные
и совершенные.
На рис. 24
вы видите формулу Бергхольта для ассоциативных квадратов, она получена из
формулы с рис. 21 при дополнительных условиях для ассоциативных квадратов.
Кроме того, необходимо потребовать выполнение условия: A + C = B + D.
|
A — a |
C + a + c |
B + a + c |
D – a – 2c |
|
D — c |
B |
C |
A + c |
|
C — c |
A |
D |
B + c |
|
B + a + 2c |
D — a — c |
A — a — c |
C + a |
Рис. 24
Я
составила программу для построения ассоциативных магических квадратов 4-го
порядка по формуле, изображённой на рис. 24. В программе задействован массив из
50 чисел; можно ввести в программу любой массив чисел, но чем больше чисел в
массиве, тем дольше будет выполняться программа. По этой программе построен
наименьший ассоциативный квадрат из простых чисел. Смотрите этот квадрат на
рис. 25.
|
17 |
113 |
37 |
73 |
|
79 |
31 |
107 |
23 |
|
97 |
13 |
89 |
41 |
|
47 |
83 |
7 |
103 |
Рис. 25
Магическая
константа квадрата равна 240.
Из чисел
Смита мне не удалось получить ассоциативный квадрат, составленный из разных
чисел; надо увеличивать исходный массив смитов. Получен только ассоциативный
квадрат с повторяющимися числами (рис. 26).
|
94 |
690 |
85 |
627 |
|
654 |
58 |
663 |
121 |
|
627 |
85 |
690 |
94 |
|
121 |
663 |
58 |
654 |
Рис. 26
Предлагаю
решить эту задачу читателям.
Задача:
построить наименьший ассоциативный
магический квадрат 4-го порядка из чисел Смита.
Можно воспользоваться
формулой Бергхольта, а можно придумать свой алгоритм построения такого
квадрата.
Далее из
общей формулы Бергхольта получим формулу для построения совершенных магических
квадратов 4-го порядка, применив указанные условия. Вы видите эту формулу на
рис. 27.
|
A — a |
C + a + c |
B + a — c |
D — a |
|
D — c |
B |
C |
A + c |
|
C + c |
A |
D |
B — c |
|
B + a |
D — a — c |
A — a + c |
C + a |
Рис. 27
Кроме того, необходимо
потребовать выполнение условия: A – B – C + D = 2a.
Вот какой
наименьший совершенный квадрат из простых чисел у меня получился по программе,
составленной по формуле с рис. 27 (рис. 28):
|
13 |
83 |
31 |
113 |
|
97 |
47 |
79 |
17 |
|
89 |
7 |
107 |
37 |
|
41 |
103 |
23 |
73 |
Рис. 28
Магическая
константа этого квадрата равна 240. Кстати, традиционный магический квадрат,
показанный на рис. 23, тоже построен по этой программе, он является
совершенным.
Совершенный квадрат из
смитов построить не удалось. И вот читателям ещё одна
Задача:
построить наименьший совершенный
магический квадрат 4-го порядка из чисел Смита.
Наконец, ещё одна сложная
задача о нетрадиционных магических квадратах 4-го порядка:
Задача:
построить наименьший магический
квадрат 4-го порядка из последовательных чисел Смита.
Этот
квадрат не должен обладать никакими дополнительными свойствами, то есть для его
построения надо брать самую общую формулу (рис. 21). Понятно, что значения
переменных A, B, C, D должны принадлежать
множеству смитов; значения переменных a, b, c, d – произвольные целые числа;
а все элементы, расположенные в квадрате на рис. 21, тоже должны принадлежать
множеству смитов. И, наконец, по условию задачи, элементы, из которых
составляется квадрат, должны представлять собой 16 последовательных чисел
Смита.
Задача
непростая. Я проверила по своей программе 800 первых кандидатов в такой
магический квадрат, квадрат не найден. Дальше не могу проверять: у меня
закончился массив смитов, я сгенерировала смиты в интервале от 1 до 100000.
В
заключение приведу наименьший магический квадрат 4-го порядка из произвольных
смитов (рис. 29). Этот квадрат построен участником форума dxdy.ru (ник tolstopuz). Магическая константа
квадрата равна 1195.
|
22 |
346 |
562 |
265 |
|
778 |
274 |
85 |
58 |
|
4 |
454 |
382 |
355 |
|
391 |
121 |
166 |
517 |
Рис. 29
Разумеется,
автор этого магического квадрата строил его по своему алгоритму. Однако квадрат
получается по общей формуле Бергхольта при следующих значениях переменных:
A = 454, B = 274, C = 85, D = 382, a = 432, b = 117, c = -171, d = 36.
Проверьте!
Таким
образом, если вы запрограммируете общую формулу Бергхольта, приведённую на рис.
21, то легко построите магический квадрат, показанный на рис. 29.
ОБЩИЕ ФОРМУЛЫ
МАГИЧЕСКИХ КВАДРАТОВ 5-го ПОРЯДКА
Начну опять
с магического квадрата, построенного из чисел, составляющих арифметическую
прогрессию (рис. 30). Это прогрессия из простых чисел.
|
6171054912832631 |
7969283390638391 |
6906693835571351 |
7233644467899671 |
7478857442145911 |
|
7315382125981751 |
7642332758310071 |
6252792570914711 |
7805808074474231 |
6743218519407191 |
|
7887545732556311 |
6579743203243031 |
7151906809817591 |
7724070416392151 |
6416267887078871 |
|
7560595100227991 |
6498005545160951 |
8051021048720471 |
6661480861325111 |
6988431493653431 |
|
6824956177489271 |
7070169151735511 |
7397119784063831 |
6334530228996791 |
8132758706802551 |
Рис. 30
Понятно,
что для построения магического квадрата 5-го порядка нужна арифметическая
прогрессия длины 25. Из смитов ещё не найдена прогрессия такой длины, поэтому
мы не можем пока построить аналогичный магический квадрат из смитов.
Далее,
магический квадрат можно построить из 5 арифметических прогрессий длины 5 с
одинаковой разностью, так что первые члены этих прогрессий тоже образуют
арифметическую прогрессию. В этом случае 25 чисел можно записать следующими
алгебраическими формулами:
a a
+ b a + 2b a + 3b a + 4b
a + c a
+ b + c a + 2b + c a + 3b + c a + 4b + c
a + 2c a
+ b + 2c a + 2b + 2c a + 3b + 2c a + 4b + 2c
a + 3c a
+ b + 3c a + 2b + 3c a + 3b + 3c a + 4b + 3c
a + 4c a
+ b + 4c a + 2b + 4c a + 3b + 4c a + 4b + 4с
В магическом квадрате эти
элементы можно разместить, например, так (рис. 31):
|
a |
a + 2b + 4c |
a + 4b + c |
a + 3b + 2c |
a + b + 3c |
|
a + 4b + 2c |
a + 3b + 3c |
a + b |
a + 4c |
a + 2b + c |
|
a + b + 4c |
a + c |
a + 2b + 2c |
a + 4b + 3c |
a + 3b |
|
a + 2b + 3c |
a + 4b |
a + 3b + 4c |
a + b + c |
a + 2c |
|
a + 3b + c |
a + b + 2c |
a + 3c |
a + 2b |
a + 4b + 4c |
Рис. 31
Магические
квадраты, построенные по формуле с рис. 31, будут обладать свойствами
ассоциативности и пандиагональности, то есть это формула идеальных магических
квадратов 5-го порядка. Магическая константа квадратов, задаваемых формулой с
рис. 31, определяется по формуле:
S = 5a + 10(b +c)
Понятно,
что в случае c = 5b все 25 чисел образуют одну арифметическую
прогрессию с разностью b. Примером такого квадрата является квадрат,
показанный на рис. 30.
При a = 1, b = 1, c = 5 получаем традиционный
магический квадрат (рис. 32).
|
1 |
23 |
10 |
14 |
17 |
|
15 |
19 |
2 |
21 |
8 |
|
22 |
6 |
13 |
20 |
4 |
|
18 |
5 |
24 |
7 |
11 |
|
9 |
12 |
16 |
3 |
25 |
Рис. 32
А теперь
возьмём произвольные значения переменных a, b, c и построим нетрадиционный
идеальный магический квадрат по формуле с рис. 31. Пусть a = 8, b = 10,
c = 13.
Сразу
можем вычислить магическую константу будущего квадрата: S = 5*8 + 10*(10 + 13) = 270. Магический квадрат получится
такой (рис. 33):
|
8 |
80 |
61 |
64 |
57 |
|
74 |
77 |
18 |
60 |
41 |
|
70 |
21 |
54 |
87 |
38 |
|
67 |
48 |
90 |
31 |
34 |
|
51 |
44 |
47 |
28 |
100 |
Рис. 33
Далее
будем строить магические квадраты из чисел, составляющих пять арифметических
прогрессий с одинаковой разностью, но первые члены этих прогрессий никак не
связаны между собой. В этом случае 25 чисел можно представить следующими
алгебраическими выражениями:
a1 a1 + b a1 + 2b a1 + 3b a1 + 4b
a2 a2 + b a2 + 2b a2 + 3b a2 + 4b
a3 a3 + b a3 + 2b a3 + 3b a3 + 4b
a4 a4 + b a4 + 2b a4 + 3b a4 + 4b
a5 a5 + b a5 + 2b a5 + 3b a5 + 4b
В квадрате эти числа можно
разместить, например, так (рис. 34):
|
a1 |
a5 + 2b |
a2 + 4b |
a3 + 3b |
a4 + b |
|
a3 + 4b |
a4 + 3b |
a1 + b |
a5 |
a2 + 2b |
|
a5 + b |
a2 |
a3 + 2b |
a4 + 4b |
a1 + 3b |
|
a4 + 2b |
a1 + 4b |
a5 + 3b |
a2 + b |
a3 |
|
a2 + 3b |
a3 + b |
a4 |
a1 + 2b |
a5 + 4b |
Рис. 34
Легко
видеть, что магический квадрат, задаваемый формулой с рис. 34, является
пандиагональным, а вот свойством ассоциативности в общем случае такой квадрат
не обладает. Приведу пример (рис. 35) магического квадрата, построенного по
формуле с рис. 34. Числа, составляющие этот квадрат, являются числами Смита.
Они образуют пять арифметических прогрессий длины 5 с одинаковой разностью b = 9. Первая из этих прогрессий
627 +
9n, n = 0, 1, …, 4 найдена мной, остальные
взяты на форуме Портала Естественных Наук (ссылка дана выше).
|
627 |
11989273 |
4619515 |
4653553 |
6633247 |
|
4653562 |
6633265 |
636 |
11989255 |
4619497 |
|
11989264 |
4619479 |
4653544 |
6633274 |
654 |
|
6633256 |
663 |
11989282 |
4619488 |
4653526 |
|
4619506 |
4653535 |
6633238 |
645 |
11989291 |
Рис. 35
Этот квадрат является
пандиагональным, но не обладает ассоциативностью.
Чтобы
магический квадрат, задаваемый формулой с рис. 34, обладал свойством
ассоциативности, необходимо и достаточно выполнение следующего условия: a1 + a5 = a2 + a4 = 2a3. То есть первые члены пяти
арифметических прогрессий должны быть связаны между собой определённой
зависимостью. Найти такие прогрессии из произвольных натуральных чисел очень
просто. Например:
a1 = 3, a2 = 1, a3 = 4, a4 = 7, a5 = 5, b = 5.
При таких
значениях переменных мы получим по формуле с рис. 34 следующий нетрадиционный
идеальный магический квадрат (рис. 36):
|
3 |
15 |
21 |
19 |
12 |
|
24 |
22 |
8 |
5 |
11 |
|
10 |
1 |
14 |
27 |
18 |
|
17 |
23 |
20 |
6 |
4 |
|
16 |
9 |
7 |
13 |
25 |
Рис. 36
Найти
арифметические прогрессии с указанной зависимостью между первыми членами,
состоящие из простых чисел или из смитов, мне не удалось; арифметические
прогрессии из простых чисел длиной 25, конечно, не считаются. Предлагаю
читателям сделать это.
Наконец,
можно не озадачиваться поиском каких бы то ни было арифметических прогрессий, а
просто выбрать произвольные значения переменных и применить формулу с рис. 34.
Мы получим нетрадиционный пандиагональный квадрат 5-го порядка с магической
константой, вычисляемой по следующей формуле:
(2) S = a1 + a2 + a3 + a4 + a5 + 10b
Приведу пример. Пусть a1 = 6, a2 = 10, a3 = 17, a4 = 21, a5 = 28, b = 13. Сразу вычислим магическую
константу будущего квадрата:
S = 6 + 10 + 17 + 21 + 28
+ 10*13 = 212.
На рис. 37 вы видите
готовый магический квадрат, он является пандиагональным.
|
6 |
54 |
62 |
56 |
34 |
|
69 |
60 |
19 |
28 |
36 |
|
41 |
10 |
43 |
73 |
45 |
|
47 |
58 |
67 |
23 |
17 |
|
49 |
30 |
21 |
32 |
80 |
Рис. 37
Если вы
хотите получить магический квадрат с заданной магической константой, можно
подобрать значения переменных в формуле (2), чтобы получить нужное значение
магической константы.
Таким
образом, на рис. 34 представлена формула пандиагонального магического квадрата
5-го порядка. Отметим, что при следующих значениях переменных:
a1 = 1, a2 = 6, a3 = 11, a4 = 16, a5 = 21, b = 1
формула с рис. 34 даёт традиционный пандиагональный
и ассоциативный магический квадрат (см. рис. 32).
Переходим к рассмотрению
магических квадратов 5-го порядка, составляемых из произвольного массива чисел.
Общую формулу магических квадратов 5-го порядка я нашла в [2]. Эта формула
показана на рис. 38.
|
a1 |
a2 |
a3 |
a4 |
a5 |
|
a6 |
a7 |
a8 |
a9 |
b1 |
|
a10 |
a11 |
a12 |
a13 |
b2 |
|
b8 |
a14 |
b9 |
a15 |
b4 |
|
b7 |
b6 |
b10 |
b5 |
b3 |
Рис. 38
Суть этой
формулы такова: все переменные ai – свободные, все переменные
bi – зависимые, они
вычисляются через переменные ai. Как видите, свободных
переменных здесь 15. Зависимые переменные пронумерованы в том порядке, в каком
их следует вычислять. Например, при вычислении переменной b4 используется значение уже
вычисленной переменной b3.
По этой
формуле можно построить, например, все традиционные магические квадраты 5-го
порядка, если дать возможность свободным переменным принять все значения из
множества первых 25 натуральных чисел. Впрочем, если строить традиционные
магические квадраты, то число свободных переменных можно уменьшить на 1, потому
что в этом случае известна магическая константа квадрата.
Приведу
пример магического квадрата, построенного по формуле с рис. 37, при произвольном
выборе свободных переменных. Пусть свободные переменные принимают такие
значения:
a1 = 7, a2 = 12, a3 = 5, a4 = 9, a5 = 17, a6 = 1, a7 = 6, a8 = 11, a9 = 16, a10 = 21, a11 = 4, a12 = 2, a13 = 1, a14 = 19, a15 = 24.
Вычислим магическую
константу будущего квадрата: S = 7 + 12 + 5 + 9 + 17 = 50.
На рис. 38 вы видите
готовый магический квадрат.
|
7 |
12 |
5 |
9 |
17 |
|
1 |
6 |
11 |
16 |
16 |
|
21 |
4 |
2 |
1 |
22 |
|
25 |
19 |
-2 |
24 |
-16 |
|
-4 |
9 |
34 |
0 |
11 |
Рис. 38
Не очень
красивый квадрат получился, с отрицательными и с одинаковыми числами. Тем не
менее, он магический.
Понятно,
что формула, показанная на рис. 37, является общей формулой, определяющей любой
магический квадрат 5-го порядка. Рассмотрим, например, такой магический квадрат
из простых чисел (этот квадрат я построила, когда искала наименьший магический
квадрат из простых чисел). Смотрите на рис. 39.
|
101 |
971 |
929 |
1013 |
191 |
|
359 |
173 |
461 |
1019 |
1193 |
|
773 |
1229 |
641 |
53 |
509 |
|
881 |
263 |
821 |
1109 |
131 |
|
1091 |
569 |
353 |
11 |
1181 |
Рис. 39
Легко видеть, при каких
значениях свободных переменных построен данный квадрат.
Я
составила схему построения идеальных магических квадратов 5-го порядка из
массива, состоящего из 25 чисел. Массив чисел должен удовлетворять следующим
условиям: сумма всех чисел массива должна быть кратна 5. Магическая константа
квадрата S тоже должна быть кратна 5. Среди чисел массива
должно иметься число S/5, это число будет находиться в центральной ячейке
квадрата. Остальные 24 числа массива должны разбиться на 12 пар комплементарных
чисел, то есть дающих в сумме константу ассоциативности квадрата Ka = 2*S/5. Понятно, что всем этим условиям удовлетворяет,
например, массив, состоящий из 25 первых натуральных чисел.
Показываю схему идеального
квадрата 5-го порядка, составленную мной (рис. 40):
|
a1 |
a2 |
a3 |
a4 |
x1 |
|
a5 |
a6 |
a7 |
a8 |
x2 |
|
x3 |
x4 |
S/5 |
x5 |
x6 |
|
x7 |
x8 |
x9 |
x10 |
x11 |
|
x12 |
x13 |
x14 |
x15 |
x16 |
Рис. 40
Здесь ai – свободные переменные (все
они принимают 24 различных значения; одно из чисел массива равно S/5 и находится в центральной
ячейке квадрата). Переменные x1, x2, x3, x4 вычисляются по следующим
формулам:
x1 = S – a1 – a2 – a3 – a4
(3) x2 = S – a5 – a6 – a7 – a8
x3
= S/5 + a5 + a2 – a3 – a6
x4
= 6*S/5 + a1 – a4 – a5 – a6 – 2*a7 – a8
Все остальные переменные вычисляются
по ассоциативности. Например: x16 = Ka – a1, x5 = Ka – x4.
Проверим
эту схему на примере идеального квадрата, показанного на рис. 33, этот квадрат
построен по другой формуле. Продублирую этот квадрат (рис. 41):
|
8 |
80 |
61 |
64 |
57 |
|
74 |
77 |
18 |
60 |
41 |
|
70 |
21 |
54 |
87 |
38 |
|
67 |
48 |
90 |
31 |
34 |
|
51 |
44 |
47 |
28 |
100 |
Рис. 41
Имеем: a1 = 8, a2 = 80, a3 = 61, a4 = 64, a5 = 74, a6 = 77, a7 = 18, a8 = 60, S/5 = 54, S =
270, Ka = 108.
Вычисляем x1, x2, x3, x4 по формулам (3):
x1 = 270 – 8 –
80 – 61 – 64 = 57
x2 = 270 – 74 –
77 – 18 – 60 = 41
x3 =
54 + 74 + 80 – 61 – 77 = 70
x4
= 6*54 + 8 – 64 – 74
– 77 – 2*18 – 60 = 21
Легко
убедиться, что все остальные переменные, вычисляемые по ассоциативности, тоже
совпадают с элементами, расположенными в квадрате на рис. 41.
Я
запрограммировала схему, представленную на рис. 40. Программа работает, но
очень медленно (как уже знают читатели, я пишу программы на языке QBASIC, который имеет плохое
быстродействие).
Если мы
будем строить по данной схеме традиционные идеальные квадраты, тогда исходный
массив состоит из первых 25 натуральных чисел; S = 65, S/5 = 13, Ka = 26; все восемь свободных
переменных должны принять значения от 1 до 25, за исключением 13, то есть все
они пробегают 24 значения. В этом случае мы должны получить по программе все
традиционные идеальные квадраты 5-го порядка. Как известно, таких квадратов
всего 16 с учётом поворотов и отражений. Один из таких квадратов показан на
рис. 32.
Представленную
схему для идеального квадрата 5-го порядка можно применить также для построения
идеальных квадратов из массива чисел, состоящего более чем из 25 чисел. В этом
случае количество свободных переменных увеличится на 1, и они будут принимать
все значения чисел массива. Схема будет выглядеть так (рис. 42):
|
a1 |
a2 |
a3 |
a4 |
x1 |
|
a5 |
a6 |
a7 |
a8 |
x2 |
|
x3 |
x4 |
a0 |
x5 |
x6 |
|
x7 |
x8 |
x9 |
x10 |
x11 |
|
x12 |
x13 |
x14 |
x15 |
x16 |
Рис. 42
Формулы
(3) для вычисления зависимых переменных остаются в силе, с учётом того, что S = 5*a0. Понятно, что чем больше будет чисел в массиве,
тем дольше будет выполняться программа.
И,
наконец, представлю общую схему построения любого магического квадрата 5-го
порядка из заданного массива, состоящего из 25 чисел. В этом случае массив
чисел должен удовлетворять только одному условию: сумма всех чисел массива
должна быть кратна 5. Вычислив сумму всех чисел массива и разделив её на 5,
получаем магическую константу S. На рис. 43 вы видите общую схему любого
магического квадрата 5-го порядка.
|
a1 |
a2 |
a3 |
x1 |
a4 |
|
a12 |
x3 |
x5 |
a5 |
x4 |
|
x6 |
x7 |
a6 |
a14 |
a11 |
|
a13 |
x2 |
x8 |
a9 |
a10 |
|
a7 |
x9 |
x10 |
x11 |
a8 |
Рис. 43
Здесь 14
свободных переменных ai (i = 1, 2, 3, …, 14) и 11 зависимых переменных xk (k = 1, 2, 3, …, 11). Каждая свободная
переменная должна принять все 25 значений, равных числам заданного массива.
Зависимые переменные вычисляются по следующим формулам:
x1 = S – a1 – a2 – a3 – a4
x2 = S – a4 – a5 – a6 – a7
x3 = S – a1 – a6 – a8 – a9
x4 = S – a4 – a8 – a10 – a11
x5 = S – a5 – a12 – x3 – x4
(4) x6 = S – a1 – a7 – a12 – a13
x7 = S – a6 – a11 – a14 – x6
x8 = S – a9 – a10 – a13 – x2
x9 = S – a2 – x2 – x3 – x7
x10 = S – a3 – a6 – x5 – x8
x11 = S – a5 – a9 – a14 – x1
В отличие
от общей схемы, представленной на рис. 38, в рассматриваемой схеме количество
свободных переменных на 1 меньше. Это объясняется тем, что здесь магический
квадрат строится из массива, состоящего точно из 25 чисел, что даёт возможность
сразу вычислить магическую константу.
Эту схему
я тоже запрограммировала. Таким образом, имеется программа построения всех
магических квадратов 5-го порядка из заданного массива, состоящего из 25 чисел.
По этой
программе можно построить также все традиционные магические квадраты
5-го порядка. В этом случае исходный массив состоит из 25 первых натуральных
чисел, S = 65.
Интересно,
повторил ли кто-нибудь опыт американцев по построению всех традиционных
магических квадратов 5-го порядка? Как известно, они сделали это в 1973 г. Напомню читателям, что написал М. Гарднер в книге “Путешествие во времени” (М.: Мир, 1990):
“Точное число
квадратов порядка 5 не было известно до 1973 г., когда полный перебор
магических квадратов был осуществлён компьютерной программой,
разработанной Р. Шрёппелем, математиком и программистом из “Information
International”. Прогон программы на компьютере занимает около 100 часов
машинного времени. Окончательное сообщение, написанное М. Билером, появилось в
октябре 1975 г.
С точностью до поворотов и
отражений существует 275 305 224 магических квадратов порядка 5”.
Интересно
было бы посмотреть, как справится с этой задачей современный компьютер. Но для
этого, конечно, надо переписать мою программу на современный язык
программирования с хорошим быстродействием.
Можно
немного упростить задачу, построить не все магические квадраты, а только
квадраты, начинающиеся с числа 1 (число 1 находится в левой верхней ячейке
квадрата). Тогда количество свободных переменных уменьшится на 1, и все они
должны принять значения от 2 до 25.
А теперь
рассмотрим общую схему с рис. 43 на примере наименьших магических квадратов
5-го порядка из последовательных простых чисел. Эти квадраты составляются из
следующего массива простых чисел: 13, 17, …, 109, 113. Магическая константа
квадрата равна 313.
По
программе Stefano Tognon можно построить заданное
количество таких квадратов. Но можно ли построить по его программе все такие
квадраты?
На рис. 44
изображён один из квадратов, построенных по программе Stefano Tognon.
|
79 |
13 |
71 |
37 |
113 |
|
59 |
41 |
83 |
23 |
107 |
|
31 |
109 |
73 |
53 |
47 |
|
101 |
61 |
19 |
103 |
29 |
|
43 |
89 |
67 |
97 |
17 |
Рис. 44
Легко
убедиться, что этот квадрат полностью удовлетворяет схеме на рис. 43 и формулам
(4).
Понятно,
что если выполнить программу, реализующую схему с рис. 43, полностью, то
построятся все магические квадраты, составленные из чисел данного массива.
Приведу
текст программы, реализующей схему с рис. 43. Как я уже говорила, программа
написана на языке QBASIC.
ТЕКСТ ПРОГРАММЫ
(общая схема построения
всех магических квадратов 5-го порядка
из заданного массива
чисел)
10 DIM B(25), A(5, 5), C(25)
15 OPEN «MK8.txt» FOR INPUT
AS #1
20 FOR I = 1 TO 25: INPUT #1, B(I):
NEXT I
25 CLOSE #1
27 OPEN «MK10.txt» FOR
OUTPUT AS #1
30 W = 0
35 FOR I = 1 TO 25: W = W + B(I):
NEXT I
40 W = W / 5
42 FOR I = 1 TO 25
44 FOR J = 1 TO 25
45 PRINT «J»; J
46 IF J = I THEN 560
48 FOR K = 1 TO 25
50 IF K <> I THEN IF K <>
J THEN 54
52 GOTO 555
54 FOR L = 1 TO 25
56 IF L <> I THEN IF L <>
J THEN IF L <> K THEN 60
58 GOTO 550
60 A(1,
4) = W — B(I) — B(J) — B(K) — B(L)
62 IF A(1, 4) < B(1) THEN 550
64 IF A(1, 4) > B(25) THEN 550
66 IF A(1, 4) <> B(I) THEN IF
A(1, 4) <> B(J) THEN IF A(1, 4) <> B(K) THEN IF A(1, 4) <>
B(L) THEN 70
68 GOTO 550
70 FOR X = 1 TO 25
72 IF A(1, 4) = B(X) THEN 78
74 NEXT X
76 GOTO 550
78 C(1)
= B(I): C(2) = B(J): C(3) = B(K): C(4) = A(1, 4): C(5) = B(L)
80 FOR M = 1 TO 25
82 IF M <> I THEN IF M <>
J THEN IF M <> K THEN IF M <> L THEN 86
84 GOTO 545
86 FOR N = 1 TO 25
88 IF N <> I THEN IF N <>
J THEN IF N <> K THEN IF N <> L THEN IF N <> M THEN 92
90 GOTO 540
92 FOR O = 1 TO 25
94 IF O <> I THEN IF O <>
J THEN IF O <> K THEN IF O <> L THEN IF O <> M THEN IF O
<> N THEN 98
96 GOTO 535
98 C(6)
= B(M): C(7) = B(N): C(8) = B(O)
100 A(4,
2) = W — C(5) — C(6) — C(7) — C(8)
102 IF A(4, 2) < B(1) THEN 535
104 IF A(4, 2) > B(25) THEN 535
106 FOR X = 1 TO 8
108 IF A(4, 2) = C(X) THEN 535
110 NEXT X
112 FOR X = 1 TO 25
114 IF A(4, 2) = B(X) THEN 120
116 NEXT X
118 GOTO 535
120 C(9)
= A(4, 2)
122 FOR P = 1 TO 25
124 IF P <> I THEN IF P
<> J THEN IF P <> K THEN IF P <> L THEN IF P <> M THEN
IF P <> N THEN IF P <> O THEN 128
126 GOTO 530
128 FOR Q = 1 TO 25
130 IF Q <> I THEN IF Q
<> J THEN IF Q <> K THEN IF Q <> L THEN IF Q <> M THEN
IF Q <> N THEN IF Q <> O THEN IF Q <> P THEN 134
132 GOTO 525
134 C(10)
= B(P): C(11) = B(Q)
136 A(2,
2) = W — C(1) — C(7) — C(10) — C(11)
138 IF A(2, 2) < B(1) THEN 525
140 IF A(2, 2) > B(25) THEN 525
142 FOR X = 1 TO 11
144 IF A(2, 2) = C(X) THEN 525
146 NEXT X
148 FOR X = 1 TO 25
150 IF A(2, 2) = B(X) THEN 156
152 NEXT X
154 GOTO 525
156 C(12)
= A(2, 2)
158 FOR R = 1 TO 25
160 IF R <> I THEN IF R
<> J THEN IF R <> K THEN IF R <> L THEN IF R <> M THEN
IF R <> N THEN IF R <> O THEN IF R <> P THEN IF R <> Q
THEN 166
162 GOTO 520
166 FOR S = 1 TO 25
168 IF S <> I THEN IF S
<> J THEN IF S <> K THEN IF S <> L THEN IF S <> M THEN
IF S <> N THEN IF S <> O THEN IF S <> P THEN IF S <> Q
THEN IF S <> R THEN 172
170 GOTO 515
172 C(13)
= B(R): C(14) = B(S)
174 A(2,
5) = W — C(5) — C(10) — C(13) — C(14)
176 IF A(2, 5) < B(1) THEN 515
178 IF A(2, 5) > B(25) THEN 515
180 FOR X = 1 TO 14
182 IF A(2, 5) = C(X) THEN 515
184 NEXT X
186 FOR X = 1 TO 25
188 IF A(2, 5) = B(X) THEN 194
190 NEXT X
192 GOTO 515
194 C(15)
= A(2, 5)
196 FOR T = 1 TO 25
198 IF T <> I THEN IF T
<> J THEN IF T <> K THEN IF T <> L THEN IF T <> M THEN
IF T <> N THEN IF T <> O THEN IF T <> P THEN IF T <> Q
THEN IF T <> R THEN IF T <> S THEN 202
200 GOTO 510
202 C(16)
= B(T)
204 A(2,
3) = W — C(6) — C(12) — C(15) — C(16)
206 IF A(2, 3) < B(1) THEN 510
208 IF A(2, 3) > B(25) THEN 510
210 FOR X = 1 TO 16
212 IF A(2, 3) = C(X) THEN 510
214 NEXT X
216 FOR X = 1 TO 25
218 IF A(2, 3) = B(X) THEN 224
220 NEXT X
222 GOTO 510
224 C(17)
= A(2, 3)
226 FOR U = 1 TO 25
228 IF U <> I THEN IF U
<> J THEN IF U <> K THEN IF U <> L THEN IF U <> M THEN
IF U <> N THEN IF U <> O THEN IF U <> P THEN IF U <> Q
THEN IF U <> R THEN IF U <> S THEN IF U <> T THEN 232
230 GOTO 505
232 C(18)
= B(U)
234 A(3,
1) = W — C(1) — C(8) — C(16) — C(18)
236 IF A(3, 1) < B(1) THEN 505
238 IF A(3, 1) > B(25) THEN 505
240 FOR X = 1 TO 18
242 IF A(3, 1) = C(X) THEN 505
244 NEXT X
246 FOR X = 1 TO 25
248 IF A(3, 1) = B(X) THEN 254
250 NEXT X
252 GOTO 505
254 C(19)
= A(3, 1)
256 FOR V = 1 TO 25
258 IF V <> I THEN IF V
<> J THEN IF V <> K THEN IF V <> L THEN IF V <> M THEN
IF V <> N THEN IF V <> O THEN IF V <> P THEN IF V <> Q
THEN IF V <> R THEN IF V <> S THEN IF V <> T THEN IF V
<> U THEN 262
260 GOTO 500
262 C(20)
= B(V)
264 A(3,
2) = W — C(7) — C(14) — C(19) — C(20)
266 IF A(3, 2) < B(1) THEN 500
268 IF A(3, 2) > B(25) THEN 500
270 FOR X = 1 TO 20
272 IF A(3, 2) = C(X) THEN 500
274 NEXT X
276 FOR X = 1 TO 25
278 IF A(3, 2) = B(X) THEN 284
280 NEXT X
282 GOTO 500
284 C(21)
= A(3, 2)
286 A(4,
3) = W — C(9) — C(11) — C(13) — C(18)
288 IF A(4, 3) < B(1) THEN 500
290 IF A(4, 3) > B(25) THEN 500
292 FOR X = 1 TO 21
294 IF A(4, 3) = C(X) THEN 500
296 NEXT X
298 FOR X = 1 TO 25
300 IF A(4, 3) = B(X) THEN 306
302 NEXT X
304 GOTO 500
306 C(22)
= A(4, 3)
308 A(5,
2) = W — C(2) — C(12) — C(21) — C(9)
310 IF A(5, 2) < B(1) THEN 500
312 IF A(5, 2) > B(25) THEN 500
314 FOR X = 1 TO 22
316 IF A(5, 2) = C(X) THEN 500
318 NEXT X
320 FOR X = 1 TO 25
322 IF A(5, 2) = B(X) THEN 328
324 NEXT X
326 GOTO 500
328 C(23)
= A(5, 2)
330 A(5,
3) = W — C(3) — C(17) — C(7) — C(22)
332 IF A(5, 3) < B(1) THEN 500
334 IF A(5, 3) > B(25) THEN 500
336 FOR X = 1 TO 23
338 IF A(5, 3) = C(X) THEN 500
340 NEXT X
342 FOR X = 1 TO 25
344 IF A(5, 3) = B(X) THEN 350
346 NEXT X
348 GOTO 500
350 C(24)
= A(5, 3)
352 A(5,
4) = W — C(4) — C(6) — C(20) — C(11)
354 IF A(5, 4) < B(1) THEN 500
356 IF A(5, 4) > B(25) THEN 500
358 FOR X = 1 TO 24
360 IF A(5, 4) = C(X) THEN 500
362 NEXT X
364 FOR X = 1 TO 25
366 IF A(5, 4) = B(X) THEN 372
368 NEXT X
370 GOTO 500
372 IF C(8) + C(23) + C(24) + A(5, 4)
+ C(10) <> W THEN 500
374 C(25)
= A(5, 4)
376 FOR X = 1 TO 25
378 FOR Y = 1 TO 25
380 IF Y = X THEN 384
382 IF C(X) = C(Y) THEN 500
384 NEXT Y
386 NEXT X
401 A(1,
1) = C(1): A(1, 2) = C(2): A(1, 3) = C(3): A(1, 5) = C(5)
402 A(2,
1) = C(16): A(2, 4) = C(6): A(3, 3) = C(7): A(3, 4) = C(20): A(3, 5) = C(14)
403 A(4, 1) = C(18): A(4, 4) = C(11): A(4, 5) =
C(13): A(5, 1) = C(8)
404 A(5,
5) = C(10)
408 FOR X = 1 TO 5
409 FOR Y = 1 TO 5
410 PRINT A(X, Y);
411 PRINT #1, A(X, Y);
412 NEXT Y
414 PRINT : PRINT #1,
416 NEXT X
418 PRINT : PRINT #1,
500 NEXT V
505 NEXT U
510 NEXT T
515 NEXT S
520 NEXT R
525 NEXT Q
530 NEXT P
535 NEXT O
540 NEXT N
545 NEXT M
550 NEXT L
555 NEXT K
560 NEXT J
565 NEXT I
570 PRINT : PRINT W: PRINT
600 END
Выполнить
программу полностью мне не удаётся (очень долго). Тогда я прибегаю к
искусственному заданию первых 6 переменных (по известному квадрату), то есть
записываю строки программы, задающие эти переменные, так:
42 FOR I = 17 TO 17
44 FOR J = 1 TO 1
48 FOR K = 15 TO 15
54 FOR L = 25 TO 25
80 FOR M = 4 TO 4
86 FOR N = 16 TO 16
Замечу,
что значение переменной – это не сам элемент квадрата, а номер этого элемента в
массиве чисел.
Теперь в
программе изменяются только 8 переменных из 14. В этом случае программа
выполняется полностью за 4 минуты и выдаёт только один магический квадрат, тот
самый, который изображён на рис. 44; именно из этого квадрата я задала первые 6
переменных.
Выполняю
ещё один такой же эксперимент. Снова строю магический квадрат из того же
массива чисел по программе S. Tognon. Вы видите этот квадрат на рис. 45.
|
53 |
97 |
107 |
37 |
19 |
|
73 |
47 |
23 |
103 |
67 |
|
13 |
31 |
71 |
89 |
109 |
|
113 |
59 |
83 |
41 |
17 |
|
61 |
79 |
29 |
43 |
101 |
Рис. 45
Снова
задаю в программе первые 6 переменных, теперь уже по квадрату с рис. 45, на
рисунке искусственно задаваемые переменные находятся в голубых ячейках. Строки
программы с этими переменными запишутся так:
42 FOR I = 11 TO 11
44 FOR J = 20 TO 20
48 FOR K = 23 TO 23
54 FOR L = 3 TO 3
80 FOR M = 22 TO 22
86 FOR N = 15 TO 15
Запускаю
программу, она полностью выполняется и выдаёт два магических квадрата! Понятно,
что один из них с рис. 45. Но найден ещё один магический квадрат (рис. 46):
|
53 |
97 |
107 |
37 |
19 |
|
73 |
47 |
23 |
103 |
67 |
|
109 |
31 |
71 |
89 |
13 |
|
17 |
59 |
83 |
41 |
113 |
|
61 |
79 |
29 |
43 |
101 |
Рис. 46
Сравните
квадраты на рис. 45 и рис. 46. Интересный вариант квадрата с рис. 45 найден
программой: переставлены две пары чисел (эти числа в розовых ячейках). Как
видим, программа не пропускает ни одного варианта.
Ещё один
тест, для традиционного магического квадрата, изображённого на рис. 47 (квадрат
выбран произвольно).
|
1 |
14 |
22 |
18 |
10 |
|
23 |
20 |
6 |
4 |
12 |
|
9 |
2 |
13 |
25 |
16 |
|
15 |
21 |
19 |
7 |
3 |
|
17 |
8 |
5 |
11 |
24 |
Рис. 47
Теперь
строки программы, задающие первые 6 переменных, запишутся так:
42 FOR I = 1 TO 1
44 FOR J = 14 TO 14
48 FOR K = 22 TO 22
54 FOR L = 10 TO 10
80 FOR M = 4 TO 4
86 FOR N = 13 TO 13
Замечу,
что для традиционных магических квадратов номер элемента совпадает с самим
элементом.
Запускаю
программу, она работает примерно минут 20 и выдаёт несколько магических
квадратов (не поставила счётчик в программе, считать квадраты не хочется).
Показываю все эти магические квадраты, как они записаны в файл.
1 14 22 18 10
9 21 6 4 25
24 5 13 20 3
16 23 7 11 8
15 2 17 12 19
1 14 22 18 10
25 21 12 4 3
8 5 13 20 19
16 23 11 6 9
15 2 7 17 24
1 14 22 18 10
21 9 12 4 19
20 3 13 24 5
8 23 11 17 6
15 16 7 2 25
1 14 22 18 10
16 19 2 4 24
20 5 13 12 15
11 21 3 23 7
17 6 25 8 9
1 14 22 18 10
20 11 23 4 7
19 3 13 6 24
8 21 2 25 9
17 16 5 12 15
1 14 22 18 10
15 6 16 4 24
23 19 13 7 3
9 21 2 25 8
17 5 12 11 20
1 14 22 18 10
23 20 6 4 12
9 2 13 25 16
15 21 19 7 3
17 8 5 11 24
1 14 22 18 10
25 19 11 4 6
7 2 13 23 20
15 21 16 8 5
17 9 3 12 24
1 14 22 18 10
25 15 2 4 19
16 7 13 20 9
6 21 23 12 3
17 8 5 11 24
1 14 22 18 10
24 6 23 4 8
7 15 13 11 19
16 21 5 20 3
17 9 2 12 25
1 14 22 18 10
5 19 12 4 25
23 6 13 3 20
15 17 7 24 2
21 9 11 16 8
1 14 22 18 10
8 23 19 4 11
15 9 13 3 25
20 17 5 16 7
21 2 6 24 12
1 14 22 18 10
25 23 2 4 11
3 5 13 20 24
15 17 9 16 8
21 6 19 7 12
1 14 22 18 10
11 23 2 4 25
24 5 13 20 3
8 17 9 16 15
21 6 19 7 12
1 14 22 18 10
11 23 19 4 8
25 9 13 3 15
7 17 5 16 20
21 2 6 24 12
1 14 22 18 10
7 12 19 4 23
25 2 13 16 9
11 17 5 24 8
21 20 6 3 15
1 14 22 18 10
23 12 19 4 7
9 2 13 16 25
11 17 5 24 8
21 20 6 3 15
1 14 22 18 10
25 20 9 4 7
12 11 13 5 24
6 17 19 15 8
21 3 2 23 16
1 14 22 18 10
25 20 9 4 7
2 3 13 23 24
16 17 15 12 5
21 11 6 8 19
1 14 22 18 10
11 20 25 4 5
23 6 13 16 7
9 17 3 12 24
21 8 2 15 19
1 14 22 18 10
15 24 19 4 3
16 2 13 25 9
12 17 6 7 23
21 8 5 11 20
1 14 22 18 10
11 19 23 4 8
25 9 13 15 3
7 17 5 12 24
21 6 2 16 20
1 14 22 18 10
11 19 25 4 6
23 8 13 16 5
9 17 3 12 24
21 7 2 15 20
1 14 22 18 10
23 7 19 4 12
9 25 13 3 15
11 17 5 24 8
21 2 6 16 20
1 14 22 18 10
24 6 23 4 8
12 9 13 15 16
7 17 5 25 11
21 19 2 3 20
1 14 22 18 10
5 25 7 4 24
17 8 13 11 16
19 15 2 20 9
23 3 21 12 6
1 14 22 18 10
5 19 20 4 17
12 9 13 6 25
24 15 3 21 2
23 8 7 16 11
Квадрат с
рис. 47 выделен среди этих квадратов, выданных программой.
И,
наконец, последний тест. Возьмём теперь наименьший магический квадрат из
произвольных смитов. Этот квадрат построен совсем недавно участником форума dxdy.ru (ник 12d3). Вы видите этот квадрат
на рис. 48.
|
355 |
576 |
4 |
319 |
382 |
|
454 |
85 |
391 |
648 |
58 |
|
27 |
535 |
346 |
526 |
202 |
|
706 |
166 |
378 |
121 |
265 |
|
94 |
274 |
517 |
22 |
729 |
Рис. 48
Повторяю
эксперимент. Программы работает 3 секунды и выдаёт только один магический
квадрат, этот самый – с рис. 48. Вариантов здесь не найдено. Но они наверняка
будут, если не фиксировать 6 переменных. А сколько всего будет магических
квадратов, составленных из чисел данного массива, неизвестно. Автор квадрата
сообщал на форуме, что его программа тоже строит все магические квадраты из
заданного массива чисел, но сколько будет квадратов в этом конкретном случае,
он не сообщил.
Таким
образом, мы имеем работающую программу построения всех магических
квадратов 5-го порядка из заданного массива, состоящего из 25 чисел. Кто желает
повторить опыт американцев? А вдруг они ошиблись, и традиционных магических
квадратов 5-го порядка совсем не столько, сколько они насчитали. Трудно
поверить, что их так много. Когда я проделала это же самое для порядка 4 (очень
давно, ещё на старой ЭВМ), удостоверилась, что традиционных магических
квадратов 4-го порядка действительно 880 (с учётом поворотов и отражений).
Сначала тоже не верилось. А вот для порядка 5 пока не удаётся построить все
традиционные магические квадраты. Вот и программа уже есть, но не могу её
выполнить. Один участник форума dxdy.ru тоже вроде бы интересуется
этим вопросом. Он пытался построить все традиционные квадраты порядка 5 по
программе S.
Tognon. Но это ему не удалось по
вполне понятной причине: эта программа не предназначена для построения всех квадратов
из заданного массива чисел.
Кроме
того, у нас имеется нерешённая задача о наименьшем магическом квадрате 5-го
порядка из последовательных смитов. Можно использовать представленную схему для
решения этой задачи. Сначала, конечно, нужно найти подходящие массивы, из
которых может быть построен магический квадрат 5-го порядка, а затем проверять
все эти массивы по предложенному алгоритму.
Разумеется,
можно придумать ещё не один алгоритм для решения этой задачи.
Итак, ещё
одна
Задача:
построить
наименьший магический квадрат 5-го порядка из последовательных чисел Смита.
В заключение
рассказа об общих формулах магических квадратов 5-го порядка представлю ещё
один алгоритм построения магических квадратов 5-го порядка из массива,
состоящего из 25 чисел. Повторю: числа в массиве могут быть любыми, лишь бы
сумма всех чисел массива была кратна 5. Понятно, что не из любого массива,
удовлетворяющего этому условию, магический квадрат может быть построен. Это
условие является необходимым, но не является достаточным.
Для показа
этого алгоритма возьмём для наглядности магический квадрат, изображённый на
рис. 48. Этот квадрат составлен из следующих смитов:
4, 22, 27, 58, 85, 94, 121, 166, 202, 265, 274,
319, 346, 355, 378, 382, 391, 454, 517, 526, 535, 576, 648, 706, 729
Сумма всех чисел массива
равна 8180, магическая константа S = 8180/5 = 1636.
На первом
этапе сформируем все оригинальные строки по 5 чисел, так что сумма чисел в
строке равна магической константе квадрата. Строка считается оригинальной, если
числа в ней следуют в порядке возрастания. Этот этап очень просто
запрограммировать, программа выполняется быстро и выдаёт 216 нужных строк.
Покажу несколько первых строк из файла, в который они записаны программой:
4 22 346
535 729
4 22 355
526 729
4 22 378
526 706
4 27 382
517 706
4 58 319
526 729
4 58 391
454 729
4 58 391
535 648
4 85 265
576 706
4 85 382
517 648
4 85 454
517 576
4 94 274
535 729
4 94 355
454 729
4 94 355
535 648
4 94 378
454 706
4 121 265
517 729
4 121 346
517 648
4 166 202
535 729
4 166 346 391 729
4 166 355
382 729
4 166 355
535 576
4 166 378
382 706
4 202 265
517 648
4 202 319
382 729
4 202 319
535 576
.
. . . . . . . . . . . . . . . . . .
На втором
этапе из всех найденных строк сформируем оригинальные наборы из 3 строк, так
что все числа в наборе различные. Наборы считаются оригинальными, если первые
числа строк следуют в порядке возрастания.
Этот этап
тоже просто запрограммировать и программа выполняется быстро. Покажу три первых
оригинальных набора строк, выданных программой:
4 22 346 535 729
27 58 319 526 706
85 94 355 454 648
4 22 355 526 729
27 58 391 454 706
85 94 274 535 648
4 22 378 526 706
27 166 391 517 535
58 94 382 454 648
. . . . . . . . . . . . . .
. . . .
Понятно, что среди всех
оригинальных наборов должен быть такой набор:
4 319 355 382 576
27 202 346 526 535
58
85 391 454 648
Переходим
к третьему этапу алгоритма. На этом этапе каждый оригинальный набор надо
преобразовать путём перестановки строк и перестановки всех чисел в строках, а
затем каждый вариант набора достроить до магического квадрата, если это
окажется возможным. Я написала программу этого этапа только для одного оригинального
набора. Кроме того, в программу не заложена перестановка строк в наборе, в
программе выполняется только перестановка чисел в строках. Понятно, что таким
способом мы получаем 1203 вариантов набора. Если заложить ещё перестановку
строк в наборе, то вариантов будет 6*1203. Даже на Бейсике программа
третьего этапа выполняется примерно 35 — 40 минут и выдаёт магический квадрат,
если он получается. На рис. 49 показано, как выполняется достраивание квадрата.
Варьируются всего две переменные M и N, каждая из них принимает
10 значений (на две строки у нас осталось 10 чисел массива). Остальные 8
элементов xi вычисляются по значениям
варьируемых переменных и уже известным элементам.
|
355 |
576 |
4 |
319 |
382 |
|
454 |
85 |
391 |
648 |
58 |
|
27 |
535 |
346 |
526 |
202 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
M |
x6 |
x7 |
x8 |
N |
Рис. 49
Очевидно:
для того чтобы получить магический квадрат с рис. 48, надо переставить строки в
показанном выше оригинальном наборе так:
4 319 355 382 576
58
85 391 454 648
27 202 346 526 535
Итак,
введя в программу исходный массив из 25 чисел и этот оригинальный набор из 3
строк, я получаю два магических квадрата: квадрат с рис. 48 и квадрат,
получающийся из него отражением относительно вертикальной оси симметрии, то
есть вот такой эквивалентный квадрат (рис. 50):
|
382 |
319 |
4 |
576 |
355 |
|
58 |
648 |
391 |
85 |
454 |
|
202 |
526 |
346 |
535 |
27 |
|
265 |
121 |
378 |
166 |
706 |
|
729 |
22 |
517 |
274 |
94 |
Рис. 50
Чтобы не
корректировать программу, я сделала варианты наборов, переставив строки в
оригинальном наборе вручную, и проверила ещё 5 вариантов набора по программе.
Для 4 вариантов программа не выдала ни одного магического квадрата, а для
одного варианта выдала два магических квадрата, эти квадраты тоже эквивалентны,
один получается из другого отражением относительно вертикальной оси симметрии.
Покажу вариант набора, из которого получились магические квадраты:
58
85 391 454 648
4 319 355 382
576
27 202 346 526 535
И вот
какой магический квадрат получился из этого варианта набора (показываю один из
эквивалентных квадратов) (рис. 51):
|
85 |
454 |
391 |
58 |
648 |
|
576 |
355 |
4 |
382 |
319 |
|
535 |
27 |
346 |
202 |
526 |
|
274 |
94 |
517 |
729 |
22 |
|
166 |
706 |
378 |
265 |
121 |
Рис. 51
Легко видеть, что этот
квадрат получается из квадрата с рис. 48 М-преобразованием.
Таким
образом, представленный алгоритм вполне пригоден для реализации. Если
объединить все три этапа и написать программу на нормальном языке
программирования, можно довольно быстро строить все магические квадраты
из заданного массива, состоящего из 25 чисел. При этом важно отметить один
нюанс: чем меньше будет строк из 5 чисел, дающих в сумме магическую константу
квадрата, тем быстрее выполнится программа, потому что время выполнения
программы напрямую зависит от количества таких строк. Следовательно, данный
алгоритм как раз идеально подходит для построения магических квадратов из чисел
Смита, потому что числа Смита дают очень мало строк с магической суммой. Это
установлено эмпирически.
Здесь
представлены два алгоритма построения магических квадратов 5-го порядка из
массива, состоящего из 25 чисел. Разумеется, они не исчерпывают всех возможных
алгоритмов решения этой задачи. Читатели могут придумать свои интересные схемы
и реализовать их. Напомню: у нас есть нерешённая задача – не найден наименьший
магический квадрат 5-го порядка из последовательных смитов.
Подключайтесь
к решению этой задачи, а также всех задач, которые предложены в статье!
ДОБАВЛЕНИЕ
Когда я
составляла программу построения магических квадратов 4-го порядка из массива,
состоящего из 16 чисел, мне ещё не была известна формула Бергхольта. В моей
программе реализована схема, показанная на рис. 52.
|
a1 |
a2 |
x1 |
a3 |
|
a4 |
x2 |
a5 |
x5 |
|
x6 |
a6 |
a7 |
x7 |
|
x3 |
x8 |
x9 |
x4 |
Рис. 52
Здесь ai (i = 1, 2, …, 7) – свободные переменные, xk (k = 1, 2, …, 9) – зависимые переменные. Все
свободные переменные должны принять 16 значений, равных числам массива.
Магическая константа квадрата определяется массивом чисел, обозначим её S. Зависимые переменные
вычисляются по следующим формулам:
x1 = S – a1 – a2 – a3
x2 = S – a5 – a6 – a7
x3 = S – a3 – a5 – a6
x4 = S – a1 – a7 – x2
x5 = S – a4 – a5 – x2
x6 = S – a1 – a4 – x3
x7 = S – a6 – a7 – x6
x8 = S – a2 – a6 – x2
x9 = S – a5 – a7 – x1
Программа,
составленная по этой схеме, работает быстро даже на Бейсике. Если в качестве
исходного массива взять первые 16 натуральных чисел, то по этой программе можно
построить все традиционные магические квадраты 4-го порядка. По просьбе одного
читателя я построила все традиционные квадраты по этой программе и выложила их
на сайте. Причём квадраты построились с учётом поворотов и отражений, то есть
количество квадратов равно 880*8 = 7040. Смотрите эти квадраты здесь:
http://www.natalimak1.narod.ru/mk/MK4all.rtf
По этой
программе я проверила 800 первых кандидатов в наименьший магический квадрат из
последовательных смитов, о чём уже сказано выше.
Можно
использовать подобную схему для построения нетрадиционных магических квадратов
4-го порядка из массива, состоящего более чем из 16 чисел. Тогда количество
свободных переменных увеличится на 1, и все они должны принять значения, равные
всем числам массива. В этом случае время выполнения программы напрямую зависит
от количества чисел в массиве.
Далее,
запрограммировав формулу Бергхольта для традиционных пандиагональных квадратов
4-го порядка (см. рис. 27), я построила все пандиагональные квадраты данного
порядка. Они тоже построились с учётом поворотов и отражений, то есть их всего
48*8 = 384. Возможно, что пандиагональные квадраты 4-го порядка уже есть в
Приложениях (они давно были мной построены), но добавлю и эти квадраты,
построенные по формуле Бергхольта. Смотрите эти квадраты здесь:
http://www.natalimak1.narod.ru/mk/pan4all.rtf
ЕЩЁ ДОБАВЛЕНИЕ (25
декабря 2009 г.)
На рис. 43
представлена общая схема построения магических квадратов 5-го порядка из массива,
состоящего из 25 чисел. Теперь представлю схему построения пандиагональных
квадратов 5-го порядка из массива, состоящего из 25 чисел (рис. 53).
|
a1 |
a2 |
a3 |
a4 |
x1 |
|
a5 |
a6 |
a7 |
a8 |
x2 |
|
x11 |
x12 |
a9 |
a12 |
x7 |
|
x10 |
a10 |
x8 |
a11 |
x6 |
|
x3 |
x13 |
x8 |
x5 |
x4 |
Рис. 53
Здесь ai (i = 1,2, …, 12) свободные переменные, xk (k = 1, 2, …, 13) – зависимые переменные;
они пронумерованы в том порядке, в каком их следует вычислять, так как при
вычислении некоторых переменных используются уже вычисленные значения
предыдущих переменных. Все свободные переменные должны принять 25 значений,
равных числам массива. При реализации надо иметь в виду, что схема не
обеспечивает нужных сумм чисел в 6 из 8 разломанных диагоналей. Поэтому
проверку суммы чисел в этих диагоналях необходимо заложить в программу. Кроме
того, конечно, необходимо проверять принадлежность всех зависимых переменных
данному массиву чисел.
Обратите
внимание на то, что по сравнению с общей схемой (рис. 43) в рассматриваемой
схеме количество свободных переменных на 2 меньше.
Зависимые
переменные вычисляются по следующим формулам (S – магическая константа
квадрата):
x1 = S – a1 – a2 – a3 – a4
x2 = S – a5 – a6 – a7 – a8
x3 = S – a8 – a9 – a10 – x1
x4 = S – a1 – a6 – a9 – a11
x5 = S – a4 – a8 – a11 – a12
(5) x6 = S – a2 – a7 – a12 – x3
x7 = S – x1 – x2 – x4 – x6
x8 = S – a2 – a5 – a11 – x7
x9 = S – a3 – a7 – a9 – x8
x10 = S – a10 – a11 – x6 – x9
x11 = S – a1 – a5 – x3 – x10
x12 = S – a9 – a12 – x7 – x11
x13 = S – a2 – a6 – a10 – x12
Я
реализовала этот алгоритм на Бейсике; программа выполняется, но очень долго.
Для тестирования взяла идеальный магический квадрат, изображённый на рис. 33.
Квадрат продублирован на рис. 54.
|
8 |
80 |
61 |
64 |
57 |
|
74 |
77 |
18 |
60 |
41 |
|
70 |
21 |
54 |
87 |
38 |
|
67 |
48 |
90 |
31 |
34 |
|
51 |
44 |
47 |
28 |
100 |
Рис. 54
Напомню,
что в рассматриваемой схеме нам задан массив чисел, из которых строится пандиагональный
квадрат. По массиву сразу определяем магическую константу будущего квадрата,
она равна 270.
Искусственно
фиксирую в программе первые шесть свободных переменных. При таких условиях программа
выполняется быстро (несколько секунд) и выдаёт пандиагональный квадрат с рис.
54. А вот выполнить программу полностью мне не удаётся.
На рис. 55
вы видите наименьший магический квадрат 5-го порядка из простых чисел (автор
квадрата А. Лелеченко; квадрат выложен на форуме dxdy.ru).
|
3 |
43 |
107 |
7 |
73 |
|
97 |
53 |
13 |
47 |
23 |
|
61 |
59 |
5 |
71 |
37 |
|
31 |
67 |
29 |
89 |
17 |
|
41 |
11 |
79 |
19 |
83 |
Рис. 55
Можно ли
построить из данного массива простых чисел пандиагональный квадрат 5-го
порядка? Магическая константа квадрата равна 233. Предлагаю читателям решить
эту задачу.
Если из
данного массива пандиагональный квадрат построить невозможно, тогда надо
построить такой квадрат из других простых чисел, но с минимальной магической
константой. Вообще пандиагональный квадрат 5-го порядка из простых чисел
построен (см. рис. 30), этот квадрат обладает ещё и ассоциативностью, то есть
является идеальным. Можно построить пандиагональный квадрат 5-го порядка из
простых чисел и с меньшей магической константой по схеме с рис. 34, например,
такой (рис. 56):
|
7 |
337 |
131 |
197 |
181 |
|
227 |
241 |
37 |
277 |
71 |
|
307 |
11 |
167 |
271 |
97 |
|
211 |
127 |
367 |
41 |
107 |
|
101 |
137 |
151 |
67 |
397 |
Рис. 56
А вот
наименьший пандиагональный квадрат 5-го порядка из простых чисел мне
неизвестен. Я такой пока не построила.
Пандиагональный
квадрат 5-го порядка из чисел Смита тоже построен (см. рис. 35). Но это тоже
наверняка не наименьший квадрат. Так что, предлагается аналогичная задача:
построить наименьший пандиагональный квадрат 5-го порядка из чисел Смита.
ЕЩЁ ДОБАВЛЕНИЕ (4
февраля 2010 г.)
На форуме dxdy.ru решены сразу две задачи.
Обе задачи решил Макс Алексеев (ник maxal).
Первая
задача: найден наименьший магический квадрат 3-го порядка из последовательных
чисел Смита. Вы видите этот квадрат на рис. 57.
|
84138954584 |
84138954498 |
84138954532 |
|
84138954486 |
84138954538 |
84138954590 |
|
84138954544 |
84138954578 |
84138954492 |
Рис. 57
Теперь из последовательных
чисел Смита надо строить квадраты порядков 4 – 5, 7 – 9.
Алексеев
нашёл ещё один магический квадрат 3-го порядка из последовательных чисел Смита,
смотрите его на форуме.
Сложность
этой задачи была в том, что для её решения пришлось сгенерировать очень большие
числа Смита. Второй магический квадрат Алексеева из последовательных смитов
составлен из чисел на порядок больше тех, что заполняют квадрат, изображённый
на рис. 57.
Вторая задача о формуле
Ермакова (см. рис. 18). Алексеев сообщает на форуме:
“Я там обратил внимание на формулу Ермакова, которому якобы не
удалось получить по ней традиционный магический квадрат. Вот значения
параметров дающие таковой (а именно квадрат Дюрера): A = 16, B = 13, C = 4, D = 1, a = — 1, b = 0, c = 4, d = 0.”
В самом
деле, при данных значениях параметров по формуле Ермакова получается магический
квадрат Дюрера (рис. 58):
|
16 |
3 |
2 |
13 |
|
5 |
10 |
11 |
8 |
|
9 |
6 |
7 |
12 |
|
4 |
15 |
14 |
1 |
Рис. 58
Приходите
на форум dxdy.ru
в тему “Магические квадраты”:
http://dxdy.ru/topic12959.html
Принимайте
участие в решении нерешённых задач. Сообщайте о своих решениях на форуме.
Во второй части статьи вы найдёте рассказ о
формулах и схемах магических квадратов 6-го порядка.
Продолжение
читайте здесь:
http://www.natalimak1.narod.ru/formul1.htm
Л и т е р а т у р а
[1] М. Гарднер. От мозаик Пенроуза к надёжным
шифрам. – М.: Мир, 1993.
[2] Б. А. Кордемский. Математическая смекалка. –
М.: Государственное издательство технико-теоретической литературы, 1957.
[3] У. Болл, Г. Коксетер. Математические эссе и
развлечения. – М.: Мир, 1986.
[4]
Nature, 1910, vol. LXXXIII, p. 368;
см. также Chernick J.
American Mathematical Monthly, 1938, vol. XLV,
pp. 172 – 175.
[5] H. L. Nelson, A
Consecutive Prime 3 x 3 Magic Square, JRM, 1988, vol. 20:3, pp 214-216
9 – 25 декабря 2009 г.
– 4 февраля 2010 г.
г. Саратов
Пишите мне!
Приглашаю всех на форум!
На главную страницу
Магическая константа M — сумма чисел в каждой строке, столбце и на диагоналях.
Для квадрата любой размерности n∙n минимальная магическая константа вычисляется по следующей формуле:
M = n(n2 + 1)/2
I. Магический квадрат 3×3
Для квадрата размера 3×3 минимально возможная магическая константа будет равна:
3(32 + 1)/2 = 3(9 + 1)/2 = 15
Подчеркнём, что 15 — это не единственно возможная магическая константа для квадрата 3×3, а константа, меньше которой других констант для этого квадрата быть не может.
Важное правило, которое вам пригодится при построении магического квадрата 3×3:
Число в центре квадрата 3×3 всегда в три раза меньше магической константы.
То есть, если у нас магическая константа M = 15, то в центре квадрата 3×3 будет стоять
15:3 = 5.
Для дальнейшего составления магического квадрата с магической константой M=15 расставьте по углам чётные числа 2,4,8,6.
Как видим, по сумма чисел на диагоналях квадрата равна 15, то есть магической константе.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Зная магическую константу и по два числа в ряду и столбце, мы можем вписать третье число в ряд и столбец. Определить это число очень просто — надо из магической константы вычесть два числа из ряда или столбца.
Применив этот метод, мы получим полностью заполненный магический квадрат:
Ещё одно важное правило построения магических квадратов:
Если у нас есть один магический квадрат, и мы все числа этого квадрата увеличим на одно и то же число или умножим на одно и то же число, то у нас опять получится квадрат. Это правило достаточно очевидно.
Пример 1. К числам в нашем магическом квадрате с M=15 прибавим 3 и 5
Как видим, у первого квадрата сумма чисел по вертикали, горизонтали и диагонали одинакова и составляет 24 (это и есть его магическая константа), а у второго квадрата магическая константа равна 30.
У этих двух квадратов число в центре по прежнему в три раза меньше, чем магическая константа (8 у первого квадрата и 10 у второго).
Пример 2. Числа нашего магического квадрата с M=15 умножим на 2 и на 3
Как видим, в первом случае, после умножения чисел на два, мы получили квадрат с магической константой 30 — та же самая константа, что и после того, как в первом примере мы увеличили все числа на 5. Но при этом, несмотря на то, что у этих двух магических квадратах одинаковые магические константы, числа при этом в клетках разные — а вот число в центральном квадрате одно и то же — это 10.
Так и должно быть, ведь, как было сказано выше, в магическом квадрате 3×3 число в центральной клетке должно быть в три раза меньше магической константы. Т.к. магическая константа у обеих магических квадратов одинаковая, то и центральное число одно и то же.
Задача 1.
Постройте магический квадрат с магической константой 39.
Зная магическую константу, мы легко найдём число, которое должно быть в центральной клетке — нужно магическую константу разделить на 3. 39:3 = 13.
Далее можно или подбирать числа (помня о том, что сумма чисел по диагонали, по горизонтали и по вертикали должна быть равна магической константе) или, для ускорения процесса, воспользоваться знанием чисел магического квадрата с минимальной магической константой M = 15.
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Напомним этот квадрат:
В центре этого квадрата — число 5. В центре того квадрата, который мы должны построить — число 13.
Разница между этими числами составляет 8. И, как следует из правила, которое мы написали выше, если все числа одного магического квадрата увеличить на одно и то же число, то получится другой магический квадрат.
Достаточно запомнить, что в центре минимального магического квадрата — 5, а по углам — чётные числа 2, 4, 6, 8. Таким образом, нам надо увеличить эти числа на 8. Далее будет легко заполнить оставшиеся клетки (числа в них вычисляются как магическая константа минус числа в ряду или столбце).
В итоге получится вот такой квадрат:
Задача 2.
Достройте магический квадрат
В этом квадрате мы знаем число в центральной клетке (9), а, значит, мы знаем магическую константу, которая в 3 раза больше и равна 27. Ну а зная магическую константу и три первоначальных числа, вписать оставшиеся числа в клетки не составит труда.
Решение:
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
II. Магический квадрат 4×4
Мы не будем подробно останавливаться на магических квадратах 4×4 — они почти не встречаются на математических олимпиадах и вступительных экзаменах в физматшколы, но общее представление о них дадим.
Минимально возможная магическая константа вычисляется всё по той же формуле:
M = n(n2 + 1)/2
M = 4(42 + 1)/2 = 34.
У квадрата 4×4 обе стороны чётные, а это значит, что центральной клетки, в отличие от квадрата 3×3, у него нет, и нет соответствующей закономерности, с ним связанной.
Однако, у этого квадрата есть другие закономерности:
Помимо того, что у магического квадрата 4×4 равна сумма числе по диагонали, вертикали и горизонтали, у него сумма чисел в угловых квадратах 2×2 равна магической константе M, сумма чисел в центральном квадрате 2×2 также равна M, и сумма чисел в углах квадрата тоже равна M.
Сумма чисел в левом верхнем квадрате 2×2: 16+3+5+10 = 34. В трёх других угловых квадратах 2×2 сумма также равна магической константе, о чём и сказано выше.
Сумма чисел в центральном квадрате 2×2 также равна магической константе 34: 10+11+6+7 = 34.
Сумма чисел в углах магического квадрата тоже равна магической константе: 16+13+4+1 = 34
|
Ну, например есть такой квадрат 3х3 2 7 6 9 5 1 4 3 8 Имея его, запросто можно составить магический квадрат 9х9 по следующему принципу. Рисуете на бумаге большой квадрат 3х3, каждая клетка которого потому будет разбита на малые 9 квадратов 3х3. Видите, где у приведённого квадрата 3х3 находится единичка? В средней полосе справа. Потому у большого квадрата начинаем именно этот квадрат разбивать на 9 и так же заполняем в той же последовательности что была у квадрата 3х3, т.е. 2 7 6 9 5 1 4 3 8 Теперь где двойка? Вверху слева. На большом квадрате разбиваем его на 9 частей и заполняем в той же последовательности, но уже начиная с 10, т.к. закончили на 9. 11 16 15 18 14 10 13 12 17 Теперь очередь тройки. Она внизу посередине. Поступаем так же, но заполнять уже начиная с 19 20 25 24 27 23 19 22 21 26 Таким образом разобьём остальные клетки большого квадрата в нужной последовательности и заполним их аналогично. Получим полноценный магический квадрат 9х9. При желании по этому же способу можно получить магический квадрат 27х27 и т.д. автор вопроса выбрал этот ответ лучшим Mefody66 5 лет назад Nasos дал интересный ответ, но вопрос был не об этом. Дело в том, что магический квадрат 3*3 есть всего ОДИН, и Nasos его написал: 2 7 6 9 5 1 4 3 8 Конечно, не считая поворотов и отражений. Например, можно его же написать так: 6 1 8 7 5 3 2 9 4 Магическая сумма равна 15, а число 15 можно представить, как сумму трёх чисел, всего 8 способами: 15=1+5+9=1+6+8=2+4+9=2+5+8=2+6+7=3+4+8=3+5+7=4+5+6 Заметьте, что числа 1, 3, 7 и 9 встречаются по 2 раза, значит, они стоят на сторонах. Числа 2, 4, 6, 8 встречаются по 3 раза, они стоят в углах. И только 5 встречается 4 раза, она стоит в центре. После этого расставить числа на правильные места труда не составляет. -Irinka- более года назад Решение данной головоломки не вызовет у вас труда, если знать правила, которые необходимо при этом соблюдать. Итак, для решения ребуса используем цифры от 1 до 9. Записывать их нужно так, чтобы сумма чисел, как по горизонтали, так и по вертикали долга быть равна именно 15. Для простоты решения записываем в центр 5, для облегчения задачи по диагонали записываем четные цифры в свободные клетки, остальные клетки заполняем нечётными. Санитарный врач 3 года назад Раскрою некоторые секреты школ с углубленным изучение математики о решении магических квадратов. Их решают не подбором. Существуют разные виды математических квадратов 3 на 3. Так называемый простой магический квадрат, который состоит из 9 клеток (3 на 3), в который вписываются числа от 1 до 9 так, чтобы сумма числе в столбцах, строках и диагоналях была бы равна. Эта сумма еще называется «магической» суммой или магической постоянной. Числа в ячейках не повторяются. Существуют еще сложные магические квадраты 3 на 3, в которых вписываются произвольные числа, но условия о равенстве сумм чисел в строках, столбцах и диагоналях сохраняется. Решение магических квадратов проходят в 2-3 классе начальной школы, особенно этим славиться программа Гейдмана, рабочие тетради и контрольные работы. Есть четкие принципы решения магических квадратов, но не все учителя их доходчиво объясняют. Вот эти принципы решения магических квадратов 3 на 3:
Запомнив эти правила, Вы сможете решить любой магический квадрат 3 на 3. Илта 7 месяцев назад Такую задачу дают детям в третьем классе. По началу она может у ребёнка вызвать затруднения, но в принципе, зная правила, с заданием можно справиться. Для решения необходимо вписать цифры так, чтобы в сумме они давали число 15. Число 2 ставим в нижнюю правую клеточку, тройку в центр первого столбца, а 4 уже над тройкой. В центре магического квадрата ставим 5. В правом верхнем углу расположим цифру 6. Цифра 7 идёт под шестёркой. Цифра 8 в верхнем левом уголке. А цифра 9 в нижней строчке по центру. И теперь проверяем. Все в сумме даёт 15. Вот такое простое решение магического квадрата 3 на 3. Просто нужно включить воображение. 88SkyWalker88 более года назад Магический квадрат — это такой квадрат, который состоит из девяти клеточек (по три в ряду). В клеточки нужно поставить цифры таким образом, чтобы в каждом ряду, в каждом столбике, а также по диагонали была одна и та же сумма чисел. Итак, числа располагаем следующим образом: 2, 7, 6 9, 5, 1 4, 3, 8 Проверяем: 2+7+6=15 9+5+1=15 4+3+8=15 6+1+8=15 7+5+3=15 2+9+4=15 6+5+4=15 2+5+8=15 Везде сумма чисел получается 15. Точно в цель более года назад Очень интересная эта задача про магический квадрат. Дело в том, что сумма всех чисел и по диагонали, и по вертикали, и по горизонтали всегда будет равно 15. Я хочу напомнить, как выглядит магический квадрат: 2 7 6 9 5 1 4 3 8 Неважно, с какой цифры начинать отсчет и по какой линии идти — результатом всегда будет число 15. Чосик более года назад Данная загадка нередко встречается в играх, как часть головоломки. Чтобы решить магический квадрат, необходимо использовать цифры от 1 до 9, расположив их так, чтобы сумма чисел в ряду, столбике, по диагоналям была равна 15. Решить такую загадку просто, если уже делал это и знать основу. Тогда ее можно и повторить. Первый ключевой ход — поставить 5 в центре, точнее, оставить ее на своем месте. Это единственная цифра, которая сохраняет свою позицию, если бы выставляли цифры по порядку. Также помним, что четные цифры стоят по диагонали, а нечетные цифры (кроме центральной 5) в такие не попадают. После это расположить их в верном порядке просто. владсандрович более года назад Суть решения данной задачи там должна сводиться к тому, что в том квадрате, сумма всех чисел по диагонали, а так же и вертикале и горизонтали, всегда в конечном итоге, будет равняться именно пятнадцати. Пять там должно стоять в самом центре, четные цифры должны располагаться по диагонали, а что касается нечетных, то не считая пятерки, их нужно располагать более произвольно. ТаняМащинська 5 лет назад В школе на уроках информатики во втором классе моему сыну написали в домашнем задании решить магические квадраты 3*3. Если сказать коротко и просто, то это такой квадрат, в котором сума чисел равна числу 15:по диагонали, по горизонтали, или по вертикали. Знаете ответ? |
16
Существует несколько различных классификаций магических квадратов
пятого порядка, призванных хоть как-то их систематизировать. В книге
Мартина Гарднера [ГМ90, сс. 244-345] описан один из таких способов –
по числу в центральном квадрате. Способ любопытный, но не более того.
Сколько существует квадратов шестого порядка, до сих пор неизвестно, но их примерно 1.77 х 1019. Число огромное, поэтому нет никаких надежд пересчитать их с помощью полного перебора, а вот формулы для подсчёта магических квадратов никто придумать не смог.
Как составить магический квадрат?
Придумано очень много способов построения магических квадратов. Проще всего составлять магические квадраты нечётного порядка. Мы воспользуемся методом, который предложил французский учёный XVII века А. де ла Лубер (De La Loubère). Он основан на пяти правилах, действие которых мы рассмотрим на самом простом магическом квадрате 3 х 3 клетки.
Правило 1. Поставьте 1 в среднюю колонку первой строки (Рис. 5.7).
Рис. 5.7. Первое число
Правило 2. Следующее число поставьте, если возможно в клетку, соседнюю с текущей по диагонали правее и выше (Рис. 5.8).
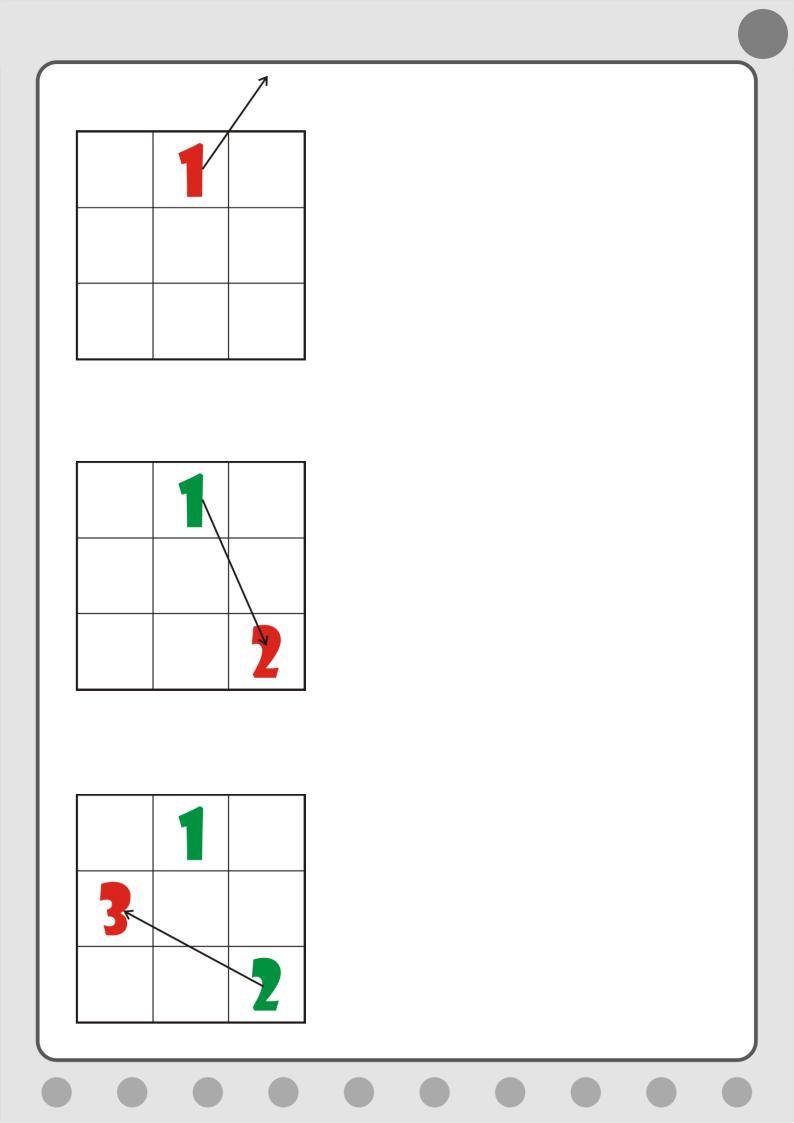
17
Рис. 5.8. Пытаемся поставить второе число
Правило 3. Если новая клетка выходит за пределы квадрата сверху, то запишите число в самую нижнюю строку и в следующую колонку (Рис. 5.9).
Рис. 5.9. Ставим второе число
Правило 4. Если клетка выходит за пределы квадрата справа, то запишите число в самую первую колонку и в предыдущую строку (Рис. 5.10).
Рис. 5.10. Ставим третье число
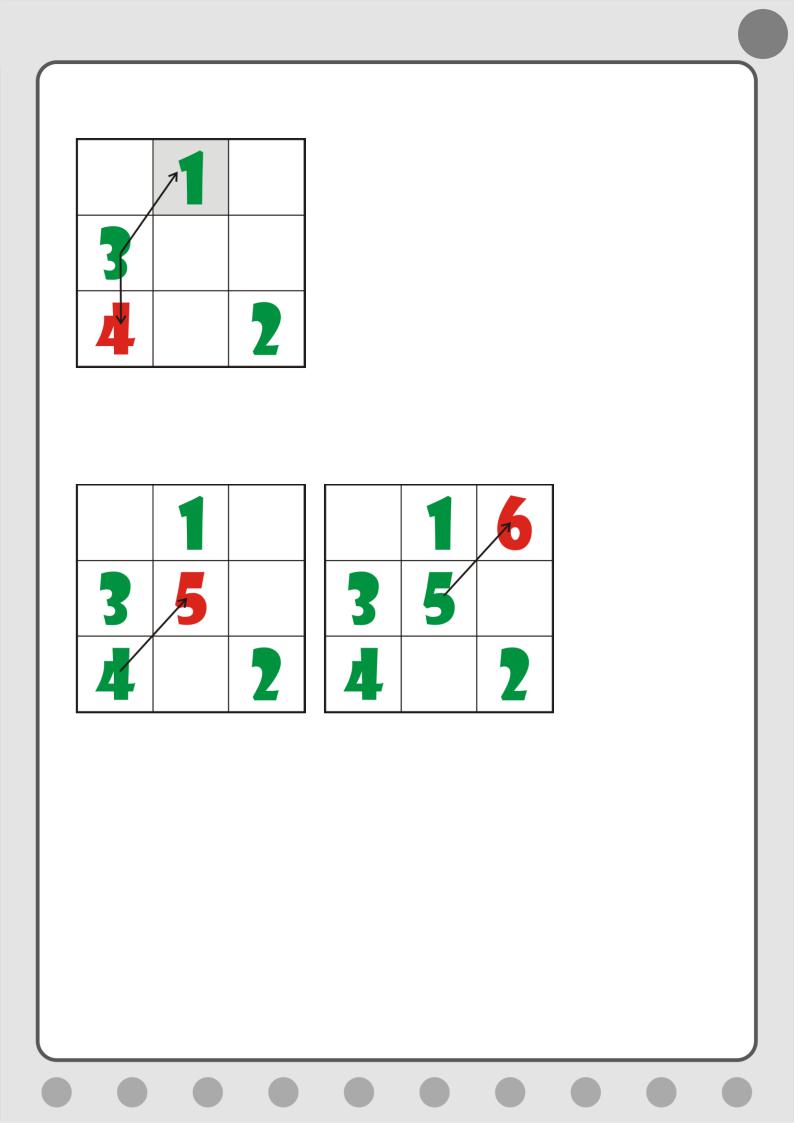
18
Правило 5. Если в клетке уже занята, то очередное число запишите под текущей клеткой (Рис. 5.11).
Рис. 5.11. Ставим четвёртое число
Далее переходите к Правилу 2 (Рис. 5.12).
Рис. 5.12. Ставим пятое и шестое число
Снова выполняйте Правила 3, 4, 5, пока не составите весь квадрат (Рис.
5.13).
Не правда ли, правила очень простые и понятные, но всё равно довольно утомительно расставлять даже 9 чисел. Однако, зная алгоритм построения магических квадратов, мы сможем легко перепоручить компьютеру всю рутинную работу, оставив себе только творческую, то есть написание программы.
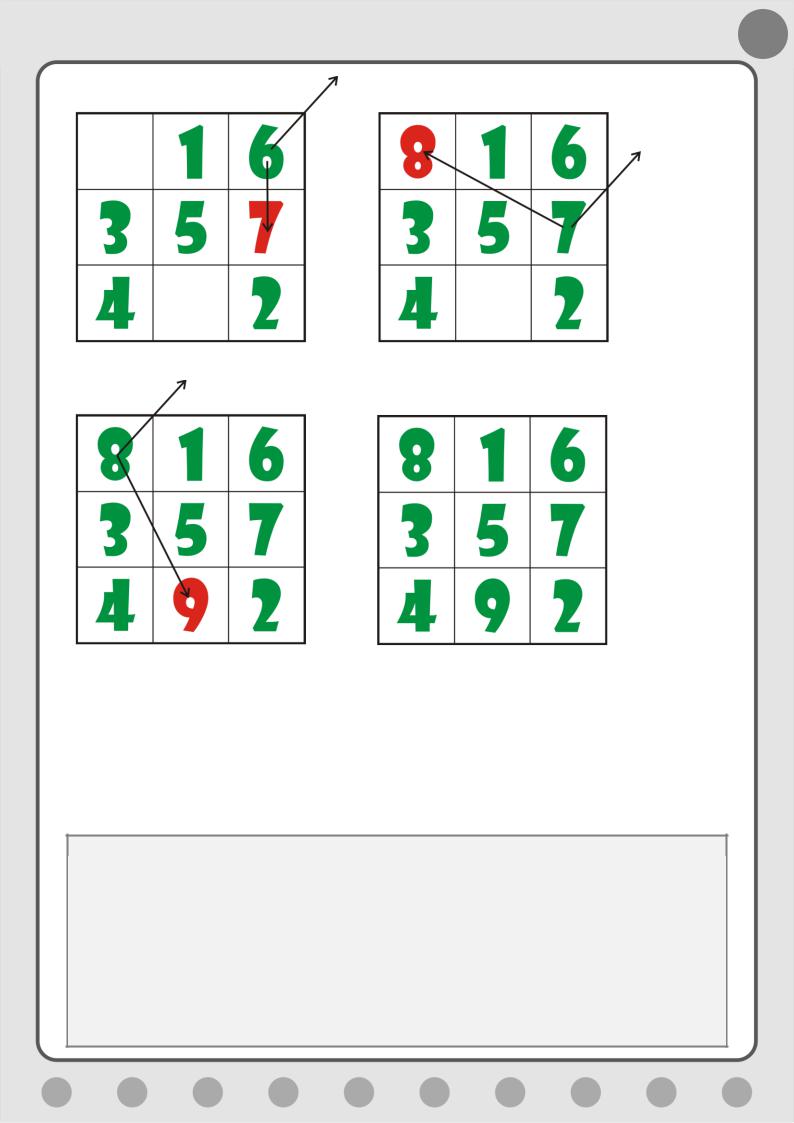
19
Рис. 5.13. Заполняем квадрат следующими числами
Проект Магические квадраты (Magic)
Набор полей для программы Магические квадраты совершенно очевиден:
//ПРОГРАММА ДЛЯ ГЕНЕРИРОВАНИЯ
//НЕЧЕТНЫХ МАГИЧЕСКИХ КВАДРАТОВ
//ПО МЕТОДУ ДЕ ЛА ЛУБЕРА
public partial class Form1 : Form
{
//макс. размеры квадрата: const int MAX_SIZE = 27; //var
int n=0; // порядок квадрата int [,] mq; // магический квадрат
int number=0;// текущее число для записи в квадрат

20
int col=0; // текущая колонка int row=0; // текущая строка
Метод де ла Лубера годится для составления нечётных квадратов любого размера, поэтому мы можем предоставить пользователю возможность самостоятельно выбирать порядок квадрата, разумно ограничив при этом свободу выбора 27-ью клетками.
После того как пользователь нажмёт заветную кнопку btnGen Генерировать!, метод btnGen_Click создаёт массив для хранения чисел и переходит в метод generate:
//НАЖИМАЕМ КНОПКУ «ГЕНЕРИРОВАТЬ»
private void btnGen_Click(object sender, EventArgs e)
{
//порядок квадрата:
n = (int)udNum.Value;
//создаем массив:
mq = new int[n+1, n+1];
//генерируем магический квадрат: generate();
lstRes.TopIndex = lstRes.Items.Count-27;
}
Здесь мы начинаем действовать по правилам де ла Лубера и записываем первое число – единицу – в среднюю клетку первой строки квадрата (или массива, если угодно):
//Генерируем магический квадрат void generate(){
//первое число: number=1;
rule1:
//колонка для первого числа — средняя: col = n / 2 + 1;
//строка для первого числа — первая: row=1;
//заносим его в квадрат: mq[row,col]= number;
Теперь мы последовательно пристраиваем по клеткам остальные числа – от двойки до n * n:
//переходим к следующему числу:
21
nextNumber:
number++;
Запоминаем на всякий случай координаты актуальной клетки
int tc=col; int tr = row;
и переходим в следующую клетку по диагонали:
col++; row—;
Проверяем выполнение третьего правила:
rule3:
if (row < 1) row= n;
А затем четвёртого:
rule4:
if (col > n) { col=1;
goto rule3;
}
И пятого:
rule5:
if (mq[row,col] != 0) { col=tc;
row=tr+1; goto rule3;
}
Как мы узнаем, что в клетке квадрата уже находится число? – Очень просто: мы предусмотрительно записали во все клетки нули, а числа в готовом квадрате больше нуля. Значит, по значению элемента массива мы сразу же определим, пустая клетка или уже с числом! Обратите внимание, что здесь нам понадобятся те координаты клетки, которые мы запомнили перед поиском клетки для следующего числа.
Рано или поздно мы найдём подходящую клетку для числа и запишем его в соответствующую ячейку массива:

22
//заносим его в квадрат: mq[row, col] = number;
Попробуйте иначе организовать проверку допустимости перехода в но-
вую клетку!
Если это число было последним, то программа свои обязанности выполнила, иначе она добровольно переходит к обеспечению клеткой следующего числа:
//если выставлены не все числа, то if (number < n*n)
//переходим к следующему числу: goto nextNumber;
И вот квадрат готов! Вычисляем его магическую сумму и распечатываем на экране:
//построение квадрата закончено: writeMQ();
} //generate()
Напечатать элементы массива очень просто, но важно учесть выравнивание чисел разной «длины», ведь в квадрате могут быть одно-, дву- и трёхзначные числа:
//Печатаем магический квадрат void writeMQ()
{
lstRes.ForeColor = Color.Black;
string s = «Магическая сумма = » + (n*n*n +n)/2; lstRes.Items.Add(s);
lstRes.Items.Add(«»);
// печатаем магический квадрат: for (int i= 1; i<= n; ++i){
s=«»;
for (int j= 1; j <= n; ++j){
if (n*n > 10 && mq[i,j] < 10) s += » «; if (n*n > 100 && mq[i,j] < 100) s += » «; s= s + mq[i,j] + » «;
}
lstRes.Items.Add(s);
}
lstRes.Items.Add(«»); }//writeMQ()
23
Запускаем программу – квадраты получаются быстро и на загляденье (Рис.
5.14).
Рис. 5.14. Изрядный квадратище!
В книге С.Гудман, С.Хидетниеми Введение в разработку и анализ алгорит-
мов, на страницах 297-299 мы отыщем тот же самый алгоритм, но в «сокращённом» изложении. Он не столь «прозрачен», как наша версия, но работает верно.
Добавим кнопку btnGen2 Генерировать 2! и запишем алгоритм на языке
Си-шарп в метод btnGen2_Click:
//Algorithm ODDMS
private void btnGen2_Click(object sender, EventArgs e)
{
//порядок квадрата: n = (int)udNum.Value;
//создаем массив:
mq = new int[n + 1, n + 1];
//генерируем магический квадрат: int row = 1;
24
int col = (n+1)/2;
for (int i = 1; i <= n * n; ++i)
{
mq[row, col] = i; if (i % n == 0)
{
++row;
}
else
{
if (row == 1) row = n;
else
—row;
if (col == n) col = 1;
else
++col;
}
}
//построение квадрата закончено: writeMQ();
lstRes.TopIndex = lstRes.Items.Count — 27;
}
Кликаем кнопку и убеждаемся, что генерируются «наши» квадраты (Рис.
5.15).
Рис. 5.15. Старый алгоритм в новом обличии
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Загрузить PDF
Загрузить PDF
Магические квадраты обрели популярность наряду с появлением математических игр, таких как судоку. Магический квадрат — это таблица, заполненная целыми числами таким образом, чтобы сумма чисел по горизонтали, вертикали и диагонали была одинакова (так называемая магическая константа). Эта статья расскажет вам, как построить квадрат нечетного порядка, квадрат порядка одинарной четности и квадрат порядка двойной четности.
-
1
Вычислите магическую константу.[1]
Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 3×3 n=3, а его магическая константа:- Магическая константа = [3 * (32 + 1)] / 2
- Магическая константа = [3 * (9 + 1)] / 2
- Магическая константа = (3 * 10) / 2
- Магическая константа = 30/2
- Магическая константа квадрата 3х3 равна 15.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
2
Напишите 1 в центральной ячейке верхней строки. Строить любой нечетный квадрат нужно именно с этой ячейки. Например, в квадрате 3х3 напишите 1 во второй ячейке верхней строки, а в квадрате 15х15 напишите 1 в восьмой ячейке верхней строки.
-
3
Следующие числа (2,3,4 и так далее по возрастанию) записывайте в ячейки по правилу: одна строка — вверх, один столбец — вправо. Но, например, чтобы записать 2, нужно «выйти» за пределы квадрата, поэтому существуют три исключения из данного правила:
- Если вы вылезли за верхний предел квадрата, напишите цифру в самой нижней ячейке соответствующего столбца.
- Если вы вылезли за правый предел квадрата, напишите цифру в самой дальней (левой) ячейке соответствующей строки.
- Если вы попали на ячейку, которая занята другой цифрой, напишите цифру непосредственно под предыдущей записанной цифрой.
Реклама
-
1
Существуют различные методики для построения квадратов порядка одинарной четности и двойной четности.
- Число строк или столбцов в квадрате порядка одинарной четности делится на 2, но не на 4.[2]
- Наименьшим квадратом порядка одинарной четности является квадрат 6х6 (квадрат 2×2 построить нельзя).
- Число строк или столбцов в квадрате порядка одинарной четности делится на 2, но не на 4.[2]
-
2
Вычислите магическую константу. Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 6×6 n=6, а его магическая константа:
- Магическая константа = [6 * (62 + 1)] / 2
- Магическая константа = [6 * (36 + 1)] / 2
- Магическая константа = (6 * 37) / 2
- Магическая константа = 222/2
- Магическая константа квадрата 6х6 равна 111.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
3
Разделите магический квадрат на четыре квадранта одинакового размера. Обозначьте квадранты через А (сверху слева), C (сверху справа), D (снизу слева) и B (снизу справа). Чтобы выяснить размер каждого квадранта, разделите n на 2.
- Таким образом, в квадрате 6х6 размер каждого квадранта равен 3×3.
-
4
В квадранте А напишите четвертую часть всех чисел; в квадранте В напишите следующую четвертую часть всех чисел; в квадранте С напишите следующую четвертую часть всех чисел; в квадранте D напишите заключительную четвертую часть всех чисел.
- В нашем примере квадрата 6х6 в квадранте А напишите числа 1-9; в квадранте В — числа 10-18; в квадранте С — числа 19-27; в квадранте D — числа 28-36.
-
5
Числа в каждом квадранте записывайте так, как вы строили нечетный квадрат. В нашем примере квадрант А начните заполнять числами с 1, а квадранты С, B, D — с 10, 19, 28, соответственно.
- Число, с которого вы начинаете заполнение каждого квадранта, всегда пишите в центральной ячейке верхней строки определенного квадранта.
- Заполняйте каждый квадрант числами так, как будто это отдельный магический квадрат. Если при заполнении квадранта доступна пустая ячейка из другого квадранта, игнорируйте этот факт и пользуйтесь исключениями из правила заполнения нечетных квадратов.
-
6
Выделите определенные числа в квадрантах А и D.[3]
На данном этапе сумма чисел в столбцах, строках и по диагонали не будет равна магической константе. Поэтому вы должны поменять местами числа в определенных ячейках верхнего левого и нижнего левого квадрантов.- Начиная с первой ячейки верхней строки квадранта А, выделите количество ячеек, равное медиане количества ячеек во всей строке. Таким образом, в квадрате 6×6 выделите только первую ячейку верхней строки квадранта А (в этой ячейке написано число 8); в квадрате 10х10 вам нужно выделить первые две ячейки верхней строки квадранта А (в этих ячейках написаны числа 17 и 24).
- Образуйте промежуточный квадрат из выделенных ячеек. Так как в квадрате 6х6 вы выделили только одну ячейку, то промежуточный квадрат будет состоять из одной ячейки. Назовем этот промежуточный квадрат как A-1.
- В квадрате 10х10 вы выделили две ячейки верхней строки, поэтому необходимо выделить две первые ячейки второй строки, чтобы образовать промежуточный квадрат 2х2, состоящий из четырех ячеек.
- В следующей строке пропустите число в первой ячейке, а затем выделите столько чисел, сколько вы выделили в промежуточном квадрате A-1. Полученный промежуточный квадрат назовем A-2.
- Получение промежуточного квадрата А-3 аналогично получению промежуточного квадрата A-1.
- Промежуточные квадраты А-1, А-2, А-3 образуют выделенную область А.
- Повторите описанный процесс в квадранте D: создайте промежуточные квадраты, которые образуют выделенную область D.
-
7
Поменяйте местами числа из выделенных областей А и D (числа из первой строки квадранта А с числами из первой строки квадранта D и так далее). Теперь сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
Реклама
-
1
Число строк или столбцов в квадрате порядка двойной четности делится на 4.[4]
- Наименьшим квадратом порядка двойной четности является квадрат 4х4.
-
2
Вычислите магическую константу. Это можно сделать при помощи простой математической формулы [n * (n2 + 1)] / 2, где n – количество строк или столбцов в квадрате. Например, в квадрате 4×4 n=4, а его магическая константа:
- Магическая константа = [4 * (42 + 1)] / 2
- Магическая константа = [4 * (16 + 1)] / 2
- Магическая константа = (4 * 17) / 2
- Магическая константа = 68/2
- Магическая константа квадрата 4х4 равна 34.
- Сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
-
3
Создайте промежуточные квадраты А-D. В каждом углу магического квадрата выделите промежуточный квадрат размером n/4, где n – количество строк или столбцов в магическом квадрате.[5]
Обозначьте промежуточные квадраты как A, B, C, D (в направлении против часовой стрелки).- В квадрате 4×4 промежуточные квадраты будут состоять из угловых ячеек (по одной в каждом промежуточном квадрате).
- В квадрате 8х8 промежуточные квадраты будут иметь размер 2×2.
- В квадрате 12х12 промежуточные квадраты будут иметь размер 3×3 (и так далее).
-
4
Создайте центральный промежуточный квадрат. В центре магического квадрата выделите промежуточный квадрат размером n/2, где n – количество строк или столбцов в магическом квадрате. Центральный промежуточный квадрат не должен пересекаться с угловыми промежуточными квадратами, но должен касаться их углов.
- В квадрате 4×4 центральный промежуточный квадрат имеет размер 2×2.
- В квадрате 8×8 центральный промежуточный квадрат имеет размер 4×4 (и так далее).
-
5
Начните строить магический квадрат (слева направо), но числа записывайте только в ячейки, расположенные в выделенных промежуточных квадратах. Например, квадрат 4×4 вы заполните так:
- Напишите 1 в первой строке первом столбце; напишите 4 в первой строке четвертом столбце.
- Напишите 6 и 7 в центре второй строки.
- Напишите 10 и 11 в центре третьей строки.
- Напишите 13 в четвертой строке первого столбца; напишите 16 в четвертой строке четвертого столбца.
-
6
Оставшиеся ячейки квадрата заполняются аналогичным образом (слева направо), но числа нужно записывать в порядке убывания и только в ячейки, расположенные вне выделенных промежуточных квадратов. Например, квадрат 4×4 вы заполните так:
- Напишите 15 и 14 в центре первой строки.
- Напишите 12 во второй строке первого столбца; напишите 9 во второй строке четвертого столбца.
- Напишите 8 в третьей строке первого столбца; напишите 5 в третьей строке четвертого столбца.
- Напишите 3 и 2 в центре четвертой строки.
- Теперь сумма чисел в любой строке, столбце и по диагонали должна быть равна магической константе.
Реклама
Советы
- Воспользуйтесь описанными методами и найдите свой способ решения магических квадратов.
Реклама
Что вам понадобится
- Карандаш
- Бумага
- Ластик
Похожие статьи
Об этой статье
Эту страницу просматривали 352 321 раз.