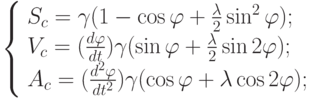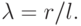Как составить математическую модель объекта

1 Основы математического моделирования

Учителю интеграция предметов позволяет воспитывать у ребят охоту к
целенаправленному преодолению трудностей на пути познания. Новые функции
педагога главным образом определяются необходимостью чёткого представлять
структуру учебной деятельности и свои действия на каждом этапе от возникновения
замысла до полного его осуществления.
Приведём пример простейшей математической модели. Представим себе, что нужно
определить площадь пола комнаты. Реальный объект – пол комнаты – заменяется
абстрактной
математической моделью – прямоугольником.
Математическая модель, основанная на некотором упрощении, никогда не бывает
тождественна рассматриваемому объекту, не передаёт всех его свойств и
особенностей, а является его приближённым отражением. Однако в результате
замены реального объекта соответствующей ему моделью появляется возможность
математически сформулировать задачу его изучения и воспользоваться для анализа
его свойств математическим аппаратом, который не зависит от конкретной природы
данного объекта. Этот аппарат позволяет единообразно описать широкий круг
фактов и наблюдений, провести их детальный количественный анализ, предсказать,
как поведёт себя объект в различных условиях, т.е. прогнозировать результаты
будущих наблюдений.
Моделирование представляет собой один из основных методов познания, является
формой отражения действительности и заключается в выяснении или воспроизведении
тех или иных свойств реальных объектов, предметов и явлений с помощью других
объектов, процессов, явлений, либо с помощью абстрактного описания в виде
изображения, плана, карты, совокупности уравнений, алгоритмов и программ.
Возможности моделирования, то есть перенос результатов, полученных в ходе
построения и исследования модели, на оригинал основаны на том, что модель в определенном
смысле отображает (воспроизводит, моделирует, описывает, имитирует) некоторые
интересующие исследователя черты объекта. Моделирование как форма отражения
действительности широко распространено, и достаточно полная классификация
возможных видов моделирования крайне затруднительна, хотя бы в силу
многозначности понятия «модель», широко используемого не только в
науке и технике, но и в искусстве, и в повседневной жизни.
Классификация в любой области знаний чрезвычайно важна. Она позволяет обобщить
накопленный опыт, упорядочить понятия предметной области.
Существует несколько подходов к классификации моделей. Выделим основные:
область использования;
учёт в модели временного фактора (динамики);
отрасль знаний;
способ представления моделей.
Классификация по области использования:
Классификация с учётом фактора времени и области использования:
Классификация по способу представления:
2 Требования, предъявляемые к математическим моделям
К математическим моделям предъявляются следующие основные требования:
Универсальности.
Точности.
Адекватности.
Экономичности.
Универсальность математической модели характеризует полноту отражения в ней
свойств реального объекта. Математическая модель отражает не все, а лишь
некоторые свойства реального объекта.
Точность математической модели оценивается степенью совпадения значений
выходных параметров реального объекта и значений тех же параметров,
рассчитанных с помощью модели.
Адекватность математической модели – это ее способность отражать заданные
свойства объекта с погрешностью, не выше заданной.
Экономичность математической модели характеризуется затратами вычислительных
ресурсов на ее реализацию. Если работа с математической моделью осуществляется
вручную, то ее экономичность определяется затратами личного времени проектировщика.
Если модель используется при автоматизированном проектировании, то затратами
машинного времени и памяти компьютера.
К математическим моделям предъявляется и целый ряд других требований, среди
которых следует выделить следующие:
Вычислимость, т.е. возможность ручного или с помощью ЭВМ исследования
качественных и количественных закономерностей функционирования объекта
(системы).
Модульность, т.е. соответствие конструкций модели структурным составляющим
объекта (системы).
Алгоритмизируемость, т.е. возможность разработки соответсвующих алгоритма и
программы, реализующей математическую модель на ЭВМ.
Наглядность, т.е. удобное визуальное восприятие модели.

Задачи математического моделирования.
Существует два основных класса задач, связанных с математическими моделями:
прямые и обратные. В первом случае все параметры модели считаются известными, и
нам остается только исследовать её поведение. Например, определение частоты
колебаний гармонического осциллятора при известном значении параметра k —
прямая задача математического моделирования.
Порой требуется решить обратную задачу: какие-то параметры модели неизвестны
(например, не могут быть измерены явно), и требуется их найти, сопоставляя
поведение реальной системы с её моделью. Ещё одна обратная задача: подобрать
параметры модели таким образом, чтобы она удовлетворяла каким-то заданным
условиям — такие задачи требуется решать при проектировании систем.

3 Примеры математического моделирования

Структурно-функциональная организация биологических макромолекул. Классическая
и квантовая динамика процессов внутримолекулярных и межмолекулярных
взаимодействий макромолекул и их комплексов.
Процессы переноса заряда, вещества и энергии в молекулярно-биологических
системах. Химическая и биологическая кинетика. Математические модели кинетики
роста популяций. Периодические процессы в биологии. Качественная теория систем
биохимических реакций.
Биологические мембраны. Моделирование структуры и основных мембранных
процессов. Моделирование проницаемости и возбудимости клеточных мембран.
Биология клетки. Создание математических моделей функционирования органелл и
клетки в целом. Модели внутриклеточной и межклеточной передачи сигналов.
Математическое моделирование регуляции функционирования клетки.
Математическая физиология. Моделирование тканей, органов, и систем организма в
норме и патологии. Моделирование иммунной, эндокринной системы, сердечно — сосудистой
системы, мышечной системы, системы свертывания крови и других систем тканей и
органов. Моделирование патофизиологических процессов: повреждения, регенерации
и старения тканей, органов и систем. Моделирование инфекционных заболеваний.
Нейросетевые модели обработки информации в структурах мозга.
Биология развития и старения. Моделирование систем контроля онтогенеза. Моделирование
процессов деления и роста клеток, дифференциации тканей и морфогенеза особи.
Моделирование процессов физиологической адаптации и старения организма.
Математическая генетика. Моделирование пространственной, временной и
функциональной организации генетических систем. Теория внутрипопуляционной
селекции. Моделирование генетического полиморфизма.
Эволюция. Математические модели эволюционной генетики. Исследования общих
закономерностей макроэволюционного процесса. Эволюционные модели
биоразнообразия. Популяционная биология. Моделирование динамики численности и
структуры популяций с учетом различных биологических механизмов взаимодействия
популяций (отношения типа хищник-жертва, конкуренция, действие лимитирующих
факторов, стимуляторов и др.). Модели взаимодействия популяций через сигнальные
системы.
Моделирование экосистем. Модели региональных и локальных экосистем.
Геоинформационные системы. Модели глобального развития. Модели массопереноса в
природных средах. Математические модели экосистем как основа экологического
прогноза. Эколого-экономические модели. Математическое моделирование процессов
в различных компонентах экосистем. Математическое моделирование искусственных
экосистем. Модели взаимодействия экосистем. Модели круговорота веществ. Модели
замкнутых экосистем. Теория подобия экосистем.
Вычислительная экология. Проблемы окружающей среды и природных ресурсов.
Интегрированные оценки взаимосвязи биосферы и климата. Экология вирусов:
моделирование межпопуляционных взаимодействий в системе вирусы-переносчики —
потенциальные хозяева в различных экологических нишах. Математические модели
эпидемического процесса. Задачи прогноза и управления эпидемическим процессом.
Системная биология. Общие проблемы моделирования сложных систем. Качественная
теория поведения биологических систем во времени. Теория редукции сложности
математических моделей. Общесистемные проблемы математического моделирования
популяций, сообществ, биоценозов. Модели пространственной синхронизации.
Автоколебания. Диссипативные структуры. Самоорганизация и саморегуляция живых
систем.

4. Составление математических моделей
Модель — это такой материальный или мысленно представляемый объект, который в
процессе познания (изучения) замещает объект-оригинал, сохраняя некоторые
важные для данного исследования типичные его черты.
Математическая модель — модель, в которой для описания свойств и типичных черт
объекта используются математические символы.
Покупая в магазине разные продукты, мы автоматически занимаемся простейшим
математическим моделированием. Запомнив цену каждого продукта, мы (или кассир)
складываем абстрактные числа, оплачиваем сумму и затем по каждому чеку (числу
на чеке) получаем конкретный продукт.
Такую же простейшую схему математического моделирования мы много раз применяли
в курсе алгебры при решении текстовых задач. Мы перекладывали практическую
задачу на математический язык, решали математическую задачу, а затем
интерпретировали математический результат.
Процесс математического моделирования — это процесс построения математической
модели. Он состоит из следующих этапов:
Переложение практической задачи на математический язык: составление уравнений,
неравенств, системы уравнений и неравенств и т. д.
Решение математической задачи: уравнения, неравенства, системы и т. д.
Интерпретация математического результата: переход от найденных чисел (корней
уравнений, решений неравенств) к их практическому смыслу в данной задаче.
Проверка результата практикой.
Первые три этапа мы все применяли при решении текстовых алгебраических задач. И
если мы не допустили ошибок, что проверяется непосредственно проверкой или по
данным в учебнике ответам, то считается, что задача решена верно. При решении
практических задач такого ответа не существует. Представьте себе, что решается
сложная задача о конструировании самолета или не менее сложная экономическая
задача. В таких случаях необходима проверка математических выводов
экспериментом.
Чтобы проверить теоретические выводы о конструкции самолета, строят его модель
— единственный (а не серийный) настоящий самолет — и сначала проверяют его
испытанием в аэродинамической трубе. Затем проводят испытания в настоящем
полете. Во время испытания выявляются недостатки, уточняются условия задачи,
уточняются и проверяются все три этапа ее решения. Затем снова эксперимент, и
так до получения хорошего для практики результата.
Таким образом, вырисовывается следующая схема математического моделирования:
Реальный Мир |1 этап – абстракция| Математическая модель|
4 этап эксперимент||2 этап решение математической проблемы
Выводы о реальном мире|3 этап – интерпретация Математические выводы|

Рассмотрим пример.
Задача. Два художника купили по одинаковому количеству краски. Первый из них
половину всей краски купил по рублей за тюбик, а другую половину – по рублей за
тюбик. Второй половину всех денег за покупку истратил на тюбики по рублей, а
другую половину денег – на тюбики по рублей. Кто из них заплатил за покупку
меньше?
Решение. I. Введем обозначения:
S — число тюбиков, купленных каждым художником;
х рублей – сумма, затраченная на покупку первым художником;
y рублей — сумма, затраченная на покупку вторым художником.
По условию задачи имеем:
S/2 +S/2 = x, (1)
y/ 2 + y/ 2 =S, (2)
Итак, нужно выяснить, какое из чисел, x или y, меньше другого, если
положительные числа , , x, y, S удовлетворяют равенствам (1), (2). Эта
математическая задача и есть математическая модель данной практической задачи.
Приведем некоторые задачи, решаемые методом моделирования
Задача о рекламе. Средства массовой информации дают рекламные объявления для
ускорения сбыта некоторой продукции, которая есть в продаже. Последующая
информация о продукции распространяется среди покупателей посредством общения
друг с другом. По какому закону распространяется известие о наличии этой
продукции?
Решение. Пусть N число потенциальных покупателей данной продукции и в момент
времени t об ее наличии в продаже знают х (t) покупателей. Хотя на самом деле
число покупателей целое, но для абстрактной математической модели можно
считать, что функция х (t) может принимать все значения от 0 до N.
Статистика показывает, что с большой степенью достоверности скорость изменения
функции х (t) прямо пропорциональна как числу знающих о продукции, так и числу
не знающих. Если условится, что время отсчитывается после рекламных объявлений,
когда о товаре узнало N / человек, то приходим к дифференциальному уравнению
x (t) = kx(t)( N x(t)) (3)
с начальными условиями х = N / при t = 0. В уравнении (3) коэффициент k это
положительный коэффициент пропорциональности, который определяется
экспериментально и зависит от интенсивности рекламы и скорости распространения
слухов.
Интегрируя уравнение (1), находим, что
1 / N ln (x /(N x)) = kt + С.
Полагая NC = C1, приходим к равенству
x / (N x) = AеNk t , где А = еC1 .
Если последнее уравнение разрешить относительно х, то получим соотношение
х (t) = N Aе Nkt / AеNkt + 1 = N / 1 + Ре Nkt , (4)
где Р = 1/ A.
Если учесть теперь начальные условия, то уравнение (4) перепишется в виде
х (t) = N / (1 + ( 1)Nkt
Задача(химия и технология производства). Через сосуд ёмкостью а литров,
наполненный водным раствором некоторой соли, непрерывно протекает жидкость,
причем в единицу времени втекает b литров чистой воды и вытекает такое же
количество раствора.
Найти закон, по которому изменяется содержание соли в сосуде в зависимости от
времени протекания жидкости через сосуд.
Решение: в данный момент времени t в сосуде содержится некоторое число x кг
соли, а в b литрах кг.
Если бы в течение единицы времени, начиная с момента t , концентрация раствора
оставалась неизменной, т.е. такой, какой она была в момент времени t, то
количество соли в сосуде за эту единицу времени уменьшилось бы на кг; такова
скорость уменьшения количества соли в сосуде для момента t.
С другой стороны, производная равна скорости прироста количества соли в момент
t; значит, скорость уменьшения количества соли в момент t будет равна . Итак,
имеем:
Разделим переменные: , откуда , или потенцируя,
(5), где — произвольная постоянная.
Предположим для определенности, что при t=0 количество соли в сосуде было равно
c кг.
Полагая в формуле (5) t=0, найдем, что и получим окончательно , т.е. количество
соли убывает с течением времени по «показательному» закону.
Ответ:
Задача (биология, процессы прироста). В культуре пивных дрожжей быстрота
прироста действующего фермента пропорциональна наличному его количеству x.
Первоначальное количество фермента было a. Через час оно удвоилось. Во сколько
раз оно увеличится через 3 часа?
Решение:
По условию дифференциальное уравнение процесса ,
где k – коэффициент пропорциональности.
Разделяя переменные, получим: .
Отсюда, общее решение .
Найдем с из начального условия: при t=0, x=a. Отсюда , или c = a.
Подставляя в общее решение, получим частное решение задачи: .
Коэффициент пропорциональности определяем из данных дополнительных условий: при
t=1час; x=2a.
Отсюда: , или .Подставляя в частное решение , получим закон рассматриваемого
процесса: .
При t = 3часа, x = 8a. Следовательно, количество фермента спустя три часа
увеличится в 8 раз.
Ответ: за три часа количество фермента увеличится в 8 раз.

5 Элементарные математические модели

Рассмотрим некоторые подходы к построению простейших математических моделей,
иллюстрирующие применение фундаментальных законов природы.
1. Фундаментальные законы природы. Наиболее распространенный метод построения
моделей состоит в применении фундаментальных законов природы к конкретной
ситуации. Эти законы общепризнаны, многократно подтверждены опытом, служат
основой множества научно-технических достижений. Поэтому их обоснованность не
вызывает сомнений, что, помимо всего прочего, обеспечивает исследователю мощную
психологическую поддержку.
а) Сохранение энергии. Этот закон известен почти двести лет и занимает,
пожалуй, наиболее почетное место среди великих законов природы. Полагаясь на
него, эксперт по баллистике, желающий быстро определить скорость револьверной
пули и не имеющий поблизости специальной лаборатории, может воспользоваться
относительно простым устройством типа маятника — груза, подвешенного на легком
жестком и свободно вращающемся стержне (рис. 1)

Рис. 1.
Пуля, застрявшая в грузе, сообщит системе «пуля—груз» свою
кинетическую энергию, которая в момент наибольшего отклонения стержня от
вертикали полностью перейдет в потенциальную энергию системы. Это описывается
цепочкой равенств

Здесь mv2/2 — кинетическая энергия пули массы m, имеющей скорость v, M — масса
груза, V — скорость системы «пуля—груз» сразу после столкновения, g —
ускорение свободного падения, I — длина стержня,α— угол наибольшего отклонения.
Искомая скорость определяется формулой
,
которая будет вполне точной, если не учитываемые нами потери энергии на
разогрев пули и груза, на преодоление сопротивления воздуха, разгон стержня и
т. д. невелики. Это, на первый взгляд, разумное рассуждение на самом деле
неверно. Процессы, происходящие при «слипании» пули и маятника, уже
не являются чисто механическими. Поэтому примененный для вычисления величины V
закон сохранения механической энергии несправедлив: сохраняется полная, а не
механическая энергия системы. Он дает лишь нижнюю границу для оценки скорости
пули (для правильного решения этой простой задачи надо воспользоваться также
законом сохранения импульса).
б) Сохранение материи. Именно этим соображением руководствуется школьник,
решающий задачу о заполнении бассейна водой, втекающей и вытекающей из двух
труб. Конечно же, область применения этого закона несравненно шире.
Пусть, например, имеется небольшое количество радиоактивного вещества (урана),
окруженного толстым слоем «обычного» материала (свинца), — ситуация
типичная либо при хранении делящихся материалов, либо при их использовании в
энергетике .
Под словом «небольшой» подразумевается упрощающее обстоятельство, а
именно то, что все продукты распада, не испытывая столкновений с атомами
вещества, беспрепятственно покидают область I. Другими словами, длина
свободного пробега продуктов распада в первом веществе значительно больше
характерных размеров самого материала LI, Т.е. . Слова «толстый слой»
означают, что в согласии с целями хранения продукты деления полностью поглощаются
в области II. Это гарантируется при выполнении противоположного условия , где —
длина пробега продуктов распада во втором веществе, LII — его характерный
размер.
Итак, все, что вылетает из области I, поглощается в области II, и суммарная
масса обоих веществ со временем не меняется. Это и есть закон сохранения
материи, примененный к данной ситуации. Если в начальный момент времени t=0
массы веществ были равны MI(0) и MII(0), то в любой момент времени справедлив
баланс
MI(0) +MII(0)= MI(t) + MII(t) (6)
Одного уравнения (6), очевидно, недостаточно для определения текущих значений
двух масс — MI(t) и MII(t). Для замыкания математической формулировки
необходимо привлечь дополнительное соображение о характере распада. Оно гласит,
что скорость распада (число атомов, распадающихся в единицу времени)
пропорционально общему числу атомов радиоактивного вещества. За небольшое время
dt между моментами t и t + dt всего распадется

атомов. Здесь вторично использован закон сохранения вещества, но применительно
не ко всему процессу, а к отрезку времени dt. В этом уравнении, описывающем
баланс атомов, в правой части стоит знак минус (вещество убывает), а величина
отвечает некоторому среднему значению числа атомов за рассматриваемое время.
Перепишем его в дифференциальной форме:

Учитывая, что , где — атомный вес вещества I, получаем
|(7) |
При самопроизвольной радиоактивности любой атом имеет некоторую не зависящую от
состояния окружающего вещества вероятность распада. Поэтому чем больше (меньше)
самого радиоактивного вещества, тем больше (меньше) выделяется продуктов
распада в единицу времени. Коэффициент пропорциональности (постоянная распада)
определяется конкретным веществом. Уравнения (6), (7) вместе с условиями , а
также величинами , MI(0), MII(0) и составляют математическую модель
рассматриваемого объекта.
Интегрируя (7), получаем, что масса делящегося материала убывает по
экспоненциальному закону и при в области I вещество полностью исчезает.
Так как суммарная масса в соответствии с (6) остается постоянной, то в области
II количество вещества растет:
и при продукты распада полностью переходят из области I в область II.
в) Сохранение импульса. Неподвижно стоящая в безветренную погоду на поверхности
озера лодка начнет двигаться вперед, если сделать несколько шагов от ее носа к
корме. Так проявляет себя закон сохранения импульса, утверждающий: полный
импульс системы, не испытывающей действия внешних сил, сохраняется. Принцип
реактивного движения положен в основу многих замечательных технических
устройств, например, ракеты, выводящей на орбиту вокруг Земли искусственный
спутник, для чего ей требуется развить скорость примерно 8 км/с. Простейшая
математическая модель движения ракеты получается из закона сохранения импульса
в пренебрежении сопротивлением воздуха, гравитацией и другими силами, исключая,
конечно, тягу реактивных двигателей.
Пусть продукты сгорания ракетного топлива покидают расположенные в кормовой
части выхлопные сопла со скоростью u (для современных топлив величина и равна
3-5 км/с). За малый промежуток времени dt между моментами t и t + dt часть
топлива выгорела, и масса ракеты изменилась на величину dm. Изменился также
импульс ракеты, однако суммарный импульс системы «ракета плюс продукты
сгорания» остался тем же, что и в момент t:

где v(t) — скорость ракеты, — средняя за промежуток dt скорость истекающих из
сопел газов (обе скорости берутся относительно Земли). Первый член в правой
части этого равенства — импульс ракеты в момент t + dt, второй — импульс,
переданный истекающим газом за время dt.
Учитывая, что m(t + dt) = m(t) + (dm/dt) dt + O(dt2), закон сохранения импульса
можно переписать в виде дифференциального уравнения

в котором член — (dm/dt)u, очевидно, не что иное, как сила тяги ракетных
двигателей, и которое, будучи преобразованным к виду

легко интегрируется:

где v0, m0 — соответственно скорость и масса ракеты в момент t = 0. Если v0=0,
то максимальная скорость ракеты, достигаемая при полном сгорании топлива, равна

(8)
Здесь mp — полезная масса (масса спутника), ms — структурная масса (масса
собственно ракетной конструкции — топливных баков, двигателей, систем
управления и т.д.).
Простая формула Циолковского (8) позволяет сделать фундаментальный вывод
оконструкции ракеты для космических полетов. Введем величину
которая характеризует при mр = 0 отношение структурной и начальной масс ракеты.
Тогда для практически реальных значений км/с получаем при mр = 0
Отсюда следует, что даже в самой идеальной ситуации (полезная масса равна нулю,
отсутствуют гравитация и сопротивление воздуха и т.д.) ракета рассматриваемого
типа не способна достичь первой космической скорости. Тем самым необходимо
использовать многоступенчатые ракеты — вывод, к которому пришли
основоположники.

Заключение.
В данной работе рассмотрены различные виды моделирования, выполнена систематизация
видов моделирования, рассмотрены приемы применения моделирования к решению
различных задач (проблем).
В ходе изучения данного вопроса мы рассмотрели способы использования
моделирования для исследования различных процессов, объектов, явлений в
различных областях.
Моделирование:
является одним из ключевых видов деятельности человека;
всегда в той или иной форме предшествует любому делу;
занимает центральное место в исследовании объекта; позволяет
обоснованно принимать решение: как совершенствовать привычные объекты, надо ли
создавать новые, как изменять процессы управления и, в конечном итоге, — как
менять окружающий мир в лучшую сторону.
Для любого вида моделирования важно не только определить цели и составить
модель, но и качественно провести сбор обработку и систематизацию информации.
При решении многих задач математики, экономики, физики и техники не всегда
удается установить функциональную зависимость между искомыми и данными
переменными величинами, но зато удается вывести дифференциальное уравнение, позволяющее
точно предсказать протекание некоторого процесса при определенных условиях.
Решение таких задач потребует от учащихся большой теоретической подготовки:
изучить теоретические основы дифференциальных уравнений, способы их решения;
рассмотреть некоторые приёмы решения задач по физике, геометрии, экономике,
биологии и химии с помощью составления дифференциальных уравнений.

Список использованной литературы

1. Алгебра и начала анализа : Учеб. для 10-11 кл. сред. шк./ Ш. А. Алимов, Ю.
М. Колягин, Ю.В. Сидоров и др. — М.: Просвещение, 1993. – 254 c.
2. Башмаков, М. И. Алгебра и начала анализа : Учеб. для 10-11 кл. сред. шк. —
М.: Просвещение, 1992. – 351 с.
3. Вольтерра В. Математическая теория борьбы за существование. М.: Наука, 1976.
4. Зельдович Я.Б., Яглом И.М. «Высшая математика для начинающих физиков и
техников». М.: Наука, 1982.
5. Задачник по курсу математического анализа : Уч. пособие для студентов заочн.
отделений физ.-мат. фак-тов пединститутов. Ч. I// Под ред. Н. Я. Виленкина. –
М.: Просвещение, 1971. – 343 с.
6. Колмогоров, А. Н. Алгебра и начала анализа : Учеб. для 10-11 кл.
общеобразоват. учреждений/ А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и
др. – М.: Просвещение, 1998. – 365 c.
7. Модели и моделирование в методике обучения физике : Материалы докладов
республиканской научно-теоретической конференции. – Киров: Изд-во Вятского ГПУ,
2000. – 90 с.
8. Мордкович, А. Г. Алгебра и начала анализа: Учеб. для 10-11 кл.
общеобразоват. учреждений. Ч. I. – М.: Мнемозина, 2003. – 375 с.
9. Никольский, С. М. Алгебра и начала анализа : Учеб. для 11 класса
общеобразоват. учреждений/ С. М. Никольский, М. К. Потапов. — М.: Просвещение,
2003.
8. Пискунов. Н.С. Дифференциальное и интегральное исчисление для втузов. Том 2.
М.: Наука, 1978.- 267с.
9. Уильямсон М.Г.. Анализ биологических популяций. М.: Мир, 1975.
10. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. М.: Наука,
1992.
11. Шубин М. А. «Математический анализ для решения физических задач» М., МЦНМО,
2003