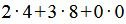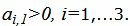Калькулятор симплекс-метода
Количество переменных:
Количество ограничений:
Очистить
Решить
В двойственную
Выполнено действий:
Как пользоваться калькулятором
- Задайте количество переменных и ограничений
- Введите коэффициенты целевой функции
- Введите коэффициенты ограничений и выберите условия (≤, = или ≥)
- Выберите тип решения
- Нажмите кнопку «Решить»
Что умеет калькулятор симплекс-метода
- Решает основную задачу линейного программирования
- Позволяет получить решение с помощью основного симплекс-метода и метода искусственного базиса
- Работает с произвольным количеством переменных и ограничений
Что такое симплекс-метод
Задача линейного программирования — это задача поиска неотрицательных значений параметров, на которых заданная линейная функция достигает своего максимума или минимума при заданных линейных ограничениях.
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Алгоритм является универсальным методом, которым можно решить любую задачу линейного программирования.
Если вам тоже ничего не понятно из этого определения, то вы на верном пути. Чаще всего статьи про симплекс-метод очень сильно углубляются в дебри теории задачи линейного программирования, из-за чего очень легко потерять суть и так ничего и не понять. Мы постараемся описать алгоритм симплекс-метода так, чтобы показать, что в нём нет ничего страшного и на самом деле он весьма простой. Но сначала нам всё-таки потребуется ввести несколько определений.
Целевая функция — функция, максимум (или минимум) которой нужно найти. Представляет собой сумму произведений коэффициентов на значения переменных: F = c1·x1 + c2·x2 + … + cn·xn
Ограничение — условие вида a1·x1 + a2·x2 + … + an·xn v b, где вместо v ставится один из знаков: ≤, = или ≥
План — произвольный набор значений переменных x1 … xn.
Алгоритм решения основной задачи ЛП симплекс-методом
Пусть в задаче есть m ограничений, а целевая функция заивисит от n основных переменных. Первым делом необходимо привести все ограничения к каноническому виду — виду, в котором все условия задаются равенствами. Для этого предварительно все неравенства с ≥ умножаются на -1, для получения неравенств с ≤.
Чтобы привести ограничения с неравенствами к каноническому виду, для каждого ограничения вводят переменную, называемую дополнительной с коэффициентом 1. В ответе эти переменные учитываться не будут, однако сильно упростят начальные вычисления. При этом дополнительные переменные являются базисными, а потому могут быть использованы для формирования начального опорного решения.
Пример 1
Привести к каноническому виду ограничения:
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 200
4·x1 + 6·x2 + 8·x3 ≥ 160
Меняем знаки у ограничений с ≥, путём умножения на -1 и добавляем дополнительные переменные к ограничениям с неравенством:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 200
-4·x1 — 6·x2 — 8·x3 + x5 = -160
Формирование начального базиса
После того как задача приведена к каноническому виду, необходимо найти начальный базис для формирования первого опорного решения. Если в процессе приведения были добавлены дополнительные переменные, то они становятся базисными.
Иначе необходимо выделить среди коэффициентов ограничений столбец, который участвует в формировании единичной матрицы в заданной строке (например, если требуется определить вторую базисную переменную, то необходимо искать столбец, в котором второе число равно 1, а остальные равны нулю). Если такой столбец найден, то переменная, соответствующая этому столбцу, становится базисной.
В противном случае можно поискать столбец, в котором все значения кроме числа в заданной строке равны нулю, и, если он будет найден, то разделить все значения строки на число, стоящее на пересечении этих строки и столбца, тем самым образовав столбец, участвующий в формировании единичной матрицы.
Пример 2
9·x1 + 5·x2 + 4·x3 + 3·x4 + 2·x5 → max
x1 — 2·x2 + 2·x3 ≤ 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 — 4·x3 + 2·x5 = 30
Для ограничения с неравенством добавляем дополнительную переменную x6.
Перепишем ограничения в каноническом виде:
x1 — 2·x2 + 2·x3 + x6 = 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 — 4·x3 + 2·x5 = 30
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Столбец 4 является частью единичной матрицы. Переменная x4 входит в начальный базис
В пятом столбце все значения кроме третьего равны нулю. Поэтому в качестве третьей базисной переменной берём x5, предварительно разделив третью строку на 2.
Симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| ? | 2 | 1 | -4 | 0 | 2 | 0 | 30 |
После преобразования получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 1 |
1 2 |
-2 | 0 | 1 | 0 | 15 |
Если такой столбец отсутствует, то для формирования базиса необходимо применить исключение Гаусса для первого ненулевого столбца, который ещё не является базисным. Для этого вся строка делится на элемент в найденном столбце, а из остальных строк вычитается полученная строка, разделённая на значение, стоящее в этом же столбце. После этой операции все значения вне данной строки будут обнулены, и столбец можно будет считать базисным.
Пример 3
4·x1 + 5·x2 + 4·x3 → max
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 160
4·x1 + 6·x2 + 8·x3 ≤ 200
Для каждого ограничения с неравенством добавляем дополнительные переменные x4 и x5.
Перепишем ограничения в каноническом виде:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 160
4·x1 + 6·x2 + 8·x3 + x5 = 200
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Начальная симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| ? | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
Для определения второй базисной переменной ищем первый ненулевой столбец, который ещё не является базисным. Первый столбец не нулевой и не является базисным. Выполняем исключение Гаусса: делим строку 2 на 4, а из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент в первом столбце.
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| x1 | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
После исключения получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 0 | 2 | 4 | 1 | 0 | 160 |
| x1 | 1 |
1 2 |
1 | 0 | 0 | 40 |
| x5 | 0 | 4 | 4 | 0 | 1 | 40 |
После того как базис сформирован, нужно построить начальную симплекс-таблицу. Она строится следующим образом:
- Для удобства в первой строке можно записать коэффициенты Ci целевой функции (для дополнительных переменных эти коэффициенты равны нулю)
- Вторая строка формирует шапку таблицы. В ней первый столбец называется базис, а остальные перечисляют основные переменные x1..xn и дополнительные xn+1..xn+k
- Затем построчно перечисляются базисные переменные и коэффициенты ограничений
Схематично начальная таблица будет выглядеть примерно так:
| C | с1 | c2 | … | cn | 0 | 0 | … | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| базис | x1 | x2 | … | xn | xn+1 | xn+2 | … | xn+k | b |
| xe1 | a11 | a12 | … | a1n | a1n+1 | a1n+2 | … | a1n+k | b1 |
| xe2 | a21 | a22 | … | a2n | a2n+1 | a2n+2 | … | a2n+k | b2 |
| … | … | … | … | … | … | … | … | … | … |
| xem | am1 | am2 | … | amn | amn+1 | amn+2 | … | amn+k | bm |
Избавляемся от отрицательных свободных коэффициентов
После приведения к каноническому виду или после алгебраических преобразований при формировании базиса некоторые из свободных коэффициентов (bi) могли стать отрицательными, что не позволяет перейти к дальнейшим вычислениям. Чтобы избавиться от отрицательных значений b необходимо:
- Найти строку, в которой находится максимальное по модулю значение b. Пусть это будет строка i;
- Найти максимальный по модулю элемент в этой строке. Пусть он находится в столбце j;
- Строку i разделить на элемент, стоящий на пересечении i-ой строки и j-го столбца;
- Из каждой оставшейся строки k вычесть строку i, умноженную на элемент строки k и столбца j;
- Переменную, соответствующую найденному столбцу j, сделать базисной (добавить в базис вместо переменной, находящейся в строке i).
Этот шаг необходимо повторять до тех пор, пока все отрицательные b не станут положительными или в строке не останется отрицательных элементов. Если строка с максимальным по модулю bi не содержит отрицательных элементов, то такая задача не имеет решений и на этом алгоритм заканчивает свою работу. В противном случае все bi положительны и алгоритм переходит к следующему этапу — расчёту дельт.
Пример 4
20·x1 + 20·x2 + 10·x3 → min
4·x1 + 3·x2 + 2·x3 ≥ 33
3·x1 + 2·x2 + x3 ≥ 23
x1 + x2 + 2·x3 ≥ 12
Меняем знаки у ограничений с ≥, путём умножения на -1:
-4·x1 — 3·x2 — 2·x3 ≤ -33
— 3·x1 — 2·x2 — x3 ≤ -23
— x1 — x2 — 2·x3 ≤ -12
Для каждого ограничения с неравенством добавляем дополнительные переменные x4..x6.
Перепишем ограничения в каноническом виде:
— 4·x1 — 3·x2 — 2·x3 + x4 = -33
— 3·x1 — 2·x2 — x3 + x5 = -23
— x1 — x2 — 2·x3 + x6 = -12
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Начальная симплекс-таблица
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x4 | -4 | -3 | -2 | 1 | 0 | 0 | -33 |
| x5 | -3 | -2 | -1 | 0 | 1 | 0 | -23 |
| x6 | -1 | -1 | -2 | 0 | 0 | 1 | -12 |
В столбце b присутствуют отрицательные значения.
Максимальное по модулю |b|max = |-33| находится в первой строке.
Максимальный по модулю элемент в первой строке = -4 находится в первом столбце.
В качестве базисной переменной x4 берём x1.
Делим первую строку на -4. Из второй и третьей строк вычитаем первую, умноженную на соответствующий элемент в первом столбце.
Обновлённая таблица:
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 |
3 4 |
1 2 |
—
1 4 |
0 | 0 |
33 4 |
| x5 | 0 |
1 4 |
1 2 |
—
3 4 |
1 | 0 |
7 4 |
| x6 | 0 | —
1 4 |
—
3 2 |
—
1 4 |
0 | 1 | —
15 4 |
В столбце b присутствуют отрицательные значения.
Максимальное по модулю |b|max = |-
| находится в третьей строке.
Максимальный по модулю элемент в третьей строке = —
находится в третьем столбце.
В качестве базисной переменной x6 берём x3.
Делим третью строку на —
. Из первой и второй строк вычитаем третью, умноженную на соответствующий элемент в третьем столбце.
Обновлённая таблица:
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 |
2 3 |
0 | —
1 3 |
0 |
1 3 |
7 |
| x5 | 0 |
1 6 |
0 | —
5 6 |
1 |
1 3 |
1 2 |
| x3 | 0 |
1 6 |
1 |
1 6 |
0 | —
2 3 |
5 2 |
Расчёт дельт
Дельты — это параметры, на основании которых проверяется оптимальность текущего решения и улучшается функция. Они рассчитываются для каждой из переменных ограничений и записываются последней строкой таблицы.
Для расчёта дельт используется следующая формула: Δi = ce1·a1i + ce2·a2i + … + cem·ami — ci. Проще говоря, чтобы вычислить дельту по заданной i-ой переменной, нужно перемножить коэффициенты условий в i-ом столбце на коэффициенты целевой функции при соответствующих базисных переменных, сложить эти произведения и вычесть из полученной суммы коэффициент целевой функции столбца i.
Пример 5
Таблица:
| C | 3 | 0 | 2 | 0 | 0 | -6 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x2 | 2 | 1 | -3 | 0 | 0 | 6 | 18 |
| x4 | -3 | 0 | 2 | 1 | 0 | -2 | 24 |
| x5 |
1 5 |
0 |
3 5 |
0 | 1 | —
4 5 |
36 5 |
Вычисляем дельты: Δi = C2·a1i + C4·a2i + C5·a3i — Ci
Симплекс-таблица с дельтами
| C | 3 | 0 | 2 | 0 | 0 | -6 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x2 | 2 | 1 | -3 | 0 | 0 | 6 | 18 |
| x4 | -3 | 0 | 2 | 1 | 0 | -2 | 24 |
| x5 |
1 5 |
0 |
3 5 |
0 | 1 | —
4 5 |
36 5 |
| Δ | -3 | 0 | -2 | 0 | 0 | 6 | 0 |
Проверка плана на оптимальность
После того как дельты рассчитаны, необходимо проверить оптимальность текущего плана. Критерий оптимальности формулируется следующим образом:
При максимизации функции: текущее решение считается оптимальным, если в таблице отсутствуют отрицательные дельты.
При минимизации функции: текущее решение считается оптимальным, если в таблице отсутствуют положительные дельты.
Пример 6
9·x1 + 5·x2 + 4·x3 + 3·x4 + 2·x5 → max
x1 — 2·x2 + 2·x3 ≤ 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 — 4·x3 + x5 = 30
Симплекс-таблица с дельтами
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Критерий оптимальности: план оптимален, если в таблице отсутствуют отрицательные дельты.
План не оптимален, так как ищется максимум функции, а Δ1 = -2 отрицательна.
Если текущий план оптимален, то алгоритм завершает свою работу. Значениям переменных соответствуют значения столбца свободных коэффициентов b. Если свободной переменной нет в базисе, то её значение считается нулевым. Значение целевой функции, принимаемой на данном наборе, находится в строке с дельтами в том же столбце. Если какое-либо из значений столбца b отрицательно, то решения задачи не существует.
Переход к более оптимальному решению
Если текущий план оказался не оптимальным, то алгоритм ищет столбец с наименьшей (с наибольшей, если ищется минимум) дельтой. После чего вычисляются симплекс-отношения Q. Для этого значения свободных коэффициентов делятся на ненулевые коэффициенты из найденного столбца. Если результат деления получается отрицательным, то такие отношение игнорируются.
Среди найденных симплекс-отношений ищется строка, в которой находится симплекс-отношение с наименьшим значением. Если таких отношений нет, то алгоритм останавливает свою работу, так как целевая функция не ограничена и решения не существует.
Пример 7
Симплекс-таблица с дельтами
| C | 2 | 1 | -2 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 | -5 | 0 | -3 | 0 | -1 | 25 |
| x5 | 0 | -16 | 0 | -7 | 1 | -3 | 57 |
| x3 | 0 | -6 | 1 | -2 | 0 | -1 | 17 |
| Δ | 0 | 1 | 0 | -2 | 0 | 0 | 16 |
Проверяем план на оптимальность: план не оптимален, так как ищется минимум функции, а Δ2 = 1 положительна.
Определяем разрешающий столбец — столбец, в котором находится максимальная дельта: 2, Δ2: 1
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения второго столбца
| C | 2 | 1 | -2 | 0 | 0 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x1 | 1 | -5 | 0 | -3 | 0 | -1 | 25 | — |
| x5 | 0 | -16 | 0 | -7 | 1 | -3 | 57 | — |
| x3 | 0 | -6 | 1 | -2 | 0 | -1 | 17 | — |
| Δ | 0 | 1 | 0 | -2 | 0 | 0 | 16 |
Все значения второго столбца отрицательны. Функция не ограничена. Оптимальное решение отсутствует.
В противном случае строка с наименьшим отношением считается разрешающей и, аналогично избавлению от отрицательных свободных коэффициентов, делится на разрешающий элемент, расположенный в найденных столбце и строке, и из остальных строк вычитается найденная строка, разделённая на значения, стоящие в этом же столбце соответствующей строки. Переменная, стоящая в разрешающем столбце заменяет базисную переменную, находящуюся в найденной строке.
После этого вычисляются новые дельты и проверяется новый план. Так продолжается до тех пор пока не будет выполнен критерий оптимальности плана или не будет установлено, что решение не существует.
Пример 8
Симплекс-таблица с дельтами
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -2 отрицательна.
Итерация 1
Определяем разрешающий столбец — столбец, в котором находится минимальная дельта: 3, Δ3: -9
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения третьего столбца
В найденном столбце ищем строку с наименьшим значением Q: Qmin = 3, строка 1.
На пересечении найденных строки и столбца находится разрешающий элемент: 2
В качестве базисной переменной x6 берём x3.
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 | 1 | -2 | 2 | 0 | 0 | 1 | 6 | 6 / 2 = 3 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 | 24 / 1 = 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 | — |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Делим первую строку на 2. Из второй и третьей строк вычитаем первую, умноженную на соответствующий элемент в третьем столбце.
Вычисляем новые дельты: Δi = C3·a1i + C4·a2i + C5·a3i — Ci
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
1 2 |
-1 | 1 | 0 | 0 |
1 2 |
3 | 3 |
| x4 |
1 2 |
3 | 0 | 1 | 0 | —
1 2 |
21 | 24 |
| x5 | 4 | -3 | 0 | 0 | 1 | 2 | 42 | — |
| Δ |
5 2 |
-6 | 0 | 0 | 0 |
9 2 |
159 |
Текущий план X: [ 0, 0, 3, 21, 42, 0 ]
Целевая функция F: 9·0 + 5·0 + 4·3 + 3·21 + 2·42 + 0·0 = 159
Проверяем план на оптимальность: план не оптимален, так как Δ2 = -6 отрицательна.
Итерация 2
Определяем разрешающий столбец — столбец, в котором находится минимальная дельта: 2, Δ2: -6
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения второго столбца
В найденном столбце ищем строку с наименьшим значением Q: Qmin = 7, строка 2.
На пересечении найденных строки и столбца находится разрешающий элемент: 3
В качестве базисной переменной x4 берём x2.
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
1 2 |
-1 | 1 | 0 | 0 |
1 2 |
3 | — |
| x2 |
1 2 |
3 | 0 | 1 | 0 | —
1 2 |
21 | 21 / 3 = 7 |
| x5 | 4 | -3 | 0 | 0 | 1 | 2 | 42 | — |
| Δ |
5 2 |
-6 | 0 | 0 | 0 |
9 2 |
159 |
Делим вторую строку на 3. Из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент во втором столбце.
Вычисляем новые дельты: Δi = C3·a1i + C2·a2i + C5·a3i — Ci
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
2 3 |
0 | 1 |
1 3 |
0 |
1 3 |
10 | — |
| x2 |
1 6 |
1 | 0 |
1 3 |
0 | —
1 6 |
7 | 7 |
| x5 |
9 2 |
0 | 0 | 1 | 1 |
3 2 |
63 | — |
| Δ |
7 2 |
0 | 0 | 2 | 0 |
7 2 |
201 |
Текущий план X: [ 0, 7, 10, 0, 63, 0 ]
Целевая функция F: 9·0 + 5·7 + 4·10 + 3·0 + 2·63 + 0·0 = 201
Проверяем план на оптимальность: отрицательные дельты отсутствуют, следовательно план оптимален.
Ответ: x1 = 0, x2 = 7, x3 = 10, x4 = 0, x5 = 63, F = 201
Метод искусственного базиса
Очень часто при решении задачи линейной оптимизации бывает довольно сложно выполнять алгебраические преобразования над коэффициентами ограничений для поиска начального базиса. Для упрощения вычислений существует альтернативный метод решения, называемый методом искусственного базиса. Его суть заключается в том, что вместо того, чтобы искать базис среди имеющихся основных и дополнительных переменных, ввести так называемые искусственные переменные, которые сформируют начальный базис. Возможно, звучит сложно и непонятно, но сейчас мы всё объясним.
Подготовительный этап
Аналогично базовому симплекс-методу для всех ограничений с неравентством вводятся дополнительные переменные, причём для ограничений с ≥ они берутся с коэффициентом -1, а для ограничений с ≤ с коэффициентом 1. Ограничения с равенством остаются без изменений. Если свободный коэффициент какого-либо из ограничений меньше нуля, то такое ограничение умножается на -1 (знак неравенства при этом меняется на противоположный). После этого приступают к поиску базиса.
Пример 9
3·x1 + 2·x2 + 3·x3 → min
-2·x1 — x2 — x3 ≥ -2
3·x1 + 8·x2 + 2·x3 ≥ 8
2·x1 + x3 = 1
Меняем знаки у ограничений с отрицательными свободными коэффициентами, путём умножения на -1:
2·x1 + x2 + x3 ≤ 2
3·x1 + 8·x2 + 2·x3 ≥ 8
2·x1 + x3 = 1
Для каждого ограничения с неравенством добавляем дополнительные переменные x4 и x5.
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство с ≥. Базисная переменная для этого ограничения будет определена позднее.
Ограничение 3 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Начальная симплекс-таблица
| C | 3 | 2 | 3 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 2 |
| ?1 | 3 | 8 | 2 | 0 | -1 | 8 |
| ?2 | 2 | 0 | 1 | 0 | 0 | 1 |
Формирование начального базиса
Для того, чтобы сформировать начальный базис в первую очередь можно поискать столбец, у которого одно значение равно единице, а все значения остальные значения равны нулю, и сделать соответствующую переменную базисной для этой строки. Однако такое случается довольно редко, поэтому проще сразу перейти к следующему пункту. Для всех ограничений, не имеющих базисной переменной, добавляем искусственную переменную с коэффициентом 1. В целевую функцию добавляем эту же переменную с коэффициентов -M, если ищется максимум или с коэффициентом M, если ищется минимум. M всего лишь является очень большим числом.
Пример 10
x1 — x2 → min
2·x1 + x2 = 1
x1 — 3·x2 + x3 = 3
x1 + 11·x2 = 11
Ограничение 1 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Столбец 3 является частью единичной матрицы. Переменная x3 входит в начальный базис
Ограничение 3 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Начальная симплекс-таблица
| C | 1 | -1 | 0 | 0 |
| базис | x1 | x2 | x3 | b |
|---|---|---|---|---|
| ?1 | 2 | 1 | 0 | 1 |
| x3 | 1 | -3 | 1 | 3 |
| ?3 | 1 | 11 | 0 | 11 |
Для ограничения 1 добавляем искусственную переменную u1 и делаем её базисной.
Для ограничения 3 добавляем искусственную переменную u2 и делаем её базисной.
В целевую функцию добавляем искусственные пременные с коэффициентом M, где M — очень большое число.
Таблица с искусственными переменными
| C | 1 | -1 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | u1 | u2 | b |
|---|---|---|---|---|---|---|
| u1 | 2 | 1 | 0 | 1 | 0 | 1 |
| x3 | 1 | -3 | 1 | 0 | 0 | 3 |
| u2 | 1 | 11 | 0 | 0 | 1 | 11 |
Перепишем условие задачи с учётом добавленных искусственных переменных:
F = 1x1 -1x2 + Mu1 + Mu2 → min
2·x1 + x2 + u1 = 1
x1 — 3·x2 + x3 = 3
x1 + 11·x2 + u2 = 11
Расчёт дельт и проверка плана на оптимальность
После того, как начальный базис сформирован необходимо вычислить дельты. Дельты вычисляются полностью аналогично базовому методу: Δi = ce1·a1i + ce2·a2i + … + cem·ami — ci. Единственным отличием будет тот факт, что результат может содержать значения с M. Когда дельты будут получены необходимо проверить текущий опорный план на оптимальность (см. проверку плана на оптимальность в базовом симплекс-методе). Если план оптимален, то алгоритм завершает свою работу, иначе формирует более оптимальное решение и повторяет процесс.
Пример 11
Таблица с искусственными переменными
| C | 3 | 2 | 3 | 0 | 0 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | u1 | u2 | b |
|---|---|---|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| u1 | 3 | 0 | 2 | 0 | -1 | 0 | 1 | 0 | 3 |
| u2 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
Вычисляем дельты: Δi = C4·a1i + C7·a2i + C8·a3i — Ci
Δ1 = C4·a11 + C7·a21 + C8·a31 — C1 = 0·2 + M·3 + M·0 — 3 = -3 + 3M
Δ2 = C4·a12 + C7·a22 + C8·a32 — C2 = 0·1 + M·0 + M·0 — 2 = -2
Δ3 = C4·a13 + C7·a23 + C8·a33 — C3 = 0·1 + M·2 + M·1 — 3 = -3 + 3M
Δ4 = C4·a14 + C7·a24 + C8·a34 — C4 = 0·1 + M·0 + M·0 — 0 = 0
Δ5 = C4·a15 + C7·a25 + C8·a35 — C5 = 0·0 + M·(-1) + M·0 — 0 = -M
Δ6 = C4·a16 + C7·a26 + C8·a36 — C6 = 0·0 + M·0 + M·(-1) — 0 = -M
Δ7 = C4·a17 + C7·a27 + C8·a37 — C7 = 0·0 + M·1 + M·0 — M = 0
Δ8 = C4·a18 + C7·a28 + C8·a38 — C8 = 0·0 + M·0 + M·1 — M = 0
Δb = C4·b1 + C7·b2 + C8·b3 — C9 = 0·2 + M·3 + M·1 — 0 = 4M
Симплекс-таблица с дельтами
| C | 3 | 2 | 3 | 0 | 0 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | u1 | u2 | b |
|---|---|---|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| u1 | 3 | 0 | 2 | 0 | -1 | 0 | 1 | 0 | 3 |
| u2 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
| Δ | -3 + 3M | -2 | -3 + 3M | 0 | -M | -M | 0 | 0 | 4M |
Текущий план X: [ 0, 0, 0, 2, 0, 0, 3, 1 ]
Целевая функция F: 3·0 + 2·0 + 3·0 + 0·2 + 0·0 + 0·0 + M·3 + M·1 = 4M
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -3 + 3M положительна.
Графический метод решения ЗЛП
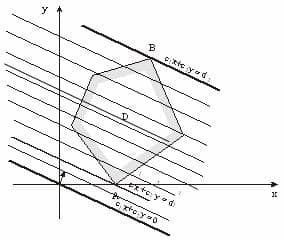
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).
Назначение сервиса. С помощью данного сервиса можно в онлайн режиме решить задачу линейного программирования геометрическим методом, а также получить решение двойственной задачи (оценить оптимальность использования ресурсов). Дополнительно создается шаблон решения в Excel.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
- Также решают
Инструкция. Выберите количество строк (количество ограничений). Если количество переменных больше двух, необходимо систему привести к СЗЛП (см. пример и пример №2). Если ограничение двойное, например, 1 ≤ x1 ≤ 4, то оно разбивается на два: x1 ≥ 1, x1 ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса.
Решение задачи линейного программирования графическим методом включает следующие этапы:
- На плоскости X10X2 строят прямые.
- Определяются полуплоскости.
- Определяют многоугольник решений;
- Строят вектор N(c1,c2), который указывает направление целевой функции;
- Передвигают прямую целевую функцию c1x2 + c2x2 = 0 в направлении вектора N до крайней точки многоугольника решений.
- Вычисляют координаты точки и значение целевой функции в этой точке.
При этом могут возникать следующие ситуации:
- Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.
- Целевая функция принимает экстремальное значение в любой точке отрезка АВ.
- Целевая функция не ограничена сверху (при поиске на максимум) или снизу (на минимум)
- Система ограничений задачи несовместна
Пример. Компания изготавливает два вида продукции – П1 и П2. Для производства продукции используются два вида сырья – С1 и С2. Оптовые цены единицы продукции равна: 5 д.е. для П1 и 4 д.е. для П2. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.
Таблица — Расход сырья на производство продукции
| Сырье | Расход сырья на 1 ед. продукции | Максимальный запас сырья, ед. | |
| П1 | П2 | ||
| М1 | 6 | 4 | 24 |
| М2 | 1 | 2 | 6 |
Установлены ограничения на спрос продукции: ежедневный объем производства продукции П2 не должен превышать ежедневный объем производства продукции П1 не более чем на 1 тонну; максимальный ежедневный объем производства П2 не должен превышать 2 т.
Требуется определить:
Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?
- Сформулировать математическую модель задачи линейного программирования.
- Решить задачу линейного программирования графическим способом (для двух переменных).
Решение.
Сформулируем математическую модель задачи линейного программирования.
x1 – производство продукции П1, ед.
x2 – производство продукции П2, ед.
x1, x2 ≥ 0
Ограничения по ресурсам
6x1 + 4x2 ≤ 24
x1 + 2x2 ≤ 6
Ограничения по спросу
x1 +1 ≥ x2
x2 ≤ 2
Целевая функция
5x1 + 4x2 → max
Тогда получаем следующую ЗЛП:
6x1 + 4x2 ≤ 24
x1 + 2x2 ≤ 6
x2 — x1 ≤ 1
x2 ≤ 2
x1, x2 ≥ 0
5x1 + 4x2 → max
Примеры решения задачи линейного программирования графически.
Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
F(X) = 3x1 — 2x2 + 5x3 — 4x5 → max при ограничениях:
x1 + x2 + x3=12
2x1 — x2 + x4=8
— 2x1 + 2x2 + x5=10
F(X) = 3x1 — 2x2 + 5x3 — 4x5
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 1 | 1 | 1 | 0 | 0 | 12 |
| 2 | -1 | 0 | 1 | 0 | 8 |
| -2 | 2 | 0 | 0 | 1 | 10 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x3.
2. В качестве базовой переменной можно выбрать x4.
3. В качестве базовой переменной можно выбрать x5.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x1 + x2 + x3 = 12
2x1 — x2 + x4 = 8
— 2x1 + 2x2 + x5 = 10
Выразим базисные переменные через остальные:
x3 = — x1 — x2+12
x4 = — 2x1 + x2+8
x5 = 2x1 — 2x2+10
Подставим их в целевую функцию:
F(X) = 3x1 — 2x2 + 5(- x1 — x2+12) — 4(2x1 — 2x2+10)
или
F(X) = — 10x1 + x2+20 → max
Система неравенств:
— x1 — x2+12 ≥ 0
— 2x1 + x2+8 ≥ 0
2x1 — 2x2+10 ≥ 0
Приводим систему неравенств к следующему виду:
x1 + x2 ≤ 12
2x1 — x2 ≤ 8
— 2x1 + 2x2 ≤ 10
F(X) = — 10x1 + x2+20 → max
Особенности решения задач линейного программирования графическим методом
Пример №1. Записать задачу в стандартной форме и решить ее графическим методом.
f=x1+13x2-x3+2x4+3x5
-x2+x3-x5=-3
x1-4x2+3x3-x4+2x5=3
4x2-x3+x4-x5=6
Из первого уравнения выражаем x5:
x5 = -x2+x3+3
и подставим во все выражения:
f=x1+13x2-x3+2x4+3(-x2+x3+3)
x1-4x2+3x3-x4+2(-x2+x3+3)=3
4x2-x3+x4-(-x2+x3+3)=6
или
f=x1+10x2+2x3+2x4+9
x1-6x2+5x3-x4=-3
5x2-2x3+x4=9
Из второго уравнения выражаем x4:
x4=9-5x2+2x3
и подставим во все выражения:
f=x1+6x3+27
x1-x2+3x3=6
Переменную x2 принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x1 + 6x3+ 27
x1 + 3x3≥6
Далее задача решается графическом способом.
Пример №2
F(X) = 3x1 — 2x2 + 5x3 — 4x5 → max при ограничениях:
x1 + x2 + x3=12
2x1 — x2 + x4=8
— 2x1 + 2x2 + x5=10
F(X) = 3x1 — 2x2 + 5x3 — 4x5
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 1 | 1 | 1 | 0 | 0 | 12 |
| 2 | -1 | 0 | 1 | 0 | 8 |
| -2 | 2 | 0 | 0 | 1 | 10 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x3.
2. В качестве базовой переменной можно выбрать x4.
3. В качестве базовой переменной можно выбрать x5.
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x1 + x2 + x3 = 12
2x1 — x2 + x4 = 8
— 2x1 + 2x2 + x5 = 10
Выразим базисные переменные через остальные:
x3 = — x1 — x2+12
x4 = — 2x1 + x2+8
x5 = 2x1 — 2x2+10
Подставим их в целевую функцию:
F(X) = 3x1 — 2x2 + 5(- x1 — x2+12) — 4(2x1 — 2x2+10)
или
F(X) = — 10x1 + x2+20 → max
Система неравенств:
— x1 — x2+12 ≥ 0
— 2x1 + x2+8 ≥ 0
2x1 — 2x2+10 ≥ 0
Приводим систему неравенств к следующему виду:
x1 + x2 ≤ 12
2x1 — x2 ≤ 8
— 2x1 + 2x2 ≤ 10
F(X) = — 10x1 + x2+20 → max
Пример №3. Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.
- Составить систему математических зависимостей (неравенств) и целевую функцию.
- Изобразить геометрическую интерпретацию задачи.
- Найти оптимальное решение.
- Провести аналитическую проверку.
- Определить существенные и несущественные ресурсы и их избытки.
- Определить значение целевой функции.
- Вычислить объективно обусловленные оценки.
- Составить соотношение устойчивости.
| Наимен. показат. | Нормы на одно изделие | Прибыль на одно изделие | ||
| Рес. 1 | Рес. 2 | Рес. 3 | ||
| Изделие 1 | 10.0 | 14.0 | 3.8 | 40 |
| Изделие 2 | 22.0 | 7.5 | 14.5 | 75 |
| Наличие ресурсов | 450 | 310 | 360 | — |
Пример решения
F(x) = 3x1 + 4x2 → max
| 000 | 2x1 + x2 ≤ 600 |
| 0x1 + 0x2 ≤ 225 | |
| 5x1 +4x2 ≤ 1000 | |
| 2x2 ≥ 150 | |
| 0x1 + 0x2 ≥ 0 |
F(x) = 3x1 + 4x2 + 0x3 + 0x4 + 0x5 + 0x6 + 0x7 — Mx8 — Mx9 → max
| 000 | 2x1 + x2 + x3 = 600 |
| + x4 = 225 | |
| 5x1 + 4x2 + x5 = 1000 | |
| 2x2 — x6 + x8 = 150 | |
| — x7 + x9 = 0 |
Предварительный этап:
Предварительный этап начинается с того что необходимо избавиться от отрицательных значений(если таковые имеются) в правой части ограничений. Для чего соответствующие ограничения умножаем на -1. После данной манипуляции знак неравенства меняем на противоположный.
Далее необходимо избавиться от неравенств, для чего в левую часть неравенств вводим компенсирующие переменные. Если неравенство вида ≤, то компенсирующая переменная имеет знак +, если неравенство вида ≥, то компенсирующая переменная имеет знак -. Компенсирующие переменные входят в целевую функцию задачи с нулевым коэффициентом.
Теперь в системе ограничений необходимо найти достаточное количество базисных переменных. В каждом ограничении должна быть одна базисная переменная. Базисной является переменная, которая имеет при себе коэффициент 1 и встречается только в одном ограничении. Если в каком-то ограничении нет базисных переменных, то добавляем их искусственно, причем искусственные переменные входят в целевую функцию с коэффициентом -M, если целевая функция стремится к мах и с М, если целевая функция стремится к min.
Итерация: 1
| B | Cb | P | x1 | x2↓ | x3 | x4 | x5 | x6 | x7 | x8 | x9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x3 | 0 | 600 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 600 |
| x4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ∞ |
| x5 | 0 | 1000 | 5 | 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 250 |
| x8 ← |
-M | 150 | 0 | 2 | 0 | 0 | 0 | -1 | 0 | 1 | 0 | 75 |
| x9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | ∞ |
| max | -150M | -3 | -2M-4 | 0 | 0 | 0 | M | M | 0 | 0 |
Вычисление элементов таблицы:
Элементы колонки базис(B)
Переносим в таблицу базовые элементы, которые мы определили на предварительном этапе:
B1 = x3;
B2 = x4;
B3 = x5;
B4 = x8;
B5 = x9;
Элементы колонки Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Cb1 = 0;
Cb2 = 0;
Cb3 = 0;
Cb4 = -M;
Cb5 = -M;
Значения упрявляемых переменных и колонки P
На данном этапе никаких вычислений не нужно, просто переносим значения из предварительного этапа в соответствующие ячейки таблицы:
P1 = 600;
P2 = 225;
P3 = 1000;
P4 = 150;
P5 = 0;
x1,1 = 2;
x1,2 = 1;
x1,3 = 1;
x1,4 = 0;
x1,5 = 0;
x1,6 = 0;
x1,7 = 0;
x1,8 = 0;
x1,9 = 0;
x2,1 = 0;
x2,2 = 0;
x2,3 = 0;
x2,4 = 1;
x2,5 = 0;
x2,6 = 0;
x2,7 = 0;
x2,8 = 0;
x2,9 = 0;
x3,1 = 5;
x3,2 = 4;
x3,3 = 0;
x3,4 = 0;
x3,5 = 1;
x3,6 = 0;
x3,7 = 0;
x3,8 = 0;
x3,9 = 0;
x4,1 = 0;
x4,2 = 2;
x4,3 = 0;
x4,4 = 0;
x4,5 = 0;
x4,6 = -1;
x4,7 = 0;
x4,8 = 1;
x4,9 = 0;
x5,1 = 0;
x5,2 = 0;
x5,3 = 0;
x5,4 = 0;
x5,5 = 0;
x5,6 = 0;
x5,7 = -1;
x5,8 = 0;
x5,9 = 1;
Значение целевой функции
Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений.
MaxP = (Cb1 * P1) + (Cb11 * P2 + (Cb21 * P3 + (Cb31 * P4 + (Cb41 * P5 = (0 * 600) + (0 * 225) + (0 * 1000) + (-M * 150) + (-M * 0) = -150M;
Оценки управляемых переменных
Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной.
Maxx1 = ((Cb1 * x1,1) + (Cb2 * x2,1) + (Cb3 * x3,1) + (Cb4 * x4,1) + (Cb5 * x5,1) ) — kx1 = ((0 * 2) + (0 * 0) + (0 * 5) + (-M * 0) + (-M * 0) ) — 3 = -3;
Maxx2 = ((Cb1 * x1,2) + (Cb2 * x2,2) + (Cb3 * x3,2) + (Cb4 * x4,2) + (Cb5 * x5,2) ) — kx2 = ((0 * 1) + (0 * 0) + (0 * 4) + (-M * 2) + (-M * 0) ) — 4 = -2M-4;
Maxx3 = ((Cb1 * x1,3) + (Cb2 * x2,3) + (Cb3 * x3,3) + (Cb4 * x4,3) + (Cb5 * x5,3) ) — kx3 = ((0 * 1) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * 0) ) — 0 = 0;
Maxx4 = ((Cb1 * x1,4) + (Cb2 * x2,4) + (Cb3 * x3,4) + (Cb4 * x4,4) + (Cb5 * x5,4) ) — kx4 = ((0 * 0) + (0 * 1) + (0 * 0) + (-M * 0) + (-M * 0) ) — 0 = 0;
Maxx5 = ((Cb1 * x1,5) + (Cb2 * x2,5) + (Cb3 * x3,5) + (Cb4 * x4,5) + (Cb5 * x5,5) ) — kx5 = ((0 * 0) + (0 * 0) + (0 * 1) + (-M * 0) + (-M * 0) ) — 0 = 0;
Maxx6 = ((Cb1 * x1,6) + (Cb2 * x2,6) + (Cb3 * x3,6) + (Cb4 * x4,6) + (Cb5 * x5,6) ) — kx6 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * -1) + (-M * 0) ) — 0 = M;
Maxx7 = ((Cb1 * x1,7) + (Cb2 * x2,7) + (Cb3 * x3,7) + (Cb4 * x4,7) + (Cb5 * x5,7) ) — kx7 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * -1) ) — 0 = M;
Maxx8 = ((Cb1 * x1,8) + (Cb2 * x2,8) + (Cb3 * x3,8) + (Cb4 * x4,8) + (Cb5 * x5,8) ) — kx8 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 1) + (-M * 0) ) — -M = 0;
Maxx9 = ((Cb1 * x1,9) + (Cb2 * x2,9) + (Cb3 * x3,9) + (Cb4 * x4,9) + (Cb5 * x5,9) ) — kx9 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * 1) ) — -M = 0;
Элементы колонки Q
Поскольку среди оценок управляемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис введем переменную с наименьшей отрицательной оценкой.
Количество переменных в базисе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базиса, для чего мы рассчитываем Q.
Элементы столбика Q рассчитываем поделив значения из колонки P на значение с колонки, соответствующие переменной которая вводится в базис:
Q1 = P1 / x1,2 = 600 / 1 = 600;
Q2 = P2 / x2,2 = 225 / 0 = ∞;
Q3 = P3 / x3,2 = 1000 / 4 = 250;
Q4 = P4 / x4,2 = 150 / 2 = 75;
Q5 = P5 / x5,2 = 0 / 0 = ∞;
Выводим из базиса переменную с наименьшим положительным значением Q.
На пересечении строки, которая соответствует переменной что выводится из базиса, и столбца который соответствует переменной что вводится в базис, расположен разрешающий элемент.
Данный элемент позволит нам рассчитать элементы таблицы следующей итерации.
Итерация: 2
| B | Cb | P | x1↓ | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x3 | 0 | 525 | 2 | 0 | 1 | 0 | 0 | 0.5 | 0 | -0.5 | 0 | 262.5 |
| x4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ∞ |
| x5 ← |
0 | 700 | 5 | 0 | 0 | 0 | 1 | 2 | 0 | -2 | 0 | 140 |
| x2 | 4 | 75 | 0 | 1 | 0 | 0 | 0 | -0.5 | 0 | 0.5 | 0 | ∞ |
| x9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | ∞ |
| max | 300 | -3 | 0 | 0 | 0 | 0 | -2 | M | M+2 | 0 |
Вычисление элементов таблицы:
Элементы колонки базис(B)
За результатами вычислений предыдущей итерации убираем с базиса переменную x8 и ставим на ее место x2. Все остальные ячейки остаются без изменений.
Элементы колонки Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Cb1 = 0;
Cb2 = 0;
Cb3 = 0;
Cb4 = 4;
Cb5 = -M;
Значения упрявляемых переменных и колонки P(В качестве исходных данных берутся данные из предыдущей итерации)
Заполняем нулями все ячейки, соответствующие переменной, которая только что была введена в базис:(Разрешающий элемент остается без изменений)
x1,2 = 0;
x2,2 = 0;
x3,2 = 0;
x5,2 = 0;
Переносим в текущую таблицу строку с разрешающим элементом с предыдущей таблицы, поэлементно поделив ее значения на разрешающий элемент:
P4 = P4 / x4,2 = 150 / 2 = 75;
x4,1 = x4,1 / x4,2 = 0 / 2 = 0;
x4,2 = x4,2 / x4,2 = 2 / 2 = 1;
x4,3 = x4,3 / x4,2 = 0 / 2 = 0;
x4,4 = x4,4 / x4,2 = 0 / 2 = 0;
x4,5 = x4,5 / x4,2 = 0 / 2 = 0;
x4,6 = x4,6 / x4,2 = -1 / 2 = -0.5;
x4,7 = x4,7 / x4,2 = 0 / 2 = 0;
x4,8 = x4,8 / x4,2 = 1 / 2 = 0.5;
x4,9 = x4,9 / x4,2 = 0 / 2 = 0;
Остальные пустые ячейки, за исключением строки оценок и колонки Q, рассчитываем методом прямоугольника, относительно разрешающего элемента:
P1 = (P1 * x4,2) — (x1,2 * P4) / x4,2 = ((600 * 2) — (1 * 150)) / 2 = 525;
P2 = (P2 * x4,2) — (x2,2 * P4) / x4,2 = ((225 * 2) — (0 * 150)) / 2 = 225;
P3 = (P3 * x4,2) — (x3,2 * P4) / x4,2 = ((1000 * 2) — (4 * 150)) / 2 = 700;
P5 = (P5 * x4,2) — (x5,2 * P4) / x4,2 = ((0 * 2) — (0 * 150)) / 2 = 0;
x1,1 = ((x1,1 * x4,2) — (x1,2 * x4,1)) / x4,2 = ((2 * 2) — (1 * 0)) / 2 = 2;
x1,2 = ((x1,2 * x4,2) — (x1,2 * x4,2)) / x4,2 = ((1 * 2) — (1 * 2)) / 2 = 0;
x1,4 = ((x1,4 * x4,2) — (x1,2 * x4,4)) / x4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
x1,5 = ((x1,5 * x4,2) — (x1,2 * x4,5)) / x4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
x1,6 = ((x1,6 * x4,2) — (x1,2 * x4,6)) / x4,2 = ((0 * 2) — (1 * -1)) / 2 = 0.5;
x1,7 = ((x1,7 * x4,2) — (x1,2 * x4,7)) / x4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
x1,8 = ((x1,8 * x4,2) — (x1,2 * x4,8)) / x4,2 = ((0 * 2) — (1 * 1)) / 2 = -0.5;
x1,9 = ((x1,9 * x4,2) — (x1,2 * x4,9)) / x4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
x2,1 = ((x2,1 * x4,2) — (x2,2 * x4,1)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x2,2 = ((x2,2 * x4,2) — (x2,2 * x4,2)) / x4,2 = ((0 * 2) — (0 * 2)) / 2 = 0;
x2,4 = ((x2,4 * x4,2) — (x2,2 * x4,4)) / x4,2 = ((1 * 2) — (0 * 0)) / 2 = 1;
x2,5 = ((x2,5 * x4,2) — (x2,2 * x4,5)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x2,6 = ((x2,6 * x4,2) — (x2,2 * x4,6)) / x4,2 = ((0 * 2) — (0 * -1)) / 2 = 0;
x2,7 = ((x2,7 * x4,2) — (x2,2 * x4,7)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x2,8 = ((x2,8 * x4,2) — (x2,2 * x4,8)) / x4,2 = ((0 * 2) — (0 * 1)) / 2 = 0;
x2,9 = ((x2,9 * x4,2) — (x2,2 * x4,9)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x3,1 = ((x3,1 * x4,2) — (x3,2 * x4,1)) / x4,2 = ((5 * 2) — (4 * 0)) / 2 = 5;
x3,2 = ((x3,2 * x4,2) — (x3,2 * x4,2)) / x4,2 = ((4 * 2) — (4 * 2)) / 2 = 0;
x3,4 = ((x3,4 * x4,2) — (x3,2 * x4,4)) / x4,2 = ((0 * 2) — (4 * 0)) / 2 = 0;
x3,5 = ((x3,5 * x4,2) — (x3,2 * x4,5)) / x4,2 = ((1 * 2) — (4 * 0)) / 2 = 1;
x3,6 = ((x3,6 * x4,2) — (x3,2 * x4,6)) / x4,2 = ((0 * 2) — (4 * -1)) / 2 = 2;
x3,7 = ((x3,7 * x4,2) — (x3,2 * x4,7)) / x4,2 = ((0 * 2) — (4 * 0)) / 2 = 0;
x3,8 = ((x3,8 * x4,2) — (x3,2 * x4,8)) / x4,2 = ((0 * 2) — (4 * 1)) / 2 = -2;
x3,9 = ((x3,9 * x4,2) — (x3,2 * x4,9)) / x4,2 = ((0 * 2) — (4 * 0)) / 2 = 0;
x5,1 = ((x5,1 * x4,2) — (x5,2 * x4,1)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x5,2 = ((x5,2 * x4,2) — (x5,2 * x4,2)) / x4,2 = ((0 * 2) — (0 * 2)) / 2 = 0;
x5,4 = ((x5,4 * x4,2) — (x5,2 * x4,4)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x5,5 = ((x5,5 * x4,2) — (x5,2 * x4,5)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x5,6 = ((x5,6 * x4,2) — (x5,2 * x4,6)) / x4,2 = ((0 * 2) — (0 * -1)) / 2 = 0;
x5,7 = ((x5,7 * x4,2) — (x5,2 * x4,7)) / x4,2 = ((-1 * 2) — (0 * 0)) / 2 = -1;
x5,8 = ((x5,8 * x4,2) — (x5,2 * x4,8)) / x4,2 = ((0 * 2) — (0 * 1)) / 2 = 0;
x5,9 = ((x5,9 * x4,2) — (x5,2 * x4,9)) / x4,2 = ((1 * 2) — (0 * 0)) / 2 = 1;
Значение целевой функции
Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений.
MaxP = (Cb1 * P1) + (Cb11 * P2 + (Cb21 * P3 + (Cb31 * P4 + (Cb41 * P5 = (0 * 525) + (0 * 225) + (0 * 700) + (4 * 75) + (-M * 0) = 300;
Оценки управляемых переменных
Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной.
Maxx1 = ((Cb1 * x1,1) + (Cb2 * x2,1) + (Cb3 * x3,1) + (Cb4 * x4,1) + (Cb5 * x5,1) ) — kx1 = ((0 * 2) + (0 * 0) + (0 * 5) + (4 * 0) + (-M * 0) ) — 3 = -3;
Maxx2 = ((Cb1 * x1,2) + (Cb2 * x2,2) + (Cb3 * x3,2) + (Cb4 * x4,2) + (Cb5 * x5,2) ) — kx2 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 1) + (-M * 0) ) — 4 = 0;
Maxx3 = ((Cb1 * x1,3) + (Cb2 * x2,3) + (Cb3 * x3,3) + (Cb4 * x4,3) + (Cb5 * x5,3) ) — kx3 = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx4 = ((Cb1 * x1,4) + (Cb2 * x2,4) + (Cb3 * x3,4) + (Cb4 * x4,4) + (Cb5 * x5,4) ) — kx4 = ((0 * 0) + (0 * 1) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx5 = ((Cb1 * x1,5) + (Cb2 * x2,5) + (Cb3 * x3,5) + (Cb4 * x4,5) + (Cb5 * x5,5) ) — kx5 = ((0 * 0) + (0 * 0) + (0 * 1) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx6 = ((Cb1 * x1,6) + (Cb2 * x2,6) + (Cb3 * x3,6) + (Cb4 * x4,6) + (Cb5 * x5,6) ) — kx6 = ((0 * 0.5) + (0 * 0) + (0 * 2) + (4 * -0.5) + (-M * 0) ) — 0 = -2;
Maxx7 = ((Cb1 * x1,7) + (Cb2 * x2,7) + (Cb3 * x3,7) + (Cb4 * x4,7) + (Cb5 * x5,7) ) — kx7 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * -1) ) — 0 = M;
Maxx8 = ((Cb1 * x1,8) + (Cb2 * x2,8) + (Cb3 * x3,8) + (Cb4 * x4,8) + (Cb5 * x5,8) ) — kx8 = ((0 * -0.5) + (0 * 0) + (0 * -2) + (4 * 0.5) + (-M * 0) ) — -M = M+2;
Maxx9 = ((Cb1 * x1,9) + (Cb2 * x2,9) + (Cb3 * x3,9) + (Cb4 * x4,9) + (Cb5 * x5,9) ) — kx9 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 1) ) — -M = 0;
Элементы колонки Q
Поскольку среди оценок управляемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис введем переменную с наименьшей отрицательной оценкой.
Количество переменных в базисе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базиса, для чего мы рассчитываем Q.
Элементы столбика Q рассчитываем поделив значения из колонки P на значение с колонки, соответствующие переменной которая вводится в базис:
Q1 = P1 / x1,1 = 525 / 2 = 262.5;
Q2 = P2 / x2,1 = 225 / 0 = ∞;
Q3 = P3 / x3,1 = 700 / 5 = 140;
Q4 = P4 / x4,1 = 75 / 0 = ∞;
Q5 = P5 / x5,1 = 0 / 0 = ∞;
Выводим из базиса переменную с наименьшим положительным значением Q.
На пересечении строки, которая соответствует переменной что выводится из базиса, и столбца который соответствует переменной что вводится в базис, расположен разрешающий элемент.
Данный элемент позволит нам рассчитать элементы таблицы следующей итерации.
Итерация: 3
| B | Cb | P | x1 | x2 | x3 | x4 | x5 | x6↓ | x7 | x8 | x9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x3 | 0 | 245 | 0 | 0 | 1 | 0 | -0.4 | -0.3 | 0 | 0.3 | 0 | -816.67 |
| x4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ∞ |
| x1 ← |
3 | 140 | 1 | 0 | 0 | 0 | 0.2 | 0.4 | 0 | -0.4 | 0 | 350 |
| x2 | 4 | 75 | 0 | 1 | 0 | 0 | 0 | -0.5 | 0 | 0.5 | 0 | -150 |
| x9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | ∞ |
| max | 720 | 0 | 0 | 0 | 0 | 0.6 | -0.8 | M | M+0.8 | 0 |
Вычисление элементов таблицы:
Элементы колонки базис(B)
За результатами вычислений предыдущей итерации убираем с базиса переменную x5 и ставим на ее место x1. Все остальные ячейки остаются без изменений.
Элементы колонки Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Cb1 = 0;
Cb2 = 0;
Cb3 = 3;
Cb4 = 4;
Cb5 = -M;
Значения упрявляемых переменных и колонки P(В качестве исходных данных берутся данные из предыдущей итерации)
Заполняем нулями все ячейки, соответствующие переменной, которая только что была введена в базис:(Разрешающий элемент остается без изменений)
x1,1 = 0;
x2,1 = 0;
x4,1 = 0;
x5,1 = 0;
Переносим в текущую таблицу строку с разрешающим элементом с предыдущей таблицы, поэлементно поделив ее значения на разрешающий элемент:
P3 = P3 / x3,1 = 700 / 5 = 140;
x3,1 = x3,1 / x3,1 = 5 / 5 = 1;
x3,2 = x3,2 / x3,1 = 0 / 5 = 0;
x3,3 = x3,3 / x3,1 = 0 / 5 = 0;
x3,4 = x3,4 / x3,1 = 0 / 5 = 0;
x3,5 = x3,5 / x3,1 = 1 / 5 = 0.2;
x3,6 = x3,6 / x3,1 = 2 / 5 = 0.4;
x3,7 = x3,7 / x3,1 = 0 / 5 = 0;
x3,8 = x3,8 / x3,1 = -2 / 5 = -0.4;
x3,9 = x3,9 / x3,1 = 0 / 5 = 0;
Остальные пустые ячейки, за исключением строки оценок и колонки Q, рассчитываем методом прямоугольника, относительно разрешающего элемента:
P1 = (P1 * x3,1) — (x1,1 * P3) / x3,1 = ((525 * 5) — (2 * 700)) / 5 = 245;
P2 = (P2 * x3,1) — (x2,1 * P3) / x3,1 = ((225 * 5) — (0 * 700)) / 5 = 225;
P4 = (P4 * x3,1) — (x4,1 * P3) / x3,1 = ((75 * 5) — (0 * 700)) / 5 = 75;
P5 = (P5 * x3,1) — (x5,1 * P3) / x3,1 = ((0 * 5) — (0 * 700)) / 5 = 0;
x1,1 = ((x1,1 * x3,1) — (x1,1 * x3,1)) / x3,1 = ((2 * 5) — (2 * 5)) / 5 = 0;
x1,3 = ((x1,3 * x3,1) — (x1,1 * x3,3)) / x3,1 = ((1 * 5) — (2 * 0)) / 5 = 1;
x1,4 = ((x1,4 * x3,1) — (x1,1 * x3,4)) / x3,1 = ((0 * 5) — (2 * 0)) / 5 = 0;
x1,5 = ((x1,5 * x3,1) — (x1,1 * x3,5)) / x3,1 = ((0 * 5) — (2 * 1)) / 5 = -0.4;
x1,6 = ((x1,6 * x3,1) — (x1,1 * x3,6)) / x3,1 = ((0.5 * 5) — (2 * 2)) / 5 = -0.3;
x1,7 = ((x1,7 * x3,1) — (x1,1 * x3,7)) / x3,1 = ((0 * 5) — (2 * 0)) / 5 = 0;
x1,8 = ((x1,8 * x3,1) — (x1,1 * x3,8)) / x3,1 = ((-0.5 * 5) — (2 * -2)) / 5 = 0.3;
x1,9 = ((x1,9 * x3,1) — (x1,1 * x3,9)) / x3,1 = ((0 * 5) — (2 * 0)) / 5 = 0;
x2,1 = ((x2,1 * x3,1) — (x2,1 * x3,1)) / x3,1 = ((0 * 5) — (0 * 5)) / 5 = 0;
x2,3 = ((x2,3 * x3,1) — (x2,1 * x3,3)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x2,4 = ((x2,4 * x3,1) — (x2,1 * x3,4)) / x3,1 = ((1 * 5) — (0 * 0)) / 5 = 1;
x2,5 = ((x2,5 * x3,1) — (x2,1 * x3,5)) / x3,1 = ((0 * 5) — (0 * 1)) / 5 = 0;
x2,6 = ((x2,6 * x3,1) — (x2,1 * x3,6)) / x3,1 = ((0 * 5) — (0 * 2)) / 5 = 0;
x2,7 = ((x2,7 * x3,1) — (x2,1 * x3,7)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x2,8 = ((x2,8 * x3,1) — (x2,1 * x3,8)) / x3,1 = ((0 * 5) — (0 * -2)) / 5 = 0;
x2,9 = ((x2,9 * x3,1) — (x2,1 * x3,9)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x4,1 = ((x4,1 * x3,1) — (x4,1 * x3,1)) / x3,1 = ((0 * 5) — (0 * 5)) / 5 = 0;
x4,3 = ((x4,3 * x3,1) — (x4,1 * x3,3)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x4,4 = ((x4,4 * x3,1) — (x4,1 * x3,4)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x4,5 = ((x4,5 * x3,1) — (x4,1 * x3,5)) / x3,1 = ((0 * 5) — (0 * 1)) / 5 = 0;
x4,6 = ((x4,6 * x3,1) — (x4,1 * x3,6)) / x3,1 = ((-0.5 * 5) — (0 * 2)) / 5 = -0.5;
x4,7 = ((x4,7 * x3,1) — (x4,1 * x3,7)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x4,8 = ((x4,8 * x3,1) — (x4,1 * x3,8)) / x3,1 = ((0.5 * 5) — (0 * -2)) / 5 = 0.5;
x4,9 = ((x4,9 * x3,1) — (x4,1 * x3,9)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x5,1 = ((x5,1 * x3,1) — (x5,1 * x3,1)) / x3,1 = ((0 * 5) — (0 * 5)) / 5 = 0;
x5,3 = ((x5,3 * x3,1) — (x5,1 * x3,3)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x5,4 = ((x5,4 * x3,1) — (x5,1 * x3,4)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x5,5 = ((x5,5 * x3,1) — (x5,1 * x3,5)) / x3,1 = ((0 * 5) — (0 * 1)) / 5 = 0;
x5,6 = ((x5,6 * x3,1) — (x5,1 * x3,6)) / x3,1 = ((0 * 5) — (0 * 2)) / 5 = 0;
x5,7 = ((x5,7 * x3,1) — (x5,1 * x3,7)) / x3,1 = ((-1 * 5) — (0 * 0)) / 5 = -1;
x5,8 = ((x5,8 * x3,1) — (x5,1 * x3,8)) / x3,1 = ((0 * 5) — (0 * -2)) / 5 = 0;
x5,9 = ((x5,9 * x3,1) — (x5,1 * x3,9)) / x3,1 = ((1 * 5) — (0 * 0)) / 5 = 1;
Значение целевой функции
Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений.
MaxP = (Cb1 * P1) + (Cb11 * P2 + (Cb21 * P3 + (Cb31 * P4 + (Cb41 * P5) = (0 * 245) + (0 * 225) + (3 * 140) + (4 * 75) + (-M * 0) = 720;
Оценки управляемых переменных
Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной.
Maxx1 = ((Cb1 * x1,1) + (Cb2 * x2,1) + (Cb3 * x3,1) + (Cb4 * x4,1) + (Cb5 * x5,1) ) — kx1 = ((0 * 0) + (0 * 0) + (3 * 1) + (4 * 0) + (-M * 0) ) — 3 = 0;
Maxx2 = ((Cb1 * x1,2) + (Cb2 * x2,2) + (Cb3 * x3,2) + (Cb4 * x4,2) + (Cb5 * x5,2) ) — kx2 = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 1) + (-M * 0) ) — 4 = 0;
Maxx3 = ((Cb1 * x1,3) + (Cb2 * x2,3) + (Cb3 * x3,3) + (Cb4 * x4,3) + (Cb5 * x5,3) ) — kx3 = ((0 * 1) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx4 = ((Cb1 * x1,4) + (Cb2 * x2,4) + (Cb3 * x3,4) + (Cb4 * x4,4) + (Cb5 * x5,4) ) — kx4 = ((0 * 0) + (0 * 1) + (3 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx5 = ((Cb1 * x1,5) + (Cb2 * x2,5) + (Cb3 * x3,5) + (Cb4 * x4,5) + (Cb5 * x5,5) ) — kx5 = ((0 * -0.4) + (0 * 0) + (3 * 0.2) + (4 * 0) + (-M * 0) ) — 0 = 0.6;
Maxx6 = ((Cb1 * x1,6) + (Cb2 * x2,6) + (Cb3 * x3,6) + (Cb4 * x4,6) + (Cb5 * x5,6) ) — kx6 = ((0 * -0.3) + (0 * 0) + (3 * 0.4) + (4 * -0.5) + (-M * 0) ) — 0 = -0.8;
Maxx7 = ((Cb1 * x1,7) + (Cb2 * x2,7) + (Cb3 * x3,7) + (Cb4 * x4,7) + (Cb5 * x5,7) ) — kx7 = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * -1) ) — 0 = M;
Maxx8 = ((Cb1 * x1,8) + (Cb2 * x2,8) + (Cb3 * x3,8) + (Cb4 * x4,8) + (Cb5 * x5,8) ) — kx8 = ((0 * 0.3) + (0 * 0) + (3 * -0.4) + (4 * 0.5) + (-M * 0) ) — -M = M+0.8;
Maxx9 = ((Cb1 * x1,9) + (Cb2 * x2,9) + (Cb3 * x3,9) + (Cb4 * x4,9) + (Cb5 * x5,9) ) — kx9 = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * 1) ) — -M = 0;
Элементы колонки Q
Поскольку среди оценок управляемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис введем переменную с наименьшей отрицательной оценкой.
Количество переменных в базисе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базиса, для чего мы рассчитываем Q.
Элементы столбика Q рассчитываем поделив значения из колонки P на значение с колонки, соответствующие переменной которая вводится в базис:
Q1 = P1 / x1,6 = 245 / -0.3 = -816.67;
Q2 = P2 / x2,6 = 225 / 0 = ∞;
Q3 = P3 / x3,6 = 140 / 0.4 = 350;
Q4 = P4 / x4,6 = 75 / -0.5 = -150;
Q5 = P5 / x5,6 = 0 / 0 = ∞;
Выводим из базиса переменную с наименьшим положительным значением Q.
На пересечении строки, которая соответствует переменной что выводится из базиса, и столбца который соответствует переменной что вводится в базис, расположен разрешающий элемент.
Данный элемент позволит нам рассчитать элементы таблицы следующей итерации.
Итерация: 4
| B | Cb | P | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x3 | 0 | 350 | 0.75 | 0 | 1 | 0 | -0.25 | 0 | 0 | 0 | 0 | |
| x4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| x6 | 0 | 350 | 2.5 | 0 | 0 | 0 | 0.5 | 1 | 0 | -1 | 0 | |
| x2 | 4 | 250 | 1.25 | 1 | 0 | 0 | 0.25 | 0 | 0 | 0 | 0 | |
| x9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | |
| max | 1000 | 2 | 0 | 0 | 0 | 1 | 0 | M | M | 0 |
Вычисление элементов таблицы:
Элементы колонки базис(B)
За результатами вычислений предыдущей итерации убираем с базиса переменную x1 и ставим на ее место x6. Все остальные ячейки остаются без изменений.
Элементы колонки Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Cb1 = 0;
Cb2 = 0;
Cb3 = 0;
Cb4 = 4;
Cb5 = -M;
Значения упрявляемых переменных и колонки P(В качестве исходных данных берутся данные из предыдущей итерации)
Заполняем нулями все ячейки, соответствующие переменной, которая только что была введена в базис:(Разрешающий элемент остается без изменений)
x1,6 = 0;
x2,6 = 0;
x4,6 = 0;
x5,6 = 0;
Переносим в текущую таблицу строку с разрешающим элементом с предыдущей таблицы, поэлементно поделив ее значения на разрешающий элемент:
P3 = P3 / x3,6 = 140 / 0.4 = 350;
x3,1 = x3,1 / x3,6 = 1 / 0.4 = 2.5;
x3,2 = x3,2 / x3,6 = 0 / 0.4 = 0;
x3,3 = x3,3 / x3,6 = 0 / 0.4 = 0;
x3,4 = x3,4 / x3,6 = 0 / 0.4 = 0;
x3,5 = x3,5 / x3,6 = 0.2 / 0.4 = 0.5;
x3,6 = x3,6 / x3,6 = 0.4 / 0.4 = 1;
x3,7 = x3,7 / x3,6 = 0 / 0.4 = 0;
x3,8 = x3,8 / x3,6 = -0.4 / 0.4 = -1;
x3,9 = x3,9 / x3,6 = 0 / 0.4 = 0;
Остальные пустые ячейки, за исключением строки оценок и колонки Q, рассчитываем методом прямоугольника, относительно разрешающего элемента:
P1 = (P1 * x3,6) — (x1,6 * P3) / x3,6 = ((245 * 0.4) — (-0.3 * 140)) / 0.4 = 350;
P2 = (P2 * x3,6) — (x2,6 * P3) / x3,6 = ((225 * 0.4) — (0 * 140)) / 0.4 = 225;
P4 = (P4 * x3,6) — (x4,6 * P3) / x3,6 = ((75 * 0.4) — (-0.5 * 140)) / 0.4 = 250;
P5 = (P5 * x3,6) — (x5,6 * P3) / x3,6 = ((0 * 0.4) — (0 * 140)) / 0.4 = 0;
x1,1 = ((x1,1 * x3,6) — (x1,6 * x3,1)) / x3,6 = ((0 * 0.4) — (-0.3 * 1)) / 0.4 = 0.75;
x1,2 = ((x1,2 * x3,6) — (x1,6 * x3,2)) / x3,6 = ((0 * 0.4) — (-0.3 * 0)) / 0.4 = 0;
x1,3 = ((x1,3 * x3,6) — (x1,6 * x3,3)) / x3,6 = ((1 * 0.4) — (-0.3 * 0)) / 0.4 = 1;
x1,4 = ((x1,4 * x3,6) — (x1,6 * x3,4)) / x3,6 = ((0 * 0.4) — (-0.3 * 0)) / 0.4 = 0;
x1,5 = ((x1,5 * x3,6) — (x1,6 * x3,5)) / x3,6 = ((-0.4 * 0.4) — (-0.3 * 0.2)) / 0.4 = -0.25;
x1,6 = ((x1,6 * x3,6) — (x1,6 * x3,6)) / x3,6 = ((-0.3 * 0.4) — (-0.3 * 0.4)) / 0.4 = 0;
x1,8 = ((x1,8 * x3,6) — (x1,6 * x3,8)) / x3,6 = ((0.3 * 0.4) — (-0.3 * -0.4)) / 0.4 = 0;
x1,9 = ((x1,9 * x3,6) — (x1,6 * x3,9)) / x3,6 = ((0 * 0.4) — (-0.3 * 0)) / 0.4 = 0;
x2,1 = ((x2,1 * x3,6) — (x2,6 * x3,1)) / x3,6 = ((0 * 0.4) — (0 * 1)) / 0.4 = 0;
x2,2 = ((x2,2 * x3,6) — (x2,6 * x3,2)) / x3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0;
x2,3 = ((x2,3 * x3,6) — (x2,6 * x3,3)) / x3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0;
x2,4 = ((x2,4 * x3,6) — (x2,6 * x3,4)) / x3,6 = ((1 * 0.4) — (0 * 0)) / 0.4 = 1;
x2,5 = ((x2,5 * x3,6) — (x2,6 * x3,5)) / x3,6 = ((0 * 0.4) — (0 * 0.2)) / 0.4 = 0;
x2,6 = ((x2,6 * x3,6) — (x2,6 * x3,6)) / x3,6 = ((0 * 0.4) — (0 * 0.4)) / 0.4 = 0;
x2,8 = ((x2,8 * x3,6) — (x2,6 * x3,8)) / x3,6 = ((0 * 0.4) — (0 * -0.4)) / 0.4 = 0;
x2,9 = ((x2,9 * x3,6) — (x2,6 * x3,9)) / x3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0;
x4,1 = ((x4,1 * x3,6) — (x4,6 * x3,1)) / x3,6 = ((0 * 0.4) — (-0.5 * 1)) / 0.4 = 1.25;
x4,2 = ((x4,2 * x3,6) — (x4,6 * x3,2)) / x3,6 = ((1 * 0.4) — (-0.5 * 0)) / 0.4 = 1;
x4,3 = ((x4,3 * x3,6) — (x4,6 * x3,3)) / x3,6 = ((0 * 0.4) — (-0.5 * 0)) / 0.4 = 0;
x4,4 = ((x4,4 * x3,6) — (x4,6 * x3,4)) / x3,6 = ((0 * 0.4) — (-0.5 * 0)) / 0.4 = 0;
x4,5 = ((x4,5 * x3,6) — (x4,6 * x3,5)) / x3,6 = ((0 * 0.4) — (-0.5 * 0.2)) / 0.4 = 0.25;
x4,6 = ((x4,6 * x3,6) — (x4,6 * x3,6)) / x3,6 = ((-0.5 * 0.4) — (-0.5 * 0.4)) / 0.4 = 0;
x4,8 = ((x4,8 * x3,6) — (x4,6 * x3,8)) / x3,6 = ((0.5 * 0.4) — (-0.5 * -0.4)) / 0.4 = 0;
x4,9 = ((x4,9 * x3,6) — (x4,6 * x3,9)) / x3,6 = ((0 * 0.4) — (-0.5 * 0)) / 0.4 = 0;
x5,1 = ((x5,1 * x3,6) — (x5,6 * x3,1)) / x3,6 = ((0 * 0.4) — (0 * 1)) / 0.4 = 0;
x5,2 = ((x5,2 * x3,6) — (x5,6 * x3,2)) / x3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0;
x5,3 = ((x5,3 * x3,6) — (x5,6 * x3,3)) / x3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0;
x5,4 = ((x5,4 * x3,6) — (x5,6 * x3,4)) / x3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0;
x5,5 = ((x5,5 * x3,6) — (x5,6 * x3,5)) / x3,6 = ((0 * 0.4) — (0 * 0.2)) / 0.4 = 0;
x5,6 = ((x5,6 * x3,6) — (x5,6 * x3,6)) / x3,6 = ((0 * 0.4) — (0 * 0.4)) / 0.4 = 0;
x5,8 = ((x5,8 * x3,6) — (x5,6 * x3,8)) / x3,6 = ((0 * 0.4) — (0 * -0.4)) / 0.4 = 0;
x5,9 = ((x5,9 * x3,6) — (x5,6 * x3,9)) / x3,6 = ((1 * 0.4) — (0 * 0)) / 0.4 = 1;
Значение целевой функции
Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений.
MaxP = (Cb1 * P1) + (Cb11 * P2 + (Cb21 * P3 + (Cb31 * P4 + (Cb41 * P5 = (0 * 350) + (0 * 225) + (0 * 350) + (4 * 250) + (-M * 0) = 1000;
Оценки управляемых переменных
Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной.
Maxx1 = ((Cb1 * x1,1) + (Cb2 * x2,1) + (Cb3 * x3,1) + (Cb4 * x4,1) + (Cb5 * x5,1) ) — kx1 = ((0 * 0.75) + (0 * 0) + (0 * 2.5) + (4 * 1.25) + (-M * 0) ) — 3 = 2;
Maxx2 = ((Cb1 * x1,2) + (Cb2 * x2,2) + (Cb3 * x3,2) + (Cb4 * x4,2) + (Cb5 * x5,2) ) — kx2 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 1) + (-M * 0) ) — 4 = 0;
Maxx3 = ((Cb1 * x1,3) + (Cb2 * x2,3) + (Cb3 * x3,3) + (Cb4 * x4,3) + (Cb5 * x5,3) ) — kx3 = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx4 = ((Cb1 * x1,4) + (Cb2 * x2,4) + (Cb3 * x3,4) + (Cb4 * x4,4) + (Cb5 * x5,4) ) — kx4 = ((0 * 0) + (0 * 1) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx5 = ((Cb1 * x1,5) + (Cb2 * x2,5) + (Cb3 * x3,5) + (Cb4 * x4,5) + (Cb5 * x5,5) ) — kx5 = ((0 * -0.25) + (0 * 0) + (0 * 0.5) + (4 * 0.25) + (-M * 0) ) — 0 = 1;
Maxx6 = ((Cb1 * x1,6) + (Cb2 * x2,6) + (Cb3 * x3,6) + (Cb4 * x4,6) + (Cb5 * x5,6) ) — kx6 = ((0 * 0) + (0 * 0) + (0 * 1) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx7 = ((Cb1 * x1,7) + (Cb2 * x2,7) + (Cb3 * x3,7) + (Cb4 * x4,7) + (Cb5 * x5,7) ) — kx7 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * -1) ) — 0 = M;
Maxx8 = ((Cb1 * x1,8) + (Cb2 * x2,8) + (Cb3 * x3,8) + (Cb4 * x4,8) + (Cb5 * x5,8) ) — kx8 = ((0 * 0) + (0 * 0) + (0 * -1) + (4 * 0) + (-M * 0) ) — -M = M;
Maxx9 = ((Cb1 * x1,9) + (Cb2 * x2,9) + (Cb3 * x3,9) + (Cb4 * x4,9) + (Cb5 * x5,9) ) — kx9 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 1) ) — -M = 0;
Ответ:
Поскольку среди оценок управляемых переменных нет отрицательных значений, текущая таблица имеет оптимальное решение.
Значение целевой функции:
F* = 1000
Переменные которые присутствуют в базисе, равны соответствующим ячейкам колонки P, все остальные переменные равны нулю:
x1 = 0;
x2 = 250;
Ответ:
F* = 1000
X* = (0; 250)
Условные обозначения:
| xi↓ | — вводим переменную в базис; |
| xi ← |
— выводим переменную с базиса; |
| xi | — разрешительный елемент; |
| xi | — базисной елемент; |
| B | — базис; |
| Cb | — коэффициент при базисной переменной; |
| P | — план; |
Симплекс метод онлайн
Данный онлайн калькулятор решает задачу линейного программирования симплекс методом. Дается подробное решение с пояснениями. Для решения задачи линейного программирования задайте количество ограничений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите в статье: Решение задачи линейного программирования. Симплекс метод.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Симплекс метод
Симплекс метод − это метод решения задачи линейного программирования (ЗЛП). Суть метода заключается в нахождении начального допустимого плана, и в последующем улучшении плана до достижения максимального (или минимального) значения целевой функции в данном выпуклом многогранном множестве или выяснения неразрешимости задачи. Подробнее в статье: Решение задачи линейного программирования. Симплекс метод.
Примеры решения ЗЛП симплекс методом
Пример 1. Решить следующую задачу линейного программирования:
Р е ш е н и е. Матрица коэффициентов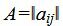 
системы уравнений имеет вид:
 |
Правая часть ограничений системы уравнений имеет вид:
 |
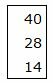Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1. Последние три векторы столбцы обазуют базис в трехмерном пространствое. Следовательно базисные переменные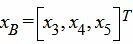 
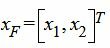
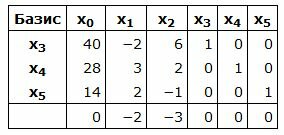, а свободные переменные 
:
 |
Запишем текущий опорный план:
 |
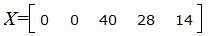Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем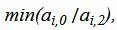 
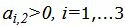
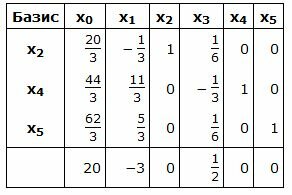
при 
. min(40:6, 28:2)=20/3 соответствует строке 1. Из базиса выходит вектор x3. Сделаем исключение Гаусса для столбца x2, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на -1/3, 1/6, 1/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
 |
Запишем текущий опорный план:
 |
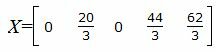Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-3), следовательно в базис входит вектор x1. Определяем, какой вектор выходит из базиса. Для этого вычисляем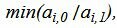 
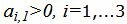
при 
. min(44/3:11/3, 62/3:5/3)=4 соответствует строке 2. Из базиса выходит вектор x4. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 2. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 3, 4 со строкой 2, умноженной на 1/11, -5/11, 9/11, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
 |
Текущий опорный план является оптимальным, так как в строках 4 под переменными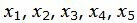 
нет отрицательных элементов.
Решение можно записать так: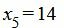 
.
Значение целевой функции в данной точке: F(X)=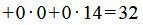
.
Пример 2. Найти максимум функции
 |
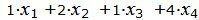при условиях
Р е ш е н и е. Матрица коэффициентов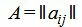 
системы уравнений имеет вид:
 |
Правая часть ограничений системы уравнений имеет вид:
 |
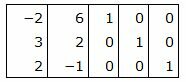
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1:
 |
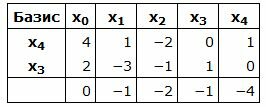Базисные векторы x4, x3, следовательно, все элементы в столбцах x4, x3, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на 4. Обнулим все элементы столбца x3, кроме ведущего элемента. Для этого сложим строку 3 со строкой 2, умноженной на 1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-11), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем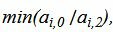 
при 
. Все 
следовательно целевая функция неограничена сверху. Т.е. задача линейного программирования неразрешима.
Примеры решения ЗЛП методом искусственного базиса
Пример 1. Найти максимум функции
при условиях
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственное переменное, а в целевую функцию добавляем это переменное, умноженное на −M, где M, очень большое число:
Матрица коэффициентов 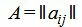системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
 |
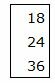Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
Базисные векторы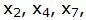 
следовательно, все элементы в столбцах ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца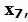 
кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-5), следовательно в базис входит вектор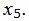 
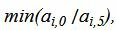
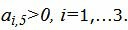
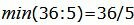
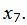
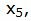
Определяем, какой вектор выходит из базиса. Для этого вычисляем 
при 
соответствует строке 3. Из базиса выходит вектор 
Сделаем исключение Гаусса для столбца 
учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строку 5 со строкой 3, умноженной на 1. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор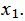 
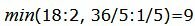
Определяем, какой вектор выходит из базиса. Для этого вычисляем 
при 
соответствует строке 1. Из базиса выходит вектор x2. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на 3/2, -1/10, 3/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-13/2), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем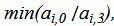 
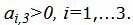
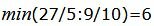
при 
соответствует строке 3. Из базиса выходит вектор x5. Сделаем исключение Гаусса для столбца x3, учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 2, 4 со строкой 3, умноженной на 5/3, 25/9, 65/9, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Текущий опорный план является оптимальным, так как в строках 4−5 под переменными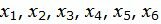 
нет отрицательных элементов.
Решение исходной задачи можно записать так:
Значение целевой функции в данной точке:
Пример 2. Найти оптимальный план задачи линейного программирования:
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственные переменные, а в целевую функцию добавляем эти переменные, умноженные на −M, где M, очень большое число:
Матрица коэффициентов 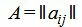системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
Базисные векторы x4, x5, x6, следовательно, все элементы в столбцах x4, x5, x6, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 4 со строкой 1, умноженной на -1. Обнулим все элементы столбца x5, кроме ведущего элемента. Для этого сложим строку 5 со строкой 2, умноженной на -1. Обнулим все элементы столбца x6, кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
В строке 5 элементы, соответствующие переменным x1, x2, x3, x4, x5, x6 неотрицательны, а число находящийся в пересечении данной строки и столбца x0 отрицательнo. Тогда исходная задача не имеет опорного плана. Следовательно она неразрешима.
Задачи линейного программирования
Краткая теория
Линейное программирование — область математики, разрабатывающая
теорию и численные методы решения задач нахождения экстремума (максимума или
минимума) линейной функции многих переменных при наличии линейных ограничений,
т. е. равенств или неравенств, связывающих эти переменные.
Методы линейного программирования применяют к практическим задачам,
в которых:
- необходимо выбрать наилучшее решение (оптимальный план) из
множества возможных; - решение можно выразить как набор значений некоторых переменных
величин; - ограничения, накладываемые на допустимые решения специфическими
условиями задачи, формулируются в виде линейных уравнений или неравенств; - цель выражается в форме линейной функции основных переменных.
Значения целевой функции, позволяя сопоставлять различные решения, служат
критерием качества решения.
Для практического решения экономической задачи математическими
методами ее прежде всего следует записать с помощью математических выражений:
уравнений, неравенств и тому подобное, то есть составить
экономико-математическую модель. Исходя из отмеченных выше особенностей задач
линейного программирования, можно наметить следующую общую схему формирования
модели:
- выбор некоторого числа переменных величин, заданием числовых
значений которых однозначно определяется одно из возможных состояний
исследуемого явления; - выражение взаимосвязей, присущих исследуемому явлению, в виде
математических соотношений (уравнений, неравенств); эти соотношения образуют
систему ограничений задачи; - количественное выражение выбранного критерия оптимальности в
форме целевой функции; - математическая формулировка задачи как задачи отыскания
экстремума целевой функции при условии выполнения ограничений, накладываемых на
переменные.
Модель задачи линейного программирования может быть записана в
одной из приведенных ниже форм:
1. Общая или произвольная
форма записи задачи линейного программирования:
при ограничениях:
– произвольные
2. Симметричная или стандартная форма записи
задачи линейного программирования:
3. Каноническая или основная
форма записи задачи линейного программирования:
Указанные выше три формы записи ЗЛП эквивалентны в том смысле, что
каждая из них с помощью несложных преобразований может быть сведена к другой
форме, то есть если имеется способ нахождения оптимального решения задачи в
одной из указанных форм, то тем самым может быть определен оптимальный план
задачи в любой другой форме (говорят о стратегической эквивалентности задачи в
любой из форм).
Так, при необходимости задачу минимизации можно заменить задачей
максимизации, и наоборот.
Неравенство типа
путем умножения левых и правых частей на -1
можно превратить в неравенство типа
и наоборот. Ограничения-неравенства
преобразуются в ограничения-равенства путем прибавления (вычитания)
к левым частям дополнительных (балансовых) неотрицательных переменных
:
В случае необходимости ограничение-равенство
можно записать в виде системы неравенств:
Если в задаче линейного программирования какая-то переменная
не подчинена условию неотрицательности, ее
заменяют разностью двух других неотрицательных переменных
и
:
Способы решения задач линейного программирования подробно рассмотрены на соседних страницах сайта:
- графический метод
- симплексный метод
- транспортная задача
Примеры решения задач
Задача 1
Имеются
корма двух видов и силос. Их можно использовать для кормления скота в
количестве не более 50 и 80 кг соответственно. Стоимость 1 кг сена -12 ден.ед.,
а силоса -8 ден.ед. Составить кормовой рацион минимальной стоимости. Данные
приведены в таблице:
|
Питательные вещества |
Корма |
Минимальное содержание питательных веществ |
|
| Сено | Силос | ||
| Кормовые ед., кг | 0,5 | 0,3 | 30 |
| Протеин, г | 40 | 10 | 1000 |
| Кальций, г | 1,25 | 2,5 | 100 |
| Фосфор, г | 2 | 1 | 80 |
Решение
Через
и
обозначим количество сена и силоса
соответственно. Тогда целевая функция, выражающая стоимость рациона:
Ограничения:
Кроме
того, по смыслу задачи:
Получаем
следующую задачу линейного программирования:
Задача 2
Построить
экономико-математическую модель задачи и найти оптимальный план раскроя с точки
зрения минимизации отходов.
Куски
искусственной кожи по 60 дм разрезать на части по 20 дм, 25 дм и 30 дм так,
чтобы частей по 20 дм было не менее 6 штук, частей по 25 дм было не менее 10
штук и частей по 30 дм было не менее 4 штук.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Обозначим через
искомые величины количества заготовок из
кожи, раскраиваемых соответствующим
образом.
Тогда целевая функция экономико-математической
модели:
Экономико-математическая модель имеет следующие ограничения:
Кроме
того, по смыслу задачи:
Задача 3
Составить
экономико-математическую модель задачи линейного программирования.
Найти
оптимальное сочетание посевов трех культур: пшеницы, гречихи и картофеля.
Эффективность возделывания названных культур (в расчете на 1 га) характеризуется
показателями, значения которых приведены в таблице. Производственные ресурсы:
6000 га пашни, 5000 чел.-дней труда механизаторов, 9000 чел.-дней ручного
труда. Критерий оптимальности – максимум прибыли.
| Показатель | Пшеница | Гречиха | Картофель |
| Урожайность, ц | 20 | 10 | 100 |
|
Затраты механизаторов, чел.-дней |
0.5 | 1 | 5 |
|
Затраты ручного труда, чел.дней |
0.5 | 0.5 | 20 |
|
Прибыль от реализации 1 ц продукции, ден.ед. |
4 | 10 | 3 |
Решение
Через
и
обозначим количество собираемой пшеницы,
гречихи и картофеля соответственно.
Тогда
ограничение на количество пашни:
Ограничение
на затраты труда механизаторов:
Ограничения
на затраты ручного труда:
Кроме
того, по смыслу задачи:
Целевая
функция, выражающая получаемую от реализации прибыль:
Получаем
следующую экономико-математическую модель: