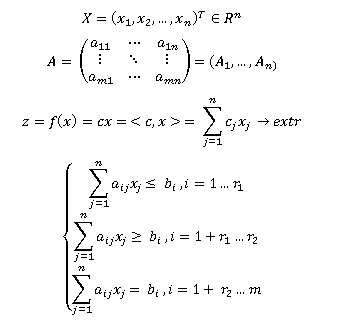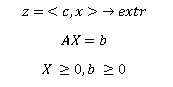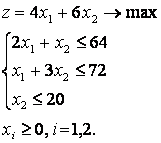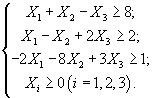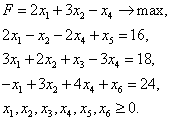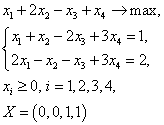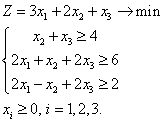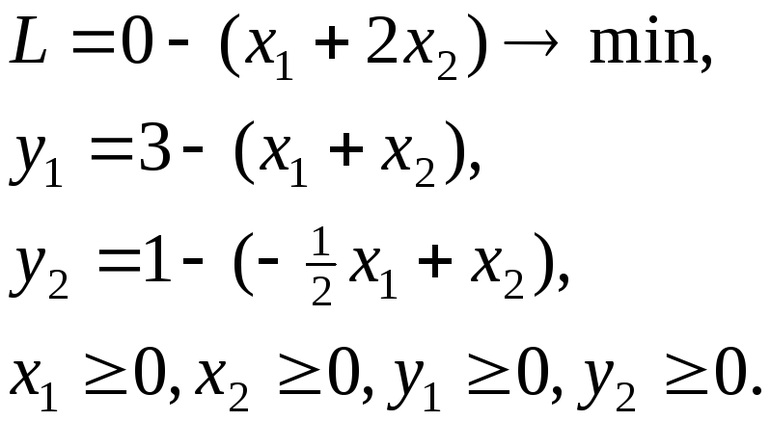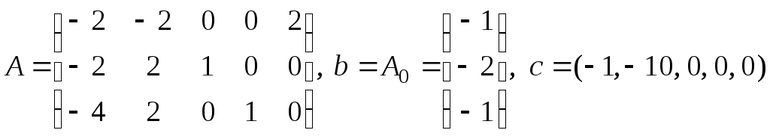Как составить математическую модель задачи симплекс методом

Подробный разбор симплекс-метода

Пролог

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение:

Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

Замечание:

Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

1. Неравенства с отрицательными умножаем на (-1).
2. Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
3. Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
4. Делаем замену переменных:

Замечание:

Будем нумеровать

по номеру неравенства, в которое мы его добавили.

Замечание:

≥0.

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение:

Точка

называется угловой точкой, если представление

возможно только при

.

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит

(т.е.

– не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

Определение:

Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.

§4. Симплекс-метод

Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.

Необходимые условия для применения симплекс-метода:

1. Задача должна иметь каноническую форму.
2. У задачи должен быть явно выделенный базис.

Определение:

Явно выделенным базисом будем называть вектора вида:

, т.е. только одна координата вектора ненулевая и равна 1.

Замечание:

Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.

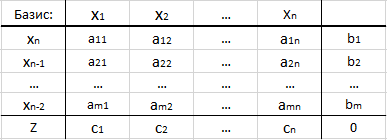
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:

• В первой строке указывают «наименование» всех переменных.
• В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
• В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
• Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
• Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.

Замечание:

Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.

Замечание:

Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.

Замечание:

Коэффициенты в строке функционала берутся со знаком “-”.

Алгоритм симплекс-метода:

1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:

• Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
• Если задача на максимум – выбираем минимальный отрицательный.

Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.

Замечание:

Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.

Определение:

Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.

2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:

• Вектор правых частей почленно делится на ведущий столбец
• Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)

Определение:

Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.

Замечание:

Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.

3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.

Определение:

Такой элемент называется ведущим элементом.

4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.

5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.

• Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
• Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка

Замечание:

Преобразование такого вида направлено на введение выбранной переменной в базис, т.е. представление ведущего столбца в виде базисного вектора.

6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.

§5. Интерпретация результата работы симплекс-метода

1. Оптимальность

Условие оптимальности полученного решения:

• Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
• Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).

2. Неограниченность функционала

Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:

При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.

Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.

3. Альтернативные решения

При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).

Алгебраический признак существования альтернативы:

После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.

Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.

Эпилог

Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.

Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.

Спасибо за внимание!

P.S.

Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.

Симплекс-метод, примеры решения задач

Здесь приведено ручное
(не апплетом) решение двух задач
симплекс-методом (аналогичным решению
апплетом) с подробными объяснениями
для того, чтобы понять алгоритм решения
задач симплекс-методом. Первая задача
содержит знаки неравенства только »
≤ » (задача с начальным базисом),
вторая может содержить знаки » ≥ «,
» ≤ » или » = » (задача с
искусственным базисом), они решаются
по разному.

Симплекс-метод, решение задачи с начальным базисом

1)Симплекс-метод
для задачи с
начальным базисом (все знаки
неравенств-ограничений » ≤ «).

Запишем задачу в
канонической
форме, т.е. ограничения-неравенства
перепишем в виде равенств, добавляя
балансовые
переменные:

Эта система является
системой с базисом (базис s₁,
s₂,
s₃,
каждая из них входит только в одно
уравнение системы с коэффициентом 1),
x₁
и x₂
— свободные переменные. Задачи, при
решении которых применяется симплекс-метод,
должны обладать следующими двумя
свойствами:
-система ограничений
должна быть системой уравнений с
базисом;
-свободные члены всех уравнений
в системе должны быть неотрицательны.

Полученная система
— система с базисом и ее свободные члены
неотрицательны, поэтому можно применить
симплекс-метод.
Составим первую симплекс-таблицу
(Итерация 0) для решения задачи на
симплекс-метод,
т.е. таблицу коэффициентов целевой
функции и системы уравнений при
соответствующих переменных. Здесь «БП»
означает столбец базисных переменных,
«Решение» — столбец правых частей
уравнений системы. Решение не является
оптимальным, т.к. в z – строке есть
отрицательные коэффициенты.

симплекс-метод итерация
0

БП	x1	x2	s1	s2	s3	Решение	Отношение
z	-4	-6	0	0	0	0	—
s1	2	1	1	0	0	64	64/1=64
s2	1	3	0	1	0	72	72/3=24
s3	0	1	0	0	1	20	20/1=20

Для улучшения решения
перейдем к следующей итерации
симплекс-метода,
получим следующую симплекс-таблицу.
Для этого надо выбрать разрешающий
столбец, т.е.
переменную, которая войдет в базис на
следующей итерации симплекс-метода. Он
выбирается по наибольшему по модулю
отрицательному коэффициенту в z-строке
(в задаче на максимум) – в начальной
итерации симплекс-метода это столбец
x₂
(коэффициент -6).

Затем выбирается
разрешающая
строка, т.е.
переменная, которая выйдет из базиса
на следующей итерации симплекс-метода.
Она выбирается по наименьшему отношению
столбца «Решение» к соответствующим
положительным элементам разрешающего
столбца (столбец «Отношение») – в
начальной итерации это строка s₃
(коэффициент 20).

Разрешающий элемент
находится на пересечении разрешающего
столбца и разрешающей строки, его ячейка
выделена цветом, он равен 1. Следовательно,
на следующей итерации симплекс-метода
переменная x₂
заменит в базисе s₁.
Заметим, что в z-строке отношение не
ищется, там ставится прочерк » — «.
В случае если есть одинаковые минимальные
отношения, то выбирается любое из них.
Если в разрешающем
столбце все коэффициенты меньше или
равны 0, то решение задачи бесконечно.

Заполним следующую
таблицу «Итерация 1». Её мы получим из
таблицы «Итерация 0». Цель дальнейших
преобразований — превратить разрешающий
столбец х₂
в единичный (с единицей вместо разрешающего
элемента и нулями вместо остальных
элементов).

1)Вычисление строки
х₂
таблицы «Итерация 1». Сначала делим
все члены разрешающей строки s₃
таблицы «Итерация 0» на разрешающий
элемент (он равен 1 в данном случае) этой
таблицы, получим строку x₂
в таблице «Итерации 1». Т.к. разрешающий
элемент в данном случае равен 1, то строка
s₃
таблицы «Итерация 0» будет совпадать
со строкой х₂
таблицы «Итерация 1». Строку x₂
таблицы «Итерации 1» мы получили 0
1
0 0 1 20, остальные строки таблицы «Итерация
1» будут получены из этой строки и
строк таблицы «Итерация 0» следующим
образом:

2) Вычисление z-строки
таблицы «Итерация 1». На месте -6
в первой строке (z-строке) в столбце х₂
таблицы «Итерация 0» должен быть 0
в первой строке таблицы «Итерация
1». Для этого все элементы строки х₂
таблицы «Итерация 1» 0 1
0 0 1 20 умножим на 6, получим 0 6
0 0 6 120 и сложим эту строку с первой строкой
(z — строкой) таблицы «Итерация 0» -4
-6
0 0 0 0, получим -4 0
0 0 6 120. В столбце x₂
появился ноль
0, цель
достигнута. Элементы разрешающего
столбца х₂
выделены красным цветом.

3) Вычисление строки
s₁
таблицы «Итерация 1». На месте 1
в s₁
строке таблицы «Итерация 0» должен
быть 0 в таблице «Итерация 1». Для
этого все элементы строки х₂
таблицы «Итерация 1» 0 1
0 0 1 20 умножим на -1, получим 0 -1
0 0 -1 -20 и сложим эту строку с s₁
— строкой таблицы «Итерация 0» 2 1
1 0 0 64, получим строку 2 0
1 0 -1 44. В столбце х₂
получен необходимый 0.

4) Вычисление строки
s₂
таблицы «Итерация 1». На месте 3
в s₂
строке таблицы «Итерация 0» должен
быть 0 в таблице «Итерация 1». Для
этого все элементы строки х₂
таблицы «Итерация 1» 0 1
0 0 1 20 умножим на -3, получим 0 -3
0 0 -3 -60 и сложим эту строку с s₁
— строкой таблицы «Итерация 0» 1 3 0
1 0 72, получим строку 1 0
0 1 -3 12. В столбце х₂
получен нужный 0. Столбец х₂
в таблице «Итерация 1» стал единичным,
он содержит одну 1 и остальные 0.

Строки таблицы
«Итерация 1» получаем по следующему
правилу:

Новая строка = Старая
строка – (Коэффициент разрешающего
столбца старой строки)*(Новая разрешающая
строка).

Например для z-строки
имеем:

Старая z-строка  
                 
                 
       (-4   -6
0 0 0 0)
-(-6)*Новая разрешающая
строка               
 -(0 -6
0 0 -6
-120)
=Новая z-строка
(-4 0
0 0 6 120).

Для следующих таблиц
пересчет элементов таблицы делается
аналогично, поэтому мы его опускаем.

симплекс-метод итерация
1

БП	x1	x2	s1	s2	s3	Решение	Отношение
z	-4	0	0	0	6	120	—
s1	2	0	1	0	-1	44	44/2=22
s2	1	0	0	1	-3	12	12/1=12
x2	0	1	0	0	1	20	—

Разрешающий столбец
х₁,
разрешающая строка s₂,
s₂
выходит из базиса, х₁
входит в базис. Совершенно аналогично
получим остальные симплекс-таблицы,
пока не будет получена таблица со всеми
положительными коэффициентами в
z-строке. Это признак оптимальной таблицы.

симплекс-метод итерация
2

БП	x1	x2	s1	s2	s3	Решение	Отношение
z	0	0	0	4	-6	168	—
s1	0	0	1	-2	5	20	20/5=4
x1	1	0	0	1	-3	12	—
x2	0	1	0	0	1	20	20/1=20

Разрешающий столбец
s₃,
разрешающая строка s₁,
s₁
выходит из базиса, s₃
входит в базис.

симплекс-метод итерация
3

БП	x1	x2	s1	s2	s3	Решение	Отношение
z	0	0	6/5	8/5	0	192	—
s3	0	0	1/5	-2/5	1	4	—
x1	1	0	3/5	-1/5	0	24	—
x2	0	1	-1/5	2/5	0	16	—

В z-строке все
коэффициенты неотрицательны, следовательно,
получено оптимальное решение x₁
= 24, x₂
= 16, z_max
= 192.

Соседние файлы в папке типовое решение задач

• #
• #
• #
• #
• #

Решение задач линейного программирования
симплексным методом

Если вы уже разобрались с графическим методом решения задач линейного программирования, самое время переходить к симплекс-методу. В отличие от первого, он практически не имеет ограничений на задачу (любое количество переменных, разные знаки и т.п.) и модифицируется в зависимости от типа задачи (например, М-метод или метод искусственного базиса).

При решении задачи симплекс методом вычисления обычно ведутся (для компактности и наглядности) в таблицах (табличный симплекс-метод), причем последняя таблица с оптимальным решением содержит важную дополнительную информацию: решение двойственной задачи, остатки ресурсов, сведения о дефицитных ресурсах и т.п., которая позволяет провести экономический анализ задачи линейного программирования (см. ниже пример 3).

Примеры решений задач симплекс-методом выложены бесплатно для вашего удобства — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении подобных заданий, перейдите в раздел: решение линейного программирования на заказ.

Решение задач симплекс-методом: примеры онлайн

Задача 1. Компания производит полки для ванных комнат двух размеров — А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В — 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В — 30 мин; машину можно использовать 160 час в неделю. Если прибыль от продажи полок типа А составляет 3 денежных единицы, а от полок типа В — 4 ден. ед., то сколько полок каждого типа следует выпускать в неделю?

Задача 2. Решить задачу линейного программирования симплекс-методом.

Задача 3. Предприятие производит 3 вида продукции: А1, А2, А3, используя сырьё двух типов. Известны затраты сырья каждого типа на единицу продукции, запасы сырья на планируемый период, а также прибыль от единицы продукции каждого вида.

Сырьё	Затраты сырья на единицу продукции	Запас сырья
	А1	А2	А3
I	3,5	7	4,2	1400
II	4	5	8	2000
Прибыль от ед. прод.	1	3	3

1. Сколько изделий каждого вида необходимо произвести, чтобы получить максимум прибыли?
2. Определить статус каждого вида сырья и его удельную ценность.
3. Определить максимальный интервал изменения запасов каждого вида сырья, в пределах которого структура оптимального плана, т.е. номенклатура выпуска, не изменится.
4. Определить количество выпускаемой продукции и прибыль от выпуска при увеличении запаса одного из дефицитных видов сырья до максимально возможной (в пределах данной номенклатуры выпуска) величины.
5. Определить интервалы изменения прибыли от единицы продукции каждого вида, при которых полученный оптимальный план не изменится.

Задача 4. Решить задачу линейного программирования симплексным методом:

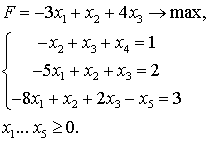
Задача 5. Решить задачу линейного программирования симплекс-методом:

Задача 6. Решить задачу симплекс-методом, рассматривая в качестве начального опорного плана, план, приведенный в условии:

Задача 7. Решить задачу модифицированным симплекс-методом.
Для производства двух видов изделий А и Б используется три типа технологического оборудования. На производство единицы изделия А оборудование первого типа используется а1=4 часов, оборудование второго типа а2=8 часов, а оборудование третьего типа а3=9 часов. На производство единицы изделия Б оборудование первого типа используется б1=7 часов, оборудование второго типа б2=3 часов, а оборудование третьего типа б3=5 часов.
На изготовление этих изделий оборудование первого типа может работать не более чем t1=49 часов, оборудование второго типа не более чем t2=51 часов, оборудование третьего типа не более чем t3=45 часов.
Прибыль от реализации единицы готового изделия А составляет АЛЬФА=6 рублей, а изделия Б – БЕТТА=5 рублей.
Составить план производства изделий А и Б, обеспечивающий максимальную прибыль от их реализации.

Задача 8. Найти оптимальное решение двойственным симплекс-методом

Понятие и алгоритм

Под симплексным методом понимается последовательный переход от одного базисного нахождения системы решений к другому. Эта перестановка повторяется до тех пор, пока переменная величина цели не достигнет своего наибольшего или наименьшего значения. Такой подход является универсальным, его можно использовать для решения любой задачи последовательного программирования.

Метод был разработан в 1947 году математиком из США Бернардом Данцигом. Предложенный способ оказался весьма эффективным для решения задач, связанных с оптимизацией использования ограниченных ресурсов. То есть он позволяет оценить и откорректировать параметры системы, а также получить качественные аналитические результаты.

Существует два подхода решения задачи:

• графический;
• симплексный.

Первый можно использовать для оптимизационного решения двухмерных задач. Например, существует два производственных цикла по сборке ящиков. Выпуск товара характеризуется ограничением в поставках древесины и временем формовки изделия. Для одного необходимо 30 досок, а для другого — 40. Поставщики доставляют в неделю 2 тыс. единиц материала. Первый ящик собирается за 15 минут, а второй — за 30. Нужно определить, какое количество ящиков необходимо производить за неделю на первом конвейере и на втором. При этом первое изделие приносит 10 рублей прибыли, а второе — пять. Время изготовление ограничено 160 часами.

Решение заключается в принятии за Х1 и Х2 количество выпущенных ящиков. Затем — в нахождении максимальной еженедельной прибыли и описании процесса ограничения в виде уравнения.

Это типовая двухмерная задача, условия неотрицательности которой определяются границами прямых: 30*Х1 + 4 0*Х 2 ≤ 2000 (для досок) и 20*Х 1 ≤ 50*Х 2 = 1600 (для сборки). Отложив по оси ординат Х1, а Х2 по абсцисс, и указав на них точки соответствующие уравнениям, можно будет подобрать оптимальное решение для использования сырья и времени.

Графический метод удобно применять для двухмерных задач, но его невозможно использовать при решениях, связанных с размерностью, превышающей три. При этом во всех алгоритмах оптимальный результат принимается допустимым базисному. Симплекс-метод же является вычислительной процедурой, использующей принятое положение, описываемое в алгебраической форме.

Симплекс-метод при базисном решении

Впервые способ был изложен Данцигом в книге «Линейное программирование, его обобщения и применения», изданной на русском языке в 1966 году. Эта теория основывалась на вычислительной процедуре и представлялась в виде стандартных алгебраических форм. Основное направление метода заключается в указании способа нахождения опорного решения, переходе к другому, более оптимальному расчёту и определении критериев, позволяющих остановить перебор опорных вариантов.

Алгоритм решения задачи линейного программирования симплекс методом следующий:

1. Свести поставленную задачу к канонической форме путём переноса свободных членов в правую часть и ввода дополнительных переменных. В случае отрицательных переменных неравенство умножается на -1. Если в записи используется знак «меньше или равно», переменная используется положительная, в противном случае — отрицательная.
2. В зависимости от количества вводимых значений все переменные принимаются за основные. Их необходимо выразить через неосновные и перейти к базовому решению.
3. Через неосновные переменные выражается функция цели.
4. Если при решении отыскивается ответ с максимумом или минимумом линейной формы и все неосновные переменные получаются только положительными, то задача считается выполненной.
5. Если найденный максимум (минимум) линейной формы в функции имеет одну или несколько неосновных переменных с отрицательными коэффициентами, необходимо перейти к новому базисному решению.
6. Из переменных, входящих в форму с отрицательными или положительными коэффициентами, выбирается наибольшая (по модулю) и переводится в основные.

Другими словами, указывается оптимальное опорное решение, способ перехода от одного нахождения ответа к другому, варианты улучшения расчётов. После нахождения первоначального решения с «единичным базисом» вычисляется оценка разложения векторов по базису и заполняется симплексная таблица.

В тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи, используют метод с искусственным базисом. Это симплекс-метод с так называемой М-задачей (ММЭ), решаемый способом добавления к левой части системы уравнений искусственных единичных векторов. При этом новая матрица должна содержать группу единичных линейно-независимых векторов.

Двухфазный способ

Двойственный метод используется при анализе задач линейного программирования, записанного в форме основной задачи. При этом среди векторов, m уравнений, составленных из коэффициентов, должны быть единичные. Такой метод можно использовать, когда свободные члены уравнений являются любыми числами.

Например, существует ограниченность, описываемая функцией:

F = C 1 X 1+ C 2 X 2+…+ CnXn. Используется условие, что Х1Р1+Х2Р2+…+Х(m +1) P (m +1)+ +… XnPn = Р0, где Х j больше либо равно 0 (j =1, n). Принимается, что среди чисел bi (i =1, m) имеются отрицательные.

Решением будет выражение: х= (b1; b2;…; bm ;0;…;0), однако этот ответ не будет разрешать задание, так как к нему могут относиться и отрицательные числа. Так как векторы Р1, Р2… Рм единичные, то каждый из них можно описать линейной областью, состоящей из них же. При этом коэффициентами разложения векторов Рj по области будут числа: Xij = aij (i =1, m; j =1, n) по модулю.

Выражение х= ( b1; b2;…; bm ;0;…;0) определяется базисом. Называют его псевдоплан. Считается, что если дельта j больше либо равна нулю, то для любого: j ( j =1, n ) по модулю. В то же время если в псевдоплане с находимым базисом существует хотя бы одно отрицательное число, то тогда задача вообще не будет иметь планов. Но когда для этих отрицательных чисел верно, что аij меньше нуля, то можно будет перейти к новому псевдоплану.

Объяснение псевдоплана помогает построить алгоритм двойственного метода. Если взять за основу х = (b1; b2;…; bm ;0;…;0) и представить это выражение псевдопланом, то, учитывая исходные данные, можно составить симплекс-таблицу. В ней часть элементов будет отрицательная. Так как дельта j должна быть больше либо равна нулю, то при отсутствии таких чисел в таблице уже будет записан оптимальный план. В обратном случае выбирается по модулю наибольшее из чисел с минусом.

Принцип решения задачи включает следующее:

• нахождение псевдоплана;
• проверка его на оптимальность;
• выбор разрешающей строки путём нахождения абсолютной величины отрицательного числа, отношения элементов (m+1) и соответствующей им строке;
• нахождение нового псевдоплана.

Если анализ оптимален, считается, что найдено верное решение. В другом случае устанавливается неразрешимость задачи либо составляется новый псевдоплан. Делается это в результате пересчёта табличных данных, например, методом Жордана-Гаусса.

Пример задачи

Использование метода линейного программирования распространено в решениях транспортных задач. Он помогает в целевых расчётах и нужен для минимизации затрат в условиях ограниченной грузоподъёмности и времени обслуживания заказчиков.

Задачи линейного программирования (ЗЛП) позволяют выбрать оптимальную загрузку при перемещении какого-либо товара из одних мест в другие. Во вводных данных указывается число пунктов отправления (м) и количество мест назначения (n). Первые обозначаются как А1, А2…Ам, а вторые – В1, В2…Вn. За аi принимается объём продукции на складе, а bi – потребность. Затраты на перевозку с i пункта в j обозначаются Сij.

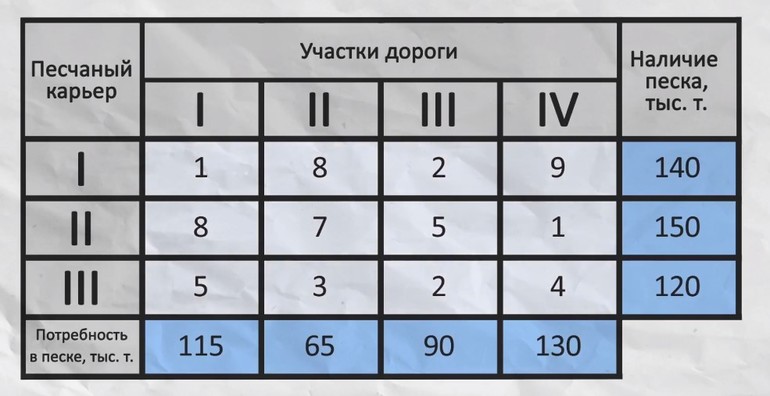
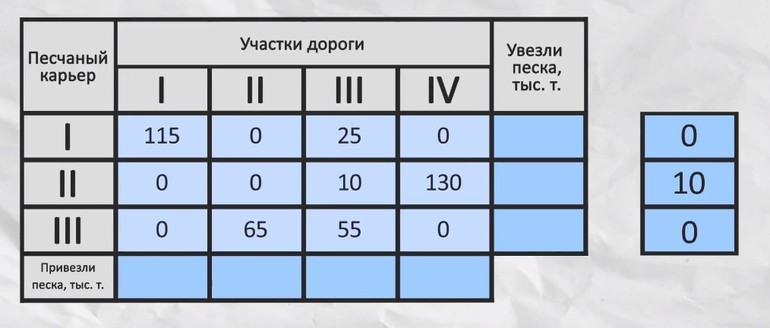
Главная задача — составить план таким образом, чтобы общая стоимость была минимальна. Пусть дано четыре песчаных карьера, с которых необходимо поставить песок на четыре склада. При этом осуществляться перевозки должны за определённую стоимость. Составляем таблицу.

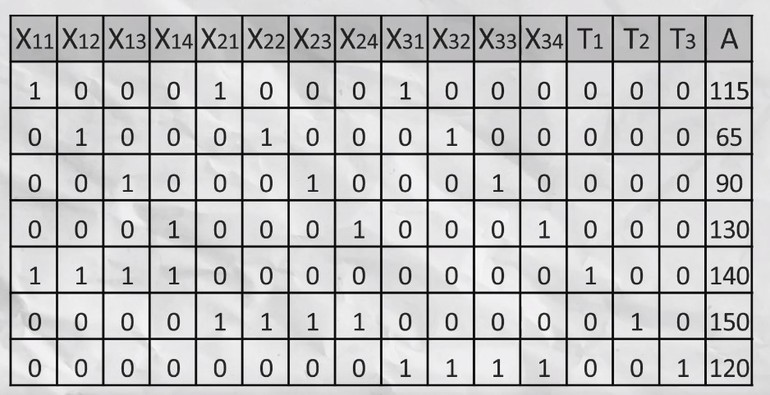
Записываем уравнение ограничения. Сумма всего перевезённого песка с первого карьера должна быть меньше или равна 140. Поэтому можно записать: x11+x12+x12+x14+T1 = 140, где Т1 переменная для хранения остатка. Сумма ограничений будет записана как х11+х21+х31 =115. Аналогичные уравнения составляют и для оставшихся карьеров.

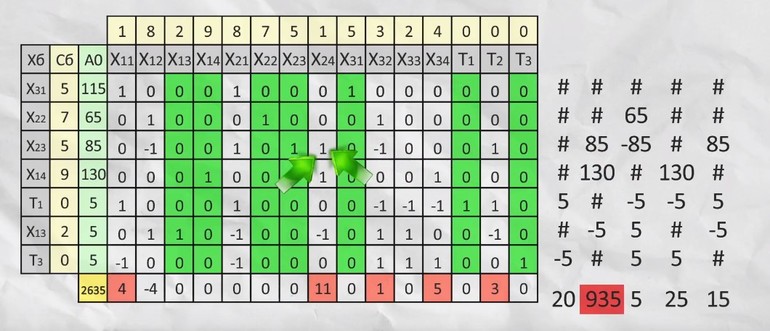
Теперь формируют матрицу, на основании которой с помощью свойства матриц ищется единичный базис. Например, вычесть из одной строки другую. Все отрицательные значения последнего столбца убирают. Для этого из каждой строки вычитают наименьшее значение, а последнее отрицательное число умножают на -1. Теперь составляют подробную симплекс-таблицу, где:

• A0 – последний столбец из матрицы;
• Сб – стоимость перевозок;
• Х11, Т3 – данные из полученной матрица.

В последней строчке прямоугольника проставляют сумму произведений Сб на этот столбец и вычитают значение суммы перемножения Сб с А0. Делают дополнительное вычисление. Для каждой строки А0 делят на выделенное число, ищут наименьший результат и умножают его на положительные числа из последней строки.

Наибольшее число определяется пересечением ранее выбранных значений, на базе которых создают новый базис. После в соответствии с единичными базисами меняют Сб и Хб. Операцию повторяют до тех пор, пока не исчезнут все положительные числа из последней строки. Заполняют новую таблицу.

Расчёт в Excel

Для включения пакета анализа в программе необходимо перейти в раздел «Параметры» и выбрать строчку «Перейти». В новом окне найти строчку «Пакет анализа», кликнуть по ней и нажать кнопку ОК.

Затем понадобится загрузить и открыть шаблон для проверки в Excel. Используя манипулятор типа «мышь» или клавиатуру, выбрать ячейку G4 и выполнить команду «Сервис/Поиск решения». Далее указать исходные данные, а после нажать кнопку «Выполнить».

Полученное решение можно представить в форме отчёта, содержащего:

1. Результаты – содержит информацию об исходных и конечных значениях целевой и влияющих ячеек, дополнительные сведения об ограничениях.
2. Устойчивость — отчёт, включающий данные о чувствительности решения к малым изменениям.
3. Пределы – включают исходные и конечные значения, а также верхние и нижние границы значений, которые принимают влияющие ячейки при введённых ограничениях.

Онлайн-сервис для чайников

Метод решения относится к высшей математике, поэтому в нём довольно трудно разобраться даже подготовленному человеку, не говоря уже о чайнике. Существует некоторое количество сайтов с подробным онлайн-решением методом симплекса. На таких сервисах предлагается ввести количество переменных и строк (ограничений). А далее просто заполнить симплекс-таблицу и нажать расчёт. Причём при необходимости вводимые данные можно править, тем самым видеть, как изменяется результат от изменения исходной информации.

Удобным является ещё и то, что обычно на сайтах предлагается создать шаблон решения в Excel или Maple. Решаться любая задача будет почти мгновенно. Подробно можно выполнить расчёт онлайн-калькулятор по методу симплекса на следующих сайтах:

1. «Семестр» (semestr.ru).
2. «Мир математики» (matworld.ru).
3. «Высшая математика» (math-pr.com).
4. «Матзона» (mathzone.ru).
5. «Контрольная работа» (kontrolnaya-rabota.ru).

Выполнить расчёт с помощью онлайн-сервисов сможет любой. При этом вероятность ошибки в ответе стремится к нулю. Тем более что для решения задачи даже необязательно знать принцип симплекс-метода.