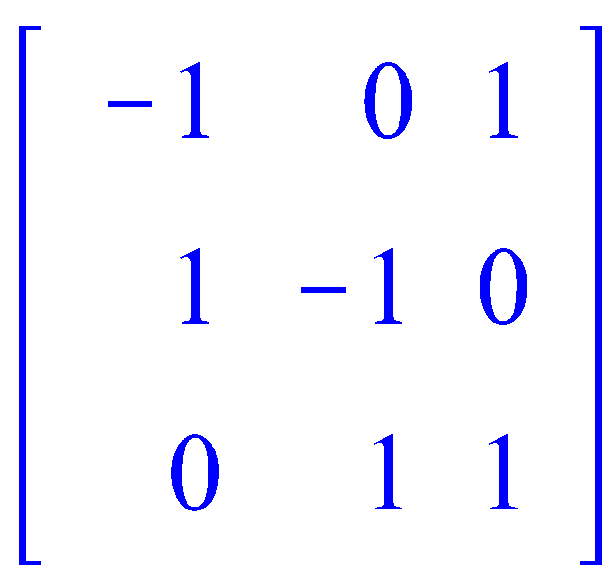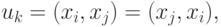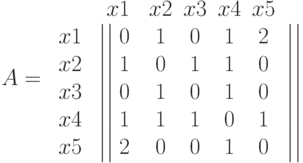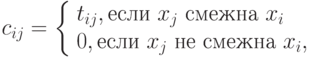Как составить матрицу инцидентности по матрице смежности - Исправление недочетов и поиск решений вместе с Examum.ru

Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор

В этой статье:

Матрица смежности

Матрица инцидентности

Список смежности (инцидентности)

Взвешенный граф (коротко)

Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.

Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).

Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).

Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.

Матрица смежности

Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.

Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.

Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.

Каждая ячейка матрицы равна либо 1, либо 0;

Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.

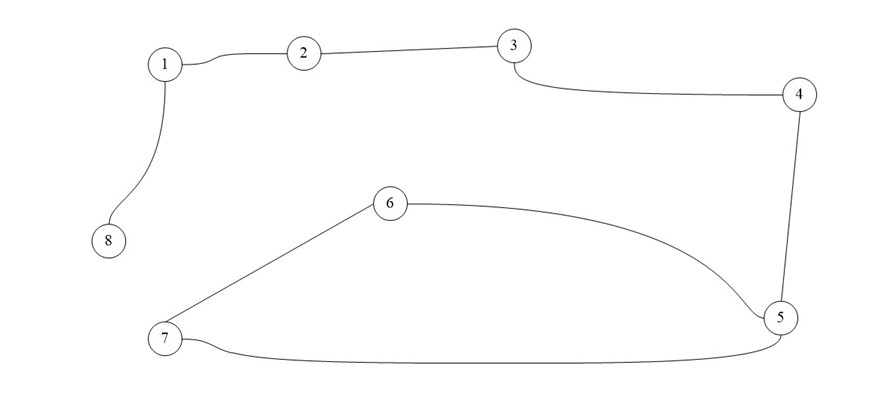
Для практического примера возьмем самый обыкновенный неориентированный граф:

А теперь представим его в виде матрицы:

Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.

С одной стороны объем памяти будет:

Но используя вышеописанный подход получается:

Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.

Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.

Если мы используем ориентированный граф, то кое-что меняется.

Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.

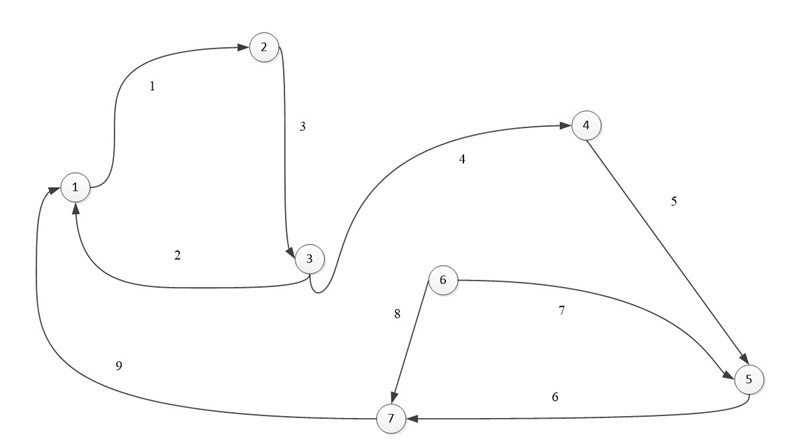
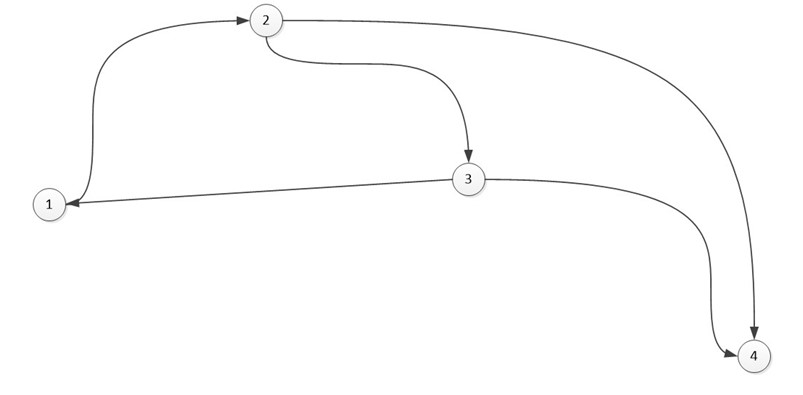
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:

В виде матрицы:

Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.

Объем памяти:

Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.

Используя петли мы должны запомнить, что в неориентированном графе петля учитывается дважды, а в ориентированном — единожды.

Матрица инцидентности

Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.

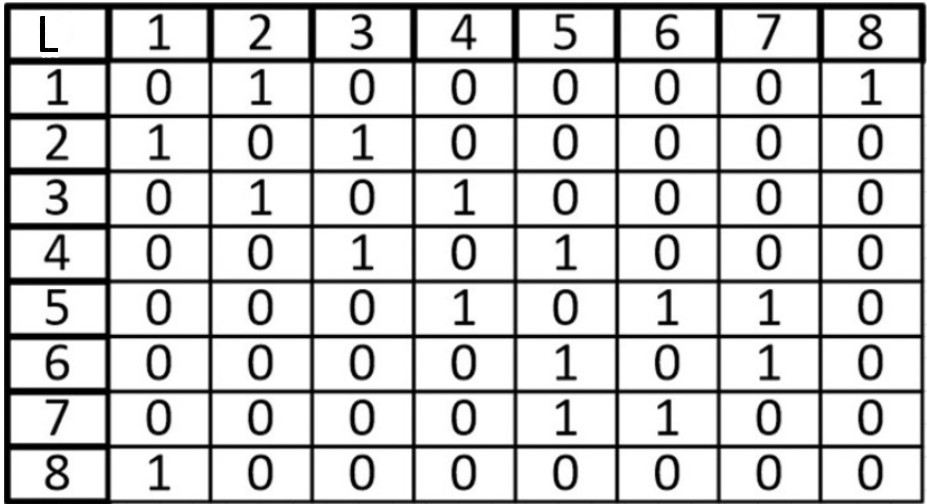
Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.

Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.

Сразу же иллюстрируем данное правило:

В виде матрицы:

Сумма элементов i-ой строки равна степени вершины.

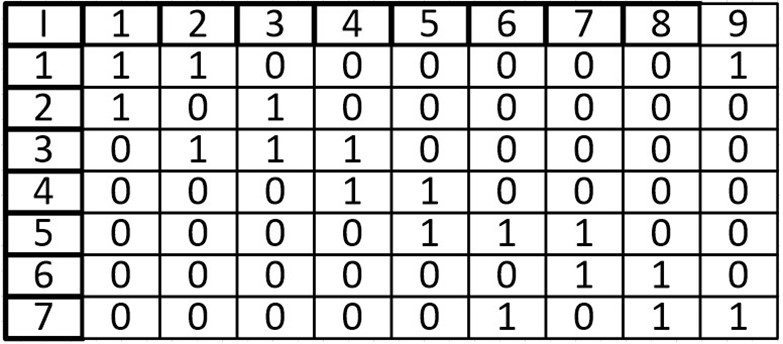
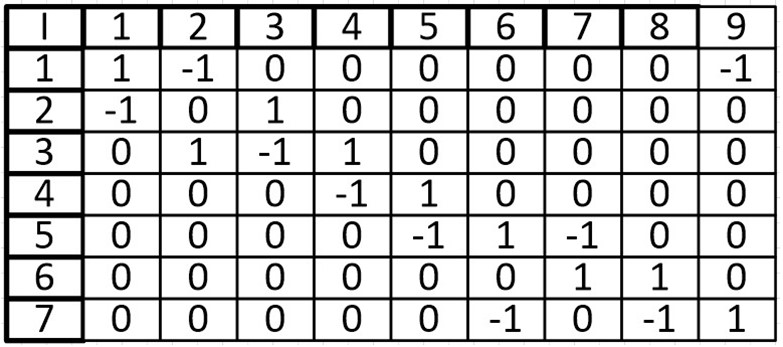
При ориентированным графе, ячейка I (i, j) равна 1, если вершина V (i) начало дуги E(j) и ячейка I (i, j) равна -1 если вершина V (i) конец дуги E (j), иначе ставится 0.

Ориентированный граф:

В виде матрицы:

Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.

При суммировании строки, ячейки со значением -1, могут складываться только с ячейками, также имеющими значение -1, то же касается и 1, мы можем узнать степень входа и степень выхода из вершины. Допустим при сложении первой вершины, мы узнаем, что из нее исходит 1 ребро и входят два других ребра. Это является еще одной особенностью (при том очень удобной) данной матрицы.

Объем памяти:

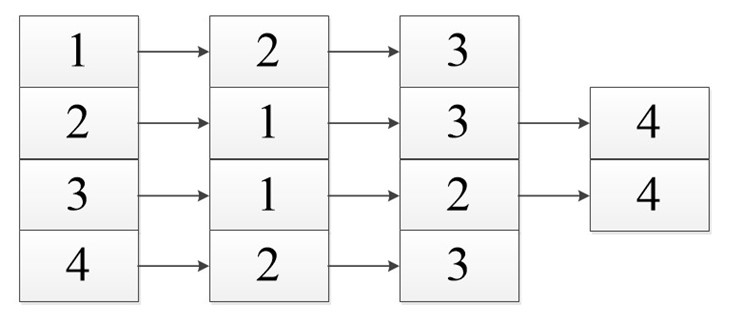
Список смежности (инцидентности)

Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.

В виде списка это будет выглядеть так:

Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.

Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:

Объем памяти:

Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).

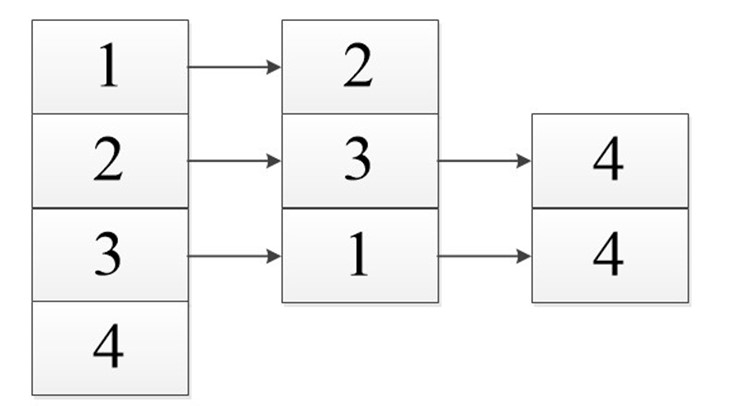
В виде списка:

Сумма длин всех списков:

Объем памяти:

Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.

К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.

Взвешенность графа

Взвешенный граф — это граф, в котором вместо 1 обозначающее наличие связи между вершинами или связи между вершиной и ребром, хранится вес ребра, то есть определённое число с которым мы будем проводить различные действия.

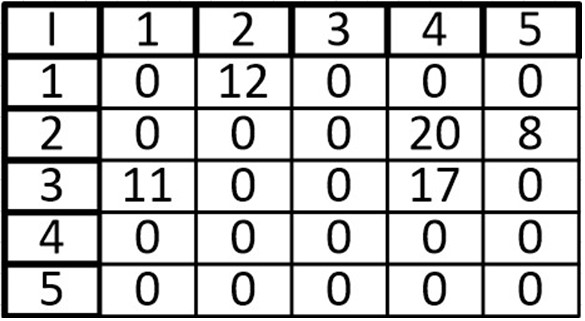
К примеру, возьмем граф с весами на ребрах:

И сделаем матрицу смежности:

В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.

Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.

Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.

Если заметили ошибку или есть предложения пишите в комментарии.

Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.

На каком языке программирования проводить операции с графами

21.28%
Использовать оба
10

Проголосовали 47 пользователей.

Воздержались 8 пользователей.

Источник

#include <iostream>
#include <fstream>
#include <string>
#include <iomanip>
using namespace std;

int** matrix(string fileName, int& N, int& M)
{
    ifstream in(fileName);
    if (in.is_open())
    {
        int i, j;
        in >> N >> M;
        int** a = new int* [N];
        for (i = 0; i < N; i++)
        {
            a[i] = new int[M];
            for (j = 0; j < M; j++)
                in >> a[i][j];
        }
        cout << endl;
        in.close();
        return a;
    }
    else
    {
        cout << "Unable to open file text.txt";
        return nullptr;
    }
}
int** matrix2(string fileName, int& N, int& M)
{
    ifstream in(fileName);
    if (in.is_open())
    {
        int i, j;
        in >> N;
        int M = 0;
        int** a = new int* [N];
        for (i = 0; i < N; i++)
        {
            a[i] = new int[N];
            for (j = 0; j < N; j++)
                in >> a[i][j];
            M += a[i][j];
        }
        M /= 2;
        int I[N][M];
        int C = 0;
        for (int i = 0; i < N; i++)
            for (int j = i + 1; j < N; j++)
                if (a[i][j]) {
                    I[i][C] = 1;
                    I[j][C++] = 1;
                }
        cout << endl;
        in.close();
        return a;
    }
    else
    {
        cout << "Unable to open file text.txt";
        return nullptr;
    }
}
void printMatrix(int** a, int N, int M)
{
    int i, j;
    for (i = 0; i < N; i++)
    {
        for (j = 0; j < M; j++)
            cout << setw(5) << a[i][j];
        cout << endl;
    }
}

int main()
{
    int N = 0, M = 0;
    int** a = matrix("text.txt", N, M);
    if (a)
    {
        printMatrix(a, N, M);
    }
    int** b = matrix2("text2.txt", N, M);
    if (b)
    {
        printMatrix(a, N, M);
    }

    system("pause");
    return 0;
}

задан 27 апр 2021 в 17:33

Имеется матрица смежности A[N][N]

Считаете количество единиц в ней (это можно сделать при вводе), делите пополам, получаете M — количество рёбер (я подразумеваю неориентированный граф.)

int M = 0;
...
  in >> a[i][j];
  M += a[i][j];
...
M /= 2;

Создаёте матрицу I[N][M] — т.е. c M столбцами, заполненную нулями

Устанавливаете C = 0 — номер текущего ребра

Обходите половину A выше диагонали (c j>i), если A[i][j]==1, то ставите две единицы в ячейки I[i][C] и I[j][C] и делаете C++

for (int i=0; i < n; i++)
   for (int j=i+1; j < n; j++)
       if (a[i][j])  {
          I[i][C] = 1;
          I[j][C++] = 1;
       }

ответ дан 28 апр 2021 в 1:35

MBoMBo

47.9k1 золотой знак17 серебряных знаков40 бронзовых знаков

Источник

Говорить о том, что ребро g и каждая из вершин u и y инцидентна g, стоит лишь в том случае, если g соединяет u и y. Уяснив это, перейдем к рассмотрению данного метода. Матрица инцидентности строиться по похожему, но не по тому же принципу, что и матрица смежности. Так если последняя имеет размер n×n, где n – число вершин, то матрица инцидентности – n×m, здесь n – число вершин графа, m – число ребер. То есть теперь чтобы задать значение какой-либо ячейки, нужно сопоставить не вершину с вершиной, а вершину с ребром.

В каждой ячейки матрицы инцидентности неориентированного графа стоит 0 или 1, а в случае ориентированного графа, вносятся 1, 0 или -1. То же самое, но наиболее структурировано:

1) Неориентированный граф

a. 1 – вершина инцидентна ребру

b. 0 – вершина не инцидентна ребру

2) Ориентированный граф

a. 1 – вершина инцидентна ребру, и является его началом

b. 0 – вершина не инцидентна ребру

c. -1 – вершина инцидентна ребру, и является его концом

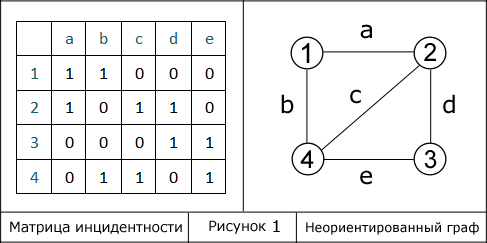
Построим матрицу инцидентности сначала для неориентированного графа, а затем для орграфа.

Ребра обозначены буквами от a до e, вершины – цифрами. Все ребра графа не направленны, поэтому матрица инцидентности заполнена положительными значениями.

Для орграфа графа матрица имеет немного другой вид. В каждую из ее ячеек внесено одно из трех значений. Обратите внимание, что нули в двух этих матрицах (рис. 1 и 2) занимают одинаковые позиции, ведь в обоих случаях структура графа одна. Но некоторые положительные единицы сменились на отрицательные, например, в неориентированном графе ячейка (1, b) содержит 1, а в орграфе -1. Действительно, это уместно, т. к. в первом случае ребро b не направленное, а во втором – направленное, и, причем вершиной входа для него является вершина «1».

Каждый столбец отвечает за какое-либо одно ребро, поэтому граф, описанный при помощи матрицы инцидентности, всегда будет иметь следующий признак: любой из столбцов матрицы инцидентности содержит две единицы, либо 1 и -1 когда это ориентированное ребро, все остальное в нем – нули.

В программе матрица инцидентности задается, также как и матрица смежности, а именно при помощи двумерного массива. Его элементы могут быть инициализированы при объявлении, либо по мере выполнения программы.

( 2 оценки, среднее 5 из 5 )

Источник

Между
множествами вершин V
и рёбер Е
определено
отношение инцидентности.
Каждое ребро е
из Е
инцидентно ровно двум вершинам

и
,
которые оно соединяет. При этом вершина

и ребро е
(а также вершина

и ребро е)
называются инцидентными друг другу, а
вершины

и

называются смежными. Отношения
инцидентности между вершинами и рёбрами
графа можно задать с помощью матрицы
инцидентности (incidence
matrix)
I.
Число
строк этой матрицы равно числу вершин
графа, а число столбцов – числу рёбер.

Для
неориентированного
графа элемент матрицы
,
если вершина

инцидентна ребру е,
в противном случае
.

Для
ориентированного
графа элемент матрицы
,
если вершина

является концом дуги е
(т.е. дуга входит в вершину);
,
если вершина

является началом дуги е
(т.е.
дуга исходит из вершины);
,
если вершина

не инцидентна дуге е.

Рис.
5

Составим
матрицу инцидентности для орграфа с
рис. 5. По вертикали запишем вершины, по
горизонтали рёбра.

	AB	AC	BC	BE	DD	EC
A	1	1	0	0	0	0
B	-1	0	1	1	0	0
C	0	-1	-1	0	0	-1
D	0	0	0	0	-1	0
E	0	0	0	-1	0	1

Заметим,
что для вершины D
дуга DD
является петлёй, для неё значение
элемента матрицы инцидентности
принимается равным единице.

4. Графы в Maple

Операции
с графами в среде Maple
выполняются с помощью команд, находящихся
в пакетах networks
(сети) и GraphTheory
(теория графов). Вызовем первый пакет:

_>

:

1.
Зададим новый граф G
командой new
и добавим последовательность его вершин
командой addvertex:

Соединим
некоторые вершины командой connect,
запросим список названий рёбер (команда
edges)
и нарисуем граф:

Команда
connect
соединяет каждую вершину из первого
списка [1,3] с каждой вершиной из второго
списка [4,6]. По умолчанию наш граф является
неориентированным. Запросим список
полученных рёбер
командой
ends:

Убедимся
в том, что начало и конец рёбер не
определены:

На
команды «хвост» и «голова» ребра ответа
нет.

Зададим
матрицы смежности и инцидентности:

Убедитесь
в том, что матрицы выводятся правильно.

ЗАДАНИЕ
1. Придумать граф G1,
вершины задавать командой addvertex,
рёбра – командой addedge,
например: addedge([[1,2],[1,4],[2,3]],G1).
Определить начало и конец каждой дуги
с помощью команд tail
и head
(если ребро задаётся в квадратных
скобках, то это ориентированная дуга).
Вывести список дуг. Начертить граф.
Составить матрицы смежности и
инцидентности.

2.
Зададим полный
граф командой complete.
Полный граф означает, что все вершины
соединены между собой.

Матрица
смежности:

Матрица
инцидентности не выводится из-за большого
объёма:

Исключим
из графа некоторые рёбра (фигурные
скобки означают, что рёбра не ориентированы):

ЗАДАНИЕ
2. Задать полный граф с пятью вершинами,
определить его характеристики. Исключить
2 ребра, исследовать полученный граф.

3.
Ориентированный
граф. Зададим дуги графа с помощью
упорядоченных пар вершин, их поместим
в квадратные скобки.

Построим
другой ориентированный граф.

₂

ЗАДАНИЕ
3-1. Придумать и исследовать ориентированный
граф.

ЗАДАНИЕ
3-2. Объяснить действия следующих команд:

ЗАДАНИЕ
3-3. Построить и сравнить графы gg
и ggd,
описанные ниже. Объяснить действия
следующих команд:

Соседние файлы в папке ЛАБ MAPLE ИС

Источник

17. 2. Части графа

Граф $G^{/ }= (X^{/}, U^{/})$ является частью графа , если $X^{/} subset X$ и $U^{/} subset U$ , т.е. граф содержит все вершины и рёбра любой его части.

Часть, которая наряду с некоторым подмножеством рёбер графа содержит и все инцидентные им вершины, называется подграфом.

Часть, которая наряду с некоторым подмножеством рёбер графа содержит все вершины графа ( $X^{/} = X$ , $U^{/} subset U$ ), называется суграфом.

Исходный граф по отношению к его подграфу называют надграфом, а по отношению к суграфу — сверхграфом.

Совокупность всех рёбер графа, не принадлежащих его подграфу (вместе с инцидентными вершинами ), образует дополнение подграфа (рис. 17.12).

Рис.
17.12.
Граф и его составляющие: а) граф; б) часть графа; в) подграф; г) суграф

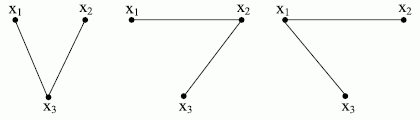
Связный неориентированный граф, не содержащий циклов, называют деревом.

Несвязный граф без циклов, отдельные компоненты связности которого являются деревьями, называют лесом.

Рис.
17.13.
Три различных дерева, которые можно построить на множестве из трёх вершин

Все приведённые деревья изоморфны друг другу, т.е. на трёх вершинах можно построить только одно неизоморфное дерево.

17. 3. Способы задания графов

Уже отмечалось, что произвольный граф можно задать совокупностью двух множеств: — множества вершин и — множества рёбер ( дуг ) графа или множества и отображения множества в .

Условные обозначения таких графов и , соответственно.

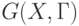
Другой удобной формой описания графов является представление их с помощью матриц, методика формальной разработки которых хорошо разработана.

Матрица смежности

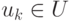
Из ранее сказанного известно, что две вершины $x_{i}$ и $х_{j} in X$ графа называются смежными, если они являются граничными вершинами ребра $u_{k} in U$ .

Отношение смежности на множестве вершин графа можно определить, представив каждое ребро как пару смежных вершин, т.е.

$u_{k} = (x_{i} , x_{j}) , k=l,2,..., q.$

Для неориентированных графов такие пары неупорядочены, так что

$u_{k} = (x_{i} , x_{j}) = (x_{j} , x_{i}),$

а для орграфов — упорядочены, причём, $x_{i}$ и $x_{j}$ означают, соответственно, начальную и конечную вершины дуги $u_{k}$ .
Петля при вершине $x_{j}$ в обоих случаях представляется неупорядоченной парой $(х_{i }, x_{j})$ .

Множество вершин вместе с определённым на нём отношением смежности полностью определяет граф.

Граф можно представить матрицей смежности.

Строки и столбцы матрицы соответствуют вершинам графа, а её (i j) элемент равен числу кратных рёбер, связывающих вершины $х_{i }$ и $x_{j}$ (или направленных от вершины $x_{i}$ к вершине $x_{j}$ для орграфов).

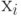
Например, для графа рис. 17.2, а, матрица смежности имеет вид

$A = begin{array}{ccccccc} & x1& x2& x3& x4& x5 &\ begin{array}{c} x1\ x2\ x3\ x4\ x5 end{array} & left| left| begin{array}{c} 0\1\0\1\2end{array} & begin{array}{c} 1\0\1\1\0end{array} & begin{array}{c} 0\1\0\1\0end{array} & begin{array}{c} 1\1\1\0\1end{array} & begin{array}{c} 2\0\0\1\0end{array} & left| left| begin{array}{c} \ \ \ \ \end{array} end{array}$

Матрица смежности неориентированного графа всегда симметрична, а орграфа — в общем случае несимметрична. Неориентированным рёбрам соответствуют пары ненулевых элементов, симметричных относительно главной диагонали матрицы, а петлям — ненулевые элементы главной диагонали.

В столбцах и строках, соответствующих изолированным вершинам, все элементы равны нулю. Элементы матрицы простого графа равны 0 или 1, причём, элементы главной диагонали равны 0.

Правильность составления матрицы легко проверить: для неориентированного графа сумма элементов в каждом i -том столбце или строке соответствует степени вершины 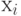$х_{i}$ . Если элементы матрицы $a_{ii},$ расположенные на главной диагонали, отличны от нуля, то это свидетельствует о наличии петель в вершине $x_{i}$ .

Для неориентированного графа матрица смежности симметрична относительно главной диагонали, так как $a_{ij} = a_{ji}$ .

При решении целого класса задач проектирования РЭС приходится оперировать матрицами, которые строятся аналогично матрицам смежности, но значения их элементов определяются мерой (весом), связанной с ребром ( дугой ) графа.

В САПР широко используют две разновидности таких матриц: матрицу весовых соотношений и матрицу длин.

Матрица весовых соотношений

Это квадратная матрица $С = с_{i j} _{n times n}$ , общий элемент которой

$c_{i j }= left{ begin{array}{l} t_{i j },text{если } x_{j}text{ смежна }x_{i}\ 0 , text{если }x_{j}text{ не смежна }x_{i} , end{array}$

где $t _{i j }$ — вес связи $(x_{i} , x_{j})$ .

Применение матриц весовых соотношений позволяет учитывать различные требования к сокращению длины тех или иных электрических соединений в конструкциях РЭС, условия тепловой и электромагнитной совместимости отдельных элементов схемы и другие.

Матрица длин

Это квадратная матрица 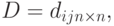$D = d_{i j } _{ntimes n},$ общий элемент которой

$d_{i j} = left{ begin{array}{l} l_{i j },text{ если }x_{i} text{ и }x_{j}text{ смежны};\ 0 ,text{ если }x_{i}text{ не смежна }x_{j}, end{array}$

где $l_{i j}$ — длина ребра $(X_{i} , x_{j})$ .

В евклидовой метрике расстояние между двумя точками на плоскости

$l_{ij }= sqrt{(s_i - s_j)^2 + (t_i - t_j)^2},$

где $s_{i} , t_{i}$ и $s_{j}, t_{j}$ — координаты вершин $x_{j}$ и $x_{j}$ , соответственно.

Это выражение неудобно для использования в машинных программах, так как извлечение квадратного корня на ЭВМ требует больших затрат времени. Поэтому часто пользуются линейной метрикой, тем более, что при решении многих конструкторских задач она вполне оправдана.

Пример. При проектировании многослойных печатных плат трассировка соединений ведётся в каждом из слоёв во взаимно перпендикулярных направлениях, в связи с чем длина электрических связей между элементами с координатами $(s_{i}, t_{i}) и (s_{j}, t_{j})$

$l_{ij} = s_{i} - s_{j} | + t_{i} - t_{j} .$

Линейная метрика оказывается непригодной для решения задач, в которых имеет место вычисление производных по координатам (оптимизация нелинейных функций).

В этом случае расстояние между двумя точками представляется в виде степенной функции:

$l_{i j} = (s_{i} - s_{j})^{k} + (t_{i} - t_{j})^{k} ,$

где — показатель степени (как правило, k = 2 ).

Матрицу длин используют при решении задач оптимизации размещения конструктивных элементов на плате, когда одним из критериев качества является минимум суммарной длины соединений.

Матрица инцидентности

Если вершина $x_{i}$ является концом ребра $u_{k},$ то говорят, что они инцидентны: вершина $x_{i}$ инцидентна ребру $u_{k}$ и ребро $u_{k}$ инцидентно вершине. В то время как смежность представляет собой отношение между однородными объектами ( вершинами ), инцидентность — это отношение между разнородными объектами ( вершинами и рёбрами).

При рассмотрении орграфов различают положительную инцидентность ( дуга исходит из вершины ) и отрицательную инцидентность ( дуга заходит в вершину ).

Рассматривая инцидентность вершин и рёбер графа, можно представить его матрицей инцидентности размера , строки которой соответствуют вершинам, а столбцы — рёбрам.

Для неориентированного графа элементы этой матрица определяются по следующему правилу: ij — элемент равен 1, если вершина $x_{i}$ инцидентна ребру $u_{i }$ и равен нулю, если $x_{i}$ и $u_{i}$ не инцидентны.

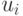
В случае орграфа ненулевой 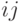— элемент равен , если $x_{i}$ — начальная вершина дуги $u_{i}$ , и равен , если $x_{i}$ — конечная вершина дуги $u_{i}$ .

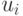
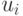
Приведём пример: составим матрицу инцидентности для рис. 17.2,а.

$S = begin{array}{cccccccc} & u1& u2& u3& u4& u5 &u6&\ begin{array}{c} x1\ x2\ x3\ x4\ x5 end{array} & left| left| begin{array}{c} 1\1\0\0\0end{array} & begin{array}{c} 0\1\1\0\0end{array} & begin{array}{c} 0\1\1\0\0end{array} & begin{array}{c} 0\1\0\0\1end{array} & begin{array}{c} 0\0\1\0\1end{array} & begin{array}{c} 0\0\0\0\0end{array} & left| left| begin{array}{c} \ \ \ \ \end{array} end{array}$

Каждый столбец матрицы содержит обязательно два единичных элемента (для орграфа эти элементы всегда имеют различные знаки и равны, соответственно, и ).

Количество единиц в строке равно степени соответствующей вершины (для орграфа количество положительных единиц определяет положительную степень, а количество отрицательных единиц — отрицательную степень).

Нулевая строка соответствует изолированной вершине, а нулевой столбец — петле.

Следует иметь в виду, что нулевой столбец матрицы инцидентности лишь указывает на наличие петли, но не содержит сведений том, с какой вершиной эта петля связана (в практических приложениях это может быть несущественно).

Правильность составления матрицы легко проверить: число единиц в i-ой строке матрицы соответствует степени вершины $x_{i}$ графа, а число единиц в каждом столбце — двум, так как каждое ребро соединяет две вершины графа. Единственное исключение составляет петля, дважды инцидентная одной и той же вершине.

Столбец, соответствующий петле, состоит из нулей, в результате чего матрица не указывает на существование петель. Поэтому при изучении свойств графа с помощью этой матрицы необходимо исключить из него петли.

Граф однозначно задаётся матрицами смежности и инцидентности. В свою очередь, каждая из этих матриц полностью определяет граф.

Существуют простые приёмы перехода от одной матрицы к другой.

Кроме выше перечисленных разновидностей матриц используются также матрицы контуров, сечений и так далее. Эти матрицы используются, как правило, при анализе электронных схем, поэтому далее они не будут рассматриваться.

Контрольные вопросы

На какие понятия опираются понятия теории графов?
Для каких целей используются графы?
Сформулируйте понятие графа.
Как представляется граф геометрически?
Что представляют собой ориентированные и неориентированные графы?
В каких случаях и почему используются ориентированные и неориентированные графы?
Какие вершины называют смежными?
Какие вершины называют инцидентными?
Что называют локальной степенью вершины?
Что называют несвязным графом?
Что называют маршрутом?
Что входит в понятие » цепь «?
Как составляется матрица смежности графа?
Как составляется матрица инцидентности?

Источник