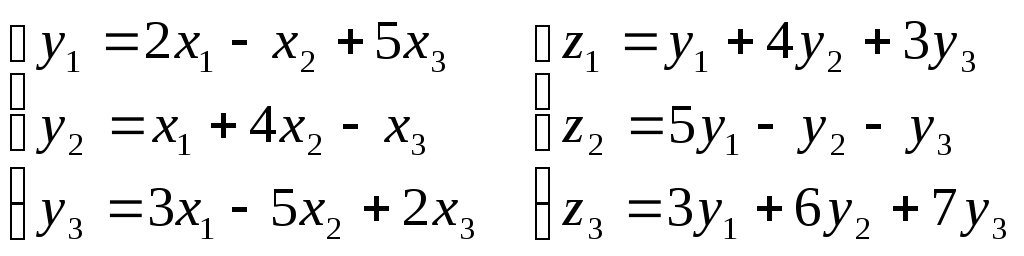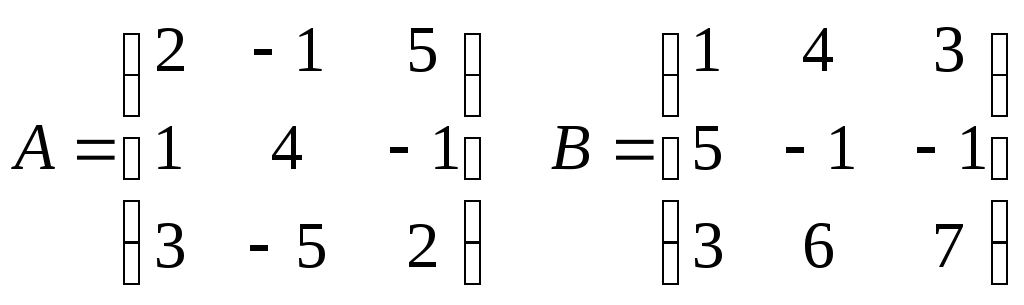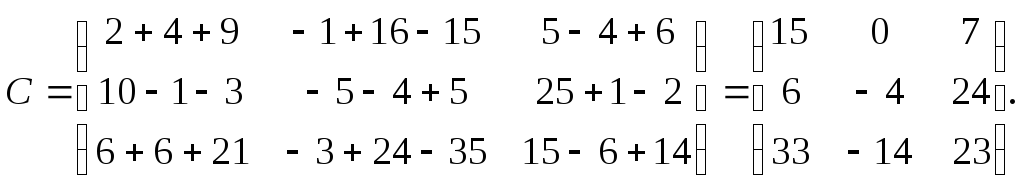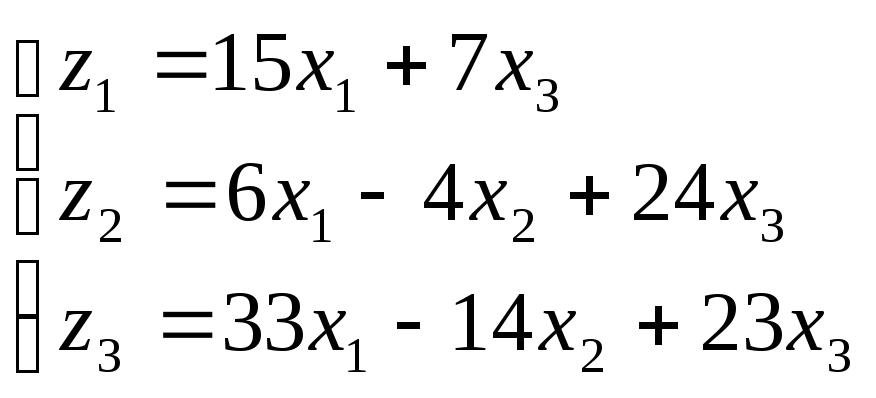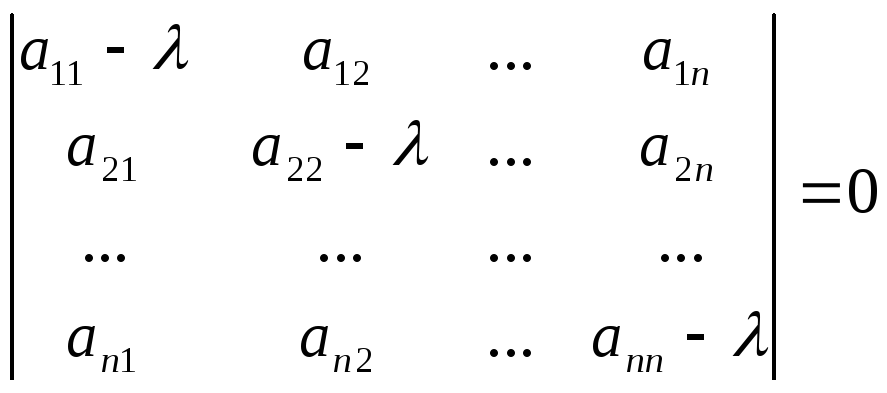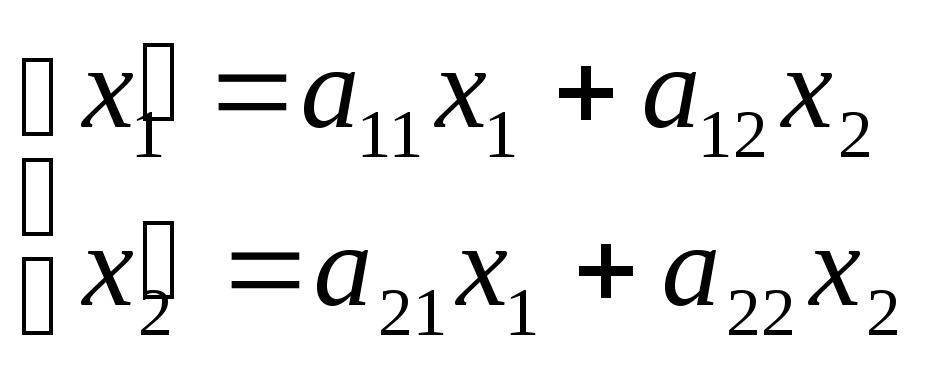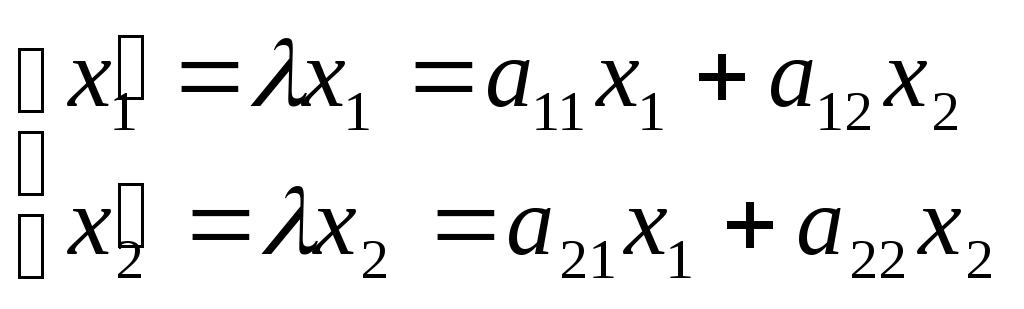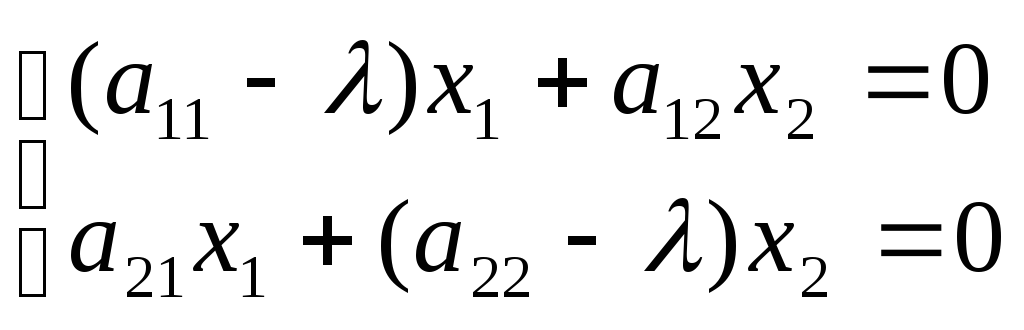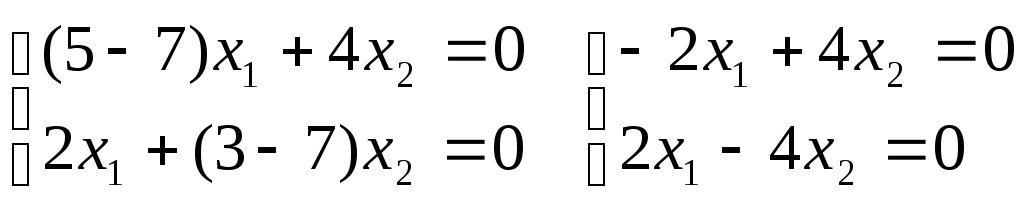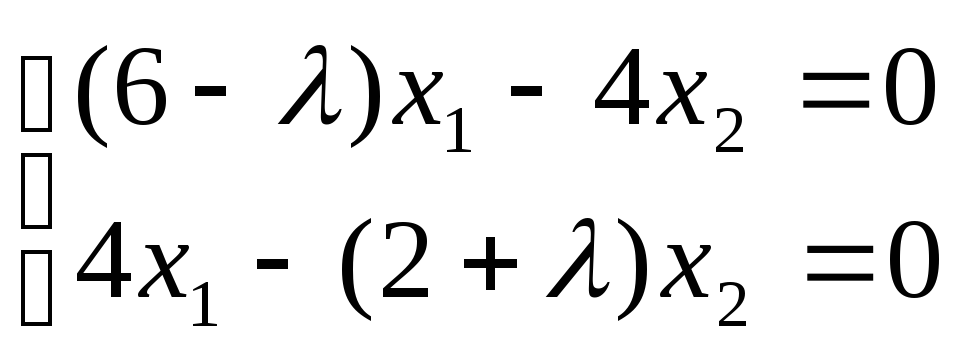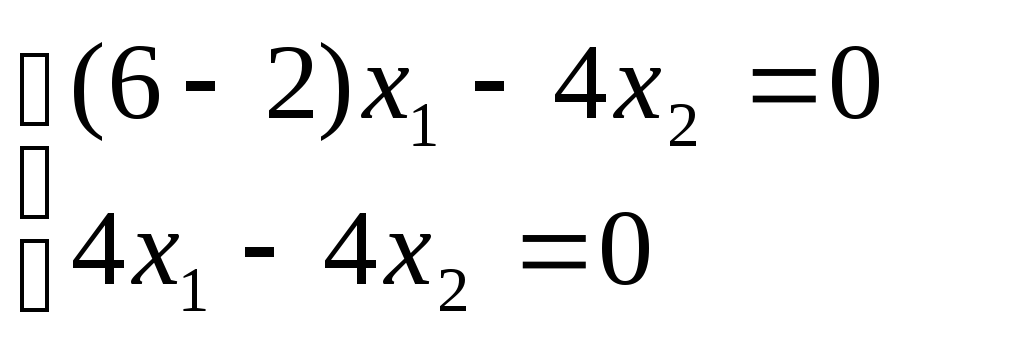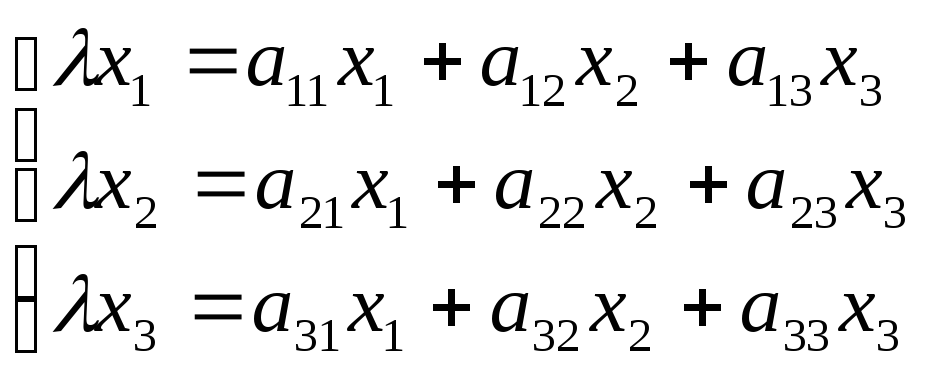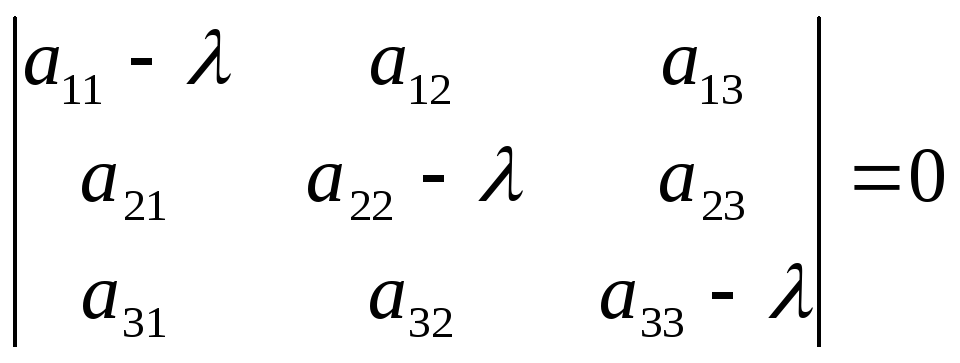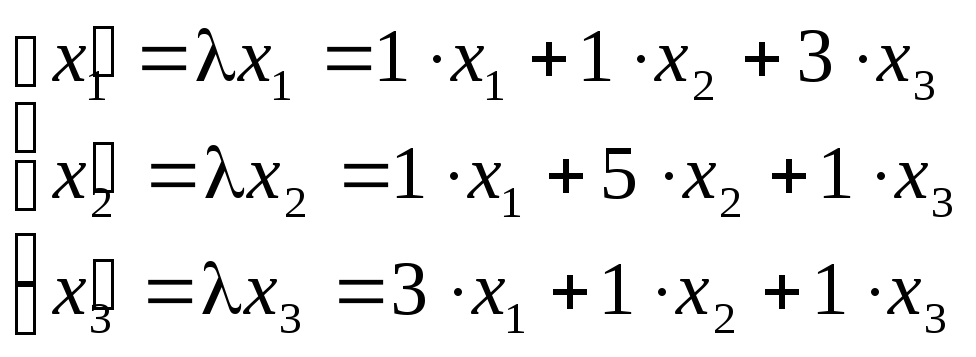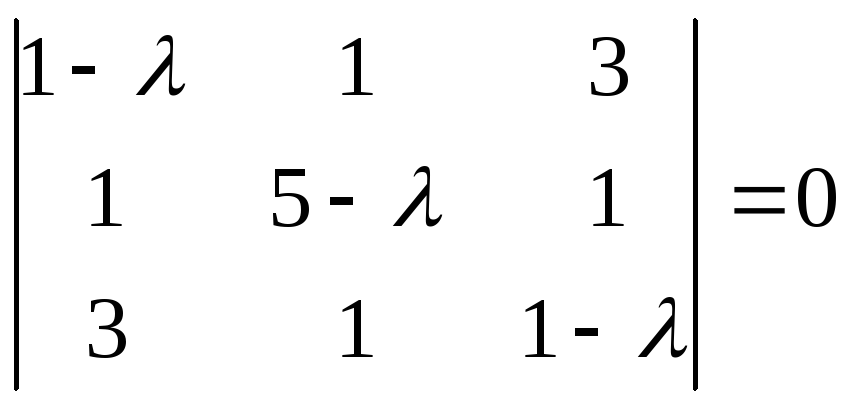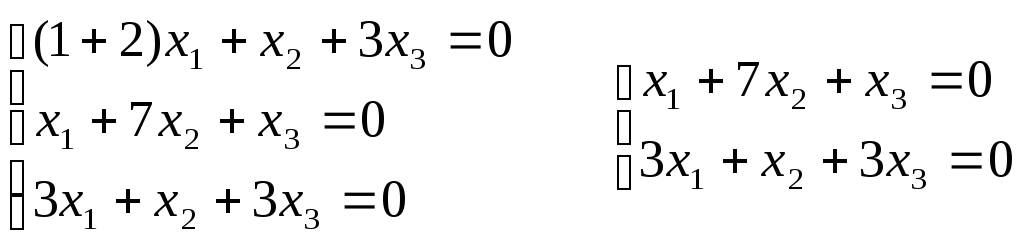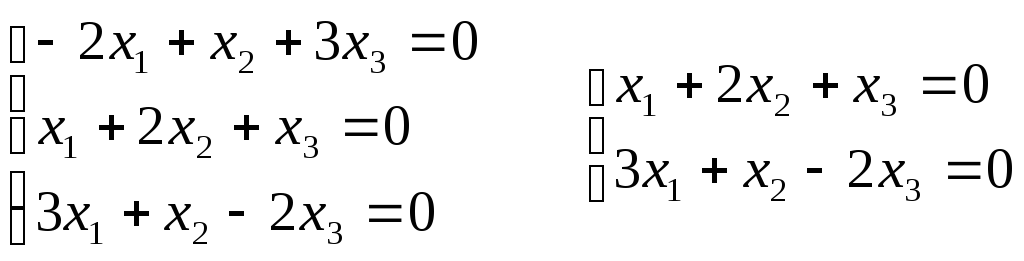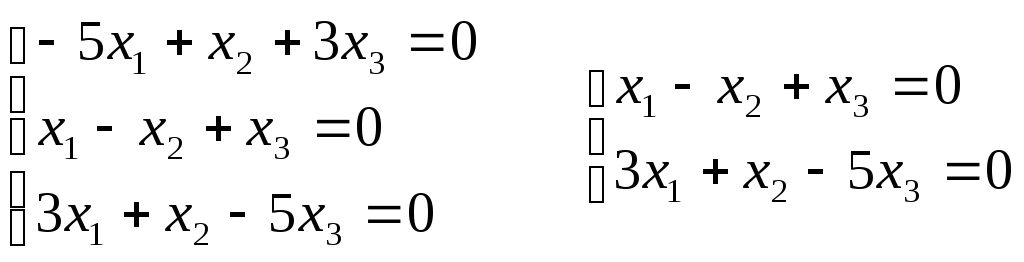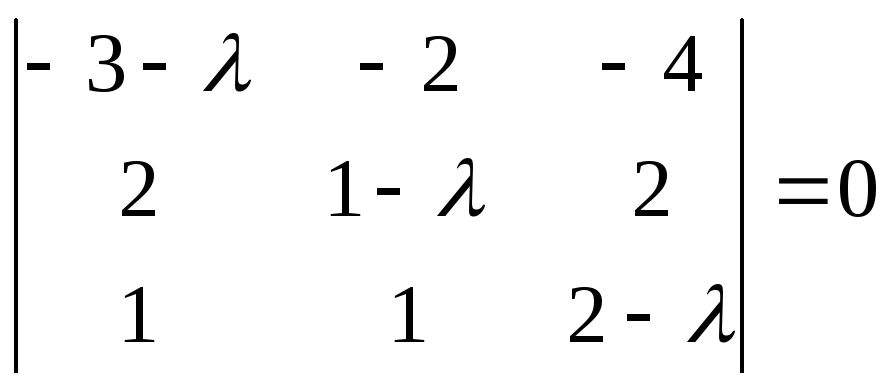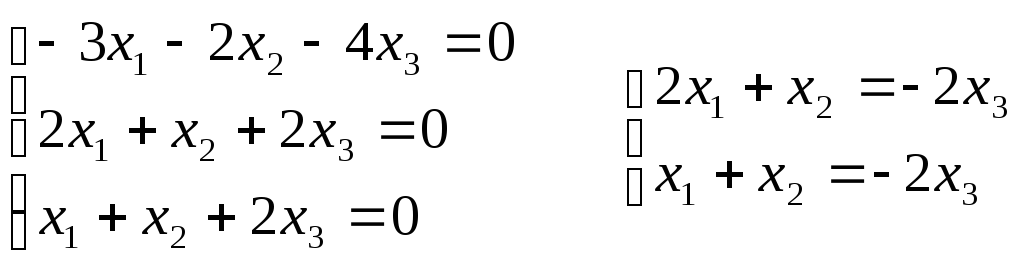Как составить матрицу преобразования

In linear algebra, linear transformations can be represented by matrices. If T is a linear transformation mapping mathbb {R} ^{n} to mathbb {R} ^{m} and mathbf {x} is a column vector with n entries, then

{displaystyle T(mathbf {x} )=Amathbf {x} }

for some mtimes n matrix A, called the transformation matrix of T.[citation needed] Note that A has m rows and n columns, whereas the transformation T is from mathbb {R} ^{n} to mathbb {R} ^{m}. There are alternative expressions of transformation matrices involving row vectors that are preferred by some authors.[1][2]

Uses[edit]

Matrices allow arbitrary linear transformations to be displayed in a consistent format, suitable for computation.[3] This also allows transformations to be composed easily (by multiplying their matrices).

Linear transformations are not the only ones that can be represented by matrices. Some transformations that are non-linear on an n-dimensional Euclidean space Rn can be represented as linear transformations on the n+1-dimensional space Rn+1. These include both affine transformations (such as translation) and projective transformations. For this reason, 4×4 transformation matrices are widely used in 3D computer graphics. These n+1-dimensional transformation matrices are called, depending on their application, affine transformation matrices, projective transformation matrices, or more generally non-linear transformation matrices. With respect to an n-dimensional matrix, an n+1-dimensional matrix can be described as an augmented matrix.

In the physical sciences, an active transformation is one which actually changes the physical position of a system, and makes sense even in the absence of a coordinate system whereas a passive transformation is a change in the coordinate description of the physical system (change of basis). The distinction between active and passive transformations is important. By default, by transformation, mathematicians usually mean active transformations, while physicists could mean either.

Put differently, a passive transformation refers to description of the same object as viewed from two different coordinate frames.

Finding the matrix of a transformation[edit]

If one has a linear transformation T(x) in functional form, it is easy to determine the transformation matrix A by transforming each of the vectors of the standard basis by T, then inserting the result into the columns of a matrix. In other words,

{displaystyle A={begin{bmatrix}T(mathbf {e} _{1})&T(mathbf {e} _{2})&cdots &T(mathbf {e} _{n})end{bmatrix}}}

For example, the function T(x) = 5x is a linear transformation. Applying the above process (suppose that n = 2 in this case) reveals that

{displaystyle T(mathbf {x} )=5mathbf {x} =5Imathbf {x} ={begin{bmatrix}5&0\0&5end{bmatrix}}mathbf {x} }

The matrix representation of vectors and operators depends on the chosen basis; a similar matrix will result from an alternate basis. Nevertheless, the method to find the components remains the same.

To elaborate, vector mathbf {v} can be represented in basis vectors, {displaystyle E={begin{bmatrix}mathbf {e} _{1}&mathbf {e} _{2}&cdots &mathbf {e} _{n}end{bmatrix}}} with coordinates {displaystyle [mathbf {v} ]_{E}={begin{bmatrix}v_{1}&v_{2}&cdots &v_{n}end{bmatrix}}^{mathrm {T} }}:

{displaystyle mathbf {v} =v_{1}mathbf {e} _{1}+v_{2}mathbf {e} _{2}+cdots +v_{n}mathbf {e} _{n}=sum _{i}v_{i}mathbf {e} _{i}=E[mathbf {v} ]_{E}}

Now, express the result of the transformation matrix A upon mathbf {v} , in the given basis:

{displaystyle {begin{aligned}A(mathbf {v} )&=Aleft(sum _{i}v_{i}mathbf {e} _{i}right)=sum _{i}{v_{i}A(mathbf {e} _{i})}\&={begin{bmatrix}A(mathbf {e} _{1})&A(mathbf {e} _{2})&cdots &A(mathbf {e} _{n})end{bmatrix}}[mathbf {v} ]_{E}=Acdot [mathbf {v} ]_{E}\[3pt]&={begin{bmatrix}mathbf {e} _{1}&mathbf {e} _{2}&cdots &mathbf {e} _{n}end{bmatrix}}{begin{bmatrix}a_{1,1}&a_{1,2}&cdots &a_{1,n}\a_{2,1}&a_{2,2}&cdots &a_{2,n}\vdots &vdots &ddots &vdots \a_{n,1}&a_{n,2}&cdots &a_{n,n}\end{bmatrix}}{begin{bmatrix}v_{1}\v_{2}\vdots \v_{n}end{bmatrix}}end{aligned}}}

The a_{i,j} elements of matrix A are determined for a given basis E by applying A to every {displaystyle mathbf {e} _{j}={begin{bmatrix}0&0&cdots &(v_{j}=1)&cdots &0end{bmatrix}}^{mathrm {T} }}, and observing the response vector

{displaystyle Amathbf {e} _{j}=a_{1,j}mathbf {e} _{1}+a_{2,j}mathbf {e} _{2}+cdots +a_{n,j}mathbf {e} _{n}=sum _{i}a_{i,j}mathbf {e} _{i}.}

This equation defines the wanted elements, a_{i,j}, of j-th column of the matrix A.[4]

Eigenbasis and diagonal matrix[edit]

Yet, there is a special basis for an operator in which the components form a diagonal matrix and, thus, multiplication complexity reduces to n. Being diagonal means that all coefficients a_{i,j} except a_{i,i} are zeros leaving only one term in the sum {textstyle sum a_{i,j}mathbf {e} _{i}} above. The surviving diagonal elements, a_{i,i}, are known as eigenvalues and designated with lambda _{i} in the defining equation, which reduces to {displaystyle Amathbf {e} _{i}=lambda _{i}mathbf {e} _{i}}. The resulting equation is known as eigenvalue equation.[5] The eigenvectors and eigenvalues are derived from it via the characteristic polynomial.

With diagonalization, it is often possible to translate to and from eigenbases.

Examples in 2 dimensions[edit]

Most common geometric transformations that keep the origin fixed are linear, including rotation, scaling, shearing, reflection, and orthogonal projection; if an affine transformation is not a pure translation it keeps some point fixed, and that point can be chosen as origin to make the transformation linear. In two dimensions, linear transformations can be represented using a 2×2 transformation matrix.

Stretching[edit]

A stretch in the xy-plane is a linear transformation which enlarges all distances in a particular direction by a constant factor but does not affect distances in the perpendicular direction. We only consider stretches along the x-axis and y-axis. A stretch along the x-axis has the form x’ = kx; y’ = y for some positive constant k. (Note that if k > 1, then this really is a «stretch»; if k < 1, it is technically a «compression», but we still call it a stretch. Also, if k = 1, then the transformation is an identity, i.e. it has no effect.)

The matrix associated with a stretch by a factor k along the x-axis is given by:

{displaystyle {begin{bmatrix}k&0\0&1end{bmatrix}}}

Similarly, a stretch by a factor k along the y-axis has the form x’ = x; y’ = ky, so the matrix associated with this transformation is

{displaystyle {begin{bmatrix}1&0\0&kend{bmatrix}}}

Squeezing[edit]

If the two stretches above are combined with reciprocal values, then the transformation matrix represents a squeeze mapping:

{displaystyle {begin{bmatrix}k&0\0&1/kend{bmatrix}}.}

A square with sides parallel to the axes is transformed to a rectangle that has the same area as the square. The reciprocal stretch and compression leave the area invariant.

Rotation[edit]

For rotation by an angle θ counterclockwise (positive direction) about the origin the functional form is x' = x cos theta - y sin theta and {displaystyle y'=xsin theta +ycos theta }. Written in matrix form, this becomes:[6]

{displaystyle {begin{bmatrix}x'\y'end{bmatrix}}={begin{bmatrix}cos theta &-sin theta \sin theta &cos theta end{bmatrix}}{begin{bmatrix}x\yend{bmatrix}}}

Similarly, for a rotation clockwise (negative direction) about the origin, the functional form is x' = x cos theta + y sin theta and {displaystyle y'=-xsin theta +ycos theta } the matrix form is:

{displaystyle {begin{bmatrix}x'\y'end{bmatrix}}={begin{bmatrix}cos theta &sin theta \-sin theta &cos theta end{bmatrix}}{begin{bmatrix}x\yend{bmatrix}}}

These formulae assume that the x axis points right and the y axis points up.

Shearing[edit]

For shear mapping (visually similar to slanting), there are two possibilities.

A shear parallel to the x axis has x' = x + ky and y' = y. Written in matrix form, this becomes:

{displaystyle {begin{bmatrix}x'\y'end{bmatrix}}={begin{bmatrix}1&k\0&1end{bmatrix}}{begin{bmatrix}x\yend{bmatrix}}}

A shear parallel to the y axis has x' = x and y' = y + kx, which has matrix form:

{displaystyle {begin{bmatrix}x'\y'end{bmatrix}}={begin{bmatrix}1&0\k&1end{bmatrix}}{begin{bmatrix}x\yend{bmatrix}}}

Reflection[edit]

For reflection about a line that goes through the origin, let {displaystyle mathbf {l} =(l_{x},l_{y})} be a vector in the direction of the line. Then use the transformation matrix:

{displaystyle mathbf {A} ={frac {1}{lVert mathbf {l} rVert ^{2}}}{begin{bmatrix}l_{x}^{2}-l_{y}^{2}&2l_{x}l_{y}\2l_{x}l_{y}&l_{y}^{2}-l_{x}^{2}end{bmatrix}}}

Orthogonal projection[edit]

To project a vector orthogonally onto a line that goes through the origin, let {displaystyle mathbf {u} =(u_{x},u_{y})} be a vector in the direction of the line. Then use the transformation matrix:

{displaystyle mathbf {A} ={frac {1}{lVert mathbf {u} rVert ^{2}}}{begin{bmatrix}u_{x}^{2}&u_{x}u_{y}\u_{x}u_{y}&u_{y}^{2}end{bmatrix}}}

As with reflections, the orthogonal projection onto a line that does not pass through the origin is an affine, not linear, transformation.

Parallel projections are also linear transformations and can be represented simply by a matrix. However, perspective projections are not, and to represent these with a matrix, homogeneous coordinates can be used.

Examples in 3D computer graphics[edit]

Rotation[edit]

The matrix to rotate an angle θ about any axis defined by unit vector (x,y,z) is [7]

{displaystyle {begin{bmatrix}xx(1-cos theta )+cos theta &yx(1-cos theta )-zsin theta &zx(1-cos theta )+ysin theta \xy(1-cos theta )+zsin theta &yy(1-cos theta )+cos theta &zy(1-cos theta )-xsin theta \xz(1-cos theta )-ysin theta &yz(1-cos theta )+xsin theta &zz(1-cos theta )+cos theta end{bmatrix}}.}

Reflection[edit]

To reflect a point through a plane ax + by + cz = 0 (which goes through the origin), one can use {displaystyle mathbf {A} =mathbf {I} -2mathbf {NN} ^{mathrm {T} }}, where mathbf {I} is the 3×3 identity matrix and mathbf {N} is the three-dimensional unit vector for the vector normal of the plane. If the L2 norm of a, b, and c is unity, the transformation matrix can be expressed as:

{displaystyle mathbf {A} ={begin{bmatrix}1-2a^{2}&-2ab&-2ac\-2ab&1-2b^{2}&-2bc\-2ac&-2bc&1-2c^{2}end{bmatrix}}}

Note that these are particular cases of a Householder reflection in two and three dimensions. A reflection about a line or plane that does not go through the origin is not a linear transformation — it is an affine transformation — as a 4×4 affine transformation matrix, it can be expressed as follows (assuming the normal is a unit vector):

{displaystyle {begin{bmatrix}x'\y'\z'\1end{bmatrix}}={begin{bmatrix}1-2a^{2}&-2ab&-2ac&-2ad\-2ab&1-2b^{2}&-2bc&-2bd\-2ac&-2bc&1-2c^{2}&-2cd\0&0&0&1end{bmatrix}}{begin{bmatrix}x\y\z\1end{bmatrix}}}

where {displaystyle d=-mathbf {p} cdot mathbf {N} } for some point mathbf {p} on the plane, or equivalently, {displaystyle ax+by+cz+d=0}.

If the 4th component of the vector is 0 instead of 1, then only the vector’s direction is reflected and its magnitude remains unchanged, as if it were mirrored through a parallel plane that passes through the origin. This is a useful property as it allows the transformation of both positional vectors and normal vectors with the same matrix. See homogeneous coordinates and affine transformations below for further explanation.

Composing and inverting transformations[edit]

One of the main motivations for using matrices to represent linear transformations is that transformations can then be easily composed and inverted.

Composition is accomplished by matrix multiplication. Row and column vectors are operated upon by matrices, rows on the left and columns on the right. Since text reads from left to right, column vectors are preferred when transformation matrices are composed:

If A and B are the matrices of two linear transformations, then the effect of first applying A and then B to a column vector mathbf {x} is given by:

{displaystyle mathbf {B} (mathbf {A} mathbf {x} )=(mathbf {BA} )mathbf {x} .}

In other words, the matrix of the combined transformation A followed by B is simply the product of the individual matrices.

When A is an invertible matrix there is a matrix A−1 that represents a transformation that «undoes» A since its composition with A is the identity matrix. In some practical applications, inversion can be computed using general inversion algorithms or by performing inverse operations (that have obvious geometric interpretation, like rotating in opposite direction) and then composing them in reverse order. Reflection matrices are a special case because they are their own inverses and don’t need to be separately calculated.

Other kinds of transformations[edit]

Affine transformations[edit]

Effect of applying various 2D affine transformation matrices on a unit square. Note that the reflection matrices are special cases of the scaling matrix.

Affine transformations on the 2D plane can be performed in three dimensions. Translation is done by shearing parallel to the xy plane, and rotation is performed around the z axis.

To represent affine transformations with matrices, we can use homogeneous coordinates. This means representing a 2-vector (x, y) as a 3-vector (x, y, 1), and similarly for higher dimensions. Using this system, translation can be expressed with matrix multiplication. The functional form x' = x + t_x; y' = y + t_y becomes:

{displaystyle {begin{bmatrix}x'\y'\1end{bmatrix}}={begin{bmatrix}1&0&t_{x}\0&1&t_{y}\0&0&1end{bmatrix}}{begin{bmatrix}x\y\1end{bmatrix}}.}

All ordinary linear transformations are included in the set of affine transformations, and can be described as a simplified form of affine transformations. Therefore, any linear transformation can also be represented by a general transformation matrix. The latter is obtained by expanding the corresponding linear transformation matrix by one row and column, filling the extra space with zeros except for the lower-right corner, which must be set to 1. For example, the counter-clockwise rotation matrix from above becomes:

{displaystyle {begin{bmatrix}cos theta &-sin theta &0\sin theta &cos theta &0\0&0&1end{bmatrix}}}

Using transformation matrices containing homogeneous coordinates, translations become linear, and thus can be seamlessly intermixed with all other types of transformations. The reason is that the real plane is mapped to the w = 1 plane in real projective space, and so translation in real Euclidean space can be represented as a shear in real projective space. Although a translation is a non-linear transformation in a 2-D or 3-D Euclidean space described by Cartesian coordinates (i.e. it can’t be combined with other transformations while preserving commutativity and other properties), it becomes, in a 3-D or 4-D projective space described by homogeneous coordinates, a simple linear transformation (a shear).

More affine transformations can be obtained by composition of two or more affine transformations. For example, given a translation T’ with vector {displaystyle (t'_{x},t'_{y}),} a rotation R by an angle θ counter-clockwise, a scaling S with factors (s_{x},s_{y}) and a translation T of vector {displaystyle (t_{x},t_{y}),} the result M of T’RST is:[8]

{displaystyle {begin{bmatrix}s_{x}cos theta &-s_{y}sin theta &t_{x}s_{x}cos theta -t_{y}s_{y}sin theta +t'_{x}\s_{x}sin theta &s_{y}cos theta &t_{x}s_{x}sin theta +t_{y}s_{y}cos theta +t'_{y}\0&0&1end{bmatrix}}}

When using affine transformations, the homogeneous component of a coordinate vector (normally called w) will never be altered. One can therefore safely assume that it is always 1 and ignore it. However, this is not true when using perspective projections.

Perspective projection[edit]

Comparison of the effects of applying 2D affine and perspective transformation matrices on a unit square.

Another type of transformation, of importance in 3D computer graphics, is the perspective projection. Whereas parallel projections are used to project points onto the image plane along parallel lines, the perspective projection projects points onto the image plane along lines that emanate from a single point, called the center of projection. This means that an object has a smaller projection when it is far away from the center of projection and a larger projection when it is closer (see also reciprocal function).

The simplest perspective projection uses the origin as the center of projection, and the plane at z=1 as the image plane. The functional form of this transformation is then x' = x / z; y' = y / z. We can express this in homogeneous coordinates as:

{displaystyle {begin{bmatrix}x_{c}\y_{c}\z_{c}\w_{c}end{bmatrix}}={begin{bmatrix}1&0&0&0\0&1&0&0\0&0&1&0\0&0&1&0end{bmatrix}}{begin{bmatrix}x\y\z\1end{bmatrix}}}

After carrying out the matrix multiplication, the homogeneous component {displaystyle w_{c}} will be equal to the value of z and the other three will not change. Therefore, to map back into the real plane we must perform the homogeneous divide or perspective divide by dividing each component by {displaystyle w_{c}}:

{displaystyle {begin{bmatrix}x'\y'\z'\1end{bmatrix}}={frac {1}{w_{c}}}{begin{bmatrix}x_{c}\y_{c}\z_{c}\w_{c}end{bmatrix}}}

More complicated perspective projections can be composed by combining this one with rotations, scales, translations, and shears to move the image plane and center of projection wherever they are desired.

See also[edit]

  • 3D projection
  • Change of basis
  • Image rectification
  • Pose (computer vision)
  • Rigid transformation
  • Transformation (function)
  • Transformation geometry

References[edit]

  1. ^ Rafael Artzy (1965) Linear Geometry
  2. ^ J. W. P. Hirschfeld (1979) Projective Geometry of Finite Fields, Clarendon Press
  3. ^ Gentle, James E. (2007). «Matrix Transformations and Factorizations». Matrix Algebra: Theory, Computations, and Applications in Statistics. Springer. ISBN 9780387708737.
  4. ^ Nearing, James (2010). «Chapter 7.3 Examples of Operators» (PDF). Mathematical Tools for Physics. ISBN 978-0486482125. Retrieved January 1, 2012.
  5. ^ Nearing, James (2010). «Chapter 7.9: Eigenvalues and Eigenvectors» (PDF). Mathematical Tools for Physics. ISBN 978-0486482125. Retrieved January 1, 2012.
  6. ^ http://ocw.mit.edu/courses/aeronautics-and-astronautics/16-07-dynamics-fall-2009/lecture-notes/MIT16_07F09_Lec03.pdf[bare URL PDF]
  7. ^ Szymanski, John E. (1989). Basic Mathematics for Electronic Engineers:Models and Applications. Taylor & Francis. p. 154. ISBN 0278000681.
  8. ^ Cédric Jules (February 25, 2015). «2D transformation matrices baking».

External links[edit]

  • The Matrix Page Practical examples in POV-Ray
  • Reference page — Rotation of axes
  • Linear Transformation Calculator
  • Transformation Applet — Generate matrices from 2D transformations and vice versa.
  • Coordinate transformation under rotation in 2D
  • Excel Fun — Build 3D graphics from a spreadsheet
Источник

Все курсы > Линейная алгебра > Занятие 3

На прошлых занятиях мы поговорили про векторы и векторные пространства. Сегодня рассмотрим матрицы и линейные преобразования.

Ноутбук к сегодняшнему занятию⧉

Как матрицы преобразовывают пространство

Посмотрим, как матрица может изменить положение вектора.

Преобразование базисных векторов

Начнем с базисных векторов. Возьмем матрицу $A$ и два базисных вектора $mathbf i$ и $mathbf j$.

A = np.array([[2, 3],

              [5, 1]])

i = np.array([1, 0])

j = np.array([0, 1])

Если поочередно умножить матрицу на каждый из векторов, то первый столбец матрицы $A$ определит новые координаты вектора $mathbf i$, второй столбец — вектора $mathbf j$.

$$ begin{bmatrix} 2 & 3 \ 5 & 1 end{bmatrix} cdot begin{bmatrix} 1 \ 0 end{bmatrix} = begin{bmatrix} 2 \ 5 end{bmatrix} $$

$$ begin{bmatrix} 2 & 3 \ 5 & 1 end{bmatrix} cdot begin{bmatrix} 0 \ 1 end{bmatrix} = begin{bmatrix} 3 \ 1 end{bmatrix} $$

Так трансформационная матрица (transformation matrix, левый множитель) оказывает влияние на базисные (и все остальные) векторы и, таким образом, меняет пространство.

Посмотрим на результат на графике.

ax = plt.axes()

plt.xlim([—0.5, 5])

plt.ylim([—0.5, 6])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

# найдем координаты с помощью произведения

arrow_a = ax.arrow(0, 0, np.dot(A, i)[0], np.dot(A, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’)

arrow_b = ax.arrow(0, 0, np.dot(A, j)[0], np.dot(A, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’)

plt.show()

преобразование базисных векторов с помощью матрицы

Продемонстрируем, что при преобразовании любого вектора, мы по сути меняем базисные векторы, умноженные на скаляр. Рассмотрим, как в результате умножения матрицы A на вектор $mathbf r$, мы получим новый вектор $mathbf r’$.

$$A cdot mathbf r = mathbf r’ $$

Очевидно, мы можем умножать векторы $mathbf r$ и $mathbf r’$ на скаляр $n$ или представить их в виде суммы двух (базисных) векторов.

$$A cdot n mathbf r = n mathbf r’ $$

$$A cdot (mathbf i + mathbf j) = (mathbf i + mathbf j)’ $$

Тогда справедливо, что

$$A cdot (n mathbf i+m mathbf j) = (n mathbf i+m mathbf j)’ $$

Выполним умножение.

$$ A cdot (n mathbf i + m mathbf j) = (nA mathbf i+mA mathbf j) = n mathbf i’ + m mathbf j’ $$

Обратите внимание, что умножение матрицы на скаляр коммутативно, то есть $A n mathbf i = n A mathbf i $.

Таким образом, можно сказать, что при преобразовании пространства матрица преобразует масштабированные (scaled) базисные векторы. Приведем пример.

$$  begin{bmatrix} 2 & 3 \ 5 & 1 end{bmatrix} begin{bmatrix} 2 \ 4 end{bmatrix} = begin{bmatrix} 16 \ 14 end{bmatrix} $$

$$  begin{bmatrix} 2 & 3 \ 5 & 1 end{bmatrix} left( 2 begin{bmatrix} 1 \ 0 end{bmatrix} + 4 begin{bmatrix} 0 \ 1 end{bmatrix} right)  = begin{bmatrix} 16 \ 14 end{bmatrix} $$

$$ 2 begin{bmatrix} 2 & 3 \ 5 & 1 end{bmatrix} begin{bmatrix} 1 \ 0 end{bmatrix} + 4 begin{bmatrix} 2 & 3 \ 5 & 1 end{bmatrix} begin{bmatrix} 0 \ 1 end{bmatrix} = begin{bmatrix} 16 \ 14 end{bmatrix} $$

$$ 2 begin{bmatrix} 2 \ 5 end{bmatrix} + 4 begin{bmatrix} 3 \ 1 end{bmatrix} = begin{bmatrix} 16 \ 14 end{bmatrix} $$

Иначе говоря, «новые», преобразованные векторы будут иметь те же координаты относительно нового базиса, что и исходный вектор, относительно исходного базиса (потому что $n$ и $m$ или 2 и 4 в примере выше не изменяются при преобразовании).

Свойства преобразований

Вначале дадим описательное определение линейной трансформации пространства.

При линейном преобразовании начало координат не смещается, а линии координатной сетки остаются параллельными и сохраняют исходное расстояние друг от друга (origin remains fixed, grid lines remain parallel and evenly spaced).

Более формально свойства трансформации ($T$), которую также можно назвать функцией (function) или отображением (mapping) относительно векторов $mathbf v$ и $mathbf w$ можно выразить через две заданные в линейном пространстве операции сложения и умножения на скаляр.

  1. $ T(mathbf v + mathbf w) = T(mathbf v) + T(mathbf w) $
  2. $ T(c mathbf v) = c T(mathbf v) $

Примечение. Несмещение начала координат можно рассматривать как частный случай свойства 2, так как преобразование нулевого вектора должно дать нулевой вектор $T(mathbf 0) = mathbf 0 $. Приведем пример линейного и нелинейного преобразований.

Пример 1. Проекция

Рассмотрим проекцию $T: mathbb R^2 rightarrow mathbb R^2 $.

пример линейного преобразования: проекция

Проверим приведенные выше свойства:

  • $ T(mathbf v + mathbf w) = T(mathbf v) + T(mathbf w) $
  • если, например, вектор $mathbf v$ увеличить в два раза, то и проекция увеличится в два раза
  • начало координат при проекции не смещается, то есть $T(mathbf 0) = mathbf 0 $

Пример 2. Нелинейное преобразование

Предположим, что мы хотим сместить каждый вектор проскости (в частности, вектор $ mathbf v $) на некоторый вектор $ mathbf d $.

пример нелинейного преобразования

Очевидно нарушается второе свойство, например, $ T(2 mathbf v) not= 2T(mathbf v) $. Более того, смещается начало координат, $T(mathbf 0) = mathbf d $.

Умножение матрицы на вектор

Важно, что умножение матрицы $A$ на векторы $mathbf v$ и $mathbf w$, т.е. $T(mathbf v) = A mathbf v$ и $T(mathbf w) = A mathbf w$ всегда линейно, так как

  • $ A(mathbf v + mathbf w) = A(mathbf v) + A(mathbf w) $
  • $ A(c mathbf v) = c A(mathbf v) $

Соответственно, задача линейного преобразования сводится к нахождению правильной трансформационной матрицы (причем в известной, заданной системе координат).

Например, если мы хотим перейти от трех измерений к двум, $T: mathbb R^3 rightarrow mathbb R^2$, то нам потребуется матрица $2 times 3$:

пример линейного преобразования: умножение матрицы на вектор

В общем случае матрица $A$ размерностью $m times n$ соответствует $ T: R^n rightarrow R^m $.

Смена базиса

Как уже было сказано, если линейное преобразование задано матрицей, то введена система координат (базис).

  • На вход матрица получает базис $ mathbf v_1,…, mathbf v_n in R^n $
  • На выходе выдает $ mathbf w_1,…, mathbf w_m in R^m $

Другими словами, при преобразовании линейной комбинации $mathbf v_1,…, mathbf v_n$ в линейную комбинацию $mathbf w_1,…, mathbf w_m$ происходит смена базиса. Например,

$$ mathbf v = c_1 mathbf v_1 + c_2 mathbf v_2 rightarrow T(mathbf v) = c_1 mathbf w_1 + c_2 mathbf w_2 $$

Пример 3. Производная как линейное преобразование

Интересно, что взятие производной линейно. Предположим, что у нас есть некоторая функция $ f(x) = c_1 + c_2 x + c_3 x^2 $. Ее базис: ${ 1, x, x^2 }$. Тогда производной будет $f'(x) = c_2 + 2 c_3 x $ с базисом ${ 1, x }$. Найти производную можно с помощью матрицы

$$ begin{bmatrix} 0 & 1 & 0 \ 0 & 0 & 2 end{bmatrix} begin{bmatrix} c_1 \ c_2 \ c_3 end{bmatrix} = begin{bmatrix} c_2 \ 2c_3 end{bmatrix} $$

Решение системы уравнений как преобразование

Теперь рассмотрим решение системы линейных уравнений (simultaneous equations) с точки зрения трансформации пространства.

$$ begin{bmatrix} 2 & 3 \ 5 & 1 end{bmatrix} begin{bmatrix} a \ b end{bmatrix} = begin{bmatrix} 8 \ 13 end{bmatrix}$$

По сути, нам нужно найти такой вектор $begin{bmatrix} a \ b end{bmatrix}$, при умножении матрицы на который мы окажемся в точке $ begin{bmatrix} 8 \ 13 end{bmatrix} $.

Виды преобразований

Можно выделить некоторые часто встречающиеся виды преобразований. Создадим вектор $mathbf x$.

Единичная матрица

Если умножить единичную матрицу (identity matrix) на вектор $mathbf x$, ничего не произойдет.

I = np.array([[1, 0],

              [0, 1]])

np.dot(I, x)

Обратите внимание, мы легко можем догадаться, что с вектором после преобразования ничего не произойдет, потому что столбцы трансформационной матрицы в точности повторяют векторы базиса $mathbf i$ и $mathbf j$.

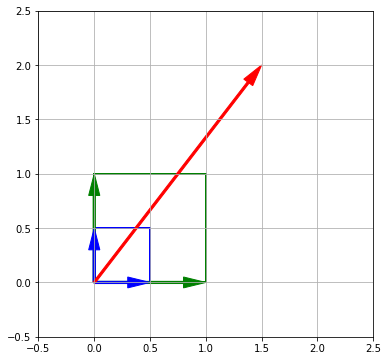
Сжатие и растяжение

При сжатии или растяжении (scaling) координаты вектора соответственно уменьшаются или увеличиваются в размере. В случае базисных векторов, они не меняют направления. Приведем пример растяжения.

# столбцы — это тот же базис, но

# единицы увеличены в три и два раза соответственно

Scale = np.array([[3, 0],

                  [0, 2]])

np.dot(Scale, x)

Посмотрим, как это выглядит на графике.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

ax = plt.axes()

plt.xlim([—0.5, 9.5])

plt.ylim([—0.5, 9.5])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, np.dot(Scale, i)[0], np.dot(Scale, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.arrow(0, 0, np.dot(Scale, j)[0], np.dot(Scale, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2))

ax.add_patch(Rectangle((0, 0), 3, 2, fill = False, edgecolor = ‘b’, lw = 2))

ax.arrow(0, 0, np.dot(Scale, x)[0], np.dot(Scale, x)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’)

plt.show()

растяжение

Дадим некоторые пояснения. Преобразования пространства удобно описывать с помощью площади, образованной двумя (в пространстве $R^2$) векторами.

  • Зеленый квадрат: площадь базисных векторов
  • Синий квадрат: площадь масштабированных базисных векторов
  • Красный вектор: масштабированный вектор $mathbf x$

Обратите внимание, векторы базиса $mathbf i$ и $mathbf j$ после трансформации сохранили направление, вектор $ mathbf r $ сместился выше. Понимание того, что некоторые векторы сохраняют направление, а некоторые — нет, очень пригодится позднее.

Приведем пример сжатия. Для этого нужно, чтобы ненулевые координаты матрицы были меньше единицы.

Squish = np.array([[.5, 0],

                   [0, .5]])

np.dot(Squish, x)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

ax = plt.axes()

plt.xlim([—0.5, 2.5])

plt.ylim([—0.5, 2.5])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, np.dot(Squish, i)[0], np.dot(Squish, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.arrow(0, 0, np.dot(Squish, j)[0], np.dot(Squish, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2))

ax.add_patch(Rectangle((0, 0), .5, .5, fill = False, edgecolor = ‘b’, lw = 2))

ax.arrow(0, 0, np.dot(Squish, x)[0], np.dot(Squish, x)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘r’, ec = ‘r’)

plt.show()

сжатие

Отражение

Отражение (reflection) как бы «перекидывает» вектор на другую сторону от осей координат. Посмотрим на отражение относительно оси y (то есть «перекидывать» мы будем вектор $mathbf i$). Для этого в первом столбце трансформационной матрицы 1 меняется на $-1$.

Reflect_y = np.array([[—1, 0],

                      [0, 2]])

# посмотрим, где окажется вектор x

np.dot(Reflect_y, x)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

ax = plt.axes()

plt.xlim([—1.5, 1.5])

plt.ylim([—0.2, 2.5])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

# отражается относительно оси y

ax.arrow(0, 0, np.dot(Reflect_y, i)[0], np.dot(Reflect_y, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

# вектор j мы растягиваем

ax.arrow(0, 0, np.dot(Reflect_y, j)[0], np.dot(Reflect_y, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2))

ax.add_patch(Rectangle((0, 0), —1, 2, fill = False, edgecolor = ‘b’, lw = 2))

plt.show()

отражение относительно оси y

Выполним отражение относительно обеих осей.

Invert = np.array([[—1, 0],

                   [0, —1]])

np.dot(Invert, x)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

ax = plt.axes()

plt.xlim([—1.5, 1.5])

plt.ylim([—1.5, 1.5])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

# отражается относительно оси y

ax.arrow(0, 0, np.dot(Invert, i)[0], np.dot(Invert, i)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

# отражается относительно оси x

ax.arrow(0, 0, np.dot(Invert, j)[0], np.dot(Invert, j)[1], width = 0.02, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2))

ax.add_patch(Rectangle((0, 0), —1, —1, fill = False, edgecolor = ‘b’, lw = 2))

plt.show()

отражение относительно обеих осей

Матрица перестановки

Матрица перестановки (permutation matrix) позволяет поменять векторы $mathbf i$ и $mathbf j$ местами.

P = np.array([[0, 1],

              [1, 0]])

# посмотрим, где окажется вектор x

np.dot(P, x)

# а также базисные векторы

np.dot(P, i), np.dot(P, j)

(array([0, 1]), array([1, 0]))

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

ax = plt.axes()

plt.xlim([—0.5, 1.5])

plt.ylim([—0.5, 1.5])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

# i и j меняются местами

ax.arrow(0, 0, np.dot(P, i)[0], np.dot(P, i)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.arrow(0, 0, np.dot(P, j)[0], np.dot(P, j)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2))

ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘b’, lw = 1))

plt.show()

матрица перестановки

Сдвиг (трансвекция)

Сдвиг или трансвекция (shear) предполагает, что один из базисных векторов остается на месте, второй сдвигается.

# вектор i остается на месте, j сдвигается

Shear = np.array([[1, 1],

                  [0, 1]])

np.dot(Shear, x)

ax = plt.axes()

plt.xlim([—0.5, 2.5])

plt.ylim([—0.5, 1.5])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, np.dot(Shear, i)[0], np.dot(Shear, i)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.arrow(0, 0, np.dot(Shear, j)[0], np.dot(Shear, j)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2))

ax.add_patch(Polygon([[0, 0], [1, 0], [2, 1], [1, 1]], fill = False, edgecolor = ‘b’, lw = 2))

plt.show()

сдвиг

Вращение

Посмотрим, как можно повернуть (rotate) базисные векторы на 90 градусов против часовой стрелки.

# поворот на 90 градусов против часовой стрелки

Rotate = np.array([[0, —1],

                   [1, 0]])

np.dot(Rotate, x)

ax = plt.axes()

plt.xlim([—1.5, 1.5])

plt.ylim([—0.5, 1.5])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, np.dot(Rotate, i)[0], np.dot(Rotate, i)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.arrow(0, 0, np.dot(Rotate, j)[0], np.dot(Rotate, j)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.add_patch(Rectangle((0, 0), 1, 1, fill = False, edgecolor = ‘g’, lw = 2))

ax.add_patch(Rectangle((0, 0), —1, 1, fill = False, edgecolor = ‘b’, lw = 2))

plt.show()

поворот на 90 градусов

Поворот на определенный угол против часовой стрелки.

theta = np.radians(90)

Rotate = np.array([[np.cos(theta), —np.sin(theta)],

                   [np.sin(theta), np.cos(theta)]])

np.dot(Rotate, x)

Смысл такой трансформации представлен на схеме ниже. Для поворота на 90 градусов против часовой стрелки вспомним, что

  • для вектора $mathbf i quad cos(90^{circ}) = 0, quad -sin(90^{circ}) = -1$
  • для вектора $mathbf j quad sin(90^{circ}) = 1, quad cos(90^{circ}) = 0$

матрица вращения

Видео про линейные преобразования⧉.

Композиция преобразований

Посмотрим, что произойдет, если применить сначала поворот на 90 градусов по часовой стрелке, затем отражение относительно оси y.

Так как матрица преобразования стоит слева от преобразуемого вектора, то для применения двух преобразований, матрица второго преобразования будет стоять слева от матрицы первого.

$$ Reflect_y cdot (Rotate cdot mathbf x ) $$

Подготовим матрицы.

# поворот по часовой стрелки

theta = np.radians(90)

Rotate = np.array([[np.cos(theta), np.sin(theta)],

                   [—np.sin(theta), np.cos(theta)]]).round()

Rotate

array([[ 0.,  1.],

       [-1.,  0.]])

# отражение относительно оси y

Reflect_y = np.array([[—1, 0],

                      [0, 1]])

Reflect_y

array([[-1,  0],

       [ 0,  1]])

Выполним преобразование.

np.dot(Reflect_y, np.dot(Rotate, i)), np.dot(Reflect_y, np.dot(Rotate, j))

(array([ 0., -1.]), array([-1.,  0.]))

Посмотрим на этот процесс графически. Вначале первое преобразование (вращение).

ax = plt.axes()

plt.xlim([—1.5, 1.5])

plt.ylim([—1.5, 1.5])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

# поворот по часовой стрелке

ax.arrow(0, 0, np.dot(Rotate, i)[0], np.dot(Rotate, i)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.arrow(0, 0, np.dot(Rotate, j)[0], np.dot(Rotate, j)[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

plt.show()

композиция преобразований: вращение

Теперь применим второе преобразование (отражение) к результату первого.

ax = plt.axes()

plt.xlim([—1.5, 1.5])

plt.ylim([—1.5, 1.5])

plt.grid()

ax.arrow(0, 0, i[0], i[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

ax.arrow(0, 0, j[0], j[1], width = 0.03, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘g’, ec = ‘g’)

# отображение относительно оси y

ax.arrow(0, 0, np.dot(Reflect_y, np.dot(Rotate, i))[0], np.dot(Reflect_y, np.dot(Rotate, i))[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

ax.arrow(0, 0, np.dot(Reflect_y, np.dot(Rotate, j))[0], np.dot(Reflect_y, np.dot(Rotate, j))[1], width = 0.01, head_width = 0.1, head_length = 0.2, length_includes_head = True, fc = ‘b’, ec = ‘b’)

plt.show()

композиция преобразований: отражение

Запишем, где оказались векторы $mathbf i$ и $mathbf j$ после второго преобразования и соединим эти координаты в матрицу. Затем умножим на исходные векторы $mathbf i$ и $mathbf j$.

Composition = np.array([[0, —1],

                        [—1, 0]])

np.dot(Composition, i), np.dot(Composition, j)

(array([ 0, -1]), array([-1,  0]))

Результат аналогичен последовательному применению предыдущих преобразований.

# то же самое мы получим, перемножив матрицы преобразований

np.dot(Reflect_y, Rotate)

array([[ 0., -1.],

       [-1.,  0.]])

Обратите внимание, что порядок операций важен. Поменяв матрицы преобразований местами, мы получим другой результат.

# выполнив отражение, а затем поворот,

# мы вернем векторы в исходное положение

np.dot(Rotate, np.dot(Reflect_y, i)), np.dot(Rotate, np.dot(Reflect_y, j))

(array([0., 1.]), array([1., 0.]))

Это еще раз демонстрирует некоммутативность, но ассоциативность умножения матриц.

Приведем ссылки на видео:

  • Умножение матриц как последовательность преобразований⧉
  • Линейные преобразования в трехмерном пространстве⧉

Подведем итог

Мы посмотрели, как матрицы преобразовывают пространство и на примерах изучили, чем линейные преобразования отличаются от нелинейных. Кроме того, мы познакомились с основными видами линейных преобразований.

Рассмотрим системы линейных уравнений.

Источник

Матрицы линейных преобразований

Пусть
в n-
мерном линейном пространстве с базисом
,,…,
задано линейное преобразование А. Тогда
векторы А,А,…,А—
также векторы этого пространства и их
можно представить в виде линейной
комбинации векторов базиса:

A=
a11+
a21+…+
an1

A=
a12+
a22+…+
an2

……………………………….

A=
an1+
an2+…+
ann

Тогда
матрица А =

называется матрицей
линейного преобразования А.

Если
в пространстве L
взять вектор
=
x1+
x2+…+
xn,
то A
L.

,
где

……………………………..

Эти
равенства можно назвать линейным
преобразованием в базисе
,,…,.

В
матричном виде:

,
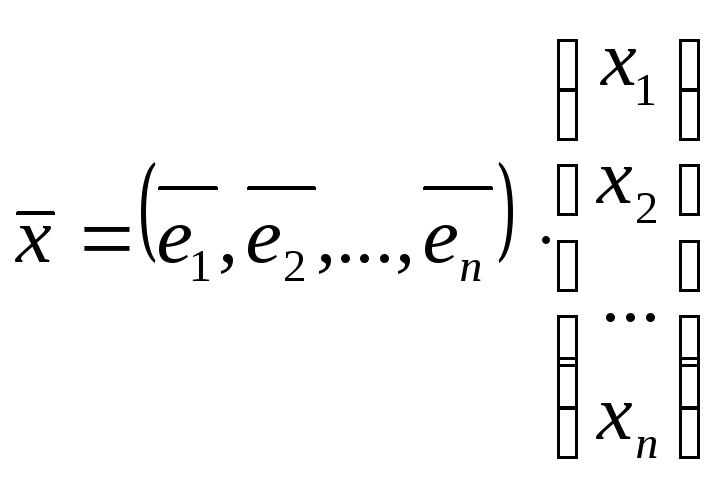
А,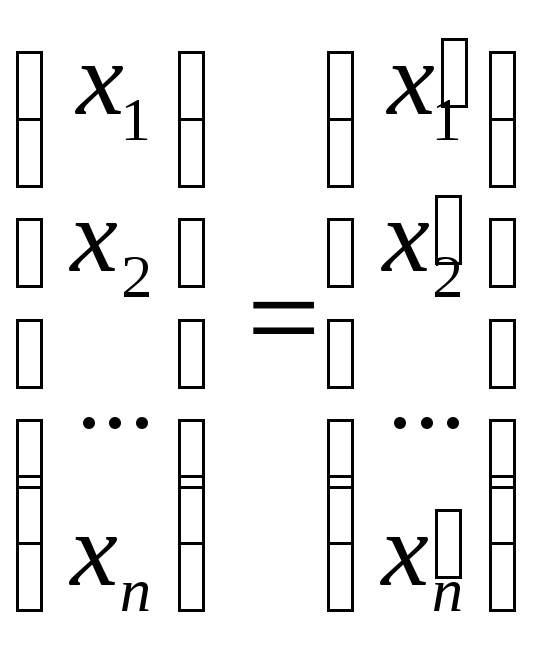

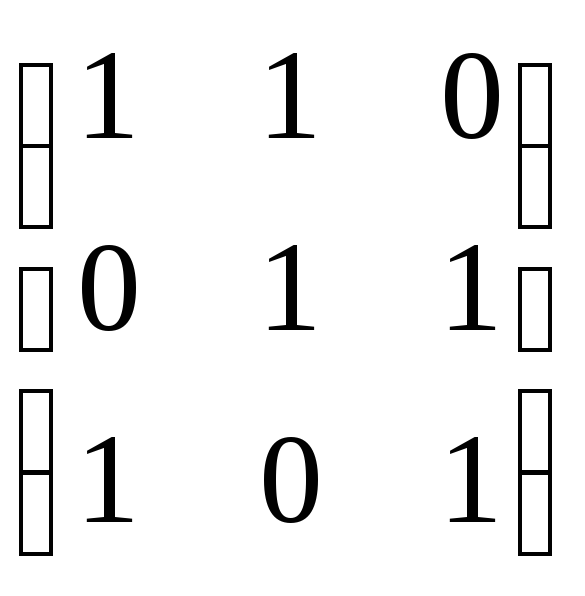
Пример.
Найти матрицу линейного преобразования,
заданного в виде:

x
= x + y

y
= y + z

z
= z + x

x
= 1x
+ 1y
+ 0z

y
= 0x
+ 1y
+ 1z

z
= 1x
+ 0y
+ 1z

A
=

На практике действия
над линейными преобразованиями сводятся
к действиям над их матрицами.

Определение:
Если вектор
переводится
в вектор

линейным преобразованием с матрицей
А, а вектор

в вектор

линейным преобразованием с матрицей
В, то последовательное применение этих
преобразований равносильно линейному
преобразованию, переводящему вектор

в вектор
(оно
называется произведением
составляющих преобразований).

С
= ВА

Пример.
Задано линейное преобразование А,
переводящее вектор
в
вектор

и линейное преобразование В, переводящее
вектор

в вектор
.
Найти матрицу линейного преобразования,
переводящего вектор

в вектор
.

С
= ВА

Т.е.

Примечание:
Если А=
0, то преобразование вырожденное, т.е.,
например, плоскость преобразуется не
в целую плоскость, а в прямую.

Собственные значения и собственные векторы линейного преобразования

Определение:
Пусть L
– заданное n-
мерное линейное пространство. Ненулевой
вектор
L
называется собственным
вектором
линейного преобразования А, если
существует такое число ,
что выполняется равенство:

A.

При
этом число 
называется собственным
значением (характеристическим числом)
линейного преобразования А, соответствующего
вектору
.

Определение:
Если линейное преобразование А в
некотором базисе
,,…,
имеет матрицу А =
,
то собственные значения линейного
преобразования А можно найти как корни
1,
2,
… ,n
уравнения:

Это
уравнение называется характеристическим
уравнением,
а его левая часть- характеристическим
многочленом
линейного преобразования А.

Следует
отметить, что характеристический
многочлен линейного преобразования не
зависит от выбора базиса.

Рассмотрим
частный
случай. Пусть
А – некоторое линейное преобразование
плоскости, матрица которого равна
.
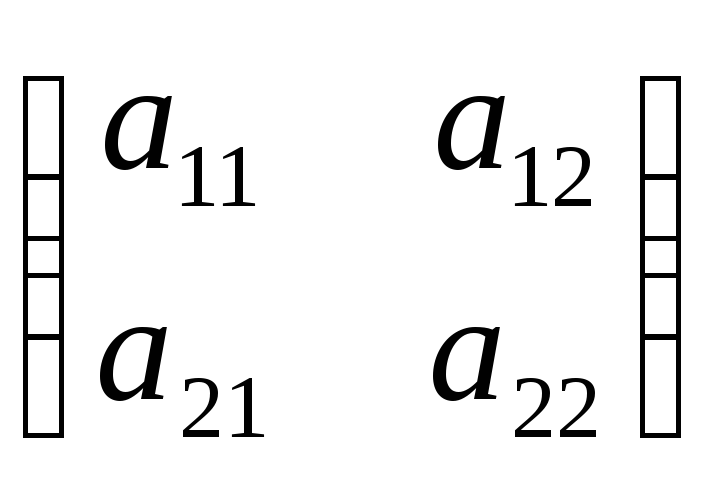
Тогда преобразование А может быть задано
формулами:

;

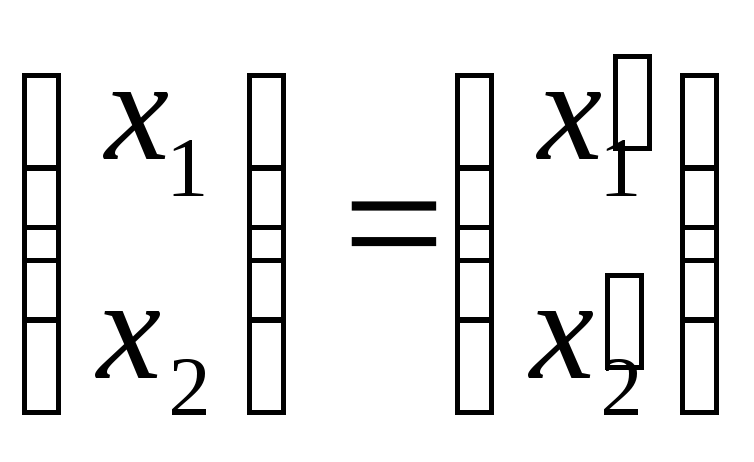
в
некотором базисе
.

Если
преобразование А имеет собственный
вектор с собственным значением ,
то А.


или

Т.к.
собственный вектор
ненулевой,
то х1
и х2
не равны нулю одновременно. Т.к. данная
система однородна, то для того, чтобы
она имела нетривиальное решение,
определитель системы должен быть равен
нулю. В противном случае по правилу
Крамера система имеет единственное
решение – нулевое, что невозможно.

Полученное
уравнение является характеристическим
уравнением линейного преобразования
А.

Таким
образом, можно найти собственный вектор
(х1,
х2)
линейного преобразования А с собственным
значением ,
где 
— корень характеристического уравнения,
а х1
и х2
– корни системы уравнений при подстановке
в нее значения .

Понятно,
что если характеристическое уравнение
не имеет действительных корней, то
линейное преобразование А не имеет
собственных векторов.

Следует
отметить, что если
—
собственный вектор преобразования А,
то и любой вектор ему коллинеарный –
тоже собственный с тем же самым собственным
значением .

Действительно,
.
Если учесть, что векторы имеют одно
начало, то эти векторы образуют так
называемое собственное
направление или
собственную
прямую.

Т.к.
характеристическое уравнение может
иметь два различных действительных
корня 1
и 2,
то в этом случае при подстановке их в
систему уравнений получим бесконечное
количество решений. (Т.к. уравнения
линейно зависимы). Это множество решений
определяет две собственные
прямые.

Если
характеристическое уравнение имеет
два равных корня 1
= 2
= ,
то либо имеется лишь одна собственная
прямая, либо, если при подстановке в
систему она превращается в систему
вида:
.
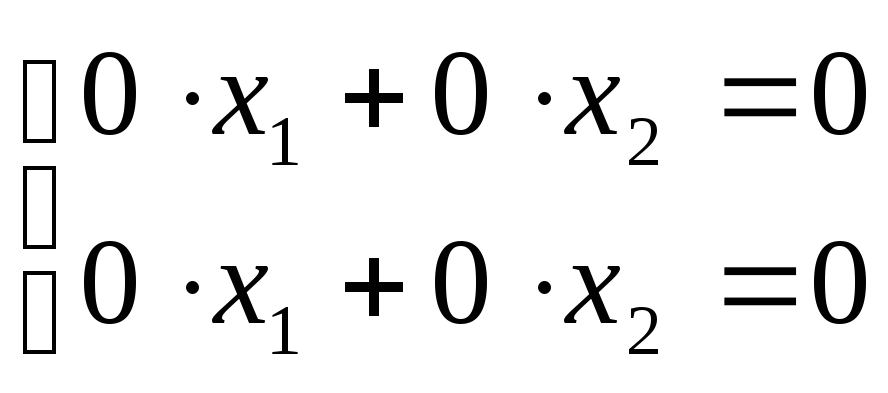
Эта система удовлетворяет любым значениям
х1
и х2.
Тогда все векторы будут собственными,
и такое преобразование называется
преобразованием
подобия.

Пример.
Найти характеристические числа и
собственные векторы линейного
преобразования с матрицей А =
.

Запишем
линейное преобразование в виде:

Составим
характеристическое уравнение:

2
— 8
+ 7 = 0;

Корни
характеристического уравнения: 1
= 7; 2
= 1;

Для
корня 1
= 7:

Из
системы получается зависимость: x1
– 2x2
= 0. Собственные
векторы для первого корня характеристического
уравнения имеют координаты: (t;
0,5t)
где t—
параметр.

Для
корня 2
= 1:

Из
системы получается зависимость: x1
+ x2
= 0. Собственные
векторы для второго корня характеристического
уравнения имеют координаты: (t;
—t)
где t—
параметр.

Полученные
собственные векторы можно записать в
виде:

Пример.
Найти характеристические числа и
собственные векторы линейного
преобразования с матрицей А =
.

Запишем
линейное преобразование в виде:

Составим
характеристическое уравнение:

2
— 4
+ 4 = 0;

Корни
характеристического уравнения: 1
= 2
= 2;

Получаем:

Из
системы получается зависимость: x1
– x2
= 0. Собственные
векторы для первого корня характеристического
уравнения имеют координаты: (t;
t)
где t—
параметр.

Собственный
вектор можно записать:
.

Рассмотрим
другой частный
случай. Если
—
собственный вектор линейного преобразования
А, заданного в трехмерном линейном
пространстве, а х1,
х2,
х3
– компоненты этого вектора в некотором
базисе
,
то

,

где 
— собственное значение (характеристическое
число) преобразования А.

Если
матрица линейного преобразования А
имеет вид:

,
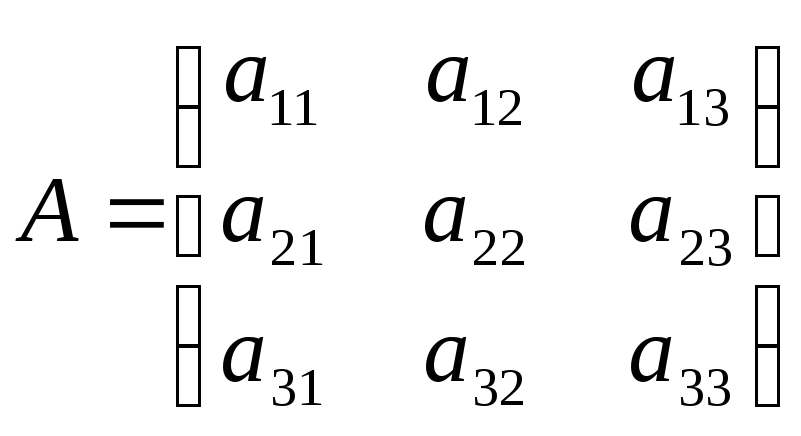
то

Характеристическое
уравнение:

Раскрыв
определитель, получим кубическое
уравнение относительно .
Любое кубическое уравнение с действительными
коэффициентами имеет либо один, либо
три действительных корня.

Тогда
любое линейное преобразование в
трехмерном пространстве имеет собственные
векторы.

Пример.
Найти характеристические числа и
собственные векторы линейного
преобразования А, матрица линейного
преобразования А =
.

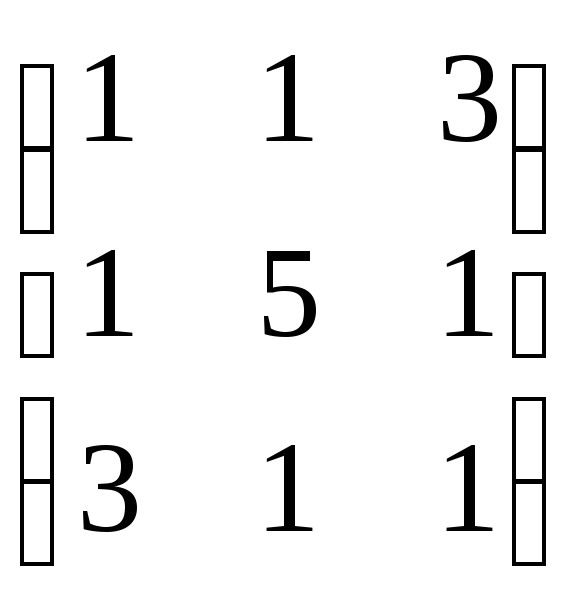
Составим
характеристическое уравнение:

(1
— )((5
— )(1
— )
— 1) — (1 — 
— 3) + 3(1 — 15 + 3)
= 0

(1
— )(5
— 5
— 
+ 2
— 1) + 2 + 
— 42 + 9
= 0

(1
— )(4
— 6
+ 2)
+ 10
— 40 = 0

4
— 6
+ 2
— 4
+ 62
— 3
+ 10
— 40 = 0

-3
+ 72
– 36 = 0

-3
+ 92
— 22
– 36 = 0

-2(
+ 2) + 9(2
– 4) = 0

(
+ 2)(-2
+ 9
— 18) = 0

Собственные
значения: 1
= -2; 2
= 3; 3
= 6;

1)
Для 1
= -2:

Если
принять х1
= 1, то

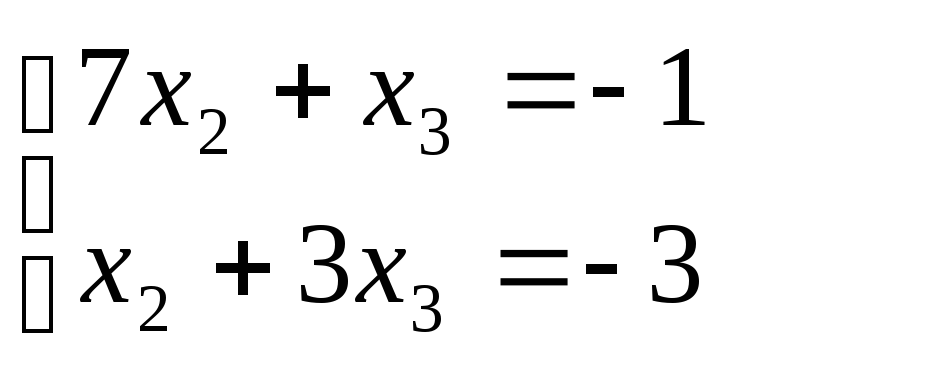
х2
= 0; x3
= -1;

Собственные
векторы:

2)
Для 2
= 3:

Если
принять х1
= 1, то

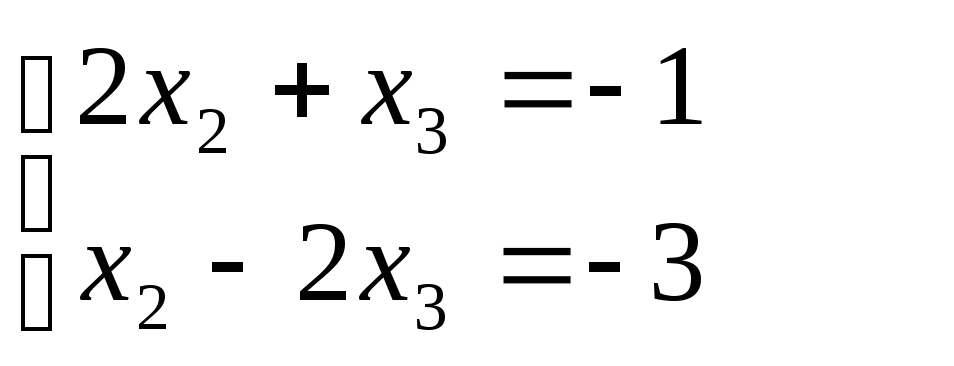
х2
= -1; x3
= 1;

Собственные
векторы:

3)
Для 3
= 6:

Если
принять х1
= 1, то

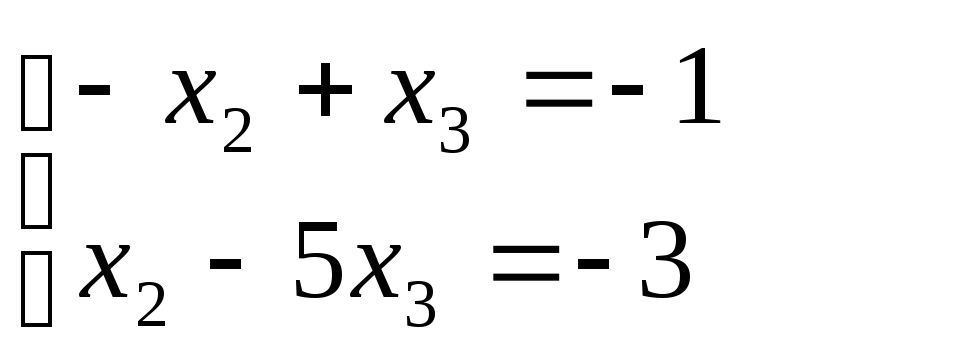
х2
= 2; x3
= 1;

Собственные
векторы:

Пример.
Найти характеристические числа и
собственные векторы линейного
преобразования А, матрица линейного
преобразования А =
.

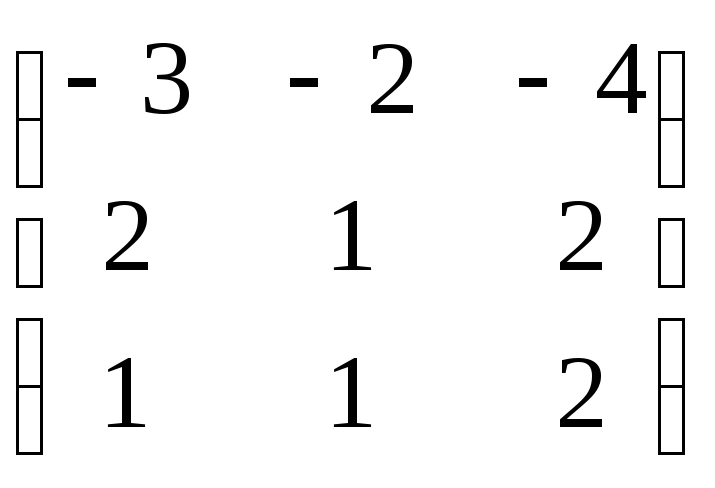
Составим
характеристическое уравнение:

-(3
+ )((1
— )(2
— )
– 2) + 2(4 — 2
— 2) — 4(2 — 1 + )
= 0

-(3
+ )(2
— 
— 2
+ 2
— 2) + 2(2 — 2)
— 4(1 + )
= 0

-(3
+ )(2
— 3)
+ 4 — 4
— 4 — 4
= 0

-32
+ 9
— 3
+ 32
— 8
= 0

-3
+ 
= 0

1
= 0; 2
= 1; 3
= -1;

Для
1
= 0:

Если
принять х3
= 1, получаем х1
= 0, х2
= -2

Собственные
векторы
t,
где t
– параметр.

Для
самостоятельного решения:
Аналогично найти
и

для 2
и 3.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Будем рассматривать двумерный случай.

Матрица преобразования — это некоторая матрица . Мы будем рассматривать матрицы вида

Допустим есть какое-то преобразование , и (к точке применили преобразование и получили точку ).

Тогда матрица преобразования , умноженная на однородные координаты , даёт однородные координаты .

В каком-то смысле, любое линейное преобразование одновременно является матрицей, так же как точка — это набор координат.

Посмотрим как меняются координаты при преобразовании.

.

То есть новые координаты как-то линейно зависят от старых.

Рассмотрим частные случаи преобразований.

Содержание

  • 1 Базовые преобразования
    • 1.1 Параллельный перенос
    • 1.2 Масштабирование вдоль осей
    • 1.3 Поворот относительно начала координат
    • 1.4 Тождественное преобразование
  • 2 Композиция преобразований

Базовые преобразования

Параллельный перенос

Задаёт преобразование .

Обозначается , где — вектор параллельного переноса.

Пример
Задача: Найдите новые координаты точки после параллельного переноса плоскости на вектор .

Решение:

Вполне ожидаемый ответ.

Масштабирование вдоль осей

Задаёт преобразование .

Будем обозначать как . Числа и называются коэффициентами масштабирования.

Пример

Задача: Найдите новые координаты точки после масштабирования по оси с коэффициентом 2 (по оси масштаб остаётся таким же).

Решение:

Поворот относительно начала координат

Обозначается , где — угол поворота.
Как обычно, при повороте против часовой стрелки, и при повороте по часовой стрелке.

Пример
Задача: Найдите новые координаты точки после поворота плоскости на °.

Решение:

Замечание

, то есть центральная симметрия относительно начала координат меняет координаты точки на противоположные.

Тождественное преобразование

Это преобразование, оставляющее все точки неподвижными.

Его матрица:

Композиция преобразований

Задача: к точке применили осевую симметрию относительно , и затем применили параллельный перенос на . Какие новые координаты у точки?

Решение: обозначим нашу точку за , новую точку за

Посчитаем двумя способами.

1)

2) Воспользуемся ассоциативностью умножения матриц (сочетательный закон)

Заметим, что — тоже какая-то матрица преобразования, в данном случае «осевая симметрия относительно , с последующим параллельным переносом на »

Действительно,

Тогда матрица для будет .

Получается, при композиции преобразований их матрицы перемножаются.

Источник

Линейные операторы (преобразования)

Определение линейных операторов (преобразований)

Линейным преобразованием (линейным оператором) линейного пространства {V} называется линейное отображение mathcal{A}colon Vto V пространства {V} в себя.

Поскольку линейное преобразование является частным случаем линейного отображения, к нему применимы все понятия и свойства, рассмотренные для отображений: инъективность, сюръективность, биективность, обратимость, ядро, образ, дефект, ранг и т.д.

Матрицей линейного оператора (преобразования) mathcal{A}colon Vto V в базисе mathbf{e}_1,ldots,mathbf{e}_n пространства {V} называется квадратная матрица A, составленная из координатных столбцов образов базисных векторов mathcal{A}(mathbf{e}_1),ldots,mathcal{A}(mathbf{e}_n), найденных относительно базиса mathbf{e}_1,ldots,mathbf{e}_n.

Матрица биективного линейного оператора (преобразования) обратима, т.е. невырождена. Поэтому биективное (обратимое) преобразование называют также невырожденным.

Примеры линейных операторов (преобразований)

1. Обозначим mathcal{O}colon Vto V — нулевое преобразование n-мерного пространства {V}, которое ставит в соответствие любому вектору mathbf{v}in V нулевой элемент boldsymbol{o} пространства {V}. Это преобразование не является инъективным, сюръективным, биективным, обратимым. Матрица нулевого преобразования (в любом базисе) нулевая, ядро преобразования ker mathcal{O}=V, образ преобразования operatorname{im} mathcal{O}={boldsymbol{o}}, дефект d=n, ранг r=0.

2. Обозначим mathcal{E}colon Vto V — тождественное преобразование n-мерного пространства {V}, которое ставит в соответствие каждому вектору mathbf{v}in V этот же вектор mathcal{E}(mathbf{v})=mathbf{v}. Это преобразование является инъективным, сюръективным, биективным, обратимым. Матрица тождественного преобразования (в любом базисе) единичная n-го порядка, ядро преобразования ker mathcal{E}={boldsymbol{o}}, образ преобразования operatorname{im} mathcal{E}=V, дефект d=0, ранг r=n.

3. Обозначим mathcal{Z}_{boldsymbol{o}}colon Vto V — центральную симметрию n-мерного пространства V (относительно нулевого вектора boldsymbol{o}), т.е. преобразование, которое каждому вектору ставит в соответствие противоположный ему вектор: mathcal{Z}_{boldsymbol{o}}(mathbf{v})=-mathbf{v}. Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Матрица преобразования противоположна единичной (в любом базисе): Z_0=E; ядро преобразования ker mathcal{Z}_{boldsymbol{o}}={boldsymbol{o}}, образ преобразования operatorname{im} mathcal{Z}_{boldsymbol{o}}=V, дефект d=o, ранг r=n.

4. Обозначим mathcal{H}_{lambda}colon Vto V — гомотетию n-мерного пространства {V} (с коэффициентом lambda), т.е. преобразование, которое каждому вектору ставит в соответствие коллинеарный ему вектор: mathcal{H}_{lambda} (mathbf{v})=lambdacdot mathbf{v}. Это преобразование линейное. При lambdane0 оно инъективное, сюръективное, биективное, обратимое. Матрица преобразования пропорциональна единичной (в любом базисе): H_{lambda}=lambdacdot E, ядро преобразования ker mathcal{H}_{lambda}= {boldsymbol{0}}, образ преобразования operatorname{im} mathcal{H}_{lambda}= V, дефект d=0, ранг r=n. При lambda=0colon, mathcal{H}_{0}=mathcal{O} (см. пункт 1); при lambda=1colon, mathcal{H}_1= mathcal{E} (см. пункт 2); при lambda=-1colon, mathcal{H}_{(-1)}= mathcal{Z}_{boldsymbol{o}} (см. пункт 3).

5. Рассмотрим линейное пространство V_2 радиус-векторов (с общим началом в точке O), принадлежащих одной плоскости (рис. 9.1). Обозначим mathcal{R}_{varphi}colon V_2to V_2 — поворот вокруг точки O (на угол varphi в положительном направлении (против часовой стрелки)). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу поворота в стандартном ортонормированием базисе vec{i},vec{j}. Раскладывая образы vec{i},'= mathcal{R}_{varphi}(vec{i}),~ vec{j},'= mathcal{R}_{varphi}(vec{j}) базисных векторов по базису, получаем

Линейное пространство радиус-векторов

begin{cases} vec{i},'= vec{i}cdot cosvarphi+vec{j}cdot sinvarphi,,\ vec{j},'= -vec{i}cdot sinvarphi+ vec{j}cdot cosvarphi,.end{cases}

Составляем матрицу (9.1) преобразования (оператора), записывая найденные координаты образов по столбцам:

R_{varphi}= begin{pmatrix}cosvarphi&-sinvarphi\ sinvarphi& cosvarphi end{pmatrix}!.

Ядро оператора (преобразования) ker mathcal{R}_{varphi}={boldsymbol{o}}, образ преобразования operatorname{im} mathcal{R}_{varphi}=V_2, дефект d=0, ранг r=2. При varphi=2pi k,~ kin mathbb{Z}colon mathcal{R}_{2pi k}= mathcal{E} (см. пункт 2); при varphi=pi+2pi k,~ kin mathbb{Z}colon mathcal{R}_{pi+2pi k}= mathcal{Z}_{boldsymbol{o}} (см. пункт 3).

6. Обозначим mathcal{D}colon P_n(mathbb{R})to P_{n}(mathbb{R}) — оператор дифференцирования, который каждому многочлену степени не выше и ставит в соответствие его производную, рассматриваемую как многочлен степени не выше ncolon, mathcal{D}(p(x))= p'(x). Это преобразование линейное, неинъективное, несюръективное, небиективное, необратимое. Квадратная матрица ((n+l)-го порядка) преобразования в стандартном базисе имеет вид

D=begin{pmatrix} 0&1&0&cdots&0\ 0&0&2&cdots&0\ vdots&vdots&vdots& ddots&vdots\ 0&0&0&cdots&n\ 0&0&0&cdots&0 end{pmatrix}!.

Ядро преобразования ker mathcal{D}=P_0(mathbb{R}) — пространство многочленов нулевой степени, образ operatorname{im} mathcal{D}=P_{n-1}(mathbb{R}) — пространство многочленов степени не выше (n-1), дефект d=1, ранг r=1, dim P_n(mathbb{R})=n+1.

Рассмотрим преобразование mathcal{D}colon T_{omega}(mathbb{R})to T_{omega} (mathbb{R}) линейного пространства тригонометрических многочленов (частоты omegane0) с действительными коэффициентами: T_{omega}(mathbb{R})= operatorname{Lin} (sinomega t,cosomega t), т.е. T_{omega}(mathbb{R}) — множество функций вида f(t)=asinomega t+bcosomega t, где a,bin mathbb{R}. Заметим, что это множество является двумерным вещественным линейным пространством. Стандартный базис пространства T_{omega}(mathbb{R}) образуют функции mathbf{e}_1(t)=sinomega t, mathbf{e}_2(t)=cosomega t, поскольку они линейно независимы (тождественное равенство нулю asinomega t+bcosomega tequiv0 возможно только в тривиальном случае a=b=0). При дифференцировании функции f(t) получаем функцию f'(t)=-bomega sinomega t+aomegacosomega t того же вида. Следовательно, преобразование mathcal{D}colon T_{omega}(mathbb{R})to T_{omega} (mathbb{R}) определено. Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу преобразования в стандартном базисе mathbf{e}_1(t)=sinomega t, mathbf{e}_2(t)=cosomega t. Раскладывая образы базисных векторов, получаем

begin{aligned} mathcal{D}(mathbf{e}_1)&= omegacosomega t= 0cdotsinomega t+omegacosomega t,,\[5pt] mathcal{D}(mathbf{e}_2)&= -omegasinomega t= -omegasinomega t+0cdotcosomega t,.end{aligned}

Составляем матрицу (9.1) преобразования, записывая найденные координаты образов по столбцам: D=begin{pmatrix}0&-omega\ omega&0end{pmatrix}. Ядро преобразования ker mathcal{D}= {boldsymbol{o}(t)} — нулевое подпространство, образ operatorname{im} mathcal{D}=T_{omega}(mathbb{R}), дефект d=0, ранг r=2, boldsymbol{o}(t)= 0cdotsinomega t+0cdotcosomega t.

Аналогичными свойствами обладает преобразование mathcal{D}colon T_{omega} (mathbb{C})to T_{omega}(mathbb{C}), где T_{omega}(mathbb{C})= operatorname{Lin} (sinomega t,cosomega t) — множество функций вида asinomega t+bcosomega t с комплексными коэффициентами ain mathbb{C} и bin mathbb{C}. Множество T_{omega}(mathbb{C}) является двумерным комплексным линейным пространством.

7. Пусть линейное пространство разлагается в прямую сумму подпространств V=L_1oplus L_2. Обозначим Pi_{L_1}colon Vto V — оператор проектирования на подпространство L_1 параллельно подпространству L_2, который каждому вектору mathbf{v}=mathbf{v}_1+mathbf{v}_2, где mathbf{v}_1in L_1,~ mathbf{v}_2in L_2, ставит в соответствие его составляющую (проекцию) mathbf{v}_1in L_1, т.е. Pi_{L_1}(mathbf{v}_1+mathbf{v}_2)= mathbf{v}_1 (рис.9.2). Это преобразование линейное. При L_1ne V оно неинъективное, несюръективное, небиективное, необратимое. Ядро преобразования ker Pi_{L_1}=L_2, образ преобразования operatorname{im} Pi_{L_1}=L_1, дефект d=dim{L_2}, Ранг r=dim{L_1},. При L_1=Vcolon, Pi_V=mathcal{E}; при L_2=Vcolon, Pi_{{boldsymbol{o}}}= mathcal{O}.

Оператор проектирования на подпространство параллельно подпространству

8. Пусть линейное пространство разлагается в прямую сумму подпространств V=L_1oplus L_2. Обозначим mathcal{Z}_{L_1}colon Vto V — оператор отражения в подпространстве L_1 параллельно подпространству L_2 (или преобразование симметрии относительно подпространства L_1 параллельно подпространству L_2), который каждому вектору mathbf{v}=mathbf{v}_1+ mathbf{v}_2, где mathbf{v}_1in L_1,~ mathbf{v}_2in L_2, ставит в соответствие вектор (mathbf{v}_1-mathbf{v}_2), т.е. mathcal{Z}_{L_1} (mathbf{v}_1+mathbf{v}_2)= mathbf{v}_1-mathbf{v}_2 (рис. 9.3). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Ядро преобразования ker mathcal{Z}_{L_1}={boldsymbol{o}}, образ преобразования operatorname{im} mathcal{Z}_{L_1}=V, дефект d=0, ранг r=dim{V}. При L_1=Vcolon, mathcal{Z}_{L_1}= mathcal{E}.

Матрицы линейного оператора (преобразования) в разных базисах

Найдем связь матриц одного и того же линейного оператора (преобразования) в разных базисах.

Пусть в базисе (mathbf{e})=(mathbf{e}_1,ldots,mathbf{e}_n) преобразование mathcal{A}colon Vto V имеет матрицу mathop{A}limits_{(mathbf{e})}, а в базисе (mathbf{f})=(mathbf{f}_1,ldots, mathbf{}_n) — матрицу mathop{A}limits_{(mathbf{f})}. Если S — матрица перехода от базиса (mathbf{e}) к базису (mathbf{f}), то

mathop{A}limits_{(mathbf{f})}= S^{-1}cdot mathop{A}limits_{(mathbf{e})} cdot S.

(9.4)

Докажем формулу (9.4). Пусть векторы mathbf{v} и mathbf{w} в базисах (mathbf{e}) и (mathbf{f}) имеют координатные столбцы mathop{v}limits_{(mathbf{e})}, mathop{v}limits_{(mathbf{f})} и mathop{w}limits_{(mathbf{e})}, mathop{w}limits_{(mathbf{f})} соответственно. Если w=mathcal{A}(mathbf{v}), то по формуле (9.2) имеем

mathop{w}limits_{(mathbf{e})}= mathop{A}limits_{(mathbf{e})}cdot mathop{v}limits_{(mathbf{e})},qquad mathop{w}limits_{(mathbf{f})}= mathop{A}limits_{(mathbf{f})}cdot mathop{v}limits_{(mathbf{f})}.

Подставляя в первое равенство связи координат векторов в разных базисах mathop{v}limits_{(mathbf{e})}= Scdot mathop{v}limits_{(mathbf{f})}, mathop{w}limits_{(mathbf{e})}= Scdot mathop{w}limits_{(mathbf{f})} получаем Scdot mathop{w}limits_{(mathbf{f})}= mathop{A}limits_{(mathbf{e})}cdot Scdot mathop{v}limits_{(mathbf{f})} или, учитывая обратимость матрицы Scolon mathop{w}limits_{(mathbf{f})}= S^{-1}cdot mathop{A}limits_{(mathbf{e})}cdot Scdot mathop{v}limits_{(mathbf{f})}. Сравнивая последнее равенство с mathop{w}limits_{(mathbf{f})}= mathop{A}limits_{(mathbf{f})}cdot mathop{v}limits_{(mathbf{f})}, убеждаемся в справедливости (9.4).

Замечания 9.2

1. Матрицы линейного преобразования в разных базисах оказываются подобными. И наоборот, любые две подобные матрицы являются матрицами некоторого линейного преобразования, найденными относительно разных базисов.

2. Для матриц преобразований справедливы свойства, рассмотренные ранее. В частности, при фиксированном базисе матрица суммы преобразований равна сумме их матриц, матрица произведения преобразования на число равна произведению матрицы преобразования на это же число, матрица композиции преобразований равна произведению матриц преобразований, матрица обратного преобразования является обратной для матрицы обратимого преобразования.

Алгебра линейных операторов (преобразований)

Рассмотрим множество mathcal{L}(V) — линейных преобразований (операторов) n-мерного линейного пространства V. Напомним, что два преобразования mathcal{A}colon Vto V и mathcal{B}colon Vto V называются равными, если mathcal{A}(mathbf{v})= mathcal{B}(mathbf{v})~ forall mathbf{v}in V.

На множестве mathcal{L}(V) определены две линейные операции: сложение преобразований и умножение преобразования на число, поскольку в результате этих операций получается линейное преобразование.

Нетрудно показать, что эти операции удовлетворяют условиям:

1. mathcal{A}+mathcal{B}= mathcal{B}+mathcal{A}quad forall mathcal{A},mathcal{B}in mathcal{L}(V);

2. mathcal{A}+(mathcal{B}+mathcal{C})= (mathcal{A}+mathcal{B})+mathcal{C}quad forall mathcal{A},mathcal{B},mathcal{C}in mathcal{L}(V);

3. существует нулевое преобразование mathcal{O}inmathcal{L}(V) такое, что mathcal{A}+mathcal{O}=mathcal{A}~ forall mathcal{A}in mathcal{L}(V);

4. для каждого преобразования mathcal{A} существует противоположное преобразование (-mathcal{A})=(-1)cdot mathcal{A} такое, что mathcal{A}+(-mathcal{A})=mathcal{O};

5. lambdacdot(mathcal{A}+mathcal{B})= lambdacdot mathcal{A}+lambdacdot mathcal{B}~ forall mathcal{A},mathcal{B}in mathcal{L}(V) и любого числа lambda;

6. (lambda+mu)cdot mathcal{A}= lambdacdot mathcal{A}+mucdot mathcal{A}~ forall mathcal{A}in mathcal{L}(V) и любых чисел lambda,,mu;

7. lambdacdot (mucdot mathcal{A})=(lambdamu)cdot mathcal{A}~ forall mathcal{A}in mathcal{L}(V) и любых чисел lambda,,mu;

8. 1cdot mathcal{A}quad forall mathcal{A}in mathcal{L}(V).

В условиях 5-7 говорится о числах из того же числового поля, над которым определено линейное пространство {V}.

Условия 1-8 повторяют аксиомы линейного пространства. Поэтому множество mathcal{L}(V) с линейными операциями является линейным пространством. Если пространство {V} вещественное (комплексное), то и пространство mathcal{L}(V) вещественное (комплексное).

Найдем размерность пространства mathcal{L}(V). При фиксированном базисе имеется взаимно однозначное соответствие между линейными преобразованиями и их матрицами, причем это соответствие сохраняет линейные операции. Следовательно, пространство mathcal{L}(V) изоморфно пространству M_{ntimes n} — квадратных матриц n-го порядка. Размерность пространства M_{ntimes n} равна n^2. По теореме 8.3:

dimmathcal{L}(V)= dim M_{ntimes n}=n^2, то есть dimmathcal{L}(V)= (dim{V})^2.

Кроме линейных операций в множестве mathcal{L}(V) определена операция умножения элементов. Произведением преобразований mathcal{A} и mathcal{B} назовем их композицию, т.е. mathcal{A}mathcal{B}= mathcal{A}circ mathcal{B}. В результате композиции линейных преобразований получается линейное преобразование. Операция умножения удовлетворяет следующим условиям:

1. mathcal{A}(mathcal{B}mathcal{C})= (mathcal{A}mathcal{B})mathcal{C}quad forall mathcal{A},mathcal{B},mathcal{C}in mathcal{L}(V);

2. mathcal{A}(mathcal{B}+mathcal{C})= mathcal{A}mathcal{B}+mathcal{A} mathcal{C} quad forall mathcal{A},mathcal{B},mathcal{C}in mathcal{L}(V);

3. (mathcal{A}+mathcal{B})mathcal{C}= mathcal{A}mathcal{C}+mathcal{B}mathcal{C} quad forall mathcal{A},mathcal{B},mathcal{C}in mathcal{L}(V);

4. существует тождественное преобразование mathcal{E} такое, что mathcal{A} mathcal{E}= mathcal{E}mathcal{A}= mathcal{A}~ forall mathcal{A}in mathcal{L}(V).

Первое условие выражает ассоциативность операции умножения, условия 2 и 3 — законы дистрибутивности, условие 4 — существование нейтрального элемента. Множество mathcal{L}(V) с операциями сложения и умножения элементов является кольцом с единицей (вообще говоря, некоммутативное, так как в общем случае mathcal{A} mathcal{B}ne mathcal{B}mathcal{A}).

Операции умножения операторов (преобразований) и произведения операторов на число (из заданного числового поля) удовлетворяют условию:

5. (lambdacdot mathcal{A})mathcal{B}= mathcal{A}(lambdacdot mathcal{B})= lambdacdot (mathcal{A}mathcal{B}).

Линейное пространство, которое является кольцом, удовлетворяющим условию 5, называется алгеброй. Поэтому множество mathcal(V) называют алгеброй линейных операторов (преобразований).

Многочлены от линейного оператора (преобразования)

В алгебре mathcal(V) можно определить целую неотрицательную степень оператора mathcal{A}colon Vto V , полагая по определению

mathcal{A}^0=mathcal{E},quad mathcal{A}^1=mathcal{A},quad mathcal{A}^2=mathcal{A}mathcal{A},ldots, mathcal{A}^n=mathcal{A}^{n-1}mathcal{A}.

Пусть p(lambda)=a_m lambda^m+ldots+a_1 lambda+a_0 — многочлен переменной lambda. Многочленом p(mathcal{A}) от линейного преобразования mathcal{A} называется преобразование p(mathcal{A})= a_m mathcal{A}^m+ldots+ a_1 mathcal{A}+ a_0 mathcal{E}.

Многочлен p(lambda)=a_m lambda^m+ldots+a_1 lambda+a_0 называется аннулирующим для линейного преобразования mathcal{A}, если p(mathcal{A})= mathcal{O} — нулевое преобразование. Заметим, что у каждого линейного преобразования mathcal{A}colon Vto V n-мерного линейного пространства V существует аннулирующий многочлен степени не выше n^2. Действительно, система из (n^2+1) элементов mathcal{E}, mathcal{A},ldots,mathcal{A}^{n^2} линейного пространства mathcal{L}(V) линейно зависима (так как dimmathcal{L}(V)=n^2). Поэтому существуют такие числа a_0,a_1,ldots,a_{n^2}, не все равные нулю одновременно, что a_{n^2} mathcal{A}^{n^2}+ ldots+ a_1 mathcal{A}+a_0 mathcal{E}=mathcal{O}. Следовательно, многочлен p(lambda)= a_{n^2}lambda^{n^2}+ldots+ a_1 lambda+a_0 — аннулирующий для преобразования mathcal{A}.

Замечания 9.3

1. При фиксированном базисе каждому преобразованию (оператору) можно сопоставить его матрицу. Свойства линейных операций 1-8, записанные для матриц преобразований, повторяют свойства линейных операций с матрицами, а свойствам 1-5 произведения операторов отвечают свойства операции умножения матриц.

2. При фиксированном базисе многочлен p(mathcal{A}) от линейного преобразования mathcal{A} имеет матрицу p(A)=a_m A^m+ldots +a_1A+a_0E, где A — матрица преобразования mathcal{A} в том же базисе. Поэтому свойства многочленов от матриц переносятся на многочлены от линейного преобразования. В частности, многочлены от одного преобразования перестановочны:

begin{aligned}p(mathcal{A})cdot q(mathcal{A})&= Biggl(sum_{i=1}^{m}a_i mathcal{A}^iBiggr)cdot Biggl(sum_{j=1}^{k}b_j mathcal{A}^jBiggr)= sum_{i=1}^{m} sum_{j=1}^{k} a_ib_j mathcal{A}^{i+j}=\[2pt] &= sum_{j=1}^{k} sum_{i=1}^{m} b_ja_i mathcal{A}^{j+i}= Biggl(sum_{j=1}^{k}b_j mathcal{A}^jBiggr)cdot Biggl(sum_{i=1}^{m} a_{i}mathcal{A}^iBiggr)= q(mathcal{A})cdot p(mathcal{A}). end{aligned}

3. Функции от матриц определяются при помощи многочленов от матриц. Поэтому можно определить функции от линейных преобразований.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти нотариуса в егрюл
  • Как найти синус угла по теореме косинусов
  • Как найти неповторяющиеся комбинации
  • Портфолио нмо образец как составить
  • Как найти артефакты на оазисе