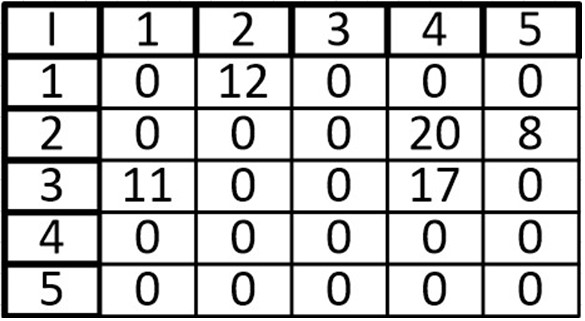
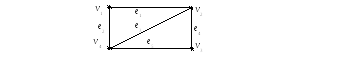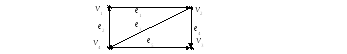Как составить матрицу смежности вершин графа - Исправление недочетов и поиск решений вместе с Examum.ru

Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор

В этой статье:

Матрица смежности

Матрица инцидентности

Список смежности (инцидентности)

Взвешенный граф (коротко)

Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.

Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).

Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).

Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.

Матрица смежности

Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.

Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.

Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.

Каждая ячейка матрицы равна либо 1, либо 0;

Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.

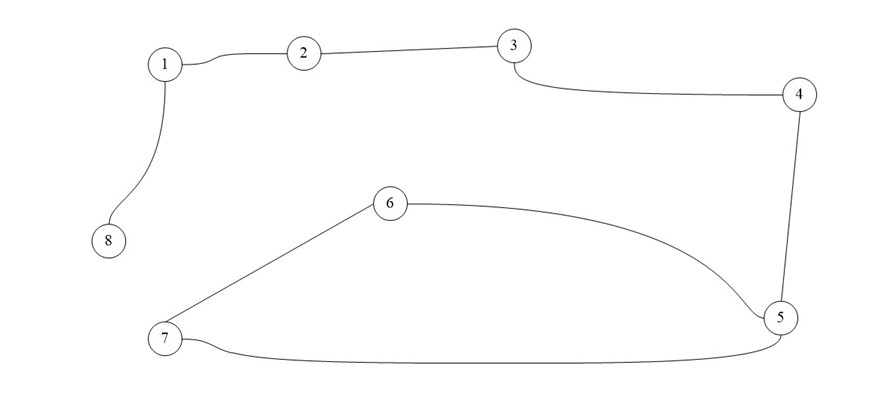
Для практического примера возьмем самый обыкновенный неориентированный граф:

А теперь представим его в виде матрицы:

Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.

С одной стороны объем памяти будет:

Но используя вышеописанный подход получается:

Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.

Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.

Если мы используем ориентированный граф, то кое-что меняется.

Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.

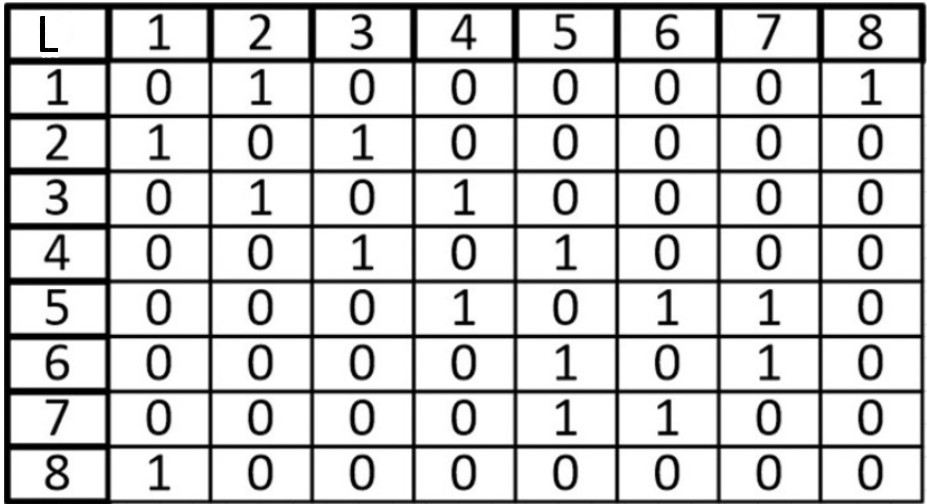
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:

В виде матрицы:

Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.

Объем памяти:

Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.

Используя петли мы должны запомнить, что в неориентированном графе петля учитывается дважды, а в ориентированном — единожды.

Матрица инцидентности

Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.

Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.

Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.

Сразу же иллюстрируем данное правило:

В виде матрицы:

Сумма элементов i-ой строки равна степени вершины.

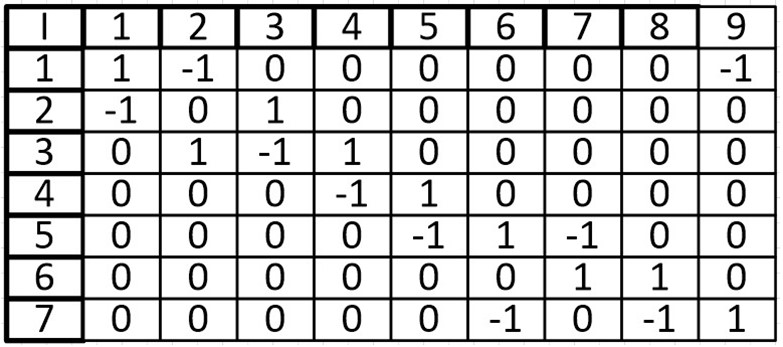
При ориентированным графе, ячейка I (i, j) равна 1, если вершина V (i) начало дуги E(j) и ячейка I (i, j) равна -1 если вершина V (i) конец дуги E (j), иначе ставится 0.

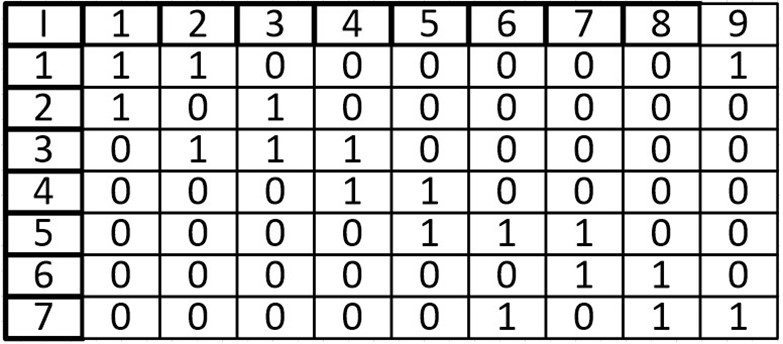
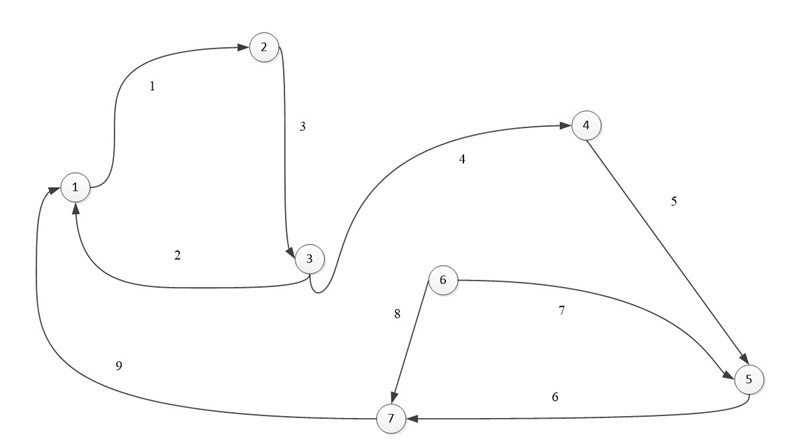
Ориентированный граф:

В виде матрицы:

Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.

При суммировании строки, ячейки со значением -1, могут складываться только с ячейками, также имеющими значение -1, то же касается и 1, мы можем узнать степень входа и степень выхода из вершины. Допустим при сложении первой вершины, мы узнаем, что из нее исходит 1 ребро и входят два других ребра. Это является еще одной особенностью (при том очень удобной) данной матрицы.

Объем памяти:

Список смежности (инцидентности)

Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.

В виде списка это будет выглядеть так:

Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.

Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:

Объем памяти:

Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).

В виде списка:

Сумма длин всех списков:

Объем памяти:

Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.

К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.

Взвешенность графа

Взвешенный граф — это граф, в котором вместо 1 обозначающее наличие связи между вершинами или связи между вершиной и ребром, хранится вес ребра, то есть определённое число с которым мы будем проводить различные действия.

К примеру, возьмем граф с весами на ребрах:

И сделаем матрицу смежности:

В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.

Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.

Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.

Если заметили ошибку или есть предложения пишите в комментарии.

Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.

На каком языке программирования проводить операции с графами

21.28%
Использовать оба
10

Проголосовали 47 пользователей.

Воздержались 8 пользователей.

Источник

From Wikipedia, the free encyclopedia

In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.

In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is undirected (i.e. all of its edges are bidirectional), the adjacency matrix is symmetric.
The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory.

The adjacency matrix of a graph should be distinguished from its incidence matrix, a different matrix representation whose elements indicate whether vertex–edge pairs are incident or not, and its degree matrix, which contains information about the degree of each vertex.

Definition[edit]

For a simple graph with vertex set U = {u₁, …, u_n}, the adjacency matrix is a square n × n matrix A such that its element A_ij is one when there is an edge from vertex u_i to vertex u_j, and zero when there is no edge.^[1] The diagonal elements of the matrix are all zero, since edges from a vertex to itself (loops) are not allowed in simple graphs. It is also sometimes useful in algebraic graph theory to replace the nonzero elements with algebraic variables.^[2] The same concept can be extended to multigraphs and graphs with loops by storing the number of edges between each two vertices in the corresponding matrix element, and by allowing nonzero diagonal elements. Loops may be counted either once (as a single edge) or twice (as two vertex-edge incidences), as long as a consistent convention is followed. Undirected graphs often use the latter convention of counting loops twice, whereas directed graphs typically use the former convention.

Of a bipartite graph[edit]

The adjacency matrix A of a bipartite graph whose two parts have r and s vertices can be written in the form

${displaystyle A={begin{pmatrix}0_{r,r}&B\B^{mathsf {T}}&0_{s,s}end{pmatrix}},}$

where B is an r × s matrix, and 0_r,r and 0_s,s represent the r × r and s × s zero matrices. In this case, the smaller matrix B uniquely represents the graph, and the remaining parts of A can be discarded as redundant. B is sometimes called the biadjacency matrix.

Formally, let G = (U, V, E) be a bipartite graph with parts U = {u₁, …, u_r}, V = {v₁, …, v_s} and edges E. The biadjacency matrix is the r × s 0–1 matrix B in which b_i,j = 1 if and only if (u_i, v_j) ∈ E.

If G is a bipartite multigraph or weighted graph, then the elements b_i,j are taken to be the number of edges between the vertices or the weight of the edge (u_i, v_j), respectively.

Variations[edit]

An (a, b, c)-adjacency matrix A of a simple graph has A_i,j = a if (i, j) is an edge, b if it is not, and c on the diagonal. The Seidel adjacency matrix is a (−1, 1, 0)-adjacency matrix. This matrix is used in studying strongly regular graphs and two-graphs.^[3]

The distance matrix has in position (i, j) the distance between vertices v_i and v_j. The distance is the length of a shortest path connecting the vertices. Unless lengths of edges are explicitly provided, the length of a path is the number of edges in it. The distance matrix resembles a high power of the adjacency matrix, but instead of telling only whether or not two vertices are connected (i.e., the connection matrix, which contains boolean values), it gives the exact distance between them.

Examples[edit]

Undirected graphs[edit]

The convention followed here (for undirected graphs) is that each edge adds 1 to the appropriate cell in the matrix, and each loop adds 2.^[4] This allows the degree of a vertex to be easily found by taking the sum of the values in either its respective row or column in the adjacency matrix.

Labeled graph	Adjacency matrix
	${displaystyle {begin{pmatrix}2&1&0&0&1&0\1&0&1&0&1&0\0&1&0&1&0&0\0&0&1&0&1&1\1&1&0&1&0&0\0&0&0&1&0&0end{pmatrix}}}$ Coordinates are 1–6.
Nauru graph	Coordinates are 0–23. White fields are zeros, colored fields are ones.

Labeled graph

Adjacency matrix

${displaystyle {begin{pmatrix}2&1&0&0&1&0\1&0&1&0&1&0\0&1&0&1&0&0\0&0&1&0&1&1\1&1&0&1&0&0\0&0&0&1&0&0end{pmatrix}}}$

Coordinates are 1–6.

Symmetric group 4; Cayley graph 1,5,21 (Nauru Petersen); numbers.svg

Nauru graph

Symmetric group 4; Cayley graph 1,5,21 (adjacency matrix).svg

Coordinates are 0–23.

White fields are zeros, colored fields are ones.

Directed graphs[edit]

The adjacency matrix of a directed graph can be asymmetric. One can define the adjacency matrix of a directed graph either such that

a non-zero element A_ij indicates an edge from i to j or
it indicates an edge from j to i.

The former definition is commonly used in graph theory and social network analysis (e.g., sociology, political science, economics, psychology).^[5] The latter is more common in other applied sciences (e.g., dynamical systems, physics, network science) where A is sometimes used to describe linear dynamics on graphs.^[6]

Using the first definition, the in-degrees of a vertex can be computed by summing the entries of the corresponding column and the out-degree of vertex by summing the entries of the corresponding row. When using the second definition, the in-degree of a vertex is given by the corresponding row sum and the out-degree is given by the corresponding column sum.

Labeled graph	Adjacency matrix
Directed Cayley graph of S₄	Coordinates are 0–23. As the graph is directed, the matrix is not necessarily symmetric.

Labeled graph

Adjacency matrix

Symmetric group 4; Cayley graph 4,9; numbers.svg

Directed Cayley graph of S₄

Symmetric group 4; Cayley graph 4,9 (adjacency matrix).svg

Coordinates are 0–23.

As the graph is directed, the matrix is not necessarily symmetric.

Trivial graphs[edit]

The adjacency matrix of a complete graph contains all ones except along the diagonal where there are only zeros. The adjacency matrix of an empty graph is a zero matrix.

Properties[edit]

Spectrum[edit]

The adjacency matrix of an undirected simple graph is symmetric, and therefore has a complete set of real eigenvalues and an orthogonal eigenvector basis. The set of eigenvalues of a graph is the spectrum of the graph.^[7] It is common to denote the eigenvalues by ${displaystyle lambda _{1}geq lambda _{2}geq cdots geq lambda _{n}.}$

The greatest eigenvalue $lambda _{1}$ is bounded above by the maximum degree. This can be seen as result of the Perron–Frobenius theorem, but it can be proved easily. Let v be one eigenvector associated to $lambda _{1}$ and x the component in which v has maximum absolute value. Without loss of generality assume v_x is positive since otherwise you simply take the eigenvector , also associated to $lambda _{1}$ . Then

${displaystyle lambda _{1}v_{x}=(Av)_{x}=sum _{y=1}^{n}A_{x,y}v_{y}leq sum _{y=1}^{n}A_{x,y}v_{x}=v_{x}deg(x).}$

For d-regular graphs, d is the first eigenvalue of A for the vector v = (1, …, 1) (it is easy to check that it is an eigenvalue and it is the maximum because of the above bound). The multiplicity of this eigenvalue is the number of connected components of G, in particular ${displaystyle lambda _{1}>lambda _{2}}$ for connected graphs. It can be shown that for each eigenvalue $lambda _{i}$ , its opposite ${displaystyle -lambda _{i}=lambda _{n+1-i}}$ is also an eigenvalue of A if G is a bipartite graph.^[8] In particular −d is an eigenvalue of any d-regular bipartite graph.

The difference ${displaystyle lambda _{1}-lambda _{2}}$ is called the spectral gap and it is related to the expansion of G. It is also useful to introduce the spectral radius of denoted by ${displaystyle lambda (G)=max _{left|lambda _{i}right|<d}|lambda _{i}|}$ . This number is bounded by . This bound is tight in the Ramanujan graphs, which have applications in many areas.

Isomorphism and invariants[edit]

Suppose two directed or undirected graphs G₁ and G₂ with adjacency matrices A₁ and A₂ are given. G₁ and G₂ are isomorphic if and only if there exists a permutation matrix P such that

$PA_{1}P^{-1}=A_{2}.$

In particular, A₁ and A₂ are similar and therefore have the same minimal polynomial, characteristic polynomial, eigenvalues, determinant and trace. These can therefore serve as isomorphism invariants of graphs. However, two graphs may possess the same set of eigenvalues but not be isomorphic.^[9] Such linear operators are said to be isospectral.

Matrix powers[edit]

If A is the adjacency matrix of the directed or undirected graph G, then the matrix Aⁿ (i.e., the matrix product of n copies of A) has an interesting interpretation: the element (i, j) gives the number of (directed or undirected) walks of length n from vertex i to vertex j. If n is the smallest nonnegative integer, such that for some i, j, the element (i, j) of Aⁿ is positive, then n is the distance between vertex i and vertex j. A great example of how this is useful is in counting the number of triangles in an undirected graph G, which is exactly the trace of A³ divided by 6. We divide by 6 to compensate for the overcounting of each triangle (3! = 6 times). The adjacency matrix can be used to determine whether or not the graph is connected.

Data structures[edit]

The adjacency matrix may be used as a data structure for the representation of graphs in computer programs for manipulating graphs. The main alternative data structure, also in use for this application, is the adjacency list.^[10]^[11]

The space needed to represent an adjacency matrix and the time needed to perform operations on them is dependent on the matrix representation chosen for the underlying matrix. Sparse matrix representations only store non-zero matrix entries and implicitly represent the zero entries. They can, for example, be used to represent sparse graphs without incurring the space overhead from storing the many zero entries in the adjacency matrix of the sparse graph. In the following section the adjacency matrix is assumed to be represented by an array data structure so that zero and non-zero entries are all directly represented in storage.

Because each entry in the adjacency matrix requires only one bit, it can be represented in a very compact way, occupying only |V |² / 8 bytes to represent a directed graph, or (by using a packed triangular format and only storing the lower triangular part of the matrix) approximately |V |² / 16 bytes to represent an undirected graph. Although slightly more succinct representations are possible, this method gets close to the information-theoretic lower bound for the minimum number of bits needed to represent all n-vertex graphs.^[12] For storing graphs in text files, fewer bits per byte can be used to ensure that all bytes are text characters, for instance by using a Base64 representation.^[13] Besides avoiding wasted space, this compactness encourages locality of reference.
However, for a large sparse graph, adjacency lists require less storage space, because they do not waste any space representing edges that are not present.^[11]^[14]

An alternative form of adjacency matrix (which, however, requires a larger amount of space) replaces the numbers in each element of the matrix with pointers to edge objects (when edges are present) or null pointers (when there is no edge).^[14] It is also possible to store edge weights directly in the elements of an adjacency matrix.^[11]

Besides the space tradeoff, the different data structures also facilitate different operations. Finding all vertices adjacent to a given vertex in an adjacency list is as simple as reading the list, and takes time proportional to the number of neighbors. With an adjacency matrix, an entire row must instead be scanned, which takes a larger amount of time, proportional to the number of vertices in the whole graph. On the other hand, testing whether there is an edge between two given vertices can be determined at once with an adjacency matrix, while requiring time proportional to the minimum degree of the two vertices with the adjacency list.^[11]^[14]

References[edit]

^ Biggs, Norman (1993), Algebraic Graph Theory, Cambridge Mathematical Library (2nd ed.), Cambridge University Press, Definition 2.1, p. 7.
^ Harary, Frank (1962), «The determinant of the adjacency matrix of a graph», SIAM Review, 4 (3): 202–210, Bibcode:1962SIAMR…4..202H, doi:10.1137/1004057, MR 0144330.
^ Seidel, J. J. (1968). «Strongly Regular Graphs with (−1, 1, 0) Adjacency Matrix Having Eigenvalue 3». Lin. Alg. Appl. 1 (2): 281–298. doi:10.1016/0024-3795(68)90008-6.
^ Shum, Kenneth; Blake, Ian (2003-12-18). «Expander graphs and codes». Volume 68 of DIMACS series in discrete mathematics and theoretical computer science. Algebraic Coding Theory and Information Theory: DIMACS Workshop, Algebraic Coding Theory and Information Theory. American Mathematical Society. p. 63. ISBN 9780821871102.
^
Borgatti, Steve; Everett, Martin; Johnson, Jeffrey (2018), Analyzing Social Networks (2nd ed.), SAGE, p. 20
^
Newman, Mark (2018), Networks (2nd ed.), Oxford University Press, p. 110
^ Biggs (1993), Chapter 2 («The spectrum of a graph»), pp. 7–13.
^ Brouwer, Andries E.; Haemers, Willem H. (2012), «1.3.6 Bipartite graphs», Spectra of Graphs, Universitext, New York: Springer, pp. 6–7, doi:10.1007/978-1-4614-1939-6, ISBN 978-1-4614-1938-9, MR 2882891
^ Godsil, Chris; Royle, Gordon Algebraic Graph Theory, Springer (2001), ISBN 0-387-95241-1, p.164
^ Goodrich & Tamassia (2015), p. 361: «There are two data structures that people often use to represent graphs, the adjacency list and the adjacency matrix.»
^ ^a ^b ^c ^d Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), «Section 22.1: Representations of graphs», Introduction to Algorithms (Second ed.), MIT Press and McGraw-Hill, pp. 527–531, ISBN 0-262-03293-7.
^ Turán, György (1984), «On the succinct representation of graphs», Discrete Applied Mathematics, 8 (3): 289–294, doi:10.1016/0166-218X(84)90126-4, MR 0749658.
^ McKay, Brendan, Description of graph6 and sparse6 encodings, archived from the original on 2001-04-30, retrieved 2012-02-10.
^ ^a ^b ^c Goodrich, Michael T.; Tamassia, Roberto (2015), Algorithm Design and Applications, Wiley, p. 363.

External links[edit]

Weisstein, Eric W. «Adjacency matrix». MathWorld.
Fluffschack — an educational Java web start game demonstrating the relationship between adjacency matrices and graphs.
Open Data Structures — Section 12.1 — AdjacencyMatrix: Representing a Graph by a Matrix, Pat Morin
Café math : Adjacency Matrices of Graphs : Application of the adjacency matrices to the computation generating series of walks.

Источник

Лекция 7.

п.7. Графы. Орграфы.

7.5. Представление графов в
компьютере.

Известны различные способы представления
графов в памяти компьютера, которые
различаются объемом занимаемой памяти
и скорости выполнения операций над
графами. Преставление выбирается, исходя
из потребностей конкретной задачи. В
подавляющем большинстве случаев граф
задается матрицей. Чаще всего графы
представляют либо матрицей смежности,
либо матрицей инциденций.

Определение 7.12. Матрица смежности
вершин орграфа G,
содержащего n вершин-
это квадратная матрица A=a_ij
n-го порядка, у которой
строки и столбцы матрицы соответствуют
вершинам орграфа. Элементы a_ij
матрицы A равны числу
дуг, направленных из i-й
вершины в j-ю. Если
орграф состоит из однократных дуг, то
элементы матрицы равны либо 0, либо 1.

Матрицей смежности вершин
неориентированного графа G,
содержащего n вершин,
называют квадратную матрицу A=a_ij
n-го порядка, у которой
строки и столбцы матрицы соответствуют
вершинам неориентированного графа.
Элементы a_ij
матрицы A равны числу
ребер, направленных из i-й
вершины в j-ю. В случае
неориентированного графа G
ему вместе с ребром (v_i,
v_j)
принадлежит и ребро (v_j,
v_i),
поэтому матрица смежности вершин A=a_ij
будет симметрична относительно главной
диагонали.

Определение 7.13. Матрица смежности
дуг орграфа —
это квадратная матрица B=b_ij
m-го порядка, у которой
строки и столбцы матрицы соответствуют
дугам орграфа. Элементы b_ij
матрицы B равны 1, если
дуга e_i
непосредственно предшествует дуге e_j
и 0 в остальных случаях.

Матрицей смежности ребер
неориентированного графа является
матрица B=b_ij
m-го порядка, у которой
строки и столбцы матрицы соответствуют
ребрам графа. Элементы b_ij
матрицы B равны 1, если
ребра e_i
и e_j
имеют общую вершину, и 0 в остальных
случаях.

Определение 7.14. Матрицей инциденций
(инцидентности) неориентирован-ного
помеченного графа с

вершинами и

ребрами называется матрица

размерности
,
строки которой соответствуют вершинам,
а столбцы – ребрам. Элементы

матрицы инциденций неориентированного
графа равны 1, если вершина

инцидентна ребру
,
и 0 в противном случае.

Матрицей инциденций (инцидентности)
орграфа с

вершинами и

дугами называется матрица

размерности nm,
строки которой соответствуют вершинам,
а столбцы -дугам
орграфа. Элементы c_ij
равны 1, если дуга e_j
исходит из i-й вершины;
-1, если дуга e_j
заходит в i-ю вершину;
0, если дуга не инцидентна i-й
вершине:

Если каждому ребру графа приписано
некоторое положительное число, то такое
число называется весом, а сам граф
называется взвешенным графом. Простой
взвешенный граф (сеть) может быть
представлен также своей матрицей
весов
,
где _ij
– вес ребра, соединяющего вершины v_i
и v_j.
Весы несуществующих ребер (дуг) полагают
равными нулю или бесконечности в
зависимости от приложений.

Пример 7.7.
1) Для заданного неориентированного
графа построить матрицы смежностей и
матрицы инциденций.

2) Для заданного ориентированного графа
построить матрицы смежностей и матрицы
инциденций.

Решение. 1) Строим матрицу смежности
вершин, которая будет размерности 44.
Строим матрицу смежности ребер, которая
будет размерности 55.

Строим матрицу инциденций, которая
будет размерности 45.

2) Строим матрицу смежности вершин,
которая будет размерности 44.
Строим матрицу смежности ребер, которая
будет размерности 55.

Строим матрицу инциденций, которая
будет размерности 45.



7.6. Выявление маршрутов с заданным
количеством ребер (дуг).

С помощью матрицы смежности вершин
можно найти все маршруты, содержащие
заданное количество ребер (дуг).
Справедлива следующая теорема, которую
примем без доказательства.

Теорема 7.3. Для определения маршрутов,
состоящих из k ребер
(дуг), необходимо возвести в k-ю
степень матрицу смежности вершин P.
Тогда элемент

матрицы

даст количество маршрутов длины k
(состоящих из k ребер)
из вершины

в вершину
.

Пример 7.8.
Для неориентированного графа,
изображенного на рисунке, найти все
маршруты длины 2.

Решение. Составим матрицу смежности
вершин P и возведем
ее в квадрат. Результат возведения:

Рассмотрим первую строку. Например,
элемент
.
Это значит, что существует три маршрута
из v₁ в v₁
длиной в два ребра. Действительно, это
маршруты
.
Из v₁ в v₂
существует два маршрута:
.

Если использовать числовую матрицу
смежности вершин, то для нахождения
самих маршрутов необходимо работать с
графом. Если воспользоваться
модифициро-ванной матрицей смежности,
в ячейки которой записаны названия
ребер, то можно получить не только
количество маршрутов, но и сами маршруты.

Действительно, для данного примера
имеем



Аналогично обстоит дело с орграфом,
хотя у него матрица смежности вершин
несимметрическая.

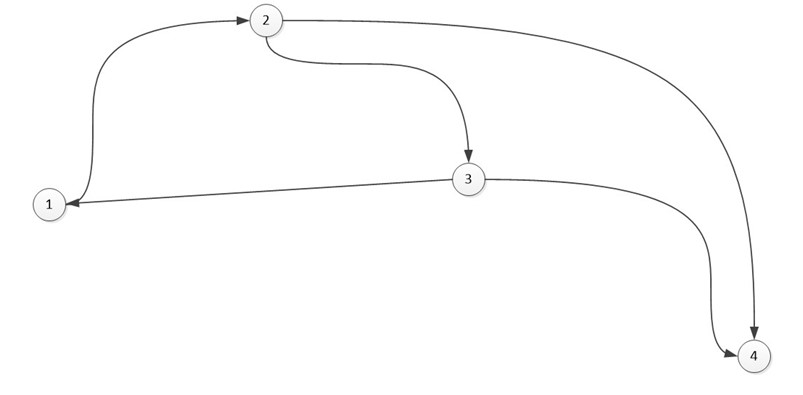
Пример 7.9.
Для орграфа, изображенного на рисунке,
найти все маршруты с тремя дугами.

Решение. Матрица смежности P
и результаты ее возведения в квадрат и
куб имеют следующий вид:

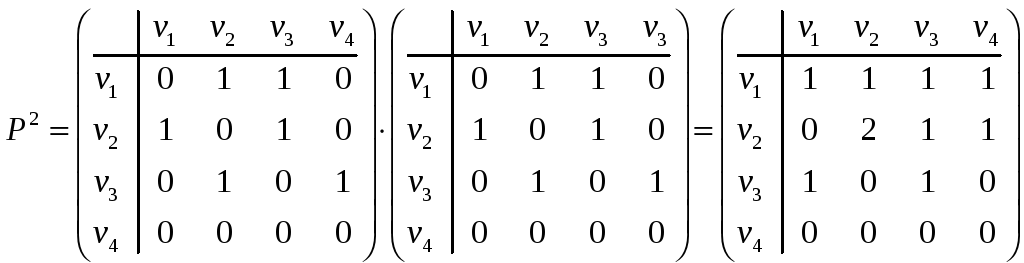
Рассмотрим, например, элемент

после возведения матрицы смежности
вершин в квадрат. Это значит, из вершины
v₂ в вершину v₂
есть два маршрута длиной две дуги. Это
маршруты

и
.
После возведения матрицы в куб сохраняется
та же картина. Например,
.
Это значит, что есть два маршрута длиной
три дуги из вершины v₁
в вершину v₂. Это
маршруты

и
.


Для получения цепей (маршрутов, в которых
каждое ребро встречается один раз) нужно
в модифицированной матрице P
³ вычеркнуть те слагаемые, в
которых какой-либо сомножитель встречается
более одного раза.

7.7. Упорядочивание вершин и дуг
орграфа.

Расчеты в задачах, связанных с графами,
заметно упрощаются, если их элементы
упорядочены. Под упорядочиванием
вершин связного орграфа без циклов
понимают такое разбиение его вершин на
группы, при котором:

1) вершины первой группы не имеют
предшествующих вершин, а вершины
последней группы последующих;

2) вершины любой другой группы не имеют
предшествующих в следующей группе;

3) вершины одной и той же группы дугами
не соединяются.

Аналогичным образом вводится понятие
упорядочения дуг. В результате
упорядочения элементов получают орграф,
изоморфный исходному. Упорядочение
элементов выполняется графическим или
матричным способом. Графический способ
упорядочивание вершин, дуг орграфа
носит название алгоритма Фалкерсона.

Алгоритм Фалкерсона для упорядочения
вершин:

1. Находят вершины графа, в которые не
входит ни одна дуга. Они образуют первую
группу. Нумеруют вершины группы в
натуральном порядке 1, 2, … . При этом
присвоение номеров вершинам внутри
группы может быть сделано не единственным
образом, что не имеет значения.

2. Мысленно вычеркиваем все пронумерованные
вершины и дуги, из них выходящие. В
получившемся графе найдется, по крайней
мере, одна вершина, в которую не входит
ни одна дуга. Этой вершине, входящей во
вторую группу, присваивается очередной
номер и т.д. Этот шаг повторяется до тех
пор, пока все вершины не будут упорядочены
(пронумерованы).

Алгоритм Фалкерсона для упорядочения
дуг:

1. Найти дуги, не имеющие непосредственно
предшествующих (они образуют I
группу).

2. Вычеркнуть найденные дуги; после
этого появится, по крайней мере, одна
новая дуга, не имеющая непосредственно
предшествующей (в графе без дуг I
группы). Такие дуги составляют II
группу. Повторять этот шаг, пока все
дуги не будут разбиты на группы. В
заключение упорядочения дугам присваивают
новые обозначения с индексами 1, 2, … .

__________________________________

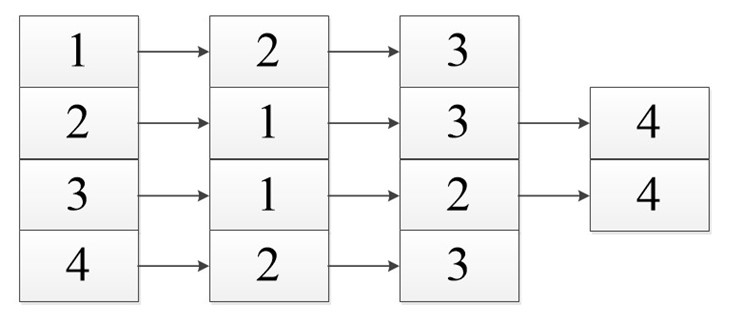
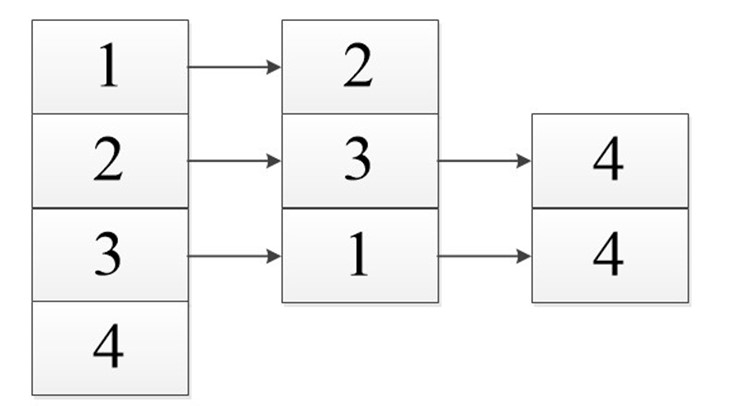
Пример 7.11.
Графическим способом упорядочить
вершины и дуги заданного орграфа.

Решение. Используя алгоритм
Фалкерсона, упорядочим вершины и дуги
заданного орграфа.

_________________________________

Соседние файлы в папке дискретка

Источник

В чем особенности представления графа матрицей смежности

Содержание:

Матрица смежности для графов
- В чем особенности представления
Списки смежности и списки ребер, плюсы и минусы
Классификация графов
Способы представления графа, алгоритмы обхода
Как построить граф по матрице смежности

Матрица смежности для графов

Матрица смежности графа является квадратной матрицей с элементами, каждый из которых имеет одно из двух значений: 0 или 1.

Простой пример матрицы смежности изображен на рисунке.

Простой пример матрицы смежности изображен на рисунке

Источник: kvodo.ru

Данная матрица является двоичной квадратной, то есть количество строк в единичном случае соответствует количеству столбцов, а также строки и столбы имеют значения либо 1, либо 0. Первая строка и первый столбец, не состоящие в матрице, а записанные для легкости восприятия, содержат номера, на пересечении которых расположен каждый из элементов, и они определяют индексное значение последних. Достаточно просто выполнить построение матрицы данного типа, зная соответствующий ей граф.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Достаточно просто выполнить построение матрицы данного типа

Источник: kvodo.ru

В левой стороне на рисунке представлена аналогичная матрица смежности с размерностью 4х4. Числа, выделенные синим цветом, допустимо рассматривать в виде вершин смешанного графа, записанного в правой стороне – того, представлением которого является матрица.

Отобразить граф можно путем вычисления по матрице смежности числа его вершин и применения специального правила. В том случае, когда из одной вершины в другую проход свободен, то есть имеется ребро, в ячейку записывают 1, в противном случае – 0. Таким образом:

если из i в j существует ребро, то (A[i][j]:=1), в противном случае (A[i][j]:=0.)

Заметим, что для элементов, расположенных на главной диагонали, характерно нулевое значение. Это является следствием отсутствия у графа петель. Однако, в информатике нет ограничений для записи некоторых или всех элементов на главной диагонали в виде единиц.

В чем особенности представления

В программе матрицу смежности задают с помощью обычного двумерного массива. Его размерность соответствует n x n, где n является числом вершин графа.

В программе матрицу смежности задают с помощью обычного двумерного массива

Источник: kvodo.ru

В том случае, когда граф неизвестен заранее, а определен пользователем, необходимо вводить двумерный массив вручную. Это объясняется условиями работы конкретного языка программирования. При необходимости предоставления графа в виде матрицы смежности требуется (O(|V|^{2})) памяти, так как ее размер соответствует квадрату числа всех вершин.

Если количество ребер графа в сравнении с числом вершин является небольшим, значения многих элементов матрицы смежности будут соответствовать нулю. Таким образом, применение рассматриваемой методики нецелесообразно, в связи с наличием для подобных графов наиболее эффективных способов представления.

Списки смежности и списки ребер, плюсы и минусы

Относительно памяти, списки смежности менее требовательны по сравнению с матрицами смежности. Объем памяти для их хранения составляет (O(|V|+|E|)). Такой перечень целесообразно представить как таблицу с двумя столбцами и строками в количестве, не превышающем число вершин в графе. Для примера можно рассмотреть граф смешанного типа:

Для примера можно рассмотреть граф смешанного типа

Источник: kvodo.ru

В данном случае, граф состоит из 6 вершин (|V|) и 5 ребер (|E|). Из последних 2 ребра являются направленными и 3 ненаправленными. При этом из каждой вершины выходит, как минимум одно ребро в другую вершину. Таким образом, список смежности рассматриваемого графа содержит |V| строк.

Таким образом, список смежности рассматриваемого графа содержит |V| строк

Источник: kvodo.ru

В i строке и 1 столбце указана вершина выхода, а в i строке и 2 столбце – вершина входа. Например, из вершины 5 выходят два ребра, входящие в вершины 1 и 4.

В процессе программной реализации списка смежности число вершин и ребер задают с помощью клавиатуры. Можно установить лимиты, то есть задать пару констант, одна из которых определяет максимально допустимое число вершин (Vmax), другая – ребер (Emax). Затем следует использовать три одномерных целочисленных массива:

terminal[1..Emax] – для хранения вершин, содержащих ребра;
next [1..Emax] – включает указатели на элементы массива terminal;
head[1..Vmax] – состоит из указателей на начало подсписков, то есть такие вершины, записанные в массив terminal, с которых начинается процесс перечисления всех вершин, смежных одной i-ой вершине.

Примечание

Допустимым действием является выделение в программе двух ключевых частей. К ним относят ввод ребер для дальнейшего добавления их в список смежности и вывод полученного списка смежности на экран.

В первую очередь выполняют запрос на ввод суммы вершин (n) и ребер (m) графа (данная информация должна быть у пользователя). Следующим шагом является запуск цикла ввода ребер, то есть смежных вершин. Условие в этом цикле нужно для того, чтобы узнать, какое введено ребро.

Если введено направленное ребро, то функция add вызывается 1 раз, иначе – 2, тем самым внося сведения, что есть ребро как из вершины v в вершину u, так и из u в v. По окончанию формирования списка смежности происходит его отображение программой на экране.

По окончанию формирования списка смежности происходит его отображение программой на экране.

Источник: kvodo.ru

Код

Источник: kvodo.ru

Вывод на экран осуществляется:

по циклу от 1 до n, где n – является количеством вершин;
согласно вложенному в него циклу, который прекращает свою работу тогда, когда указатель на следующий элемент для i-ой вершины отсутствует, то есть все смежные ей вершины уже выведены.

Функция add производит добавление ребер в изначально пустой список смежности:

(Add(v, u))

(k:=k+1)

(terminal[k]:=u)

(next[k]:=head[v])

(head[v]:=k)

Действия реализуются, согласно алгоритму с формальными параметрами, вспомогательной переменной k и тремя одномерными целочисленными массивами:

значение переменной k увеличивается на 1;
в k-ый элемент массива terminal добавляют конечную для какого-либо ребра вершина (u);
в строке №3 для k-ого элемента массива next определяется адрес следующего элемента массива terminal;
массив head заполняют указателями на стартовые элементы, которые являются началом подсписка (строки в таблице) смежных вершин с некоторой i-ой вершиной.

В ячейке, где пересекаются i-ая строка и 2-ой столбец, могут быть записи нескольких элементов в соответствии с несколькими смежными вершинами. Можно обозначить каждую строку из списка смежности его подсписком. В результате выведенный список смежности будет включать элементы подсписков, отсортированные в обратном порядке. Обычно порядок вывода смежных вершин (в подсписках) не имеет принципиального значения.

Список со строками, содержащими запись двух смежных вершин и вес ребра, которое их соединяет, называют списком ребер графа. В качестве примера можно рассмотреть связный граф G=(V, E). Множество ребер E следует сгруппировать следующим образом:

d – подмножество, включающее только неориентированные ребра графа G;
k – подмножество, включающее только ориентированные ребра графа G.

Допустим, какая-либо величина p равна количеству всех ребер, которые включены в подмножество d, а s – то же самое относительно k. Тогда для графа G высотой списка ребер будет являться величина:

s+p*2

Таким образом, число строк из списка ребер в любом случае должно соответствовать величине, определенной по итогам сложения ориентированных ребер с неориентированными, умноженными на 2. Рассматриваемый способ представления графа предполагает хранение в каждой строке пары смежных вершин, а неориентированное ребро, которое соединяет вершины v и u, идет как из v в u, так и из u в v.

Например, имеется некий граф смешанного типа с 5 вершинами и 4 ребрами, каждому из которых соответствует определенное целое значение (для наглядности оно составлено из номеров вершин):

для наглядности оно составлено из номеров вершин

Источник: kvodo.ru

Граф содержит 3 направленных ребра и 1 ненаправленное. Путем подстановки значений в формулу можно определить высоту списка ребер: 3+1*2=5

Путем подстановки значений в формулу можно определить высоту списка ребер

Источник: kvodo.ru

На рисунке изображен список ребер для рассматриваемого графа. Таблица в размерах составляет n×3, где n= s+p*2=3+1*2=5. Элементы в первом столбце расположены по возрастанию, во втором – порядок расположения элементов определен первым, а в третьем – зависит от двух предыдущих.

Список ребер реализуется программой. Процесс схож с операциями при реализации списка смежностей. В первую очередь организуют ввод данных, которые с помощью особой функции распределяются среди массивов. Затем происходит вывод полученного списка смежности на экран. В связи с необходимостью в использовании дополнительного массива, функция добавления ребер организована по-другому.

В связи с необходимостью в использовании дополнительного массива, функция добавления ребер организована по-другому

Источник: kvodo.ru

Код программы

Источник: kvodo.ru

Максимально допустимое число вершин в графе определено с помощью константы Vmax, а количество ребер – Emax. Вторая константа инициализируется формулой Vmax*(Vmax-1)/2, вычисляющей количество ребер в полном графе при известном числе вершин.

Далее, в программах описываются 5 массивов:

terminal – массив вершин, включающий ребра;
weight – массив весов ребер;
head[i]=k – для хранения i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – является первой вершиной, смежной с i-ой, а weight[k] – вес инцидентного ей ребра;
last[i]=k – для хранения i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – является последней вершиной, смежной с i-ой, а weight[k] – вес инцидентного ей ребра;
point[i]=k – хранит для i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – следующая вершина, смежная с i-ой, а weight[k] – вес инцидентного ей ребра.

По результатам ввода числа вершин (n) и ребер (m) графа будет запущен цикл, каждый этап которого сопровождается вводом пользователем с клавиатуры пары смежных вершин и веса ребра, расположенного между ними. Если ребро ориентированное, функция записи в список ребер (Add) вызывается единожды, при неориентированном ребре – дважды. Суммарное количество вызовов функции определяется по формуле:

s+(p*2)

где s – является ориентированными ребрами графа

p – неориентированные ребра

По итогам формирования списка ребер следует умножить на 2 переменную m. Это связано с тем, что при чисто неориентированном графе высота списка составляет:

0+(m*2)

Завершающим этапом является отображение на экране результирующей конструкции. В связи с тем, что на номер первой вершины, смежной с i-ой вершиной, указывает элемент head[i], каждая новая итерация внешнего цикла начинается с взятия этого номера (k=head[i]). Внутренний цикл прекращает реализацию в том случае, когда отсутствует смежная с i-ой вершины (k станет равной нулю), а внешний – по окончанию вывода списка ребер.

Ключевые действия, включая добавление ребра, удаление ребра, проверку наличия ребра от вершины i до вершины j, отличаются высокой эффективностью и являются операциями с постоянным временем. В том случае, когда граф плотный, а количество ребер большое, матрица смежности представляет собой наиболее целесообразное решение. Даже когда граф и матрица смежности разрежены, можно представить ее с помощью структур данных для разреженной матрицы.

Главное достоинство методики заключается в применении матриц. Благодаря передовым разработкам в сфере аппаратного обеспечения, представляется возможным реализовывать даже дорогостоящие матричные операции на графическом процессоре (GPU). В процессе выполнения операций со смежной матрицей можно получить ценные данные о природе графа и том, как связаны его вершины.

К минусам матрицы смежности можно отнести риски возникновения недостатка объема памяти по причине наличия требований к пространству матрицы смежности VxV. Однако, зачастую графы не обладают чрезмерно большим числом соединений, что является основным поводом выбрать списки смежности для решения распространенных задач.

С другой стороны, несмотря на простоту базовых операций, существуют такие операции, как inEdges и outEdges, которые отличаются дороговизной при использовании для представления матрицы смежности.

Классификация графов

Ярким примером графа является схема метро или некий другой маршрут. Программисты знакомы с компьютерной сетью, которая также представляет собой граф. Общим в этих примерах является наличие точек, соединенных линиями.

В случае компьютерной сети точками являются отдельные серверы, а линиями – разные типы электрических сигналов. В метрополитене точки можно принять за станции, а линии – за туннели, проложенные между станциями. Согласно теории графов, точки представляют собой вершины или узлы, а линии – ребра или дуги.

Граф является совокупностью вершин, которые соединены ребрами.

В математике преимущественно рассматривают не содержание, а структуру вещей, отделяя ее от всего остального. Данный прием позволяет определять какие-либо объекты, как графы. В случае компьютерной сети можно отметить наличие определенной топологии и возможности условного представления в виде некоторого количества компьютеров и соединительных путей. На рисунке изображена полносвязная топология:

На рисунке изображена полносвязная топология

Источник: kvodo.ru

Фактически такая топология является графом. Пять компьютеров представляют собой вершины, а соединения или пути передачи сигналов являются ребрами. Ели выполнить замену компьютеров на вершины, то в результате получится математический объект или граф с 10 ребрами и 5 вершинами. Нумерацию вершин допустимо выполнять произвольно.

В рассматриваемом примере не используются петли, то есть такие ребра, которые выходят из вершины и сразу же водят в нее. В теории графов существует ряд обозначений:

G=(V, E), здесь G – граф, V – его вершины, E – ребра;
|V| – порядок (число вершин);
|E| – размер графа (число рёбер).

Применительно к рисунку:

|V|=5, |E|=10.

Классификация графов:

связные, в которых между какой-либо парой вершин расположено от одного и более путей;
несвязные – хотя бы с одной вершиной, не связанной с другими.

В том случае, когда из любой вершины доступна другая вершина, граф является неориентированным и связным. При невыполнении данного условия для связного графа, его называет ориентированным или орграфом.

Примечание

Степень вершины определяется числом ребер, которые соединяют ее с другими вершинами.

В сумме все степени графа соответствуют удвоенному количеству всех его ребер. К примеру, на рисунке изображен граф со суммой степеней, равной 20:

К примеру, на рисунке изображен граф со суммой степеней, равной 20

Источник: kvodo.ru

Орграф отличается от неориентированного графа возможностью перемещаться из вершины h в вершину s без промежуточных вершин лишь тогда, когда ребро выходит из h и входит в s, но не наоборот. Форма записи ориентированного графа:

G=(V, A)

где V – является вершинами, A – определяет направленные ребра.

К третьему типу относят смешанные графы. Такие графы включают направленные и ненаправленные ребра. Формальная запись смешанного графа:

G=(V, E, A)

Формальная запись смешанного графа

Источник: kvodo.ru

На рисунке изображен граф с направленными [(e, a), (e, c), (a, b), (c, a), (d, b)] и ненаправленными [(e, d), (e, b), (d, c)…] дугами. Предположим, что имеются два графа:

Предположим, что имеются два графа

Источник: kvodo.ru

Данные графы эквиваленты друг другу, так как без изменений в структуре одного графа можно построить второй. Такие графы являются изоморфными, то есть обладают следующим свойством: какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом. На приведенном выше рисунке изображена пара изоморфных графов.

В случае, когда каждое ребро графа соответствует некоторому значению в виде веса ребра, граф является взвешенным. При решении задач можно встретить примеры, когда за вес принимают длину, цену маршрута и другие виды измерений. При графическом изображении графа принято указывать весовые значения около ребер.

Путь – последовательность вершин, каждая из которых связана с последующей с помощью ребра.

При совпадении первой и последней вершины путь называют циклом. Длина пути равна количеству составляющих его ребер. К примеру, на рисунке путь является последовательностью [(e), (a), (b), (c)]. Этот путь представляет собой подграф, так как к нему применимо определение последнего, а именно: граф G’=(V’, E’) является подграфом графа G=(V, E), только тогда когда V’ и E’ принадлежат V, E.

Способы представления графа, алгоритмы обхода

Граф, как и другие распространенные типы математических объектов, можно представить на компьютере, то есть сохранить в его памяти. Наиболее известные способы интерпретации графов:

матрица смежности;
матрица инцидентности;
список смежности;
список ребер.

Первые два метода заключаются в хранении графа в виде двумерного массива или матрицы. Размеры этих массивов определяются числом вершин и/или ребер в определенном графе. Таким образом, размер матрицы смежности – n×n (где n – число вершин), а матрицы инцидентности – n×m (n – число вершин, m – число ребер в графе).

В процессе решения многих задач с применением графов требуется обходить все вершины и ребра, то есть дуги. Обойти граф – значит, пройти все его вершины точно по одному разу. Алгоритмы обхода:

в глубину;
в ширину.

Реализация алгоритма обхода заключается в последовательном посещении вершин и исследовании ребер. Не посещенную вершину называют новой. После посещения вершину считают открытой до момента исследования всех инцидентных ей ребер. По итогу манипуляций вершина становится закрытой.

Обход в глубину выполняют, согласно следующим правилам:

при нахождении в вершине х следует перемещаться в какую-либо другую вершину, не посещенную ранее, с одновременным запоминанием первой дуги;
в том случае, когда невозможно переместиться в ранее не посещенную вершину из вершины х, требуется вернуться в вершину z, из которой впервые удалось попасть в х, и продолжить обход в глубину из вершины z.

Примечание

Поиск в ширину отличается тем, что за активную принимается такая открытая вершина, которая была посещена последней. В том случае, когда выполняется обход в глубину, чем позднее будет посещена вершина, тем раньше она будет использована.

В качестве примера можно рассмотреть неориентированный граф, изображенный на рисунке:

В качестве примера можно рассмотреть неориентированный граф, изображенный на рисунке

Источник: pandia.ru

Обход следует начинать со стартовой вершины 1. Она является активной и единственной, которая открыта. Другие вершины: 2,3,4,5,6 – новые. Вершина 1 обладает тремя инцидентными ребрами – 1–2, 1–4 и 1–6. Можно начать с ребра 1–2. В результате его прохождения открывается вершина 2. Она обладает одним инцидентным ребром 2–1, которое просмотрено. Вершина 2 была просмотрена, в результате чего она преобразуется в закрытую.

Затем по ребру 2–1 можно вернуться в вершину 1. По ребру 1– 4 легко попасть в вершину 4, которая становится открытой. Вершина 4 обладает четырьмя инцидентными ребрами: 4–1, 4–3, 4–5, 4–6. Таким образом, ребро 4–1 просмотрено.

Далее следует рассмотреть ребро 4–3. С его помощью удобно попасть в вершину 3, которая в результате становится открытой. Вершина 3 обладает одним инцидентным ребром 3–4. Данная вершина просмотрена. В результате вершина 3 закрыта, а по ребру 3–4 можно вернуться в вершину 4. Затем следует рассмотреть ребро 4 – 5.

Вершина 5 обладает двумя инцидентными ей ребрами: просмотренным (4–5) и ребром 5–6, по которому можно попасть в вершину 6. Вершина 6 обладает тремя инцидентными ей ребрами: просмотренным 6–5, 6–1 и 6–4. С помощью ребра 6–1 можно попасть в просмотренную вершину 1. По ребру 6–4 просто попасть в просмотренную вершину 4. В результате все вершины графа просмотрены. Порядок посещения вершин: 1, 2, 4, 3, 5, 6.

Основной особенностью и отличием поиска в ширину является выбор в виде активной вершины – такой, которая посещалась раньше, чем остальные. Таким образом, можно сформулировать ключевое свойство обхода в ширину: чем ближе вершина к старту, тем раньше она будет посещена.

Вершина используется путем просмотра одновременно всех вершин, которые ранее не были просмотрены и являются смежными с рассматриваемой вершиной. В результате поиск реализуют по всем вероятным направлением сразу. В первую очередь посещается вершина А, далее смежные с ней вершины, удаленные от А на 1.

Затем посещаются вершины, которые расположены на расстоянии 2 от А, и так далее. Чем ближе вершина к стартовой вершине, тем раньше она будет посещена. Поиск в ширину направлен на определение наиболее короткого из возможных путей.

В качестве примера можно рассмотреть неориентированный граф, изображенный на рисунке:

В качестве примера можно рассмотреть неориентированный граф, изображенный на рисунке

Источник: pandia.ru

Обход следует начать со стартовой вершины 1, которая является просмотренной. Вершины 2, 4, 6 и стартовая вершина – смежные. Данные вершины можно отметить, как просмотренные, и поместить в очередь. При рассмотрении вершины 2 можно заметить, что она не обладает смежными вершинами.

Затем нужно рассмотреть вершину 4 с двумя смежными вершинами 3 и 5. Их можно поместить в очередь и отметить, как просмотренные. В результате просмотрены все вершины графа. Порядок посещения вершин: 1, 2, 4, 6, 3, 5.

Как построить граф по матрице смежности

Данная методика отличается удобством, что позволяет представлять плотные графы с количеством ребер (|E|), которое приблизительно соответствует числу вершин в квадрате (|V|2). В процессе требуется заполнить матрицу размером |V| x |V| следующим образом:

A[i][j] = 1 (Если существует ребро из i в j)

A[i][j] = 0 (Иначе)

Метод допустим к применению в случае ориентированных и неориентированных графов. Во втором варианте матрица A имеет вид симметричной, то есть A[i][j] == A[j][i]. Это объясняется тем, что при существовании ребра между i и j, оно является и ребром из i в j, и ребром из j в i. С помощью данного свойства сокращают практически вдвое объем требуемой памяти, в связи с тем, что элементы хранятся лишь в верхней части матрицы, над главной диагональю.

С помощью данного свойства сокращают практически вдвое объем требуемой памяти

Источник: habrastorage.org

Источник

Definition[edit]

Of a bipartite graph[edit]

Variations[edit]

Examples[edit]

Undirected graphs[edit]

Directed graphs[edit]

Trivial graphs[edit]

Properties[edit]

Spectrum[edit]

Isomorphism and invariants[edit]

Matrix powers[edit]

Data structures[edit]

See also[edit]

References[edit]

External links[edit]

В чем особенности представления графа матрицей смежности

Матрица смежности для графов

В чем особенности представления

Списки смежности и списки ребер, плюсы и минусы

Классификация графов

Способы представления графа, алгоритмы обхода

Как построить граф по матрице смежности