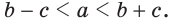Вспомним
теорему о соотношениях между сторонами и
углами треугольника:
В
треугольнике против большей стороны лежит больший угол, и
наоборот, против большего угла лежит большая сторона.
Воспользуемся
этой теоремой при доказательстве неравенства треугольника.
Теорема:
Длина
любой стороны треугольника меньше суммы двух других его сторон.
Доказательство:
Пусть
АВС — произвольный треугольник. Докажем, что сторона АВ меньше суммы сторон АС
и ВС.
Отложим
на луче АС отрезок СЕ=ВС.
Получили,
что треугольник ВСЕ — равнобедренный, а значит, углы при основании равны.
В
треугольнике АВЕ угол ∠АВЕ>∠1,
следовательно, ∠АВЕ>∠2.
А
так как в треугольнике против большего угла лежит большая сторона, то АВ<АЕ.
У
нас АЕ=АС+СЕ, а также по построению СЕ=ВС. Тогда получаем, что сторона
АВ<АС+ВС.
Теорема
доказана.
Следствие:
Для
любых трёх точек А, В и С, не лежащих на одной прямой,
справедливы следующие неравенства:
Следствие:
Длина
каждой стороны треугольника больше разности длин двух других его сторон.
Пример.
Доказать,
что медиана АЕ треугольника АВС меньше полусуммы двух
соседних его сторон.
Докажем,
что для медианы АЕ справедливо неравенство:
Продлим
медиану АЕ на её длину, то есть отрезок AЕ=ЕD. Рассмотрим треугольники СЕD
и
АЕВ.
У
них СЕ=ЕВ, так как АЕ — медиана. АЕ=ED по построению, а углы АЕВ и CED равны как вертикальные. А значит,
треугольники СЕD
и
АЕВ равны по первому признаку равенства треугольников. Следовательно, сторона CD=АВ.
В
треугольнике CAD
по равенству треугольника, получаем:
Что
и требовалось доказать.
Пример.
Доказать,
что сторона треугольника АВС меньше его полупериметра.
Каждая
сторона треугольника меньше суммы двух других его сторон. В нашем треугольнике
АВС для стороны АВ имеем:
Прибавим
к обеим частям этого неравенства АВ:
Получаем:
Что
и требовалось доказать.
- Альфашкола
- Уроки по математике
- Планиметрия
- Неравенство треугольника.
Неравенство треугольника. — онлайн урок
Тема:Неравество треугольника 7 класс. В данном уроке рассмотрена теорема о неравенстве треугольника. Показано как составлять неравенство для треугольника. Условие существования треугольника. Рассмотрен один из элементов треугольника — средняя линия, теорема о средней линии треугольника. Рассмотрена задача на нахождение средней линии треугольника. Также рассмотрена задача как найти периметр треугольника.
Отзывы:
Очень понравился преподаватель.
ОГРОМНАЯ БЛАГОДАРНОСТЬ!!!
Спасибо огромное Галине Павловне за занятия!
Похожие уроки
Содержание:
Неравенство треугольника:
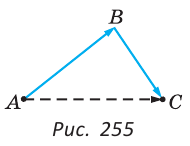
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС <АВ + ВС. Докажем это.
Теорема (о неравенстве треугольника).
Любая сторона треугольника меньше суммы двух других его сторон.
Дано:
Доказать: АС <АВ+ВС, АВ<АС+ВС, ВС < АВ+АС.
Доказательство:
Пусть АС — наибольшая сторона 


Для сторон 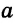
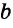
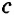
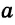
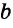
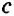
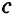
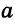
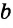
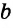
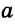
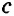
Следствие 1.
Если для точек А, В и С верно, что АВ=АС+ВС, то эти точки лежат на одной прямой. При этом точка С лежит между точками А и В.
Следствие 2.
Длина отрезка, соединяющего концы незамкнутой ломаной, меньше длины ломаной.
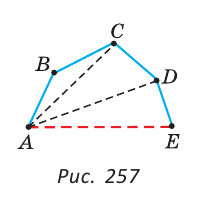
На рисунке 257 изображена незамкнутая ломаная ABCDE.
Докажем, что АЕ<АВ+ВС+CD+DE. Соединим точку А с точками С и D отрезками. По неравенству треугольника АС<АВ+ВС и AD<АС+CD. Значит, AD<АВ+ВС+CD. Так как по неравенству треугольника АЕ
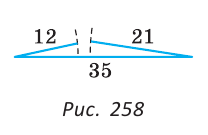
Чтобы доказать, что данные три числа не могут быть длинами сторон треугольника, достаточно убедиться, что большее из этих чисел не меньше суммы двух других чисел. Например, треугольника со сторонами 21, 12, 35 не существует, так как не выполняется неравенство треугольника: 35>12+21 (рис. 258).
Замечание. Из неравенств треугольника 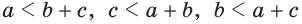
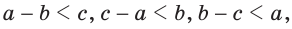
Пример:
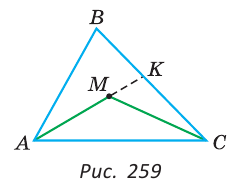
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.
Решение:
Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС < АВ + ВС. Продлим сторону AM до пересечения со стороной ВС в точке К. Из 

Пример:
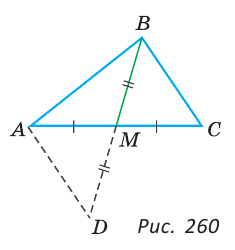
Доказать, что медиана треугольника меньше полусуммы двух соседних сторон.
Доказательство:
Докажем, что для медианы ВМ треугольника ABC справедливо неравенство: ВМ < 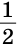
Продлим медиану ВМ на ее длину, MD = ВМ, BD = 2ВМ. Треугольники AMD и СМВ равны по первому признаку равенства треугольников (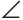

Теоремы о соотношениях между сторонами и углами треугольника.
Теорема 1. В треугольнике против большей стороны лежит больший угол.
Доказательство.
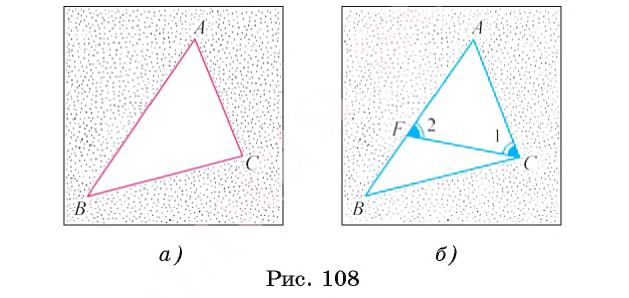
1) Пусть в треугольнике АВС сторона АВ больше стороны АС. Докажем, что 

2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).
3) Так как АF < АВ, то точка F лежит между точками А и В. Отсюда следует, что 


4) Угол 2 является внешним углом треугольника ВFС, следовательно, 

5) Так как треугольник FАС является равнобедренным, то 

Таким образом, 





Отсюда получаем, что 

Теорема доказана.
Теорема 2. В треугольнике против большего угла лежит большая сторона.
Доказательство.
1) Пусть в треугольнике АBС 

2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ < АС.
3) Если АВ = АС, то данный треугольник АBС является равнобедренным, а, значит, 



В каждом из этих случаев получаем противоречие с условием: 

Теорема доказана.
Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.
Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.
Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.
Доказательство.
Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.
Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.
Теорема доказана.
Неравенство треугольника
Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.
Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.
Доказательство.
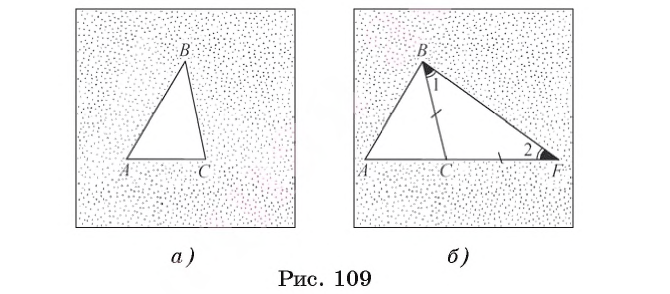
1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ < АС + СВ (рис. 109, а).
2) Отложим на луче АС отрезок CF, равный стороне ВС (рис. 109, б).
3) В равнобедренном треугольнике ВСF угол 1 равен углу 2, а в треугольнике АВF 



4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ < АF. Но так как АF = АС + СF, то АВ < АС + СВ.
Теорема доказана.
Следствие 1. Для любых трех точек А, В, С, не лежащих на одной прямой, справедливы следующие три неравенства, которые называются неравенствами треугольника:
АВ < АС + СB; АС < АВ + ВС; АВ < ВА+АС.
Следствие 2. Длина каждой стороны треугольника больше разности длин двух других его сторон.
Признаки равенства прямоугольных треугольников
На основании первого и второго признаков равенства треугольников можно доказать следующие признаки равенства прямоугольных треугольников.
Теорема 1 (о равенстве прямоугольных треугольников по двум катетам). Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Доказательство.
Так как в прямоугольном треугольнике угол между катетами прямой, а любые два прямых угла равны, то по первому признаку равенства треугольников следует утверждение данной теоремы.
Теорема доказана.
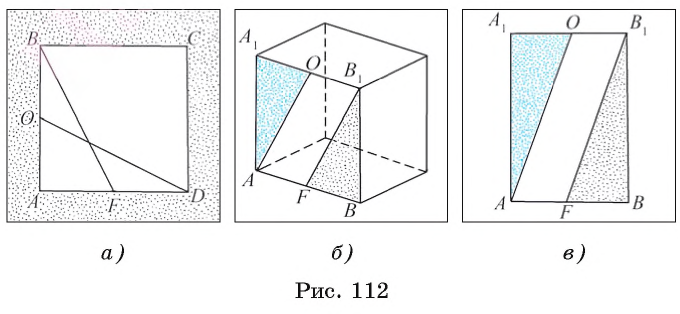
Например, пусть ABCD — квадрат, а точки О и F — середины сторон АВ и AD соответственно (рис. 112, а). Тогда прямоугольные треугольники OAD и FAB равны. Действительно, поскольку каждый угол квадрата прямой, а его стороны равны, то АD =АВ и АО = АF, т. е. эти треугольники равны по двум катетам.
Пусть точки О и F — середины ребер А1В1 и АВ соответственно прямоугольного параллелепипеда (рис. 112, б). Тогда равны прямоугольные треугольники АА1O и В1ВF, содержащиеся в грани АA1B1B прямоугольного параллелепипеда. Действительно, так как каждый угол прямоугольника АA1B1B прямой (рис. 112, в), а противоположные стороны равны, то верны равенства 

Теорема 2 (о равенстве прямоугольных треугольников по катету и прилежащему острому углу). Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого треугольника, то такие треугольники равны.
Доказательство.
Учитывая условие теоремы и тот факт, что прямые углы равны, получаем, что катет и два прилежащих к нему угла одного прямоугольного треугольника соответственно равны катету и двум прилежащим к нему углам второго прямоугольного треугольника. Следовательно, по второму признаку равенства треугольников эти треугольники равны.
Теорема доказана.
Докажем еще два признака равенства прямоугольных треугольников.
Теорема 3 (о равенстве прямоугольных треугольников по гипотенузе и острому углу). Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Доказательство.
1) Пусть в прямоугольных треугольниках АBС и А1В1С1 равны гипотенузы АВ и А1В1, а также 

2) Так как сумма градусных мер углов любого треугольника равна 180°, то в треугольнике ABC 







3) Таким образом, гипотенуза AB и два прилежащих к ней угла треугольника ABC соответственно равны гипотенузе А1В1 и двум прилежащим к ней углам треугольника А1В1С1. Следовательно, на основании второго признака равенства треугольников получаем, что 

Теорема доказана.
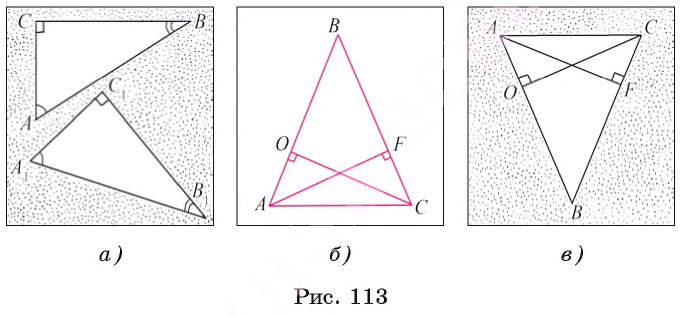
Например, пусть отрезки СО и AF — высоты равнобедренного треугольника ABC с основанием АС. Тогда 

Действительно, АС — общая гипотенуза этих треугольников, а 

Теорема 4 (о равенстве прямоугольных треугольников по гипотенузе и катету). Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Доказательство.
1) Пусть в прямоугольных треугольниках АСВ и А1С1 В1 

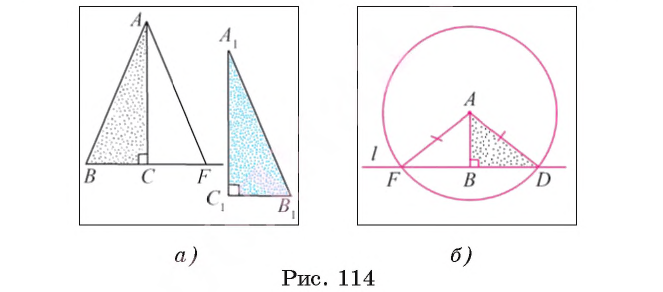
2) На луче, противоположном лучу СB, отложим отрезок СF, равный отрезку С1В1. Тогда треугольники А1В1С1 и АСF равны по двум катетам.
3) Следовательно, АF =А1В1=АВ, т. е. треугольник АВF является равнобедренным и 

Теорема доказана.
Например, пусть прямая l пересекает окружность, центром которой является точка А, в точках D и F (рис. 114, б). Отрезок АВ — перпендикуляр, проведенный из точки А к прямой l. Тогда треугольники ABF и ABD равны по гипотенузе и катету. Действительно, AF = AD как радиусы окружности, отрезок АВ — общий катет этих треугольников.
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой
- Задачи на построение по геометрии
- Серединный перпендикуляр к отрезку
- Второй и третий признаки равенства треугольников
- Параллельные прямые
- Соотношения между сторонами и углами треугольника
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Цель урока: изучить теорему о
неравенстве треугольника и показать ее
применение при решении задач.
Задачи:
- Образовательные:
- относительно учащихся: научиться применять
свойство «неравенство треугольника» и
определять несуществующие треугольники; - относительно педагога: объяснить новую тему с
первичным закреплением новых знаний; включить
учеников в исследовательскую деятельность; - показать практическое применение полученных
знаний; создать условия для формирования
целостной картины мира.
- относительно учащихся: научиться применять
- Развивающие:
- развитие речи, мышления, сенсорной (восприятие
внешнего мира через органы чувств) сферы
личности и потребностно-мотивационной области; - развитие умственной деятельности (выполнять
операции анализа, синтеза, способность
наблюдать, делать выводы, выделять существенные
признаки объектов, цели и способы деятельности,
выдвигать гипотезы).
- развитие речи, мышления, сенсорной (восприятие
- Воспитательные:
- повысить интерес к традициям края;
- развивать самостоятельность, умение работать
парами; - способствовать формированию коммуникативной
компетенции.
Тип урока: урок изучения и первичного
закрепления новых знаний.
Оборудование: доска, компьютер,
интерактивная доска или мультимедийный
проектор, презентация, учебники, рабочие тетради
(Приложение 1), 14
наборов полосок из картона по 5 см, 7 см (2 шт.), 9
см, 12 см, 14 см, 16 см, таблички с треугольниками, смайлики (Приложение
2).
ХОД УРОКА
1. Организационный этап
2. Подготовка к основному этапу урока (обеспечение
мотивации и принятия учащимися цели
учебно-познавательной деятельности,
актуализация опорных знаний)

Посмотрите на рисунок, выполненный на доске. Как
называется эта фигура? (Это треугольник.)
– Какая фигура называется треугольником? (Треугольник
– фигура, состоящая из трех точек, не лежащих на
одной прямой и трех отрезков, попарно
соединяющих эти точки.)
– Что возникает в вашей памяти? Что вы можете
рассказать об этом треугольнике? Если
обозначить треугольник АВС, назовите большую
сторону. (Ребята отвечают на вопросы учителя.)
– А почему именно эту фигуру я предложила вам
вспомнить? (Будем изучать какие-то свойства
треугольника.)
– Совершенно верно, сегодня мы будем изучать
свойство «неравенство треугольника».
3.Усвоение новых знаний и способов действий
3.1. Постановка проблемы, выдвижение
гипотезы
Еслиб только меня спросили,
Я б ответил предельно кратко,
Что не видел Земли красивей
И загадочней, чем Камчатка.Где вулканы царапают небо,
Низвергая к подножьм лавы,
Где сплетаются быль и небыль,
И где в рост человека травы.
– Эти замечательные стихи Анатолия Старикана
посвящены нашей малой родине Камчатке. Камчатка
имеет свои традиции, и одной из них является
ежегодное проведение Берингии.

ставшая традиционной гонка на собачьих упряжках,
которая проводится с 1990 года.)
– Обычно Берингия проводится в марте и вместе с
началом весны приходит в населенные пункты на
своем пути, принося радость их обитателям. Стоит
заметить, что гонка помимо состязательной
составляющей, имеет еще и гуманитарное значение
для жителей сел и поселков Камчатского края, где
отдыхают участники гонки. Детям и школам
отдаленных уголков Камчатки оказывают
спонсорскую помощь.
В этом году Беригиня проходила с 7 по 21 марта.
Проблемная ситуация.
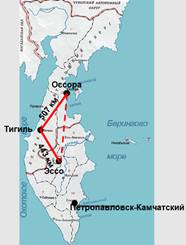
стартовала из села Эссо, и одним из пунктов
остановки стал поселок Тигиль. Расстояние между
этими населенными пунктами 443 км. Далее каюры
отправились в поселок Оссора. На каком
расстоянии от села Эссо может находиться поселок
Оссора, если расстояние между поселком Тигиль и
поселком Оссора 507 км?
Какую фигуру необходимо построить, чтобы
решить эту проблему? (Необходимо построить
треугольник.) Какова может быть длина третьей
стороны? Выскажите свои гипотезы, мы проверим их
в конце урока.
Ученики отвечают на вопросы учителя, строят
треугольник в рабочей тетради и высказывают свои
гипотезы, например, расстояние между с. Эссо и п.
Оссора меньше 950 км.
- 3.2. Проведение исследования, формулирование
нового свойства сторон треугольника

рассматриваемой проблеме является треугольник.
Я уверена, что вы очень наблюдательны. Скажите, а
где еще в повседневной жизни вам встречались
треугольные формы? В архитектуре? (Знак
аварийной остановки и т.д. Крыши имеют
треугольную форму.)
– Вы правы. Основу крыш составляют наклонные и
горизонтальные балки, которые соединены между
собой и образуют треугольник.
Давайте сконструируем макеты собственных крыш.
Представьте, что те полоски, которые лежат перед
вами – это балки для построения крыши дома.
Исследовательская работа
– Перед вами лежат макеты сторон
треугольников.
Постройте, используя эти макеты треугольники со
сторонами:
а) 7, 12, 9;
б) 7, 14, 7;
в) 5, 16, 7.
В первой задаче треугольник построить легко. Во
второй получился отрезок. Почему? (Т.к. три
вершины лежат на одной прямой, а треугольник –
это фигура, составленная из трех точек, не
лежащих на одной прямой, попарно соединенных
отрезками. Длина большего отрезка равна сумме
длин меньших.)
– Можно ли построить треугольник в третьем
случае? (В третьем случае треугольник построить
нельзя, так как длина большей стороны больше
суммы длин меньших сторон.)
Учитель выслушивает версии учеников. В
случае затруднения можно предложить детям
сравнить длину стороны, построенной первой и
сумму двух других сторон треугольника.
версия детей: «Если сторона, построенная
первой, меньше суммы двух других сторон, то
треугольник строится».
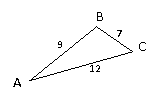
– Итак, треугольник, с какими сторонами мы смогли
построить? (Треугольник со сторонами 7, 12, 9.)
AB < BC + АС, так как 9 см < 7 см + 12 см
ВС < АВ + АС, так как 7 см < 9 см + 12 см
АС < АВ + ВС, так как 12 см < 9 см + 7 см.
Ученики обозначают стороны треугольника,
записывают неравенства в тетради.
– Как называются выражения, записанные на
доске? (Неравенства.)
– Что связывают эти три неравенства? (Стороны
треугольника.)
– Какова тема урока? (Неравенство
треугольника.)
– Сформулируйте это свойство. (Каждая сторона
треугольника меньше суммы двух других сторон.)
– Молодцы ребята, хорошо поработали, но впереди
еще серьезная работа по доказательству теоремы.
Энергизатор
Отложите ручки, повернитесь парами лицом друг
другу. На счет «один», поднимите правую руку с
вытянутым указательным пальцем. На счет «два»,
накройте левой ладонью указательный палец
соседа. На счет «три», успейте убрать свою руку и
схватить палец соседа. Начали!
Ребята с удовольствием выполняют
упражнение, которое снимает напряжение и
создает доброжелательную атмосферу, повышает
энергетический потенциал учащихся.
3.3. Доказательство теоремы
– Откройте учебник на стр. 74, прочитайте
формулировку теоремы о неравенстве
треугольника.
Ученики работают над формулировкой теоремы,
выясняют, что дано и что требуется доказать,
строят рисунок и доказывают теорему вместе с
учителем в рабочих тетрадях. Отвечают на
наводящие вопросы учителя.
Теорема. Каждая сторона треугольника
меньше суммы двух других сторон.
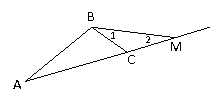
Доказать: АВ<АС+СВ
Доказательство:
Строим отрезок СМ равный отрезку СВ на продолжении стороны АС.
В равнобедренном Δ ВСМ ∟1 =∟2
(по свойству углов в равнобедренном треугольнике).
∟1< ∟АВМ, то ∟2<∟АВМ.
Рассмотрим треугольник АВМ.
– Каким соотношением в треугольнике связаны
стороны и углы? (В треугольнике против большего
угла лежит большая сторона.)
– Какая сторона лежит против угла АВМ? (Сторона
АМ.)
– Какая сторона лежит против угла 2? (Сторона
АВ.)
– Сравните стороны АВ и АМ? (АВ < АМ)
АВ < АМ
АВ < АС + СМ
АВ < АС + ВС
Аналогично доказывается, что ВС < АВ + АС;
АС < АВ + ВС. Теорема доказана.
Целесообразно сначала провести доказательство
теоремы устно, а потом записать доказательство
на доске и в рабочих тетрадях.
4.Физкультминутка, повторение
Победителем Берингии в 2011 году стал каюр
Карагинского района, и чтобы узнать имя
победителя поиграем с вами в математическое поле
чудес. Находите ответы на мои вопросы на
рисунках, развешенных по периметру класса и
называйте только букву.
(Ребята играют стоя.)

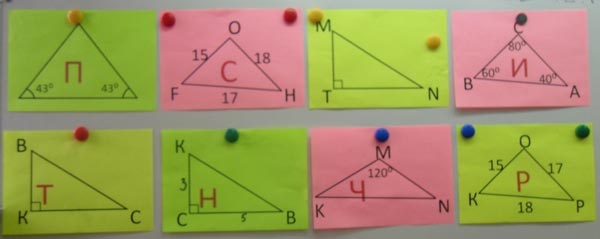
– Какой треугольник является равнобедренным?
(П)
– В каком треугольнике больший угол О? (Р)
– В каком треугольнике меньшая сторона ВС?
(И)
– В каком прямоугольном треугольнике катет ВК,
гипотенуза ВС? (Т)
– Какой треугольник является тупоугольным?
(Ч)
– В прямоугольном треугольнике МNT назовите
угол, противолежащий катету ТМ (L N)
– Совершенно верно, победителем является
Андрей Притчин, который преодолел весь путь за 90
часов.
5. Первичная проверка понимания и
закрепление знаний
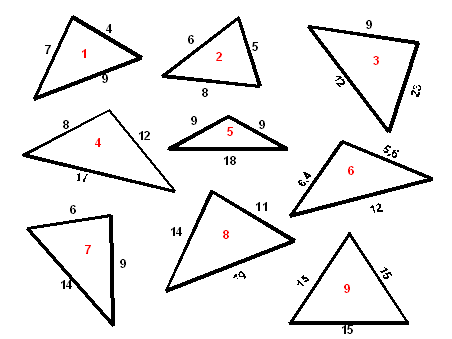
– Выберите, какие треугольники не существуют?
(Ученики работают самостоятельно,
один человек работает у доски, потом проверка.)
Ответ: не существуют треугольники с
номерами 3, 5, 6.
– Ребята, что вы заметили? Как быстро
применить теорему о неравенстве треугольника?
(Высказывают свои версии.) – Сумма
двух сторон, должна быть больше третьей стороны.
Например, 10 + 3 > 5, но треугольник построить
нельзя, почему? (Так как 3 + 5 < 10.) То есть, для того
чтобы быстро проверить существует ли
треугольник, надо сравнить большую сторону с
суммой двух меньших сторон.
– Молодцы, ребята! Быстро справились с
заданием!
6. Обобщение и систематизация знаний (решение
проблемы, проверка гипотезы)
– Итак, какое условие должно выполняться, чтобы
можно было построить треугольник? (Большая
сторона треугольника должна быть меньше суммы
двух меньших сторон.)
– Какую проблему я поставила перед вами в начале
урока? (Берингия стартовала из села Эссо, и
одним из пунктов остановки стал поселок Тигиль.
Расстояние между этими населенными пунктами
443 км. Далее каюры отправились в поселок
Оссора. На каком расстоянии от села Эссо может
находиться поселок Оссора, если расстояние между
поселком Тигиль и поселком Оссора 507 км?)
– Предложите решение этой проблемы, используя
новые знания. (Расстояние между Эссо и
Оссорой должно быть меньше, чем 950 км.)
– Какую гипотезу мы выдвигали? (Расстояние
между Эссо и Оссорой должно быть меньше, чем 950
км.)
– Подтвердилась ли гипотеза? (Да.)
Дополнительное задание: с какой
средней скоростью двигался победитель, если весь
путь он преодолел за 90 часов?
7. Постановка домашнего задания
- Выучить теорему п. 33, стр. 74.
- Исследовательское: Найти все треугольники,
длины сторон которых выражены натуральными
числами и а) не превосходят числа 2; б) периметр
треугольника равен 5. Ответы: а)1,1,1; 2,
2,2; 1, 2, 2 б) 1,2,2. - Творческое (по желанию): сочинить сказку,
рассказ или стихотворение по изученной теме.
8. Итоги урока, оценка знаний, рефлексия
Фронтальным опросом учитель вместе с
учащимися подводит итоги урока и активным
ребятам ставит оценки.
– Какую тему мы сегодня изучили? (Неравенство
треугольника.)
– Что нового вы узнали на уроке? (Любая сторона
треугольника меньше суммы двух других сторон.)
– Какие свойства треугольника повторили? (В
треугольнике против большей стороны лежит
больший угол, и обратно. В прямоугольном
треугольнике гипотенуза всегда больше катета.
Если в треугольнике два угла равны, то
треугольник равнобедренный.)
– Как называется гонка на собачьих упряжках? (Берингия.)
– Из какого села стартует? (Из села Эссо.)
– В каком поселке финиш? (В поселке Оссора.)
– Как зовут победителя 2011 года? (Андрей
Притчин.)
– Молодцы! Андрей Притчин является
четырехкратным победителем Берингии, и я
уверена, что каждый из вас обязательно станет
победителем в той или иной области. Главное очень
захотеть и добиваться поставленной цели.
– Какие цели мы ставили в начале урока? Достигли
ли их? Какую жизненную проблему решили?
– Какие трудности возникли у вас на уроке? Как вы
их преодолевали? Понятна ли вам тема урока? (Ребята
отвечают на вопросы учителя, участвуют в
рефлексии.)
– А теперь еще раз сосредоточьтесь на своих
ощущениях и эмоциях, на том насколько понятна вам
тема урока, возьмите соответствующий смайлик
(Приложение 2), и повесьте его на доску.
– Спасибо, ребята, за работу! Урок окончен, до
свидания! Успехов вам и побед.
Литература:
Атанасян Л.С. и др. Геометрия 7-9.: учеб. для
общеобразоват.учреждений / Л.С. Атанасян,
В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение,
2006.
Интернет-ресурсы:
- http://www.beringia.ru
- http://rian.ru/society
- http://huskomania.ru/category/tags/kamchatka/beringiya