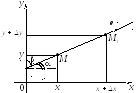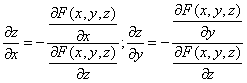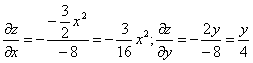Уравнение касательной плоскости и нормали к поверхности
Как найти?
Постановка задачи
Найти уравнение касательной плоскости и нормали к поверхности $ F(x,y,z) = 0 $ в точке $ M(x_0,y_0,z_0) $
План решения
Уравнение касательной плоскости к поверхности записывается следующем образом:
$$ F’_x bigg |_M (x-x_0) + F’_y bigg |_M (y-y_0) + F’_z bigg |_M (z-z_0) = 0 $$
Уравнение нормали к поверхности составляется по формуле:
$$ frac{x-x_0}{F’_x Big |_M} = frac{y-y_0}{F’_y Big |_M} = frac{z-z_0}{F’_z Big |_M} $$
- Находим частные производные $ F’_x, F’_y, F’_z $ в точке $ M(x_0,y_0,z_0) $
- Подставляем найденные значения производных в формулы для составления уравнений
ЗАМЕЧАНИЕ
Если в условии задачи задана точка $ M (x_0,y_0) $ с двумя координатами, то необходимо дополнительно вычислить координату $ z_0 $ из уравнения $ F(x_0,y_0,z_0) = 0 $, подставив в него известные координаты $ x_0 $ и $ y_0 $.
Примеры решений
| Пример 1 |
| Найти уравнение касательной плоскости и нормали к поверхности $ z = x^2 + y^2 $ в точке $ M(1,-2,5) $ |
| Решение |
|
Переносим $ z $ в правую часть и записываем поверхность в виде: $$ F(x,y,z) = x^2 + y^2 — z $$ Находим частные производные первого порядка функции $ F(x,y,z) $: $$ F’_x = 2x $$ $$ F’_y = 2y $$ $$ F’_z = -1 $$ Вычисляем значения полученных производных в точке $ M(1,-2,5) $: $$ F’_x Big |_M = F’_x(1,-2,5) = 2 cdot 1 = 2 $$ $$ F’_y Big |_M = F’_y (1,-2,5) = 2 cdot (-2) = -4 $$ $$ F’_z Big |_M = F’_z (1,-2,5) = -1 $$ Подставляем полученные данные в формулу касательной плоскости: $$ 2(x-1) + (-4)(y+2) + (-1)(z-5) = 0 $$ Раскрываем скобки и записываем окончательное уравнение плоскости: $$ 2x — 4y — z — 5 = 0 $$ Теперь запишем уравнение нормали к поверхности с помощью второй формулы: $$ frac{x-1}{2} = frac{y+2}{-4} = frac{z-5}{-1} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
|
$$ 2x — 4y — z — 5 = 0 $$ $$ frac{x-1}{2} = frac{y+2}{-4} = frac{z-5}{-1} $$ |
| Пример 2 |
| Составить уравнение касательной плоскости и нормали к поверхности $ z = e^{xcos y} $ в точке $ M(1,pi, frac{1}{e}) $ |
| Решение |
|
Записываем поверхность в виде: $$ F = e^{xcos y} — z $$ Находим частные производные от функции $ F(x,y,z) $: $$ F’_x = e^{xcos y} cdot (xcos y)’_x = cos y e^{xcos y} $$ $$ F’_y = e^{xcos y} cdot (xcos y)’_y = -xsin y e^{xcos y} $$ $$ F’_z = -1 $$ Вычисляем значения производных в точке $ M(1,pi,frac{1}{e}) $: $$ F’_x Big |_M = F’_x (1,pi,frac{1}{e}) = cos pi cdot e^{1 cdot cos pi} = -1 cdot e^{(-1)} = -e^{-1} $$ $$ F’_y Big |_M = F’_y (1,pi, frac{1}{e}) = -1 cdot sin pi cdot e^{1 cdot cos pi} = -1 cdot 0 cdot e^1 = 0 $$ $$ F’_z Big |_M = -1 $$ Подставляем в первую формулу касательной плоскости полученные ранее неизвестные данные: $$ -e^{-1}(x-1) + 0 cdot (y-pi) + (-1) cdot (z-frac{1}{e}) = 0 $$ Раскрываем скобки: $$ -xfrac{1}{e} + frac{1}{e} — z + frac{1}{e} = 0 $$ Домножаем обе части уравнения на $ -e $ и получаем окончательное уравнение плоскости: $$ x + ez — 2 = 0 $$ Используя вторую формулу находим уравнение нормали к поверхности: $$ frac{x-1}{-e^{-1}} = frac{y-pi}{0} = frac{z-e^{-1}}{-1} $$ Умножим уравнение на дробь $ frac{1}{-e} $: $$ frac{x-1}{1} = frac{y-pi}{0} = frac{z-e^{-1}}{e} $$ |
| Ответ |
| $$ x + ez — 2 = 0 $$ $$ frac{x-1}{1} = frac{y-pi}{0} = frac{z-e^{-1}}{e} $$ |
Касательная плоскость и нормаль к поверхности
Пусть M0(x0;
y0;
z0)
– фиксированная точка на поверхности,
заданной функцией z
= f(x;
y)
или уравнением F(x;
y;
z)
= 0.
Касательной
плоскостью к
поверхности в точке M0
называется плоскость, в которой
расположены касательные к всевозможным
кривым, проведенным на поверхности
через точку M0.
Нормалью называется
прямая, проходящая через точку M0
перпендикулярно касательной плоскости.
Из
определений следует, что нормальный
вектор касательной плоскости
и направляющий вектор нормали совпадают.
Если поверхность
задана уравнением z
= f(x;
y),
то уравнение
касательной плоскости в
точке M0(x0;
y0;
z0)
к данной поверхности имеет вид
(1)
а
канонические
уравнения нормали,
проведенной через точку M0(x0;
y0;
z0)
поверхности, имеют вид
(2)
В случае, когда
уравнение гладкой поверхности задано
в неявном виде: F(x;
y;
z)
= 0 и F(x0;
y0;
z0)
= 0, то уравнение
касательной плоскости в
точке M0(x0;
y0;
z0)
имеет вид
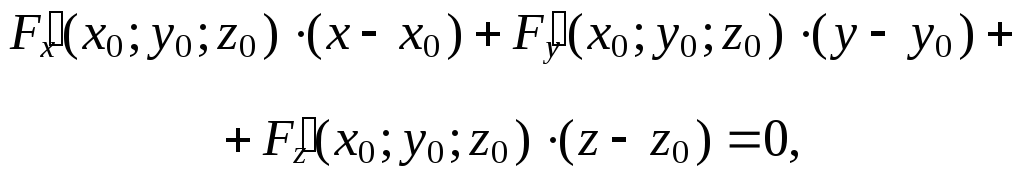
(3)
а уравнение
нормали
(4)
Пример 15.Найти уравнение касательной плоскости
и уравнения нормали к поверхностив точкеM0(1; 2;
–1).
Решение
Вычисляем значения
частных производных в точке M0(1;
2; –1)
Подставляя их в
уравнения (3) и (4), получаем соответственно
уравнение касательной плоскости:
канонические уравнения нормали:
Тест 11. Уравнение
касательной плоскости к поверхности
в точкеP0(2;
–3; 2) имеет следующий вид:
1)
2)
3)
4)
5)
Производная по направлению. Градиент
Частные производные
и
представляют собой производные от
функцииz
= f(x;
y)
по двум частным направлениям осей Ox
и Oy
(рисунок 43).
Рисунок 43
Пусть функция z
= f(x;
y)
определена в некоторой окрестности
точки М(х;
у),
– некоторое направление, задаваемое
единичным векторомгде
ибо
(или
);cos ,
cos
– косинусы углов, образуемых вектором
е
с осями координат и называемые
направляющими
косинусами.
При перемещении
в данном направлении
точкиM(x;
y)
в точку M1(x
+ x;
y
+ y)
функция z
получит приращение
z
= f(x
+ x;
y
+
+ y)
– f(x;
y),
называемое приращением
функции
в данном направлении
Если
то, очевидно, что
следовательно,
Производной
по направлению
функции двух переменных
z
= f(x;
y)
называется предел отношения приращения
функции в этом направлении к величине
перемещения
при стремлении последней к нулю, т. е.
Производная
характеризует
скорость
изменения функции в направлении
Формула для
производной функции z
= f(x;
y)
по
направлению
имеет вид
Пример 16.
Дана
функция z
= x2
+ y2,
в точке M(1;
1) направление составляет с осью Ox
угол
Найти производную функции по указанному
направлению в этой точке.
Решение
Так как
то угол
По формуле производной функции по
направлению получим
В точке M(1;
1) получаем:
Градиентом grad
z
функции z
= f(x;
y)
называется вектор с координатами
Рассмотрим скалярное
произведение векторов
и единичного вектора
Получим
Итак, производная
по направлению
есть скалярное произведение градиента
grad
z
и единичного вектора, задающего
направление
Градиент функции
grad
z
в данной точке характеризует направление
максимальной скорости изменения функции
в этой точке.
Пример 17.
Найти
градиент функции
в точкеM(0;
1).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Касательная плоскость и нормаль к поверхности.
Пусть поверхность задана в неявном виде: $F(x,y,z)=0$ и пусть точка $M_0(x_0,y_0,z_0)$ принадлежит данной поверхности. Тогда уравнение касательной плоскости к этой поверхности в точке $M_0$ таково:
$$
begin{equation}
F_{x}^{‘}(M_0)cdot(x-x_0)+F_{y}^{‘}(M_0)cdot(y-y_0)+F_{z}^{‘}(M_0)cdot(z-z_0)=0
end{equation}
$$
Уравнение нормали имеет вид:
$$
begin{equation}
frac{x-x_0}{F_{x}^{‘}(M_0)}=frac{y-y_0}{F_{y}^{‘}(M_0)}=frac{z-z_0}{F_{z}^{‘}(M_0)}
end{equation}
$$
Если же уравнение поверхности задано в явном виде $z=f(x,y)$, то уравнение касательной плоскости имеет вид:
$$
begin{equation}
f_{x}^{‘}(x_0,y_0)cdot(x-x_0)+f_{y}^{‘}(x_0,y_0)cdot(y-y_0)-(z-z_0)=0
end{equation}
$$
Уравнение нормали в случае явного задания поверхности таково:
$$
begin{equation}
frac{x-x_0}{f_{x}^{‘}(x_0,y_0)}=frac{y-y_0}{f_{y}^{‘}(x_0,y_0)}=frac{z-z_0}{-1}
end{equation}
$$
Примечание (желательное для более полного понимания текста): показатьскрыть
Пример №1
Найти уравнение касательной плоскости и нормали к поверхности $z=3x^2y^4-6xy^3+5x-4y+10$ в точке $M_0(-2;1;20)$.
Решение
Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$, $y_0$, $z_0$ (координаты точки $M_0$) в нашем случае таковы: $x_0=-2$, $y_0=1$, $z_0=20$. Но перед тем, как переходить к решению, осуществим небольшую проверку. Убедимся, что точка $M_0$ действительно лежит на заданной поверхности. Эта проверка не является обязательной, но желательна, ибо ошибка в условиях подобных задач – дело вовсе не редкое. Подставим $x=x_0$, $y=y_0$ в уравнение нашей поверхности и убедимся, что $z_0$ действительно равно 20:
$$
z_0=3x_{0}^{2}y_{0}^{4}-6x_0y_{0}^{3}+5x_0-4y_0+10=3cdot (-2)^2cdot 1^4-6cdot (-2)cdot 1^3-4cdot 1+10=12+12-4=20.
$$
Проверка пройдена, точка $M_0$ действительно лежит на заданной поверхности. Теперь найдём частные производные, т.е. $z_{x}^{‘}$ и $z_{y}^{‘}$:
$$
z_{x}^{‘}=6xy^4-6y^3+5;\
z_{y}^{‘}=12x^2y^3-18xy^2-4.
$$
Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ в выражения частных производных:
$$
z_{x}^{‘} left(x_0, y_0right)=6x_0y_{0}^{4}-6y_{0}^{3}+5=-12-6+5=-13;\
z_{y}^{‘}left(x_0, y_0right)=12x_{0}^{2}y_{0}^{3}-18x_0y_{0}^{2}-4=48-(-36)-4=80.
$$
Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_{x}^{‘} left(x_0, y_0right)=-13$, $z_{y}^{‘} left(x_0, y_0right)=80$ в формулу (3) получим уравнение касательной плоскости:
$$
-13cdot(x-(-2))+80cdot(y-1)-(z-20)=0;\
-13x+80y-z-86=0.
$$
Подставляя $x_0=-2$, $y_0=1$, $z_0=20$, $z_{x}^{‘} left(x_0, y_0right)=-13$, $z_{y}^{‘} left(x_0, y_0right)=80$ в формулу (4) получим уравнение нормали:
$$
frac{x-(-2)}{-13}=frac{y-1}{80}=frac{z-20}{-1}; frac{x+2}{-13}=frac{y-1}{80}=frac{z-20}{-1}.
$$
Ответ: Касательная плоскость: $-13x+80y-z-86=0$; нормаль: $frac{x+2}{-13}=frac{y-1}{80}=frac{z-20}{-1}$.
Пример №2
Найти уравнение касательной плоскости и нормали к поверхности $z=5sqrt{x^2+y^2}-2xy-39$ в точке $M_0(3;-4;z_0)$.
Решение
Поверхность задана в явном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (3) и (4). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=3$, $y_0=-4$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:
$$
z_0=5sqrt{x_{0}^{2}+y_{0}^{2}}-2x_0y_0-39=5sqrt{25}+24-39=10.
$$
Теперь, как и в предыдущем примере, перейдём к нахождению частных производных $z_{x}^{‘}$ и $z_{y}^{‘}$. После того, как мы найдём эти производные в общем виде, укажем их значения при $x=x_0$ и $y=y_0$:
$$
z_{x}^{‘}=frac{10x}{sqrt{x^2+y^2}}-2y; z_{x}^{‘} left(x_0, y_0right)=frac{10cdot 3}{sqrt{3^2+(-4)^2}}-2cdot(-4)=11;\
z_{y}^{‘}=frac{10y}{sqrt{x^2+y^2}}-2x; z_{y}^{‘} left(x_0, y_0right)=frac{10cdot (-4)}{sqrt{3^2+(-4)^2}}-2cdot 3=-10.\
$$
Подставляя $x_0=3$, $y_0=-4$, $z_0=10$, $z_{x}^{‘} left(x_0, y_0right)=11$, $z_{y}^{‘} left(x_0, y_0right)=-10$ в формулы (3) и (4) получим уравнения касательной плоскости и нормали:
$$
11cdot(x-3)+(-10)cdot(y-(-4))-(z-10)=0; 11x-10y-z-63=0; \
frac{x-3}{11}=frac{y-(-4)}{-10}=frac{z-10}{-1}; frac{x-3}{11}=frac{y+4}{-10}=frac{z-10}{-1}.
$$
Ответ: Касательная плоскость: $11x-10y-z-63=0$; нормаль: $frac{x-3}{11}=frac{y+4}{-10}=frac{z-10}{-1}$.
Пример №3
Найти уравнение касательной плоскости и нормали к поверхности $3xy^2z+5xy+z^2=10xz-2y+1$ в точке $M_0(1;-2;3)$.
Решение
Перенесём все слагаемые в левую часть равенства и обозначим полученное в левой части выражение как $F(x,y,z)$:
$$
3xy^2z+5xy+z^2-10xz+2y-1=0.
$$
$$F(x,y,z)=3xy^2z+5xy+z^2-10xz+2y-1$$
Используем формулы (1) и (2). Значения $x_0$, $y_0$ и $z_0$ как и ранее обозначают координаты точки $M_0$, т.е. $x_0=1$, $y_0=-2$, $z_0=3$.
Проверим, действительно ли точка $M_0$ лежит на данной поверхности. Для этого подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражение $3xy^2z+5xy+z^2-10xz+2y-1$ и выясним, равен ли нулю полученный результат:
$$
3x_0y_{0}^{2}z_0+5x_0y_0+z_{0}^{2}-10x_0z_0+2y_0-1=36-10+9-30-4-1=0.
$$
Итак, точка $M_0$ действительно лежит на данной поверхности. Естественно, что данная проверка не является обязательной, но она крайне желательна. Перейдём к дальнейшему решению. Нам нужно найти $F_{x}^{‘}$, $F_{y}^{‘}$ и $F_{z}^{‘}$:
begin{aligned}
& F_{x}^{‘}=3y^2z+5y-10z;\
& F_{y}^{‘}=6xyz+5x+2; \
& F_{z}^{‘}=3xy^2+2z-10x. end{aligned}
Нас интересуют значения частных производных именно в точке $M_0$, посему подставим $x=x_0$, $y=y_0$ и $z=z_0$ в выражения частных производных:
begin{aligned}
& F_{x}^{‘}(M_0)=3y_{0}^{2}z_0+5y_0-10z_0=-4;\
& F_{y}^{‘}(M_0)=6x_0y_0z_0+5x_0+2=-29; \
& F_{z}^{‘}(M_0)=3x_0y_{0}^{2}+2z_0-10x_0=8. end{aligned}
Подставляя $x_0=1$, $y_0=-2$, $z_0=3$, $F_{x}^{‘} left(M_0right)=-4$, $F_{y}^{‘} left(M_0right)=-29$ и $F_{z}^{‘} left(M_0right)=8$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:
$$
-4cdot(x-1)-29cdot(y-(-2))+8(z-3)=0; -4x-29y+8z-78=0.\
frac{x-1}{-4}=frac{y-(-2)}{-29}=frac{z-3}{8}; frac{x-1}{-4}=frac{y+2}{-29}=frac{z-3}{8}.
$$
Ответ: Касательная плоскость: $-4x-29y+8z-78=0$; нормаль: $frac{x-1}{-4}=frac{y+2}{-29}=frac{z-3}{8}$.
Пример №4
Найти уравнение касательной плоскости и нормали к поверхности $z^3+4xyz=-3x^2+5y+7$ в точке $M_0(0;-3;z_0)$.
Решение
Поверхность задана в неявном виде, посему для нахождения уравнений касательной плоскости и нормали будем применять формулы (1) и (2). Значения $x_0$ и $y_0$ (первая и вторая координаты точки $M_0$) заданы по условию: $x_0=0$, $y_0=-3$. Третью координату (т.е. $z_0$) нужно определить самостоятельно, подставив в заданное уравнение $x=x_0$ и $y=y_0$:
$$
z_{0}^{3}+4x_0y_0z_0=-3x_{0}^{2}+5y_0+7;\
z_{0}^{3}=-15+7; z_{0}^{3}=-8; z_0=-2.
$$
Перенесём все слагаемые в левую часть равенства:
$$
z^3+4xyz+3x^2-5y-7=0.
$$
Обозначим $F(x,y,z)=z^3+4xyz+3x^2-5y-7$ и применим формулы (1) и (2). Найдём частные производные первого порядка $F_{x}^{‘}$, $F_{y}^{‘}$ и $F_{z}^{‘}$. После того, как мы найдём эти производные в общем виде, укажем их значения в точке $M_0$:
begin{aligned}
& F_{x}^{‘}=4yz+6x; ; F_{x}^{‘}(M_0)=4y_0z_0+6x_0=-24;\
& F_{y}^{‘}=4xz-5; ; F_{y}^{‘}(M_0)=4x_0z_0-5=-5;\
& F_{z}^{‘}=3z^2+4xy; ; F_{z}^{‘}(M_0)=3z_{0}^{2}+4x_0y_0=12.
end{aligned}
Подставляя $x_0=0$, $y_0=-3$, $z_0=-2$, $F_{x}^{‘} left(M_0right)=-24$, $F_{y}^{‘} left(M_0right)=-5$ и $F_{z}^{‘} left(M_0right)=12$ в формулы (1) и (2) получим уравнения касательной плоскости и нормали:
$$
-24cdot(x-0)-5cdot(y-(-3))+12(z-(-2))=0; -24x-5y+12z+9=0.\
frac{x-0}{-24}=frac{y-(-3)}{-5}=frac{z-(-2)}{12}; frac{x}{-24}=frac{y+3}{-5}=frac{z+2}{12}.
$$
Ответ: Касательная плоскость: $-24x-5y+12z+9=0$; нормаль: $frac{x}{-24}=frac{y+3}{-5}=frac{z+2}{12}$.
Пусть имеем поверхность, заданную уравнением вида
Введем следующее определение.
Определение 1. Прямая линия называется касательной к поверхности в некоторой точке , если она является
касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку .
Так как через точку Р проходит бесконечное число различных кривых, лежащих на поверхности, то и касательных к поверхности, проходящих через эту точку, будет, вообще говоря, бесконечное множество.
Введем понятие об особых и обыкновенных точках поверхности
Если в точке все три производные равны нулю или хотя бы одна из этих производных не существует, то точка М называется особой точкой поверхности. Если в точке все три производные существуют и непрерывны, причем хотя бы одна из них отлична от нуля, то точка М называется обыкновенной точкой поверхности.
Теперь мы можем сформулировать следующую теорему.
Теорема. Все касательные прямые к данной поверхности (1) в ее обыкновенной точке Р лежат в одной плоскости.
Доказательство. Рассмотрим на поверхности некоторую линию L (рис. 206), проходящую через данную точку Р поверхности. Пусть рассматриваемая кривая задана параметрическими уравнениями
Касательная к кривой будет касательной к поверхности. Уравнения этой касательной имеют вид
Если выражения (2) подставить в уравнение (1), то это уравнение превратится в тождество относительно t, так как кривая (2) лежит на поверхности (1). Дифференцируя его по получим
Проекции этого вектора зависят от — координат точки Р; заметим, что так как точка Р обыкновенная, то эти проекции в точке Р одновременно не обращаются в нуль и потому
касательный к кривой, проходящей через точку Р и лежащей на поверхности. Проекции этого вектора вычисляются на основании уравнений (2) при значении параметра t, соответствующем точке Р.
Вычислим скалярное произведение векторов N и которое равно сумме произведений одноименных проекций:
На основании равенства (3) выражение, стоящее в правой части, равно нулю, следовательно,
Из последнего равенства следует, что вектор ЛГ и касательный вектор к кривой (2) в точке Р перпендикулярны. Проведенное рассуждение справедливо для любой кривой (2), проходящей через точку Р и лежащей на поверхности. Следовательно, каждая касательная к поверхности в точке Р перпендикулярна к одному и тому же вектору N и потому все эти касательные лежат в одной плоскости, перпендикулярной к вектору ЛГ. Теорема доказана.
Определение 2. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную ее точку Р, называется касательной плоскостью к поверхности в точке Р (рис. 207).
Заметим, что в особых точках поверхности может не существовать касательной плоскости. В таких точках касательные прямые к поверхности могут не лежать в одной плоскости. Так, например, вершина конической поверхности является особой точкой.
Касательные к конической поверхности в этой точке не лежат в одной плоскости (они сами образуют коническую поверхность).
Напишем уравнение касательной плоскости к поверхности (1) в обыкновенной точке. Так как эта плоскость перпендикулярна вектору (4), то, следовательно, ее уравнение имеет вид
Если уравнение поверхности задано в форме или уравнение касательной плоскости в этом случае примет вид
Замечание. Если в формуле (6) положим , то эта формула примет вид
ее правая часть представляет собой полный дифференциал функции . Следовательно, . Таким образом, полный дифференциал функции двух переменных в точке соответствующий приращениям независимых переменных х и у, равен соответствующему приращению аппликаты касательной плоскости к поверхности, которая является графиком данной функции.
О пределение 3. Прямая, проведенная через точку поверхности (1) перпендикулярно к касательной плоскости, называется нормалью к поверхности (рис. 207).
Напишем уравнения нормали. Так как ее направление совпадает с направлением вектора N, то ее уравнения будут иметь вид
Скачать с Depositfiles
4. ТЕОРИЯ ПОВЕРХНОСТЕЙ.
4.1 УРАВНЕНИЯ ПОВЕРХНОСТЕЙ.
Поверхность в трёхмерном пространстве может быть задана:
1) неявно:
F
(
x
,
y
,
z
)
=0 (4.1)
2) явно:
z
=
f
(
x
,
y
)
(4.2)
3) параметрически: (4.3)
или: 
где скалярные аргументы 


4.2 КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ.
Если линия лежит на поверхности (4.1), то координаты её точек удовлетворяют уравнению поверхности:
Дифференцируя это тождество, получим:
(4.4)
или 
’
)
в каждой точке кривой на поверхности. Таким образом, вектор градиента в неособых точках поверхности (в которых функция (4.5) дифференцируема и 
0
(x
0
,
y
0
,
z
0
) поверхности
(4.6)
и в качестве направляющего вектора в уравнении нормали:

В случае явного (4.2) задания поверхности уравнения касательной плоскости и нормали соответственно примут вид:
(4.8)
и
При параметрическом представлении поверхности (4.3) векторы 

а в качестве направляющего вектора нормали может быть принято их векторное произведение:
и уравнение нормали может быть записано в виде:
(4.11)
где 
0
.
В дальнейшем мы ограничимся рассмотрением лишь таких точек поверхности, где векторы
не равны нулю и не параллельны.
Пример 4.1
Составить уравнения касательной плоскости и нормали в точке М
0
(1,1,2) к поверхности параболоида вращения 
Решение: Так как уравнение параболоида задано в явном виде, то согласно (4.8) и (4.9) нужно найти 
0
:

0

0
примет вид:
2(x
-1)+2(y
-1)-(z
-2)=0 или 2
x
+2
y
–
z
‑ 2=0, а уравнение нормали 
Пример 4.2
Составить уравнения касательной плоскости и нормали в произвольной точке геликоида 
Решение. Здесь ,
Уравнение касательной плоскости:
или
Уравнения нормали:

4.3 ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.
Если поверхность задается уравнением
то кривая 

Дифференциал радиус-вектора 
0
в близлежащую точку М, равен

Так как 
(4.14)
где .
Выражение в правой части (4.14) называется первой квадратичной формой поверхности и играет в теории поверхностей огромную роль.
Интегрирую дифференциал
ds
в пределах от
t
0
(соответствует точке М
0
) до
t
(соответствует точке М), получим длину соответствующего отрезка кривой

Зная первую квадратичную форму поверхности, можно находить не только длины, но и углы между кривыми.
Если
du
,
dv
— дифференциалы криволинейных координат, отвечающие бесконечно малому смещению по одной кривой, а 
(4.16)
С помощью формулы

первая квадратичная форма дает возможность вычислить площадь области 
Пример 4.3
На геликоиде , найти длину винтовой линии 
Решение. Поскольку на винтовой линии 

v
=
t
,
получим уравнение данной винтовой линии в виде . Квадратичная форма:
= ‑ первая квадратичная форма.
Здесь . В формуле (4.15) в данном случае 
=
4.4 ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.
Обозначим 


.
(4.23)
Линия на поверхности называется линией кривизны, если ее направление в каждой точке является главным направлением.
4.6 ПОНЯТИЕ О ГЕОДЕЗИЧЕСКИХ ЛИНИЯХ НА ПОВЕРХНОСТИ.
Определение 4.1
. Кривая на поверхности называется геодезической, если ее главная нормаль 

Через каждую точку поверхности в любом направлении проходит, и при том только одна геодезическая. На сфере, например, геодезическими являются большие круги.
Параметризация поверхности называется полугеодезической, если одно семейство координатных линий состоит из геодезических, а второе ему ортогонально. Например, на сфере меридианы (геодезические) и параллели.
Геодезическая на достаточно малом отрезке является кратчайшей среди всех близких к ней кривых, соединяющих те же точки.
Уравнение нормальной плоскости
1.
4.
Касательная плоскость и нормаль к поверхности
Пусть дана некоторая поверхность, A — фиксированная точка поверхности и B — переменная точка поверхности,
(рис. 1).
Ненулевой вектор
называется нормальным вектором
к поверхности в точке A , если
Точка поверхности F (x , y , z) = 0 называется обыкновенной
, если в этой точке
- частные производные F » x
, F » y
, F » z
непрерывны; - (F » x
)2
+ (F » y
)2
+ (F » z
)2
≠ 0 .
При нарушении хотя бы одного из этих условий точка поверхности называется особой точкой поверхности
.
Теорема 1.
Если M (x 0
, y 0
, z 0
) — обыкновенная точка поверхности F (x , y , z) = 0 , то вектор
|
= grad F (x 0 |
(1) |
является нормальным к этой поверхности в точке M (x 0
, y 0
, z 0
) .
Доказательство
приведено
в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова
«Курс высшей математики: Интегральное исчисление. Функции нескольких
переменных. Дифференциальные уравнения. М.: Изд-во МЭИ, 2002
(стр. 128).
Нормалью к поверхности
в
некоторой ее точке называется прямая, направляющий вектор которой
является нормальным к поверхности в этой точке и которая проходит через
эту точку.
Канонические уравнения нормали
можно представить в виде
=
=
. |
(2) |
Касательной плоскостью
к
поверхности в некоторой точке называется плоскость, которая проходит
через эту точку перпендикулярно нормали к поверхности в этой точке.
Из этого определения следует, что уравнение касательной плоскости
имеет вид:
(3)
Если точка поверхности является особой, то в этой точке нормальный к
поверхности вектор может не существовать, и, следовательно, поверхность
может не иметь нормали и касательной плоскости.
Геометрический смысл полного дифференциала функции двух переменных
Пусть функция z = f (x , y) дифференцируема в точке a (x 0
, y 0
) . Ее графиком является поверхность
f (x , y) − z = 0.
Положим z 0
= f (x 0
, y 0
) . Тогда точка A (x 0
, y 0
, z 0
) принадлежит поверхности.
Частные производные функции F (x , y , z) = f (x , y) − z суть
F » x
= f » x
, F » y
= f » y
, F » z
= − 1
и в точке A (x 0
, y 0
, z 0
)
- они непрерывны;
- F «2
x
+ F «2
y
+ F «2
z
= f «2
x
+ f «2
y
+ 1 ≠ 0 .
Следовательно, A — обыкновенная точка поверхности F (x , y , z) и в этой точке существует касательная плоскость к поверхности. Согласно (3), уравнение касательной плоскости имеет вид:
f » x
(x 0
, y 0
) (x − x 0
) + f » y
(x 0
, y 0
) (y − y 0
) − (z − z 0
) = 0.
Вертикальное смещение точки на касательной плоскости при переходе из точки a (x 0
, y 0
) в произвольную точку p (x , y) есть B Q (рис. 2). Соответствующее приращение аппликаты есть
(z − z 0
) = f » x
(x 0
, y 0
) (x − x 0
) + f » y
(x 0
, y 0
) (y − y 0
)
Здесь в правой части стоит дифференциалd
z функции z = f (x , y) в точке a (x 0
, x 0
). Следовательно,
d
f (x 0
, y 0
). есть приращение аппликаты точки плоскости касательной к графику функции f (x , y) в точке (x 0
, y 0
, z 0
= f (x 0
, y 0
)).
Из определения дифференциала следует, что расстояние между точкой P на графике функции и точкой Q на касательной плоскости есть бесконечно малая более высокого порядка, чем расстояние от точки p до точки a .
Рассмотрим геометрические приложения производной функции нескольких переменных. Пусть функция двух переменных задана неявно: . Эта функция в области своего определения изображается некоторой поверхностью (п. 5.1). Возьмем на данной поверхности произвольную точку , в которой все три частных производных , , существуют и непрерывны, причем хотя бы одна из них не равна нулю.
Точка с такими характеристиками называется обыкновенной
точкой поверхности. Если хотя бы одно из указанных выше требований не выполняется, то точка называется особой
точкой поверхности.
Через выбранную на поверхности точку можно провести множество кривых, к каждой из которых может быть проведена касательная.
Определение 5.8.1
. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через некоторую точку , называется касательной плоскостью к данной поверхности в точке
.
Чтобы провести данную плоскость достаточно иметь две касательных прямых, то есть две кривых на поверхности. Это могут быть кривые, полученные в результате сечения данной поверхности плоскостями , (рис. 5.8.1).
Запишем уравнение касательной линии к кривой, лежащей на пересечении поверхности и плоскости . Поскольку данная кривая лежит в системе координат , то уравнение касательной к ней в точке , в соответствии с п. 2.7, имеет вид:
. (5.8.1)
Соответственно, уравнение касательной к кривой, лежащей на пересечении поверхности и плоскости , в системе координат в той же точке имеет вид:
. (5.8.2)
Воспользуемся выражением для производной неявно заданной функции (п. 5.7). Тогда , а . Подставляя эти производные в (5.8.1) и (5.8.2), получим, соответственно:


Поскольку полученные выражения не что иное, как уравнения прямых в канонической форме (п. 15), то из (5.8.3) получаем направляющий вектор , а из (5.8.4) –
. Векторное произведение даст вектор, нормальный к данным касательным линиям, а, следовательно, и к касательной плоскости:
Отсюда следует, что уравнение касательной плоскости к поверхности в точке имеет вид (п. 14):
Определение 5.8.2
. Прямая, проведенная через точку поверхности перпендикулярно касательной плоскости в этой точке, называется нормалью к поверхности
.
Так как направляющий вектор нормали к поверхности совпадает с нормалью к касательной плоскости , то уравнение нормали имеет вид:

Скалярное поле
Пусть в пространстве задана область , занимающая часть или все это пространство. Пусть каждой точке этой области по какому-то закону поставлена в соответствие некоторая скалярная величина (число).
Определение 5.9.1
. Область в пространстве, каждой точке которой ставится в соответствие по известному закону некоторая скалярная величина , называется скалярным полем
.
Если с областью связана какая-то система координат, например, прямоугольная декартовая, то каждая точка приобретает свои координаты. В этом случае скалярная величина становится функцией координат: на плоскости – , в трехмерном пространстве – . Скалярным полем часто называют и саму функцию , описывающую данное поле. В зависимости от размерности пространства, скалярное поле может быть плоским, трехмерным и т.д.
Необходимо подчеркнуть, что величина скалярного поля зависит лишь от положения точки в области , но не зависит от выбора системы координат.
Определение 5.9.2
. Скалярное поле, зависящее только от положения точки в области , но не зависящее от времени, называется стационарным
.
Нестационарные скалярные поля, то есть зависящие от времени, в данном разделе нами рассматриваться не будут.
В качестве примеров скалярных полей можно назвать поле температур, поле давлений в атмосфере, поле высот над уровнем океана.
Геометрически скалярные поля часто изображаются с помощью так называемых линий или поверхностей уровня.
Определение 5.9.3
. Множество всех точек пространства, в которых скалярное поле имеет одно и то же значение называется поверхностью уровня или эквипотенциальной поверхностью. В плоском случае для скалярного поля это множество называется линией уровня или эквипотенциальной линией
.
Очевидно, что уравнение поверхности уровня имеет вид , линии уровня – . Придавая в данных уравнениях константе разные значения, получаем семейство поверхностей или линий уровня. Например,
(вложенные друг в друга сферы с разными радиусами) или (семейство эллипсов).
В качестве примеров линий уровня из физики можно привести изотермы (линии равных температур), изобары (линии равных давлений); из геодезии – линии равных высот и т.д.
Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.
Рассмотрим поверхность σ
, заданную уравнением z = f(x,y) , где f(x,y) – дифференцируемая функция, и пусть M 0 (x 0 ,y 0 ,z 0) – фиксированная точка на поверхности σ , т.е. z 0 = f(x 0 ,y 0).
Назначение
. Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности
. Решение оформляется в формате Word
. Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис .
Правила ввода функций
:
Правила ввода функций
:
Касательной плоскостью к поверхности
σ
в её точке М
0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ
через точку М
0 .
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M 0 (x 0 ,y 0 ,z 0) имеет вид:
z – z 0 = f’ x (x 0 ,y 0)(x – x 0) + f’ y (x 0 ,y 0)(y – y 0)
Вектор называется вектором нормали к поверхности σ
в точке М 0 . Вектор нормали перпендикулярен касательной плоскости.
Нормалью к поверхности
σ
в точке М
0 называется прямая, проходящая через эту точку и имеющая направление вектора N.
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y) , в точке M 0 (x 0 ,y 0 ,z 0), где z 0 = f(x 0 ,y 0), имеют вид:
Пример №1
. Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M 0 (0;1).
Решение
. Запишем уравнения касательной в общем виде: z — z 0 = f» x (x 0 ,y 0 ,z 0)(x — x 0) + f» y (x 0 ,y 0 ,z 0)(y — y 0)
По условию задачи x 0 = 0 , y 0 = 1 , тогда z 0 = 5
Найдем частные производные функции z = x^3+5*y:
f» x (x,y) = (x 3 +5 y)» x = 3 x 2
f» x (x,y) = (x 3 +5 y)» y = 5
В точке М 0 (0,1) значения частных производных:
f» x (0;1) = 0
f» y (0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0: z — 5 = 0(x — 0) + 5(y — 1) или -5 y+z = 0
Пример №2
. Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M 0 (1;0;1).
Решение
. Находим частные производные функции . Поскольку функция задана в неявном виде, то производные ищем по формуле:
Для нашей функции:
Тогда:
В точке М 0 (1,0,1) значения частных производных:
f» x (1;0;1) = -3 / 16
f» y (1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0: z — 1 = -3 / 16 (x — 1) + 0(y — 0) или 3 / 16 x+z- 19 / 16 = 0
Пример
. Поверхность σ
задана уравнением z
= y/x + xy
– 5x
3 . Найти уравнение касательной плоскости и нормали к поверхности σ
в точке М
0 (x
0 , y
0 , z
0), принадлежащей ей, если x
0 = –1, y
0 = 2.
Найдем частные производные функции z
= f
(x
, y
) = y/x + xy
– 5x
3:
f x ’(x
, y
) = (y/x + xy
– 5x
3)’ x = – y/x 2 + y
– 15x
2 ;
f y ’ (x
, y
) = (y/x + xy
– 5x
3)’ y = 1/x + x
.
Точка М
0 (x
0 , y
0 , z
0) принадлежит поверхности σ
, поэтому можно вычислить z
0 , подставив заданные x
0 = –1 и y
0 = 2 в уравнение поверхности:
z
= y/x + xy
– 5x
3
z
0 = 2/(-1) + (–1) 2 – 5 (–1) 3 = 1.
В точке М
0 (–1, 2, 1) значения частных производных:
f x ’(М
0) = –1/(-1) 2 + 2 – 15(–1) 2 = –15; f y ’(М
0) = 1/(-1) – 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ
в точке М
0:
z
– 1= –15(x
+ 1) – 2(y
– 2) z
– 1= –15x
– 15 – 2y +
4 15x
+ 2y
+ z
+ 10 = 0.
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ
в точке М
0: .
Ответы: уравнение касательной плоскости: 15x
+ 2y
+ z
+ 10 = 0; уравнения нормали: .
Пример №1
. Дана функция z=f(x,y) и две точки А(х 0 , y 0) и В(х 1 ,y 1). Требуется: 1) вычислить значение z 1 функции в точке В; 2) вычислить приближенное значение z 1 функции в точке В исходя из значения z 0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x 0 ,y 0 ,z 0).
Решение.
Запишем уравнения касательной в общем виде:
z — z 0 = f» x (x 0 ,y 0 ,z 0)(x — x 0) + f» y (x 0 ,y 0 ,z 0)(y — y 0)
По условию задачи x 0 = 1, y 0 = 2, тогда z 0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f» x (x,y) = (x 2 +3 x y +y 2)» x = 2 x+3 y 3
f» x (x,y) = (x 2 +3 x y +y 2)» y = 9 x y 2
В точке М 0 (1,2) значения частных производных:
f» x (1;2) = 26
f» y (1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М 0:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26 x-36 y+z+73 = 0
Пример №2
. Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Касательная плоскость и нормаль к поверхности
Графиком функции 2-х переменных z = f(x,y) является поверхность, проектирующаяся на плоскость XOY в область определения функции D.
Рассмотрим поверхность σ, заданную уравнением z = f(x,y), где f(x,y) – дифференцируемая функция, и пусть M0(x0,y0,z0) – фиксированная точка на поверхности σ, т.е. z0 = f(x0,y0).
Назначение. Онлайн-калькулятор предназначен для нахождения уравнения касательной плоскости и нормали к поверхности. Решение оформляется в формате Word. Если необходимо найти уравнение касательной к кривой (y = f(x)), то необходимо использовать данный сервис.
- Решение онлайн
- Видеоинструкция
Правила ввода функций:
- Все переменные выражаются через x,y,z
Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0) имеет вид:
z – z0 = f’x(x0,y0)(x – x0) + f’y(x0,y0)(y – y0)
Вектор называется вектором нормали к поверхности σ в точке М0. Вектор нормали перпендикулярен касательной плоскости.
Нормалью к поверхности σ в точке М0 называется прямая, проходящая через эту точку и имеющая направление вектора N.
Канонические уравнения нормали к поверхности, заданной уравнением z = f(x,y), в точке M0(x0,y0,z0), где z0 = f(x0,y0), имеют вид:
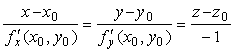
Пример №1. Поверхность задана уравнением x3+5y. Найти уравнение касательной плоскости к поверхности в точке M0(0;1).
Решение. Запишем уравнения касательной в общем виде: z - z0 = f'x(x0,y0,z0)(x - x0) + f'y(x0,y0,z0)(y - y0)
По условию задачи x0 = 0, y0 = 1, тогда z0 = 5
Найдем частные производные функции z = x^3+5*y:
f'x(x,y) = (x3+5•y)'x = 3•x2
f’x(x,y) = (x3+5•y)’y = 5
В точке М0(0,1) значения частных производных:
f'x(0;1) = 0
f'y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z - 5 = 0(x - 0) + 5(y - 1) или -5•y+z = 0
Пример №2. Поверхность задана неявным образом y2-1/2*x3-8z. Найти уравнение касательной плоскости к поверхности в точке M0(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:
Для нашей функции:
Тогда:
В точке М0(1,0,1) значения частных производных:
f'x(1;0;1) = -3/16
f'y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z - 1 = -3/16(x - 1) + 0(y - 0) или 3/16•x+z-19/16 = 0
Пример. Поверхность σ задана уравнением z= y/x + xy – 5x3. Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x3:
fx’(x, y) = (y/x + xy – 5x3)’x = – y/x2 + y – 15x2;
fy’ (x, y) = (y/x + xy – 5x3)’y = 1/x + x.
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
z= y/x + xy – 5x3
z0 = 2/(-1) + (–1) 2 – 5 (–1)3 = 1.
В точке М0(–1, 2, 1) значения частных производных:
fx’(М0) = –1/(-1)2 + 2 – 15(–1)2 = –15; fy’(М0) = 1/(-1) – 1 = –2.
Пользуясь формулой (5) получаем уравнение касательной плоскости к поверхности σ в точке М0:
z – 1= –15(x + 1) – 2(y – 2) z – 1= –15x – 15 – 2y +4
15x + 2y + z + 10 = 0.
Пользуясь формулой (6) получаем канонические уравнения нормали к поверхности σ в точке М0: .
Ответы: уравнение касательной плоскости: 15x + 2y + z + 10 = 0; уравнения нормали: .
Пример №1. Дана функция z=f(x,y) и две точки А(х0, y0) и В(х1,y1). Требуется: 1) вычислить значение z1 функции в точке В; 2) вычислить приближенное значение z1 функции в точке В исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x0,y0,z0).
Решение.
Запишем уравнения касательной в общем виде:
z — z0 = f’x(x0,y0,z0)(x — x0) + f’y(x0,y0,z0)(y — y0)
По условию задачи x0 = 1, y0 = 2, тогда z0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’x(x,y) = (x2+3•x•y•+y2)’x = 2•x+3•y3
f’x(x,y) = (x2+3•x•y•+y2)’y = 9•x•y2
В точке М0(1,2) значения частных производных:
f’x(1;2) = 26
f’y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0
Пример №2. Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x2 + y2 в точке (1;-1;3).
Скачать решение