Как составить обратную теорему

Рассмотрим четыре схемы теорем:

1.

2.

3.

4.

Две теоремы, у которых условие одной
является заключением другой, а условие
второй заключением первой, называется
взаимно обратимыми, т.е. (1) и (2) взаимно
обратимы и (3) и (4) – также взаимно
обратимы. Первая теорема обычно называется
прямой теоремой, а вторая – обратной.
Две теоремы, у которых условие и заключение
одной являются отрицанием условия и
заключение другой, называютсявзаимно
противоположными. Теорема (1) и (3), (2)
и (4) – взаимно противоположными. Прямая
и обратная теоремы в общем случае не
равносильны, то есть одна из них может
быть истинной, а другая ложность. Но
теоремы (1) и (4), (2) и (3) всегда равносильны.
Это можно доказать.

.

5.5 Формулировка необходимых и достаточных условий.

В теореме
,
предикатQ(x)логически следует из предикатаР(х),
поэтомуР(х), называютдостаточным
условием дляQ(x),
а

Q(x)– называютнеобходимым условием дляР(х):.

Если теорема имеет вид
,
то можно записать

то есть Р(х)– является необходимым
и достаточным условием дляQ(x),
аQ(x)необходимо и достаточно дляР(х).

Пример:

1) Рассмотрим утверждение: «Если число
натуральное делится на 4, то оно четное».
Оно делимое.

:
«делимостьх на 4»

:
«числохчетное»;

Следовательно, делимость числа на 4
является достаточным условием его
четности, а четность числа – необходимым
условием его делимости на 4.

2) «В следующих предложениях поставить
слова «необходимо, но недостаточно»,
«достаточно, но необходимо», «не
необходимо и недостаточно» или «необходимо
и достаточно».

«Для
того чтобы,
чтобы».

Пусть
,.
Корни уравненияравны.
Рассмотрим.
При,,,то есть.
Следовательно, дляне является необходимым. Теперь рассмотрим
противоположную импликацию.
Здесь при:;;и при:,,,
вторая импликация верна. Значит дляявляется достаточным условием. Итак
предложение может быть сформулировано
«Для того, чтобыдостаточно, но не обходимо, чтобы».

Вопросы и задания:

1. Введя подходящие одноместные предикаты
на соответствующих областях, переведите
следующие высказывания на язык логики
предикатов:

а) Все рациональные числа действительные;

б) Некоторые рациональные числа
действительны;

в) Некоторые рациональные числа не
являются действительными.

2. Записать на язык логики предикатов,
следующие определения:

а) Строго монотонной последовательности:

«называетсявырастающей (убывающей),если при.
Вырастающие и убывающие последовательности
называются строго монотонными».

б) Периодической функции:

«Функция
называютсяпериодической, если
существует такое числоТ0,
что при любомхиз области определения
функции числаипринадлежат этой области и выполняется
условие»

в) Монотонно вырастающей функции:

«Функция
называется монотонно вырастающей, если
из неравенстваследуют, что».

3. Пусть
означает «х– простое число»,означает «х – четное число»,:
«х – нечетное число»,:
«хделиту». Переведите на русский
язык следующие символические записи
на языке логики предикатов, учитывая,
что переменныехиу пробегают
множество натуральных чисел:

а)
;

б)
;

в)
;

г);

д)
.

4. Доказать несправедливость утверждений:

а) «Если функция
дифференцируемая в точке,
то она имеет в этой точке локальный
экстремум».

б) «Если дифференцируемая функция
имеет в точкевторую производную, равную нулю,
то точка— точка экстремума функции».

5. Используя приведенную основную
теорему, сформулировать к ней обратную,
противоположную и обратную к противоположной
теореме.

а) «Если в четырехугольнике диагонали
взаимно перпендикулярны, то этот
четырехугольник ромб».

б) «Если числовой ряд
сходится, то егоn-ый
член стремится к нулю при».

в) «Во всяком параллелограмме есть центр
симметрии».

6. Дополнить следующие предложения
словами «необходимо и достаточно»,
«необходимо и недостаточно», «достаточно,
но необходимо», или «не необходимо и
недостаточно».

а) «Для того чтобы два треугольника были
равны ,…., чтобы все углы одного
треугольника были равны соответствующим
углам другого».

б) «Для того чтобы все стороны многоугольника
были равны ,.., чтобы этот многоугольник
был правильным».

в) «Для того чтобы четырехугольник был
прямоугольником ,…, чтобы все его углы
были равны».

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Муниципальное бюджетное общеобразовательное
учреждение

«Средняя общеобразовательная школа № 17

города Новоалтайска Алтайского края»

Урок геометрии в 7 классе

Тема: Прямая и обратная теорема

(урок обобщения знаний по  теме «Параллельные прямые»)

Учитель: Уварова Светлана Михайловна

г.Новоалтайск

2014г.

Урок геометрии в 7 классе

Учитель: Уварова С.М.(МБОУ «СОШ№17 г.Новоалтайска»)

Тема: Прямая и
обратная теорема

Тип урока: Урок
обобщения знаний по теме «Параллельные прямые»

Цели урока:

·      
Обобщить теоретический
материал I—II глав, способствовать прочному усвоению
учащимися изученного материала, пониманию логического построения геометрии,
развитию навыков применения теории к решению задач

·      
Развивать логическое
мышление учащихся, культуру речи, создавать условия для формирования их
познавательных, коммуникативных компетенций

·      
Воспитывать культуру
общения, любознательность, понимание необходимости и полезности изучения
математики. 

                                  
План урока

1.       
Оргмомент.

Записать число, тему урока

Записать в дневник домашнее задание

2.       
Целеполагание

3.       
Актуализация опорных
знаний (устная работа по готовым чертежам),

Постановка проблемы

4.       
Изучение материала «Прямая
и обратная теорема», фронтальная работа, определение понятий «свойство» и
«признак»

5.       
Практическая работа –
составление теорем, выражающих свойства матем. понятий ( работа в парах) с
последующей проверкой

          (
приложение 1)

6.       
Составление утверждений,
обратных данному. Контрпример.

7.       
Практическая работа в
парах: составление теорем, выражающих признаки матем. понятий (приложение 2)

8.       
Контроль.

— вопросы по теме (фронтально)

— Проверочная работа ( в тетрадях по готовым чертежам на доске)

9.       
Итог урока, рефлексия

Оформление:  

1. Эпиграфы:

«Математику уже затем учить надо, что она ум в порядок приводит»

                                                                         М.В.Ломоносов

«В математике все, что не обосновано до конца, расценивается как
абсолютно необоснованное»

                                                                        
А.Я.Хинчин

2. Стенд «Изучаем на уроке»:

         — Высказывание «Без доказательства истина в науке

           остается гипотезой»

— Толкование понятий  определение, аксиома, теорема, свойство,
признак, доказательство

           3. 
Магнитная или интерактивная доска, таблички с терминами:

                    Теорема,
свойство, признак, условие, заключение,   

                   
доказательство, рассуждение, аксиомы, определения,

                    теоремы

           4.
Демонстрационная таблица «Равнобедренный треугольник»

           5. На столах
у учащихся – раздаточный материал:

                на
карточках – условия и заключения изученных теорем для

               
составления свойств и признаков(прямых и обратных теорем)

           6. На
доске:

               —
Чертежи равнобедренных треугольников для работы с

                
теоремами

               —
Задания по готовым чертежам для самостоятельной работы

                  (
на закрытой доске или в презентации к уроку)

Ход урока

I.                
Оргмомент

     — Приветствие,
запись числа, темы урока

      — Запись
домашнего задания: Вопросы на с. 49, №154б,в, №162

II.  Целеполагание

Учитель: Мы
заканчиваем изучение II главы учебника. Сегодня –

                последний
урок перед контрольной работой.

                Является
ли новой для вас тема урока?

                Что
вы уже знаете по этой теме?

                Какие
ключевые слова можно в связи с этим вспомнить?

                Какие
цели поставим перед собой на урок?

Примерные ответы
учеников:

1)  
Закрепить и повторить весь
теоретический метериал

2)  
Научиться работать с
прямой и обратной теоремой, различать «свойство» и «признак»

Учитель обращает
внимание на эпиграф к уроку:

    «Математику уже затем учить надо, что она ум в порядок приводит»

                                        
                                М.В.Ломоносов

            
Попробуем же и мы, ребята, привести в порядок наши еще пока

          небогатые
знания.

III. Актуализация опорных знаний

1.  
Повторение теоретического
метериала

1) 
Что такое теорема?

2) 
 Что выражает теорема?

3) 
Из каких двух частей
обычно состоит ее формулировка?

4) 
Что такое доказательство?

5) 
На что можно опираться при
доказательстве?

По мере ответов ребят учитель составляет таблицу на магнитной доске или
демонстрирует слайд презентации:

                                                                                  

2.  Решение задач по
готовым чертежам

     — Есть ли на
чертеже равнобедренные треугольники? (Найти и доказать):

  1)                                                    2)

 3)
                                                        4)

                                   Р=19

   В задании №4
возможен ответ учащихся: да, треугольник

   равнобедренный,
так как у него углы при основании равны.

Проблема: Какой теоремой воспользовались?(возможны ошибки

при ответе)

-Если в треугольнике два угла равны, то он равнобедренный.

-Доказана ли нами такая теорема?

-Нет.

IV. Изучение нового материала

      1) Сформулиоуйте свойство равнобедренного
троеугольника со словами  «если, то»

        (Демонстрируется
таблица «Равнобедренный треугольник»)

      —  Если
треугольник равнобедренный, то углы при основании равны.

       -Выделите
условие и заключение этой теоремы.

       -Что такое
«свойство» фигуры?

       — Качество,
отличительная особенность чего-нибудь (из словаря

          Ожегова)
 

       -Что дано в
этой теореме, а что надо доказать? ( Дано, что треугольник равнобедренный, а
надо доказать его свойство, т.е. какой характеристикой еще обладает
равнобедренный треугольник)

       2) Как
составить теорему, обратную данной?

      — Надо
поменять условие и заключение теоремы.

       — Если два
угла треугольника равны, то он равнобедренный

    — Выделите
условие и заключение. Какой треугольник дан?

    — произвольный

    —  Что надо
доказать?

    — Что он
равнобедренный.

     — Как можно
назвать эту теорему?

    —Признак
равнобедренного треугольника.

    -Что такое
признак?

    — Это
показатель, примета, знак, по которым можно определить

        что-нибудь ( из словаря Ожегова)

 Учащиеся
предпринимают попытки доказательства теоремы, но

    безуспешно.

  Учитель: Для
доказательства этой теоремы нам не хватает знаний. Но  теорема верна, и мы убедимся
в этом на последующих уроках. А пока можем ли мы пользоваться этой теоремой?

-Нет

  Учитель

    —  обращает
внимание учащихся на слова А.Я.Хинчина

  «В математике все, что не обосновано до конца, расценивается как
абсолютно необоснованное»

    — А как можно
назвать научное предположение, которое пока не доказано?

 — Гипотеза.

— Значит, мы с вами
стоим на пороге маленького научного открытия.

   А как вообще
совершаются научные открытия?

— Наблюдение –
эксперимент, опыт – предположение (гипотеза) –

   доказательство-
научное положение(теория, теорема, закон и т.п.)

 3) Обратимся еще к
одному свойству равнобедренного треугольника

   — Если
треугольник равнобедренный, то биссектриса, проведенная из вершины, является
медианой и высотой.

( ученик доказывает теорему устно у доски на заготовленном ранее
чертеже равнобедренного треугольника или с помощью слайда презентации)

    — Составьте
обратное утверждение

  — Если
биссектриса треугольника является его медианой и высотой, то этот треугольник
равнобедренный.

 ( ученик доказывает теорему устно у доски на заготовленном ранее
чертеже равнобедренного треугольника или с помощью слайда)

    — Нет ли в
теореме лишнего условия?

    — Достаточно,
чтобы биссектриса являлась высотой, медиану мы в доказательстве не
использовали.

   — Итак, мы
рассмотрели две взаимно обратные теоремы, обе они верны.

      Что выражает
первая из этих теорем?

  — Свойство
равнобедренного треугольника.

 — Что выражает обратная ей теорема?

   — Признак равнобедренного
треугольника.

  — Значит, чем является теорема, обратная
свойству? А теорема, обратная

   признаку?

V. Практическая работа (в парах)

  Задание:

  Используя карточки
с условиями и заключениями теорем, изученных ранее, составить теоремы, выражающие
свойства фигур. ( 5 минут)

— Какие теоремы
получились?

    1) Если углы
смежные, то их сумма 180°.

    2) Если углы
вертикальные, то они равны

  3) Если
треугольники равны, то их соответственные углы и стороны равны

  4) Если
треугольник равнобедренный, то  углы при основании равны.

  5) Если
треугольник равнобедренный, то  биссектриса, проведенная к основанию, является
медианой и высотой.

  6) Если
треугольник равнобедренный, то  медиана, проведенная к основанию, является
биссектрисой и высотой

  7) Если
треугольник равнобедренный, то  высота, проведенная к основанию, является
биссектрисой и медианой

 VI.
Составление утверждений, обратных данному. Контрпример.

   — Составьте
утверждение, обратное свойству вертикальных углов.

    —Если углы
равны, то они вертикальные.

  — Верно ли это
утверждение?

        Ученики сами
пытаются опровергнуть это утверждение с помощью контрпримера:

-Приведите еще примеры неверных обратных утверждений.

                       (
о смежных углах)

  VII.
Практическая работа в парах.

    — Составьте из оставшихся карточек признаки
фигур.

— Первый признак
равенства треугольников

 — Второй признак
равенства треугольников

— Третий признак
равенства треугольников

— Если две прямые
перпендикулярны третьей прямой, то они параллельны.

-Составьте
утверждение, обратное первому признаку равенства треугольников

— Если
треугольники равны, то две стороны и угол между ними одного треугольника
соответственно равны двум сторонам и углу между ними другого треугольника.

— Верно ли это
утверждение? Докажите. Как его можно назвать?

— Свойство равных
треугольников

— Сформулируйте
известное нам более общее свойство равных треугольников.

— В равных
треугольниках соответственные углы и стороны равны.

VIII. Контроль

1. Фронтальный опрос

 — Какова структура теоремы?

 — Как составить
утверждение, обратное данному?

 — Всякая ли теорема
имеет обратную?

 — Как можно доказать
ложность утверждения?

 — Для каких теорем
первой части (свойства) практической работы верны

   обратные
утверждения? Как эти утверждения называются?

Выставляются оценки
активно работавшим ученикам

 2. Проверочная
работа

По готовым чертежам
определить, какая теорема проиллюстрирована и записать ее название в
соответствующую колонку:

Ответы:

           
Свойство:                                      Признак

                                      1
вариант

2) равноб.
треугольника                 1)3 признак равенства треугольников

3) равных
треугольников                4)  равнобедренного треугольника

5) вертикальных углов

                                        2
вариант

1) равноб.
треугольника                  2) 1 признак равенства треугольников

4) смежных
углов                             3) параллельных прямых

                                                           
5) равнобедренного треугольника

3.Самопроверка с
помощью ответов на экране

 IX.
Рефлексия

 — Ребята, на полях
своей тетради нарисуйте смайл, выражающий ваше настроение по результатам урока:

    Улыбка или сомнение или печаль,
затруднение

Приложение 1. Задания для работы в парах( разрезать)

углы
смежные                                              сумма углов равна 180°

углы
вертикальные                                      эти углы равны

две прямые
перпендикулярны                    эти прямые не пересекаются

к третьей прямой

треугольники
равны                                      их соответственные углы и

                                                                            стороны
равны

треугольник
равнобедренный                     углы при основании равны

треугольник
равнобедренный                    биссектриса, проведенная
к                                                                                                       

                                                                            основанию,
является медианой

                                                                      
и высотой

треугольник равнобедренный                     высота,
проведенная к основа-

                                                                     
нию, является биссектрисой и

                                                                      
медианой

треугольник
равнобедренный                    медиана, проведенная к основа-

                                                                     
нию, является биссектрисой и

                                                                      
высотой

две стороны и угол
между ними

одного треугольника
соответ-                           треугольники равны

ственно равны двум
сторонам и

углу между ними
другого треу-

гольника,

сторона и два
прилежащих к ней

угла одного
треугольника соот-                       треугольники равны

ветственно равны двум
сторонам

и углу между ними
другого тре-

угольника,

три стороны одного
треуголь-

ника соответственно
равны                                  треугольники равны

трем сторонам другого
треу-

гольника,

Приложение 2. Задания для работы в парах (разрезать)

углы
смежные,                                              сумма углов равна 180°

углы
вертикальные,                                     эти углы равны

две прямые
перпендикулярны                    эти прямые не пересекаются

к третьей прямой,

треугольники
равны,                                      их соответственные углы и

                                                                            стороны
равны

треугольник
равнобедренный,                     углы при основании равны

треугольник
равнобедренный,                    биссектриса, проведенная
к                                                                                                       

                                                                            основанию,
является медианой

                                                                      
и высотой

треугольник
равнобедренный,                    высота, проведенная к основа-

                                                                     
нию, является биссектрисой и

                                                                      
медианой

треугольник
равнобедренный,                    медиана, проведенная к основа-

                                                                     
нию, является биссектрисой и

                                                                      
высотой

две стороны и угол
между ними

одного треугольника
соответ-                           треугольники равны

ственно равны двум
сторонам и

углу между ними
другого треу-

гольника,

сторона и два прилежащих
к ней

угла одного
треугольника соот-                       треугольники равны

ветственно равны 
стороне

и  двум прилежащим к
ней углам

  другого
треугольника,

три стороны одного
треуголь-

ника соответственно
равны                                  треугольники равны

трем сторонам другого
треу-

гольника, 

Обратная теорема или обратное утверждение к данной теореме — это утверждение, в котором условие исходной теоремы (прямого утверждения) поставлено заключением, а заключение — условием.^[1]

Обратной к обратной теореме является исходная (прямая) теорема. Справедливость обоих взаимно обратных теорем означает, что выполнения условий любой из них необходимо и достаточно для справедливости заключения.^[1]

Каждая теорема может быть выражена в форме импликации [math]displaystyle{ A Rightarrow B }[/math], в которой посылка [math]displaystyle{ A }[/math] является условием теоремы, а следствие [math]displaystyle{ B }[/math] является заключением теоремы. Тогда теорема, записанная в виде [math]displaystyle{ B Rightarrow A }[/math] является обратной к ней^[2].

Часто используется более общее определение обратной теоремы: если [math]displaystyle{ (A land C) Rightarrow B }[/math] является прямой теоремой, то обратной называется не только теорема [math]displaystyle{ B Rightarrow (A land C) }[/math], но и теоремы [math]displaystyle{ (B land A) Rightarrow C }[/math], [math]displaystyle{ (B land C) Rightarrow A }[/math]^[3].

Если условие и/или заключение теоремы являются сложными суждениями, то обратная теорема допускает множество не равносильных друг другу формулировок.
Например, если условием теоремы является [math]displaystyle{ A }[/math], а заключением [math]displaystyle{ Y Rightarrow Z }[/math]:
[math]displaystyle{ A Rightarrow (Y Rightarrow Z) }[/math], то для обратной теоремы существует пять форм:^[4]

1. [math]displaystyle{ (Y Rightarrow Z) Rightarrow A }[/math]
2. [math]displaystyle{ (A Rightarrow Z) Rightarrow Y }[/math]
3. [math]displaystyle{ Z Rightarrow (A And Y) }[/math]
4. [math]displaystyle{ A Rightarrow (Z Rightarrow Y) }[/math]
5. [math]displaystyle{ Y Rightarrow (Z Rightarrow A) }[/math]

Вообще говоря, обратная теорема может не быть истинной, даже если прямая теорема верна. Так, теорема «вертикальные углы равны» (иначе: «если углы вертикальные, то они равны»), как известно, верна. Но обратное к ней утверждение «если углы равны, то они вертикальные», вообще говоря, неверно.

Даже если обратное утверждение истинно, то его доказательство может быть гораздо сложнее доказательства прямого.
Например, теорема о четырёх вершинах была доказана в 1912 году, а её обратная только в 1998 году.

Свойства

• Прямая теорема эквивалентна теореме, противоположной обратной: [math]displaystyle{ ( A Rightarrow B ) Leftrightarrow ( overline{B} Rightarrow overline{A} ) }[/math]
• Обратная теорема эквивалентна противоположной прямой: [math]displaystyle{ ( B Rightarrow A ) Leftrightarrow ( overline{A} Rightarrow overline{B} ) }[/math]^[5]

Примеры

• Теорему Пифагора можно сформулировать следующим образом:

Если в треугольнике со сторонами длиной [math]displaystyle{ a }[/math], [math]displaystyle{ b }[/math] и [math]displaystyle{ c }[/math] угол, противолежащий стороне [math]displaystyle{ c }[/math], прямой, то [math]displaystyle{ a^2+b^2=c^2 }[/math].

Обратная к этой теореме появляется в «Началах» Евклида (книга I, предложение 48), может быть сформулирована следующим образом:

Если в треугольнике со сторонами длиной [math]displaystyle{ a }[/math], [math]displaystyle{ b }[/math] и [math]displaystyle{ c }[/math] выполняется [math]displaystyle{ a^2+b^2=c^2 }[/math], то угол, противолежащий стороне [math]displaystyle{ c }[/math], прямой.

• Теорема Абеля и теорема Абеля — Таубера
• Теоремы о вершинах подерного треугольника
• Прямая и обратная предельная теорема
• В ином смысле: теоремы Шеннона для источника общего вида

См. также

• Противоположная теорема

Примечания

Литература

• Эдельман С.Л. Математическая логика. — М.: Высшая школа, 1975. — 176 с.
• Гиндикин С.Г. Алгебра логики в задачах. — М.: Наука, 1972. — 288 с.
• Градштейн И.С. Прямая и обратная теоремы. Элементы алгебры логики. — М.: Наука, 1965. — 127 с.

Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Обратная теорема. Полные уроки

---

ТЕМА УРОКА: Обратная теорема

Цели урока:

• Выработка основных навыков.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока:

• Формировать навыки в понимании заданий, и решении задач.
• Проверить умение учащихся решать задачи.

План урока:

1. Обратная теорема.
2. Необходимые и достаточные условия (математические).
3. Лобачевского геометрия.
4. Примет обратной теоремы с доказательством.

Обратная теорема.

Обратная теорема, теорема, условием которой служит заключение исходной теоремы, а заключением — условие. Обратной к Обратная теорема будет исходная теорема. Таким образом, Обратные теоремы взаимно обратны. Например, теоремы: «если два угла треугольника равны, то их биссектрисы равны» и «если две биссектрисы треугольника равны, то соответствующие им углы равны» — являются обратными друг другу. Из справедливости какой-нибудь теоремы, вообще говоря, не следует справедливость обратной к ней теоремы. Например, теорема: «если число делится на 6, то оно делится на 3» — верна, а Обратная теорема: «если число делится на 3, то оно делится на 6» — неверна. Даже если Обратная теорема верна, для её доказательства могут оказаться недостаточными средства, используемые при доказательстве прямой теоремы. Например, в евклидовой геометрии верны как теорема «две прямые на плоскости, имеющие общий перпендикуляр, не пересекаются», так и обратная к ней теорема «две непересекающиеся прямые на плоскости имеют общий перпендикуляр». Однако вторая (обратная) теорема основывается на евклидовой аксиоме параллельных, тогда как для доказательства первой эта аксиома не нужна. В Лобачевского геометрии вторая просто неверна, тогда как первая остаётся в силе. Обратная теорема равносильна теореме, противоположной к прямой, т. е. теореме, в которой условие и заключение прямой теоремы заменены их отрицаниями. Поэтому прямая теорема равносильна теореме, противоположной к обратной, т. е. теореме, утверждающей, что если неверно заключение прямой теоремы, то неверно и её условие. Известный способ «доказательства от противного» как раз и представляет собой замену доказательства прямой теоремы доказательством теоремы, противоположной к обратной. Справедливость обеих взаимно обратных теорем означает, что выполнение условия любой из них не только достаточно, но и необходимо для справедливости заключения.

Теперь немного подробней рассмотрим Лобачевского геометрию, о какой мы вспоминали выше.

Лобачевского геометрия, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. Евклидова аксиома о параллельных гласит: через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её. В Лобачевского геометрия вместо неё принимается следующая аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Казалось бы, эта аксиома противоречит чрезвычайно привычным представлениям. Тем не менее как эта аксиома, так и вся Лобачевского геометрия имеет вполне реальный смысл.

Рассмотрим реальный примет обратной теоремы с доказательством.

Файл:T.gif Теорема о трех перпендикулярах.

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной.

Файл:14122010 0.GIF

Доказательство.

Пусть АВ – перпендикуляр к плоскости «a», АС – наклонная и «с» — прямая в плоскости «a», проходящая через основание наклонной СK. Проведем прямую СК, параллельно прямой АВ. Прямая СК перпендикулярна плоскости «a» (по этой теореме, так как она параллельна АВ), а значит и любой прямой этой плоскости, следовательно, СК перпендикулярна прямой «с». Проведем через параллельные прямые АВ и СК плоскость «b» (параллельные прямые определяют плоскость, причем только одну). Прямая с перпендикулярна двум прямым лежащим  в плоскости «b», это ВС по условию и СК по построению,  значит она  перпендикулярна и любой прямой, принадлежащей этой плоскости, значит перпендикулярна и прямой АС. Другими словами наклонная АС перпендикулярна прямой «с», лежащей в плоскости «a».

Файл:T.gif Обратная теореме о трех перпендикулярах.

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.

Файл:14122010 1.GIF

Доказательство.

Пусть АВ – перпендикуляр к плоскости «a», АС – наклонная и «с» – прямая в плоскости «a», проходящая через основание наклонной СK. Проведем прямую СК, параллельно прямой АВ. Прямая СК перпендикулярна плоскости «a» (по этой теореме, так как она параллельна АВ), а значит и любой прямой этой плоскости, следовательно, СК перпендикулярна прямой «с». Проведем через параллельные прямые АВ и СК плоскость «b» (параллельные прямые определяют плоскость, причем только одну). Прямая «с» перпендикулярна двум прямым  лежащим  в плоскости «b», это АС по условию и СК по построению,  значит она перпендикулярна и  любой прямой, принадлежащей этой плоскости, значит перпендикулярна и прямой ВС. Другими словами проекция ВС перпендикулярна прямой «с», лежащей в плоскости «a».

Еще один вид интерпретации данной теоремы:

Файл:T.gif Теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

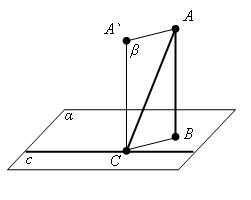
Доказательство.

Аналогично теореме о трех перпендикулярах если прямая с перпендикулярна наклонной CA, то она, будучи перпендикулярна и прямой CA`, перпендикулярна плоскости β, а значит, и проекции наклонной BC. Теорема доказана.

---

Интересный факт:

Определения, изложенные в «Началах» Евклида, не удовлетворяют тре-бованиям современной науки. Вот некоторые из 23 определений, которыми на-чинается первая книга «Начал».

1. Точка есть то, что не имеет частей (такое аналитическое определение точки, по- видимому, заимствовано Евклидом у предшественников и восходит к Демокриту).
2. Линия есть длина без ширины.
3. Границы линии суть точки.
4. Прямая есть такая линия, которая одинаково расположена по отноше-нию ко всем своим точкам.
5. Поверхность есть то, что имеет только длину и ширину.
6. Границы поверхности суть линии.
7. Плоскость есть поверхность, которая одинаково расположена по от-ношению ко всем прямым, на ней лежащим.
8. Плоский угол есть взаимное наклонение двух встречающихся линий, расположенных  в одной плоскости.

Такие определения нельзя считать логически конкретными.

Во-первых, в этих определениях употребляются такие понятия (часть, длина, ширина, грани-ца и т.д.), которые сами должны быть определены. Во-вторых, идея основных понятий (в современном смысле) у Евклида вообще отсутствует.

---

Вопросы:

1. Что такое Обратная теорема?
2. В чем отличие между необходимыми и достаточными условиями?
3. Что гласит теорема о трех перпендикулярах?

Список использованных источников:

1. Урок на тему «Наглядная геометрия» Автор: Самылина Марина Валентиновна., г. Киев
2. Геометрия: Рабочая тетрадь для 7 класса общеобразовательных учреждений Автор: Дудницын Юрий Павлович
3. Уроки геометрии Кирилла и Мефодия. 7 класс (2005)
4. Геометрия. 7 класс. Комплексная зачетная тетрадь. Стадник Л. Г.
   

---

Над уроком работали:

Самылина М.В.

Потурнак С.А.

Муха Р.Л.

---

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов  высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

Предмети > Математика > Математика 7 класс

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: