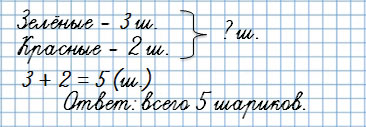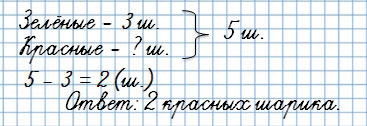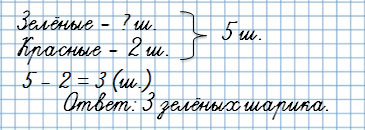|
Что значит «обратная задача» в математике (1, 2, 3, 4 класс)? Как записать и решить обратную задачу, пример? В математике обратная задача составляется на основании какой-либо имеющейся задачи. В обратных задачах искомые данные уже известны. Требуется найти одну из величин, которые были даны в условии исходной задачи. Пример 1 Исходная задача. В магазине яблоки стоят 120 рублей за 1 килограмм, а груши стоят 150 рублей за 1 килограмм. Требуется узнать, на сколько груши дороже яблок. Для решения этой задачи нужно найти разницу между 2 числами — стоимостью груш и стоимостью яблок. 150 — 120 = 30 (руб.) Таким образом, груши дороже яблок на 30 рублей. _ Обратная задача. Здесь нам будет известна разница в стоимости фруктов, то есть 30 рублей. Будем находить либо стоимость яблок, либо стоимость груш — то есть можно составить 2 разных обратных задачи. 1) Яблоки стоят 120 рублей, а груши на 30 рублей дороже. Сколько стоят груши? Решение: 120 + 30 = 150 (руб.) 2) Груши стоят 150 рублей, а яблоки на 30 рублей дешевле. Сколько стоят яблоки? Решение: 150 — 30 = 120 (руб.) Пример 2 Исходная задача. Покупатель хочет купить 500 грамм говядины, которая стоит 200 рублей за 1 килограмм. Сколько он должен заплатить? Для решения данной задачи нужно вспомнить соотношение между граммами и килограммами. 1 килограмм = 1000 грамм. 500 грамм — это ровно половина от 1000 грамм (или 1 килограмма): 500 / 1000 = 1/2. Таким образом, покупатель заплатит не 200 рублей, а только половину: 200 / 2 = 100 (руб.) _ Обратная задача. Здесь нам будет известна цена покупки, то есть 100 рублей. Можно найти, например, стоимость за 1 килограмм. Вот формулировка подобной задачи: Покупатель купил 500 грамм говядины за 100 рублей. Сколько стоит 1 килограмм говядины? Решение: 1) 1 килограмм — это 1000 грамм. 1000 / 500 = 2, то есть 1 килограмм будет в 2 раза больше, чем 500 грамм. 2) Стоимость 1 килограмма составляет 100 * 2 = 200 (руб.) модератор выбрал этот ответ лучшим Математический термин «обратная задача» включает два слова. С существительным задача все понятно. Возникает вопрос: что значит обратная. Данное прилагательное по отношению к задаче можно определить как противоположная или ведущая назад, к исходному состоянию. Для того, чтобы составить обратную задачу, нужно иметь задачу исходную. И исходную задачу необходимо решить. Это нужно для того, чтобы использовать полученный результат в качестве исходных данных для обратной задачи. Если сказать еще проще, то то, что дано ( известно ) в исходной задача, в обратной ей нужно будет искать. А решение исходной задачи станет тем, что известно по условию обратной задачи. Это мое определение термину «обратная задача», простого определения для начальной школы я не нашла. Проще пояснить на примерах. Исходная задача: Мама купила 5 пирожных и 7 кексов к чаю. Сколько всего кексов и пирожных купила мама? Решение 5+7=12 (шт.) выпечки купила мама. Обратная ей задача: Обратных задач можно в этом случае составить две: 1) Мама всего купила 12 пирожных и кексов к чаю, из них 5 пирожных. Сколько кексов купила мама? Решение 12-5=7 (к.) купила мама. 2) Мама всего купила 12 пирожных и кексов к чаю, из них 7 кексов. Сколько пирожных купила мама? Решение 12-7=5 (п.) купила мама. Марина Вологда 3 года назад Обратная задача — это такая задача, в которой все искомые величины уже известны. Из этих известных величин и составляем обратную задачу. Например, нам дана задача: В автопарк заехало три красных машины и пять белых. Сколько всего машин заехало в автопарк? Решение: 3+5 = 8 машин. Составляем обратную задачу: 1) Сколько машин заехало в автопарк красного цвета, если известно, что всего машин было 8. А белых машин было 5. Решение: 8-5 = 3 машины красного цвета. 2) Известно, что в автопарк заехало 8 машин. Из них три были красного цвета. Остальные машины были белые. Сколько машин белого цвета? Решение: 8-3 = 5 машин белого цвета. Алиса в Стране 3 года назад Многие из нас, наверное, уже забыли, что такое обратная задача, но на самом деле ничего сложного в ней нет. Приведу пример. Допустим, у нас есть расстояние (путь) и время, за которое человек его прошел, все мы знаем, как просто определить скорость, нужно расстояние (путь) разделить на время. Так вот к этой элементарной задачке можно составить две обратные задачи: на определение пути (расстояния), если известна скорость и время (чтобы решить эту задачу, нужно скорость умножить на время): Второй обратной задачей будет задача на определение времени, если известно расстояние (путь) и скорость (нужно путь поделить на скорость): Не знаю, кто их назвал «обратными» потому что задача это всегда, как минимум, поиск третьего неизвестного по двум известным, и какая разница какое из них будет неизвестным. Составить их проще простого, просто поменять неизвестное с известным, ну и вероятно математическое действие будет другое — вместо сложения — вычитание, вместо деления — умножение (как и наоборот) Вот пример. У Васи было две конфеты, Валя дала Васе еще три конфеты, сколько у Васи конфет теперь? Ответ — пять. Якобы обратная задача. У Васи было пять конфет, две из которых были его, сколько конфет ему дала Валя что бы у него получилось пять? Ответ — три. Zummy out off 3 года назад Обратная задача в математике — это такая задача, которая составляется по исходной задаче, но ответ исходной задачи включается в условие обратной задачи, а требуется найти то, что было одним из условий исходной задачи. Составление обратных задач тренирует «мозги» для решения задач в математике. Пример составления обратной задачи. Исходная задача. У Маши было 20 рублей, она купила тетрадь за 12 рублей. Сколько денег осталось у Маши? Решение: 20-12=8. Ответ: 8 рублей осталось у Маши. Обратная задача. В условие задачи надо включить сумму сдачи 8 руб. Составляем задачу: Маша купила тетрадь за 12 руб и у неё осталась сдача 8 руб. Сколько денег было у Маши до покупки тетради? Решение: 12+8=20. Ответ: 20 рублей было у Маши. Бархатные лапки 3 года назад Обратная задача составляется на основе уже имеющейся решенной задачи. В обратной задаче требуется узнать то, что было известно в нашей задаче. Объясним, что такое обратная задача, на примере простейшей задачки для начальных классов. У Иры 10 яблок, у Маши 5 яблок. Нужно найти, сколько яблок у обоих девочек вместе. Это наша задача, решается она так: общее количество яблок равно: яблоки Иры плюс яблоки Маши = 5 + 10 + 15 Обратная задача к этой задаче: у двух девочек, Иры и Маши 15 яблок, сколько яблок у Иры, если у Маши 5 яблок. Решение: 15 — 5 = 10 яблок у Иры. Также обратную задачу можно составить и так: у Иры и Маши 15 яблок, сколько яблок у Маши, если у Иры 10 яблок. Решение: 15 — 10 = 5, у Маши 5 яблок. KritikSPb 4 года назад Обратная задача в математике требует найти то, что было известно в первоначальной задаче. То есть обязательным условием составления обратной задачи является наличие прямо задачи, от которой и отталкиваются для составления обратной. Например, первоначально известно, что человеку нужно дойти из дома до магазина. Расстояние 10 км. Идёт он со скоростью 5 км в час. Через сколько времени он будет на месте? Решение: 10 / 5 = 2 часа. А теперь обратная задача: За два часа человек дошёл от дома до магазина. Определите расстояние, если известно, что скорость человека 5 км в час. Решение: 2 * 5 = 10 км. Для составления обратной задачи необходимо решить исходную. Бекки Шарп 3 года назад Обратные задачи бывают в разных науках и в математике тоже. Обратная составляется на основании уже полученных данных. Когда то что требовалось найти уже известно. Например. У Миши было 7 яблок, а у Васи 8 яблок. Сколько всего было яблок у мальчиков. Решение: 7+8=15 (яблок) Обратная задача к нашей будет такая. Всего у Миши и Васи 15 яблок. У Миши — 7 яблок. Сколько у Васи яблок? Решение: 15-7=8 (яблок) Еще одна обратная задача к нашей. У Миши и Васи 15 яблок, у Васи — 8. Сколько яблок у Миши? Решение: 15-8=7 (яблок) Val111111 4 года назад Обратная задача- это когда то, что требовалось найти, теперь известно, а то, что было в дано нужно найти. Пример, есть три яблока. Два забрали. Сколько осталось? Обратная задачка: Забрали два яблока, осталось одно, сколько было? TheSun 3 года назад В обратной задаче неизвестным является дано, именно его и нужно найти. Но, при этом известен результат. Рассмотрим на примере. У Маши было 4 синих мяча и 3 зелёных мяча. Сколько всего у Маши мячей? 4+3=7 (шт.) мячей у Маши. Теперь обратная задача. У Маши всего 7 мячей. Из них синих мячей 4, а остальные мячи зелёного цвета. Сколько у Маши зелёных мячей? 7-4=3 (шт.) зелёных мяча у Маши. Знаете ответ? |
О.Д. Юрковец
студентка 5 курса ЛПИ Филиала СФУ
Г. Лесосибирска Российской федерации
МЕТОДИЧЕСКИЕ ПРИЕМЫ В
ОБУЧЕНИИ МЛАДШИХ ШКОЛЬНИКОВ СОСТАВЛЕНИЮ ТЕКСТОВЫХ ЗАДАЧ ОБРАТНЫХ ДАННЫМ
К сожалению, очень часто в обучении
детей решению задач учителя пользуются только показом способов решения
определенных видов задач и добиваются их закрепления решения механически, при
этом решение задач развивает логическое мышление, сообразительность, смекалку;
при работе над текстовой задачей у школьника идет формирование логического
умения проводить анализ и синтез, совершенствуется умение обобщать и
конкретизировать, раскрывать основное, выделять главное и отбрасывать
несущественное, второстепенное в тексте; воспитываются личностные качества –
воля, терпение, настойчивость.
С первых дней ребенка в школе его
учат решать текстовые задачи. Первые шаги при решении простых задач не вызывают
затруднения. При этом у многих возникают трудности при самостоятельном решении составных
задач, и из года в год эти дети испытывают всё большие затруднения. Главной причиной
этих трудностей является то, что у детей в значительной степени не сформировано
умение анализировать текст задачи, правильно выделять известное и неизвестное,
устанавливать взаимосвязи между ними, которые являются основой выбора действия
для решения текстовой задачи. Из-за этого же возникает сложность в составлении
текстовых задач обратных данным.
При изучении задач в курсе
математики, как простых, так и сложных, как обычных арифметических, так и
типовых оказывается высокоэффективным систематическое применение так
называемого метода обратных задач.
Положительный результат обучения
решению задач посредством преображения прямой задачи в обратные задачи
объясняется как первопричиной тем, что такого рода подход заставляет поднимать
из сферы подсознания максимальное разнообразие связей, заключенных в содержании
задачи. Это гарантирует – на языке дидактики – глубокое и прочное усвоение
материала.
Однако многие учителя не всегда
связывают составление и решение обратных задач с проверкой решения прямых
задач. Скорее всего, причинами этого является громоздкость метода и частичное
владение методикой составления обратных задач. Именно это не дает педагогу
полностью использовать возможности обратных задач, либо ведет лишь к
формальному выполнению проверки.
При выполнении проверки решения
прямой задачи способом составлением обратной задачи и ее решения, учащиеся
должны знать следующий алгоритм:
1. решить исходную задачу;
2. подставить результат в текст
исходной задачи в качестве известного данного;
3. обозначить новое неизвестное в
задаче;
4. составить новую задачу по
отношению к данной;
5. решить составленную задачу;
6. сравнить полученный результат с
тем данным, которое сделали неизвестным;
7. сделать соответствующий вывод
(если числовые значения совпадут, то задача решена верно).
Учащиеся очень редко допускают ошибки,
при составлении обратных задач к задачам, в основе решения которых лежат знания
конкретного смысла арифметических действий. Однако часто делают ошибки в
составлении обратных задач к задачам, в которых содержатся отношения «больше» и
«меньше», заменяя не полученные числа, а само отношение. Это говорит о том, что
у ребенка, который смог допустить такую ошибку, не сформировано понятие
«обратная задача».
Для устранения этой распространённой
ошибки важно использовать в сравнении кратких записей условия как прямой, так
и обратной задачи.
Схематическое изображение задачи
позволит школьнику пронаблюдать, что при составлении обратной задачи изменяются
только числовые значения, отношения в задаче остаются неизменными.
Бывает такое, что школьник, выполнив
решение задачи, и проверив ее решение действием, обратным к выполненному, не
составляет текст обратной задачи. Это приводит лишь к проверке правильности
вычисления, но не может помочь убедиться в правильности решения прямой задачи и
правильности выбора арифметического действия. Так же бывает, что задача
содержащая слова «улетели», «вышли в море», «съели» и т.д. вызывает затруднение
у учеников, у которых не сформирован конкретный смысл арифметических действий,
так как они, не вникая в условие данной задачи, выполняют ее решение действием
вычитания, хотя вопрос в задаче стоит, сколько всего выехало, улетело, ушло и
т.д.
Эту ошибку можно избежать, если ученик
при проверке решения задачи составит условие обратной задачи, а не остановится
на составлении только обратного действия.
Главная причина такого рода ошибок это
то, что у ученика не сформирован алгоритм проверки решения задачи. Алгоритм
проверки решения арифметических задач надо рассматривать специальным курсом,
раскрывая при этом содержание каждого действия, которое имеет место в процессе
проверки, при этом давать обоснование порядку их выполнения. Это приводит к
пониманию и осознанию приема работы.
Составление и решение обратных задач
это один из самых интересных способов проверки решения прямой задачи, а так же
творческая работа над ней. Благодаря ему можно насытить урок задачами.
П. М. Эрдниев в своей методике
рассматривает организацию работы над обратными задачами с первого класса. В его
методике имеются укрупненные задания, состоящие из выполнения трех
последовательных пунктов.
Проходя тему — задачи обратные
данным, по методике Эрдниева или по традиционной, у детей могут возникнуть
следующие трудности при формулировке текста обратных задач. Школьники часто
составляют обратную задачу по аналогии с прямой задачей.
Учащимся нужно рассказывать, про
существование различных формулировок задач, делая акцент на том, что задача
должна быть понятной всем, кто будет ее решать. Текст задачи должен быть
«красивым», «благозвучным», четко выраженным и без лишней информации.
Так же возможно использование при
работе над задачами краткой записи (в основном школьники ее и используют).
Можно применять мобильные схемы, например
такие как схемы С.Н. Лысенковой, смысл которых в смене чисел и знаков вопроса в
соответствующих «квадратиках» на демонстрационной схеме и на схемах на столах у
школьников.
Таким образом, существует большое многообразие
методов и приемов работы над текстовыми задачами обратными данным с младшими
школьниками. К сожалению, в настоящее время много учителей до сих пор не
понимают возможности и ценности использования обратных задач. Это объясняется многими
факторами: нехваткой времени, литературы и методик по этой теме и др. Так же мы
выяснили что, у детей при работе с обратными задачами возникает много ошибок,
избежать которых возможно при использовании определенных методов и приемов.
Можно утверждать, что применение обратных задач в работе с детьми, это и способ
проверки правильности решения прямой задачи, и способ развития творчества,
разносторонности, мотивации к учению и много другого у школьников.
Список использованной литературы:
Истомина Н.Б. Формирование умения
решать задачи различными способами// Начальная школа. 1985. №9.
Клименченко Д.В. Решение задач
различными способами// Начальная школа. 1986. №4.
Соснина Г.М. Один из способов
проверки решения задач // Начальная школа. 1983. №1.
© О.Д. Юрковец, 2018
Математика, 2 класс
Урок № 10. Задачи, обратные данной
Перечень вопросов, рассматриваемых в теме:
- Что такое задачи, обратные данной?
- Как составлять и решать обратные задачи?
Глоссарий по теме:
Задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17
3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31
Теоретический материал для самостоятельного изучения
Решим три задачи.
Составим по рисунку первую задачу.
В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?
Составим схематический рисунок.
Решим задачу:
10 + 8 = 18 (д.)
Ответ: 18 детей в классе.
Составим вторую задачу.
В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?
Решим задачу:
18 – 10 = 8 (м.)
Ответ: 8 мальчиков в классе.
Составим третью задачу.
В классе 18 детей. Мальчиков 8, остальные — девочки. Сколько девочек в классе?
Решим задачу:
18 – 8 = 10 (д.)
Ответ: 10 девочек в классе.
Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.
Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.
Сделаем вывод: задачи, обратные данной — считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Тренировочные задания.
1. Решите задачу. Выберите задачи, обратные данной.
Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?
Варианты ответов:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
Правильные варианты:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
2 . Восстановите пропуски в задачах.
1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?
2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?
3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?
Варианты ответов:
30, 20, ясных, пасмурных, июне
Правильный вариант:
1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?
2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?
3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Обратные задачи
В обратной задаче одна из искомых величин становится известной, а одна из данных величин становится неизвестной.
Прямая задача:
У Тани было 3 зелёных шарика и 2 красных. Сколько всего шариков было у Тани?
Первая обратная задача:
У Тани было 5 шариков, 3 шарика были зелёными, а остальные красные. Сколько красных шариков было у Тани?
Ты видишь, что известная величина — красные шарики — стала неизвестной.
А неизвестная величина — общее количество шариков — стало известной.
Вторая обратная задача:
У Тани было 5 шариков, 2 шарика были красными, а остальные зелёные. Сколько зелёных шариков было у Тани?
Ты видишь, что известная величина — зелёные шарики — стала неизвестной.
А неизвестная величина — общее количество шариков — стало известной.
ТАКИЕ ЗАДАЧИ НАЗЫВАЮТСЯ ОБРАТНЫМИ.
Советуем посмотреть:
Образцы оформления задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 48. Урок 25,
Петерсон, Учебник, часть 2
Страница 50. Урок 26,
Петерсон, Учебник, часть 2
Страница 53. Урок 27,
Петерсон, Учебник, часть 2
Страница 60. Урок 31,
Петерсон, Учебник, часть 2
Страница 63. Урок 32,
Петерсон, Учебник, часть 2
Страница 8. Урок 5,
Петерсон, Учебник, часть 3
Страница 25. Урок 13,
Петерсон, Учебник, часть 3
Страница 33. Урок 17,
Петерсон, Учебник, часть 3
Страница 65. Урок 33,
Петерсон, Учебник, часть 3
Страница 91. Повторение,
Петерсон, Учебник, часть 3
2 класс
Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 39,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 51,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 9. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 106,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 14,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 38,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 32,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 35,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 10,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 21,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 40. Урок 15,
Петерсон, Учебник, часть 1
4 класс
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 87,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 49,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 68,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2
Применение метода обратных задач при изучении тем:
« Задачи на дроби» и «Нахождение части целого и целого по
его части». ( 5 класс ).
Большинство людей согласны с тем, что нет «царского пути в Математику». Много труда и терпения, настойчивости и внимания требуется от учителя и обучающегося, чтобы последний мог усвоить программный минимум знаний по этому предмету на среднем или на высоком и достаточном уровне.
Добиться того, чтобы человек за меньшее, чем прежде, время овладел большим объемом основательных и действенных знаний, — таково одно из главных направлений современной етодики.
В математике для реализации этого направления успешно используется педагогами система укрупнения дидактических единиц (УДЕ), которая была разработана педагогом, математиком-методистом, академиком Российской академии образования (1989), заслуженным деятелем науки РСФСР, доктором педагогических наук, профессором П.М. Эрдниевым.
Одной из характерных особенностей системы УДЕ является метод обратных задач. Этот метод заключается в том, что работу над задачей нецелесообразно завершать получением ответа к ней; необходимо приемом обращения составлять и решать в сравнении с исходной (прямой) задачей новую, обратную задачу, извлекая тем самым дополнительную информацию, заключающуюся в связях между величинами решений исходной задачи.
Для того, чтобы обучающиеся четко представляли себе сам механизм или алгоритм составления обратной задачи, учитель помогает ученикам оформить и заполнить таблицу, в которую входят все величины исходной задачи, а затем познакомиться с алгоритмом составления обратных задач.
Таким образом, для составления обратной задачи надо неизвестную величину рассматривать как известную, а известную – как неизвестную.
Далее ученики под руководством учителя заполняют таблицу, содержащую все величины исходной задачи, которые поочередно из разряда «известных» будут переходить в разряд «неизвестных».
Этот метод позволяет обучающимся более глубоко и существенно осознавать и понимать взаимосвязь между величинами.
В данной статье я хочу поделиться опытом использования этого метода при изучении таких тем: «Задачи на дроби» и «Нахождение части целого и целого по его части». (Математика. 5 класс: учеб. для общеобразовательных организаций / [ С.М.Никольский, М.К. Потапов].
При изложении темы «Задачи на дроби» авторы учебника приводят примеры решения двух типов задач. Однако обучающихся не знакомят с названиями этих типов задач, что в дальнейшем, на мой взгляд, затрудняет подход к их решению.
Кроме того, рассматриваемые задачи не связаны по своему содержанию, что затрудняет ученикам видеть взаимосвязь между величинами.
Вот почему, излагая тему «Задачи на дроби», я предлагаю обучающимся такой план решения задачи.
Задача
В классе было 30 учеников, из которых хорошисты составляли всего класса. Сколько было в классе хорошистов?
Ход работы
Записываем краткое условие этой задачи и определяем величины, которые будут использоваться при решении исходной и обратных задач. Данные величины заносятся в таблицу.
Таблица величин.
|
Всего |
Хорошистов |
Части |
|
3о уч |
? уч |
|
|
? уч |
18 уч |
|
|
30 уч |
18уч |
?ч |
Проанализировав содержание таблицы, ученики согласно алгоритму определяют, сколько можно составить обратных задач с данными величинами.
При составлении опорного конспекта для более наглядной взаимосвязи величин записываем его на развороте двух тетрадных листов, поделенных на три колонки, развернув тетрадь на 90 градусов.
Обязательным в решении исходной и обратных задач является рисунок, который более чем информативно и наглядно позволяет обучающимся определить тип задачи и план ее решения.
Опорный конспект
|
Тип: На нахождение дроби от числа |
||
|
Решение 1 способ 1.Сколько учеников приходится на 30 : 5=6 (уч) 2.Сколько учеников приходится на или 2.Сколько было хорошистов? 6 ∙ 3=18 (уч) Ответ: 18 учеников. ПРАВИЛО Чтоб найти дробь от числа, надо:
|
После решения задачи первого типа, который ученики записали в первой колонке таблицы, они самостоятельно составляют обратную задачу и записывают ее во вторую колонку, предварительно заполнив следующую строку таблицы величин.
|
Тип: На нахождение дроби от числа |
Тип: На нахождение числа по величине дроби |
Тип: Какую часть одно число составляет от другого. |
|
Всего – 30 уч. Хорошистов — Решение: 1 способ 1.Сколько учеников приходится на 30: 5=6 (уч.) 2.Сколько учеников приходится на или 2.Сколько было хорошистов? 6 ∙ 3=18 (уч.) Ответ: 18 учеников. ПРАВИЛО Чтоб найти дробь от числа, надо:
|
Всего – ? уч. Хорошистов —
Решение 1 способ 1.Сколько учеников приходится на 18: 3=6 (уч.) 2.Сколько учеников приходится на или Сколько учеников было в классе? 6 ∙ 5=30 (уч.) Ответ: 30 учеников. ПРАВИЛО Чтобы найти число по величине дроби, надо:
числитель.
тат умножить на зна менатель |
Всего – 30 уч. Хорошистов–18 уч.-? ч.
|
Несмотря на то что обучающиеся еще не изучали умножение и деление обыкновенных дробей, они заполняют таблицу до конца, формулируя обратную задачу и заполняя следующую строку таблицы величин, а также
третью колонку (тип задачи, краткое условие, чертеж), только без решения.
Учитель информирует обучающихся, что с решением данного типа задач они познакомятся, когда будет усвоена тема умножения и деления обыкновенных дробей.
При изучении темы «Нахождение части целого и целого по его части» пятиклассникам она излагается не как новая, а как продолжение уже ранее изученной темы « Задачи на дроби », только с применением более рационального способа решения.
|
Тип: На нахождение дроби от числа |
Тип: На нахождение числа по величине дроби |
Тип: Какую часть одно число составляет от другого. |
|
Хорошистов — Решение 1 способ 1.Сколько учеников приходится на 30 : 5=6 (уч) 2.Сколько учеников приходится на или 2.Сколько было хорошистов? 6 ∙ 3=18 (уч) Ответ: 18 учеников. ПРАВИЛО Чтоб найти дробь от числа, надо:
2способ Сколько было хороши стов? или Сколько учеников при- ходится на 30: 5 ∙ 3= 30 ∙ или 30 ∙ Ответ: 18 учеников. ПРАВИЛО Дробь от числа находится умножением этого числа на дробь. |
Всего – ? уч. Хорошистов-
Решение 1 способ 1.Сколько учеников приходится на 18 : 3=6 (уч) 2.Сколько учеников приходится на или Сколько было учеников в классе? 6 ∙ 5=30 (уч) Ответ: 30 учеников. ПРАВИЛО Чтобы найти число по величине дроби, надо: 1)Число разделить на числитель. 2)Полученный резуль тат умножить на зна менатель 2способ Сколько учеников в классе? или Сколько учеников при- ходится на 18: 3∙5= 18: или 18 : Ответ: 30 учеников. ПРАВИЛО Число по величине дроби находится делением этого числа на дробь |
Всего – 30 уч. Хорошистов–18 уч.-? ч
Решение 1.Какую часть от всех учеников составляет один ученик? 1:30 = 2.Какую часть составляют хорошисты? Ответ: ПРАВИЛО Чтобы найти, какую часть одно число составляет от другого, надо: 1)Первое число разделить на второе. 2) Полученную в результате дробь сократить. или 1)«Одно» число разделить на «другое». 2) Полученную в результате дробь сократить. |
Таким образом, применение метода обратных задач при изложении двух взаимосвязанных тем: «Задачи на дроби» и «Нахождение части целого и целого по его части» — сможет позволить учителю добиться того, чтобы обучающиеся восприняли данный материал как единый организм, в котором все его элементы функционируют взаимосвязано.